A Dual-Species Bose-Einstein Condensate with Attractive Interspecies Interactions
Abstract
1. Introduction
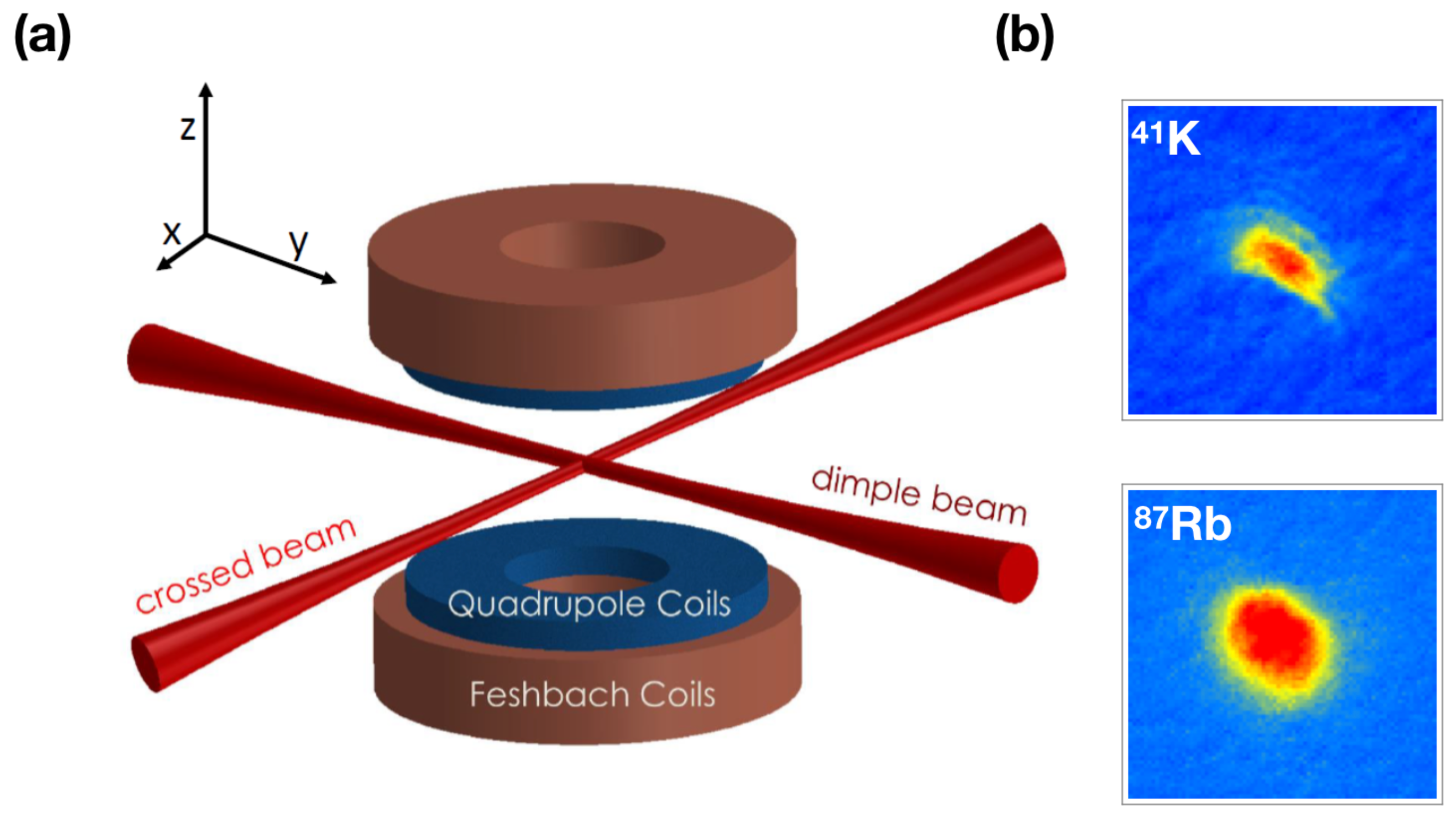
2. Experiment
3. Tuning the Interspecies Interaction
4. Compensating for the Gravitational Sag
5. The Attractive Regime
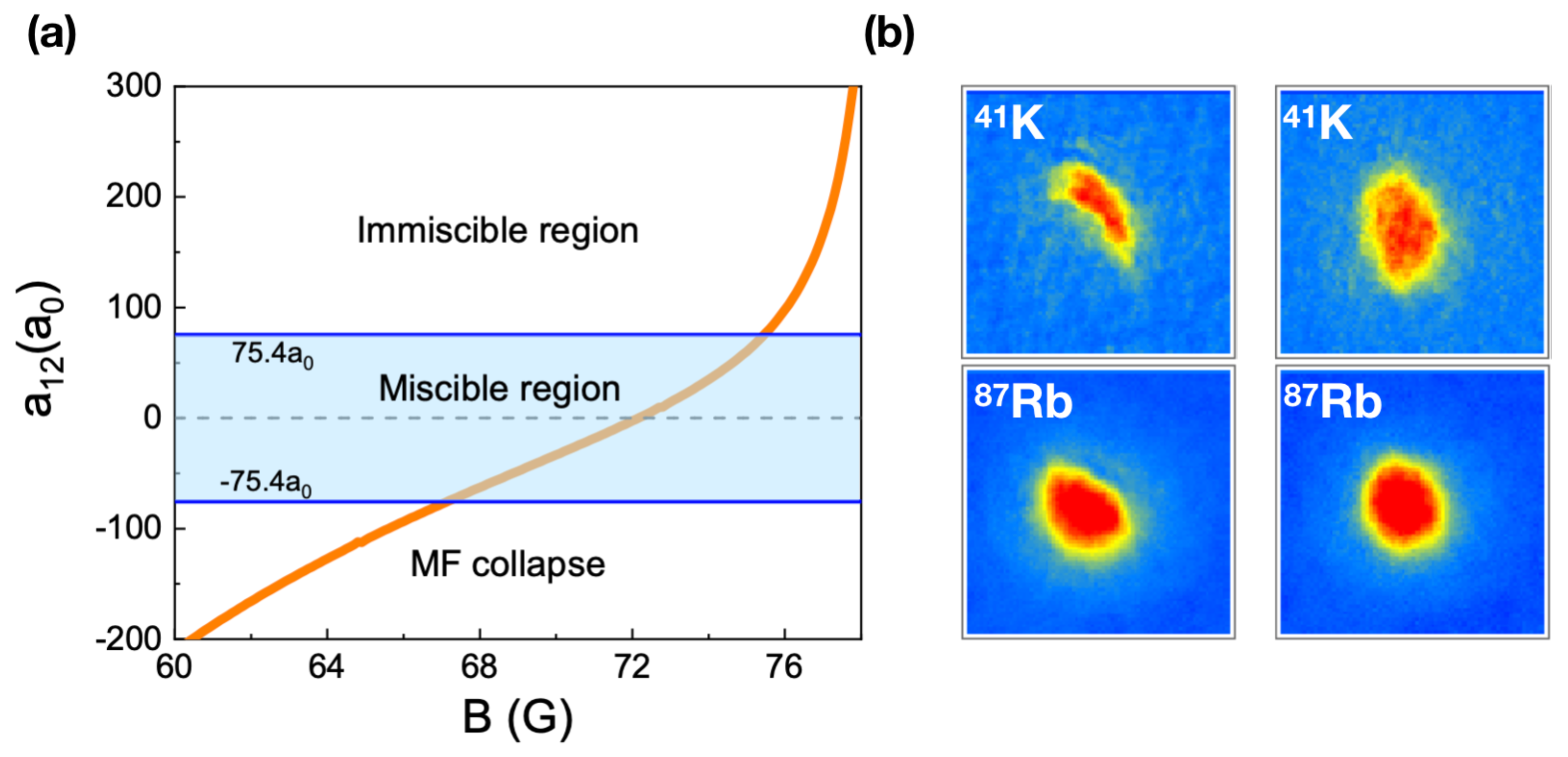
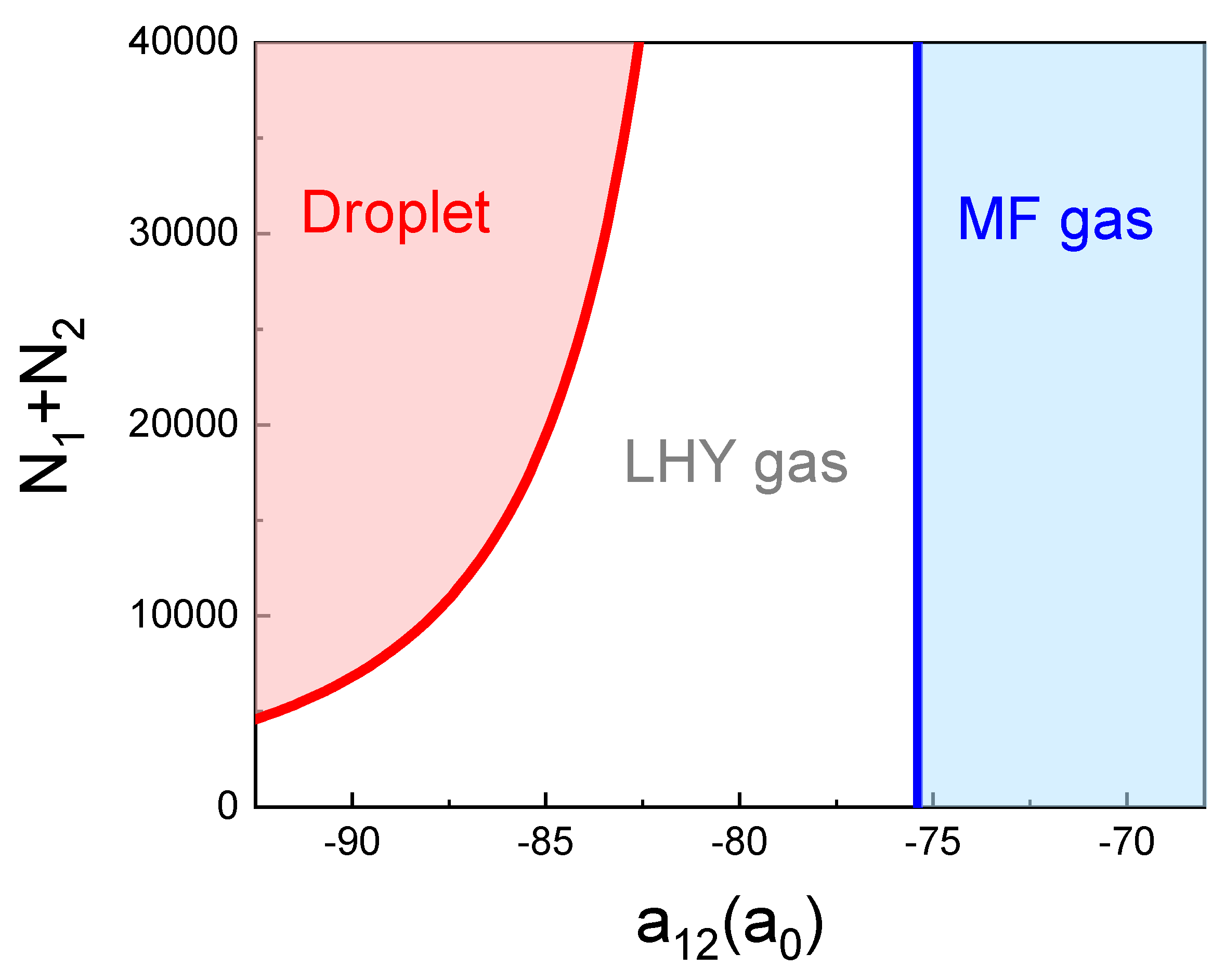
5.1. Phase Diagram: Free Space
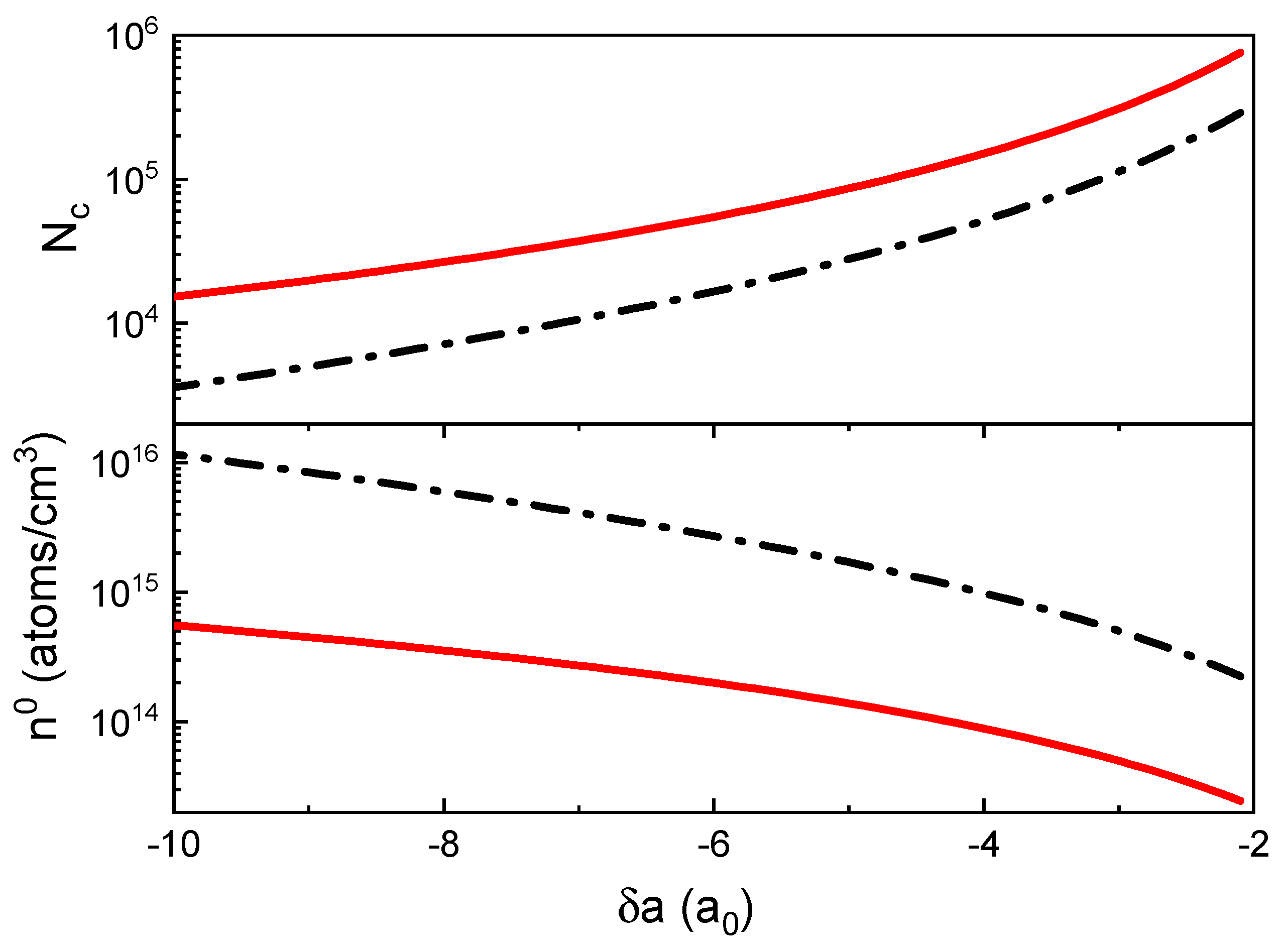
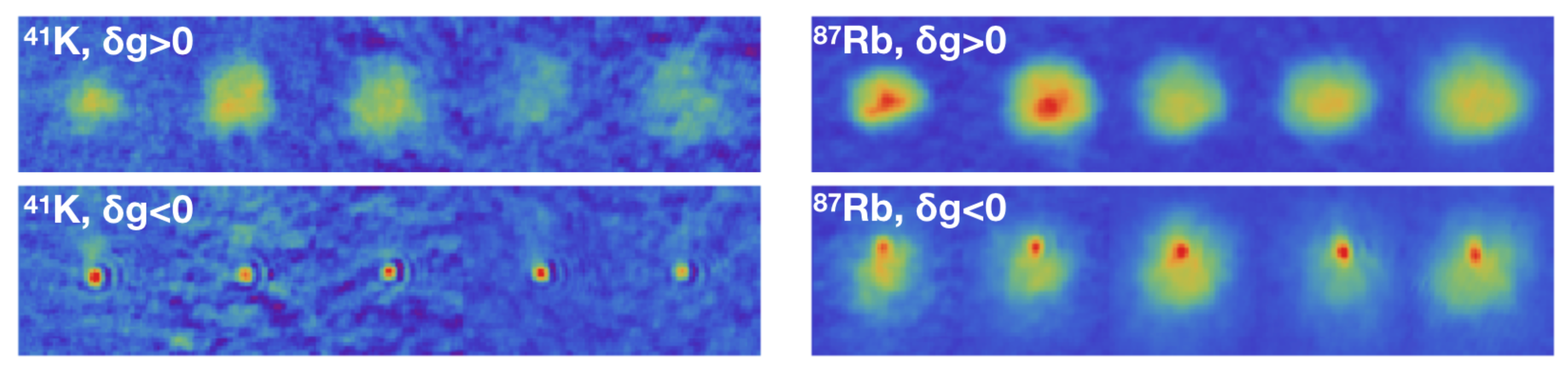
5.2. Observation of K-Rb Droplets in Free Space
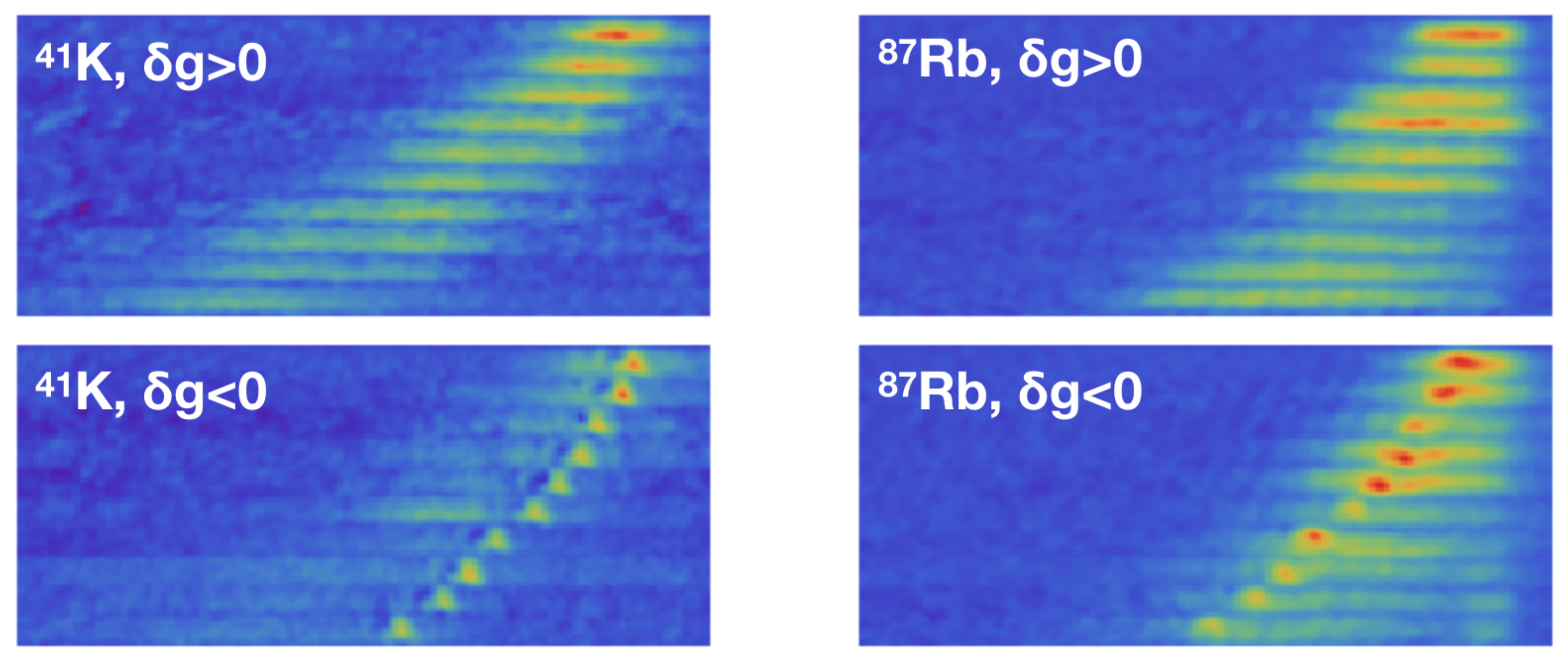
5.3. Observation of K-Rb Droplets in a Waveguide
6. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BEC | Bose–Einstein Condensate |
| ODT | optical dipole trap |
| TOF | time of flight |
| MF | mean-field |
| GP | Gross–Pitaevskii |
References
- Catani, J.; De Sarlo, L.; Barontini, G.; Minardi, F.; Inguscio, M. Degenerate Bose-Bose mixture in a three-dimensional optical lattice. Phys. Rev. A 2008, 77, 011603. [Google Scholar] [CrossRef]
- Kato, Y.; Yamamoto, D.; Danshita, I. Quantum Tricriticality at the Superfluid-Insulator Transition of Binary Bose Mixtures. Phys. Rev. Lett. 2014, 112, 055301. [Google Scholar] [CrossRef] [PubMed]
- Ota, M.; Giorgini, S.; Stringari, S. Magnetic Phase Transition in a Mixture of Two Interacting Superfluid Bose Gases at Finite Temperature. Phys. Rev. Lett. 2019, 123, 075301. [Google Scholar] [CrossRef] [PubMed]
- Richaud, A.; Zenesini, A.; Penna, V. The mixing-demixing phase diagram of ultracold heteronuclear mixtures in a ring trimer. Sci. Rep. 2019, 9, 6908. [Google Scholar] [CrossRef] [PubMed]
- Modugno, G.; Modugno, M.; Riboli, F.; Roati, G.; Inguscio, M. Two Atomic Species Superfluid. Phys. Rev. Lett. 2002, 89, 190404. [Google Scholar] [CrossRef] [PubMed]
- Ferrier-Barbut, I.; Delehaye, M.; Laurent, S.; Grier, A.T.; Pierce, M.; Rem, B.S.; Chevy, F.; Salomon, C. A mixture of Bose and Fermi superfluids. Science 2014, 345, 1035–1038. [Google Scholar] [CrossRef]
- Roy, R.; Green, A.; Bowler, R.; Gupta, S. Two-Element Mixture of Bose and Fermi Superfluids. Phys. Rev. Lett. 2017, 118, 055301. [Google Scholar] [CrossRef]
- Schweikhard, V.; Coddington, I.; Engels, P.; Tung, S.; Cornell, A.E. Vortex-Lattice Dynamics in Rotating Spinor Bose-Einstein Condensates. Phys. Rev. Lett. 2004, 93, 210403. [Google Scholar] [CrossRef]
- Hamner, C.; Chang, J.J.; Engels, P.; Hoefer, M.A. Generation of Dark-Bright Soliton Trains in Superfluid-Superfluid Counterflow. Phys. Rev. Lett. 2011, 106, 065302. [Google Scholar] [CrossRef]
- Yao, X.C.; Chen, H.Z.; Wu, Y.P.; Liu, X.P.; Wang, X.Q.; Jiang, X.; Deng, Y.; Chen, Y.A.; Pan, J.W. Observation of Coupled Vortex Lattices in a Mass-Imbalance Bose and Fermi Superfluid Mixture. Phys. Rev. Lett. 2016, 117, 145301. [Google Scholar] [CrossRef]
- Altman, E.; Hofstetter, W.; Demler, E.; Lukin, M.D. Phase diagram of two-component bosons on an optical lattice. New J. Phys. 2003, 5, 1–19. [Google Scholar] [CrossRef]
- Kuklov, A.B.; Svistunov, B.V. Counterflow Superfluidity of Two-Species Ultracold Atoms in a Commensurate Optical Lattice. Phys. Rev. Lett. 2003, 90, 100401. [Google Scholar] [CrossRef] [PubMed]
- Stamper-Kurn, D.M.; Ueda, M. Spinor Bose gases: Symmetries, magnetism, and quantum dynamics. Rev. Mod. Phys. 2013, 85, 1191–1244. [Google Scholar] [CrossRef]
- Jin, D.S.; Ye, J. Introduction to Ultracold Molecules: New Frontiers in Quantum and Chemical Physics. Chem. Rev. 2012, 112, 4801–4802. [Google Scholar] [CrossRef]
- Catani, J.; Lamporesi, G.; Naik, D.; Gring, M.; Inguscio, M.; Minardi, F.; Kantian, A.; Giamarchi, T. Quantum dynamics of impurities in a one-dimensional Bose gas. Phys. Rev. A 2012, 85, 023623. [Google Scholar] [CrossRef]
- Hu, M.G.; Van de Graaff, M.J.; Kedar, D.; Corson, J.P.; Cornell, E.A.; Jin, D.S. Bose Polarons in the Strongly Interacting Regime. Phys. Rev. Lett. 2016, 117, 055301. [Google Scholar] [CrossRef]
- Jørgensen, N.B.; Wacker, L.; Skalmstang, K.T.; Parish, M.M.; Levinsen, J.; Christensen, R.S.; Bruun, G.M.; Arlt, J.J. Observation of Attractive and Repulsive Polarons in a Bose-Einstein Condensate. Phys. Rev. Lett. 2016, 117, 055302. [Google Scholar] [CrossRef]
- Inguscio, M.; Ketterle, W.; Salomon, C. (Eds.) Proceedings of the International School of Physics Enrico Fermi, Course CLXIV; IOS Press: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Iskin, M.; Sá de Melo, C.A.R. Two-band superfluidity from the BCS to the BEC limit. Phys. Rev. B 2006, 74, 144517. [Google Scholar] [CrossRef]
- Tajima, H.; Yerin, Y.; Perali, A.; Pieri, P. Enhanced critical temperature, pairing fluctuation effects, and BCS-BEC crossover in a two-band Fermi gas. Phys. Rev. B 2019, 99, 180503. [Google Scholar] [CrossRef]
- Yerin, Y.; Tajima, H.; Pieri, P.; Perali, A. Coexistence of giant Cooper pairs with a bosonic condensate and anomalous behavior of energy gaps in the BCS-BEC crossover of a two-band superfluid Fermi gas. Phys. Rev. B 2019, 100, 104528. [Google Scholar] [CrossRef]
- Salasnich, L.; Shanenko, A.A.; Vagov, A.; Aguiar, J.A.; Perali, A. Screening of pair fluctuations in superconductors with coupled shallow and deep bands: A route to higher-temperature superconductivity. Phys. Rev. B 2019, 100, 064510. [Google Scholar] [CrossRef]
- Tajima, H.; Perali, A.; Pieri, A. BCS-BEC Crossover and Pairing Fluctuations in a Two Band Superfluid/Superconductor: A T Matrix Approach. Condens. Matter 2020, 5, 10. [Google Scholar] [CrossRef]
- Petrov, D.S. Quantum Mechanical Stabilization of a Collapsing Bose-Bose Mixture. Phys. Rev. Lett. 2015, 115, 155302. [Google Scholar] [CrossRef] [PubMed]
- Kadau, H.; Schmitt, M.; Wenzel, M.; Wink, C.; Maier, T.; Ferrier-Barbut, I.; Pfau, T. Observing the Rosensweig instability of a quantum ferrofluid. Nature 2016, 530, 194–197. [Google Scholar] [CrossRef]
- Ferrier-Barbut, I.; Kadau, H.; Schmitt, M.; Wenzel, M.; Pfau, T. Observation of Quantum Droplets in a Strongly Dipolar Bose Gas. Phys. Rev. Lett. 2016, 116, 215301. [Google Scholar] [CrossRef]
- Schmitt, M.; Wenzel, M.; Böttcher, F.; Ferrier-Barbut, I.; Pfau, T. Self-bound droplets of a dilute magnetic quantum liquid. Nature 2016, 539, 259–262. [Google Scholar] [CrossRef]
- Chomaz, L.; Baier, S.; Petter, D.; Mark, M.J.; Wächtler, F.; Santos, L.; Ferlaino, F. Quantum-Fluctuation-Driven Crossover from a Dilute Bose-Einstein Condensate to a Macrodroplet in a Dipolar Quantum Fluid. Phys. Rev. X 2016, 6, 041039. [Google Scholar] [CrossRef]
- Ferrier-Barbut, I.; Schmitt, M.; Wenzel, M.; Kadau, H.; Pfau, T. Liquid quantum droplets of ultracold magnetic atoms. J. Phys. B 2016, 49, 214004. [Google Scholar] [CrossRef]
- Wenzel, M.; Böttcher, F.; Langen, T.; Ferrier-Barbut, I.; Pfau, T. Striped states in a many-body system of tilted dipoles. Phys. Rev. A 2017, 96, 053630. [Google Scholar] [CrossRef]
- Cheiney, P.; Cabrera, C.R.; Sanz, J.; Naylor, B.; Tanzi, L.; Tarruell, L. Bright Soliton to Quantum Droplet Transition in a Mixture of Bose-Einstein Condensates. Phys. Rev. Lett. 2018, 120, 135301. [Google Scholar] [CrossRef]
- Cabrera, C.R.; Tanzi, L.; Sanz, J.; Naylor, B.; Thomas, P.; Cheiney, P.; Tarruell, L. Quantum liquid droplets in a mixture of Bose-Einstein condensates. Science 2018, 359, 301–304. [Google Scholar] [CrossRef] [PubMed]
- Semeghini, G.; Ferioli, G.; Masi, L.; Mazzinghi, C.; Wolswijk, L.; Minardi, F.; Modugno, M.; Modugno, G.; Inguscio, M.; Fattori, M. Self-Bound Quantum Droplets of Atomic Mixtures in Free Space. Phys. Rev. Lett. 2018, 120, 235301. [Google Scholar] [CrossRef] [PubMed]
- D’Errico, C.; Burchianti, A.; Prevedelli, M.; Salasnich, L.; Ancilotto, F.; Modugno, M.; Minardi, F.; Fort, C. Observation of quantum droplets in a heteronuclear bosonic mixture. Phys. Rev. Res. 2019, 1, 033155. [Google Scholar] [CrossRef]
- Petrov, D.S.; Astrakharchik, G.E. Ultradilute Low-Dimensional Liquids. Phys. Rev. Lett. 2016, 117, 100401. [Google Scholar] [CrossRef] [PubMed]
- Kartashov, Y.V.; Malomed, B.A.; Tarruell, L.; Torner, L. Three-dimensional droplets of swirling superfluids. Phys. Rev. A 2018, 98, 013612. [Google Scholar] [CrossRef]
- Astrakharchik, G.E.; Malomed, B.A. Dynamics of one-dimensional quantum droplets. Phys. Rev. A 2018, 98, 013631. [Google Scholar] [CrossRef]
- Cappellaro, A.; Macrì, T.; Salasnich, L. Collective modes across the soliton-droplet crossover in binary Bose mixtures. Phys. Rev. A 2018, 97, 053623. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Z.; Luo, Z.; Huang, C.; Tan, H.; Pang, W.; Malomed, B.A. Two-dimensional vortex quantum droplets. Phys. Rev. A 2018, 98, 063602. [Google Scholar] [CrossRef]
- Tengstrand, M.N.; Stürmer, P.; Karabulut, E.O.; Reimann, S.M. Rotating Binary Bose-Einstein Condensates and Vortex Clusters in Quantum Droplets. Phys. Rev. Lett. 2019, 123, 160405. [Google Scholar] [CrossRef]
- Ferioli, G.; Semeghini, G.; Masi, L.; Giusti, G.; Modugno, G.; Inguscio, M.; Gallemí, A.; Recati, A.; Fattori, M. Collisions of Self-Bound Quantum Droplets. Phys. Rev. Lett. 2019, 122, 090401. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Malomed, B.A.; Torner, L. Metastability of Quantum Droplet Clusters. Phys. Rev. Lett. 2019, 122, 193902. [Google Scholar] [CrossRef] [PubMed]
- Ferioli, G.; Semeghini, G.; Terradas-Briansó, S.; Masi, L.; Fattori, M.; Modugno, M. Dynamical formation of quantum droplets in a 39K mixture. Phys. Rev. Res. 2020, 2, 013269. [Google Scholar] [CrossRef]
- Juliá-Díaz, B.; Morera, I.; Astrakharchik, G.E.; Polls, A. Quantum droplets of bosonic mixtures in a one-dimensional optical lattice. arXiv 2020, arXiv:cond-mat.quant-gas/2001.04796. [Google Scholar]
- Parisi, L.; Giorgini, S. Quantum droplets in one-dimensional Bose mixtures: A quantum Monte-Carlo study. arXiv 2020, arXiv:cond-mat.quant-gas/2003.05231. [Google Scholar]
- Tylutki, M.; Astrakharchik, G.E.; Malomed, B.A.; Petrov, D.S. Collective Excitations of a One-Dimensional Quantum Droplet. arXiv 2020, arXiv:cond-mat.quant-gas/2003.05803. [Google Scholar]
- Burchianti, A.; D’Errico, C.; Rosi, S.; Simoni, A.; Modugno, M.; Fort, C.; Minardi, F. Dual-species Bose-Einstein condensate of 41K and 87Rb in a hybrid trap. Phys. Rev. A 2018, 98, 063616. [Google Scholar] [CrossRef]
- Thalhammer, G.; Barontini, G.; De Sarlo, L.; Catani, J.; Minardi, F.; Inguscio, M. Double Species Bose-Einstein Condensate with Tunable Interspecies Interactions. Phys. Rev. Lett. 2008, 100, 210402. [Google Scholar] [CrossRef]
- D’Errico, C.; Zaccanti, M.; Fattori, M.; Roati, G.; Inguscio, M.; Modugno, G.; Simoni, A. Feshbach resonances in ultracold39K. New J. Phys. 2007, 9, 223. [Google Scholar] [CrossRef]
- Marte, A.; Volz, T.; Schuster, J.; Dürr, S.; Rempe, G.; van Kempen, E.G.M.; Verhaar, B.J. Feshbach Resonances in Rubidium 87: Precision Measurement and Analysis. Phys. Rev. Lett. 2002, 89, 283202. [Google Scholar] [CrossRef]
- Riboli, F.; Modugno, M. Topology of the ground state of two interacting Bose-Einstein condensates. Phys. Rev. A 2002, 65, 063614. [Google Scholar] [CrossRef]
- Simoni, A.; Zaccanti, M.; D’Errico, C.; Fattori, M.; Roati, G.; Inguscio, M.; Modugno, G. Near-threshold model for ultracold KRb dimers from interisotope Feshbach spectroscopy. Phys. Rev. A 2008, 77, 052705. [Google Scholar] [CrossRef]
- Thalhammer, G.; Barontini, G.; Catani, J.; Rabatti, F.; Weber, C.; Simoni, A.; Minardi, F.; Inguscio, M. Collisional and molecular spectroscopy in an ultracold Bose–Bose mixture. New J. Phys. 2009, 11, 055044. [Google Scholar] [CrossRef]
- Lee, T.D.; Huang, K.; Yang, C.N. Eigenvalues and Eigenfunctions of a Bose System of Hard Spheres and Its Low-Temperature Properties. Phys. Rev. 1957, 106, 1135–1145. [Google Scholar] [CrossRef]
- Minardi, F.; Ancilotto, F.; Burchianti, A.; D’Errico, C.; Fort, C.; Modugno, M. Effective expression of the Lee-Huang-Yang energy functional for heteronuclear mixtures. Phys. Rev. A 2019, 100, 063636. [Google Scholar] [CrossRef]
- Wacker, L.J.; Jorgensen, N.B.; Birkmose, D.; Winter, N.; Mikkelsen, M.; Sherson, J.; Zinner, N.; Arlt, J.J. Universal Three-Body Physics in Ultracold KRb Mixtures. Phys. Rev. Lett. 2016, 117, 163201. [Google Scholar] [CrossRef] [PubMed]
- Gross, E.P. Hydrodynamics of a Superfluid Condensate. J. Math. Phys. 1963, 4, 195–207. [Google Scholar] [CrossRef]
- Pitaevskii, L.P. Vortex Lines in an Imperfect Bose Gas. Sov. Phys. JETP 1961, 13, 451–454. [Google Scholar]
- Ancilotto, F.; Barranco, M.; Guilleumas, M.; Pi, M. Self-bound ultradilute Bose mixtures within local density approximation. Phys. Rev. A 2018, 98, 053623. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burchianti, A.; D’Errico, C.; Prevedelli, M.; Salasnich, L.; Ancilotto, F.; Modugno, M.; Minardi, F.; Fort, C. A Dual-Species Bose-Einstein Condensate with Attractive Interspecies Interactions. Condens. Matter 2020, 5, 21. https://doi.org/10.3390/condmat5010021
Burchianti A, D’Errico C, Prevedelli M, Salasnich L, Ancilotto F, Modugno M, Minardi F, Fort C. A Dual-Species Bose-Einstein Condensate with Attractive Interspecies Interactions. Condensed Matter. 2020; 5(1):21. https://doi.org/10.3390/condmat5010021
Chicago/Turabian StyleBurchianti, Alessia, Chiara D’Errico, Marco Prevedelli, Luca Salasnich, Francesco Ancilotto, Michele Modugno, Francesco Minardi, and Chiara Fort. 2020. "A Dual-Species Bose-Einstein Condensate with Attractive Interspecies Interactions" Condensed Matter 5, no. 1: 21. https://doi.org/10.3390/condmat5010021
APA StyleBurchianti, A., D’Errico, C., Prevedelli, M., Salasnich, L., Ancilotto, F., Modugno, M., Minardi, F., & Fort, C. (2020). A Dual-Species Bose-Einstein Condensate with Attractive Interspecies Interactions. Condensed Matter, 5(1), 21. https://doi.org/10.3390/condmat5010021






