Singular Mean-Field States: A Brief Review of Recent Results
Abstract
1. Introduction
1.1. Singular States Pulled to the Center by Attractive Fields
1.1.1. Outline of the Topic
1.1.2. New Results Included in the Review
1.2. Singular Solitons: Previously Known Results
1.2.1. Singular Solitons in Free Space
1.2.2. Solitons Pinned to a Singular Potential
1.2.3. New Results Included in the Review
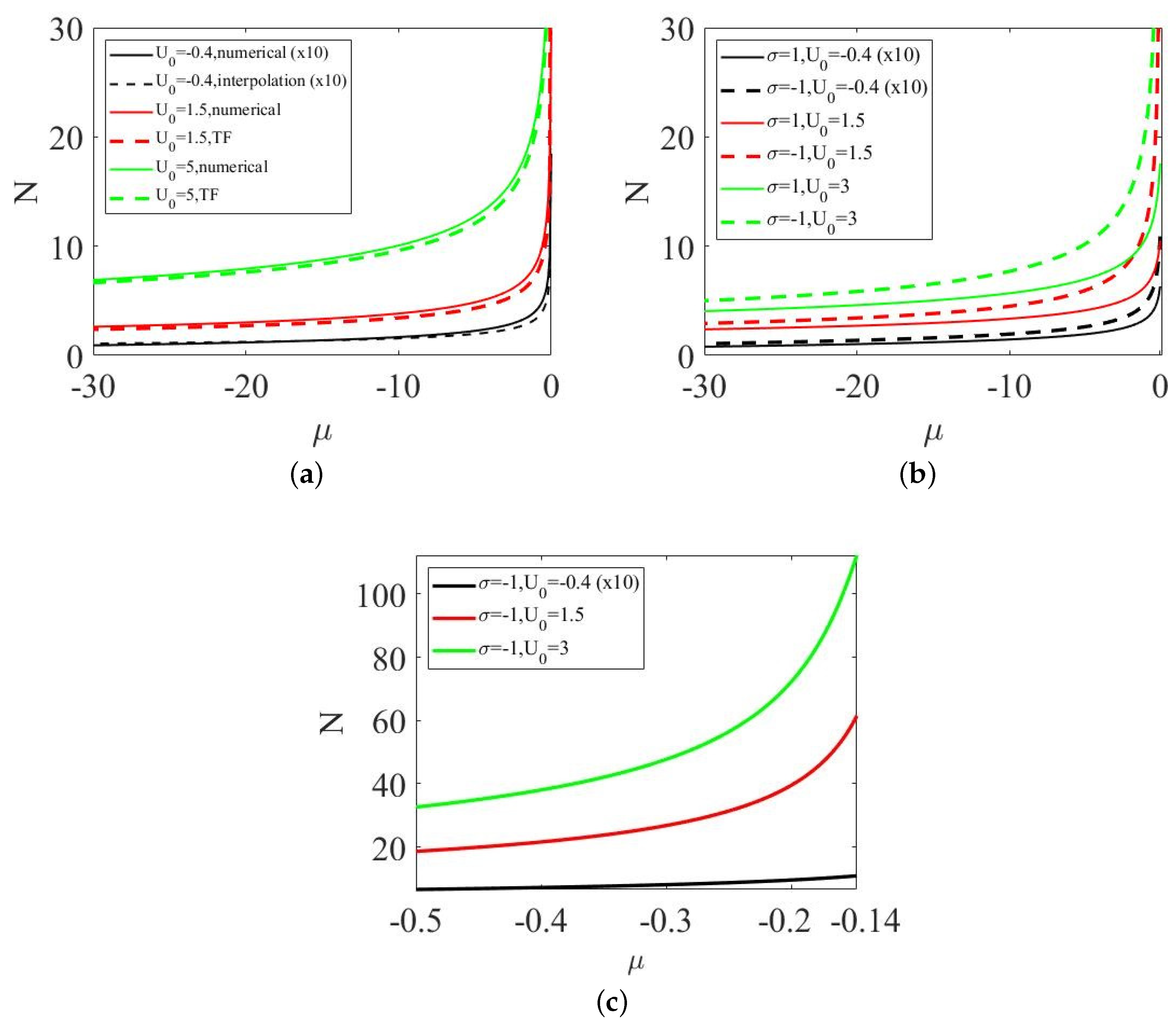
2. Two-Dimensional Singular Modes in the Attractive Potential, Stabilized by the Lee–Huang–Yang (LHY) Term
2.1. Analytical Approximations
2.1.1. The Asymptotic Form of the Solutions at and
2.1.2. The Thomas–Fermi (TF) Approximation
2.2. Numerical Results for the 2D Modes Stabilized by the LHY Term
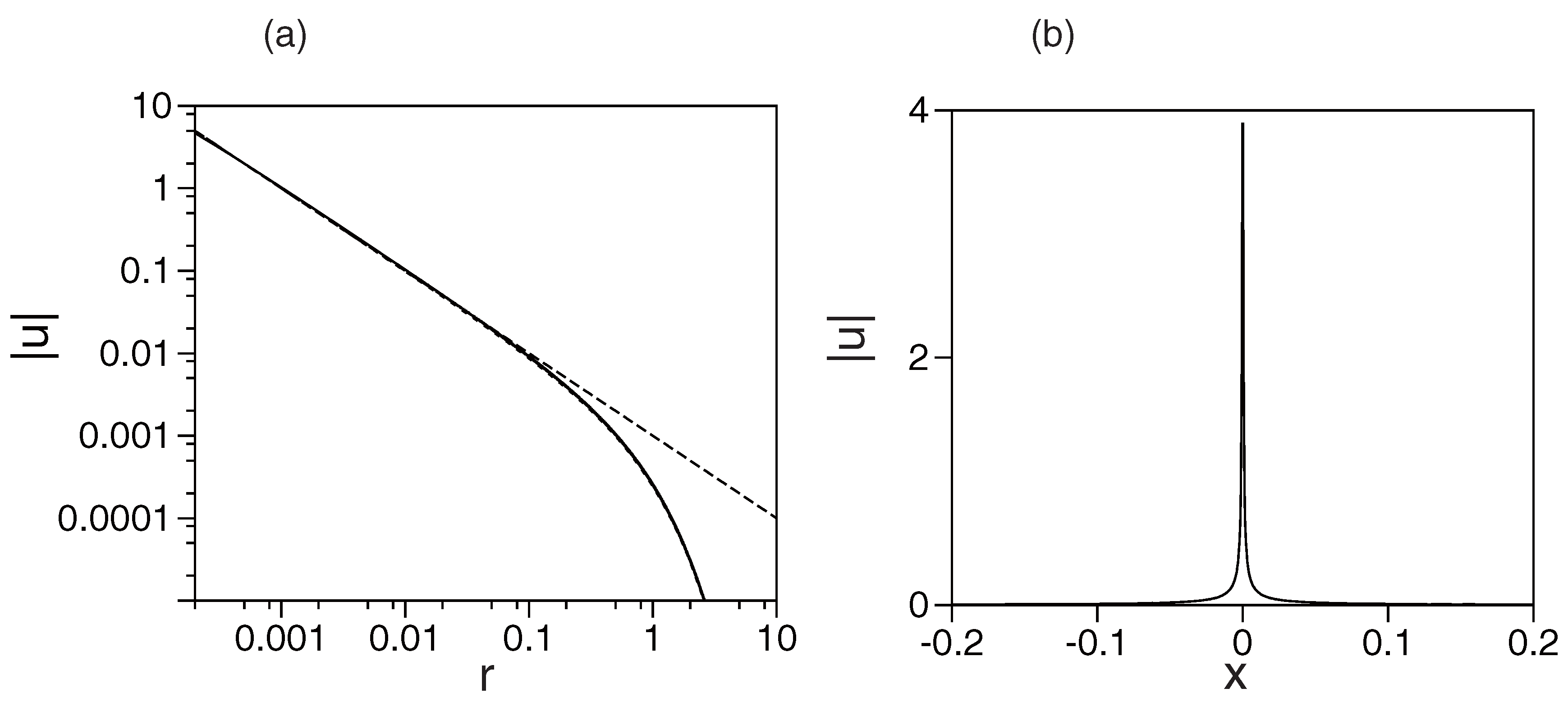
3. Singular Solitons in One, Two, and Three Dimensions
3.1. Analytical Results
3.1.1. The One-Dimensional Model with the Septimal Nonlinearity
3.1.2. Physical Interpretation of the 1D Singular Soliton: Screening of a “Bare” -Functional Potential
3.1.3. The Two-Dimensional Model with the Quintic Nonlinearity
3.1.4. Interpretation of the 2D Singular Soliton: Screening of a Ring-Shaped Attractive Potential
3.1.5. Effects of Additional Nonlinear Terms on 1D and 2D Singular Solitons
3.1.6. The 3D Model with the Cubic Nonlinearity
3.1.7. Interpretation of the 3D Singular Solitons: Screening of an Attractive Spherical Potential
4. Numerical Results for the 1D, 2D, and 3D Singular Solitons
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | two-dimensional |
| 3D | three-dimensional |
| BEC | Bose–Einstein condensate |
| GPE | Gross-Pitaevskii equation |
| GS | ground state |
| LHY | Lee–Huang–Yang (correction to the mean-field theory) |
| MF | mean field |
| NLSE | nonlinear Schrödinger equation |
| TF | Thomas–Fermi (approximation) |
| VK | Vakhitov–Kolokolov (stability criterion) |
References
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Nonrelativistic Theory; Nauka Publishers: Moscow, Russia, 1974. [Google Scholar]
- Sakaguchi, H.; Malomed, B.A. Suppression of the quantum-mechanical collapse by repulsive interactions in a quantum gas. Phys. Rev. A 2011, 83, 013607. [Google Scholar] [CrossRef]
- Denschlag, J.; Schmiedmayer, J. Scattering a neutral atom from a charged wire. Europhys. Lett. 1997, 38, 405–410. [Google Scholar] [CrossRef]
- Denschlag, J.; Umshaus, G.; Schmiedmayer, J. Probing a singular potential with cold atoms: A neutral atom and a charged wire. Phys. Rev. Lett. 1998, 81, 737. [Google Scholar] [CrossRef]
- Gupta, K.S.; Rajeev, S.G. Renormalization in quantum mechanics. Phys. Rev. D 1993, 48, 5940–5945. [Google Scholar] [CrossRef]
- Camblong, H.E.; Epele, L.N.; Fanchiotti, H.; García Canal, C.A. Renormalization of the Inverse Square Potential. Phys. Rev. Lett. 2000, 85, 1590. [Google Scholar] [CrossRef]
- Camblong, H.E.; Epele, L.N.; Fanchiotti, H.; García Canal, C.A. Dimensional transmutation and dimensional regularization in quantum mechanics: II. rotational invariance. Ann. Phys. (N. Y.) 2001, 287, 57. [Google Scholar] [CrossRef]
- Yafaev, D.R. On a zero-range interaction of a quantum particle with the vacuum. J. Phys. A 1999, 25, 963–978. [Google Scholar] [CrossRef]
- Noja, D.; Posilicano, A. On the point limit of the Pauli-Fierz model. Ann. Inst. Henri Poincaré. 1999, 71, 425–457. [Google Scholar]
- Pitaevskii, L.; Stringari, S. Bose-Einstein Condensation; Clarendon Press: Oxford, UK, 2003. [Google Scholar]
- Astrakharchik, G.E.; Malomed, B.A. Quantum versus mean-field collapse in a many-body system. Phys. Rev. A 2015, 92, 043632. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Malomed, B.A. Suppression of the quantum collapse in an anisotropic gas of dipolar bosons. Phys. Rev. A 2011, 84, 033616. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Malomed, B.A. Suppression of the quantum collapse in binary bosonic gases. Phys. Rev. A 2013, 88, 043638. [Google Scholar] [CrossRef]
- Adhikari, S.K.; Salasnich, L. One-dimensional superfluid Bose-Fermi mixture: Mixing, demixing, and bright solitons. Phys. Rev. A 2007, 76, 023612. [Google Scholar] [CrossRef]
- Bulgac, A. Local-density-functional theory for superfluid fermionic systems: The unitary gas. Phys. Rev. A 2007, 76, 050402. [Google Scholar] [CrossRef]
- Adhikari, S.K. Superfluid Fermi-Fermi mixture: Phase diagram, stability, and soliton formation. Phys. Rev. A 2007, 76, 053609. [Google Scholar] [CrossRef]
- Adhikari, S.K. Nonlinear Schrödinger equation for a superfluid Fermi gas in the BCS-BEC crossover. Phys. Rev. A 2008, 77, 045602. [Google Scholar] [CrossRef]
- Abdullaev, F.K.; Gammal, A.; Tomio, L.; Frederico, T. Stability of trapped Bose-Einstein condensates. Phys. Rev. A 2001, 63, 043604. [Google Scholar] [CrossRef]
- Abdullaev, F.K.; Salerno, M. Gap-Townes solitons and localized excitations in low-dimensional Bose-Einstein condensates in optical lattices. Phys. Rev. A 2005, 72, 033617. [Google Scholar] [CrossRef]
- Burt, E.A.; Ghrist, R.W.; Myatt, C.J.; Holland, M.J.; Cornell, E.A.; Wieman, C.E. Coherence, correlations, and collisions: What one learns about Bose-Einstein condensates from their decay. Phys. Rev. Lett. 1997, 79, 337. [Google Scholar] [CrossRef]
- Stamper-Kurn, D.M.; Andrews, M.R.; Chikkatur, A.P.; Inouye, S.; Miesner, H.J.; Stenger, J.; Ketterle, W. Optical confinement of a Bose-Einstein condensate. Phys. Rev. Lett. 1998, 80, 2027. [Google Scholar] [CrossRef]
- Roberts, J.L.; Claussen, N.R.; Cornish, S.L.; Wieman, C.E. Magnetic field dependence of ultracold inelastic collisions near a Feshbach resonance. Phys. Rev. Lett. 2000, 85, 728. [Google Scholar] [CrossRef]
- Malomed, B.A. Suppression of quantum-mechanical collapse in bosonic gases with intrinsic repulsion: A brief review. Condensed Matter. 2018, 3, 15. [Google Scholar] [CrossRef]
- Petrov, D.S. Quantum mechanical stabilization of a collapsing Bose-Bose mixture. Phys. Rev. Lett. 2015, 115, 155302. [Google Scholar] [CrossRef] [PubMed]
- Petrov, D.S.; Astrakharchik, G.E. Ultradilute low-dimensional liquids. Phys. Rev. Lett. 2016, 117, 100401. [Google Scholar] [CrossRef] [PubMed]
- Żin, P.; Pylak, M.; Wasak, T.; Gajda, M.; Idziaszek, Z. Quantum Bose-Bose droplets at a dimensional crossover. Phys. Rev. A 2018, 98, 051603. [Google Scholar] [CrossRef]
- Ilg, T.; Kumlin, J.; Santos, L.; Petrov, D.S.; Üchler, H.P.B. Dimensional crossover for the beyond-mean-field correction in Bose gases. Phys. Rev. A 2018, 98, 051604. [Google Scholar] [CrossRef]
- Lee, T.D.; Huang, K.; Yang, C.N. Eigenvalues and eigenfunctions of a Bose system of hard spheres and its low-temperature properties. Phys. Rev. 1957, 106, 1135–1145. [Google Scholar] [CrossRef]
- Roy, S.; Landini, M.; Trenkwalder, A.; Semeghini, G.; Spagnolli, G.; Simoni, A.; Fattori, M.; Inguscio, M.; Modugno, G. Test of the universality of the three-body Efimov parameter at narrow Feshbach resonances. Phys. Rev. Lett. 2013, 111, 053202. [Google Scholar] [CrossRef]
- Cabrera, C.; Tanzi, L.; Sanz, J.; Naylor, B.; Thomas, P.; Cheiney, P.; Tarruell, L. Quantum liquid droplets in a mixture of Bose-Einstein condensates. Science 2018, 359, 301–304. [Google Scholar] [CrossRef]
- Cheiney, P.; Cabrera, C.R.; Sanz, J.; Naylor, B.; Tanzi, L.; Tarruell, L. Bright soliton to quantum droplet transition in a mixture of Bose-Einstein condensates. Phys. Rev. Lett. 2018, 120, 135301. [Google Scholar] [CrossRef]
- Semeghini, G.; Ferioli, G.; Masi, L.; Mazzinghi, C.; Wolswijk, L.; Minardi, F.; Modugno, M.; Modugno, G.; Inguscio, M.; Fattori, M. Self-bound quantum droplets of atomic mixtures in free space. Phys. Rev. Lett. 2018, 120, 235301. [Google Scholar] [CrossRef]
- Ferioli, G.; Semeghini, G.; Masi, L.; Giusti, G.; Modugno, G.; Inguscio, M.; Gallemi, A.; Recati, A.; Fattori, M. Collisions of self-bound quantum droplets. Phys. Rev. Lett. 2019, 122, 090401. [Google Scholar] [CrossRef] [PubMed]
- D’Errico, C.; Burchianti, A.; Prevedelli, M.; Salasnich, L.; Ancilotto, F.; Modugno, M.; Minardi, F.; Fort, C. Observation of quantum droplets in a heteronuclear bosonic mixture. Phys. Rev. Res. 2019, 1, 033155. [Google Scholar] [CrossRef]
- Li, Y.; Luo, Z.; Lio, Y.; Chen, Z.; Huang, C.L. Fu, S.; Tan, H.; Malomed, B.A. Two-dimensional solitons and quantum droplets supported by competing self- and cross-interactions in spin-orbit-coupled condensates. New J. Phys. 2017, 19, 113043. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Z.; Luo, Z.; Huang, C.; Tan, H.; Pang, W.; Malomed, B.A. Two-dimensional vortex quantum droplets. Phys. Rev. A 2018, 98, 063602. [Google Scholar] [CrossRef]
- Nilsson Tengstrand, M.; Stürmer, P.; Karabulut, E.Ö.; Reimann, S.M. Rotating binary Bose-Einstein condensates and vortex clusters in quantum droplets. Phys. Rev. Lett. 2019, 123, 160405. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Malomed, B.A.; Tarruell, L.; Torner, L. Three-dimensional droplets of swirling superfluids. Phys. Rev. A 2018, 98, 013612. [Google Scholar] [CrossRef]
- Kadau, H.; Schmitt, M.; Wentzel, M.; Wink, C.; Maier, T.; Ferrier-Barbut, I.; Pfau, T. Observing the Rosenzweig instability of a quantum ferrofluid. Nature 2016, 530, 194–197. [Google Scholar] [CrossRef]
- Schmitt, M.; Wenzel, M.; Böttcher, F.; Ferrier-Barbut, I.; Pfau, T. Self-bound droplets of a dilute magnetic quantum liquid. Nature 2016, 539, 259–262. [Google Scholar] [CrossRef]
- Ferrier-Barbut, I.; Kadau, H.; Schmitt, M.; Wenzel, M.; Pfau, T. Observation of quantum droplets in a strongly dipolar Bose gas. Phys. Rev. Lett. 2016, 116, 215301. [Google Scholar] [CrossRef]
- Wächtler, F.; Santos, L. Ground-state properties and elementary excitations of quantum droplets in dipolar Bose-Einstein condensates. Phys. Rev. A 2016, 94, 043618. [Google Scholar] [CrossRef]
- Baillie, D.; Blakie, P.B. Droplet crystal ground states of a dipolar Bose gas. Phys. Rev. Lett. 2018, 121, 195301. [Google Scholar] [CrossRef] [PubMed]
- Cidrim, A.; dos Santos, F.E.A.; Henn, E.A.L.; Macrí, T. Vortices in self-bound dipolar droplets. Phys. Rev. A 2018, 98, 023618. [Google Scholar] [CrossRef]
- Shamriz, E.; Chen, Z.; Malomed, B.A. Suppression of the quasi-two-dimensional quantum collapse in the attraction field by the Lee-Huang-Yang effect. to be published.
- Salasnich, L.; Parola, A.; Reatto, L. Effective wave equations for the dynamics of cigar-shaped and disk-shaped Bose condensates. Phys. Rev. A 2002, 65, 043614. [Google Scholar] [CrossRef]
- Muñoz Mateo, A.; Delgado, V. Effective mean-field equations for cigar-shaped and disk-shaped Bose-Einstein condensates. Phys. Rev. A 2008, 77, 013617. [Google Scholar] [CrossRef]
- Jørgensen, N.B.; Bruun, G.M.; Arlt, J.J. Dilute fluid governed by quantum fluctuations. Phys. Rev. Lett. 2018, 121, 173403. [Google Scholar] [CrossRef] [PubMed]
- Bergé, L. Wave collapse in physics: Principles and applications to light and plasma waves. Phys. Rep. 1998, 303, 259–370. [Google Scholar] [CrossRef]
- Veron, L. Singular solutions of some nonlinear elliptic equations. Nonlinear Anal. Theory Methods Appl. 1981, 5, 225–242. [Google Scholar] [CrossRef]
- Lions, P.L. Isolated singularities in semilinear problems. J. Diff. Eq. 1980, 18, 441–450. [Google Scholar] [CrossRef]
- Gidas, B.; Spruck, J. Global and local behavior of positive solutions of nonlinear elliptic equations. Comm. Pure Appl. Math. 1981, 34, 525–581. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Malomed, B.A. Singular solitons. Phys. Rev. E 2020, 101, 012211. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Malomed, B.A. Solitons in combined linear and nonlinear lattice potentials. Phys. Rev. A 2010, 81, 013624. [Google Scholar] [CrossRef]
- Vakhitov, N.G.; Kolokolov, A.A. Stationary solutions of the wave equation in a medium with nonlinearity saturation. Radiophys. Quantum Electron. 1973, 16, 783–789. [Google Scholar] [CrossRef]
- Wang, L.; Malomed, B.A.; Yan, Z. Attraction centers and PT-symmetric delta-functional dipoles in critical and supercritical self-focusing media. Phys. Rev. E 2019, 99, 052206. [Google Scholar] [CrossRef] [PubMed]
- Lam, C.-K.; Malomed, B.A.; Chow, K.W.; Wai, P.K.A. Spatial solitons supported by localized gain in nonlinear optical waveguides. Eur. Phys. J. Spec. Top. 2009, 173, 233–243. [Google Scholar] [CrossRef]
- Tsang, C.H.; Malomed, B.A.; Lam, C.-K.; Chow, K.W. Solitons pinned to hot spots. Eur. Phys. J. D 2010, 59, 81–89. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Konotop, V.V.; Vysloukh, V.A.; Zezyulin, D.A. Guided modes and symmetry breaking supported by localized gain. In Spontaneous Symmetry Breaking, Self-Trapping, and Josephson Oscillations; Malomed, B.A., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 167–200. [Google Scholar]
- Malomed, B.A. Spatial solitons supported by localized gain. J. Opt. Soc. Am. B 2014, 31, 2460–2475. [Google Scholar] [CrossRef]
- Yang, J. Nonlinear Waves in Integrable and Nonintegrable Systems; SIAM: Philadelphia, PA, USA, 2010. [Google Scholar]
- Quiroga-Texeiro, M.; Michinel, H. Stable azimuthal stationary state in quintic nonlinear optical media. J. Opt. Soc. Am. B 1997, 14, 2004–2009. [Google Scholar] [CrossRef]
- Boudebs, G.; Cherukulappurath, S.; Leblond, H.; Troles, J.; Smektala, F.; Sanchez, F. Experimental and theoretical study of higher-order nonlinearities in chalcogenide glasses. Opt. Commun. 2003, 219, 427–433. [Google Scholar] [CrossRef]
- Malomed, B.A.; Mihalache, D.; Wise, F.; Torner, L. Spatiotemporal optical solitons. J. Opt. B Quant. Semicl. Opt. 2005, 7, R53–R72. [Google Scholar] [CrossRef]
- Falcão-Filho, L.E.; de Araújo, C.B.; Boudebs, G.; Leblond, H.; Skarka, V. Robust two-dimensional spatial solitons in liquid carbon disulfide. Phys. Rev. Lett. 2013, 110, 013901. [Google Scholar] [CrossRef]
- Reyna, A.S.; de Araújo, C.B. Spatial phase modulation due to quintic and septic nonlinearities in metal colloids. Opt. Exp. 2014, 22, 22456–22469. [Google Scholar] [CrossRef] [PubMed]
- Reyna, A.S.; Jorge, K.C.; de Araújo, C.B. Two-dimensional solitons in a quintic-septimal medium. Phys. Rev. A 2014, 90, 063835. [Google Scholar] [CrossRef]
- Reyna, A.S.; de Araújo, C.B. High-order optical nonlinearities in plasmonic nanocomposites —-A review. Adv. Opt. Photon. 2017, 9, 720–774. [Google Scholar] [CrossRef]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shamriz, E.; Chen, Z.; Malomed, B.A.; Sakaguchi, H. Singular Mean-Field States: A Brief Review of Recent Results. Condens. Matter 2020, 5, 20. https://doi.org/10.3390/condmat5010020
Shamriz E, Chen Z, Malomed BA, Sakaguchi H. Singular Mean-Field States: A Brief Review of Recent Results. Condensed Matter. 2020; 5(1):20. https://doi.org/10.3390/condmat5010020
Chicago/Turabian StyleShamriz, Elad, Zhaopin Chen, Boris A. Malomed, and Hidetsugu Sakaguchi. 2020. "Singular Mean-Field States: A Brief Review of Recent Results" Condensed Matter 5, no. 1: 20. https://doi.org/10.3390/condmat5010020
APA StyleShamriz, E., Chen, Z., Malomed, B. A., & Sakaguchi, H. (2020). Singular Mean-Field States: A Brief Review of Recent Results. Condensed Matter, 5(1), 20. https://doi.org/10.3390/condmat5010020





