Theory of Time-Resolved Optical Conductivity of Superconductors: Comparing Two Methods for Its Evaluation
Abstract
1. Introduction
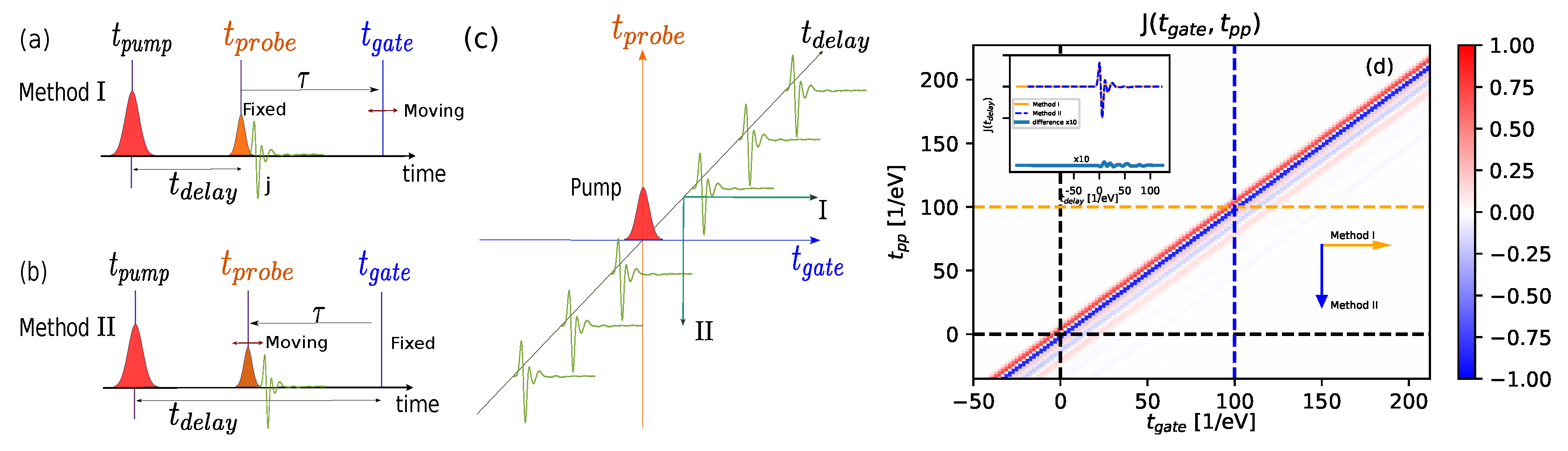
2. Methods
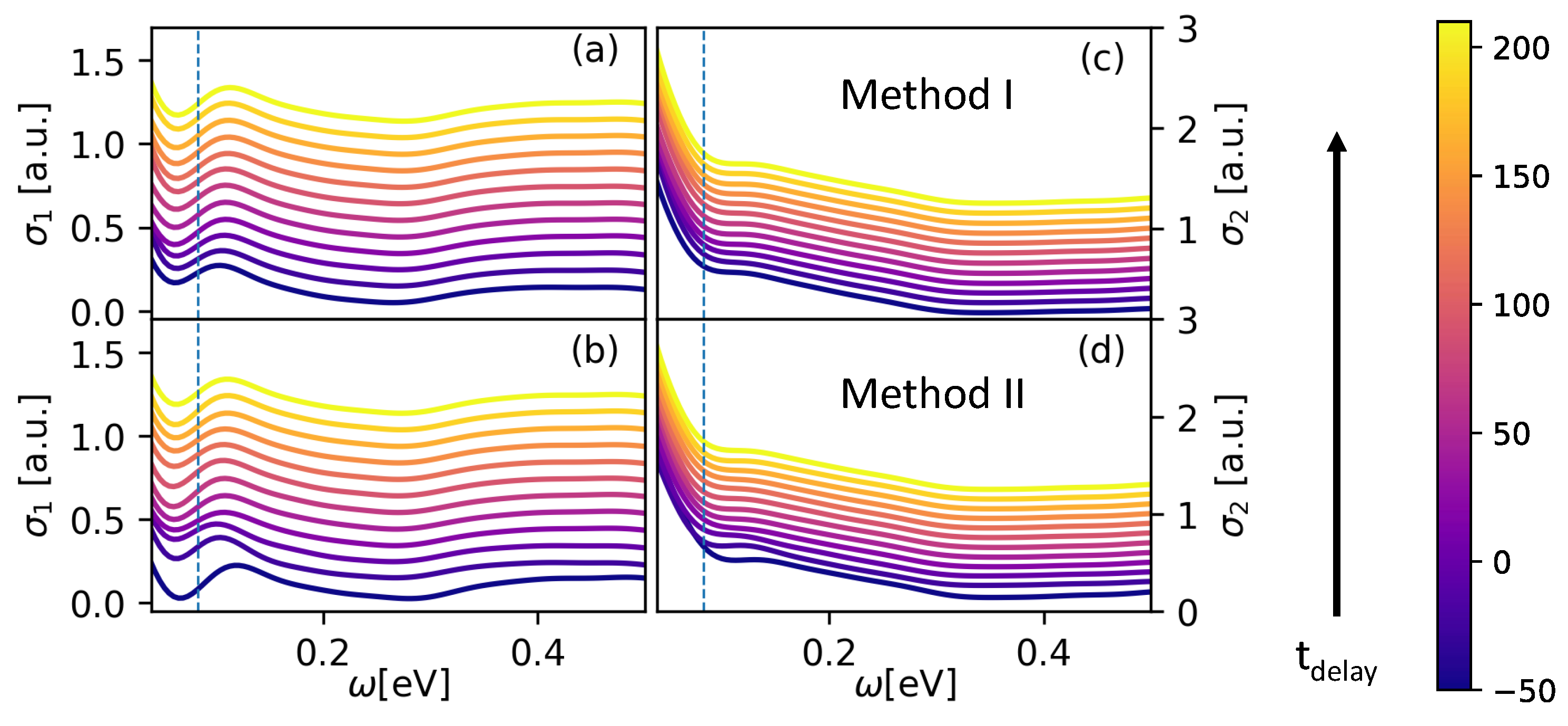
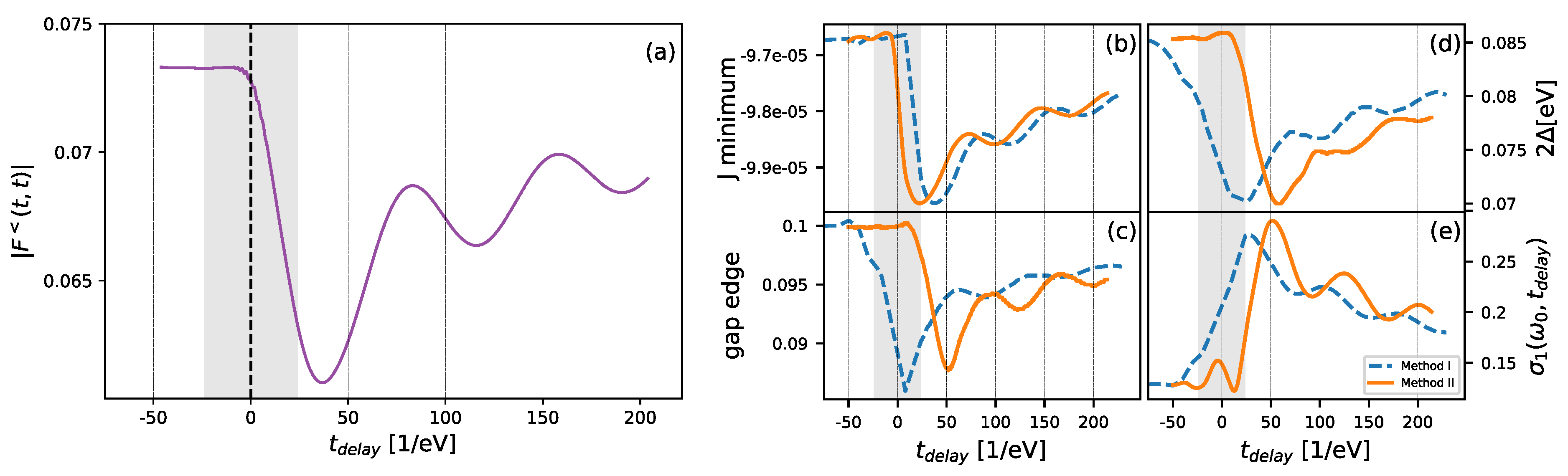
3. Results
- The location of the gap edge in , which we define to the the point on the frequency axis, where the mean of and is located within the range from to .
- The location of the minimum about the phonon frequency (measured with respect to ).
- The conductivity at a fixed frequency: .
4. Summary
5. Materials and Methods
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mitrano, M.; Cantaluppi, A.; Nicoletti, D.; Kaiser, S.; Perucchi, A.; Lupi, S.; Di Pietro, P.; Pontiroli, D.; Riccò, M.; Clark, S.R.; et al. Possible light-induced superconductivity in K3C60 at high temperature. Nature 2016, 530, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Matsunaga, R.; Hamada, Y.I.; Makise, K.; Uzawa, Y.; Terai, H.; Wang, Z.; Shimano, R. Higgs Amplitude Mode in the BCS Superconductors Nb1−xTixN Induced by Terahertz Pulse Excitation. Phys. Rev. Lett. 2013, 111, 057002. [Google Scholar] [CrossRef] [PubMed]
- Matsunaga, R.; Tsuji, N.; Fujita, H.; Sugioka, A.; Makise, K.; Uzawa, Y.; Terai, H.; Wang, Z.; Aoki, H.; Shimano, R. Light-induced collective pseudospin precession resonating with Higgs mode in a superconductor. Science 2014, 345, 1145–1149. [Google Scholar] [CrossRef] [PubMed]
- Murakami, Y.; Werner, P.; Tsuji, N.; Aoki, H. Multiple amplitude modes in strongly coupled phonon-mediated superconductors. Phys. Rev. B 2016, 93, 094509. [Google Scholar] [CrossRef]
- Tsuji, N.; Murakami, Y.; Aoki, H. Nonlinear light–Higgs coupling in superconductors beyond BCS: Effects of the retarded phonon-mediated interaction. Phys. Rev. B 2016, 94, 224519. [Google Scholar] [CrossRef]
- Kennes, D.M.; Wilner, E.Y.; Reichman, D.R.; Millis, A.J. Nonequilibrium optical conductivity: General theory and application to transient phases. Phys. Rev. B 2017, 96, 054506. [Google Scholar] [CrossRef]
- Silaev, M. Nonlinear electromagnetic response and Higgs-mode excitation in BCS superconductors with impurities. Phys. Rev. B 2019, 99, 224511. [Google Scholar] [CrossRef]
- Murotani, Y.; Shimano, R. Nonlinear optical response of collective modes in multiband superconductors assisted by nonmagnetic impurities. Phys. Rev. B 2019, 99, 224510. [Google Scholar] [CrossRef]
- Shimano, R.; Tsuji, N. Higgs Mode in Superconductors. arXiv 2019, arXiv:1906.09401. [Google Scholar]
- Jujo, T. Quasiclassical Theory on Third-Harmonic Generation in Conventional Superconductors with Paramagnetic Impurities. J. Phys. Soc. Jpn. 2017, 87, 024704. [Google Scholar] [CrossRef]
- Cea, T.; Castellani, C.; Seibold, G.; Benfatto, L. Nonrelativistic Dynamics of the Amplitude (Higgs) Mode in Superconductors. Phys. Rev. Lett. 2015, 115, 157002. [Google Scholar] [CrossRef]
- Cea, T.; Castellani, C.; Benfatto, L. Nonlinear optical effects and third-harmonic generation in superconductors: Cooper pairs versus Higgs mode contribution. Phys. Rev. B 2016, 93, 180507. [Google Scholar] [CrossRef]
- Udina, M.; Cea, T.; Benfatto, L. Theory of coherent oscillations detection in THz pump-probe spectroscopy: From phonons to electronic collective modes. arXiv 2019, arXiv:1907.06092. [Google Scholar]
- Krull, H.; Manske, D.; Uhrig, G.S.; Schnyder, A.P. Signatures of nonadiabatic BCS state dynamics in pump-probe conductivity. Phys. Rev. B 2014, 90, 014515. [Google Scholar] [CrossRef]
- Orenstein, J.; Dodge, J.S. Terahertz time-domain spectroscopy of transient metallic and superconducting states. Phys. Rev. B 2015, 92, 134507. [Google Scholar] [CrossRef]
- Shao, C.; Tohyama, T.; Luo, H.G.; Lu, H. Numerical method to compute optical conductivity based on pump-probe simulations. Phys. Rev. B 2016, 93, 195144. [Google Scholar] [CrossRef]
- Eckstein, M.; Kollar, M. Theory of time-resolved optical spectroscopy on correlated electron systems. Phys. Rev. B 2008, 78, 205119. [Google Scholar] [CrossRef]
- Tsuji, N.; Oka, T.; Aoki, H. Nonequilibrium Steady State of Photoexcited Correlated Electrons in the Presence of Dissipation. Phys. Rev. Lett. 2009, 103, 047403. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Kemper, A. Higgs Oscillations in time-resolved Optical Conductivity. arXiv 2019, arXiv:1902.09549. [Google Scholar]
- Kindt, J.T.; Schmuttenmaer, C.A. Theory for determination of the low-frequency time-dependent response function in liquids using time-resolved terahertz pulse spectroscopy. J. Chem. Phys. 1999, 110, 8589–8596. [Google Scholar] [CrossRef]
- Němec, H.; Kadlec, F.; Kužel, P. Methodology of an optical pump-terahertz probe experiment: An analytical frequency-domain approach. J. Chem. Phys. 2002, 117, 8454–8466. [Google Scholar] [CrossRef]
- Coslovich, G.; Kemper, A.F.; Behl, S.; Huber, B.; Bechtel, H.A.; Sasagawa, T.; Martin, M.C.; Lanzara, A.; Kaindl, R.A. Ultrafast dynamics of vibrational symmetry breaking in a charge-ordered nickelate. Sci. Adv. 2017, 3, e1600735. [Google Scholar] [CrossRef] [PubMed]
- Kemper, A.; Sentef, M.; Moritz, B.; Freericks, J.; Devereaux, T. Effect of dynamical spectral weight redistribution on effective interactions in time-resolved spectroscopy. Phys. Rev. B 2014, 90, 075126. [Google Scholar] [CrossRef]
- Kemper, A.F.; Sentef, M.A.; Moritz, B.; Freericks, J.K.; Devereaux, T.P. Direct observation of Higgs mode oscillations in the pump-probe photoemission spectra of electron-phonon mediated superconductors. Phys. Rev. B 2015, 92, 224517. [Google Scholar] [CrossRef]
- Mattis, D.C.; Bardeen, J. Theory of the Anomalous Skin Effect in Normal and Superconducting Metals. Phys. Rev. 1958, 111, 412–417. [Google Scholar] [CrossRef]
- Zimmermann, W.; Brandt, E.H.; Bauer, M.; Seider, E.; Genzel, L. Optical conductivity of BCS superconductors with arbitrary purity. Phys. C Supercond. 1991, 183, 99–104. [Google Scholar] [CrossRef]
- Akima, H. A new method of interpolation and smooth curve fitting based on local procedures. J. ACM 1970, 17, 589–602. [Google Scholar] [CrossRef]
- Yang, X.; Vaswani, C.; Sundahl, C.; Mootz, M.; Gagel, P.; Luo, L.; Kang, J.H.; Orth, P.P.; Perakis, I.E.; Eom, C.B.; et al. Terahertz-light quantum tuning of a metastable emergent phase hidden by superconductivity. Nat. Mater. 2018, 17, 586–591. [Google Scholar] [CrossRef] [PubMed]
- Kemper, A.; Sentef, M.A.; Moritz, B.; Devereaux, T.; Freericks, J. Review of the Theoretical Description of Time-Resolved Angle-Resolved Photoemission Spectroscopy in electron-phonon Mediated Superconductors. Annalen der Physik 2017, 529, 1600235. [Google Scholar] [CrossRef]
- Stahl, C.; Eckstein, M. Noise correlations in time- and angle-resolved photoemission spectroscopy. Phys. Rev. B 2019, 99, 241111. [Google Scholar] [CrossRef]
- GRENDEL Development Team. Available online: https://github.com/kemperlab/grendel/ (accessed on 26 August 2019).
| Phonon frequency | 0.20 eV |
| Phonon coupling | 0.12 eV |
| Impurity coupling () | 0.01 eV |
| Band parameters | eV, eV |
| Temperature | eV |
| Pump pulse | eV, eV |
| Probe pulse | eV, eV |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Revelle, J.P.; Kumar, A.; Kemper, A.F. Theory of Time-Resolved Optical Conductivity of Superconductors: Comparing Two Methods for Its Evaluation. Condens. Matter 2019, 4, 79. https://doi.org/10.3390/condmat4030079
Revelle JP, Kumar A, Kemper AF. Theory of Time-Resolved Optical Conductivity of Superconductors: Comparing Two Methods for Its Evaluation. Condensed Matter. 2019; 4(3):79. https://doi.org/10.3390/condmat4030079
Chicago/Turabian StyleRevelle, John P., Ankit Kumar, and Alexander F. Kemper. 2019. "Theory of Time-Resolved Optical Conductivity of Superconductors: Comparing Two Methods for Its Evaluation" Condensed Matter 4, no. 3: 79. https://doi.org/10.3390/condmat4030079
APA StyleRevelle, J. P., Kumar, A., & Kemper, A. F. (2019). Theory of Time-Resolved Optical Conductivity of Superconductors: Comparing Two Methods for Its Evaluation. Condensed Matter, 4(3), 79. https://doi.org/10.3390/condmat4030079





