1. Introduction
The frustrated magnet (insulator) herbertsmithite
is one of the best candidates for identification as a material that hosts a quantum spin liquid (QSL), thereby determining the nature of its thermodynamic, relaxation, and transport properties. The insulating nature of
has been established: There is a 3.3 eV charge gap (see e.g., [
1,
2]). In our review, we focus on a spin gap of QSL, and for brevity will call it “spin gap”. At low temperatures
T, a QSL may have or may not have a gap in its excitation spectrum of spinons, which are fermion quasiparticles of zero charge that occupy the corresponding Fermi sphere with Fermi momentum
. We note that, in contrast to metals, spinons cannot support charge current, but these, for instance, can carry heat, as electrons of metals do. The influence of a gap on the properties is huge, for at low
T the properties of herbertsmithite are similar to those of common insulators, while the properties resemble those of metals, provided that the gap is absent. Thus, it is a challenge to experimentally establish the presence of the gap and its value, for current theoretical and experimental studies of herbertsmithite are controversial and cannot give a definite answer to the challenge. In the present review, based primarily on our own theoretical work, we offer a number of experiments that can discern unambiguously the presence of a gapless QSL in
and other geometrically frustrated magnets. Our aim here is to let the readers to make their own qualified judgments about the presented theoretical approach and its ability to deliver an adequate description of many seemingly different experiments in a uniform manner.
In a magnet with geometric frustration, where the spins cannot be ordered even at temperatures close to absolute zero, they stay in a liquid quantum spin state. Herbertsmithite is an antiferromagnet with a kagome lattice of spins
. Recent experimental studies have shown its unusual properties [
3,
4,
5,
6,
7,
8].
The balance of electrostatic forces for the
ions in the kagome structure is such that they occupy distorted octahedral sites. The magnetic planes formed by the
ions are interspersed with nonmagnetic
layers. In samples,
defects occupy the nonmagnetic
sites between the kagome layers with
probability, thus introducing randomness and inhomogeneity into the lattice [
9]. As we shall see, the starring role of impurities in the formation of QSL is not clearly understood and is now under thorough investigation [
10,
11,
12,
13,
14,
15]. However, we suggest that the influence of impurities induced by the homogeneity on the properties of
can be tested by varying
x. We note that the impurities randomly located at the nanoscale level can support QSL as it is observed in measurements on
with
, while at
, glassy dynamics emerge [
5]. Moreover, the impurities randomly located at the nanoscale level can stabilize QSL as it is observed in measurements on the verdazyl-based complex
[
15] and make QSL stable in highly magnetic fields, as in the case of
-doped
[
14].
The experiments done on
have not found any traces of magnetic order in it. Nor they have found the spin freezing down to temperatures of around 50 mK. In these respects, herbertsmithite is the best candidate among quantum magnets to contain QSL described above [
3,
4,
5,
6,
7,
8]. These assessments are supported by model calculations indicating that an antiferromagnet on a kagome lattice has a gapless spin liquid ground state [
16,
17,
18,
19,
20,
21,
22,
23]. At the same time, recent suggestions [
9,
24,
25] that there can exist a small spin-gap in the kagome layers may stand in conflict to this emerging picture (see also refs. [
26,
27,
28] for a recent review). The obtained results are a combination of experimental and theoretical ones. The latter have been obtained in the framework of the model, which takes the presence of Cu impurities into account. The experimental data has been obtained by inelastic neutron scattering on
crystals. It is assumed that the influence of the Cu impurity ensemble on the observed properties of herbertsmithite may be disentangled from that of the kagome lattice geometry [
9,
24,
25]. It is further assumed that the impurity ensemble may be represented as a result of the dilution of some prototypic cubic lattice. The model supposes that the spin gap occurs in magnetic fields up to 9 T. We note that measurements of the local spin susceptibility of
show that the kagome spins exhibit a spin gap [
24], while the measurements of the bulk spin susceptibility evidence the absence of the gap [
3]. We shall see below that it is not possible to separate contributions coming from the local and bulk susceptibility, for both the kagome and the impurities spins form an integral system.
At the same time, without a magnetic field, the spin susceptibility
shows behavior in many respects similar to the Curie law. The latter behavior demonstrates that the copper spin ensemble plays the role of weakly interacting impurities [
9,
24,
25]. The same behavior was recently reported in a new kagome quantum spin liquid candidate,
[
29]. As a result, we observe a challenging contradiction between two sets of experimental data when some of them state the absent of a gap while the others present evidence in favor of a gap. Subsequently, we shall demonstrate that the model based on the Cu spin ensemble is rather synthetic. In other words, this model does not have the possibility of distinguishing the Cu ensemble and kagome lattice contributions. This is because the impurities, being embedded in the kagome host lattice, form a single integral entity at nanoscale. The above model may contradict the accumulated knowledge about the physical properties of
. This knowledge is the result of vast theoretical and experimental efforts related to static and dynamic properties of herbertsmithite [
3,
4,
5,
6,
7,
8,
16,
17,
18,
19,
20,
21,
22,
23]. Thus, when analyzing the physics of quantum spin liquid in the herbertsmithite, it is of crucial importance to verify the existence of a spin gap by experimental and theoretical studies, for the gap strongly influences all its thermodynamic, transport, and relaxation properties. To analyze QSL behavior theoretically, we employ the strongly correlated quantum spin liquid (SCQSL) [
16,
17,
18,
20,
23] model. A simple kagome lattice may host a dispersionless topologically protected branch of the quasiparticle spectrum with zero excitation energy, known as a flat band [
16,
18,
23,
30,
31,
32]. In that case, the topological fermion condensation quantum phase transition (FCQPT) can be considered as a quantum critical point (QCP) of the
spinon-composed QSL. Spinons have zero charge, occupying the Fermi sphere up to the Fermi momentum
[
16,
17,
32]. Taking into account that we are dealing with the real chemical compound
rather than with an ideal kagome lattice, we have to bear in mind that the actual magnetic interaction in the compound can shift QSL away from FCQPT, before or beyond QCP. Thus, the actual critical point location has to be established by experimental data analysis. The real part of the optical conductivity
, measured at low frequency on geometrically frustrated magnetic insulators, can yield important experimental clues to the nature of spinon-based QSL [
33,
34], especially at a wide range of temperatures
T and magnetic fields
B. Note that the consistent interpretation of the above data is a difficult theoretical problem [
33].
The main aim of the present review is to expose QSL as a new state of matter, also formed by heavy fermion (HF) metals, and to attract attention to experimental studies of that have the potential to reveal both the underlying physics of QSL and the presence or absence of a gap in spinon excitations that form the thermodynamic, transport, and relaxation properties. To clarify the nature of QSL in herbertsmithite, we recommend measurements of heat transport, low-energy inelastic neutron scattering, and optical conductivity in single crystals subject to an external magnetic field at low temperatures. We show that QSL is situated near FCQPT, which stems from the dependence of on the external magnetic field. We argue that the general physical picture inherent in QSL can be “purified” of the microscopic contributions coming both from phonons and the impurities polluting each specific sample being studied. We suggest that the influence of impurities on the properties of , induced by the inhomogeneity, can be tested by varying x.
In the following sections on thermodynamic properties, relaxation, and optical conductivity, we shall demonstrate that the existence of a gap within the impurity model of herbertsmithite may contradict recent experimental data collected on this material; instead, the impurities and kagome planes can form a genuine SCQSL. Accordingly, the observed gap [
24] related to the kagome planes may not be a real one as it is not a physical mechanism for the observed thermodynamic, relaxation, and conductivity properties of
.
3. Thermodynamic Properties
If QSL-forming quasiparticles are approximately dispersionless spinons (uncharged fermions), this state of matter becomes an SCQSL [
17,
18,
20,
35,
36]. As we have mentioned above, the geometrical frustration in herbertsmithite promotes the SCQSL formation [
18,
19,
20], while the presence of randomly scattered impurities can facilitate the frustration (see e.g., [
15]). Note that in real chemical compounds with many lattice imperfections, the actual SCQSL emergence point is shifted from the theoretically predicted FCQPT. This means that the mutual location of the SCQSL and FCQPT can only be extracted from the experimental data.
Famous Fermi liquid theory, proposed by Landau (the so-called Landau Fermi liquid (LFL) theory) [
41], has de facto been the universal tool to describe the itinerant fermionic systems. It maps the ensemble of strongly interacting electrons in a solid to the effective quasiparticle gas with not so strong an interaction. In such an approach, the excitations are represented in terms of the above quasiparticles so that the low-temperature properties of the system under consideration depend on the latter. The quasiparticles possess certain effective mass
, which is a parameter of the theory [
41,
42,
43], being approximately independent of external stimuli including temperature, pressure, or an electromagnetic field. The LFL theory cannot, however, explain the experimental results related to strong temperature and/or magnetic field dependence of the effective mass
, as observed in strongly correlated Fermi systems [
16,
44]. At the same time, deviations from LFL behavior are observed in the vicinity of an FCQPT [
16,
17,
44]. The above peculiarities are usually addressed as non-Fermi-liquid (NFL) properties. They are due to large effective mass, which actually becomes infinite at the FCQPT point (see [
16,
17] for details).
Let us describe the physical mechanism yielding the temperature and field dependences of the effective mass of the Landau quasiparticle
. Again, the key point is that upon approach to the FCQPT from the LFL regime, the effective mass becomes strongly external-stimuli-dependent. The aforementioned stimuli are the temperature, the magnetic field, and the external pressure
P, to name a few [
16,
17]. This is indeed a consequence of an additional instability channel of a normal Fermi liquid (to those of Pomeranchuk, [
42]). Note that the new channel is activated when the effective mass approaches infinity.
To avoid unphysical situations related, for instance, to the negativity of the effective mass, the system alters the topology of its Fermi surface [
32,
38,
39] so that the effective mass starts to depend on the above external stimuli [
16,
17]. For our studies of the effective mass properties in SCQSL, we adopt the so-called homogeneous Fermi liquid model. Such a description avoids consideration of nonuniversal (and highly irrelevant in our analysis) features like the exact structure of a specific sample [
16,
17]. In such a model, the LFL equation for
reads [
16,
17,
41]
In this expression,
M is the free electron mass,
is the Landau interaction function, depending on
p (momentum),
(constant Fermi momentum), and
, which is the quasiparticle distribution function for the spin projection
. The quasiparticle interaction
, assumed here to be spin-independent, is phenomenological. Without loss of generality, here we assume that
is independent of temperature so that
has the Fermi–Dirac form
where
is a single-particle energy spectrum. In addition,
is a chemical potential, which is spin-dependent via Zeeman splitting
, where
is the Bohr magneton. As usual, the spectrum
is obtained variationally from the system energy
,
In describing herbertsmithite as a strongly correlated quantum spin liquid, the choice of the function
is dictated by its possession of FCQPT [
16]. Thus, the sole role of the Landau interaction is to drive the system to the FCQPT point, at which the topology of the Fermi surface is altered in such a way that the effective mass ceases to be a constant parameter obtaining the aforementioned dependence on external stimuli [
16,
17]. Performing the variation (
3), we arrive at the expression for a single-particle energy spectrum
Equations (
2) and (
4) constitute the closed set to find
and
. In this case, the effective mass enters through the expression
. At the FCQPT point, the analytical solution of Equation (
1) is possible [
16,
17]. Namely, in contrast to the LFL approach with
being a constant parameter, here at zero magnetic field,
becomes temperature dependent. The latter feature comprises the strong deviation from the LFL picture, determining the NFL regime
At elevated temperatures, the system undergoes a transition to the LFL region of the phase diagram, and being subjected to the magnetic field, exhibits the behavior
of the effective mass.
The introduction of “internal” (or natural) scales greatly simplifies the analysis of the problem under consideration. We first observe that near the FCQPT, the effective mass
(i.e., the solution to Equation (
1)) has a maximum
at a temperature
[
16,
17]. This means that it is convenient to measure the effective mass and temperature in the units
and
, respectively. Thus, we arrive at normalized effective mass
and temperature
. Near FCQPT, the dependence
can be rendered as a universal interpolating function [
16,
17]. This function describes the transition from LFL to NFL states, given by Equations (
5) and (
6), and presents the universal scaling behavior of
[
16,
17]
Here,
and
, where
and
are free parameters. The magnetic field
B enters Equation (
1) only in the combination
, making
. It follows from Equation (
7) that
where
is a dimensionless quantity. In this case, the variable
y becomes
. The Equation (
8) permits us to assert Equation (
7), giving the scaling properties of temperature and magnetic field dependence of the effective mass. This implies, in turn, that at different fields
B, the curves
form a single one as a function of the normalized variable
. As
T and
B enter symmetrically in Equation (
7), it also manifests the scaling behavior of
as a function of
:
The schematic phase diagram is portrayed in
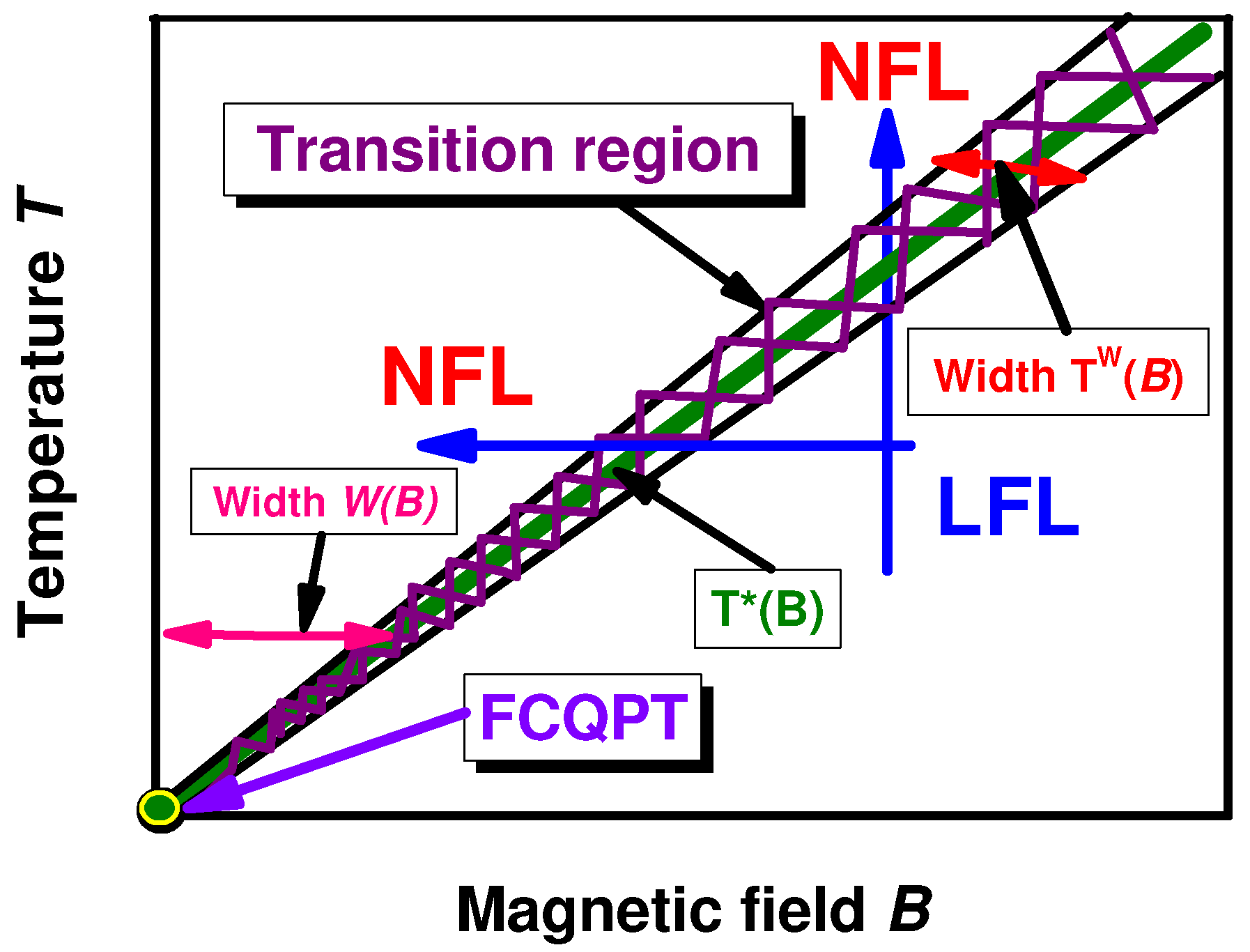
Figure 2. We assume for simplicity that at
and
, the system is near FCQPT. The external magnetic field and temperature are indeed the parameters controlling the system position on the phase diagram relatively to the FCQPT point. The same parameters are responsible for the transitions between the NFL and LFL regions of the phase diagram (see the arrows in
Figure 2). The horizontal arrow corresponds to fixed temperatures so that the system motion along this arrow from the NFL to LFL region corresponds to a magnetic field increase. On the contrary, the vertical arrow fixes the magnetic field so that the motion along it signifies the elevated temperatures. The shaded area reports the region where the NFL state transits to a weakly polarized LFL one. The temperature
of the transition is defined by the expression
which directly follows from Equation (
8). The line Equation (
10) is indeed the function
, so that the width
of the NFL region is proportional to the temperature. It can be shown similarly that the transition region width
is also
[
16,
17]. We note here that in essence, the transition region represents the crossover between LFL and NFL phases. In our case, the NFL phase is formed by quasiparticles that occupy the so-called fermion condensate (FC) state, in analogy to the Bose condensate for particles obeying Bose–Einstein statistics. (See [
16,
17] for a comprehensive explanation.) In a “pure” FC state, all fermions (quasiparticles) having momenta in a finite interval embracing the Fermi surface have energies pinned to the chemical potential. In reality, this state cannot be reached because of the Nernst theorem [
45], and the NFL features arise from “traces” of the FC state manifested at finite temperatures. Moreover, at low but finite temperatures, the magnetic field acts to suppress NFL behavior (i.e., the “FC traces”) and, upon growing sufficiently strong, restores the LFL phase. On the other hand, thermal fluctuations destroy LFL behavior and generate NFL features related to the FC state.
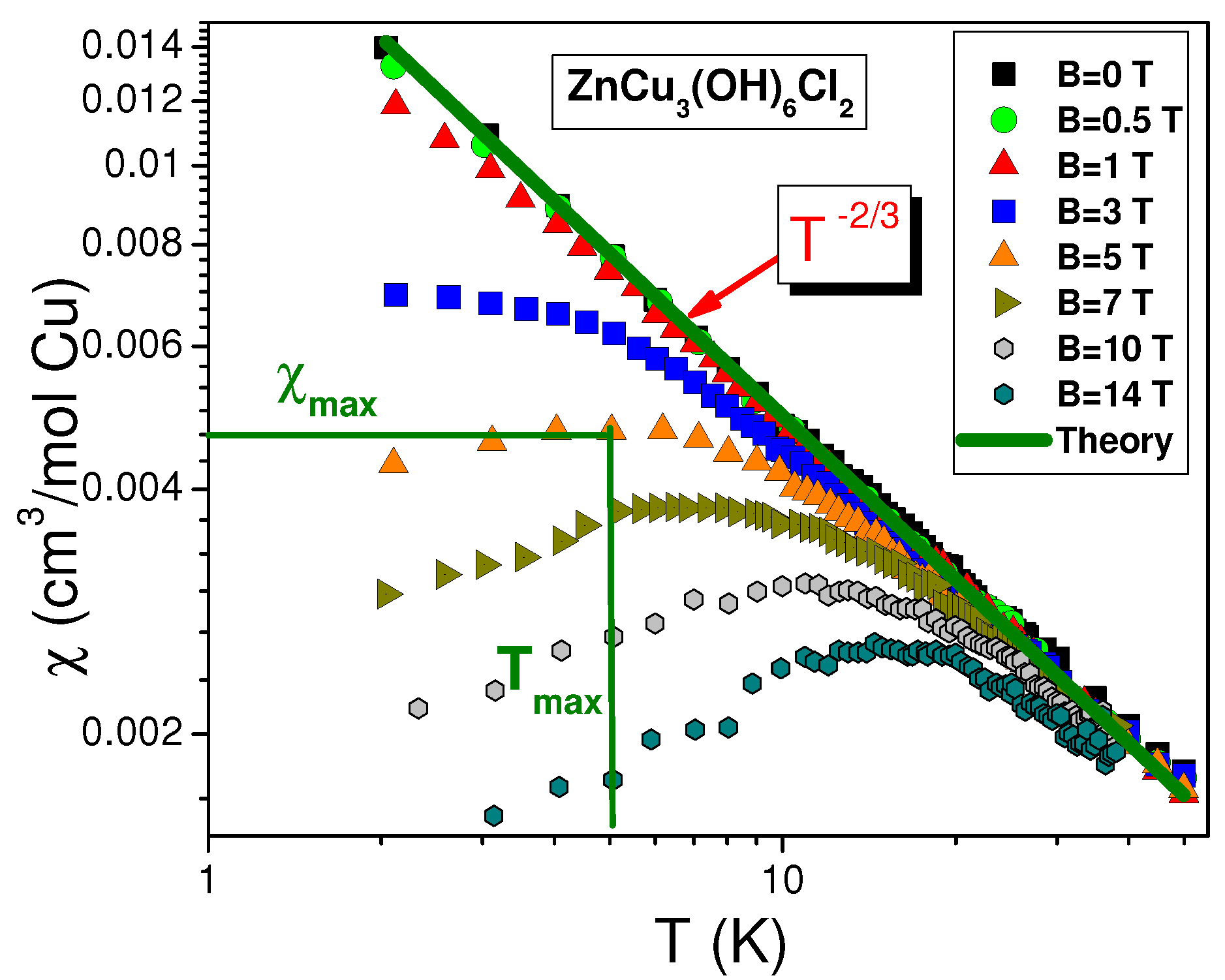
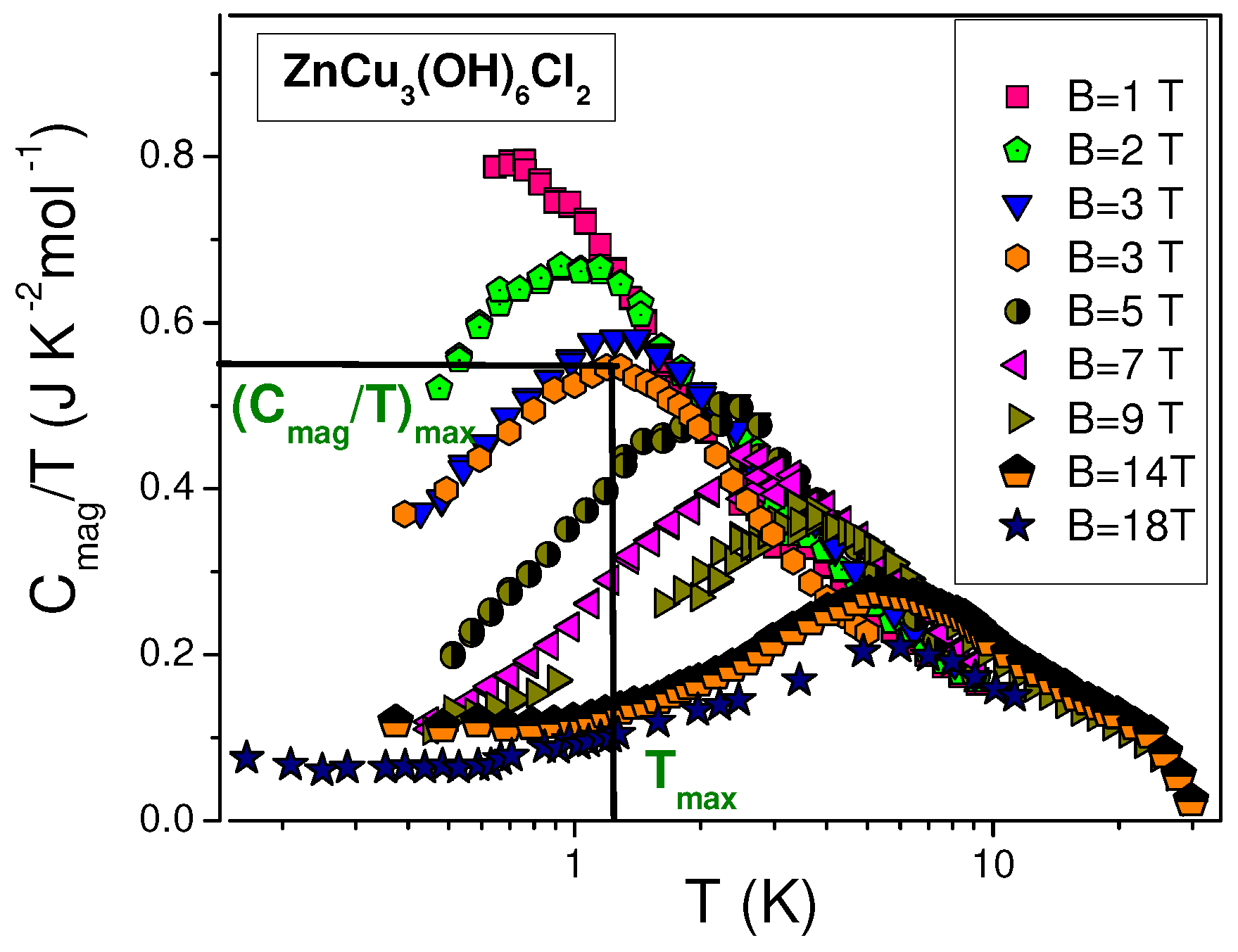
To examine the impurity model and possible gap in the spinon single particle spectrum, we consider the measured properties of herbertsmithite magnetic susceptibility
. It is seen from
Figure 3 that the magnetic susceptibility diverges as
at
T (full line). For weakly interacting impurities, it has been suggested that at low temperatures, the dependence
can be approximated by a Curie–Weiss law [
9,
24,
25], i.e.,
, where
is a Curie temperature, which turns out to be very small. At the same time, with respect to firmly established behavior
at low
B, the above Curie–Weiss approximation is in discord with both theory [
17,
18,
20] and experiment [
3]. Moreover, as seen in
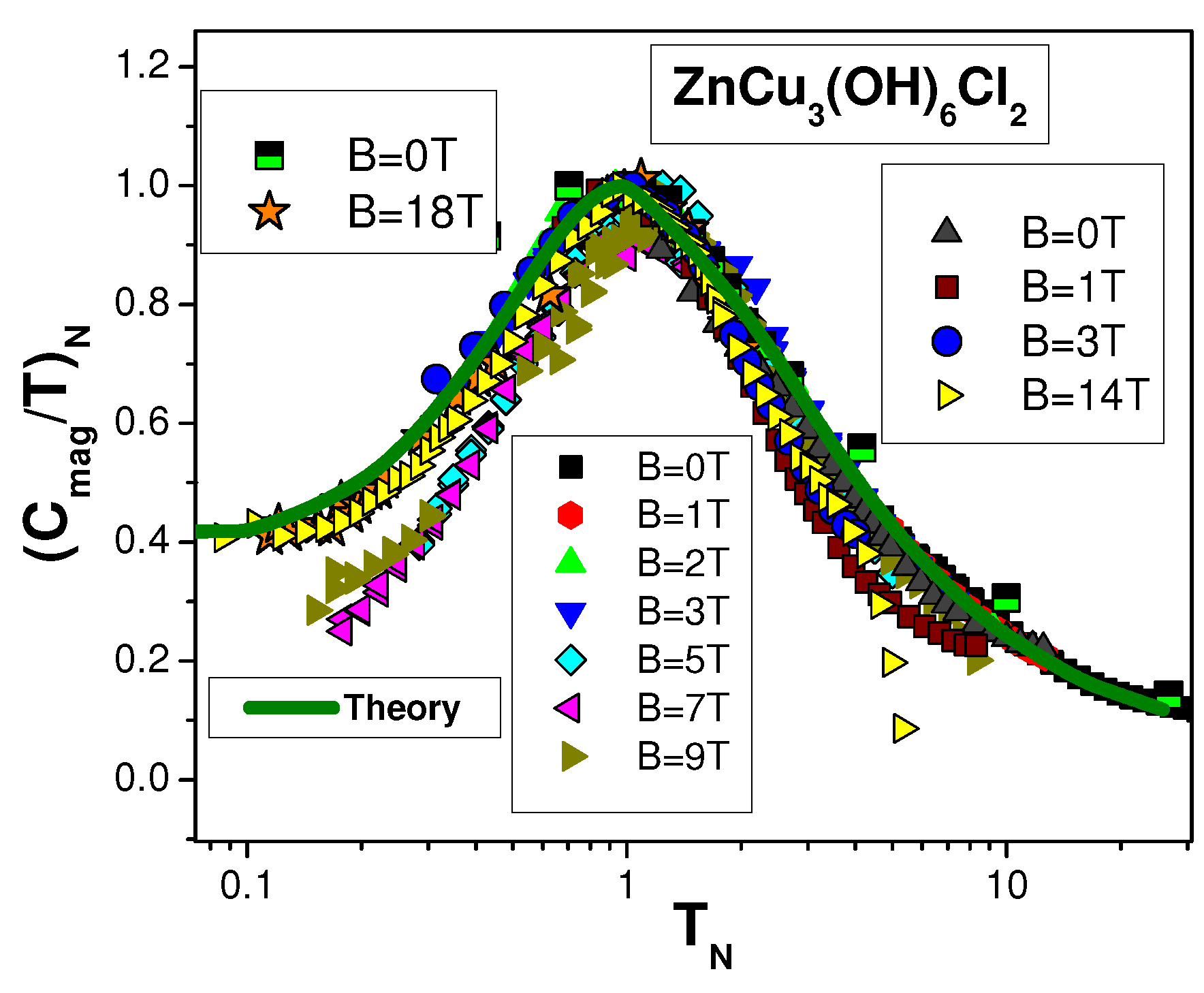
Figure 4, the normalized spin susceptibility
behaves like the normalized specific heat
extracted from measurements on
in high magnetic fields [
46] and displayed in
Figure 5a. Note that
displayed in
Figure 5a coincides approximately with
shown in
Figure 6, pointing to similarity of the electron and spinon Fermi spheres.
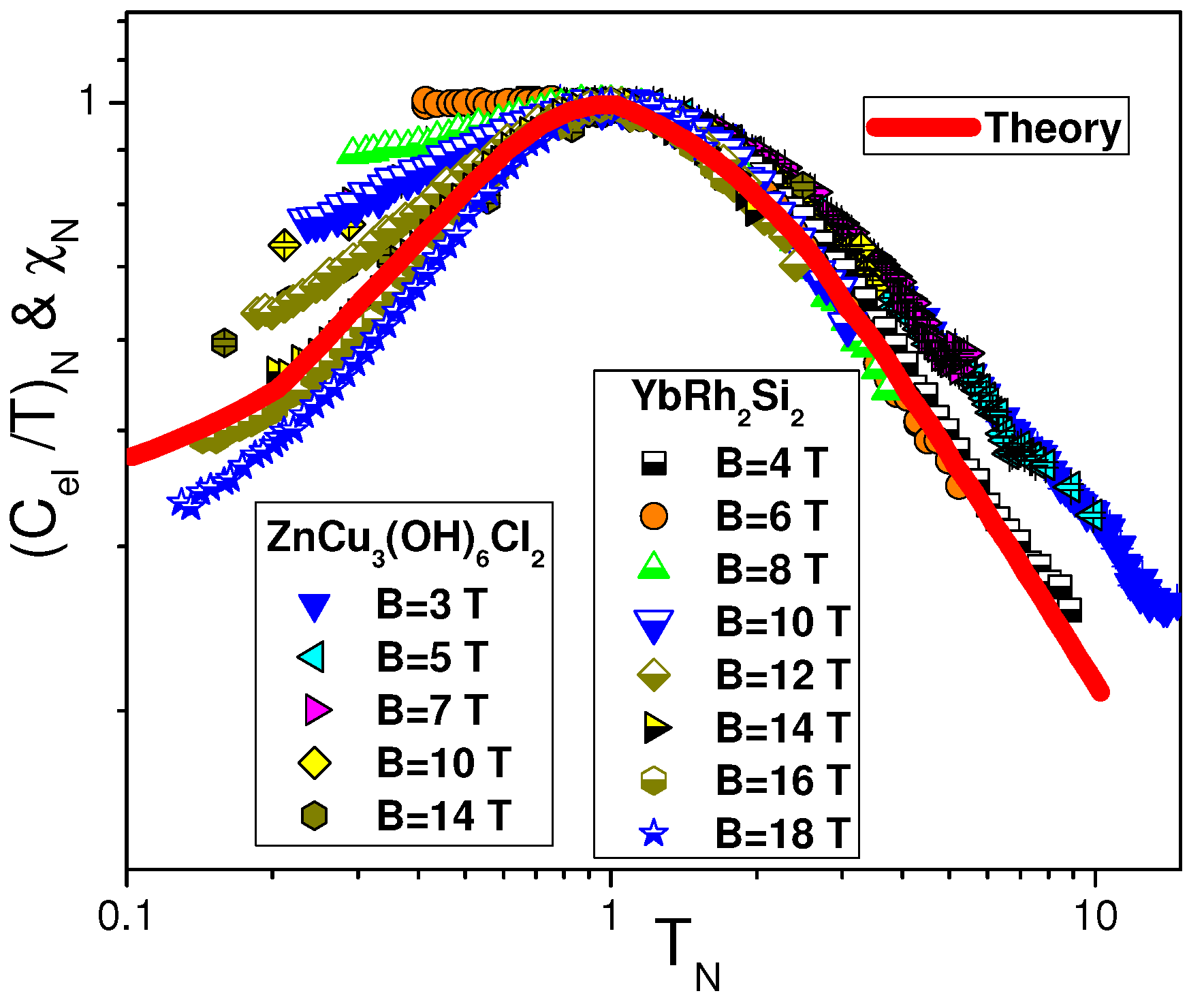
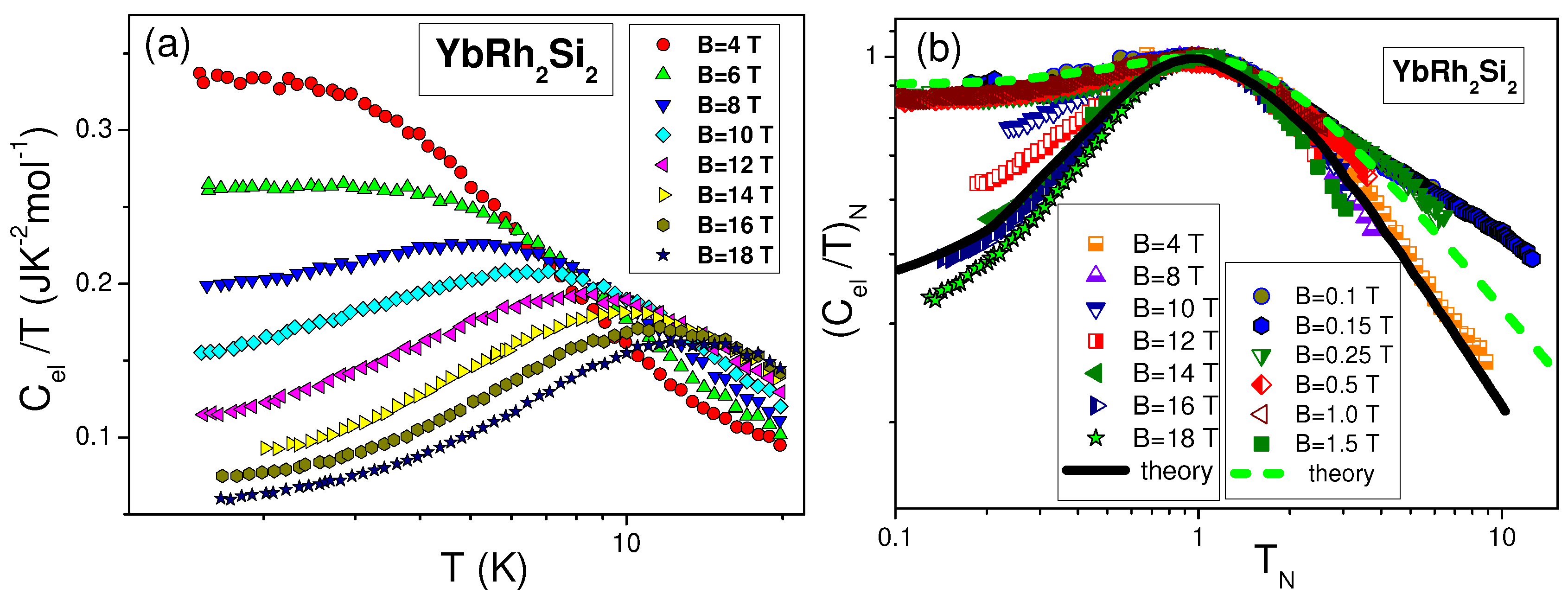
Figure 5b reports the normalized specific heat
extracted from the data [
46,
47]. It is seen that at low magnetic fields, the electronic system is not polarized as it is at high ones (black line) [
17,
48]. We note that the same behavior is exhibited by both
shown in
Figure 6 and
shown in
Figure 7. These facts support our conclusion that the SCQSL of
behaves like both the HF electron liquid of
and the insulator
[
49,
50].
In fact, at
, the FC state is represented by the superconducting state with the superconducting gap
, while the superconducting order parameter
is finite in the region
[
16,
31,
51], for in the region
.
The above observations point to a possible absence of the spin gap in
, for it is impossible to definitely separate the contributions of the impurities and of kagome planes. The impurity model implies that the intrinsic spin susceptibility of the kagome plane is decomposed as
, leading to
and the result about the existence of a putative gap [
25]. This shows that there is a problem with the impurity model as it cannot describe the firmly established behavior
[
3]. Thus, to explain the observed behavior of
, one should view the impurity ensemble embedded in the kagome host crystal lattice as an integral system [
16,
17,
18,
19,
20,
21,
23,
49,
50,
52] that acts coherently at nanoscale to produce additional frustration of the kagome planes, so as to make QSL robust at lower temperatures. Based on this analysis, we predict that QSL of quantum magnets can be stabilized by introducing a random distribution of impurities. We also note that artificially or spontaneously introducing impurities into
can both stabilize its QSL and simplify its chemical preparation.
It is instructive to plot the functions
and
of
. These functions are displayed in
Figure 8 with the data extracted from experimental facts [
4]. It is seen from
Figure 8a that the behavior of
is in accordance with Equation (
6). It is also seen from
Figure 8a that
is not located exactly at the FCQPT, for
K and the system demonstrate LFL behavior at
K [
4]. Similarly, it is seen from
Figure 8b that
, in accordance with Equations (
6) and (
7). Thus, the effect of the impurities on QSL can be analyzed basing on
Figure 8: the LFL temperature
grows if QSL is shifted by impurities from the FCQPT, while the gap is absent. It also follows from
Figure 8 that
exhibits behavior typical of HF metals under the application of a magnetic field [
16,
17]. As a result, we conclude that impurities form the single integral entity with a kagome lattice at nanoscale.
The impurity model has been utilized by the authors of reference [
9] to derive an intrinsic scattering measure
. In the latter expression,
is a total (i.e., host lattice plus impurities) scattering rate, while
is the impurity contribution with fitting parameter
a. On finding that
goes to zero as
meV (see
Figure 4b of reference [
9]), they assert the existence of a gap. However, as we have demonstrated above, such a procedure gives just a spurious gap. Indeed, the latter conclusion relies completely on the assumption of a weak inter-impurity interaction, which is unjustified empirically since the subtraction hypothesis is negated by the experimental behavior summarized in
Figure 3.
We now examine the impurity model in further detail and put its conclusion about the existence of a spin gap under scrutiny. It is seen from
Figure 3 that normal low-temperature Fermi liquid properties of the magnetic susceptibility
are confirmed experimentally at least for
T. In such strong magnetic fields and low temperatures, the impurity spins are aligned completely along the field direction. They do not have degrees of freedom, permitting them to demonstrate Curie–Weiss behavior. Thus, assuming that impurity spins are fully aligned along the magnetic field direction and hence do not contribute to
, one remains with
. Similar properties of the heat capacity follow from
Figure 6. In the above magnetic fields,
also demonstrates ordinary Fermi liquid behavior. This shows that at low temperatures and
T, the impurities show minute contributions to
and
. It becomes obvious that the main contribution in such a case comes from the host kagome lattice [
9,
24,
25]. Moreover, the impurity model implies that both
and
approach zero at
and
T. It is clear from
Figure 3,
Figure 4,
Figure 6, and
Figure 7 that this is not true. Namely, both
and
do not go to zero at
up to
T. Moreover, the scaling properties of
from
Figure 7 and the behavior of both
and
displayed in
Figure 8 confirm clearly the lack of a gap. The results of
measurements [
4,
5,
6,
7,
8] are the same for powder and bulk samples (see
Figure 6).
The aforementioned experimental results are consistent with the hypothesis that the vast majority of physical properties of herbertsmithite are due to stable SCQSL. First, there is no substantial gap in the spinon excitation spectrum. Moreover, the application of high magnetic fields 18 T does not trigger such a gap. This implies that the impurity model is inadequate. These findings are in conformity with recent measurements stating that the low-temperature plateau in the local susceptibility identifies the spin-liquid ground state as a gapless one [
53], while recent theoretical analysis confirms the absence of a gap [
22].
4. Dynamic, Relaxation, and Heat Transport Properties
Neutron scattering measurements are one more confirmation of our hypothesis’ validity. Recently, the dynamic spin susceptibility
has been measured by neutrons scattering as a function of
(momentum),
(frequency), and
T. At low temperatures, the results are consistent with the idea that these quasiparticles are spinons, which form an approximately flat band [
54].
The imaginary part
satisfies the equation [
17,
19]
where
and
are constants and
. Equation (
11) demonstrates that
has a maximum
at some
. Equation (
11) describes the scaling properties of
established in measurements in reference [
3]. As in Equation (
7), we introduce the dimensionless function
and the (dimensionless) variable
. In this case, Equation (
11) is modified to read
where
and
are fitting parameters. They should be chosen from the condition that the right-hand side of Equation (
12) should reach the maximum at
. This means that the expression
exhibits scaling as a function of
[
17,
19]. In other words, we find that
(cf. Equation (
6)) exhibits the scaling behavior with
:
Similarly,
and
are fitting parameters chosen from the condition that the function
at
. In the FCQPT point, the discussed scaling is valid almost to
.
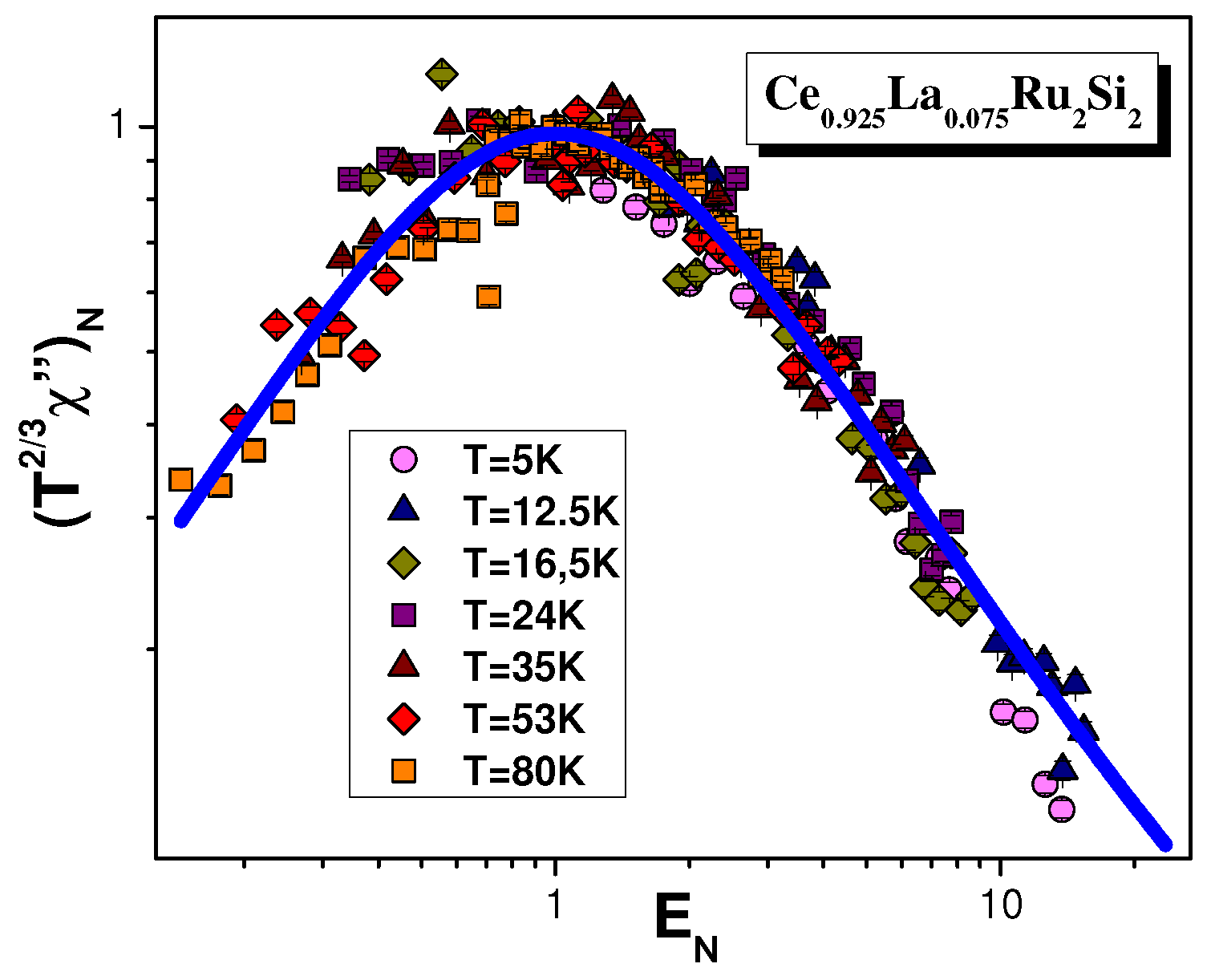
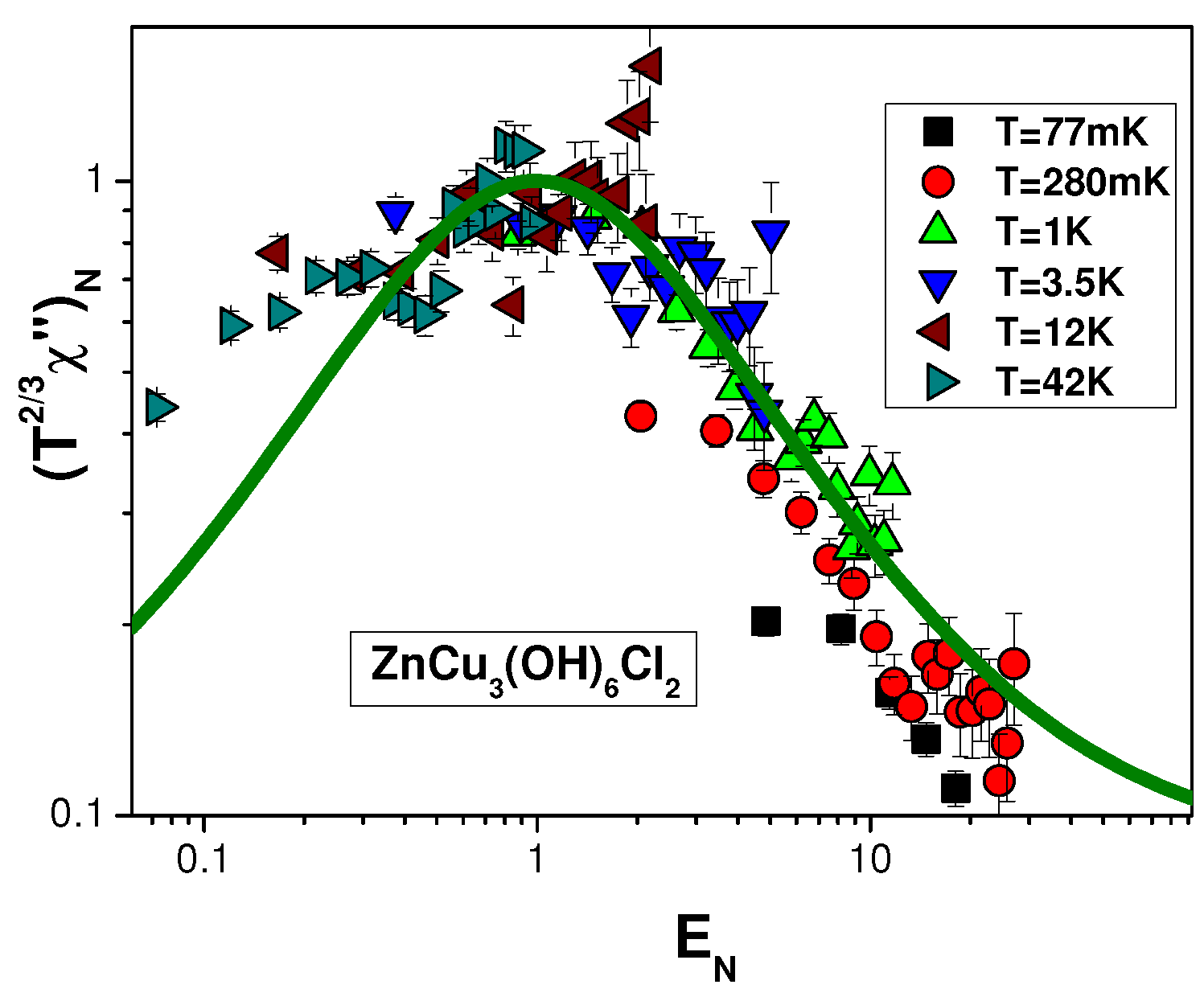
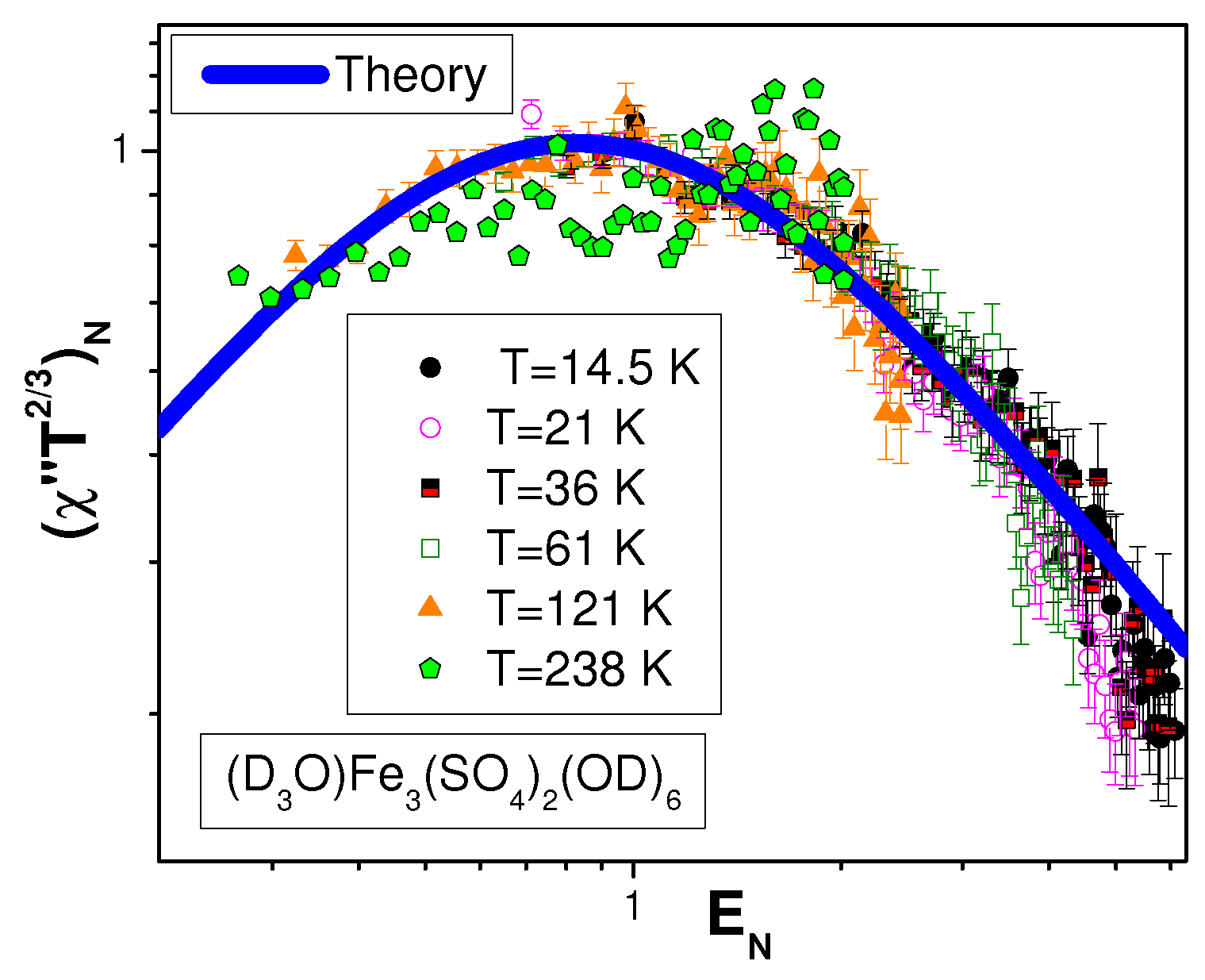
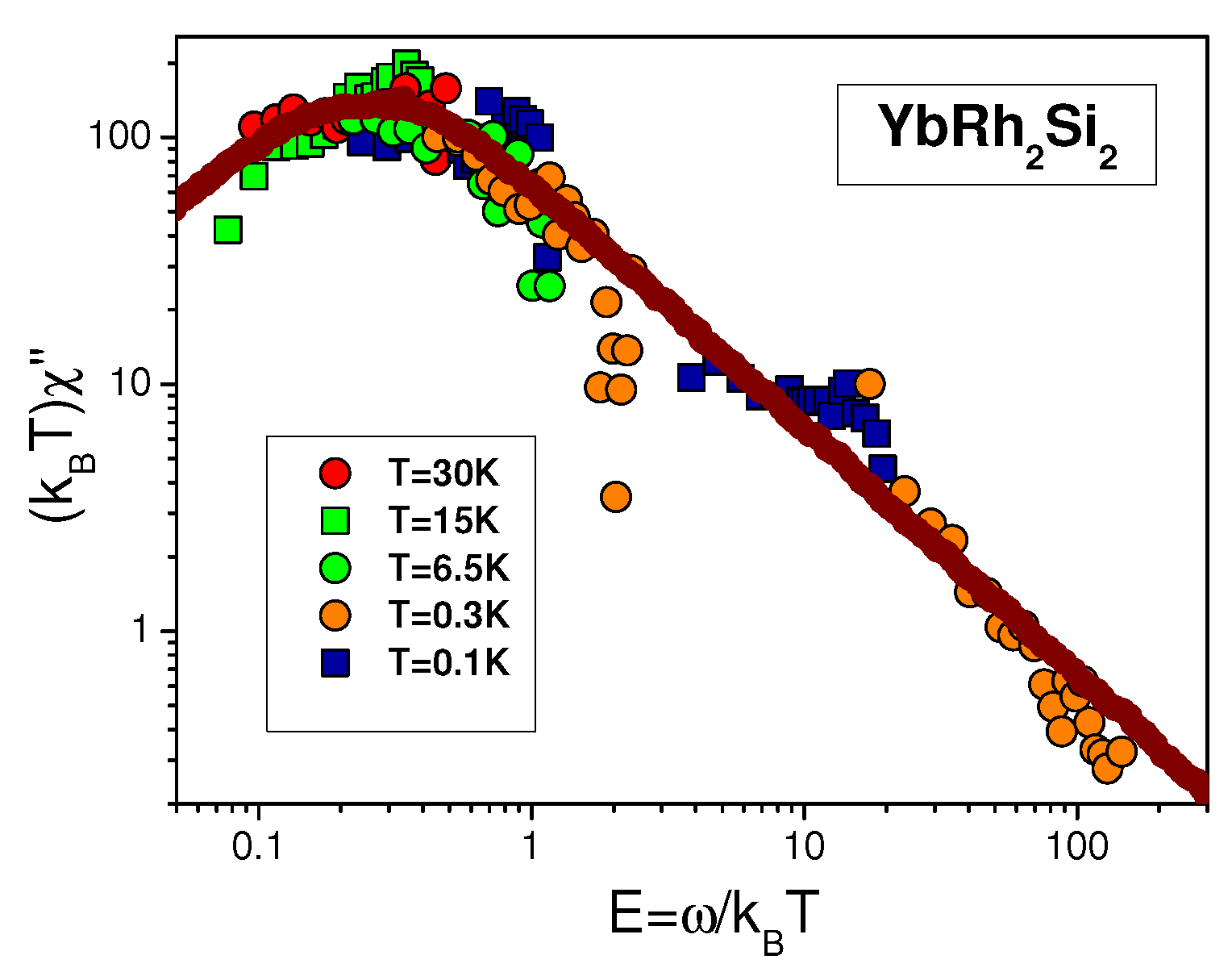
Figure 9 reports the function
extracted from neutron-scattering measurements on the HF metal
[
55]. The corresponding data collected on two systems,
[
3] and
[
56], are reported in
Figure 10 and
Figure 11. The figures show pretty good agreement between theoretical [
19] (solid curves) and experimental results on all considered chemical compounds over almost three decades in the scaled variable
. Hence
also has scaling properties. This shows that the spinons in both
and
demonstrate the same itinerant behavior as the conduction electrons in the heavy fermion compound
. The detection of the above itinerant behavior is very important as it convincingly shows the presence of a gapless SCQSL in herbertsmithite [
17,
19,
20].
Under the assumption that a fermion condensate (FC) is present in the above HF metals, the imaginary part
of the susceptibility reads [
16,
17]
where
, while
and
are adjustable parameters. Expression (
14) shows that
is a function of a single variable
. In this case, the expressions (
12) and (
14) define two types of scaling in
. The dynamic susceptibility
taken from inelastic neutron scattering measurements on the HF metal
[
57] is reported in
Figure 12. The scaling in
is clearly seen in both this function and variable
E. This confirms both the feasibility of Equation (
14) and the similarity of the HF metals and frustrated magnets properties. The scaled data acquired in measurements on such structurally different strongly correlated systems as
,
,
, and
merge in a single curve over almost three decades in the scaled variables, thus confirming that these strongly correlated Fermi systems exhibit universal scaling behavior and are symptomatic of the existence of a new state of matter [
17,
58]. This observation strengthens the credibility of the FC approach as it can reliably explain the experimental data concerned and has demonstrable predictive power [
17,
35,
58].
Indeed, it is apparent from
Figure 9,
Figure 10,
Figure 11 and
Figure 12 that the calculations within the FC approach are in conformity with th experimental results, providing strong evidence that SCQSL is the underlying mechanism defining the properties of
and
. We conclude that the spin gap apprehension is a rather artificial construction, which may contradict the acquired experimental knowledge about the
properties. The consistency of this description based on a FCQPT as the driving mechanism for the properties of herbertsmithite at low temperature can also be taken as strong evidence against the spin gap existence in this system. Note that the presence or absence of a spin gap is not that important as it does not define the physical properties of
. In particular, neither
nor
vanishes in the high magnetic fields, eliminating the contribution coming from the impurities (see
Figure 3,
Figure 4,
Figure 6, and
Figure 7). Moreover,
Figure 10 shows that such a gap does not contribute to the imaginary part of the magnetic susceptibility, which does not vanish at the lowest temperatures. Rather, all above physical properties are due to the SCQSL. This fact can be tested by magnetic field heat transport measurements similar to organic insulators
and
[
21,
59,
60]. Heat transport measurements are notably important as they probe the SCQSL excitations in
. They can also detect the itinerant spinons, which are the primary reason for heat transport. It is obvious that the above heat transport cannot do without phonons. On the other hand, the phonon contribution is barely affected by the magnetic field. To summarize, we anticipate that magnetic field dependence of heat transport measurements may be an important step forward to identify the SCQSL nature in
[
17,
20,
21].
Note that if we set the electronic charge to zero, the SCQSL in herbertsmithite becomes identically similar to the itinerant electrons ensemble in HF metals. In this case, the SCQSL thermal resistivity
w reads [
17,
20,
21]
where
comes from spinon–spinon scattering, which is similar to the contribution
from electron–electron scattering to charge transport. Here,
is the effective mass and
is the longitudinal magnetoresistivity (LMR), while
and
denote the residual thermal and electric resistivity, respectively.
Finally, we consider the magnetic field influence on the spin-lattice relaxation rate
.
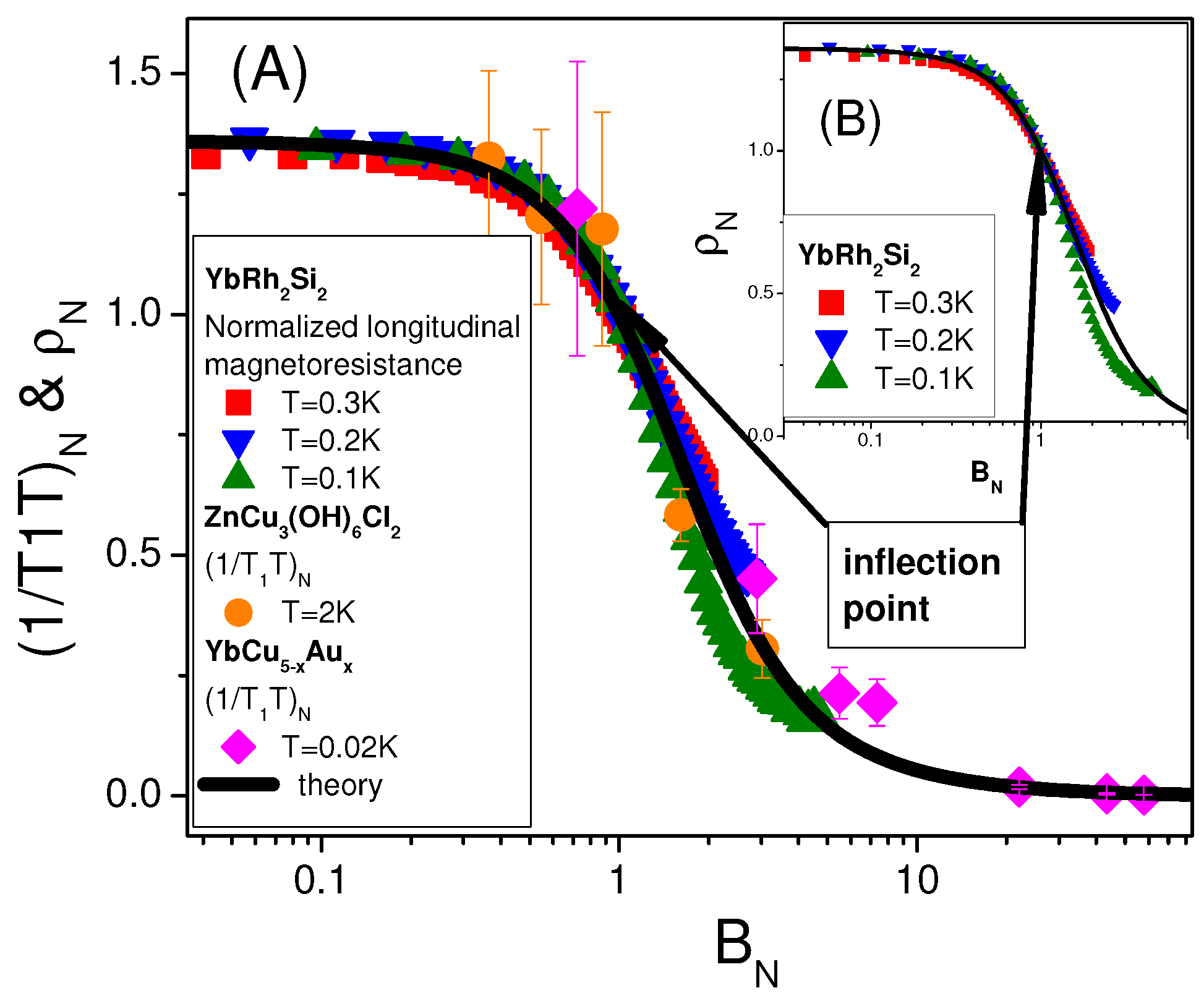
Figure 13A shows the normalized quantity
as a function of the magnetic field. It shows that with a magnetic field increase,
decays progressively. Contrary to the previous cases, where the normalization has been fulfilled in the point of maximum, here we normalize our curves in the inflection point,
, marked by the arrows in the main panel and inset. The same procedure has been performed with the normalized magnetoresistance shown in the inset to
Figure 13. The relation
shows that our system located near its QCP would exhibit similar behavior of
[
16,
17,
20,
21]. Significantly,
Figure 13A shows that the normalized spin-lattice relaxation rate of herbertsmithite [
61] and the HF metal
[
62] do exhibit the same behavior. As seen from
Figure 13A for
(or
), the quantity
is almost magnetic-field-independent. At the same time, at elevated magnetic fields it decays [
16,
17,
20,
21] according to
Thus, we hypothesize that magnetic field
B yields a crossover between NFL and LFL regimes. It also reduces substantially the relaxation rate as well as the thermal resistivity, similar to the case of the normalized LMR of
, (see
Figure 13B). Experimental data for the LMR is taken from [
63]. Also of high priority are measurements of low-energy inelastic neutron scattering on
crystalline samples under the application of a magnetic field, driving the system into the LFL sector of the phase diagram (see
Figure 2). The latter measurements permit direct observation of a possible gap, since in this case the impurity contribution is insignificant.
Recent neutron-scattering measurements on
reveal broad spin excitations covering a wide region of the Brillouin zone, thereby favoring the existence of a spinon Fermi surface [
64,
65]. At the same time, the measurements of heat transport do not show any substantial magnetic excitation contributions to thermal conductivity, thus raising doubt as to the presence of a QSL [
66]. We speculate that the observed behavior can be attributed to the emergence of a Mott insulator (see e.g., [
67]), placing the system beyond the FCQPT point in the phase diagram. At the same time, in the case of herbertsmithite, the transport and thermodynamic properties suggest that the gapless state represented by the SCQSL is situated before the FCQFT. We note that recent theoretical studies of possible gaps in the ground state of herbertsmithite lead to quite different conclusions about the presence of a gap [
18,
22,
68,
69,
70]. Recent experimental studies also indicate that the spin-liquid ground state in kagome lattice is gapless [
53], and that two distinct types of defects in herbertsmithite are found [
71]. This observation makes the impurity model vulnerable. Therefore, to probe QSL in herbertsmithite reliably, it is of crucial importance to carry out the experimental studies suggested above.
5. Charge Transport and Optical Conductivity
Our next step is the analysis of the herbertsmithite optical conductivity
at low frequencies. To avoid the contribution of phonon absorption to the conductivity, we consider low temperatures
T and frequencies
[
33]. Under such assumptions, we can neglect the lattice symmetry (kagome vs. triangular) as the wavelength is much larger than the typical crystal size. In atomic units
, the Hamiltonian of a particle having momentum
, spin
, and charge
e is given by
where
and
are the vector and scalar potentials, respectively. The nature of the vector potential
implies that
and
operators commute. Since for spinons,
, only the last term on the right-hand side of Equation (
17) contributes to
.
Equations (
5) and (
11) show that at small
, the imaginary part of the spin susceptibility reads [
19]
Observing that the energy transfer
[
36,
43] between magnetic field
and our system is due to the last term in Equation (
17), we obtain
The same quantity,
, coming from the electric field
, reads
Comparison of Equations (
19) and (
20) yields
It follows from Equation (
21) that
, and that behavior is consistent with experimental facts obtained in measurements on
and
, representing the best candidates for identification as materials that host QSL [
2,
33,
72]. We note that
(
18) at low
coincides Equation (
11) and provides a good description of the experimental data (see
Figure 9 and
Figure 10). Equations (
5) and (
21) inform us that at elevated temperatures,
is a decreasing function, which conforms with the experimental data [
33]. It also follows from Equations (
6) and (
21) that
is a decreasing function of
B. This observation seems to be contradictory as no systematic
B dependence is observed experimentally [
33].
To elucidate the
behavior, we note that corresponding experiments have been performed at
T = 3 K and
T [
33]. This means that the system is still in the transition region of the phase diagram and does not yet have the normal Fermi liquid properties, where the effective mass
is given by Equation (
6). In this case, the effective mass properties is due to Equation (
5), rather than Equation (
6). This means that the dependence
cannot be observed. Accordingly, we think that substantial
dependence can be observed at
T in the case of
K. In that case, as one sees from
Figure 6, the effective mass
is a diminishing function of the applied magnetic field. Thus, we predict that
diminishes with growing magnetic fields, as follows from Equations (
6) and (
21). Since the contribution coming from phonons does not depend on the magnetic field, we propose that measurements of the variation
, i.e.,
, can reveal both the physics of SCQSL and the ground state of
, as well as the ground state of other materials hosting a QSL. The above experiments on measurements of the heat transport and optical conductivity can be carried out on samples with varying
x. Such experiments yield information on the influence of impurities on the value of the gap. We predict that at moderate
%, the SCQSL remains robust, for both inhomogeneity and randomness facilitate frustration.