Glucose Oxidase Micropumps: Multi-Faceted Effects of Chemical Activity on Tracer Particles Near the Solid–Liquid Interface
Abstract
1. Introduction
2. Results
2.1. GOX Micropumps
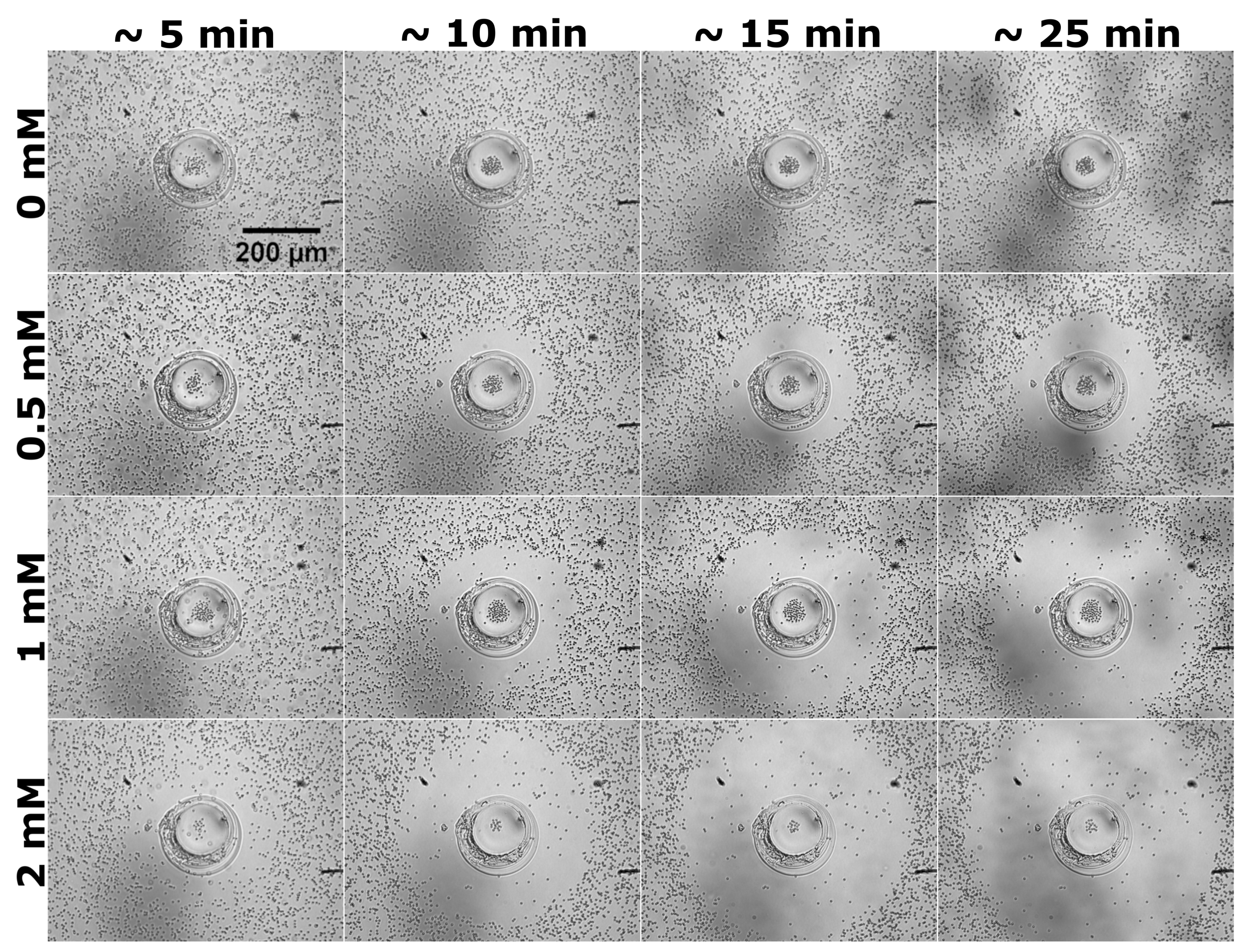
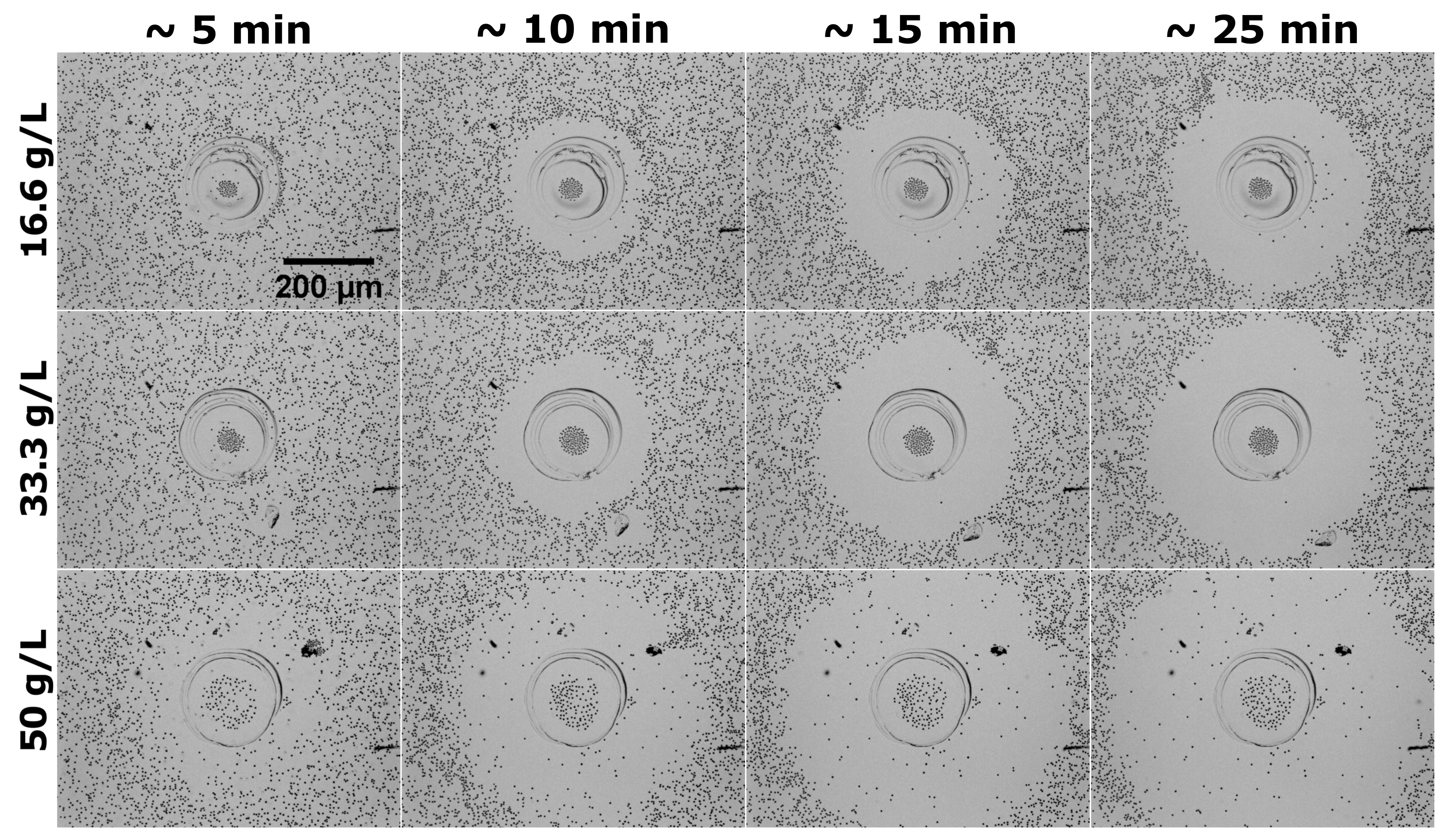
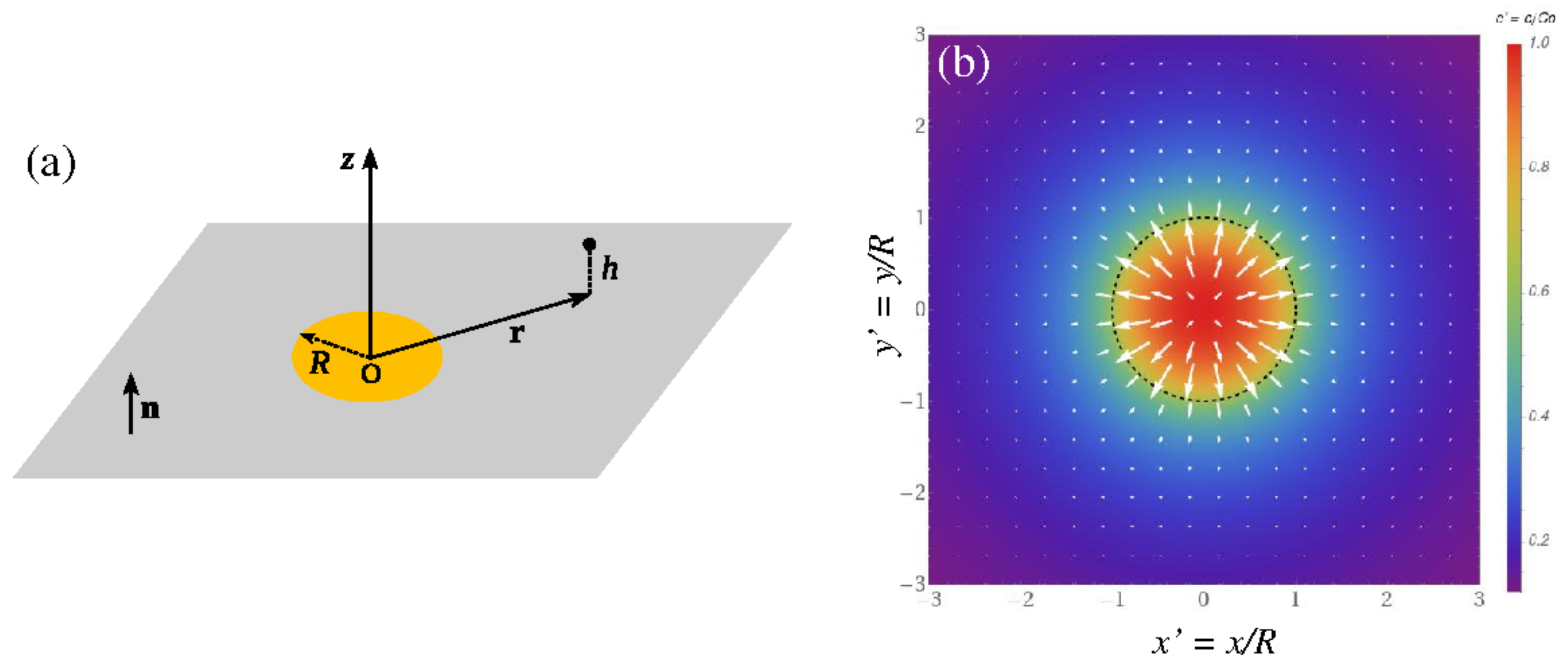
2.2. Behavior of Tracer Particles Dispersed around GOX Micropumps
- (i)
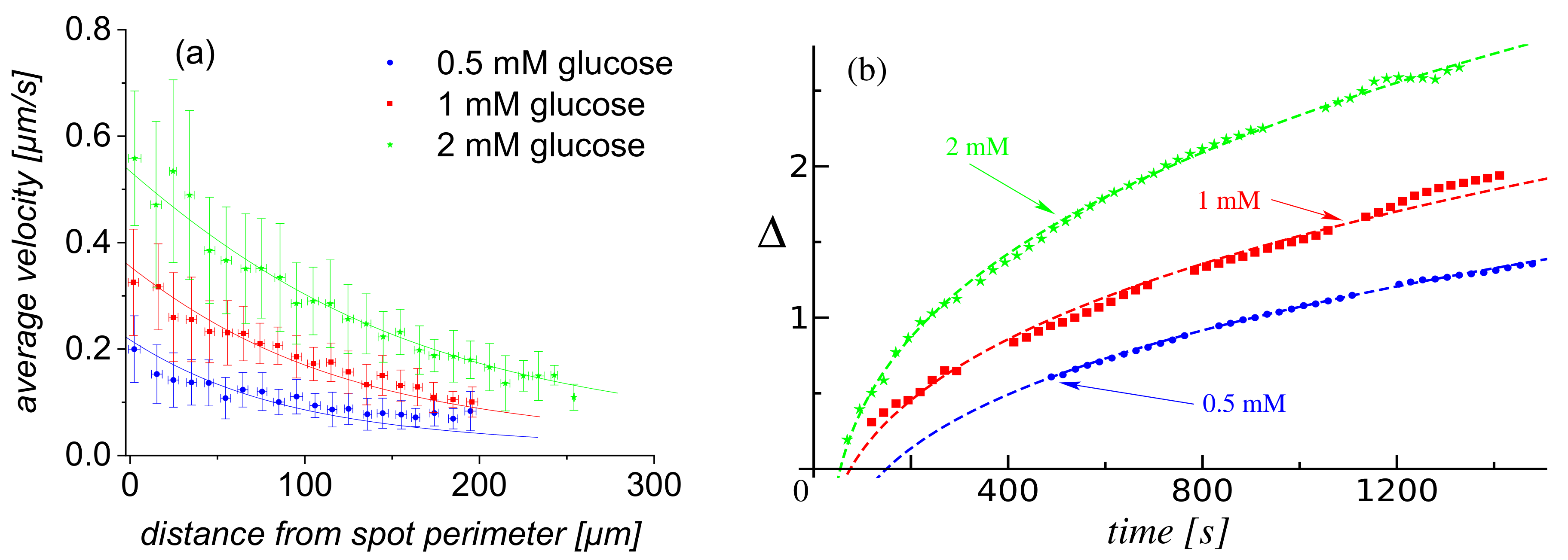
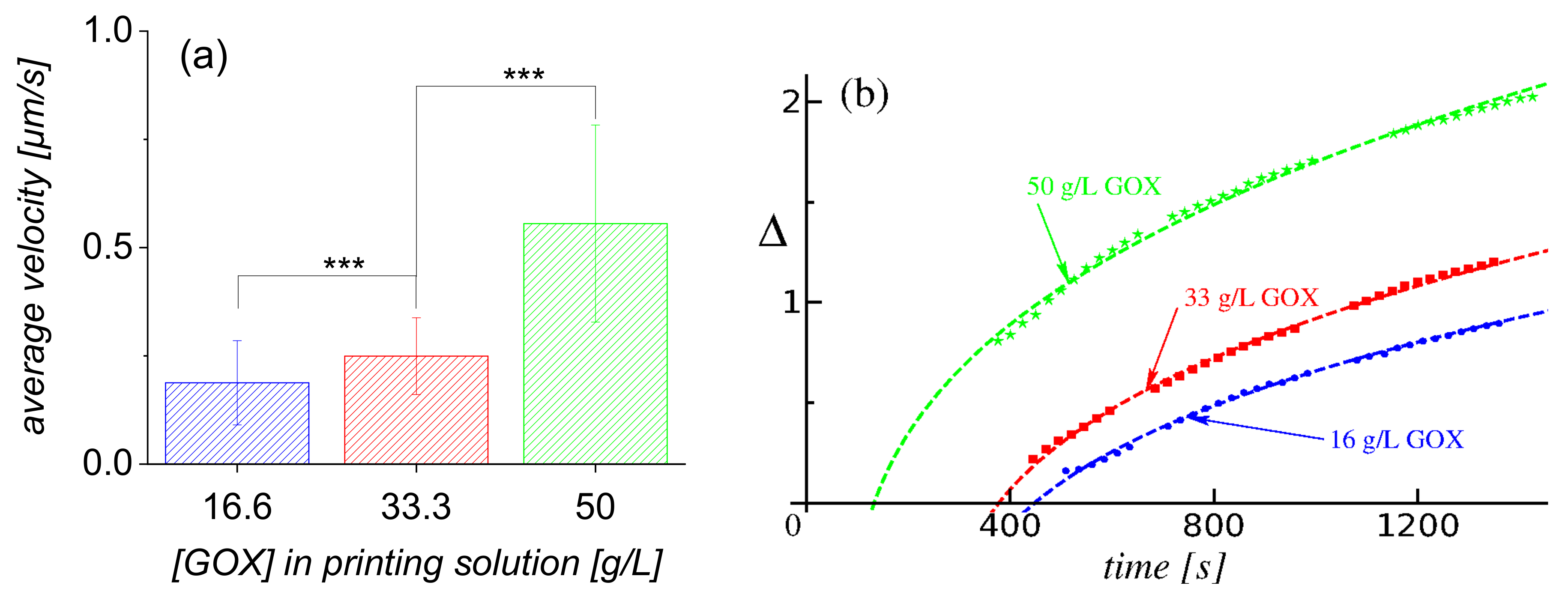
- First, by tracking individual particles (see Video S2 in the Supplementary Materials), one can extract from the video recordings a set of in-plane trajectories. While it was not possible to extract well defined instantaneous speeds along the trajectory, because of their small magnitude (see Figure 2a), the average radial velocity of motion over a distance significantly larger than the size of the tracer turned out to be less susceptible to thermal fluctuations and image resolution effects. Accordingly, we evaluated such average velocities V over trajectories starting at (to ensure that a stable steady-state regime of the enzyme pump was established; see also the results and discussion in Figure 2b) and followed up to , as a function of the initial position of the tracer, i.e., its distance d from the edge of the patch (or, equivalently, the distance from the center of the patch). In Figure 2a, we show the result of such analysis combining more than 1900 independent trajectories, starting from various locations around the patch, from nine independent experiments (three pumps, each exposed to three glucose concentrations). It is seen that the radial motion of the tracers was associated with an average velocity V, as defined above, which monotonously decreased with the distance d from the edge of the active enzyme patch from where the tracer started. These variations were noticeable for initial locations d of the order of 2–3 times the radius of the enzyme patch (i.e., up to around ). The dependence at different concentrations of substrate seemed to be similar, up to an overall magnitude factor dependent on (and increasing with) the substrate concentration. By visual inspection (particularly the tails region), one can infer that this factor is somewhat different from just a proportionality with the glucose concentration.
- (ii)
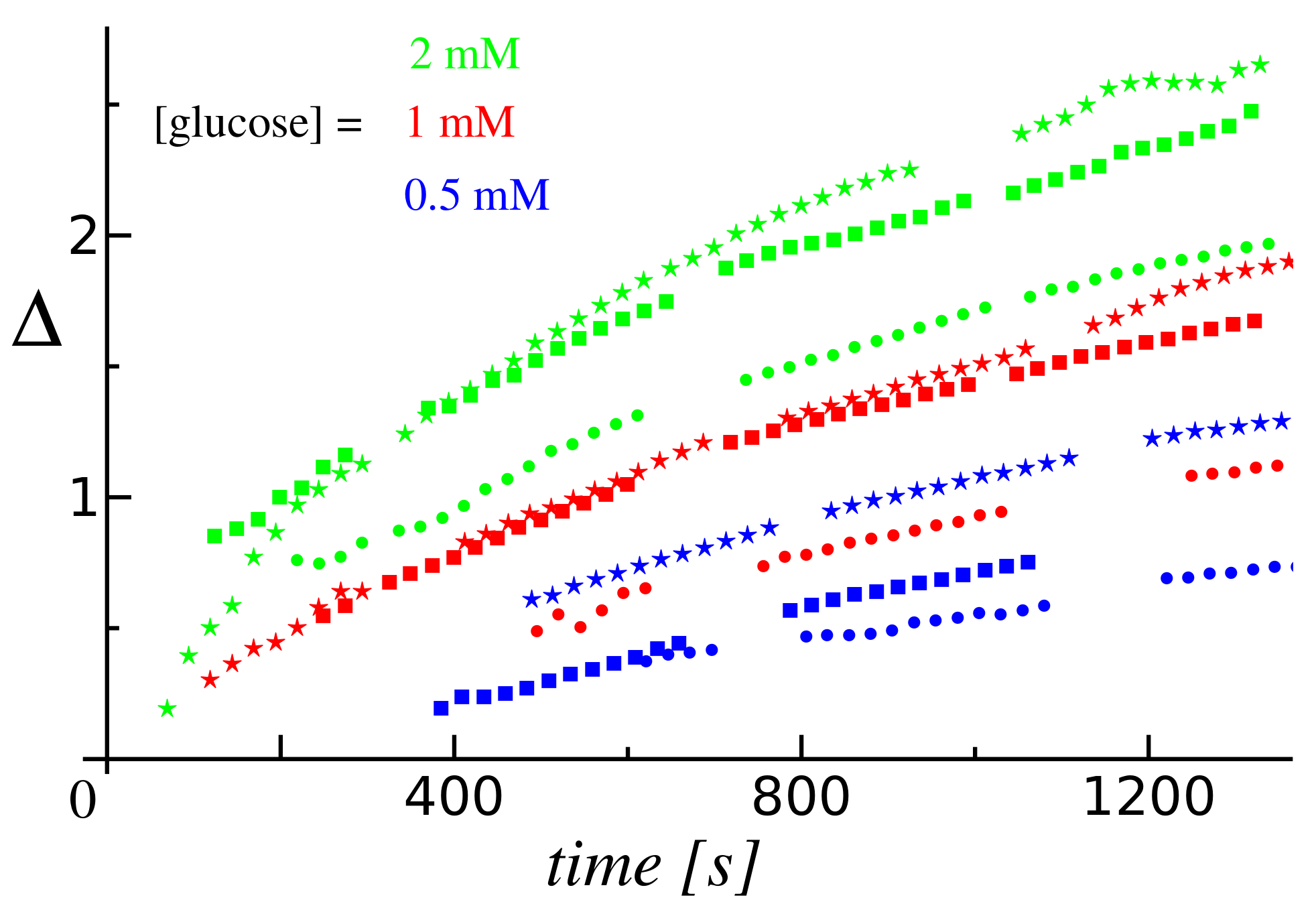
- Second, the extent of the depletion zone, the outer edge of which was defined via the in-plane radial distribution of particles as the radius at the transition between the low and high density regions, could be determined from the video recordings via image analysis (for details, see Section 4.4). We note that the rate of change of is given by the radial velocity of a tracer located at (under the assumption of a dilute monolayer). Therefore, the time-dependent behavior of the depletion zone, as well as its dependence on the concentration of substrate in solution, are correlated with the dependencies of the average velocity V of the tracers on the initial location d of the tracer and on the glucose concentration. A set of results of this analysis, in terms of the time dependence of the extent of the depletion zone for three distinct glucose concentrations, is shown in Figure 2b, and the comprehensive list of these results (i.e., from all the three experiments) in Section 4.4. (Note that only the results where the image analysis led to robust fitting (see Section 4.4) are shown, thus the depletion zone data start from non-vanishing values.) As expected, the extent of the depletion zone grows faster when the glucose concentration is larger. As in the case of the dependence of the average velocity (defined above) of the tracers, the increase in the rate of growth of the depletion zone was somewhat different from just a proportionality with the glucose concentration. There was a certain time-lag, which depended on the glucose concentration, between the start of the experiment and the emergence of the depletion zone. The value of the lag-time was, in general, less than the time needed for the complete sedimentation of the tracers (we remind that here corresponds to the start of the recording, which was 2–3 min after the addition of the solution containing glucose and the particles), and it decreased upon increasing the glucose concentration (i.e., the activity of the pump). These observations suggest that the lag relates to a transient regime of the enzyme pump, before the steady-state operation is fully developed.
3. Discussion
4. Materials and Methods
4.1. Materials
4.2. Fabrication of Enzyme Micropumps
4.3. Investigation of the Behavior of the Tracers in the Vicinity of the Active Enzyme Patch
4.4. Determination of the Extent of the Depletion Zone via Image Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| GOX | glucose oxidase |
| BSA | bovine serum albumine |
| APTES | 3-aminopropyltriethoxysilane |
Appendix A. Spatially-Dependent Number Densities of Reaction Product(s)
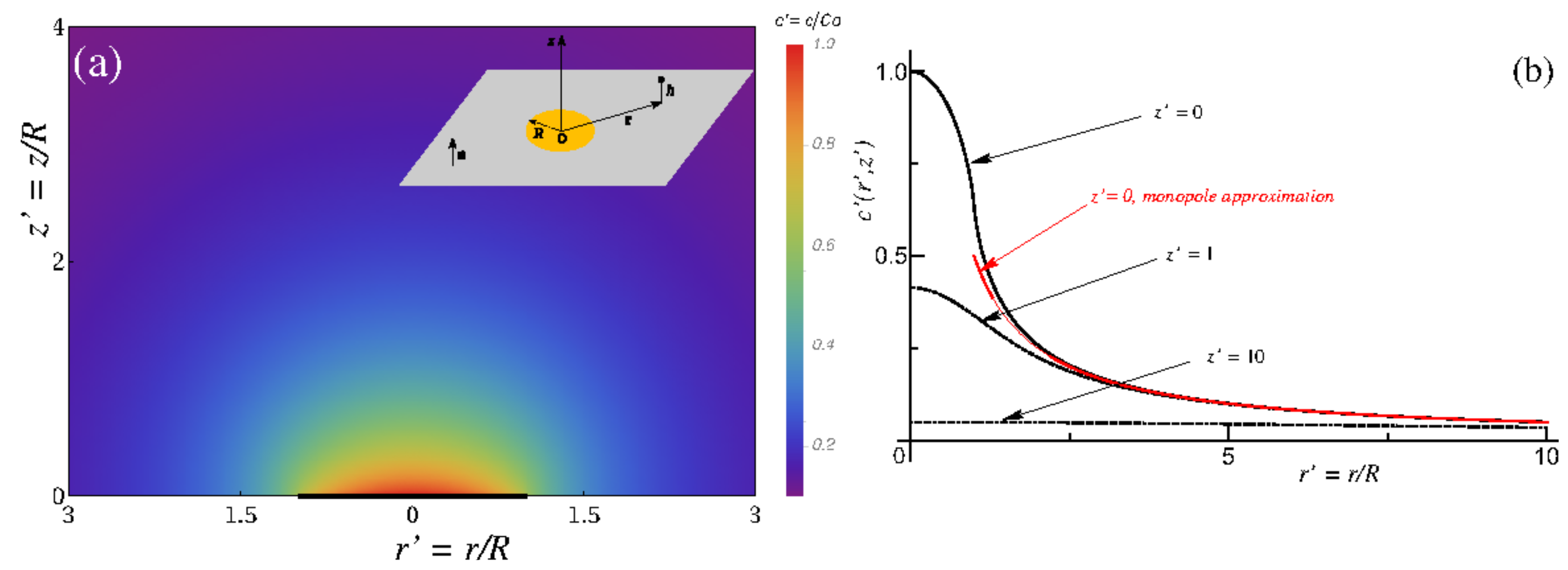
References
- Hartmeier, W. Immobilized Biocatalysts: An Introduction; Springer: New York, NY, USA, 1988. [Google Scholar]
- Sengupta, S.; Patra, D.; Ortiz-Rivera, I.; Agrawal, A.; Shklyaev, S.; Dey, K.K.; Córdova-Figueroa, U.; Mallouk, T.E.; Sen, A. Self-powered enzyme micropumps. Nat. Chem. 2014, 6, 415. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Shklyaev, O.E.; Altemose, A.; Shum, H.; Ortiz-Rivera, I.; Valdez, L.; Mallouk, T.E.; Balazs, A.C.; Sen, A. Harnessing catalytic pumps for directional delivery of microparticles in microchambers. Nat. Commun. 2017, 8, 14384. [Google Scholar] [CrossRef] [PubMed]
- Alarcón-Correa, M.; Günther, J.P.; Troll, J.; Kadiri, V.M.; Bill, J.; Fischer, P.; Rothenstein, D. Self-assembled phage-based colloids for high localized enzymatic activity. ACS Nano 2019, 13, 5810. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Tsitkov, S.; Hess, H. Complex dynamics in a two-enzyme reaction network with substrate competition. Nat. Catal. 2018, 1, 276. [Google Scholar] [CrossRef]
- Ortiz-Rivera, I.; Courtney, T.M.; Sen, A. Enzyme micropump-based inhibitor assays. Adv. Funct. Mater. 2016, 26, 2135. [Google Scholar] [CrossRef]
- Zhao, X.; Gentile, K.; Mohajerani, F.; Sen, A. Powering motion with enzymes. Acc. Chem. Res. 2018, 51, 2373. [Google Scholar] [CrossRef] [PubMed]
- Maiti, S.; Shklyaev, O.E.; Balazs, A.C.; Sen, A. Self-organization of fluids in a multienzymatic pump system. Langmuir 2019, 35, 3724. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, S.; Spiering, M.M.; Dey, K.K.; Duan, W.; Patra, D.; Butler, P.J.; Astumian, R.D.; Benkovic, S.J.; Sen, A. DNA polymerase as a molecular motor and pump. ACS Nano 2014, 8, 2410. [Google Scholar] [CrossRef]
- Valdez, L.; Shum, H.; Ortiz-Rivera, I.; Balazs, A.C.; Sen, A. Solutal and thermal buoyancy effects in self-powered phosphatase micropumps. Soft Matter 2017, 13, 2800. [Google Scholar] [CrossRef]
- Ortiz-Rivera, I.; Shum, H.; Agrawal, A.; Sen, A.; Balazs, A.C. Convective flow reversal in self-powered enzyme micropumps. Proc. Natl. Acad. Sci. USA 2016, 113, 2585. [Google Scholar] [CrossRef]
- Kline, T.R.; Paxton, W.F.; Wang, Y.; Velegol, D.; Mallouk, T.E.; Sen, A. Catalytic micropumps: Microscopic convective fluid flow and pattern formation. J. Am. Chem. Soc. 2005, 127, 17150. [Google Scholar] [CrossRef] [PubMed]
- Farniya, A.A.; Esplandiu, M.J.; Reguera, D.; Bachtold, A. Imaging the proton concentration and mapping the spatial distribution of the electric field of catalytic micropumps. Phys. Rev. Lett. 2013, 111, 168301. [Google Scholar] [CrossRef] [PubMed]
- Esplandiu, M.J.; Zhang, K.; Fraxedas, J.; Sepulveda, B.; Reguera, D. Unraveling the operational mechanisms of chemically propelled motors with micropumps. Acc. Chem. Res. 2018, 51, 1921. [Google Scholar] [CrossRef] [PubMed]
- Niu, R.; Kreissl, P.; Brown, A.T.; Rempfer, G.; Botin, D.; Holm, C.; Palberg, T.; de Graaf, J. Microfluidic pumping by micromolar salt concentrations. Soft Matter 2017, 13, 1505. [Google Scholar] [CrossRef] [PubMed]
- Niu, R.; Oğuz, E.C.; Müller, H.; Reinmüller, A.; Botin, D.; Löwen, H.; Palberg, T. Controlled assembly of single colloidal crystals using electro-osmotic micro-pumps. Phys. Chem. Chem. Phys. 2017, 19, 3104. [Google Scholar] [CrossRef] [PubMed]
- Wilson, R.; Turner, A.P.F. Glucose oxidase: an ideal enzyme. Biosens. Bioelectron. 1992, 7, 165. [Google Scholar] [CrossRef]
- Pons, A.J.; Sagués, F.; Bees, M.A.; Sørensen, P.G. Pattern formation in the methylene-blue-glucose system. J. Phys. Chem. B 2000, 104, 2251. [Google Scholar] [CrossRef]
- Pons, A.J.; Sagués, F.; Bees, M.A.; Sørensen, P.G. Quantitative analysis of chemoconvection patterns in the methylene-blue-glucose system. J. Phys. Chem. B 2002, 106, 7252. [Google Scholar] [CrossRef]
- Purcell, E. Life at low Reynolds number. Am. J. Phys. 1977, 45, 3. [Google Scholar] [CrossRef]
- Lauga, E.; Powers, T.R. The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 2009, 72, 096601. [Google Scholar] [CrossRef]
- Derjaguin, B.; Sidorenkov, G.; Zubashchenkov, E.; Kiseleva, E. Kinetic phenomena in boundary films of liquids. Kolloidn. Zh. 1947, 9, 335. [Google Scholar]
- Anderson, J. Colloid transport by interfacial forces. Ann. Rev. Fluid Mech. 1989, 21, 61. [Google Scholar] [CrossRef]
- Keh, H.J.; Anderson, J.L. Boundary effects on electrophoretic motion of colloidal spheres. J. Fluid Mech. 1985, 153, 417. [Google Scholar] [CrossRef]
- Keh, H.J.; Chen, S.B. Electrophoresis of a colloidal sphere parallel to a dielectric plane. J. Fluid Mech. 1988, 194, 377. [Google Scholar] [CrossRef]
- Merkel, T.C.; Bondar, V.I.; Nagai, K.; Freeman, B.D.; Pinnau, I. Gas sorption, diffusion, and permeation in poly(dimethylsiloxane). J. Polymer Sci. B 2000, 38, 415. [Google Scholar] [CrossRef]
- Markov, D.A.; Lillie, E.M.; Garbett, S.P.; McCawley, L.J. Variation in diffusion of gases through PDMS due to plasma surface treatment and storage conditions. Biomed. Microdev. 2014, 16, 91. [Google Scholar] [CrossRef] [PubMed]
- de Chaumont, F.; Dallongeville, S.; Chenouard, N.; Hervé, N.; Pop, S.; Provoost, T.; Meas-Yedid, V.; Pankajakshan, P.; Lecomte, T.; Le Montagner, Y. Icy: An open bioimage informatics platform for extended reproducible research. Nat. Methods 2012, 9, 690. [Google Scholar] [CrossRef]
- Golestanian, R.; Liverpool, T.B.; Ajdari, A. Designing phoretic micro- and nano-swimmers. New J. Phys. 2007, 9, 126. [Google Scholar] [CrossRef]
- Oshanin, G.; Popescu, M.N.; Dietrich, S. Active colloids in the context of chemical kinetics. J. Phys. A 2017, 50, 134001. [Google Scholar] [CrossRef]
- Kapral, R. Nanomotors without moving parts that propel themselves in solution. J. Chem. Phys. 2013, 138, 202901. [Google Scholar] [CrossRef]
- Domínguez, A.; Malgaretti, P.; Popescu, M.N.; Dietrich, S. Effective interaction between active colloids and fluid interfaces induced by Marangoni flows. Phys. Rev. Lett. 2016, 116, 078301. [Google Scholar] [CrossRef] [PubMed]
- Moran, J.L.; Posner, J.D. Phoretic self-propulsion. Ann. Rev. Fluid Mech. 2016, 49, 511. [Google Scholar] [CrossRef]
- Sneddon, I. Mixed Boundary Value Problems in Potential Theory; North-Holland: Amsterdam, The Netherlands, 1966. [Google Scholar]
| Enzyme | Dimensions | Tracer Particle | Flow (Close to Bottom Wall) | Location of Observations | Proposed Mechanism for Mass Density Variations | Ref. |
|---|---|---|---|---|---|---|
| Catalase, Lipase, Glucose oxidase | 6 mm diameter disk (in a 20 mm diameter × 1.3 mm height cell) | 2 m diameter, negatively charged polystyrene | Inward (towards the enzyme patch) | 50–100 m away from the pump, height: N/A | Exothermic reaction or solutal buoyancy | [2] |
| Urease | 6 mm diameter disk (in a 20 mm diameter × 1.3 mm height cell) | 2 m diameter, negatively charged polystyrene | Outward (away from the enzyme patch) | 50–100 m away from the pump, height: N/A | Solutal buoyancy | [2] |
| DNA polymerase | 6 mm diameter disk (in a 20 mm diameter × 1.3 mm height cell) | 2 m diameter, negatively charged polystyrene | Inward (towards the enzyme patch) | N/A | Solutal buoyancy | [9] |
| Urease, Catalase | 6 mm diameter disk (in a 20 mm diameter × 1.3 mm height cell) | 2 m diameter, negatively charged polystyrene | N/A | N/A | N/A | [6] |
| Urease | 6 mm diameter disk (in a 20 mm diameter × 1.3 mm height cell) | 2 m diameter, negatively charged polystyrene | Temporal and spatial dependent, flow reversal (outward ↔ inward) | 50 m away from the pump, height: N/A | Solutal buoyancy | [11] |
| Urease | 15 mm × 15 mm (in a 20 mm × 20 mm × 1.3 mm cell) | 2 m diameter, negatively charged, fluorescent polystyrene | N/A (external substrate gradient) | 50 m and 500 m above the enzyme-modified surface | Solutal buoyancy | [3] |
| Acid phosphatase | 6 mm diameter disk (in a 20 mm diameter × 1.3 mm height cell) | 2 m diameter, negatively charged polystyrene | Inward (towards the enzyme patch) | 0–5 mm away from the pump, height: N/A | Solutal buoyancy | [10] |
| Urease | 1 mm × 1 mm (in a 10 mm × 10 mm × 0.7 mm cell) | 1 m diameter, plain polystyrene | Outward (away from the enzyme patch) | near the edge of the patch, heights 150 m and 550 m | Solutal buoyancy | [4] |
| Glucose oxidase, Catalase, Acid phosphatase | 5 mm diameter disk (in a 20 mm diameter × 0.9 mm height cell); patch located near the lateral wall | 2 m diameter, negatively charged polystyrene | Inward (towards the enzyme patch) | 1–6 mm away from the enzyme structure, height: 200 m | Solutal buoyancy | [8] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Munteanu, R.-E.; Popescu, M.N.; Gáspár, S. Glucose Oxidase Micropumps: Multi-Faceted Effects of Chemical Activity on Tracer Particles Near the Solid–Liquid Interface. Condens. Matter 2019, 4, 73. https://doi.org/10.3390/condmat4030073
Munteanu R-E, Popescu MN, Gáspár S. Glucose Oxidase Micropumps: Multi-Faceted Effects of Chemical Activity on Tracer Particles Near the Solid–Liquid Interface. Condensed Matter. 2019; 4(3):73. https://doi.org/10.3390/condmat4030073
Chicago/Turabian StyleMunteanu, Raluca-Elena, Mihail N. Popescu, and Szilveszter Gáspár. 2019. "Glucose Oxidase Micropumps: Multi-Faceted Effects of Chemical Activity on Tracer Particles Near the Solid–Liquid Interface" Condensed Matter 4, no. 3: 73. https://doi.org/10.3390/condmat4030073
APA StyleMunteanu, R.-E., Popescu, M. N., & Gáspár, S. (2019). Glucose Oxidase Micropumps: Multi-Faceted Effects of Chemical Activity on Tracer Particles Near the Solid–Liquid Interface. Condensed Matter, 4(3), 73. https://doi.org/10.3390/condmat4030073






