A Field-Theoretical Approach to the P vs. NP Problem via the Phase Sign of Quantum Monte Carlo

Abstract

I present here a new method that allows the introduction of a discrete auxiliary symmetry in a theory in such a way that the eigenvalue spectrum of the fermion functional determinant is made up of complex conjugated pairs. The method implies a particular way of introducing and integrating over auxiliary fields related to a set of artificial shift symmetries. Gauge fixing the artificial continuous shift symmetries in the direct and dual sectors leads to the appearance of direct and dual Becchi–Rouet–Stora–Tyutin (BRST)-type global symmetries and of a symplectic structure over the field space. Such a method may allow the extension of the applicability of quantum Monte Carlo methods to some problems plagued by the fermionic sign problem.

1. Introduction

The P vs. $NP$ problem is known to have significant implications in many areas of science, including physics, mathematics, and information theory [1]. The main question is as to whether some specific classes of problems can be efficiently treated via algorithmic methods. In this paper I present a constructive approach to this problem based essentially on some topological and geometrical arguments. While researchers speculate about this question [2] and give several interpretations of possible results, there have been very few attempts to analyze the problem from perspectives other than purely algorithmic. As shown in [3] the quantum Monte Carlo phase sign problem can be mapped into a general $NP$-complete problem. I will follow this paper for a short introduction into the statistical aspects of the subject. The idea behind Monte Carlo simulations is to replace the direct calculation of sums of the form

$$\begin{array}{cc}<A>=\frac{1}{Z}\sum _{c\in \mathsf{\Omega }}A\left(c\right)p\left(c\right);\hfill & Z=\sum _{c\in \mathsf{\Omega }}p\left(c\right)\hfill \end{array}$$

(1)

over a high-dimensional space $\mathsf{\Omega }$ of configurations $\left\{c\right\}$ with the sum over a set of M configurations $\left\{c_i\right\}$ from $\mathsf{\Omega }$ according to the distribution $p\left(c_i\right)$. The average is then calculated as

$$<A>\approx \overline{A}=\frac{1}{M}\sum _{i=1}^{M}A\left(c_i\right)$$

(2)

The statistical error of the above calculation is given by

$$\mathsf{\Delta }A=\sqrt{Va{r}_A(2{\tau }_A+1)/M}$$

(3)

$Va{r}_A$ being the variance of A and ${\tau }_A$ measuring the autocorrelations of the sequence $\left\{A\left(c_i\right)\right\}$.

The Monte Carlo approach permits the evaluation of the same average in polynomial time, as long as ${\tau }_A$ does not increase faster than polynomial in the number of particles. For physical systems the sum one needs to calculate changes as follows

$$\begin{array}{cc}<A>=\frac{1}{Z}Tr[Aexp(-\beta H)];\hfill & Z=Tr\left(exp\right(-\beta H\left)\right)\hfill \end{array}$$

(4)

where $\beta$ is the inverse temperature and Z is the partition function. A Monte Carlo technique can still be applied to reduce the exponential scaling of the problem, but, as specified in [3], only after the mapping of the quantum model on a classical one. The nature of this mapping was considered by [3], and then [4], to be a Taylor expansion.

$$Z=Tr\left(exp(-\beta H)\right)=\sum _{n=0}^{\infty }\frac{{-\beta }^n}{n!}Tr\left(H^n\right)$$

(5)

$$=\sum _{n=0}^{\infty }\sum _{i_1,\dots i_n}\frac{{-\beta }^n}{n!}<i_1\left|H\right|i_2>\dots <i_n\left|H\right|i_1>$$

(6)

$$=\sum _{n=0}^{\infty }\sum _{i_1,\dots i_n}p(i_1,\dots i_n)=\sum _{c}p\left(c\right)$$

(7)

For each order n in the expansion, n sums were inserted over a complete basis set of states $\left\{\right|i>\}$. The configurations are sequences of n basis states, and the weight $p\left(c\right)$ is associated to the summand above. The average now becomes

$$<A>=\frac{1}{Z}Tr[Aexp(-\beta H)]=\frac{1}{Z}\sum _{c}A\left(c\right)p\left(c\right)$$

(8)

As long as the weight p is positive, a standard Monte Carlo technique can be applied. In fermionic systems this is not true as negative weights are possible. It is argued in [3] that although a change of the basis $\left\{\right|i>\}$ that makes the weights always positive is possible, the complexity of the method needed to find the required transformation must be exponential. Also, the authors of [3] map the sign problem into a problem that is $NP$-complete. This is of course correct if one follows the above steps. The main scope of this paper is to suggest that some assumptions in [3] can be avoided when considering a different quantization prescription and that a system can be mapped into an $NP$-complete problem but still have a polynomial solution if analyzed from the perspective of the quantization of gauge theories. Similar arguments in favor of the P = $NP$ conjecture in the context of quantum field theories have been discussed by [5] and [6]. The issue remains unsolved, and this paper makes no claim towards one side or the other. However, it is interesting to analyze the problem not only via quantum field theories as done in [5,6] but also in terms of gauge field theories. This attempt is made here. A gauge symmetry can be seen as a redundancy of the mathematical formulation. As shown by Batalin and Vilkovisky in [7], if one is willing to lose the explicit visibility of some properties, one can reduce the gauge symmetry and transform a gauge theory into a non-gauge one. In this paper, I will follow the opposite path. I construct a theory that has artificial gauge symmetries introduced in such a way that a discrete symmetry to be associated with an artificial “time reversal” invariance appears. Following [8] the presence of such a symmetry in a theory permits the avoidance of the sign problem. This construction is done by using the field–antifield [9,10] quantization of gauge theories with general algebras.

I partially follow the description by Alfaro and Damgaard [11,12] in order to show the effect of the quantization of a field theory with fermions, how the change in sign appears, and how one can relate classical and quantum descriptions in a different way. I also make the connection between geometry (symmetry) and topology (cohomology) by introducing the Becchi–Rouet–Stora–Tyutin (BRST), anti-BRST, and dual-(anti)BRST [13] operators associated to the de-Rham cohomology. I define and use the Hodge star operation [14,15] in this context in order to generate a discrete symmetry. I make use of the intrinsic symplectic structure of the general field-anti-field functional space in order to generate a Kahler structure ([16,17]). I also use the fact that the extension of the field space towards an even- dimensional space is always possible. The end result is a general quantum field theory free of the Monte Carlo sign problem and with no apparent exponential growth in complexity.

2. Mathematical Background

2.1. Hodge Star and Hodge Duality

Let $(M,g)$ be a $N=2d$-dimensional manifold, for which we can define the ∗ operator in the following way [18]:

$$\begin{array}{cc}\alpha \wedge \ast \beta =g_p(\alpha ,\beta )d{v}_g;\hfill & \alpha ,\beta \in {\wedge }^N\hfill \end{array}$$

(9)

We have also that $(\ast \ast )=1$ on ${\wedge }^N$, which means that ${\wedge }^N$ splits into eigenspaces as

$${\wedge }^N={\wedge }_{+}+{\wedge }_{-}$$

(10)

where the two eigenspaces correspond to eigenvalues $+1$ and $-1$, respectively. A d-form which belongs to ${\wedge }_{+}$ is called self-dual whereas if it belongs to the other eigenspace it is called anti-self-dual. An important remark to be done here is that given a p-vector $\lambda \in {\wedge }^{p}V$ then $\forall \theta \in {\wedge }^{d-p}V$ there exists a wedge product such that $\lambda \wedge \theta \in {\wedge }^d$. The (anti)BRST and dual-(anti)BRST operators are then equivalent to the operators:

$${\delta }_a,{\delta }_b:{\wedge }^k\to {\wedge }^{k+1}$$

(11)

$$\delta ,\overline{\delta }=\ast {\delta }_{a,b}\ast :{\wedge }^k\to {\wedge }^{k-1}$$

(12)

$$\mathsf{\Delta }={\delta }_{a,b}(\ast {\delta }_{a,b}\ast )+(\ast {\delta }_{a,b}\ast ){\delta }_{a,b}:{\wedge }^k\to {\wedge }^k$$

(13)

In the context of algebraic geometry these are ordered as follows: the exterior differential, the coexterior (dual) differential, and the Laplace operator. The exact and co-exact forms are orthogonal. The Hodge theorem allows the identification of a unique representative for each cohomology class as belonging to the kernel of the Laplacian defined for the specific complex manifold. If this is put together with the definition of the Kahler manifold, we obtain extra (discrete) symmetries in the Hodge structure of the manifold. In the main paper, the dual operators acting on the field space have been introduced in a general context. For a practical description in the context of field-spaces, see [19]. There, the author starts from a field theory with physical terms and identifies the discrete symmetry as the one induced by the Hodge-∗ operator in the physical context. In the current approach, the BV (Batalin–Vilkovisky) formalism generates the usual even-dimensional symplectic space. Dualization of the BRST–anti-BRST operators in this work is done using the extended symplectic field structure. One is not supposed to assume physicality of the terms involved.

2.2. Internal Spaces and Duality

The use of internal spaces in order to naturally define duality operations is not new. In fact I here follow [20] to show that the construction of an internal space is useful in this context and that a discrete ${\mathsf{Z}}_2$ symmetry can appear. I start by following [20] with an example of even-dimensional $\left(2n\right)$ electrodynamics. Let A be a general $(n-1)$ form and $F_{k_1\dots k_n}$ its associated field strength:

$$F_{k_1\dots k_n}={\partial }_{[k_n}{A}_{k_1\dots k_{n-1}]}$$

(14)

$$\ast F^{k_1\dots k_n}=\frac{1}{n!}{ϵ}^{k_1\dots k_{2n}}{F}_{k_{n+1}\dots k_{2n}}$$

(15)

Given the action, the equation of motion, and the Bianchi identity as

$$S=-c_n\int d^{2n}x{F}_{k_1\dots k_n}{F}^{k_1\dots k_n}$$

(16)

$${\partial }_{k_1}{F}^{k_1\dots k_n}=0$$

(17)

$${\partial }_{k_1}\ast F^{k_1\dots k_n}=0$$

(18)

respectively, ($c_n$ is a constant, $k_j$ is the tensorial index) we can see that at the level of the Bianchi identity and the equation of motion the dual operation is a symmetry. Nevertheless, in general the second power of the dual operation has a different structure depending on the dimension of the space:

$$\ast \ast F=\left\{\begin{array}{ccc}\hfill F& if& D=4k-2\hfill \\ \hfill -F& if& D=4k\hfill \end{array}\right.$$

(19)

As one can see, the dual ∗ is not well defined for the two-dimensional $\left(2D\right)$ scalar or for the $4k-2$ dimensional extensions. Its definition has been enlarged [20] by making an internal structure of the potentials in the theory manifest. One should note that this has been achieved by using a canonical transformation and that the same can be achieved via BRST. I will enlarge the set of fields (alternatively the Hilbert space) by giving them an internal structure of the form $(\alpha ,\beta )$. The dual operation is now defined as

$$\begin{array}{cc}{\tilde{F}}^{\alpha }={ϵ}^{\alpha \beta }\ast F^{\beta },\hfill & D=4k\hfill \end{array}$$

(20)

$$\begin{array}{cc}{\tilde{F}}^{\alpha }={\sigma }_1^{\alpha \beta }\ast F^{\beta },\hfill & D=4k-2\hfill \end{array}$$

(21)

$$\tilde{\tilde{F}}=F$$

(22)

with ${\sigma }_1^{\alpha \beta }$ being the first Pauli matrix. In this case self and anti-self dualities are well defined in any $D=2k$ dimensional space. One can start with the first order form of the theory:

$$S=\int d^{D}x[\mathsf{\Pi }·\dot{A}-\frac{1}{2}\mathsf{\Pi }·\mathsf{\Pi }-\frac{1}{2}B·B+A_0(\partial ·\mathsf{\Pi })]$$

(23)

Maxwell’s Gauss constraint can be generalized to precisely be the extended curl $\left(ϵ\partial \right)={ϵ}_{k_1{k}_2\dots k_{D-1}}{\partial }_{k_{D-1}}$. Then

$$\mathsf{\Pi }=\left(ϵ\partial \right)·\varphi$$

(24)

$$B=\left(ϵ\partial \right)·A$$

(25)

where $\varphi$ is a $(\frac{d}{2}-1)$-form potential, A is a generalization of the vector potential, $A_0$ is the general multiplier that enforces the Gauss constraint, the antisymmetrization of ∂ is defined as

$$\left(ϵ\partial \right)={ϵ}_{k_1{k}_2\dots k_{D-1}}{\partial }_{k_{D-1}}$$

(26)

and in general the notation

$$\mathsf{\Phi }·\mathsf{\Psi }={\mathsf{\Phi }}_{[k_1\dots k_{D-1}]}{\mathsf{\Psi }}_{[k_1\dots k_{D-1}]}$$

(27)

is used to imply antisymmetrization via the brackets. Now, I construct an internal space of potentials where duality symmetry is manifest (${\mathsf{\Phi }}^{+}$ and ${\mathsf{\Phi }}^{-}$ represent the new field structure). The dual projection can be defined now as a canonical transformation of the fields in the following way:

$$A=({\mathsf{\Phi }}^{+}+{\mathsf{\Phi }}^{-})$$

(28)

$$\mathsf{\Pi }=\eta \left(ϵ\partial \right)({\mathsf{\Phi }}^{(+)}-{\mathsf{\Phi }}^{(-)})$$

(29)

$$\eta =\pm 1$$

(30)

The action can be rewritten in terms of these fields as

$$S=\int d^{D}x\{\eta [{\dot{\mathsf{\Phi }}}^{\left(\alpha \right)}{\sigma }_3^{\alpha \beta }{B}^{\left(\beta \right)}+{\dot{\mathsf{\Phi }}}^{\left(\alpha \right)}{ϵ}^{\alpha \beta }{B}^{\left(\beta \right)}]-B^{\left(\beta \right)}·B^{\left(\beta \right)}$$

where $B^{\left(\beta \right)}=(ϵ\partial ·{\mathsf{\Phi }}^{\left(\beta \right)})$ and ${\sigma }_3^{\left(\alpha \beta \right)}$ and ${\sigma }_2^{\left(\alpha \beta \right)}=i{ϵ}^{\left(\alpha \beta \right)}$ are the Pauli marices. We see that the symplectic part factorizes in two parts: one involving the third Pauli matrix and the other one the second Pauli matrix. For a dimension $D=4k$ the first term is the generalization of the $2D$ chiral bosons. The $Z_2$ symmetry manifests itself in the transformation ${\mathsf{\Phi }}^{(\pm )}⟷{\mathsf{\Phi }}^{(\mp )}$. The second term becomes a total derivative. For $D=2k$ the first term becomes a total derivative and the second term explicitly shows the symmetry of SO(2).Although the complete diagonalization of the action in 3D cannot be done in coordinate space, a dual projection is possible in the momentum space [20]. Let me introduce a two-basis $\{{\widehat{e}}_a(k,x),$$a=1,2\}$ with $(k,x)$ being conjugate variables and the orthonormalization condition given as

$$\int dx{\widehat{e}}_a(k,x){\widehat{e}}_b(k^{\prime },x)={\delta }_{ab}\delta (k,k^{\prime })$$

(31)

The vectors in the basis can be chosen to be eigenvectors of the Laplacian, ${\mathsf{\nabla }}^2=\partial \partial$, and

$${\mathsf{\nabla }}^2{\widehat{e}}_a(k,x)=-{\omega }^2\left(k\right){\widehat{e}}_a(k,x)$$

(32)

The action of ∂ over the ${\widehat{e}}_a(k,x)$ basis is

$$\partial {\widehat{e}}_a(k,x)=\omega \left(k\right)M_{ab}{\widehat{e}}_b(k,x)$$

(33)

The two previous equations give

$$\tilde{M}M=-I$$

(34)

where ${\tilde{M}}_{ab}=M_{ba}$. The canonical scalar and its conjugate momentum have the following expansion

$$\mathsf{\Phi }\left(x\right)=\int dk{q}_a\left(k\right){\widehat{e}}_a(k,x)$$

(35)

$$\mathsf{\Pi }\left(x\right)=\int dk{p}_a\left(k\right){\widehat{e}}_a(k,x)$$

(36)

where $q_a$ and $p_a$ are the expansion coefficients. The action appears in this representation as a two-dimensional oscillator. The phase space is now four-dimensional, representing two degrees of freedom per mode,

$$S=\int dk\{p_a{\dot{q}}_a-\frac{1}{2}{p}_a{p}_a-\frac{{\omega }^2}{2}{q}_a{q}_a\}.$$

(37)

Now we can introduce the following canonical transformation

$$p_a\left(k\right)=\omega \left(k\right){ϵ}_{ab}({\phi }_b^{(+)}-{\phi }_b^{(-)})$$

(38)

$$q_a\left(k\right)=({\phi }_a^{(+)}+{\phi }_a^{(-)}).$$

(39)

The action becomes $S=S_{+}+S_{-}$ where

$$S_{\pm }=\int dk\omega \left(k\right)(\pm {\dot{q}}_a{ϵ}_{ab}{q}_b-\omega \left(k\right)q_a{q}_a).$$

(40)

As expected, this action presents the $Z_2$ symmetry under the transformation ${\phi }_a^{\alpha }\to {\sigma }_1^{\alpha \beta }{\phi }_a^{\beta }$.

This is a particular example. However, the field-anti-field prescription used in the main paper practically has a similar role and is defined in general. It generates a symplectic even-dimensional field space suitable for quantization. It also defines an analogues for the Hodge-∗ operators.

2.3. Kahler Manifolds

Kahler manifolds are particularly interesting for the current problem. In general having a differential manifold $\mathcal{M}$ and a tensor of type $(1,1)$ J such that $\forall p\in \mathcal{M}$, $J_p^2=-1$, the tensor J will give a structure to $\mathcal{M}$ with the property that the eigenvalues of it will be of the form $\pm i$. This means that $J_p$ is an even-dimensional matrix and $\mathcal{M}$ is an even manifold. From the same definition it follows that $J_p$ can divide the complexified tangent space at p in two disjoint vector subspaces

$$T_p{\mathcal{M}}^C=T_p{\mathcal{M}}^{+}\oplus T_p{\mathcal{M}}^{-}$$

(41)

$$T_p{\mathcal{M}}^{\pm }=\{Z\in T_p{\mathcal{M}}^C|J_{p}Z=\pm iZ\}$$

(42)

One can introduce two projection operators of the form

$$P^{\pm }:T_p{\mathcal{M}}^C\to T_p{\mathcal{M}}^{\pm }$$

(43)

$$P^{\pm }=\frac{1}{2}(1\pm i{J}_p)$$

(44)

which will decompose Z as $Z=Z^{+}+Z^{-}$. This construction will generate a holomorphic and an antiholomorphic sector: $Z^{\pm }=P^{\pm }Z\in T_p{\mathcal{M}}^{\pm }$, $T_p{\mathcal{M}}^{+}$ being the holomorphic sector. A complex manifold appears when demanding that given two intersecting charts $(U_i,{\gamma }_i)$ and $(U_j,{\gamma }_j)$, the map ${\psi }_{ij}={\gamma }_j{\varphi }_i^{-1}$ from ${\gamma }_i(U_i\cap U_j)$ to ${\gamma }_j(U_i\cap U_j)$ is holomorphic. Here ${\gamma }_i$ and ${\gamma }_j$ are chart homeomorphisms and ${\psi }_{ij}$ is the transition map. In this case the complex structure is given independently from the chart by

$$J_p=\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)\forall p\in \mathcal{M}$$

(45)

In the complex case there is a unique chart-independent decomposition in holomorphic and antiholomorphic parts. This means we can now choose as a local basis for those subspaces the vector $(\frac{\delta }{\delta z^{\mu }},\frac{\delta }{\delta {\overline{z}}^{\mu }})$ where ($z^{\mu },{\overline{z}}^{\mu }$) are the complex coordinates, such that the complex structure becomes

$$J_p=\left(\begin{array}{cc}i1& 0\\ 0& -i1\end{array}\right)\forall p\in \mathcal{M}$$

(46)

If we add a Riemannian metric g to the complex manifold and demand that the metric satisfies $g_p(J_{p}X,J_{p}Y)=g_p(X,Y),\forall p\in \mathcal{M}$, and $X,Y\in T_p\mathcal{M}$, then the metric is called Hermitian and $\mathcal{M}$ is called a Hermitian manifold. A complex manifold always admits a Hermitian metric. Using the base vectors of the complexified $T_p{\mathcal{M}}^C$ we can always write the metric locally as

$$g=g_{\mu \overline{\nu }}d{z}^{\mu }\otimes d{\overline{z}}^{\nu }+g_{\overline{\mu }\nu }d{\overline{z}}^{\mu }\otimes d{z}^{\nu }$$

(47)

If we have a Hermitian manifold $(\mathcal{M},g)$ with g Hermitian metric and a fundamental 2-tensor $\mathsf{\Omega }$ whose action on vectors X and $Y\in T_p\mathcal{M}$ is

$${\mathsf{\Omega }}_p(X,Y)=g_p(J_{p}X,Y)$$

(48)

then we call ${\mathsf{\Omega }}_p(X,Y)$ a Kahler form. With this definition, the Kahler form has some very useful properties. Firstly, it is antisymmetric

$$\mathsf{\Omega }(X,Y)=g(J^{2}X,JY)=-g(X,JY)=-\mathsf{\Omega }(Y,X)$$

(49)

Then it is invariant under the action of the complex structure

$$\mathsf{\Omega }(JX,JY)=\mathsf{\Omega }(X,Y)$$

(50)

and under complexification

$${\mathsf{\Omega }}_{\mu \nu }=i{g}_{\mu \nu }=0$$

(51)

$${\mathsf{\Omega }}_{\overline{\mu }\overline{\nu }}=i{g}_{\overline{\mu }\overline{\nu }}=0$$

(52)

$${\mathsf{\Omega }}_{\mu \overline{\nu }}=-{\mathsf{\Omega }}_{\overline{\nu }\mu }=i{g}_{\mu \overline{\nu }}$$

(53)

thus leading to

$$\mathsf{\Omega }=i{g}_{\mu \overline{\nu }}d{z}^{\mu }\wedge d{\overline{z}}^{\nu }$$

(54)

A Kahler manifold is a Hermitian manifold $(\mathcal{M},g)$, whose Kahler form $\mathsf{\Omega }$ is closed ($d\mathsf{\Omega }$ = 0). g is called a Kahler metric. The closing condition defines a differential equation for the metric.

$$d\mathsf{\Omega }=(\delta +\overline{\delta })i{g}_{\mu \overline{\nu }}d{z}^{\mu }\wedge d{\overline{z}}^{\nu }=$$

(55)

$$\frac{i}{2}({\delta }_{\lambda }{g}_{\mu \overline{\nu }}d{z}^{\lambda }\wedge d{z}^{\mu }\wedge d{\overline{z}}^{\nu })+\frac{i}{2}({\delta }_{\overline{\lambda }}{g}_{\mu \overline{\nu }}-{\delta }_{\overline{\nu }}{g}_{\mu \overline{\lambda }})d{\overline{z}}^{\lambda }\wedge d{z}^{\mu }\wedge d{\overline{z}}^{\nu }=0$$

(56)

This leads to the relations

$$\frac{\delta g_{\mu \overline{\nu }}}{\delta z^{\lambda }}=\frac{\delta g_{\lambda \overline{\nu }}}{\delta z^{\mu }}$$

(57)

$$\frac{\delta g_{\mu \overline{\nu }}}{\delta {\overline{z}}^{\lambda }}=\frac{\delta g_{\mu \overline{\lambda }}}{\delta {\overline{z}}^{\nu }}$$

(58)

The solution of the above equation takes the form

$$g_{\mu \overline{\nu }}={\delta }_{\mu }{\delta }_{\overline{\nu }}{K}_i$$

(59)

on a chart $U_i$ included in the manifold $\mathcal{M}$. $K_i$ is called Kahler potential.

$$K_i:U_i\to R$$

(60)

$$K_i=K_i^{\ast }$$

(61)

The Kahler form can be locally expressed in terms of the Kahler potential as

$$\mathsf{\Omega }=i\delta \overline{\delta }{K}_i$$

(62)

The definition given above is the most general one. In the main paper this method will be used for the specific case of the quantum Monte Carlo phase sign problem.

3. Quantization Prescriptions

The idea of quantization has a vast history. Originally, physical variables have been promoted to operators with specific commutation rules. These encoded the first quantizations ever performed. They were followed by the second quantization prescriptions and the anti-commutators needed for the description of fermionic particles. Finally, path integral quantization brought a completely new perspective on the procedure of quantization. While a classical theory is described by an action functional and a minimization prescription, a path-integral quantization is constructed as a functional integral of the complex exponentiated action functional

$$exp(iS[.]):C\to A$$

(63)

where C is the configuration space and A is the resulting space. This definition is very formal. In practical situations, the measure of the path integral is not always defined in the standard way. The configuration spaces are in general not even manifolds. Sometimes, in order to obtain pertinent results, a so-called “cohomological integration” is necessary. When the theory we want to quantize has redundancies (gauge symmetries) one relies on two possible approaches. When the gauge algebra is closed, a BRST quantization procedure can be implemented. In general however, the gauge algebra does not close. In this case an alternative method developed initially by Batalin and Vilkovisky is used.

The algebra of the operators of the gauge symmetry can in general be defined as

$$\frac{{\delta }^l{R}_{\alpha }^i}{\delta {\varphi }^j}{R}_{\beta }^j-{(-1)}^{{ϵ}_{\alpha }{ϵ}_{\beta }}\frac{{\delta }^l{R}_{\beta }^i}{\delta {\varphi }^j}{R}_{\alpha }^j=2R_{\gamma }^i{T}_{\alpha \beta }^{\gamma }{(-1)}^{{ϵ}_{\alpha }}-4y_j{E}_{\alpha \beta }^{ji}{(-1)}^{{ϵ}_i}{(-1)}^{{ϵ}_{\alpha }}$$

(64)

where $y_j=0$ represents the equation of motion, E and T represent coefficients, R represents the (gauge) symmetry transformation operators, and $ϵ$ encodes the Grassmann parity of the associated field. One can also define the BRST transformations of the original fields as $\delta {\varphi }^i=R_{\alpha }^i[\varphi ]c^{\alpha }$ i.e., one can define the BRST symmetry transformations via $R[\varphi ]$ and the associated ghost field $c^{\alpha }$ unambiguously. This is why, when no confusion is possible, the terms $R_{\alpha }^i$, $R[{\varphi }^i,c,\dots ]$ or the BRST transformation rule $\delta {\varphi }^A=R^A[{\varphi }^B]$ will be used alternatively as formal definitions.

If $E=0$ the algebra is closed and the nilpotency of the BRST operator is naively verified. Imposing nilpotency on the fields ${\varphi }^i$ we get

$$0={\delta }^2{\varphi }^i=R_{\alpha }^i\delta c^{\alpha }+\frac{{\delta }^l{R}_{\alpha }^i{c}^{\alpha }}{\delta {\varphi }^j}{R}_{\beta }^j{c}^{\beta }$$

(65)

If we choose now

$$\delta c^{\gamma }=T_{\alpha \beta }^{\gamma }[\varphi ]c^{\beta }{c}^{\alpha }$$

(66)

the nilpotency condition on the “physical” sector is satisfied and we obtain (considering $E=0$)

$$\frac{{\delta }^l{R}_{\alpha }^i{c}^{\alpha }}{\delta {\varphi }^j}{R}_{\beta }^j{c}^{\beta }+R_{\gamma }^i{T}_{\alpha \beta }^{\gamma }{c}^{\beta }{c}^{\alpha }=0$$

(67)

Also, using Jacobi identity one can easily show that ${\delta }^2{c}^{\gamma }=0$. It will be seen later how this can be generalized for the case of BRST-anti-BRST transformations. If the algebra depends on the last term, i.e., E is not zero, we have an open algebra and an non-nilpotent BRST transformation acting on the initial fields. The gauge fixed action constructed in the naive way would not be BRST-invariant off-shell. In order to solve this problem, one has to introduce an artificial shift symmetry and to move the non-nilpotency from the transformation rules of the original fields to the transformation rules of the collective fields. One certainly trivial way of enlarging the field space is by introducing two fields $A^l$ and $B^l$ such that

$$\begin{array}{c}\delta A^l=B^l\hfill \\ \delta B^l=0\hfill \end{array}$$

(68)

Obviously as the initial action does not depend on $A^l$, one can shift it with no practical effect. This shift would be a local symmetry and the fields $B^l$ would be the associated ghost-fields. It is precisely this idea that allows the redefinition of the field structure as will be seen further on. While it is certainly possible to move undesirable aspects of the theory to the collective sector, it is also possible to transfer desirable properties to the field structure while keeping the well-behaved properties inside. Moreover, if there are more symmetries, then the interplay between them at the level of the BRST (–anti-BRST–dual-(anti)-BRST) introduces the additional freedoms that I am using in order to avoid the sign problem practically permanently.

As one can see by now, the quantization prescription is not always trivial. One must specify what quantization means in the framework of path integrals. Essentially, the special way in which the functional integration is performed assures the correct quantization of a classical theory. Moreover, the theory, defined by an action functional, is by no means unique. It is well known that different representations can be chosen but in general in physics this amounts to the construction of effective low-energy theories. This does not always have to happen in this way. The chosen field structure can be designed such that it maps a complexity class into another.

I start with a general field theory, as described by the action $S[{\varphi }^A]$. The Batalin-Vilkovisky quantization prescription enlarges the field-space of the theory by introducing anti-fields (${\varphi }_A^{\ast }$) and gives a new canonical structure known as the anti-bracket [21]. This is defined considering two Grassmann functionals F and G as

$$(F,G)=\frac{{\delta }^{r}F}{\delta {\varphi }^A\left(x\right)}\frac{{\delta }^{l}G}{\delta {\varphi }_A^{\ast }\left(x\right)}-\frac{{\delta }^{r}F}{\delta {\varphi }_A^{\ast }\left(x\right)}\frac{{\delta }^{l}G}{\delta {\varphi }^A\left(x\right)}$$

(69)

involving alternate functional differentiation with respect to the fields and antifields. r and l superscripts stand for the right and left derivatives, respectively. I am following here the rules of [11] for the left and right derivatives. Accordingly,

$$\frac{{\delta }^l\left(FG\right)}{\delta A}=\frac{{\delta }^{l}F}{\delta A}G+{(-1)}^{{ϵ}_F{ϵ}_A}F\frac{{\delta }^{l}G}{\delta A}$$

(70)

$$\frac{{\delta }^r\left(FG\right)}{\delta A}=F\frac{{\delta }^{r}G}{\delta A}+{(-1)}^{{ϵ}_G{ϵ}_A}\frac{{\delta }^{r}F}{\delta A}G$$

(71)

which amount to the following relation between left and right derivatives in general

$$\frac{{\delta }^{l}F}{\delta A}={(-1)}^{{ϵ}_A({ϵ}_F+1)}\frac{{\delta }^{r}F}{\delta A}$$

(72)

The antibracket has some important properties: it changes the statistics as

$$ϵ[(F,G)]=ϵ\left(F\right)+ϵ\left(G\right)+1$$

(73)

and satisfies the following relation

$$(F,G)=-{(-1)}^{\left(ϵ\right(F)+1)\left(ϵ\right(G)+1)}(G,F)$$

(74)

where $ϵ$ is the Grassmann parity operator. Using this structure, the Batalin–Vilkovisky prescription can be written as

$$\frac{1}{2}(W,W)=i\hslash \mathsf{\Delta }W$$

(75)

where

$$\mathsf{\Delta }={(-1)}^{{ϵ}_A+1}\frac{{\delta }^r}{\delta {\varphi }^A}\frac{{\delta }^r}{\delta {\varphi }_A^{\ast }}$$

(76)

Here, W is called the “quantum action” and is a solution of the above equation. If it can be expanded in powers of ℏ, one obtains:

$$W=S+\sum _{n=0}^{\infty }{\hslash }^n{M}_n$$

(77)

The boundary conditions should make this coincide with the classical action when all antifields are removed $({\varphi }_A^{\ast }=0)$. To the lowest order, one recovers the classical master equation $(S,S)=0$.

If one starts with the classical action (containing the usual number of fields) $S[{\varphi }^A]$ the associated path integral is

$$Z=\int [d{\varphi }^A]exp[\frac{i}{\hslash }S[{\varphi }^A]]$$

(78)

By performing the transformations ${\varphi }^A\left(x\right)\to {\varphi }^A\left(x\right)-{\phi }^A\left(x\right)$ one constructs an action $S[{\varphi }^A-{\phi }^A]$ invariant to a local shift symmetry

$$\begin{array}{c}\delta {\varphi }^A\left(x\right)=\mathsf{\Theta }\left(x\right)\hfill \\ \delta {\phi }^A\left(x\right)=\mathsf{\Theta }\left(x\right)\hfill \end{array}$$

(79)

where $\mathsf{\Theta }\left(x\right)$ is arbitrary. In this way, I constructed another field representation that contains a collective field ${\phi }^A$. One can in principle integrate over the collective field if one fixes the introduced gauge symmetry in the standard BRST manner: adding an BRST-exact term in such a way that the local gauge symmetry is broken. This term must contain a ghost–antighost pair $(c^A\left(x\right),{\varphi }_A^{\ast }\left(x\right))$ and a Nakanishi–Lautrup field $B_A\left(x\right)$. A global BRST symmetry should emerge. The transformation rules of the fields in this theory will be

$$\begin{array}{c}\delta {\varphi }^A\left(x\right)=c^A\left(x\right)\hfill \\ \delta {\phi }^A\left(x\right)=c^A\left(x\right)\hfill \\ \delta c^A\left(x\right)=0\hfill \\ \delta {\varphi }_A^{\ast }\left(x\right)=B_A\left(x\right)\hfill \\ \delta B_A\left(x\right)=0\hfill \end{array}$$

(80)

I make no assumptions about the Grassmann parity of the initial fields ${\varphi }^A$. The ghost numbers of the new fields will be

$$\begin{array}{ccc}gh\left(c^A\right)=1;\hfill & gh\left({\varphi }_A^{\ast }\right)=-1;\hfill & gh\left(B_A\right)=0\hfill \end{array}$$

(81)

and $\delta$ is statistics changing. One can gauge fix the transformed action by adding

$$-\delta [{\varphi }_A^{\ast }{\phi }^A]={(-1)}^{ϵ\left(A\right)+1}{B}_A{\phi }^A-{\varphi }_A^{\ast }{c}^A$$

(82)

where $ϵ\left(A\right)$ is the Grassmann parity of the field ${\varphi }^A$. The partition function is now well defined:

$$\begin{array}{c}Z=\int [d{\varphi }_A][d{\phi }_A][d{\varphi }_A^{\ast }][d{c}_A][d{B}_A]\hfill \\ exp[\frac{i}{\hslash }(S[{\varphi }_A-{\phi }_A]-\int dx[{(-1)}^{ϵ\left(A\right)}{B}_A\left(x\right){\phi }^A\left(x\right)+{\varphi }_A^{\ast }\left(x\right)c^A\left(x\right)])]\hfill \end{array}$$

(83)

The collective field has been gauge fixed to zero. If one integrates out, $B_A\left(x\right)$ one obtains

$$\begin{array}{c}Z=\int [d{\varphi }^A][d{\varphi }_A^{\ast }][d{c}^A]exp\left(\frac{i}{\hslash }{S}_{ext}\right)\hfill \\ S_{ext}=S[{\varphi }^A]-\int [dx]{\varphi }_A^{\ast }{c}^A\left(x\right)\hfill \end{array}$$

(84)

where the ghosts are decoupled. From here $\frac{{\delta }^r{S}_{ext}}{\delta {\varphi }_A^{\ast }}=-c^A\left(x\right)$ or similarly $\frac{{\delta }^l{S}_{ext}}{\delta {\varphi }_A^{\ast }}=c^A\left(x\right)$. Substituting now the field equation of motion for $B_A\left(x\right)$, we obtain the symmetry transformations

$$\begin{array}{c}\delta {\varphi }^A\left(x\right)=c^A\left(x\right)\hfill \\ \delta c^A\left(x\right)=0\hfill \\ \delta {\varphi }_A^{\ast }\left(x\right)=-\frac{{\delta }^{l}S}{\delta {\varphi }^A\left(x\right)}\hfill \end{array}$$

(85)

where the superscripts l and r represent the left and right derivatives, respectively. This symmetry generates the Schwinger–Dyson equations. Starting from the identity $0=<\delta \left\{{\varphi }_A^{\ast }\left(x\right)F[{\varphi }^A]\right\}>$ and integrating over the ghosts $c^A$ and the antighosts ${\varphi }_A^{\ast }$ the Ward identity becomes

$$<\frac{{\delta }^{l}F}{\delta {\varphi }^A(x)}+(\frac{i}{\hslash })\frac{{\delta }^{l}S}{\delta {\varphi }^A\left(x\right)}F[{\varphi }^A]>=0$$

(86)

which is the most general Schwinger–Dyson equation to be associated to this theory. Now, the equation that expresses the BRST invariance of the extended action is

$$\begin{array}{c}0=\delta S_{ext}=\int dx\frac{{\delta }^r{S}_{ext}}{\delta {\varphi }^A\left(x\right)}{c}^A\left(x\right)-\int dx\frac{{\delta }^r{S}_{ext}}{\delta {\varphi }_A^{\ast }\left(x\right)}\frac{{\delta }^{l}S}{\delta {\varphi }^A\left(x\right)}=\hfill \\ =\int dx\frac{{\delta }^r{S}_{ext}}{\delta {\varphi }^A\left(x\right)}{c}^A\left(x\right)-\int dx\frac{{\delta }^r{S}_{ext}}{\delta {\varphi }_A^{\ast }\left(x\right)}\frac{{\delta }^l{S}_{ext}}{\delta {\varphi }^A\left(x\right)}\hfill \end{array}$$

(87)

where S differs from $S_{ext}$ by a term independent of ${\varphi }^A$.

Using the definition of the anti-bracket written in general for two functionals F and G as

$$(F,G)=\frac{{\delta }^{r}F}{\delta {\varphi }^A\left(x\right)}\frac{{\delta }^{l}G}{\delta {\varphi }_A^{\ast }\left(x\right)}-\frac{{\delta }^{r}F}{\delta {\varphi }_A^{\ast }\left(x\right)}\frac{{\delta }^{l}G}{\delta {\varphi }^A\left(x\right)}$$

(88)

the above identity corresponds to what is called the master equation

$$\frac{1}{2}(S_{ext},S_{ext})=-\int dx\frac{{\delta }^r{S}_{ext}}{\delta {\varphi }^A\left(x\right)}{c}^A\left(x\right)$$

(89)

The important aspect to be considered here is the right-hand side term of the above formula. In this case, the solution of the above expression implies an expansion in terms of the ghosts and the antighosts with a set of unknown coefficients

$$S_{ext}[{\varphi }^A,{\varphi }_A^{\ast },c^A]=S[{\varphi }^A]+\sum _{n=1}^{\infty }{a}_n{\varphi }_{A_1}^{\ast }\dots {\varphi }_{A_n}^{\ast }{c}^{A_1}\dots c^{A_n}$$

(90)

Of course the choice of integrating over both the ghosts and the antighosts is arbitrary. One can choose to integrate only over the ghost fields $c^A\left(x\right)$ but not over the corresponding antighosts ${\varphi }_A^{\ast }\left(x\right)$. The partition function then becomes

$$Z=\int [d{\varphi }^A][d{\varphi }_A^{\ast }]\delta \left({\varphi }_A^{\ast }\right)exp[\frac{i}{\hslash }S[{\varphi }^A]]$$

(91)

On the side of the BRST algebra this change amounts in the way in which the non-propagating fields are replaced by their corresponding equations of motion. The direct method used above must be refined when dealing with fermionic type fields. The main question with respect to how to replace $c^A$ inside the Green functions. The answer will give the transformation rules for the fields that are not integrated out. Consider the identity

$$\begin{array}{c}\int [dc]F[c^B\left(y\right)]exp[-\frac{i}{\hslash }\int dx{\varphi }_A^{\ast }\left(x\right)c^A\left(x\right)]=F(i\hslash \frac{{\delta }^l}{\delta {\varphi }_B^{\ast }\left(y\right)})exp[-\frac{i}{\hslash }\int dx{\varphi }_A^{\ast }\left(x\right)c^A\left(x\right)]\hfill \end{array}$$

(92)

It follows that the replacement of $c^A$ with its equation of motion $(c^A\left(x\right)=0)$ is not sufficient. One has to add what is called a “quantum correction” of the form $\hslash \delta /\delta {\varphi }^{\ast }$. What appears as “quantum correction” in the Green function results from our choice of integrating only over a ghost field and not over its associated antighost. Essentially, it is at this point in the quantization procedure where the difference between fermionic and bosonic fields appears. The BRST symmetry transformations have to change accordingly if the option of integrating only over the fermionic “half” of the field–antifield structure is chosen. Now, performing this replacement (meaningful only inside the path integral) the BRST transformation itself becomes

$$\begin{array}{c}\delta {\varphi }^A\left(x\right)=i\hslash {(-1)}^{{ϵ}_A}\frac{{\delta }^r}{\delta {\varphi }_A^{\ast }\left(x\right)}\hfill \\ \delta {\varphi }_A^{\ast }\left(x\right)=-\frac{{\delta }^{l}S}{\delta {\varphi }^A\left(x\right)}\hfill \end{array}$$

(93)

where ${ϵ}_A$ is the Grassmann parity associated to the fields indexed by A. It can be checked that this transformation leaves at least the combination of the measure and the action invariant. After integrating out the ghost, the antibracket structure is modified. In order to see how, one can perform a variation of an arbitrary functional $G[{\varphi }^A,{\varphi }_A^{\ast }]$. Inside the path integral we obtain

$$\begin{array}{c}\delta G[{\varphi }^A,{\varphi }_A^{\ast }]=\int dx\frac{{\delta }^{r}G}{\delta {\varphi }^A\left(x\right)}[\frac{{\delta }^l{S}_{ext}}{\delta {\varphi }_A^{\ast }\left(x\right)}+\left(i\hslash \right){(-1)}^{{ϵ}_A}\frac{{\delta }^r}{\delta {\varphi }_A^{\ast }\left(x\right)}]-\int dx\frac{{\delta }^{r}G}{\delta {\varphi }_A^{\ast }\left(x\right)}\frac{{\delta }^l{S}_{ext}}{\delta {\varphi }^A\left(x\right)}\hfill \end{array}$$

(94)

The left derivative on the left side comes from the definition of $c^A$ in $S_{ext}$. In this case, it can be considered simply as zero. I follow here closely the notation of [11]. This equation describes the “quantum deformation” introduced in the antibracket structure

$$\delta G[{\varphi }^A,{\varphi }_A^{\ast }]=\int dx[(G,S_{ext})-i\hslash \mathsf{\Delta }G]$$

(95)

where

$$\mathsf{\Delta }={(-1)}^{{ϵ}_A+1}\frac{{\delta }^r{\delta }^r}{\delta {\varphi }_A^{\ast }\left(x\right)\delta {\varphi }^A\left(x\right)}$$

(96)

Again, this term appears only as a consequence of the partial integration, which allows us to expose the operator $\delta /\delta {\varphi }_A^{\ast }$ that otherwise acts only on a $\delta$-functional. Whenever one choses to keep only half of the field–antifield components in the theory and integrates over the ghosts obeying fermi statistics, the result will be a deformation of the antibracket structure that will lead to the quantum master equation. One can already see that the mapping of the “quantum” problem to the “classical” problem as presented in [3] is correct but not unique. In the next chapter I show how one should extend the field structure of an arbitrary theory in order to obtain a sign-problem free theory. This prescription implies by no means any exponential increase in complexity if one considers what has been presented above.

4. Construction of the Theory

My method relies at a first level on the field–antifield formalism as introduced by Batalin and Vilkovisky [7] and at a second level on an innovative use of some algebraic geometry and topology theorems [14,15]. I will regard the partition function as depending on the action functional described in terms of a set of fields ${\varphi }^A$

$$Z=Z_0\int exp(-\sum _i{S}_i[{\varphi }^A])D{\varphi }^A$$

(97)

More generally, the theory may have additional internal symmetries, generated by corresponding operators. First, let me show here the main idea related to the introduction of a single shift symmetry using one set of collective fields. I will regard the partition function as depending on the action functional described in terms of a set of fields ${\varphi }^A$ (43). More generally, the theory may have additional internal symmetries, generated by corresponding operators. Let me now double the fields by introducing a collective field ${\phi }^A$ that induces a shift symmetry in the theory:

$${\varphi }^A\to {\varphi }^A-{\phi }^A$$

(98)

No assumption regarding the statistics of the ${\varphi }^A$ fields is required. They can be fermionic or bosonic. The new shift symmetry must be gauge fixed and for this I have to introduce a ghost and a trivial system in the form of a multiplet consisting of an antifield ${\varphi }_A^{\ast }$ and an auxiliary field $B_A$. After gauge fixing, a global BRST symmetry emerges in general. In the present case however, in order to maintain the triviality of the extended BRST symmetry that encompasses also the shift symmetry, the BRST transformation rules change in the following way:

$$\begin{array}{c}\delta {\varphi }^A=c^A\hfill \\ \delta {\phi }^A=c^A-R^A[{\varphi }^A-{\phi }^A]\hfill \\ \delta c^A=0\hfill \\ \delta {\varphi }_A^{\ast }=B_A\hfill \\ \delta B_A=0\hfill \end{array}$$

(99)

where $c^A$ is the ghost field and $\delta$ is the BRST transformation to be associated with the total BRST-type symmetries. $R^A[{\varphi }^A-{\phi }^A]$ represents a formal definition of the BRST symmetry associated to the possible intrinsic initial gauge symmetry. There exists a freedom to shift the original gauge symmetry $R^A[{\varphi }^A-{\phi }^A]$ between the BRST transformation of the fields and the BRST transformation of the collective fields. In this way a possible off-shell non-nilpotency in the transformation rules is transfered to the transformation rules of the collective field. This was one of the first applications of the collective field formalism to the quantization of theories involving algebras that do not close (i.e., algebras of the gauge symmetry generators depending on the form of the field equations of motion). As an example of such theories, one may quote supergravity. The ghost numbers of the new fields are

$$\begin{array}{ccc}gh\left(c^A\right)=1;\hfill & gh\left({\varphi }_A^{\ast }\right)=-1;\hfill & gh\left(B_A\right)=0\hfill \end{array}$$

(100)

Although the new artificial and certainly trivial continuous shift symmetry is easy to eliminate at this level, it is of major importance as a tool for generating new discrete symmetries. Considering the new continuous shift symmetry, one has to gauge fix it. This can be done adding the following terms in the form of BRST transformations:

$$\begin{array}{c}{S}_{gf}=S_0[{\varphi }^A-{\phi }^A]-\delta [{\varphi }_A^{\ast }{\varphi }^A]+\delta \mathsf{\Psi }[{\varphi }^A]\hfill \\ =S_0[{\varphi }^A-{\phi }^A]+{\varphi }_A^{\ast }{R}^A[{\varphi }^A-{\phi }^A]-{\varphi }_A^{\ast }{c}^A+\frac{{\delta }^l\mathsf{\Psi }}{\delta {\varphi }^A}{c}^A-{\phi }^A{B}_A\hfill \\ =S_{BV}[{\varphi }^A-{\phi }^A]-{\varphi }_A^{\ast }{c}^A+\frac{{\delta }^l\mathsf{\Psi }}{\delta {\varphi }^A}{c}^A-{\phi }^A{B}_A\hfill \end{array}$$

(101)

where $S_{BV}$ is called the Batalin–Vilkovisky action. It incorporates the original action and the terms arising from other possible internal gauge symmetries. $\mathsf{\Psi }$ is a gauge fixing bosonic functional depending only on the original fields. By this, I define a new gauge fixed action. Note that the nillpotency ${\delta }^2=0$ of the BRST transformation assures the overall invariance. The partition function is the standard one:

$$Z=\int [d{\varphi }^A][d{\varphi }_A^{\ast }]\delta ({\varphi }_A^{\ast }-\frac{{\delta }^l\mathsf{\Psi }[{\varphi }^A]}{\delta {\varphi }^A})e^{-S_{BV}[{\varphi }^A,{\varphi }_A^{\ast }]}$$

(102)

where $\mathsf{\Psi }[{\varphi }^A]$ is defined considering the condition imposed in the resulting delta-function. One must underline that the gauge fixing procedure must keep the gauge independence of the full partition function, including the integration measure.

Until now, a continuous shift-symmetry has been introduced and gauge fixed.

However, the action presents further flexibility. One can extend the field structure such that two BRST operators become manifest. In this way, one implements the BRST–anti-BRST symmetry and the associated field structure [9,10]. This method allows Schwinger–Dyson equations as Ward identities as well. Moreover, this method, also known as the “$Sp\left(2\right)$”-invariant quantization, has the property of manifestly generating a symplectic structure over the field space. This will prove to be important further on. The method is similar to what has been shown before and we obtain $S_0[\varphi ]\to S_0[{\varphi }_A-{\phi }_{A1}-{\phi }_{A2}]$. Two extra gauge symmetries arise, for which a new structure of fields is introduced: two ghostfields ($c_{A1},{\varphi }_{A2}^{\ast }$) and two antighost fields (${\varphi }_1^{\ast },c_{A2}$). Of course this extends the symmetries allowed in the theory.

$$\begin{array}{cc}{\delta }_1{\varphi }_A=c_{A1}\hfill & {\delta }_2{\varphi }_A=c_{A2}\hfill \\ {\delta }_1{\phi }_{A1}=c_{A1}-{\varphi }_{A2}^{\ast }\hfill & {\delta }_2{\phi }_{A1}=-{\varphi }_{A1}^{\ast }\hfill \\ {\delta }_1{\phi }_{A2}={\varphi }_{A2}^{\ast }\hfill & {\delta }_2{\phi }_{A2}=c_{A2}+{\varphi }_{A1}^{\ast }\hfill \\ {\delta }_1{c}_{A1}=0\hfill & {\delta }_2{c}_{A2}=0\hfill \\ {\delta }_1{\varphi }_{A2}^{\ast }=0\hfill & {\delta }_{A2}{\varphi }_{A1}^{\ast }=0\hfill \end{array}$$

(103)

Here, ${\delta }_1$ and ${\delta }_2$ are respectively the BRST and anti-BRST transformations. The next step is to impose gauge fixing. This is done in the standard way by adding more bosonic fields, calling them $B_A$ and ${\lambda }_A$. The BRST transformation rules extend according to

$$\begin{array}{cc}{\delta }_1{c}_{A2}=B_A\hfill & {\delta }_2{c}_{A1}=-B_A\hfill \\ {\delta }_1{B}_A=0\hfill & {\delta }_2{B}_A=0\hfill \\ {\delta }_1{\varphi }_1^{\ast }={\lambda }_A-\frac{B_A}{2}\hfill & {\delta }_2{\varphi }_2^{\ast }=-{\lambda }_A-\frac{B_A}{2}\hfill \\ {\delta }_1{\lambda }_A=0\hfill & {\delta }_2{\lambda }_A=0\hfill \end{array}$$

(104)

These rules imply the nillpotency conditions ${\delta }_1^2={\delta }_2^2={\delta }_1{\delta }_2+{\delta }_2{\delta }_1=0$. The action invariant under this BRST symmetry contains the terms of $S_0[{\varphi }_A-{\phi }_{A1}-{\phi }_{A2}]$, plus some gauge fixing terms

$$\begin{array}{c}{S}_{col}=\frac{1}{2}{\delta }_1{\delta }_2[{\phi }_{A1}^2-{\phi }_{A2}^2]\hfill \\ =-({\phi }_{A1}+{\phi }_{A2}){\lambda }_A+\frac{B_A}{2}({\phi }_{A1}-{\phi }_{A2})+{(-1)}^a{\varphi }_{Aa}^{\ast }{c}_{Aa}\hfill \end{array}$$

(105)

Here summation over $a=1,2$ is implied. Using the transformation

$${\phi }_{A\pm }={\phi }_{A1}\pm {\phi }_{A2}$$

(106)

we obtain the gauge fixed action

$$S_{gf}=S_0[{\varphi }_A-{\phi }_{A+}]-{\phi }_{A+}{\lambda }_A+\frac{B_A}{2}{\phi }_{A-}+{(-1)}^a{\varphi }_{Aa}^{\ast }{c}_{Aa}$$

(107)

For the sake of generality, I follow the notation in [9,10] and define

$${\delta }_a{\varphi }_A=R_{Aa}\left({\varphi }_A\right)$$

(108)

where $R_{Aa}$ is the BRST–anti-BRST symmetry transformation associated to an initial intrinsic gauge symmetry. Apart from this, the transformations associated to the additional artificial shift symmetries will be added. In the case $a=1$ we have the BRST transformation rules, whereas in the case $a=2$ we have the anti-BRST transformation rules. The two collective fields are denoted by ${\phi }_{A1}$ and ${\phi }_{A2}$ or generally ${\phi }_{Aa}$. The transformation will be ${\varphi }_A-{\phi }_{A1}-{\phi }_{A2}$. The field multiplets used are the ghosts $(c_{A1},{\varphi }_A^{\ast 2})$ and the antighosts $({\varphi }_A^{\ast 1},c_{A2})$. For $a=1$, $c_{Aa}$ is a ghost while for $a=2$, $c_{Aa}$ is an antighost. The BRST–anti-BRST transformations are

$$\begin{array}{c}{\delta }_a{\varphi }_A=c_{Aa}\\ {\delta }_a{\phi }_{Ab}={\delta }_{ab}[c_{Aa}-{ϵ}_{ac}{\varphi }_A^{\ast c}-R_{Aa}({\varphi }_A-{\phi }_{A1}-{\phi }_{A2})]+(1-{\delta }_{ab}){ϵ}_{ac}{\varphi }_A^{\ast c}\end{array}$$

(109)

Here I imply no summation over a. Also, here ${ϵ}_{ac}$ is the antisymmetric tensor. The extra fields $B_A$ and ${\lambda }_A$ are introduced and we have extra transformation rules

$$\begin{array}{c}{\delta }_a{c}_{Ab}={ϵ}_{ab}{B}_A\\ {\delta }_a{B}_A=0\\ {\delta }_a{\varphi }_A^{\ast b}=-{\delta }_a^b[{(-1)}^a{\lambda }_A+\frac{1}{2}(B_A+\frac{{\delta }^l{R}_{A1}({\varphi }_A-{\phi }_{A1}-{\phi }_{A2})}{\delta {\varphi }_B}{R}_{B2}({\varphi }_B-{\phi }_{B1}-{\phi }_{B2}))]\\ {\delta }_a{\lambda }_A=0\end{array}$$

(110)

The gauge fixing procedure must occur in a BRST–anti-BRST invariant way. The inclusion of the terms involving $\frac{{\delta }^l{R}_{A1}}{\delta {\varphi }_B}{R}_{B2}$ as well as the additional terms in Equation (56) as a modification of the traditional BRST transformation rules is done in order to encode the nilpotency of the BRST–anti-BRST transformation in a way that is independent of the gauge algebra. The additional fields $B_A$ and ${\lambda }_A$ have the role of imposing the nilpotency at the level of the transformation rules of the original fields. Any off-shell non-nilpotency is thus shifted to the transformation rules of the collective fields. There are various ways in which more than one gauge symmetry can be encoded in the BRST transformation rules. Also, parts of some transformation rules can be transfered to transformation rules of additional fields. These properties have many possible applications. Here, I make use of them in order to avoid the sign problem. One can introduce a matrix $M^{AB}$ which is invertible and has the property

$$M^{AB}={(-1)}^{{ϵ}_A{ϵ}_B}{M}_{BA}$$

(111)

It also makes all the entries between the Grassmann odd and Grassmann even sectors vanish. This means that the term ${\varphi }_A{M}^{AB}{\varphi }_B$ has ghostnumber zero and even Grassmann parity. One can gauge fix to zero the collective terms

$$\begin{array}{c}{S}_{col}=-{\phi }_{A+}{M}^{AB}{\lambda }_B+\frac{1}{2}{\phi }_{A-}{M}^{AB}{B}_B+\hfill \\ +{(-1)}^a{(-1)}^{{ϵ}_B}{\varphi }_A^{\ast a}{M}^{AB}{c}_{Ba}+\hfill \\ +\frac{1}{2}{\phi }_{A-}{M}^{AB}\frac{{\delta }^l{R}_{B1}({\varphi }_B-{\phi }_{B+})}{\delta {\varphi }_C}{R}_{C2}({\varphi }_C-{\phi }_{C+})\hfill \\ +{(-1)}^{a+1}{(-1)}^{{ϵ}_B}{\varphi }_A^{\ast a}{M}^{AB}{R}_{Ba}({\varphi }_B-{\phi }_{B+})\hfill \end{array}$$

(112)

Here, the summation over a is implied. The sum of the two collective fields is fixed to zero, ${\varphi }_A^{\ast a}$ are the source terms for the BRST–anti-BRST transformations, and the difference between the two collective fields ${\phi }_{A-}$ is the source of the mixed transformations. The original gauge symmetry can be fixed in an extended BRST-invariant way by adding the variation of a gauge boson $\mathsf{\Psi }\left(\varphi \right)$ of ghostnumber zero.

$$S_{\mathsf{\Psi }}=\frac{1}{2}{ϵ}^{ab}{\delta }_a{\delta }_b\mathsf{\Psi }\left({\varphi }_A\right)$$

(113)

The gauge fixed action can be written as:

$$S_{gf}=S_0[{\varphi }_A-{\phi }_{A+}]+S_{col}+S_{\mathsf{\Psi }}$$

(114)

where

$$S_{col}=-\frac{1}{4}{ϵ}^{ab}{\delta }_a{\delta }_b({\phi }_{A1}{M}^{AB}{\phi }_{B1}-{\phi }_{A2}{M}^{AB}{\phi }_{B2})$$

(115)

At this moment, we have a gauge fixed action with a BRST–anti-BRST symmetry. Although the matrix M can be eliminated in the end, it has the potential to introduce a metric on the space spanned by the fields of the trivial system and the ghosts [22]. The same idea can be used to introduce a Kahler structure on the field space [23]. The introduction of the internal space is required due to the definition of the Hodge dual operation. As can be seen in [20] the internal space allows the definition of the Hodge operator in any dimension. This will extend the applicability of the procedure described in [24] for arbitrary dimensions of the original theory (considering the suitable generalization of the indices of the operators). The discrete symmetry is obtained by introducing new collective fields and imposing a dual-space gauge fixing that generates a Kahler structure. The Hodge star operator that relates the direct and dual emerging global continuous symmetry transformations will induce a discrete symmetry in the final theory. This symmetry can be associated to a form of artificial discrete invariance (see [19,25]). Now, I focus on the method that generates a time reversal-type symmetry. One spans an internal space by the introduction of a new set of fields and an equivalent of the M matrix. Take the action $S_{col}$ used above. Now, introduce an internal space index for the collective fields ${\phi }_{Aa}^{\mathsf{\Omega }}$, defining their dual with respect to the internal space:

$${\tilde{\phi }}_{Aa}^{\mathsf{\Omega }}=\frac{1}{2}{ϵ}_{\mathsf{\Omega }\mathsf{\Gamma }}{\phi }_{Aa}^{\mathsf{\Gamma }}$$

(116)

and rewrite the fields as

$${\phi }_{Aa}^{\pm \mathsf{\Omega }}=\frac{1}{2}({\phi }_{Aa}^{\mathsf{\Omega }}\pm i{\tilde{\phi }}_{Aa}^{\mathsf{\Omega }})$$

(117)

In the same way, introduce another matrix N that can be factorized as:

$$\begin{array}{c}{N}^{\mathsf{\Omega }\mathsf{\Gamma }}=\frac{1}{2}(h^{\mathsf{\Omega }\mathsf{\Gamma }}-i{f}^{\mathsf{\Omega }\mathsf{\Gamma }})\\ {\overline{N}}^{\mathsf{\Omega }\mathsf{\Gamma }}=\frac{1}{2}(h^{\mathsf{\Omega }\mathsf{\Gamma }}+i{f}^{\mathsf{\Omega }\mathsf{\Gamma }})\end{array}$$

(118)

The matrices f and h are completely arbitrary as long as the matrix N can be decomposed in the above way. Replacing this into the action together with a corresponding change in the fields we obtain a Kahler structure imposed over the manifold of the field–antifield formalism. This procedure may be related to the idea of Kahler polarization in the geometric quantization. The additional terms obtained in the matrix are now of the form:

$$S_{col}=-\frac{1}{4}{ϵ}^{ab}{\delta }_a{\delta }_b\delta \overline{\delta }({\phi }_{A1}^{-\mathsf{\Omega }}{N}_{\mathsf{\Omega }\mathsf{\Gamma }}{\phi }_{B1}^{-\mathsf{\Gamma }}-{\phi }_{A2}^{+\mathsf{\Omega }}{\overline{N}}_{\mathsf{\Omega }\mathsf{\Gamma }}{\phi }_{B2}^{+\mathsf{\Gamma }})$$

(119)

where now, the $\delta$ and $\overline{\delta }$ operators correspond to the dual BRST transformations. Their form depends on the practical calculation. The most general expression that can be written here is

$$\begin{array}{c}{\delta }_{Da}{\varphi }_A={\varphi }_{Aa}^{\ast }\hfill \\ {\delta }_{Da}{\phi }_{Ab}={\delta }_{ab}[{\varphi }_{Aa}^{\ast }-{ϵ}_{ac}{c}_A^c-R_{Aa}]+(1-{\delta }_{ab}){ϵ}_{ac}{c}_A^c\hfill \\ {\delta }_{Da}{c}_{Ab}=-{\delta }_a^b[{(-1)}^a{\lambda }_A+\frac{1}{2}(B_A+\frac{{\delta }^l{R}_{A1}}{\delta {\varphi }_B}{R}_{B2})]\hfill \\ {\delta }_{Da}{B}_A=0\hfill \\ {\delta }_{Da}{\varphi }_A^{\ast b}={ϵ}_{ab}{B}_A^a\hfill \\ {\delta }_{Da}{\lambda }_A=0\hfill \end{array}$$

(120)

where the same convention remains valid as for the BRST and anti-BRST transformations. However, several expressions may be altered according to the particularities of each theory. The expressions for the case of two dimensional quantum electrodynamics ($2D$ QED) are given in the Appendix A. $S_{col}$ is the equivalent of the collective term in the action for the new degrees of freedom constructed to introduce the Kahler structure. The matrices $N_{\mathsf{\Omega }\mathsf{\Gamma }}$ and ${\overline{N}}_{\mathsf{\Omega }\mathsf{\Gamma }}$ allow me to write the gauge fixing term in such a way that a Kahler structure becomes visible. They may be compared to the choice of a polarization set over the field space although here the scope is another. $M^{AB}$ is considered implictly. The same method that allows the M matrix to vanish eliminates the N matrix as well if this is our intention. This would lead to losing the “polarization” that makes the Kahler structure visible (please note that I use the term “polarization” in a non-rigorous sense, referring only to the way in which the fields can be partitioned, see Appendix B). We now have a Kahler structure imposed on our original action. The dual-BRST symmetry is the BRST symmetry, created by the new collective fields together with their trivial system. It is the analogue of the co-derivative from algebraic geometry. In this way we obtained the so-called de-Rham cohomology operators, that are now identified with the (anti)-BRST and dual-(anti)-BRST operators.

The connection between them is given by the Hodge star operator which can be constructed independent of the dimension of the original field space if one follows the prescription of constructing the internal spaces as described above. In this case the Hodge duality plays the role of a discrete symmetry transformation.

As noted in [17,26], the field–antifield setup is amenable to the construction of a Kahlerian structure imposed on the system of fields. Here, the Hodge star induces a symmetry that can be identified with time reversal in the case of Kahlerian structures (see Appendix C). If one thinks of the Hopf algebra, one can see that there exist certain similarities between the Hodge star operator and the Hodge algebra antipode. All one has to do is to suitably introduce fields and antifields via appropriate trivial symmetries such that the antipodal structure (associated to the Hodge dual) becomes visible. In the context of the field-antifield approach the structure of the emerging fermionic determinant will be

$$det\left(D\right)=\left(\begin{array}{cc}i{T}_1& 0\\ 0& -i{T}_1\end{array}\right)$$

(121)

where $T_1$ results from the construction of the Kahler structure. This assures that for the extended field space, the sign of the fermionic determinant is always positive and allows us to avoid the sign problem. The fact that the imposed structure is reflected on the form of the determinant is explained in [27].

In order to asses the complexity of the final problem, considering the fact that the fermionic determinant does not change sign (this can be interpreted in the formalism of the first chapter as the weights $p\left(c\right)$ being positive) the increase in complexity is due to the addition of more fields. In the above constructions the number of fields has been doubled twice, so I went from a theory containing N fields to a theory containing $4N$ fields. Also, additional fields have been added each time in order to ensure the desired gauge fixing. The additional fields on the BRST and anti-BRST branches are related so the construction of the BRST–anti-BRST structure required $4N$ fields and the dual counterpart required another $4N$ fields. This amounts to a theory containing $8N$ fields globally. Considering that half of the fields live in the internal space and have a controlled behavior and also that the increase in the field number is polynomial, the method should not add exponential complexity. The analysis of the resulting Jacobian is analysed in Appendix D.

5. Practical Calculation

I present here preliminary results obtained by applying a path integral Monte Carlo method to a simple oscillator-quartic anharmonic potential. While this is not a numerical proof of validity it may be considered as a test for a known case. The results presented in the left figure have been obtained using the corrective series expansion in the form of an effective potential [28,29]. The dual gauge fixing method used to produce the right figure had no need for such corrective expansions and converged to the values obtained via the corrective series expansion. The number of iterations appears larger in the gauge fixing method but one has to consider that in the left figure the cost of constructing the effective corrective potential is not considered. That effective potential calculation introduced several other terms and became intractable for higher orders.

The classical method is based on the path integral Monte Carlo technique designed in [29], based on the addition of terms in the action functional that would vanish in the continuous limit. Adopting the same functional formalism, we write the quantum mechanical amplitude

$$A(a,b;T)={(\frac{1}{2\pi {ϵ}_N})}^{\frac{N}{2}}\int d{q}_1\dots d{q}_{N-1}{e}^{-S_N}$$

(122)

The path integral method is applied on the Euclidean time interval $[0,T]$, subdivided into N equal steps of length ${ϵ}_N=T/N$, with the boundaries given by $q_0=a$ and $q_N=b$. The discretised action of the theory is $S_N$. The initial action has the form

$$S={\int }_0^{T}dt(\frac{1}{2}{\dot{q}}^2+V\left(q\right))$$

(123)

After discretisation we obtain

$$S_N=\sum _{n=0}^{N-1}(\frac{{\delta }_n^2}{2ϵ}+{ϵ}_{N}V\left({\overline{q}}_n\right))$$

(124)

with ${\delta }_n=q_{n+1}-q_n$ and ${\overline{q}}_n=\frac{1}{2}(q_{n+1}+q_n)$. The freedom of choosing one among various discretization procedures led the authors of [28,30,31] to new insights which brought a faster convergence to the path integral Monte Carlo procedure. The main result of a path-integral Monte Carlo computation is the continuum amplitude. This result will not be modified by the choice of the point in the interval $[q_n,q_{n+1}]$ to compute the potential V. Different points correspond to different ordering prescriptions of the operator formalism [29]. Another choice that will not affect the end result is related to the discretization of the action. Indeed, one may add terms to the action functional that explicitly vanish in the continuum limit. The addition of such terms may accelerate the convergence of the path-integral computation, as has been shown in [29] and this precise computation is being used in the baseline simulation performed here and presented in Figure 1a. For example, the addition of a term defined by

$$\sum _{n=0}^{N-1}{ϵ}_N{\delta }_n^{2}g\left({\overline{q}}_n\right)$$

(125)

where g is regular when ${ϵ}_N\to 0$, will not change the continuum physics since it will vanish as ${ϵ}_N^2$ when it is employed in ${ϵ}_N^2{\int }_0^{T}dt{\dot{q}}^{2}g\left(q\right)$. However, as shown by [29], such terms will affect the speed of convergence towards the continuum limit. The authors of [29] compare the relation between $2N$ and N-fold discretisation. The relation found by [29] was

$$e^{-{\tilde{S}}_N}={(\frac{2}{\pi {ϵ}_N})}^{N/2}\int d{x}_1\dots d{x}_N{e}^{-S_{2N}}$$

(126)

where $S_{2N}$ is the $2N$ fold discretisation of the original action. Integrating this action we obtain a new type of terms in ${\tilde{S}}_N$. The class of actions that is closed with respect to the transformation presented in the above equation is of the form

$$S_N=\sum _{n=0}^{N-1}(\frac{{\delta }_n^2}{2{ϵ}_N}+{ϵ}_{N}V\left({\overline{q}}_n\right)+{ϵ}_N{\delta }_n^2{g}_1\left({\overline{q}}_n\right)+{ϵ}_N{\delta }_n^4{g}_2\left({\overline{q}}_n\right)+{ϵ}_N{\delta }_n^6{g}_3\left({\overline{q}}_n\right)+\dots )$$

(127)

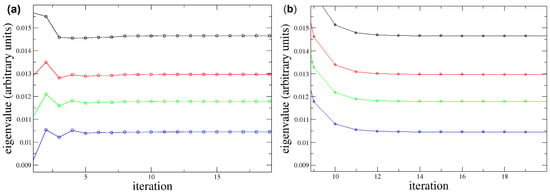
Figure 1. (a) Series-corrected solution; (b) Hodge symmetric solution; each color identifies a specific eigenvalue .

All of the functions above also depend on the time step ${ϵ}_N$ and are regular in the limit ${ϵ}_N\to 0$, making these effective actions equivalent to the starting action. For a general action, the time step is playing the role of a small parameter, ideal for an asymptotic expansion analysis. The calculations of [29] provided us with the modifications of the potential required for implementing this acceleration tool and the results of [28,30,31] have also been used as a baseline calculation. A similar idea is the foundation of this research work: Is it possible to still improve the action functional and the formulation of the theory, without altering the results, such that the sign problem could be avoided in a broader sense than what has been done until now? My approach was not to look at even finer discretizations, but instead, being guided by the fact that the sign problem appeared to be of a global nature, to employ gauge invariance and the (dual) BRST–anti-BRST symmetry to generate an artificial discrete symmetry (symmetry out of cohomology, see [32]) that would extend the classes of problems that can be analyzed by means of path integral Monte Carlo tools. The technique employed in this paper simply consists of adding a zero to the action functional, because finally all additional fields can be integrated out and the topological construction will be rendered invisible. The point of this paper is that such a topological construction, resulting in an additional (and fictitious) symmetry, is required for the theory to be numerically solvable and not plagued by the sign problem.

Of course, an important point is to understand the limitations of such a method. After all, we start with a fundamentally ill-defined theory. The sign problem, from this point of view, can be seen as a global anomaly of the form presented in [32]. The computational non-determinism is associated with precisely this global structure covered by the infinite set of paths which is intrinsic to a path integral formulation. It must be clearly said that in general, by adding more fields one does not solve the non-deterministic issues associated to the theory. The solution I propose here tries an approach that adds a physically irrelevant, yet topologically non-trivial field structure to the theory. This structure is capable of globally avoiding the sign problem and of reducing the complexity not by simply adding new fields, but by adding new fields such that a topologically non-trivial structure emerges that has the role of a topological anti-anomaly, namely an additional region of the manifold over which the paths will cancel precisely the terms that generate the sign problem on the original, unextended field manifold. The non-detectability of auxiliary topological structures has been discussed in [33,34].

With all terms added, the action functional employed for the calculation of the right side of Figure 1 is given by Equation (114) with the term of Equation (113)) properly taken into account and with the collective term as defined by Equation (119). The results presented in the figure represent convergences after several iterations towards the energy eigenvalues of the quartic anharmonic oscillator with the original potential $V\left(x\right)=\frac{1}{2}{x}^2+\lambda x^4$ for a small value of $\lambda$. This problem is certainly trivial. It has therefore been used as a benchmark calculation in [30] where it was possible to see the speedup obtained by adding the terms that vanish in the continuous limit. Here, I used the same problem in order to show that it is possible to modify the theory according to the BRST–dual-BRST prescription i.e., to add an auxiliary symmetry originating in the BRST–dual-BRST gauge fixing condition and to obtain equivalent results.

As the numerical verification above cannot make this point explicit by itself, it is worth mentioning that the sign problem only becomes important if the bosonic problem is numerically simple, while the equivalent fermionic problem is difficult precisely because of the sign problem. In the case when the bosonic problem is already hard, the sign problem will not increase the complexity of the already unsolvable problem.

I am aware that this example is not specifically related to the fermionic sign problem. The figures presented here only aim to show that my method is valid and consistent with known results. Further investigation of the effects of this method in more relevant physical situations (especially fermionic problems) is obviously desirable. It is important to understand the limitations of such an approach. The non-determinism associated to each field is not eliminated; only the effects of the sign problem are avoided by re-defining the theory in a way that is more amenable to path-integral Monte Carlo computations.

6. Conclusions

In conclusion, I showed that it is possible to introduce an auxiliary discrete symmetry that mimics time reversal and that this symmetry can be used in order to avoid the sign problem. It remains to be seen how general the applicability of such a method is. As said in the introduction, this article makes no claim about solving the P vs. $NP$ puzzle. It is however possible that gauge field theories may offer a new approach in solving apparently hard problems.