The Road Map toward Room-Temperature Superconductivity: Manipulating Different Pairing Channels in Systems Composed of Multiple Electronic Components
Abstract
1. Introduction
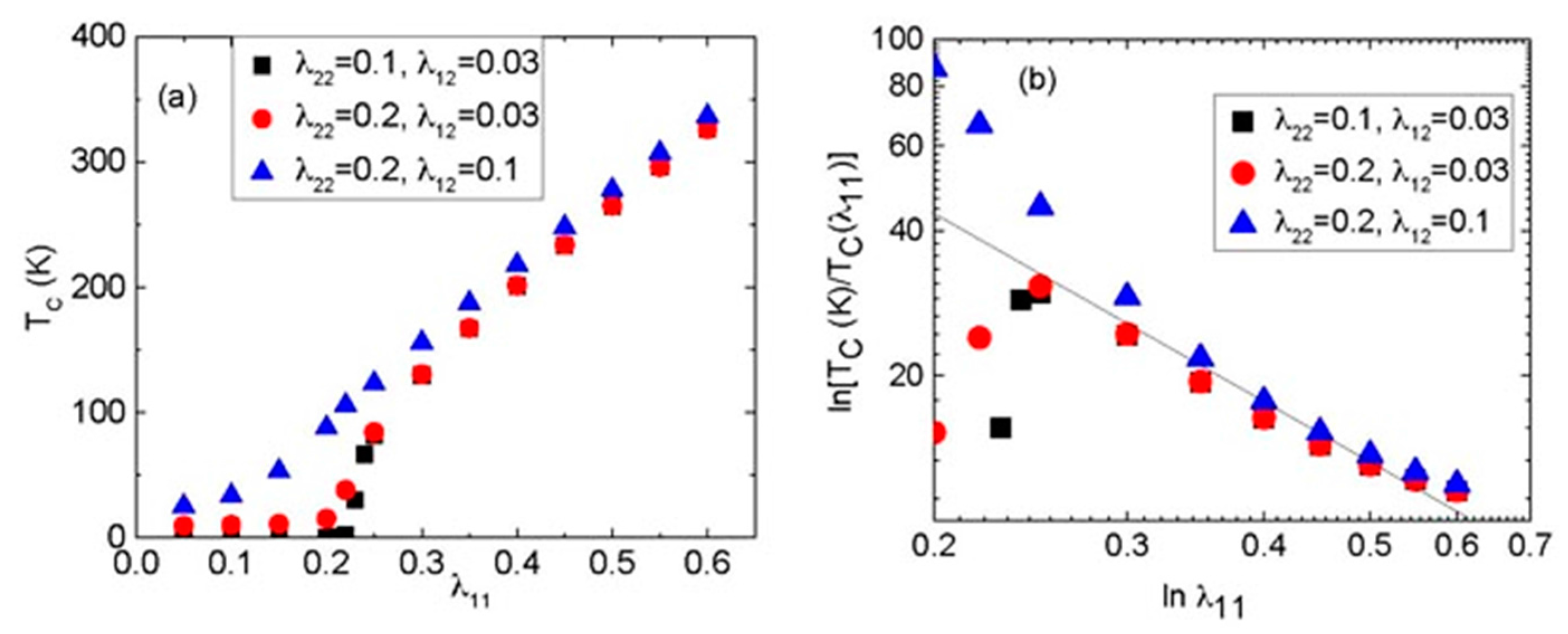
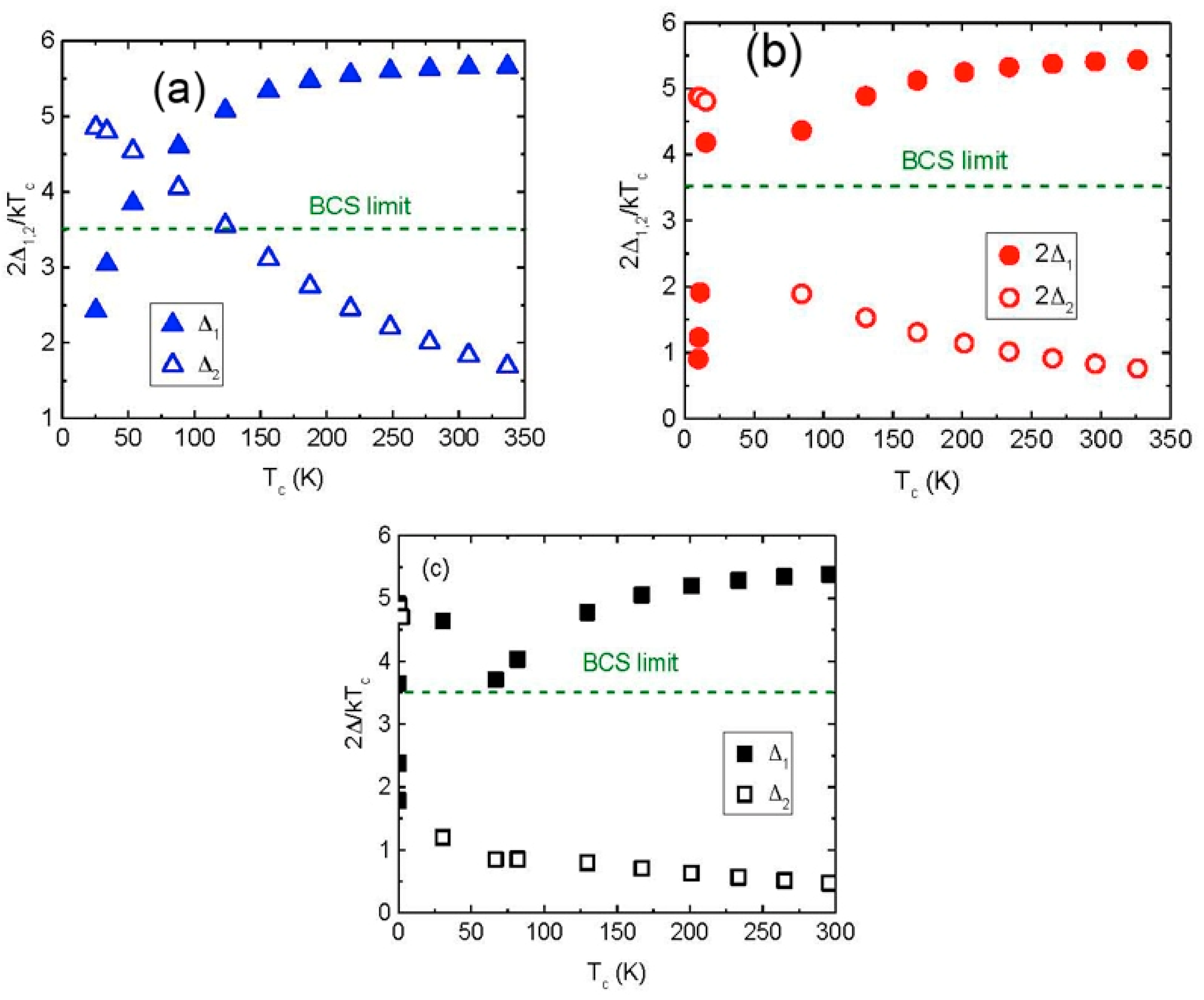
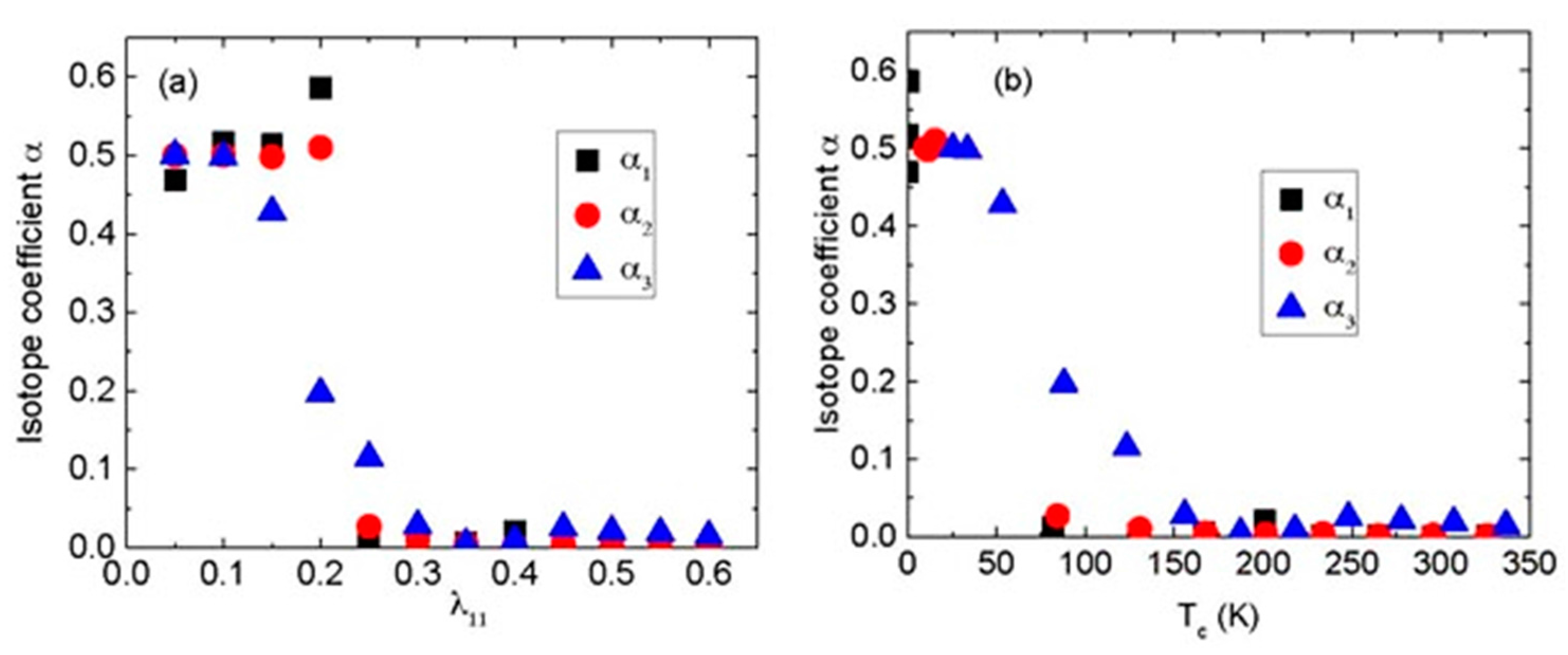
2. Results and Discussion
3. Conclusions
Author Contributions
Conflicts of Interest
References
- Bednorz, J.G.; Müller, K.A. Perovskite-type oxides the new approach to high-Tc superconductivity. Rev. Mod. Phys. 1988, 60, 585–600. [Google Scholar] [CrossRef]
- Gao, L.; Xue, Y.Y.; Chen, F.; Xiong, Q.; Meng, R.L.; Ramirez, D.; Chu, C.W.; Eggert, J.H.; Mao, H.K. Superconductivity up to 164 K in HgBa2Cam−1CumO2m+2+δ (m = 1, 2, and 3) under quasi-hydrostatic pressures. Phys. Rev. B 1994, 50, 4260–4263. [Google Scholar] [CrossRef]
- Drozdov, A.P.; Eremets, M.I.; Troyan, I.A.; Ksenofontov, V.; Shylin, S.I. Conventional superconductivity at 203 Kelvin at high pressures in the sulfur hydride system. Nature 2015, 525, 73–76. [Google Scholar] [CrossRef] [PubMed]
- Einaga, M.; Sakata, M.; Ishikawa, T.; Shimizu, K.; Eremets, M.I.; Drozdov, A.P.; Troyan, I.A.; Hirao, N.; Ohishi, Y. Crystal structure of the superconducting phase of sulfur hydride. Nat. Phys. 2016, 12, 835–838. [Google Scholar] [CrossRef] [PubMed]
- Goncharov, A.F.; Lobanov, S.S.; Kruglov, I.; Zhao, X.M.; Chen, X.J.; Oganov, A.R.; Konôpková, Z.; Prakapenka, V.B. Hydrogen sulfide at high pressure: Change in stoichiometry. Phys. Rev. B 2016, 93, 174105. [Google Scholar] [CrossRef]
- Huang, X.; Wang, X.; Duan, D.; Sundqvist, B.; Li, X.; Huang, Y.; Li, F.; Zhou, Q.; Liu, B.; Cui, T. Direct Meissner effect observation of superconductivity in compressed H2S. arXiv, 2016; arXiv:1610.02630. [Google Scholar]
- Goncharov, A.F.; Lobanov, S.S.; Prakapenka, V.B.; Greenberg, E. Stable high-pressure phases in the H-S system determined by chemically reacting hydrogen and sulfur. arXiv, 2017; arXiv:1702.02522. [Google Scholar]
- Gor’kov, L.P.; Kresin, V.Z. Pressure and high-TC superconductivity in sulfur hydrides. Sci. Rep. 2016, 6, 25608. [Google Scholar] [CrossRef] [PubMed]
- Gordon, E.E.; Xu, K.; Xiang, H.; Bussmann-Holder, A.; Kremer, R.K.; Simon, A.; Köhler, J.; Whangbo, M.-H. Structure and composition of the 200 K-Superconducting phase of H2S at ultrahigh pressure: The perovskite (SH−)(H3S+). Angew. Chem. Int. Ed. 2016, 55, 3682–3684. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, A.; Jarlborg, T. Superconductivity above the lowest Earth temperature in pressurized sulfur hydride. Europhys. Lett. 2015, 112, 37001. [Google Scholar] [CrossRef]
- Brosha, E.L.; Davies, P.K.; Garzon, F.H.; Raistrick, I.D. Metastability of Superconducting Compounds in the Y-Ba-Cu-O System. Science 1993, 260, 196–198. [Google Scholar] [CrossRef] [PubMed]
- Sleight, A.W. Room temperature superconductors. Acc. Chem. Res. 1995, 28, 103–108. [Google Scholar] [CrossRef]
- Müller, K.A.; Bussmann-Holder, A. (Eds.) Superconductivity in Complex System; Volume 114 of the Series Structure and Bonding; Springer: Berlin, Germany, 2005. [Google Scholar]
- Bianconi, A.; Missori, M.; Oyanagi, H.; Yamaguchi, H.; Nishiara, Y.; Della Longa, S. The measurement of the polaron size in the metallic phase of cuprate superconductors. Europhys. Lett. 1995, 31, 411–415. [Google Scholar] [CrossRef]
- Bianconi, A.; Saini, N.L.; Lanzara, A.; Missori, M.; Rossetti, T.; Oyanagi, H.; Yamaguchi, H.; Oka, K.; Ito, T. Determination of the local lattice distortions in the CuO2 plane of La1.85Sr0.15CuO4. Phys. Rev. Lett. 1996, 76, 3412–3415. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, A.; Bachrach, R.Z. Al surface relaxation using surface extended X-ray-absorption fine structure. Phys. Rev. Lett. 1979, 42, 104–108. [Google Scholar] [CrossRef]
- Della Longa, S.; Soldatov, A.; Pompa, M.; Bianconi, A. Atomic and electronic structure probed by X-ray absorption spectroscopy: Full multiple scattering analysis with the G4XANES package. Comput. Mater. Sci. 1995, 4, 199–210. [Google Scholar] [CrossRef]
- Bersuker, G.I.; Goodenough, J.B. Large low-symmetry polarons of the high-TC copper oxides: Formation, mobility and ordering. Phys. C Supercond. Appl. 1997, 274, 267–285. [Google Scholar] [CrossRef]
- Kusmartsev, F.V.; Di Castro, D.; Bianconi, G.; Bianconi, A. Transformation of strings into an inhomogeneous phase of stripes and itinerant carriers. Phys. Lett. A 2000, 275, 118–123. [Google Scholar] [CrossRef]
- Guidini, A.; Flammia, L.; Milošević, M.; Perali, A. BCS-BEC crossover in quantum confined superconductors. Supercond. Nov. Magn. 2016, 29, 711–715. [Google Scholar] [CrossRef]
- Bianconi, A. On the Fermi liquid coupled with a generalized Wigner polaronic CDW giving high TC superconductivity. Solid State Commun. 1994, 91, 1–5. [Google Scholar] [CrossRef]
- Muller, K.A. Possible coexistence of s- and d-wave condensates in copper oxide superconductors. Nature 1995, 377, 133–135. [Google Scholar] [CrossRef]
- Müller, K.A.; Zhao, G.-M.; Conder, K.; Keller, H. The ratio of small polarons to free carriers in derived from susceptibility measurements. J. Phys. Condens. Matter 1998, 10, L291–L296. [Google Scholar] [CrossRef]
- Perali, A.; Bianconi, A.; Lanzara, A.; Saini, N.L. The gap amplification at a shape resonance in a superlattice of quantum stripes: A mechanism for high TC. Solid State Commun. 1996, 100, 181–186. [Google Scholar] [CrossRef]
- Valletta, A.; Bianconi, A.; Perali, A.; Saini, N.L. Electronic and superconducting properties of a superlattice of quantum stripes at the atomic limit. Z. Phys. B Condens. Matter 1997, 104, 707–713. [Google Scholar] [CrossRef]
- Bianconi, A.; Valletta, A.; Perali, A.; Saini, N.L. Superconductivity of a striped phase at the atomic limit. Phys. C Supercond. 1998, 296, 269–280. [Google Scholar] [CrossRef]
- Bianconi, A. Process of Increasing the Critical Temperature TC of a Bulk Superconductor by Making Metal Heterostructures at the Atomic Limit. U.S. Patent 6,265,019, 24 July 2001. [Google Scholar]
- Bianconi, A. On the possibility of new high TC superconductors by producing metal heterostructures as in the cuprate perovskites. Solid State Commun. 1994, 89, 933–936. [Google Scholar] [CrossRef]
- Bianconi, A.; Missori, M. High TC superconductivity by quantum confinement. J. Phys. I Fr. 1994, 4, 361–365. [Google Scholar] [CrossRef]
- Cariglia, M.; Vargas-Paredes, A.; Doria, M.; Bianconi, A.; Milošević, M.; Perali, A. Shape-resonant superconductivity in nanofilms: From weak to strong coupling. J. Supercond. Nov. Magn. 2016, 29, 3081–3086. [Google Scholar] [CrossRef]
- Khasanov, R.; Strässle, S.; Di Castro, D.; Masui, T.; Miyasaka, S.; Tajima, S.; Bussmann-Holder, A.; Keller, H. Multiple gap symmetries for the order parameter of cuprate superconductors from penetration depth measurements. Phys. Rev. Lett. 2007, 99, 237601. [Google Scholar] [CrossRef] [PubMed]
- Keller, H.; Bussmann-Holder, A.; Müller, K.A. Jahn–Teller physics and high-TC superconductivity. Mater. Today 2008, 11, 38–46. [Google Scholar] [CrossRef]
- Bianconi, A. Multiband superconductivity in high TC cuprates and diborides. J. Phys. Chem. Solids 2006, 67, 567–570. [Google Scholar] [CrossRef]
- Vishik, I.M.; Hashimoto, M.; He, R.H.; Lee, W.S.; Schmitt, F.; Lu, D.; Moore, R.G.; Zhang, C.; Meevasana, W.; Sasagawa, T.; et al. Phase competition in trisected superconducting dome. Proc. Natl. Acad. Sci. USA 2012, 109, 18332–18337. [Google Scholar] [CrossRef] [PubMed]
- Inosov, D.S.; Park, J.T.; Charnukha, A.; Li, Y.; Boris, A.V.; Keimer, B.; Hinkov, V. Crossover from weak to strong pairing in unconventional superconductors. Phys. Rev. B 2011, 83, 214520. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Keller, H. Unconventional isotope effects, multi-component superconductivity and polaron formation in high temperature cuprate superconductors. J. Phys. Conf. Ser. 2008, 108, 012019. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Keller, H.; Khasanov, R.; Simon, A.; Bianconi, A.; Bishop, A.R. Isotope and interband effects in a multi-band model of superconductivity. New J. Phys. 2011, 13, 093009. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Keller, H. Isotope and multiband effects in layered superconductors. J. Phys. Condens. Matter 2012, 24, 233201. [Google Scholar] [CrossRef] [PubMed]
- Perali, A.; Innocenti, D.; Valletta, A.; Bianconi, A. Anomalous isotope effect near a 2.5 Lifshitz transition in a multi-band multi-condensate superconductor made of a superlattice of stripes. Supercond. Sci. Technol. 2012, 25, 124002. [Google Scholar] [CrossRef]
- Bianconi, A.; Filippi, M. Feshbach shape resonances in multiband high TC superconductors. In Symmetry and Heterogeneity in High Temperature Superconductors; Bianconi, A., Ed.; Springer: Dordrecht, The Netherlands, 2006; Chapter 2; pp. 21–53. [Google Scholar]
- Kristoffel, N.; Rubin, P.; Örd, T. Multiband model of cuprate superconductivity. Int. J. Mod. Phys. B 2008, 22, 5299–5327. [Google Scholar] [CrossRef]
- Deng, S.; Simon, A.; Köhler, J. Flat band–steep band scenario and superconductivity—The case of calcium. Solid State Sci. 1998, 2, 31–38. [Google Scholar] [CrossRef]
- Deng, S.; Simon, A.; Köhler, J. Calcium d States: Chemical Bonding of CaC6. Angew. Chem. Int. Ed. 2008, 47, 6703–6706. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, A.; Di Castro, D.; Agrestini, S.; Campi, G.; Saini, N.L.; Saccone, A.; De Negri, S.; Giovannini, M. A superconductor made by a metal heterostructure at the atomic limit tuned at the ‘shape resonance’: MgB2. J. Phys. Condens. Matter 2001, 13, 7383–7390. [Google Scholar] [CrossRef]
- Agrestini, S.; Di Castro, D.; Sansone, M.; Saini, N.L.; Saccone, A.; De Negri, S.; Giovannini, M.; Colapietro, M.; Bianconi, A. High TC superconductivity in a critical range of micro-strain and charge density in diborides. J. Phys. Condens. Matter 2001, 13, 11689–11695. [Google Scholar] [CrossRef]
- Di Castro, D.; Agrestini, S.; Campi, G.; Cassetta, A.; Colapietro, M.; Congeduti, A.; Continenza, A.; Negri, S.D.; Giovannini, M.; Massidda, S.; et al. The amplification of the superconducting TC by combined effect of tuning of the Fermi level and the tensile micro-strain in Al1−xMgxB2. Europhys. Lett. 2002, 58, 278–284. [Google Scholar] [CrossRef]
- Bianconi, A.; Agrestini, S.; Di Castro, D.; Campi, G.; Zangari, G.; Saini, N.; Saccone, A.; De Negri, S.; Giovannini, M.; Profeta, A.; et al. Scaling of the critical temperature with the Fermi temperature in diborides. Phys. Rev. B 2002, 65, 174515. [Google Scholar] [CrossRef]
- Deng, S.; Simon, A.; Köhler, J. Superconductivity in MgB2: A case study of the “flat Band–Steep band” scenario. J. Supercond. 2003, 16, 477–481. [Google Scholar] [CrossRef]
- Deng, S.; Simon, A.; Köhler, J. A “flat/steep band” model for superconductivity. Int. J. Mod. Phys. B 2005, 19, 29–36. [Google Scholar] [CrossRef]
- Bussmann-Holder, A.; Bianconi, A. Raising the diboride superconductor transition temperature using quantum interference effects. Phys. Rev. B 2003, 67, 132509. [Google Scholar] [CrossRef]
- Suhl, H.; Matthias, B.T.; Walker, L.R. Bardeen-Cooper-Schrieffer theory of superconductivity in the case of overlapping bands. Phys. Rev. Lett. 1959, 3, 552–554. [Google Scholar] [CrossRef]
- Ummarino, G.A.; Gonnelli, R.S.; Massidda, S.; Bianconi, A. Two-band Eliashberg equations and the experimental TC of the diboride Mg1−xAlxB2. Phys. C Supercond. 2004, 407, 121–127. [Google Scholar] [CrossRef][Green Version]
- Innocenti, D.; Poccia, N.; Ricci, A.; Valletta, A.; Caprara, S.; Perali, A.; Bianconi, A. Resonant and crossover phenomena in a multiband superconductor: Tuning the chemical potential near a band edge. Phys. Rev. B 2010, 82, 184528. [Google Scholar] [CrossRef]
- Lifshitz, I.M. Anomalies of electron characteristics of a metal in the high pressure region. Sov. Phys. JEPT 1960, 11, 1130–1135. [Google Scholar]
- Bianconi, A. Feshbach shape resonance in multiband superconductivity in heterostructures. J. Supercond. 2005, 18, 625–636. [Google Scholar] [CrossRef]
- Imada, M.; Misawa, T.; Yamaji, Y. Unconventional quantum criticality emerging as a new common language of transition-metal compounds, heavy-fermion systems, and organic conductors. J. Phys. Condens. Matter 2010, 22, 164206. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Caivano, R.; Fratini, M.; Poccia, N.; Ricci, A.; Puri, A.; Ren, Z.-A.; Dong, X.-L.; Yang, J.; Lu, W.; Zhao, Z.-X.; et al. Feshbach resonance and mesoscopic phase separation near a quantum critical point in multiband FeAs-based superconductors. Supercond. Sci. Technol. 2009, 22, 014004. [Google Scholar] [CrossRef]
- Bianconi, A.; Poccia, N.; Ricci, A. Unity in the diversity. J. Supercond. Nov. Magn. 2009, 22, 526–527. [Google Scholar] [CrossRef]
- Innocenti, D.; Valletta, A.; Bianconi, A. Shape resonance at a Lifshitz transition for high temperature superconductivity in multiband superconductors. J. Supercond. Nov. Magn. 2011, 24, 1137–1143. [Google Scholar] [CrossRef]
- Innocenti, D.; Caprara, S.; Poccia, N.; Ricci, A.; Valletta, A.; Bianconi, A. Shape resonance for the anisotropic superconducting gaps near a Lifshitz transition: The effect of electron hopping between layers. Supercond. Sci. Technol. 2011, 24, 015012. [Google Scholar] [CrossRef]
- Liu, C.; Palczewski, A.D.; Dhaka, R.S.; Kondo, T.; Fernandes, R.M.; Mun, E.D.; Hodovanets, H.; Thaler, A.N.; Schmalian, J.; Bud’ko, S.L.; et al. Importance of the Fermi-surface topology to the superconducting state of the electron-doped pnictide Ba(Fe1–xCox)2As2. Phys. Rev. B 2011, 84, 020509. [Google Scholar] [CrossRef]
- Borisenko, S.V.; Zabolotnyy, V.B.; Kordyuk, A.A.; Evtushinsky, D.V.; Kim, T.K.; Morozov, I.V.; Follath, R.; Büchner, B. One-Sign order parameter in iron based superconductor. Symmetry 2012, 4, 251–264. [Google Scholar] [CrossRef]
- Kordyuk, A.A.; Zabolotnyy, V.B.; Evtushinsky, D.V.; Yaresko, A.N.; Büchner, B.; Borisenko, S.V. Electronic band structure of Ferro-Pnictide superconductors from ARPES experiment. J. Supercond. Nov. Magn. 2013, 26, 2837–2841. [Google Scholar] [CrossRef]
- Borisenko, S.V.; Evtushinsky, D.V.; Liu, Z.H.; Morozov, I.; Kappenberger, R.; Wurmehl, S.; Büchner, B.; Yaresko, A.N.; Kim, T.K.; Hoesch, M.; et al. Direct observation of spin–orbit coupling in iron-based superconductors. Nat. Phys. 2015, 12, 311–317. [Google Scholar] [CrossRef]
- Charnukha, A.; Evtushinsky, D.V.; Matt, C.E.; Xu, N.; Shi, M.; Büchner, B.; Zhigadlo, N.D.; Batlogg, B.; Borisenko, S.V. High-temperature superconductivity from fine-tuning of Fermi-surface singularities in iron oxypnictides. Sci. Rep. 2015, 5, 18273. [Google Scholar] [CrossRef] [PubMed]
- Gonnelli, R.S.; Daghero, D.; Tortello, M.; Ummarino, G.A.; Bukowski, Z.; Karpinski, J.; Reuvekamp, P.G.; Kremer, R.K.; Profeta, G.; Suzuki, K.; et al. Fermi-Surface topological phase transition and horizontal Order-Parameter nodes in CaFe2As2 under pressure. Sci. Rep. 2016, 6, 26394. [Google Scholar] [CrossRef] [PubMed]
- Pustovit, Y.; Kordyuk, A.A. Metamorphoses of electronic structure of FeSe-based superconductors (review article). Low Temp. Phys. 2016, 42, 995–1007. [Google Scholar] [CrossRef][Green Version]
- Bianconi, A. Quantum materials: Shape resonances in superstripes. Nat. Phys. 2013, 9, 536–537. [Google Scholar] [CrossRef]
- Bianconi, A.; Jarlborg, T. Lifshitz transitions and zero point lattice fluctuations in sulfur hydride showing near room temperature superconductivity. Nov. Supercond. Mater. 2015, 1, 39–47. [Google Scholar] [CrossRef]
- Jarlborg, T.; Bianconi, A. Breakdown of the Migdal approximation at lifshitz transitions with giant zero-point motion in the H3S superconductor. Sci. Rep. 2016, 6, 24816. [Google Scholar] [CrossRef] [PubMed]
- Bussmann-Holder, A.; Köhler, J.; Whangbo, M.H.; Bianconi, A.; Simon, A. High temperature superconductivity in sulfur hydride under ultrahigh pressure: A complex superconducting phase beyond conventional BCS. Nov. Supercond. Mater. 2016, 2, 37. [Google Scholar] [CrossRef][Green Version]
- Bussmann-Holder, A.; Köhler, J.; Simon, A.; Whangbo, M.; Bianconi, A. Multigap superconductivity at extremely high temperature: A model for the case of pressurized H2S. J. Supercond. Nov. Magn. 2017, 30, 151–156. [Google Scholar] [CrossRef]
- Perali, A.; Pieri, P.; Strinati, G.C.; Castellani, C. Pseudogap and spectral function from superconducting fluctuations to the bosonic limit. Phys. Rev. B 2002, 66, 024510. [Google Scholar] [CrossRef]
- Palestini, F.; Perali, A.; Pieri, P.; Strinati, G.C. Dispersions, weights, and widths of the single-particle spectral function in the normal phase of a Fermi gas. Phys. Rev. B 2012, 85, 024517. [Google Scholar] [CrossRef]
- Guidini, A.; Perali, A. Band-edge BCS–BEC crossover in a two-band superconductor: Physical properties and detection parameters. Supercond. Sci. Technol. 2014, 27, 124002. [Google Scholar] [CrossRef]
- Shanenko, A.A.; Croitoru, M.D.; Vagov, A.V.; Axt, V.M.; Perali, A.; Peeters, F.M. Atypical BCS-BEC crossover induced by quantum-size effects. Phys. Rev. A 2012, 86, 033612. [Google Scholar] [CrossRef]
- Bianconi, A.; Di Castro, D.; Saini, N.L.; Bianconi, G. Superstripes (self organization of quantum wires in high TC superconductors). In Phase Transitions and Self-Organization in Electronic and Molecular Networks; Thorpe, M.F., Phillips, J.C., Eds.; Springer: Boston, MA, USA, 2001; Chapter 24; pp. 375–388. [Google Scholar]
- Bianconi, A.; Di Castro, D.; Bianconi, G.; Pifferi, A.; Saini, N.L.; Chou, F.C.; Johnston, D.C.; Colapietro, M. Coexistence of stripes and superconductivity: TC amplification in a superlattice of superconducting stripes. Phys. C Supercond. 2000, 341–348, 1719–1722. [Google Scholar] [CrossRef]
- Di Castro, D.; Bianconi, G.; Colapietro, M.; Pifferi, A.; Saini, N.L.; Agrestini, S.; Bianconi, A. Evidence for the strain critical point in high TC superconductors. Eur. Phys. J. B Condens. Matter Complex Syst. 2000, 18, 617–624. [Google Scholar] [CrossRef]
- Campi, G.; Bianconi, A.; Poccia, N.; Bianconi, G.; Barba, L.; Arrighetti, G.; Innocenti, D.; Karpinski, J.; Zhigadlo, N.D.; Kazakov, S.M.; et al. Inhomogeneity of charge-density-wave order and quenched disorder in a high-TC superconductor. Nature 2015, 525, 359–362. [Google Scholar] [CrossRef] [PubMed]
- Slezak, J.A.; Lee, J.; Wang, M.; McElroy, K.; Fujita, K.; Andersen, B.M.; Hirschfeld, P.J.; Eisaki, H.; Uchida, S.; Davis, J.C. Imaging the impact on cuprate superconductivity of varying the interatomic distances within individual crystal unit cells. Proc. Natl. Acad. Sci. USA 2008, 105, 3203–3208. [Google Scholar] [CrossRef] [PubMed]
- Phillips, J.C. Ineluctable complexity of high temperature superconductivity elucidated. J. Supercond. Nov. Magn. 2014, 27, 345–347. [Google Scholar] [CrossRef]
- Kresin, V.; Ovchinnikov, Y.; Wolf, S. Inhomogeneous superconductivity and the “pseudogap” state of novel superconductors. Phys. Rep. 2006, 431, 231–259. [Google Scholar] [CrossRef]
- Deutscher, G.; de Gennes, P.-G. A spatial interpretation of emerging superconductivity in lightly doped cuprates. C. R. Phys. 2007, 8, 937–941. [Google Scholar] [CrossRef]
- Kugel, K.I.; Rakhmanov, A.L.; Sboychakov, A.O.; Poccia, N.; Bianconi, A. Model for phase separation controlled by doping and the internal chemical pressure in different cuprate superconductors. Phys. Rev. B 2008, 78, 165124. [Google Scholar] [CrossRef]
- Deutscher, G. The role of Cu-O bond length fluctuations in the high temperature superconductivity mechanism. J. Appl. Phys. 2012, 111, 112603. [Google Scholar] [CrossRef]
- Bianconi, G. Superconductor-insulator transition in a network of 2d percolation clusters. Europhys. Lett. 2013, 101, 26003. [Google Scholar] [CrossRef]
- Carlson, E.W. Condensed-matter physics: Charge topology in superconductors. Nature 2015, 525, 329–330. [Google Scholar] [CrossRef] [PubMed]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bussmann-Holder, A.; Köhler, J.; Simon, A.; Whangbo, M.-H.; Bianconi, A.; Perali, A. The Road Map toward Room-Temperature Superconductivity: Manipulating Different Pairing Channels in Systems Composed of Multiple Electronic Components. Condens. Matter 2017, 2, 24. https://doi.org/10.3390/condmat2030024
Bussmann-Holder A, Köhler J, Simon A, Whangbo M-H, Bianconi A, Perali A. The Road Map toward Room-Temperature Superconductivity: Manipulating Different Pairing Channels in Systems Composed of Multiple Electronic Components. Condensed Matter. 2017; 2(3):24. https://doi.org/10.3390/condmat2030024
Chicago/Turabian StyleBussmann-Holder, Annette, Jürgen Köhler, Arndt Simon, Myung-Hwan Whangbo, Antonio Bianconi, and Andrea Perali. 2017. "The Road Map toward Room-Temperature Superconductivity: Manipulating Different Pairing Channels in Systems Composed of Multiple Electronic Components" Condensed Matter 2, no. 3: 24. https://doi.org/10.3390/condmat2030024
APA StyleBussmann-Holder, A., Köhler, J., Simon, A., Whangbo, M.-H., Bianconi, A., & Perali, A. (2017). The Road Map toward Room-Temperature Superconductivity: Manipulating Different Pairing Channels in Systems Composed of Multiple Electronic Components. Condensed Matter, 2(3), 24. https://doi.org/10.3390/condmat2030024









