Goldstone and Higgs Hydrodynamics in the BCS–BEC Crossover
Abstract
:1. Introduction
2. Functional Integration for the BCS–BEC Crossover
2.1. Loop Expansion and Gaussian Approximation
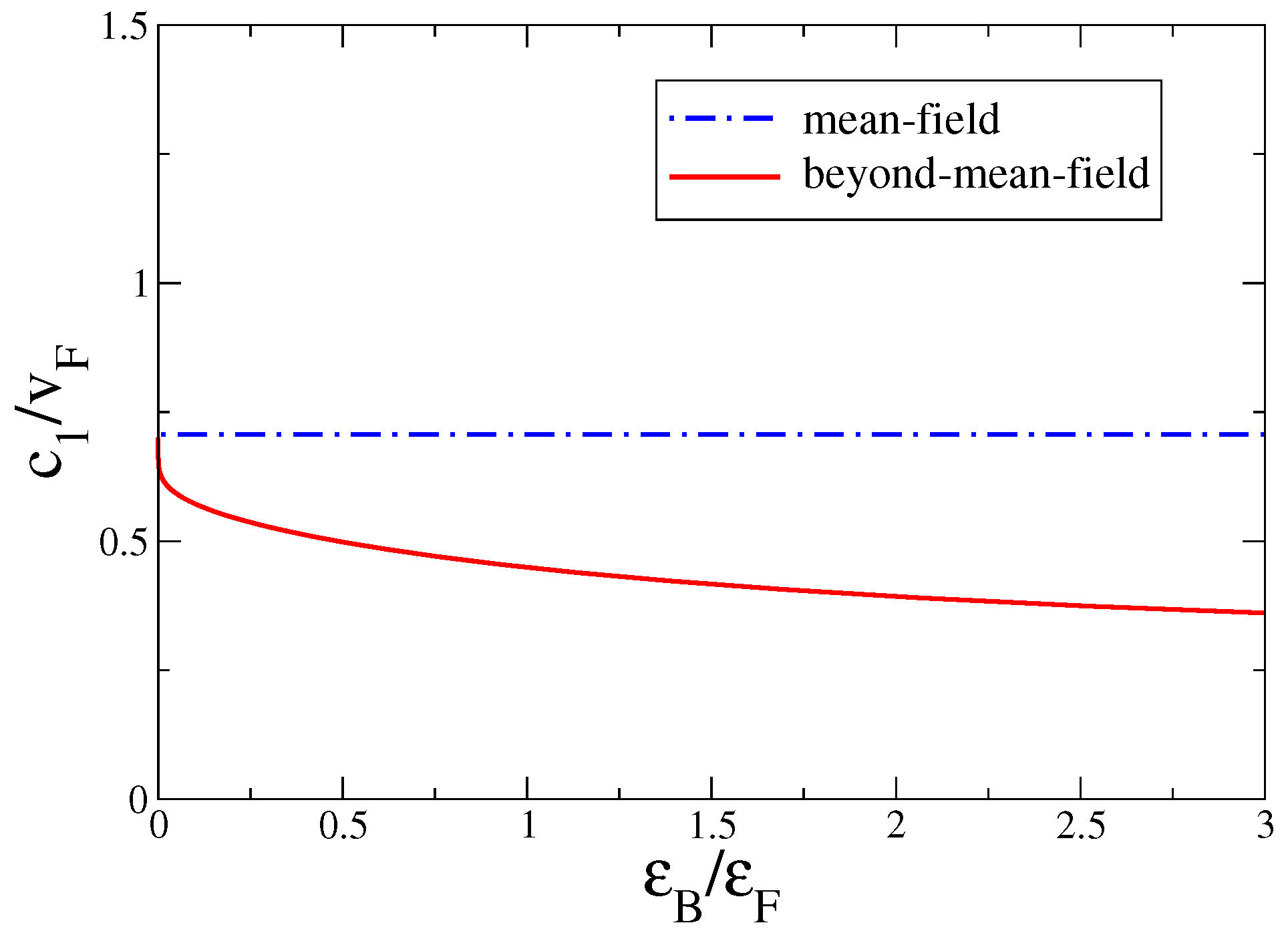
2.2. Beyond-Mean-Field Grand Potential
3. Low-Energy Gaussian Action
3.1. Connection with the Popov’s Hydrodynamic Action Functional
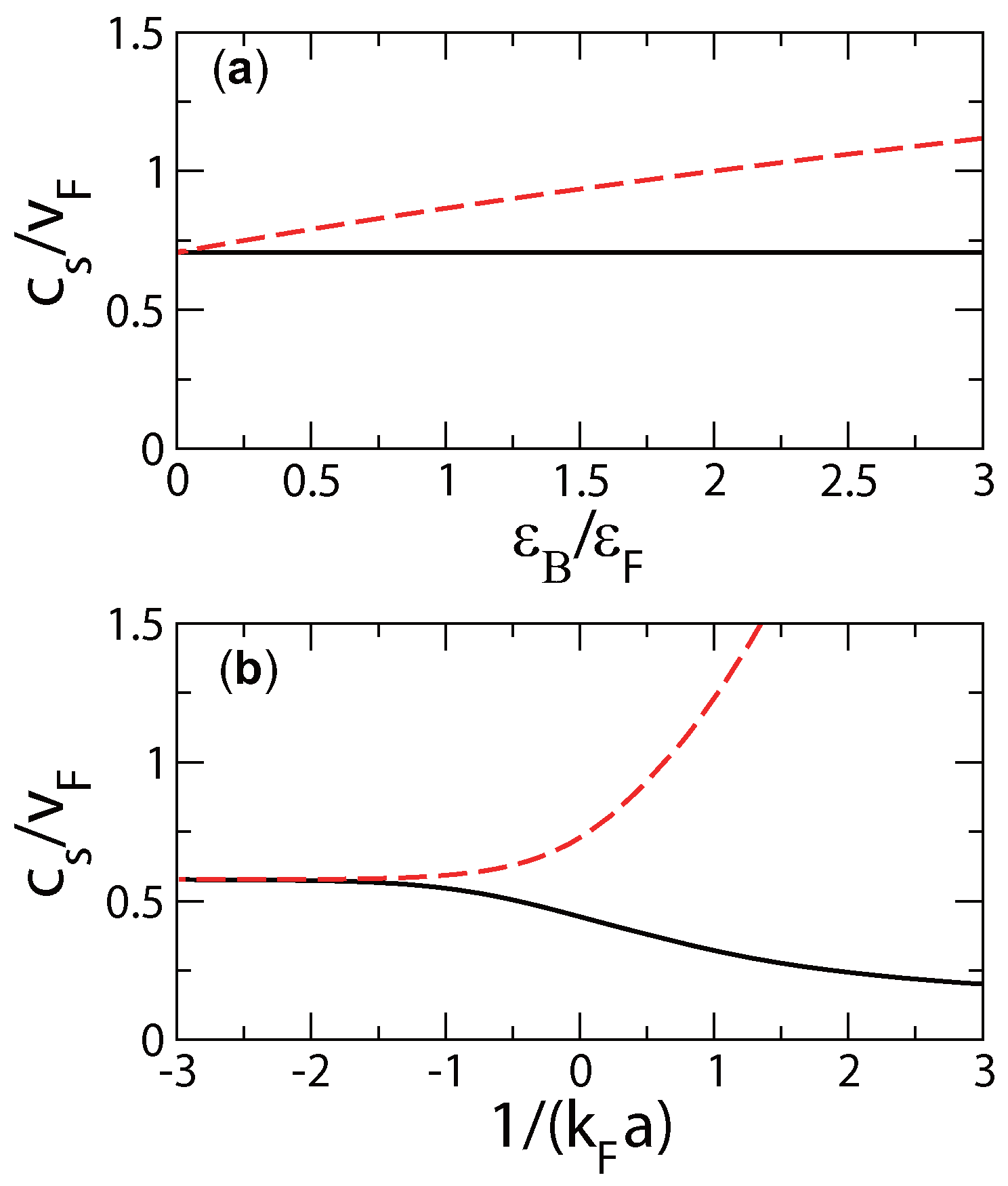
3.2. First Sound Velocity from Thermodynamics
4. Conclusions
Conflicts of Interest
References
- Greiner, M.; Regal, C.A.; Jin, D.S. Emergence of a Molecular Bose-Einstein Condensate from a Fermi Gas. Nature 2003, 426, 537–540. [Google Scholar] [CrossRef] [PubMed]
- Chin, C.; Bartenstein, M.; Altmeyer, A.; Riedl, S.; Jochim, S.; Hecker Denschlag, J.; Grimm, R. Observation of the Pairing Gap in a Strongly Interacting Fermi Gas. Science 2004, 305, 1128–1130. [Google Scholar] [CrossRef] [PubMed]
- Smerzi, A.; Fantoni, S.; Giovanazzi, S.; Shenoy, S.R. Quantum coherent atomic tunneling between two trapped Bose-Einstein condensates. Phys. Rev. Lett. 1997, 79, 4950. [Google Scholar] [CrossRef]
- Salasnich, L.; Parola, A.; Reatto, L. Bose condensate in a double-well trap: Ground state and elementary excitations. Phys. Rev. A 1999, 60, 4171–4174. [Google Scholar] [CrossRef]
- Salasnich, L.; Manini, N.; Toigo, F. Macroscopic periodic tunneling of Fermi atoms in the BCS-BEC crossover. Phys. Rev. A 2008, 77, 043609. [Google Scholar] [CrossRef]
- Valtolina, G.; Burchianti, A.; Amico, A.; Neri, E.; Xhani, K.; Seman, J.A.; Trombettoni, A.; Smerzi, A.; Zaccanti, A.; Inguscio, M.; et al. Josephson effect in fermionic superfluids across the BEC-BCS crossover. Science 2016, 350, 1505–1508. [Google Scholar] [CrossRef] [PubMed]
- Makhalov, V.; Martiyanov, K.; Turlapov, A. Ground-state pressure of quasi-2D Fermi and Bose gases. Phys. Rev. Lett. 2014, 112, 045301. [Google Scholar] [CrossRef] [PubMed]
- Murthy, P.A.; Boettcher, I.; Bayha, L.; Holzmann, M.; Kedar, D.; Neidig, M.; Ries, M.G.; Wenz, A.N.; Zurn, G.; Jochim, S. Observation of the Berezinskii-Kosterlitz-Thouless phase transition in an ultracold Fermi gas. Phys. Rev. Lett. 2015, 115, 010401. [Google Scholar] [CrossRef] [PubMed]
- Fenech, K.; Dyke, P.; Peppler, T.; Lingham, M.G.; Hoinka, S.; Hu, H.; Vale, C.J. Thermodynamics of an attractive 2D Fermi gas. Phys. Rev. Lett. 2016, 116, 045302. [Google Scholar] [CrossRef] [PubMed]
- Boettcher, I.; Bayha, L.; Kedar, D.; Murthy, P.A.; Neidig, M.; Ries, M.G.; Wenz, A.N.; Zurn, G.; Jochim, S.; Enss, T. Equation of state of ultracold fermions in the 2D BEC-BCS crossover. Phys. Rev. Lett. 2016, 116, 045303. [Google Scholar] [CrossRef] [PubMed]
- Salasnich, L.; Marchetti, P.A.; Toigo, F. Superfluidity, sound velocity, and quasicondensation in the two-dimensional BCSBEC crossover. Phys. Rev. A 2013, 88, 053612. [Google Scholar] [CrossRef]
- Salasnich, L.; Toigo, F. Composite bosons in the two-dimensional BCS-BEC crossover from Gaussian fluctuations. Phys. Rev. A 2015, 91, 011604. [Google Scholar] [CrossRef]
- He, L.; Lv, H.; Cao, G.; Hu, H.; Liu, X.-J. Quantum fluctuations in the BCS-BEC crossover of two-dimensional Fermi gases. Phys. Rev. A 2015, 92, 023620. [Google Scholar] [CrossRef]
- Mulkerin, B.C.; Fenech, K.; Dyke, P.; Vale, C.J.; Liu, X.-J.; Hu, H. Comparison of strong-coupling theories for a two-dimensional Fermi gas. Phys. Rev. A 2015, 92, 063636. [Google Scholar] [CrossRef]
- Bighin, G.; Salasnich, L. Finite-temperature quantum fluctuations in two-dimensional Fermi superfluids. Phys. Rev. B 2016, 93, 014519. [Google Scholar] [CrossRef]
- Salasnich, L.; Toigo, F. Zero-point energy of ultracold atoms. Phys. Rep. 2016, 640, 1–29. [Google Scholar] [CrossRef]
- Mulkerin, B.C.; He, L.; Dyke, P.; Vale, C.J.; Hu, H. Superfluid Density and Critical Velocity Near the Fermionic Berezinskii–Kosterlitz–Thouless Transition. Available online: http://arxiv.org/abs/1702.07091 (accessed on 30 May 2017).
- Larkin, A.; Varlamov, A. Theory of Fluctuations in Superconductors; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Chen, Q.; Stajic, J.; Tan, S.; Levin, K. BCS–BEC crossover: From high temperature superconductors to ultracold superfluids. Phys. Rep. 2005, 412, 1–88. [Google Scholar] [CrossRef]
- Okazaji, K.; Ito, Y.; Ota, Y.; Kotani, Y.; Shimojima, T.; Kiss, T.; Watanabe, S.; Chen, C.-T.; Niitaka, S.; Hanaguri, T.; et al. Superconductivity in an electron band just above the Fermi level. Sci. Rep. 2014, 4, 4109. [Google Scholar] [CrossRef] [PubMed]
- Berezinskii, V.L. Destruction of long-range order in one-dimensional and two-dimensional systems possessing a continuous symmetry group. II. Quantum systems. Sov. Phys. JETP 1972, 34, 610–616. [Google Scholar]
- Kosterlitz, J.M.; Thouless, D.J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C Solid State Phys. 1973, 6, 1181–1203. [Google Scholar] [CrossRef]
- Bighin, G.; Salasnich, L. Vortices and antivortices in two-dimensional ultracold Fermi gases. Sci. Rep. 2017, 7, 45702. [Google Scholar] [CrossRef] [PubMed]
- Nelson, D.R.; Kosterlitz, J.M. Universal jump in the superfluid density of two-dimensional superfluids. Phys. Rev. Lett. 1977, 39, 1201–1205. [Google Scholar] [CrossRef]
- Nagaosa, N. Quantum Field Theory in Condensed Matter Physics; Springer: Berlin, Germany, 1999. [Google Scholar]
- Altland, A.; Simons, B. Condensed Matter Field Theory; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Stoof, H.T.C.; Gubbels, K.B.; Dickerscheid, D.B.M. Ultracold Quantum Fields; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Pekker, D.; Varma, C.M. Amplitude/Higgs modes in condensed matter physics. Annu. Rev. Condens. Matter Phys. 2015, 6, 269–297. [Google Scholar] [CrossRef]
- Tempere, J.; Devreese, J.P.A. Superconductors—Materials, Properties and Applications; InTech: Rijeka, Croatia, 2012; pp. 1–32. [Google Scholar]
- Taylor, E.; Griffin, A.; Fukushima, N.; Ohashi, Y. Pairing fluctuations and the superfluid density through the BCS-BEC crossover. Phys. Rev. A 2006, 74, 063626. [Google Scholar] [CrossRef]
- Hu, H.; Liu, X.-J.; Drummond, P.D. Equation of state of a superfluid Fermi gas in the BCS-BEC. Europhys. Lett. 2006, 74, 574–580. [Google Scholar] [CrossRef]
- Nozieres, P.; Schmitt-Rink, S. Bose condensation in an attractive fermion gas: From weak to strong coupling superconductivity. J. Low Temp. Phys. 1985, 59, 195–211. [Google Scholar] [CrossRef]
- Engelbrecht, J.R.; Randeria, M.; Sa de Melo, C.A.R. BCS to Bose crossover: Broken-symmetry state. Phys. Rev. B 1997, 55, 15153–15156. [Google Scholar] [CrossRef]
- Diener, R.B.; Sensarma, R.; Randeria, M. Quantum Fluctuations in the Superfluid State of the BCS-BEC Crossover. Phys. Rev. A 2008, 77, 023626. [Google Scholar] [CrossRef]
- Schakel, A.M.J. Derivation of the effective action of a dilute Fermi gas in the unitary limit of the BCS-BEC crossover. Ann. Phys. 2011, 326, 193–206. [Google Scholar] [CrossRef]
- Lin, C.-Y.; Lee, D.-S.; Rivers, R.J. Spontaneous vortex production in driven condensates with narrow Feschbach resonances. Phys. Rev. A 2011, 84, 013623. [Google Scholar] [CrossRef]
- Hsiang, J.-T.; Lin, C.-Y.; Lee, D.-S.; Rivers, R.J. The role of causality in tunable Fermi gas condensates. J. Phys. Condens. Matter 2013, 25, 404211. [Google Scholar] [CrossRef] [PubMed]
- Anderson, B.M.; Boyack, R.; Wu, C.-T.; Levin, K. Correcting inconsistencies in the conventional superfluid path integral scheme. Phys. Rev. B 2016, 93, 180504. [Google Scholar] [CrossRef]
- Popov, V.N. Functional Integrals in Quantum Field Theory and Statistical Physics; Reidel: Dordrecht, The Netherlands, 1983. [Google Scholar]
- Landau, L.D. The theory of superfuidity of helium II. Phys. Rev. 1941, 60, 356–358. [Google Scholar] [CrossRef]
- Salasnich, L.; Toigo, F. Extended Thomas-Fermi density functional for the unitary Fermi gas. Phys. Rev. A 2008, 78, 053626. [Google Scholar] [CrossRef]
- Adhikari, S.K.; Salasnich, L. Effective nonlinear Schrodinger equations for cigar-shaped and disc-shaped Fermi superfluids at unitarity. New J. Phys. 2009, 11, 023011. [Google Scholar] [CrossRef]
- Khalatnikov, I.M. An Introduction to the Theory of Superfluidity; Avalon Publishing: New York, NY, USA, 1965. [Google Scholar]
- Combescot, R.; Kagan, M.Y.; Stringari, S. Collective mode of homogeneous superfluid Fermi gases in the BEC-BCS crossover. Phys. Rev. A 2006, 74, 042717. [Google Scholar] [CrossRef]
- Luick, N. Local Probing of the Berezinskii-Kosterlitz-Thouless Transition in a Two-Dimensional Bose Gas. Master Thesis, University of Hamburg, Hamburg, Germany, Unpublished work. 2014. [Google Scholar]
- Popov, V.N. On the theory of the superfluidity of two- and one-dimensional Bose systems. Theor. Math. Phys. A 1972, 11, 565–573. [Google Scholar] [CrossRef]
- Salasnich, L. Non-Universal equation of state of the two-dimensional Bose gas. Phys. Rev. Lett. 2017, 118, 130402. [Google Scholar] [CrossRef] [PubMed]
- Simonucci, S.; Strinati, G.C. Equation for the superfluid gap obtained by coarse graining the Bogoliubov—De Gennes equations throughout the BCS-BEC crossover. Phys. Rev. B 2014, 89, 054511. [Google Scholar] [CrossRef]
- Lombardi, G.; Van Alphen, W.; Klimin, S.N.; Tempere, J. Soliton-core filling in superfluid Fermi gases with spin imbalance. Phys. Rev. A 2016, 93, 013614. [Google Scholar] [CrossRef]

© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salasnich, L. Goldstone and Higgs Hydrodynamics in the BCS–BEC Crossover. Condens. Matter 2017, 2, 22. https://doi.org/10.3390/condmat2020022
Salasnich L. Goldstone and Higgs Hydrodynamics in the BCS–BEC Crossover. Condensed Matter. 2017; 2(2):22. https://doi.org/10.3390/condmat2020022
Chicago/Turabian StyleSalasnich, Luca. 2017. "Goldstone and Higgs Hydrodynamics in the BCS–BEC Crossover" Condensed Matter 2, no. 2: 22. https://doi.org/10.3390/condmat2020022
APA StyleSalasnich, L. (2017). Goldstone and Higgs Hydrodynamics in the BCS–BEC Crossover. Condensed Matter, 2(2), 22. https://doi.org/10.3390/condmat2020022





