Generation of Affine-Shifted S-Boxes with Constant Confusion Coefficient Variance and Application in the Partitioning of the S-Box Space

Abstract

Among the multiple important properties that characterize strong S-boxes for symmetric cryptography and are used in their designs, this study focuses on two: the non-linearity property, a classical security metric, and the confusion coefficient variance property, a statistical proxy for side channel resistance under the Hamming weight leakage model. Given an S-box, two sets can be created: the set of affine-shifted S-boxes, where S-boxes have the same non-linearity value, and the set of Hamming weight classes, where S-boxes have the same confusion coefficient variance value. The inherent values of these two properties ensure resistance to cryptographic attacks; however, if the value of one property increases, it will imply a decrease in the value of the other property. In view of the aforementioned fact, attaining a trade-off becomes a complex undertaking. The impetus for this research stems from the following hypothesis: if an initial S-box already exhibits a trade-off, it would be advantageous to employ a method that generates new S-boxes while preserving the balance. A thorough review of the extant literature reveals the absence of any methodology that encompasses the aforementioned elements. The present paper proposes a novel methodology for generating an affine-shifted subset of S-boxes, ensuring that the resulting subset possesses the same confusion coefficient variance value. We provide insights on the optimal search strategy to optimize non-linearity and confusion coefficient variance. The proposed methodology guarantees the preservation of constant values on the designated. It is possible to incorporate these properties into a comprehensive design scheme, in which case the remaining S-box properties are to be examined. We also demonstrate that, despite the fact that this subset contains S-boxes with the theoretical resistance to side channel attacks under the Hamming weight model, the S-boxes are in different Hamming weight classes.

1. Introduction

In the domain of symmetric cryptography, particularly in the design of block ciphers, the substitution box, also known as the S-box, plays a pivotal role. This notion has been extensively documented in the literature, with notable sources including [1,2]. The S-box’s significance extends to its recent applications in lightweight cryptography and key-dependent cryptography, as evidenced by the works of [3,4]. To ensure a secure encryption/decryption process, it is imperative that the S-boxes have optimal values for their cryptographic properties [5]. Researchers have concentrated on two properties in particular: non-linearity [6], which is the property of a cryptosystem that resists linear cryptoanalysis, and confusion coefficient variance (CCV) [7], which is the property of a cryptosystem that resists power cryptoanalysis under the Hamming weight model. It is acknowledged that other properties, such as differential uniformity, boomerang uniformity, and algebraic degree, are crucial for practical cipher design. However, the present paper is limited in scope to the exploration of the interaction between NL and CCV under a specific class of transformations.

There are several methods for the generation of S-boxes that carry good NL and/or CCV. In general, the aforementioned methods can be classified into three categories. Firstly, there is the algebraic construction method [8]. Secondly, there is the heuristic search method, which includes the random search and artificial intelligence methods [9,10,11,12]. Third, there is the hybrid approach [13,14,15]. Relative to the design of AI-assisted S-boxes, we want to mention that, in addition to the search of S-boxes using metaheuristic algorithms, only a few researches from the machine learning field tried to design S-boxes, example [16]. In our opinion, this is happening because there is no dataset of S-boxes that allows the generation of new ones with good properties.

The integrity of NL and CCV is known to provide a certain degree of protection against cryptographic attacks [1]. However, it should be noted that enhancing CCV is known to result in a corresponding deterioration of NL, and vice versa [7,17,18]. In view of the aforementioned fact, attaining a trade-off becomes a complex undertaking. The impetus for this research stems from the following hypothesis: if an initial S-box already exhibits a trade-off, any method that generates new S-boxes while preserving the balance will be of significant utility. The extant literature does not contain a methodology of this kind; therefore, one is herein presented.

It is well established that affine transformations over a fixed S-box preserve the NL property, as evidenced in the literature [19]. Consequently, in the context of constructing or searching for S-boxes that exhibit optimal NL, the space of all S-boxes can be regarded as a partition of affine classes. Furthermore, in the recent study by [20], this same space has been partitioned by equivalence classes, taking into account their hypothetical leakage in relation to the Hamming weight power consumption representation. These equivalence classes are denoted as Hamming weight (HW) classes. It is important to note that each Hamming weight class considers S-boxes with the same power representation. Consequently, the CCV remains constant across equivalent classes. The calculation of the number of equivalent classes and the cardinals of each equivalent class was also performed in [20].

The HW classes for bijective S-boxes of order n are permutations with repetition of length $2^n$, of the numbers 0, …, n, where the number (weight) k appears exactly $C(n,k)$ times. The set of repetition-based permutations does not form a group, and the search in this space has been studied in [21]. In their study, the researchers proposed a discrete algebraic differential evolutionary algorithm for repetition-based permutations. They also analyzed the behavior of these permutations during the search.

In this study, we examine affine-shifted transformations in relation to the CCV property, with a focus on those that yield S-boxes with identical CCV values. The present study relies on experimental results to statistically study the properties in terms of behavior, interaction, and common points. This research clearly ends in the formulation of a mathematical invariance and the definition of a generation method. We identify such a subset and present the method given an initial S-box, which is our main result. The S-boxes obtained have been shown to possess identical NL and CCV values. While mathematical proofs have been provided to demonstrate the method’s behavior, empirical evidence has been presented to substantiate its efficacy in the 4-bit and 8-bit spaces. The following discussion will demonstrate the application of the method in various heuristic search and optimization strategies. In conclusion, it is demonstrated that while the S-boxes exhibit equivalent theoretical resistance, they do not belong to the same Hamming weight equivalence class. This finding represents a novel outcome, as it provides evidence that there exist disparate Hamming weight classes within the S-boxes, despite the presence of equal CCV.

In addition to the above summary, we want to remark the following key points:

• Our generation method directly and quickly computes the S-boxes that have the same CCV as the initial S-box. There is no need for an extra computation to check the entire affine-shifted class. The level of resistance to side channel attacks that we provide is only in its theoretical form. However, because the property ensures minimal security in the first phase of the S-box design, then that level of practical applicability is embedded.
• Our proposal of partitioning the space of S-boxes in mega-classes (focused on the CCV property, instead of in the Hamming weight), is practical and applicable to heuristic methods and combinatorial optimization, to speed up the search, in the same manner as was carried out for Hamming weight classes [20,22]. Before this work, moving from an S-box solution to another S-box solution with the same CCV value was only possible if the move was inside the same Hamming weight class. In this work, we provide a new way of keeping the CCV value constant, with the addition of also keeping the NL value constant. In other words, having the mathematical definition of the CCV partition of the S-box space is not enough for a cipher designer to quickly obtain S-boxes with the same NL and CCV; the designer needs a generation method like ours.
• The previous points, (1) and (2), expose the technical novelty of our research.
• Our invariance statement is supported by several experiments. We consider this a theoretical result by itself that provides a new insight about the intersection between affine-shifted classes and the Hamming weight classes. Moreover, we provide another proposition where we outline a strong and novel theoretical result, also related with the intersection: we prove the existence of different Hamming weight classes in the affine-shifted set.
• Our contribution lies not in computational efficiency or generality but in structure and interpretation of the CCV landscape within this tractable class. We define the notion of CCV mega-classes, observe their empirical separation across Hamming weight classes, and propose that this structure can be used to guide or constrain S-box search algorithms. We acknowledge that this work may be considered exploratory and structural rather than a breakthrough in cryptographic design. In other words, we believe that identifying invariant metrics within subsets of S-boxes is a useful building block for future heuristic or evolutionary design strategies.
• Detailed experiments on 3-bit S-boxes were presented to analyze the joint and marginal probabilities of NL and CCV. We calculated those probabilities after generating and evaluating all the S-boxes from the entire S-box space; we did not follow any abstract or a pure math approach. In this particular case, the size of the space is computable and there are only two values for the NL property and there values for the CCV property, which helped us to obtain the insights. However, for bigger spaces like, for example, the 8-bit S-boxes, we think the combinatorial space is not computable with a personal computer, and the range of values for NL is big, but it is much bigger for CCV. The scope of our research ended in the simplest case.

This paper is structured as follows: the introduction continues with the Related Works Section 1.1 and Basic Notions Section 1.2; then, there will be a Results Section 2 and finally a Conclusions Section 3.

1.1. Related Works

The related works can be examined from two perspectives: those that provide algebraic constructions and mathematical proofs, and those that offer conjectures and empirical demonstrations.

From the very beginning of the definition of DPAs (Differential Power Attacks) and the definition of the OTO (Transparency Order, O for old definition) property, in [23], Prouff states the impossibility of designing a property that can resist in an optimal way, and at the same time, the linear, differential, and DPA attacks. Moreover, the author also proved that the OTO of balanced affine functions is not close to the best value, while the OTO of curved functions achieves the worst value, confirming that the construction of highly non-linear S-boxes with good OTO is an open problem.

Later, Chakraborty et al., in [24], proved that MTO (Transparency Order, M for modified and currently used definition) remains constant for affine permutations; on the other hand, if two S-boxes are extended affine equivalence but not affine equivalence, then their MTO are not necessarily equal. Again, it was easy to show that a bit of change in transparency order alone is not enough to ensure the security of a real implementation; therefore, it must be used in combination with other classical countermeasures. In [25], given the similarities of the RTO (Transparency Order, R for revised definition) with the MTO, the authors also prove that the value remains constant for affine transformations.

Following an exhaustive series of experiments, Picek [9] advanced a conjecture that affine equivalence does not imply equivalence in relation to DPA. In terms of the computational complexity of the affine transformation, Picek concluded that modifying the confusion coefficient is less onerous than modifying the transparency order.

A recent article [26] analyzes the affine and extended classes; the study shows that the DPA-SNR (Differential Power Analysis Signal to Noise Ratio) is not preserved.

Although affine transformations of S-boxes and their relation to DPA were not studied in [20], a new equivalence class was defined, proving that S-boxes in the same class show equal CCV. The intersection between affine equivalence and Hamming weight equivalence presents a novel and intriguing research trajectory.

1.2. Basic Notions

A bijective and vectorial Boolean function is a common mathematical definition of an S-box $S:{\{0,1\}}^n\to {\{0,1\}}^n$ [27]. This kind of bijection can be represented as a Look Up Table [28] in an efficient manner from a computational point of view and it is important in combinatorial optimization designs of S-boxes. Taking into account the output of the function, and considering the function itself as a permutation $S=(S\left(x_0\right),\dots S\left(x_{2^n-1}\right))$, is very useful for understanding the properties related to side channel attacks, while the mathematical definition is more related to algebraic properties, as will be seen in this section.

Given a Boolean function f and a Boolean vector w, the Walsh–Hadamard transform is defined as

$$W{H}_f\left(w\right)=\sum _{x\in {\{0,1\}}^n}\widehat{f}\left(x\right)\widehat{L_w}\left(x\right)$$

(1)

where the polar form of f is $\widehat{f}$ and $\widehat{L_w}$ is a linear function specified by w. The maximum value of $WH$ across all possible Boolean vectors is denoted by

$$W{H}_{max}\left(f\right)=ma{x}_{w\in {\{0,1\}}^n}\left|W{H}_f\left(w\right)\right|$$

(2)

in which |.| represents the absolute value.

The non-linearity property of the Boolean function f can be defined as

$$N{L}_f={\displaystyle \frac{1}{2}}(2^n-W{H}_{max}\left(f\right))$$

(3)

Then, the NL property of the vectorial Boolean function S is the lowest value of the non-linearity among the component functions of S (non-zero linear combinations of the n coordinates functions of S).

Affine-shifted S-boxes to a given one S are those constructed as $S_{a,b}=S(x\oplus a)\oplus b,\forall x\in {\{0,1\}}^n$, where $a,b\in {\{0,1\}}^n$. In the case $a=0^n,b=0^n$, then $S_{0,0}=S$.

Each S-box $S_{a,b}$, affine-shifted to the given S, has the same NL value as S [19].

The confusion coefficient metric was presented in [29]. This property is computed for sub-keys $k_i$ and $k_j$ as

$$\kappa (k_i,k_j)=\mathbb{E}\left[{(W\left(k_i\right)-W\left(k_j\right))}^2\right],$$

(4)

where, in (Equation (4)), W represents the leakage function of the encryption or decryption process given an arbitrary input and the sub-key k. In common symmetric cryptosystems, one way of modeling the power consumption is by using the value $HW\left(S\right(in\oplus k\left)\right)$, known as the Hamming weight leakage model, where $HW\left(y\right),y\in {\{0,1\}}^n$ computes the amount of 1’s in the binary vector y. Because the confusion coefficient property was a physical property, the confusion coefficient variance (CCV) mathematical property was presented using the confusion coefficient (Equation (4)) and the Hamming Weight model in [7]. The property takes into account all sub-keys $k_i,k_j$ and all input text $in$:

$$CCV\left(S\right)=Var\left(\mathbb{E}\left[{(HW\left(S(in\oplus k_i)\right)-HW\left(S(in\oplus k_j)\right))}^2\right]\right)$$

(5)

If two S-boxes $S_a$ and $S_b$ belong to the same Hamming weight class or, in other words, if $HW\left(S_a\left(x\right)\right)=HW\left(S_b\left(x\right)\right),\forall x\in {\{0,1\}}^n$, then they have the same theoretical resistance against power attacks under the Hamming weight leakage model [20].

A computation representation of a class can be precisely the vector of weights of the outputs of an S-box S that belongs to the class [20]

$$HW\left(S\right)=(HW\left(S\left(x_0\right)\right),\dots ,HW\left(S\left(x_{2^n-1}\right)\right))$$

(6)

There are $n+1$ sets of inputs of S such as $C_k=\{x\in {\{0,1\}}^n|HW\left(S\left(x\right)\right)=k\}$, $0\le k\le n$. For two bijective S-boxes, if their sets are equal, they belong to the same Hamming weight class [20].

2. Results: Generation of S-Boxes with the Same NL and CCV Values as an Arbitrary Initial S-Box

In the current section, we develop the study of the existing relation between affine-shifted transformations and CCV via Hamming height classes, and the achievements derived from it.

2.1. Balanced Case

To study the relationship between affine-shifted S-boxes and their respective CCV values, we analyzed all the affine-shifted S-boxes given the best S-box presented in [7], which is a bijection from ${\{0,1\}}^8$ to ${\{0,1\}}^8$ obtained by evolutionary computation and representing a local optimum (CCV = 4.057, NL = 98). We called this S-box $SPicek$. The different aspects of the study are shown in Figure 1, Figure 2, Figure 3 and Figure 4.

The HW class of $SPicek$ in its weight array representation is

$HWclass\left(SPicek\right)$ = (4, 3, 3, 4, 4, 2, 2, 4, 4, 2, 3, 3, 4, 4, 3, 4, 5, 7, 6, 5, 5, 6, 6, 5, 5, 5, 7, 4, 4, 6, 5, 4, 3, 4, 4, 3, 2, 5, 5, 3, 4, 4, 5, 3, 3, 4, 4, 3, 6, 4, 5, 6, 7, 5, 4, 5, 6, 6, 5, 5, 6, 4, 5, 6, 6, 4, 4, 5, 6, 3, 4, 5, 5, 5, 4, 5, 5, 4, 5, 6, 2, 3, 3, 1, 2, 4, 4, 1, 3, 4, 4, 3, 2, 4, 3, 2, 4, 5, 5, 4, 3, 5, 5, 4, 3, 5, 5, 3, 4, 6, 5, 3, 3, 2, 2, 3, 4, 0, 1, 3, 4, 3, 2, 3, 3, 2, 2, 2, 4, 7, 6, 5, 4, 6, 7, 5, 4, 6, 6, 4, 4, 8, 6, 5, 3, 2, 3, 4, 4, 4, 3, 4, 4, 3, 1, 3, 3, 2, 3, 5, 5, 5, 5, 6, 6, 5, 4, 4, 7, 4, 4, 6, 6, 5, 5, 7, 3, 4, 4, 2, 4, 5, 4, 3, 2, 4, 5, 3, 3, 4, 3, 3, 2, 5, 3, 2, 2, 3, 4, 3, 1, 3, 4, 2, 1, 5, 3, 2, 4, 3, 5, 5, 5, 5, 4, 5, 5, 5, 3, 7, 6, 4, 3, 6, 3, 3, 2, 4, 3, 3, 2, 4, 4, 1, 1, 4, 4, 2, 3, 4, 3, 6, 6, 2, 4, 5, 6, 4, 3, 5, 5, 4, 3, 5, 5, 2).

The S-boxes similar to $SPicek$ have, as is known, the same relatively high value of NL = 98, which provides resistance to linear attacks; however, in Figure 1, it is observed that most of them have a very low CCV value, which is a weakness that makes them vulnerable to power side channel attacks. On the other hand, it can also be seen that there are S-boxes with values of 4.057, which is equal to the CCV value of the $SPicek$ S-box. Given this behavior of the distribution of CCV values, the following question arises naturally: what are the S-boxes that preserve the CCV value of the initial S-box? The results of our experiment allow us to answer this question.

We found that all S-boxes generated when $b=0$ or $b=255$ have the same CCV value as the starting S-box. However, the amount of S-boxes following this invariant was a small fraction of all S-boxes analyzed (see Figure 1), when most CCV values were concentrated near 0. The histogram shows the gap between the CCV value of S-boxes, where $0<b<255$ and the initial (CCV = 4.057); this gap reflects the distance between a random CCV value and one obtained after an optimization process. We also noticed that the CCV value was never greater than the CCV value of $SPicek$.

In Figure 2, it can be seen more clearly that the highest CCV values are only reached for $b=0$ or $b=255$, represented by the brown color. In this 3D view, five buckets were defined (0–1, 1–2, 2–3, 3–4, and 4–5), but because two of them were empty (2–3 and 3–4), three colors were displayed. It seems that there is some kind of symmetric distribution, but we did not analyze it in depth. For a better visualization, a scatter plot was made for b versus CCV (see Figure 3).

We also examined the Hamming weight vectors for S-boxes, where $b=0$. Figure 4 shows the first 16 vectors of the affine-shifted S-boxes (including the HW class of $SPicek=SPice{k}_{0,0}$ itself), where each weight of an S-box output is a value between 0 and 8, represented by a color. We chose this first block because we noticed that the same patterns repeated every 16 vectors. The main insight we obtain is that the Hamming weight classes are not the same, because, taking the first vector as the initial HW class, the color changes for the same input x, from one row to another, while the weight should be invariant equal to $HW\left(SPicek\right(x\left)\right)$ (see [20]). This notion will be further confirmed in this paper for the AES S-box, where even the distance between classes will be studied. Another thing we noticed is that there is a kind of “inverted reflection” of the first 8 vectors into the last 8 vectors, every 16 entries. Moreover, we assumed that as a movement of weights but kept the variance. We even assumed that all of the above behavior also holds for $b=255$.

2.2. Unbalanced Case

To study the relationship between affine-shifted S-boxes and their respective CCV values in an unbalanced case, we analyzed all affine-shifted S-boxes given the AES S-box [8], which is a cryptographic primitive created via an algebraic construction. Moreover, it has very poor resistance to power consumption attacks (CCV = 0.1113, NL = 112). We denoted this S-box as $S_{AES}$.

We found that all S-boxes generated when $b=0$ or $b=255$ have the same CCV value as the starting one, again. The S-boxes following this invariant comprised a small fraction of all S-boxes analyzed (see Figure 5). The histogram shows the dispersion of the CCV value of the S-boxes; this reflects how bad the neighborhood is with respect to the side channel impedance.

For a more detailed illustration, we scattered the points of b versus $CCV$ (see Figure 6). The symmetrical pattern reappeared. Moreover, we defined some dashed intersection lines to note the behavior around $b=0$ and $b=255$. It can be seen that for other values of b, the initial CCV is reached.

2.3. Cases Comparison

Balanced and unbalanced cases can be compared using Figure 7 and Figure 8. There are clear differences in the distribution of the CCV values. The CCV values for affine-shifted S-boxes to $SPicek$ are mostly highly concentrated near zero, with a few outliers. On the other hand, the CCV values for affine-shifted S-boxes similar to the $S_{AES}$ are highly dispersed. In the first case, the median value is 0.1345 and the variance value is 0.1999; in the other case, the median value is 0.1168 and the variance value is 0.0002.

2.4. Invariance of the Confusion Coefficient Variance Under Affine-Shifted S-Boxes, and a Generation Method

The entire above analysis (balanced and unbalanced cases) led to the invariance. In this section, we also formalize a generation method from the invariance.

We recall the definition of confusion coefficient variance (CCV) for an S-box $S:{\{0,1\}}^n\to {\{0,1\}}^n$, based on the Hamming weight leakage model from 5:

$$CCV\left(S\right)=\mathrm{Var}\left(\mathbb{E}\left[{\left(HW\left(S(in\oplus k_i)\right)-HW\left(S(in\oplus k_j)\right)\right)}^2\right]\right),$$

(7)

where $HW(·)$ denotes the Hamming weight function, and the expectation is taken over all plain texts $in\in {\{0,1\}}^n$ and distinct sub-keys $k_i,k_j\in {\{0,1\}}^n$.

Proposition 1.

Let S be a bijective S-box. Define the affine-shifted subset:

$$A=\left\{S_{a,b}|S_{a,b}\left(in\right)=S(in\oplus a)\oplus b,\mathrm{with}a\in {\{0,1\}}^n,b\in \{0^n,1^n\}\right\}.$$

Then,

$$CCV\left(S_{a,b}\right)=CCV\left(S\right),\forall S_{a,b}\in A.$$

Proof. 

Let $S_{a,b}\left(in\right)=S(in\oplus a)\oplus b$. Then,

$$\begin{array}{cc}\hfill S_{a,b}(in\oplus k_i)& =S((in\oplus k_i)\oplus a)\oplus b=S(in\oplus k_i\oplus a)\oplus b,\hfill \\ \hfill S_{a,b}(in\oplus k_j)& =S(in\oplus k_j\oplus a)\oplus b.\hfill \end{array}$$

Therefore, the corresponding Hamming weights are

$$\begin{gathered} HW\left(S_{a,b}(in\oplus k_i)\right)=HW(S(in\oplus k_i\oplus a)\oplus b), \\ HW\left(S_{a,b}(in\oplus k_j)\right)=HW(S(in\oplus k_j\oplus a)\oplus b). \end{gathered}$$

We now analyze the Hamming weight difference under XOR with a fixed vector $b\in {\{0,1\}}^n$. For general $y_1,y_2$, it holds that

$${(HW(y_1\oplus b)-HW(y_2\oplus b))}^2\ne {(HW\left(y_1\right)-HW\left(y_2\right))}^2\mathrm{in}\mathrm{general}.$$

However, for $b\in \{0^n,1^n\}$, the transformation is either an identity or bitwise complement, which preserves squared Hamming weight differences:

$${(HW(y_1\oplus b)-HW(y_2\oplus b))}^2={(HW\left(y_1\right)-HW\left(y_2\right))}^2.$$

Now consider the change of variables:

$$k_i^{\prime }=k_i\oplus a,k_j^{\prime }=k_j\oplus a.$$

Since XOR with a fixed vector a defines a bijection over ${\{0,1\}}^n$, the set of all distinct key pairs $(k_i,k_j),k_i\ne k_j$ is mapped bijectively to the set of all distinct pairs $(k_i^{\prime },k_j^{\prime })$ with $k_i^{\prime }\ne k_j^{\prime }$. This mapping

• Preserves the number of pairs: $\left({\displaystyle \genfrac{}{}{0pt}{}{2^n}{2}}\right)$;
• Ensures that no pair is repeated;
• Covers all possible key pair combinations.

Hence, the expectation and variance over these key pairs remains unchanged. Therefore,

$$CCV\left(S_{a,b}\right)=CCV\left(S\right).$$

□

The subset A has a size of $2\times (2^n-1)$ S-boxes. This size grows exponentially as the size of the bits n grows (see

Table 1. Size of A in relation with n.

Size of Bits	Size of the Subset
4	30
8	510

).

Like Proposition 1, another important result of this research is the method of generating A, the subset of the affine-shifted S-boxes, such that the S-boxes of A stay invariant not only the NL property but also the CCV property, with respect to S—the initial S-box. The steps of the method are as follows (see Algorithm 1):

Algorithm 1 Generation method.

Require:  S, S-box. Ensure:  A, subset of S-boxes with equal NL and CCV than S. 1: $A\leftarrow \varnothing$ 2: for $a\in {\{0,1\}}^n\setminus 0^n$ do 3:  for $b\in \{0^n,1^n\}$ do 4:   for $x\in {\{0,1\}}^n$ do 5:    $S_{a,b}\left(x\right)\leftarrow S(x\oplus a)\oplus b$ 6:   end for 7:   $A\leftarrow A\cup \left\{S_{a,b}\right\}$ 8:  end for 9: end for 10: return A

Because each S-box on the affine-shifted subset depends only on the initial S-box, the generation method can be parallelized. Moreover, on each concurrent process for the creation of S-boxes, the remaining properties can be evaluated.

In comparison with other heuristic methods, like local search or evolution algorithms, starting from an S-box with good NL, it is better to generate affine-shifted S-boxes with the same CCV, instead of checking the neighborhood or the offspring of the S-box, because doing so will not even ensure the same NL. Although our method is not meant to search for S-boxes with a good trade-off between CCV/NL, it is the most efficient method to keep that trade-off.

The method can be applied on bijective S-boxes of all dimensions.

With the objective of finding practical evidence in favor of our invariance and showing the good behavior of the proposed generation method, the following experiment was designed and performed:

• Fix an S-box space of ($n=8$, bits) or ($n=4$, bits).
• Generation of tens of thousands of initial random S-boxes.
• For each initial random S-box, apply the generation method Algorithm 1 and obtain the resulting subset of affine-shifted S-boxes.
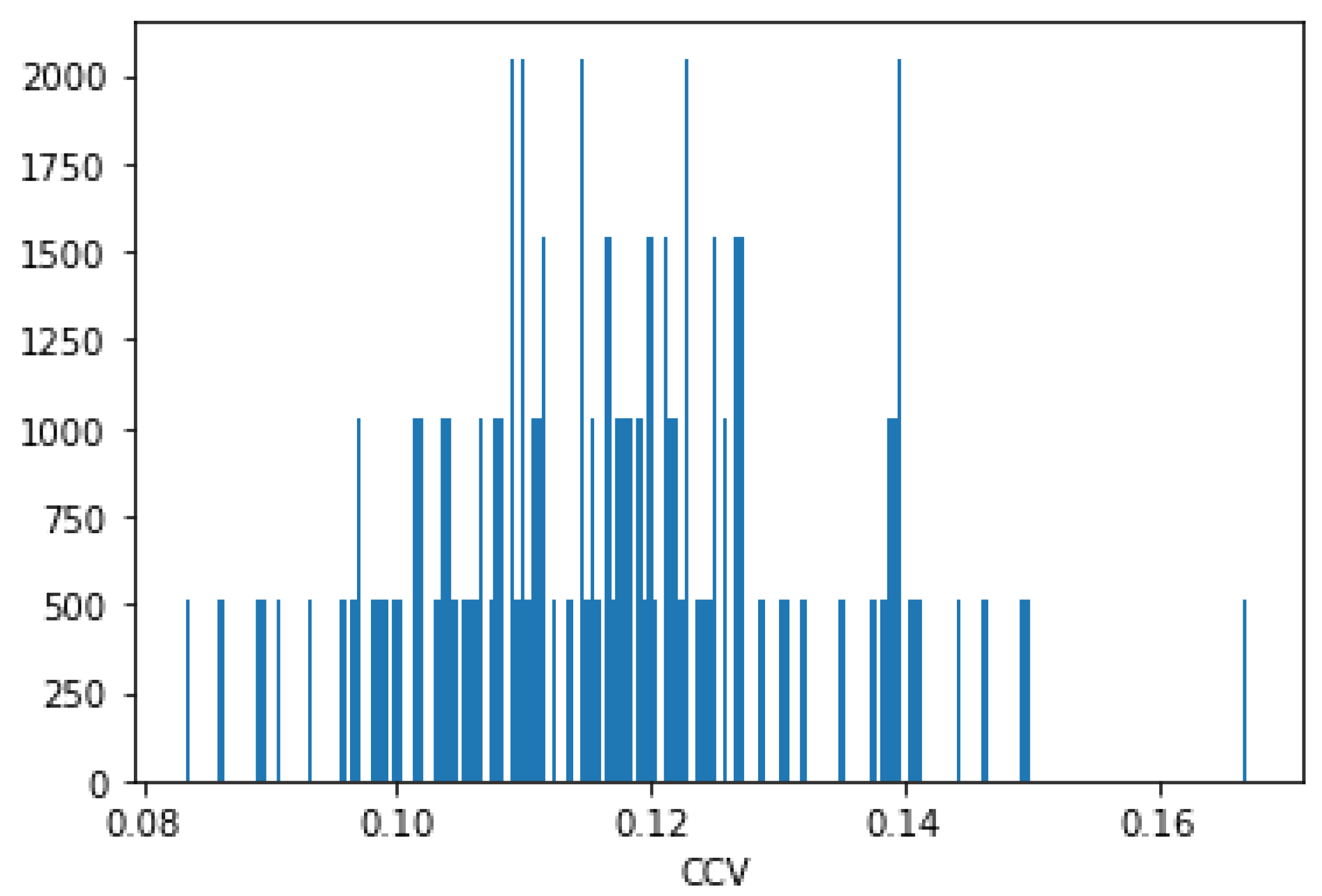
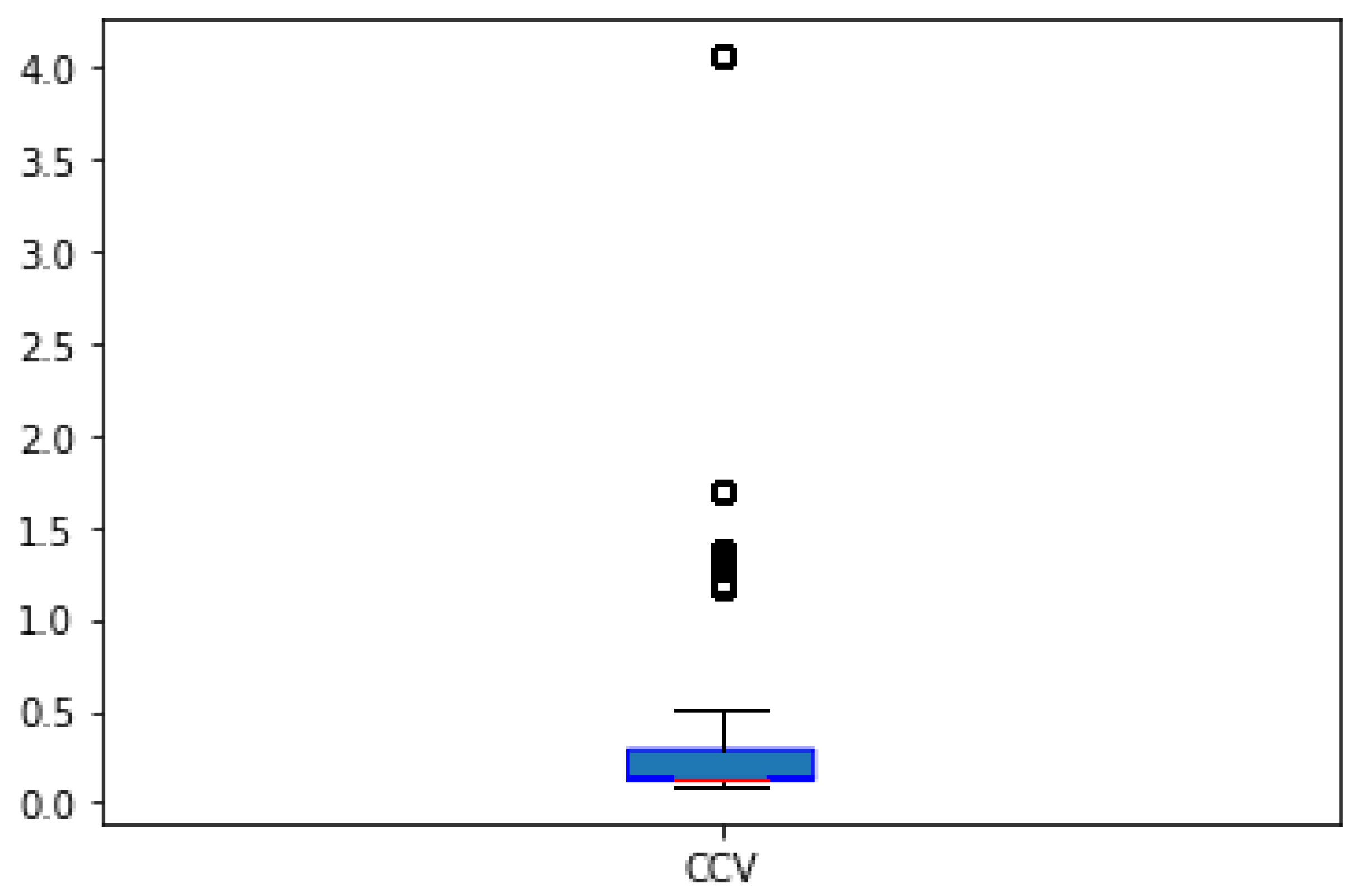
• Calculate the CCV of all the S-boxes that belong to the resulting subset.
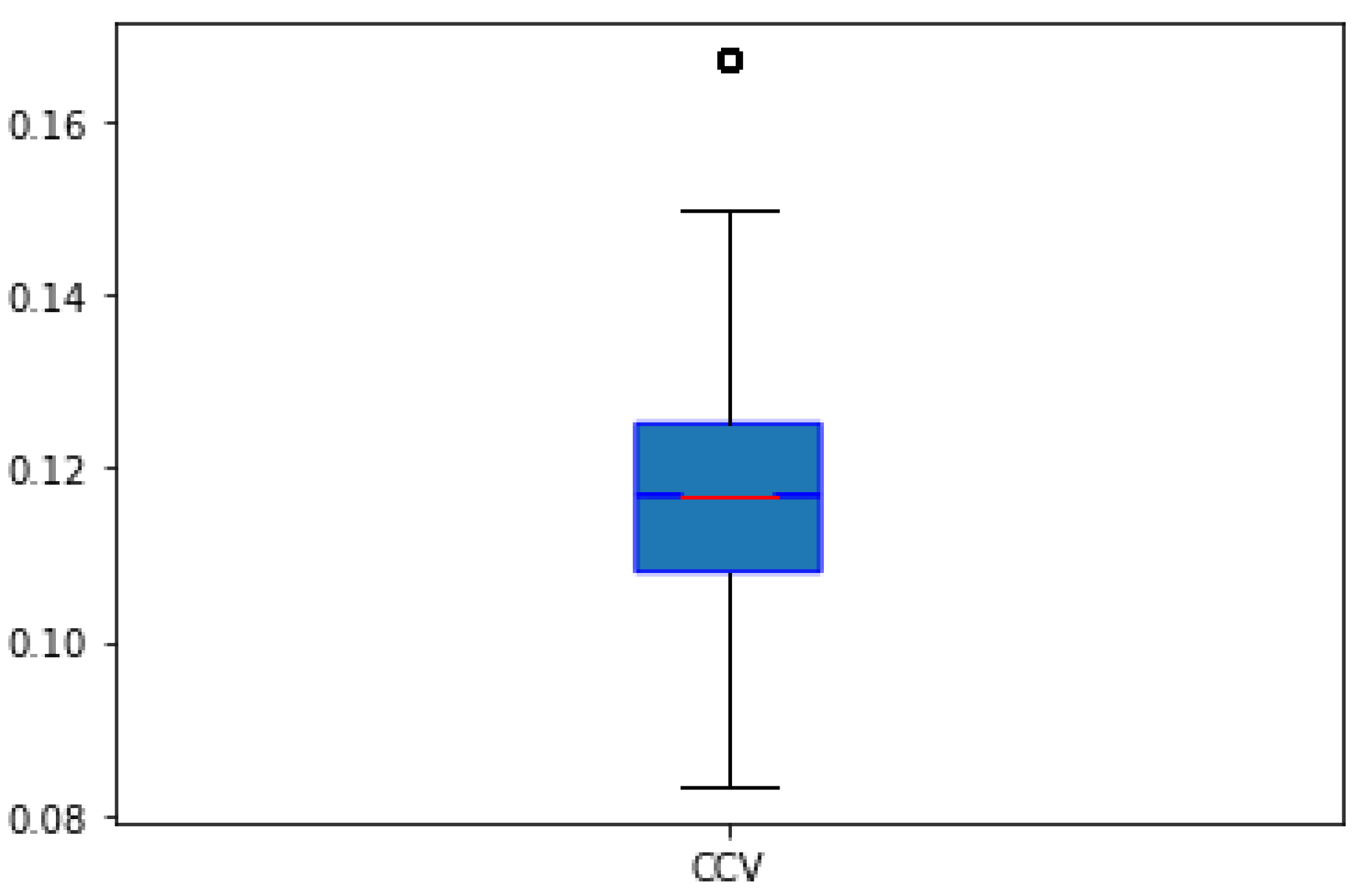
• Check if the CCV value stays constant and equal to the CCV of the initial S-box.

We applied this method 10,000 times. All the times the results were as we expected: CCV was the same for all the S-boxes inside the subset.

In terms of the practical value of the generation method, the theoretical results ensure the invariance at the affine shifted subset for S-boxes of all sizes, including 16x16 S-boxes. In order hand, the resistant we try to keep (CCV) is still needed in the design phase of the S-box; stronger attacks like the Deep Learning-Based Side Channel Analysis are present to continue undermining cryptosystems; see [30].

2.5. Generated S-Box Example

Below, we list the S-box $SPice{k}_{8,0}$ that belongs to the affine-shifted subset after applying the generation method Algorithm 1 given the initial S-box of [7]. In particular, $SPice{k}_{8,0}$ was obtained with the values $a=8$ y $b=0$; it is a cryptography primitive with a good trade-off between NL and CCV. This S-box is not suitable for practical use and is included merely to demonstrate the CCV invariance mechanism.

$SPice{k}_{8,0}$ = (85, 79, 172, 221, 61, 176, 19, 204, 89, 210, 127, 72, 8, 143, 209, 148, 10, 151, 30, 125, 203, 113, 188, 131, 123, 25, 78, 147, 84, 205, 32, 31, 74, 247, 91, 242, 23, 90, 47, 34, 235, 16, 141, 103, 165, 37, 4, 227, 76, 45, 134, 236, 117, 41, 56, 44, 216, 112, 245, 7, 65, 239, 166, 156, 27, 46, 140, 246, 118, 6, 150, 194, 163, 69, 252, 81, 64, 183, 201, 224, 58, 190, 116, 226, 77, 105, 189, 192, 255, 12, 122, 212, 234, 60, 33, 115, 162, 171, 106, 179, 173, 88, 220, 160, 243, 42, 87, 52, 164, 70, 137, 230, 83, 43, 138, 175, 207, 136, 98, 144, 248, 121, 253, 67, 68, 238, 71, 66, 177, 214, 145, 95, 119, 80, 139, 168, 240, 200, 62, 13, 132, 53, 133, 82, 35, 251, 135, 101, 153, 104, 107, 130, 223, 5, 93, 228, 155, 21, 50, 126, 152, 159, 54, 213, 202, 22, 233, 36, 219, 100, 109, 149, 146, 59, 3, 111, 39, 94, 28, 63, 185, 2, 142, 161, 186, 102, 250, 24, 96, 206, 195, 17, 75, 174, 129, 254, 187, 18, 193, 184, 232, 170, 237, 180, 40, 244, 49, 197, 20, 222, 157, 217, 208, 120, 199, 0, 249, 169, 218, 181, 73, 211, 11, 241, 9, 231, 229, 15, 108, 86, 110, 128, 191, 14, 225, 29, 198, 51, 48, 215, 92, 158, 26, 55, 167, 1, 99, 97, 124, 178, 154, 38, 196, 182, 114, 57).

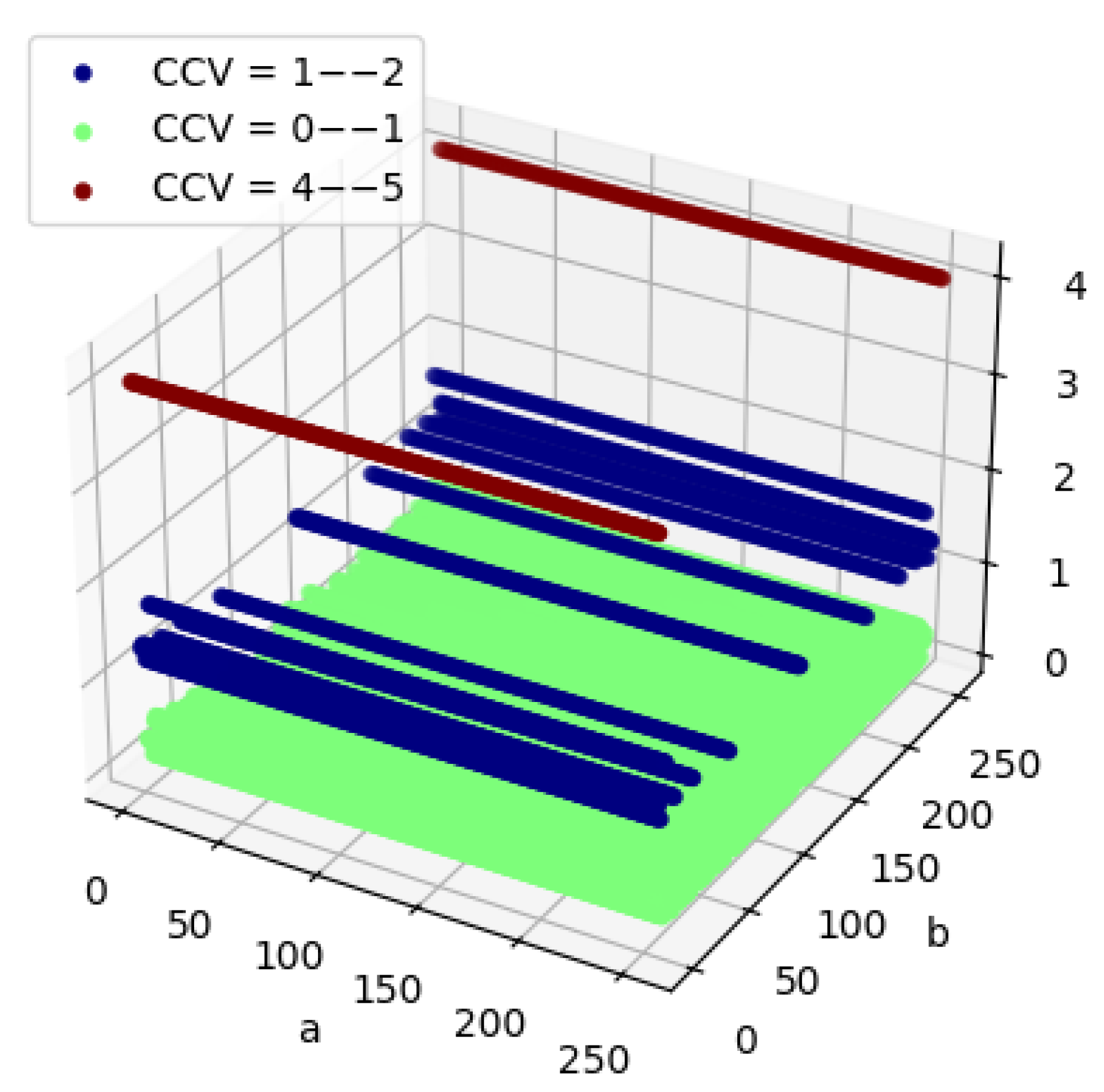
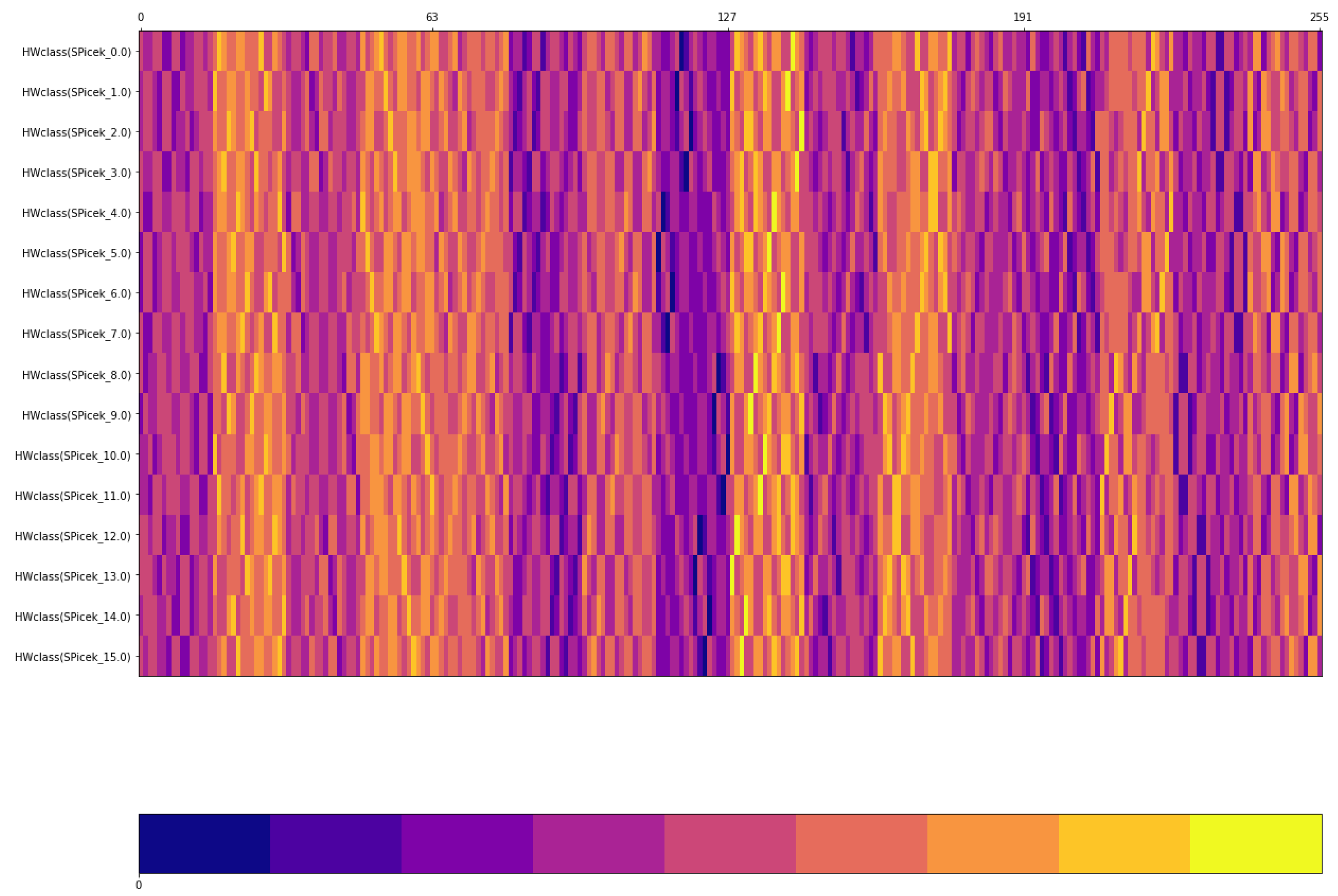
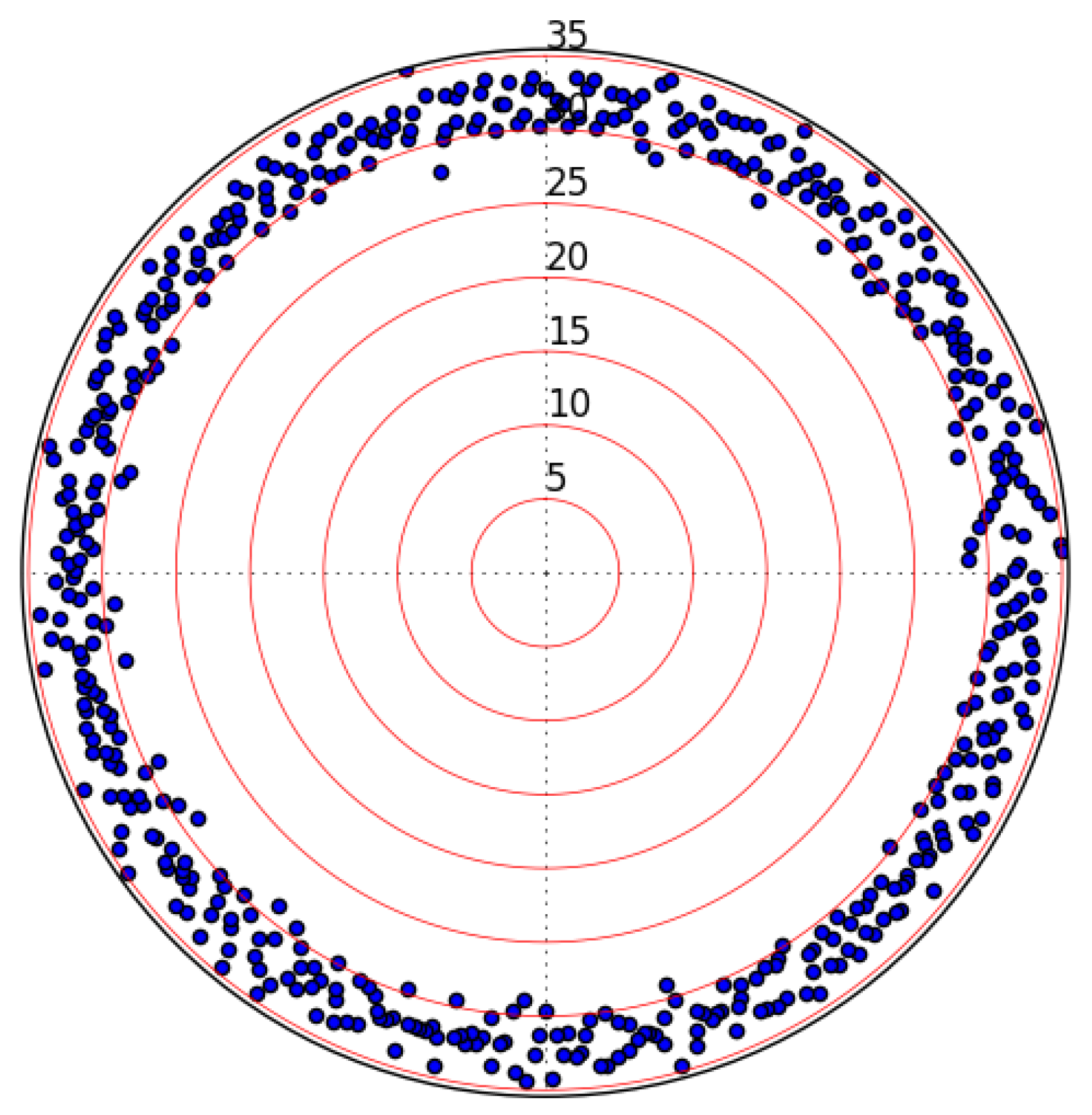
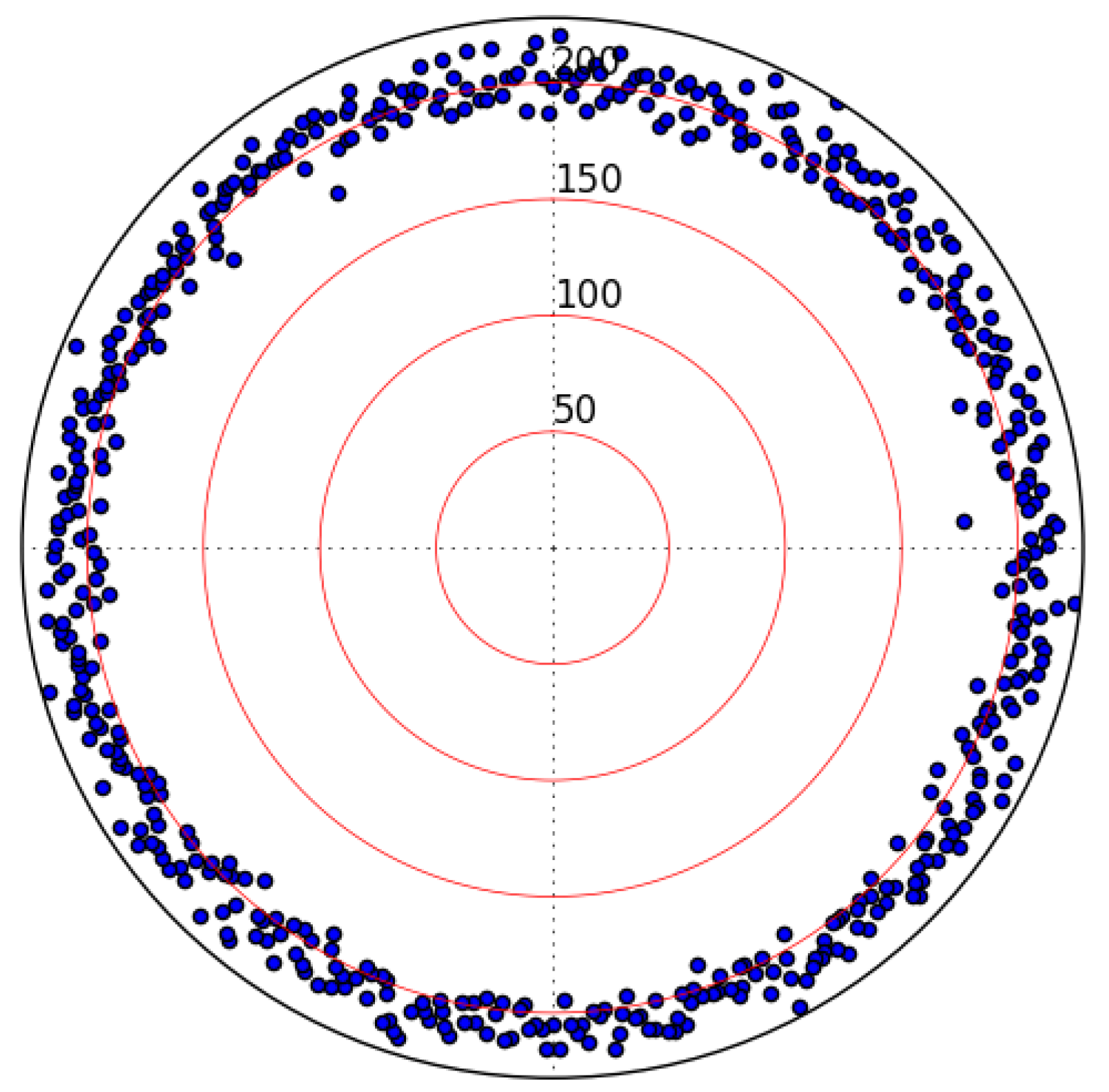
2.6. Hamming Weight Class Membership via Distance Analysis

Proposition 2.

Although the S-boxes of the subset A have the same CCV values, they are not necessarily in the same HW equivalent class.

Proof. 

This method consists of selecting an S-box (the $S_{AES}$ was taken), generating S-boxes of the correspondent set A, calculating the HW classes of the S-boxes of this set A, and proving that the HW classes are different because the distance between them is greater than zero.

1- Run the generation method Algorithm 1 to obtain the subset $A_{aes}$; however, given as an initial S-box $S_{AES}$, the S-box is used by the AES block cipher.

$$A_{aes}=\left\{S_{a,b}\right|S_{a,b}\left(x\right)=S_{AES}(x\oplus a)\oplus b\},\forall x\in {\{0,1\}}^8$$

(8)

where $a\in {\{0,1\}}^8$, $b\in \{0^8,1^8\}$ and

2- For each S-box $S_{a,b}\in A_{aes}$, calculate the Euclidean distance:

$$ED(S_a,S_b)=\sqrt{\sum _{x\in {\{0,1\}}^8}{(HW\left(S_a\left(x\right)\right)-HW\left(S_b\left(x\right)\right))}^2}$$

(9)

and the Hamming distance:

$$HD(S_a,S_b)=\sum _{x\in {\{0,1\}}^8}\left\{\begin{array}{cc}1\hfill & HW\left(S_a\left(x\right)\right)\ne HW\left(S_b\left(x\right)\right),\hfill \\ 0\hfill & \mathrm{e.}\mathrm{o.}\mathrm{c.}\hfill \end{array}\right.$$

(10)

in relation with $S_{AES}$.

□

The results were as expected. The S-boxes in $A_{aes}$ have the same CCV as $S_{AES}$, but they do not belong to the same Hamming weight class. Furthermore, they belong to different Hamming weight classes (see Figure 9 and Figure 10) considering different distance measures. In the case of the Euclidean distance, we obtain $ED(S_{a,b},S_{AES})>25,\forall S_{a,b}\in A_{aes}$; in the case of the Hamming distance, we obtain $HD(S_{a,b},S_{AES})>150,\forall S_{a,b}\in A_{aes}$.

The demonstration that there are different HW classes with an equal CCV property value is another novel result of this work from a theoretical point of view. Its practical application could further reduce the combinatorial search space for S-boxes resistant to power consumption attacks. To achieve the reduction, we propose to define, in this space of HW classes, a new equivalence relation according to the value of CCV, which immediately partitions this space of permutations with repetitions into new mega-classes, whose elements would be the HW classes with equal CCV.

If it is possible to define an efficient algorithm to build these new mega-classes and move in this reduced combinatorial space by increasing the value of CCV, the searching methods could be accelerated because all HW classes have a common and low CCV value. Partitioning the space of S-boxes using mega-classes could be better than using Hamming-Height classes. An heuristic search will optimally traverse across the space moving from mega-class to mega-class instead of moving from S-box to S-box, in the same way as has been done before using the Hamming-Weight partition.

This approach raises new questions: How to identify all the different HW classes that have the same CCV value? How to design an efficient algorithm to move in this newly reduced space of mega-classes, increasing the CCV value? How many different CCV values exist in the space of $nxn$ S-boxes? The answer to this last question is experimentally difficult due to the exponential dimension of the S-box space, which is why the samples of CCV values may be unrepresentative. These problems are suggested for future research.

2.7. Proof of Different Hamming Weight Classes for Affine-Shifted S-Boxes

Proposition 3.

Let S be an $n\times n$ bijective S-box and $S_{a,b}\left(x\right)=S(x\oplus a)\oplus b$$\forall x\in {\{0,1\}}^n$, where $a,b\in {\{0,1\}}^n$ is an affine-shifted S-box given the initial S-box S. Let $<S_{a,b}>$ also be the HW class of $S_{a,b}$ (in particular, $<S_{0,0}>=<S>$ is the HW class of S); thus, the following sentence is true:

If $a_1,a_2\in {\{0,1\}}^n,a_1\ne a_2$, then the Hamming weight classes are different to each other ($<S_{a_1,b}>\ne <S_{a_2,b}>$) and, in particular, they are different from the initial $<S_{a_1,b}>\ne <S>$.

Proof. 

Let us assume that $S_{a_1,b}$ and $S_{a_2,b}$ belong to the same Hamming weight class. $\exists k!\in {\{0,1\}}^n:S_{a_1,b}\left(k\right)=0$, which means that $S(k\oplus a_1)\oplus b=0$, while $a_1\ne a_2$. This implies that $k\oplus a_2\ne k\oplus a_1$ and, at the same time, implies $S(k\oplus a_2)\ne S(k\oplus a_1)$, as S is bijective. Then, for all values of b, we get $S(k\oplus a_2)\oplus b\ne S(k\oplus a_1)\oplus b$, leading to $S(k\oplus a_2)\oplus b\ne 0$, which means $S_{a_2,b}\left(k\right)\ne 0$. Finally, $S_{a_1,b}\left(k\right)=0$ and $S_{a_2,b}\left(k\right)\ne 0$, which contradicts the necessary condition given in [20] for S-boxes that are in the same HW class.

□

2.8. Comparison of Strategies for Optimize NL and CCV

The S-box’s space of $3\times 3$ order was generated to calculate the NL and CCV values of a total of $8!$, which equals 40,320 S-boxes. The results are shown in Figure 11 and

Table 2. Frequencies of NL and CCV in $3\times 3$ S-box’s space.

	CCV = 0.27551	CCV = 0.489796	CCV = 1.13265	Total
NL = 2	8064	0	2688	$f\left(NL\right)$ = 10,752
NL = 0	16,128	8064	5376	$f\left(NL\right)$ = 29,568
Total	$f\left(CCV\right)$ = 24,192	$f\left(CCV\right)$ = 8064	$f\left(CCV\right)=8064$	40,320

.

The space of 40,320 S-boxes was reduced in [20] to 1120 HW classes, with 36 S-boxes per class, all with the same CCV value. Table 2 shows that among all 1120 HW classes, there are only three different CCV values; in other words, there are different HW classes with an equal CCV property value that allow us to define a new partition of the S-box space.

Considering that each HW class in $3\times 3$ has exactly 36 S-boxes, the number of Hamming weight classes with the same CCV can be calculated by dividing the last row of Table 2 by 36, as shown in

Table 3. Number of HW classes with an equal CCV property value in $3\times 3$ S-box’s space.

CCV	0.27551	0.489796	1.13265	Total
$f\left(CCV\right)$	24,192	8064	8064	40,320 Number of S-boxes in $3\times 3$
$f\left(CCV\right)/36$	672	224	224	1120 Number of HW classes in $3\times 3$

. All the classes grouped by the same CCV value can be viewed in the results’ document of the experiment at http://dx.doi.org/10.13140/RG.2.2.13012.31366.

From Table 3, we can see that the number of HW classes with equal CCV is not constant and is not an increasing function of the CCV value. If we compare Table 3 with Table 2, we can see that there are 224 HW classes with $CCV=0.489796$ and 224 HW classes with $CCV=1.13265$; however, in Table 2, there is a clear difference in the NL values in these two cases. To delve deeper into this aspect, the conditional probabilities of NL given CCV were calculated, as shown in

Table 4. Joint and marginal probabilities of NL and CCV in $3\times 3$ S-box’s space.

	CCV = 0.27551	CCV = 0.489796	CCV = 1.13265	Total
NL = 2	$P=0.2$	$P=0$	$P\approx 0.07$	$P\left(NL\right)\approx 0.27$
NL = 0	$P=0.4$	$P=0.2$	$P\approx 0.13$	$P\left(NL\right)\approx 0.73$
Total	$P\left(CCV\right)=0.6$	$P\left(CCV\right)=0.2$	$P\left(CCV\right)=0.2$	$P=1$

.

Following Table 4, we obtain the following insights:

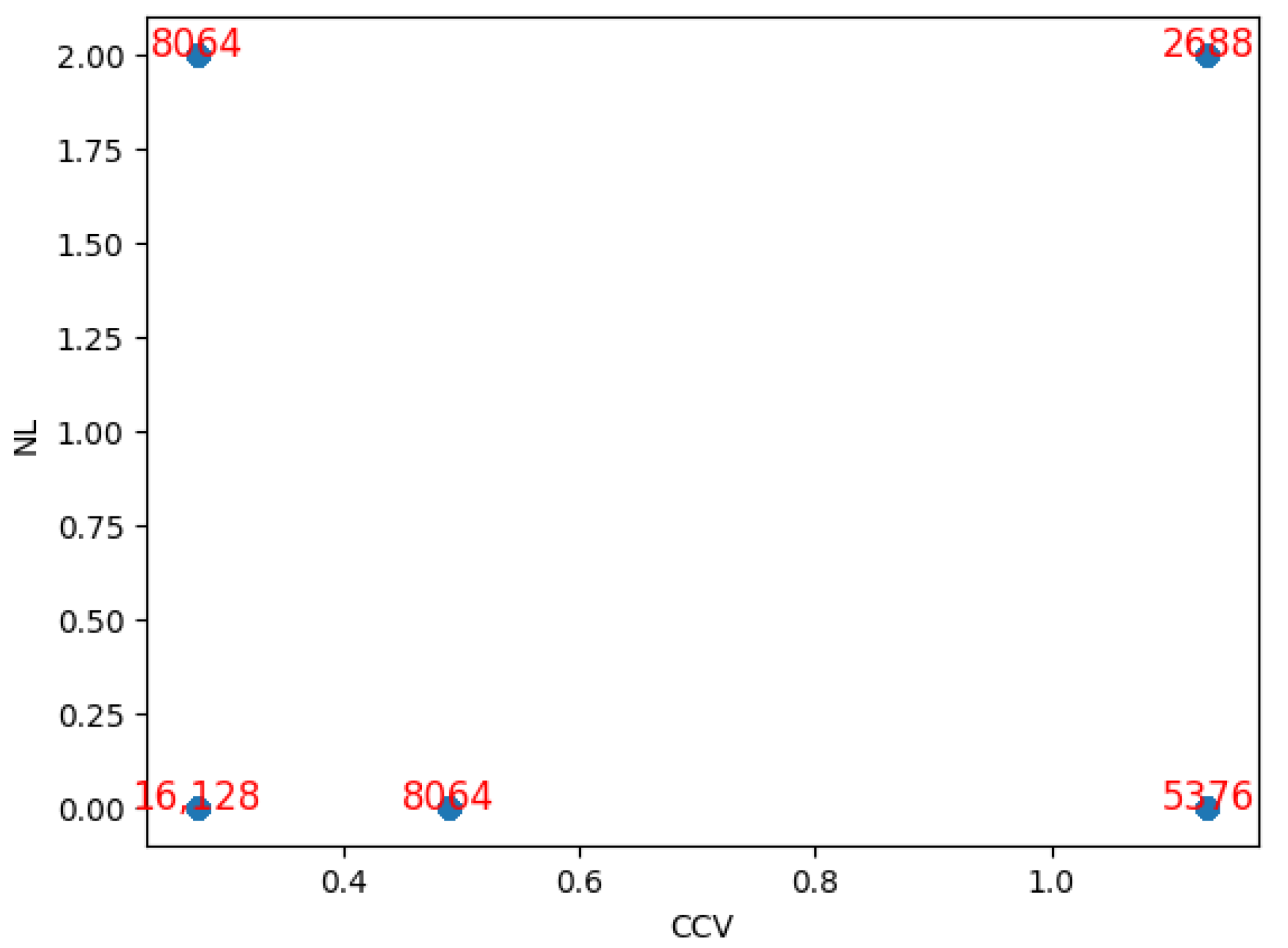
• For NL values and as for CCV values, most probabilities are the lowest they can be, $P(NL=0)\approx 0.73$ and $P(CCV=0.27551)=0.6$, which are not desirable in cryptographic terms.
• The lowest probable value, $P(NL=2,CCV=1.13265)\approx 0.07$, is reserved for the higher values of NL and CCV simultaneously, which corresponds to good cryptographic properties.
• The conditional probability for the maximum NL given the maximum CCV, $P(NL=2|CCV=1.13265)\approx 0.35$, is greater than the conditional probability for maximum CCV given the maximum NL, $P(CCV=1.13265|NL=2)\approx 0.26$.

Then, if only NL should be optimized, it is better to search for S-boxes with high CCV values first. Moreover, we sampled 1,000,000 and 100,000 S-boxes in $4\times 4$ and $8\times 8$ spaces, respectively, and we calculated the probabilities related with the maximum value of CCV and the maximum value of NL. The probabilities are shown in

Table 5. Joint and conditional probabilities of NL and CCV in $4\times 4$ and $8\times 8$ spaces.

	$4\times 4$	$8\times 8$
Total of S-boxes	1,000,000	100,000
P(NL = max , CCV = max)	0.0001	0
P(NL = max)	0.0886	0.0017
P(CCV = max)	0.0010	$1\times {10}^{-5}$
P(NL = max|CCV = max)	0.0998	0
P(CCV = max|NL = max)	0.0012	0

.

As can be seen in Table 5, in the first case it remains that $P(NL=max|CCV=max)$ has the highest value. Then, the best search strategy is to move to where S-boxes have the maximum CCV value and keeping CCV invariant through HW classes, to where S-boxes have the maximum NL value. In the second case, it is less likely that we obtain S-boxes with high CCV values; therefore, optimizing the two properties is also better to ensure we obtain high CCV first.

Prioritizing CCV optimization in higher-dimensional S-box designs (for later do NL optimization in a second step) will be very efficient if the Hamming-Weight classes or the mega-classes are used to partitioning the search space. In relation to the CCV distribution, we want to mention that, in addition to doing some explorations and getting some insights, it is still an open problem. There is a notable difference between the cardinal of the HW-classes (which is constant for all classes and was estimated at [20] as a function of n) and the cardinal of the mega-classes, because the last one is not constant and depends on the CCV, as we illustrate in our work. The estimation of the different CCV values will be studied in future research. The estimation of the cardinal of each mega-class is also open for study; for $n=3$ we just experimentally observe a symmetry of the cardinal that should be mathematically proved.

3. Conclusions

We define a new subset of affine-shifted S-boxes that have the same non-linearity and confusion coefficient variance values. Next, we resume our main theoretical and practical results. It is imperative to consider Propositions 1, 2, and 3 in conjunction with a generation method that is employed to obtain a subset, given an initial S-box. We provide several examples of S-boxes that belong to the affine-shifted subset with respect to the Picek S-box and the AES S-box, respectively. The method presented here identifies affine-shifted S-boxes that preserve both non-linearity and confusion coefficient variance, thus offering potential for heuristic search space reduction. However, the generated S-boxes are not suitable for deployment unless they also satisfy other critical cryptographic criteria, such as good differential uniformity, boomerang uniformity, and algebraic degree. Subsequent endeavors may entail the incorporation of filtering mechanisms or optimization stages with the objective of enhancing the cryptographic profile.

Furthermore, we demonstrate the existence of distinct Hamming weight classes that possess equivalent confusion coefficient values. In this paper, we put forward a definition of a mega-class and explore its potential application in the context of space-based search operations.

Future research endeavors must address the open question concerning the intersection set between the affine-shifted set and the Hamming weight class. This is due to the notion that S-boxes with the same confusion coefficient values could belong to different Hamming weight classes. Also, the study over non-bijective S-boxes should be taken into account.