Encryption Algorithm MLOL: Security and Efficiency Enhancement Based on the LOL Framework
Abstract
1. Introduction
- Integration of encryption and authentication: We improve the LOL-MINI with GHASH algorithms [13] and propose the MLOL algorithm, which seamlessly integrates encryption and authentication processes. This integrated design enhances both the efficiency and security of the algorithm. By simplifying security evaluation and making the algorithm more compatible with automated analysis tools, MLOL offers a more efficient and practical solution for AEAD algorithm design;
- Enhanced LFSR design: We introduce a new LFSR [14] design that extends the LFSR construction in the LOL framework. By replacing the original two-branch generalized Feistel structure [15] with a four-branch generalized Feistel structure, the new design supports parallel computation. This significantly reduces computational complexity, while ensuring the generated sequence maintains maximum periodicity. Compared to the LFSR in the LOL framework, the LFSR in MLOL delivers higher computational efficiency, making it particularly suitable for resource-constrained environments [16];
- Performance evaluation: We performed a detailed comparison of the implementation costs between the core component LFSR and the full MLOL algorithm, benchmarking them against the original LOL framework. By analyzing the time complexity [17] of the LFSR implementation and the overall algorithm, we assessed the implementation efficiency of the MLOL algorithm;
- Comprehensive security analysis: A detailed security analysis of the MLOL algorithm confirms that it provides 256-bit security [18] against current cryptographic attack methods, ensuring robust protection.
2. MLOL Algorithm
2.1. Definitions
2.1.1. Variables and Symbols
| Variables and Symbols | Definitions |
| n bits of 0 | |
| n bits of 1 | |
| AD | Linked data, <264 bits |
| M | Plaintext message string, <264 bits |
| C | Ciphertext message string, <264 bits |
| K | Working key, size 256 bits |
| N | Nonce value, size 128 bits |
| T | Label, size 128 bits |
| Validation tag, size 128 bits | |
| Roundload | Initialize the number of rounds to 12 |
| t | The number of iteration rounds, i.e., state moments |
| ┴ | Authentication failure symbol |
2.1.2. Conventions and Operations
| Conventions and Operations | Definitions |
| 0/1-bit string of length k bits x | |
| Bit length of x | |
| Bitwise addition modulo 2 | |
| Bitstring x spliced with y | |
| Message M’s message block number | |
| The binary representation of x | |
| bin64(X) | Express the decimal number X as a 64-bit binary number, X < 264 |
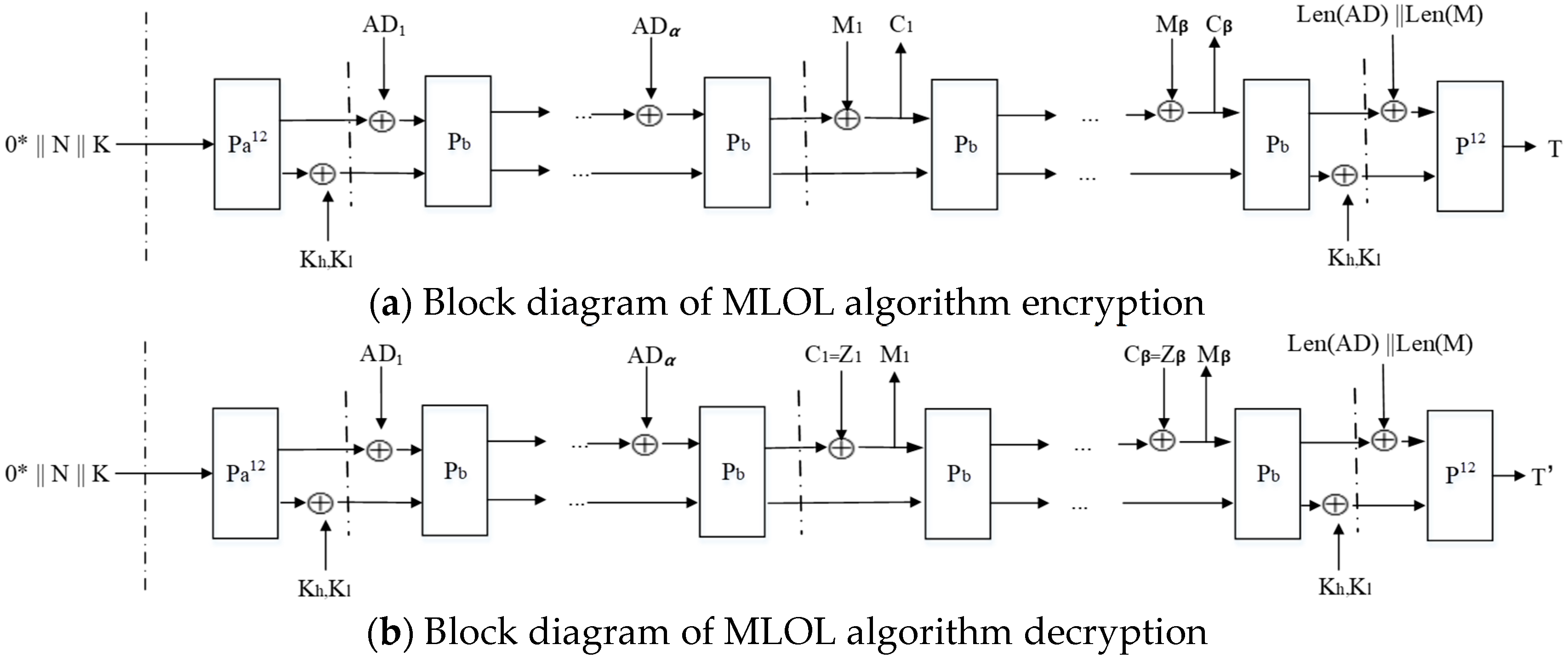
2.2. Description of Algorithm Development
2.2.1. General Framework of the Algorithm
2.2.2. Padding
2.2.3. Initialization Process
- Calculate , ;
- Update the state of registers , , whose steps are given by Equation (4);
- Update the state of registers according to Equation (5).
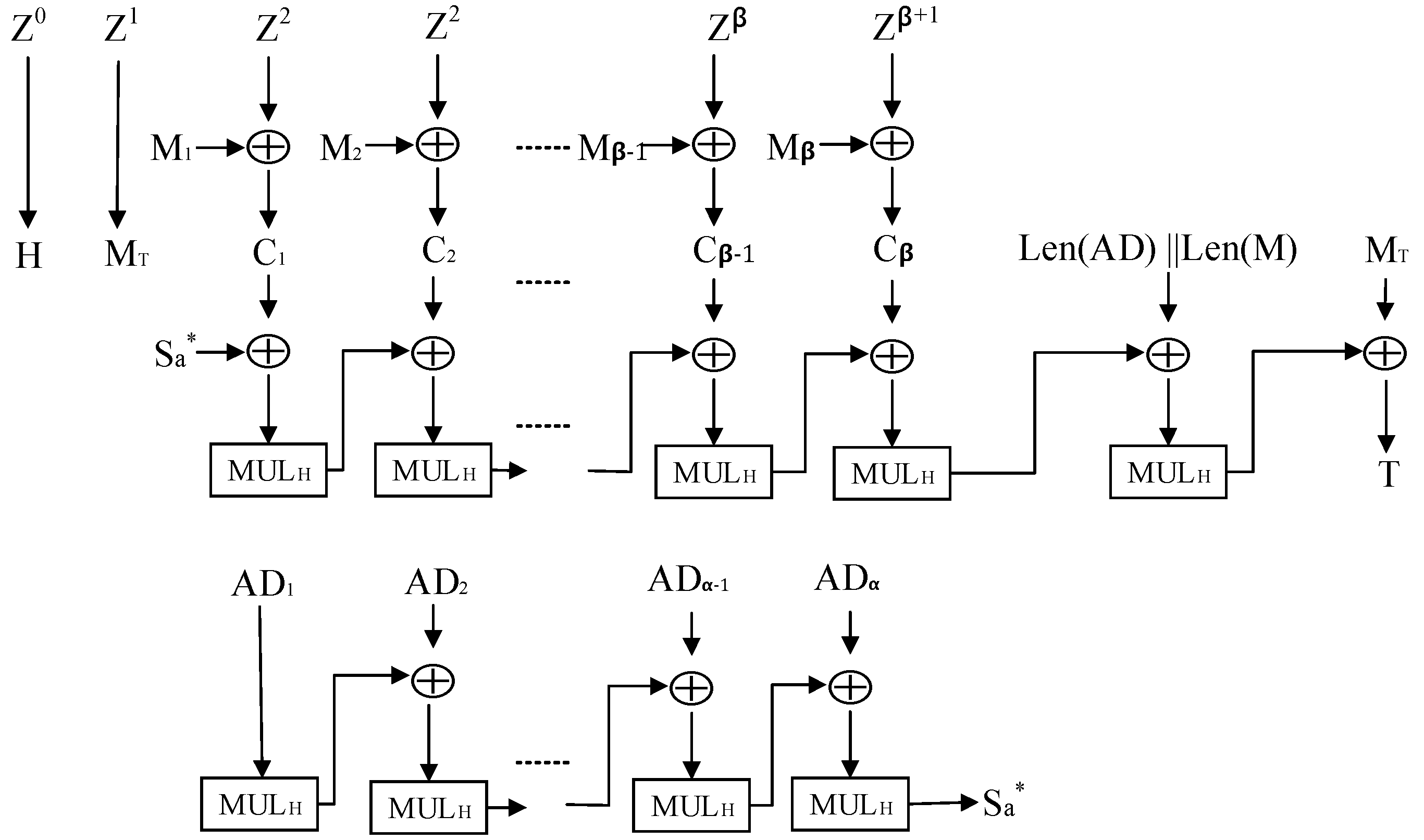
2.2.4. Associated Data Processing
- Calculate , ;
- Update the state of registers , , whose steps are given by Equation (6);
- Update the state of registers according to Equation (7);
- At time , .
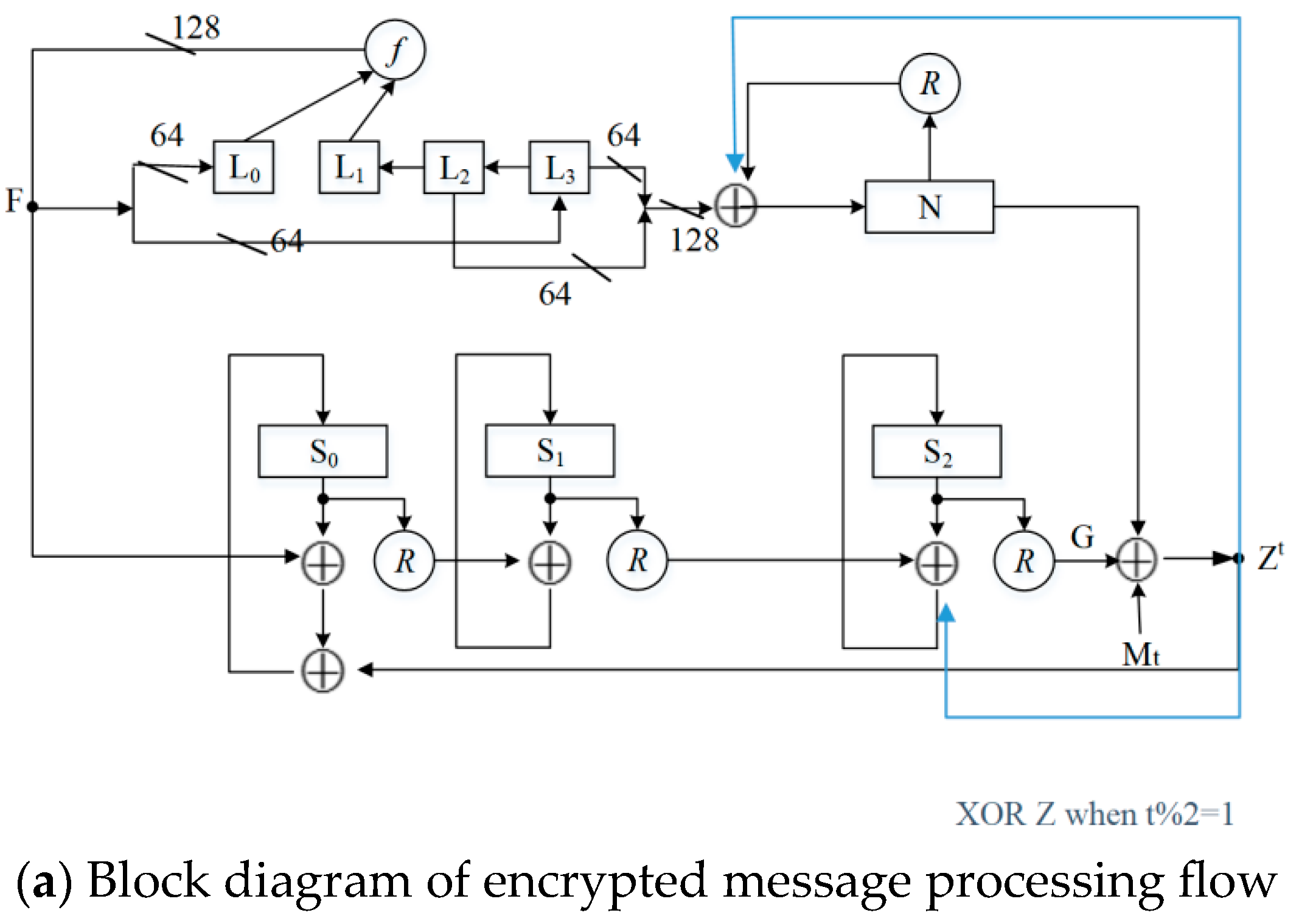
2.2.5. Message Processing
- Calculate , . Output the 128-bit ciphertext data block = at time t;
- Update the state of registers , , whose steps are given by Equation (8);
- Update the state of registers according to Equation (9);
- At time , update the final states with , .
- Calculate , ; output the 128-bit plaintext block of data = at moment t;
- Update the state of registers , whose steps are given by Equation (8);
- Update the state of registers according to Equation (9);
- At time , update the final states with , .
2.2.6. Label Generation Process
- Calculate , ;
- Update the state of registers , , whose steps are given by Equation (10);
- Update the state of registers according to Equation (11);
- At the moment of , the output label .
3. Description of Parts in the MLOL Algorithm
Improved LFSR
| Algorithm 1 LFSR Algorithm |
| Input: Initial states , , matrix C, function σ. Output: LFSR internal states and sequence output. 1: Define internal state at step t: . 2: for each time step t = 0,1,2,… do 3: Compute feedback state by 4: Generate the output sequence at step t: (12) 5: Update internal states: (13) 6: end for 7: return the sequence outputs …. |
4. Experimental Analysis and Discussion
4.1. Cost Analysis of Improved LFSR Realization
4.2. Cost Analysis of MLOL and LOL Then GHASH Algorithm Implementation
- LOL-MINI then GHASH: 12 rounds of initialization iterations, rounds of keystream output iterations, operations, 128-bit specific XOR;
- MLOL: 12 rounds of initialization iterations, 12 rounds of label generation iterations, rounds of keystream output iterations, number of 128-bit specific XOR.where , , , iterations contain the basic operations at a time as shown in Table 3.Table 3. Comparison of basic operations included in , , , (units: number of iterations).
Basic Operation 8 8 4 4 R function (math.) 4 4 4 4 128-bit specific XOR 9 7 8.5 7.5
5. Security Analysis of MLOL
5.1. Full Diffusion Round Analysis
5.2. Guess-And-Determine Attack
5.3. Algebraic Attack
5.4. Forgery Attack
5.5. Integral Analysis
5.6. Differential Analysis
- Truncated differential analysis
- 2.
- Impossible differential analysis
6. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Orhanou, G.; El Hajji, S.; Bentaleb, Y. SNOW 3G Stream cipher Operation and Complexity Study. Contemp. Eng. Sci. 2010, 3, 97–111. [Google Scholar]
- Mukherjee, C.S.; Roy, D.; Maitra, S. Design and Cryptanalysis of ZUC: A Stream Cipher in Mobile Telephony; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Pradhan, D.; Sahu, P.K.; Ghonge, M.M.; Rajeswari Tun, H.M. Security Approaches to SDN-Based Ad hoc Wireless Network Toward 5G Communication. In Software Defined Networking for Ad Hoc Networks; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Latva-aho, M.; Leppänen, K. Key Drivers and Research Challenges for 6G Ubiquitous Wireless Intelligence. 2019. Available online: https://oulurepo.oulu.fi/handle/10024/36430 (accessed on 26 January 2025).
- Shi, Y. Quantum lower bounds for the collision and the element distinctness problems. In Proceedings of the 43rd Annual IEEE Symposium on Foundations of Computer Science, Vancouver, BC, Canada, 19 November 2002. [Google Scholar]
- Damgård, I.B.; Fehr, S.; Salvail, L.; Schaffner, C. Cryptography in the bounded quantum-storage model. SIAM J. Comput. 2008, 37, 1865–1890. [Google Scholar] [CrossRef]
- Boorghany, A.; Sarmadi, S.B.; Jalili, R. On Constrained Implementation of Lattice-Based Cryptographic Primitives and Schemes on Smart Cards. ACM Trans. Embed. Comput. Syst. 2014, 14, 42. [Google Scholar] [CrossRef]
- Balogh, M.; Eaton, E.; Song, F. Quantum collision-finding in non-uniform random functions. In Proceedings of the 9th International Conference of the Post-Quantum Cryptography (PQCrypto 2018), Fort Lauderdale, FL, USA, 9–11 April 2018; Lange, T., Steinwandt, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 467–486. [Google Scholar]
- Ni, B.; Ito, G.; Dong, X.; Iwata, T. Quantum attacks against type-1 generalized Feistel ciphers and applications to CAST-256. In Progress in Cryptology—(INDOCRYPT 2019); Hao, F., Ruj, S., Gupta, S.S., Eds.; Volume 11898 of LNCS; Springer: Berlin/Heidelberg, Germany, 2019; pp. 433–455. [Google Scholar]
- Liu, Q.; Zhandry, M. On finding quantum multi-collisions. In Advances in Cryptology—EUROCRYPT 2019; Ishai, Y., Rijmen, V., Eds.; Part III, Volume 11478 of LNCS; Springer: Berlin/Heidelberg, Germany, 2019; pp. 189–218. [Google Scholar]
- Feng, D.; Jiao, L.; Hao, Y.; Zheng, Q.; Wu, W.; Qi, W.; Zhang, L.; Zhang, L.; Sun, S.; Tian, T. LOL: A Highly Flexible Framework for Designing Stream Ciphers. IACR Cryptol. Eprint Arch. 2023, 1234, 1–20. [Google Scholar] [CrossRef]
- Rogaway, P. Authenticated-encryption with associated-data. In Proceedings of the 9th ACM Conference on Computer and Communications Security (CCS 2002), Washington, DC, USA, 18–22 November 2002. [Google Scholar]
- Xue, Y. Application of GHASH function in network encryption algorithm GCM. In Network Security Technology and Application; Springer: Berlin/Heidelberg, Germany, 2009; Volume 6, pp. 92–94. [Google Scholar]
- Deb, S.; Bhuyan, B.; Gupta, N.C. Design and analysis of LFSR-based stream cipher. In Proceedings of the International Conference on Computing and Communication Systems: I3CS 2016, NEHU, Shillong, India; Springer: Singapore, 2018. [Google Scholar]
- Shibutani, K.; Isobe, T.; Hiwatari, H.; Mitsuda, A.; Akishita, T.; Shirai, T. Piccolo: An Ultra-Lightweight Blockcipher; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Suzaki, T.; Minematsu, K. Improving the generalized Feistel. In International Workshop on Fast Software Encryption; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Ye, L.; Wang, X. Cryptographic Algorithms and Their Implementations in Resource-Constrained Networks; China New Telecommunications: Beijing, China, 2008; Volume 10, pp. 63–66, 72. [Google Scholar]
- Gligoroski, D.; Ødeård, R.S.; Jensen, R.E. OBSERVATION: An explicit form for a class of second preimages for any message M for the SHA-3 candidate Keccak. IACR Cryptol. ePrint Arch. 2011, 2011, 261. [Google Scholar]
- Bao, Z.; Guo, J.; List, E. Full Diffusion Analysis of Lightweight Cryptographic Primitives. IACR Trans. Symmetric Cryptol. 2021, 2021, 1–25. [Google Scholar]
- Khazaei, S.; Moazami, F. On the Computational Complexity of Finding a Minimal Basis for the Guess and Determine Attack. Iran. Soc. Cryptol. 2017, 9, 3. [Google Scholar]
- Feng, X.; Liu, J.; Zhou, Z.; Wu, C.; Feng, D. A byte-based guess and determine attack on SOSEMANUK. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Singapore, 5–9 December 2010; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Hadipour, H.; Eichlseder, M. Autoguess: A tool for finding guess-and-determine attacks and key bridges. In Proceedings of the International Conference on Applied Cryptography and Network Security, Rome, Italy, 20–23 June 2022; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar]
- Biryukov, A.; Shamir, A. Cryptanalytic time/memory/data tradeoffs for stream ciphers. In Proceedings of the 6th International Conference on the Theory and Application of Cryptology and Information Security (Advances in Cryptology—ASIACRYPT 2000), Kyoto, Japan, 3–7 December 2000; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Ma, Z.; Tian, T.; Qi, W.F. Conditional differential attacks on Grain-128a stream cipher. IET Inf. Secur. 2017, 11, 139–145. [Google Scholar] [CrossRef]
- Courtois, B.P. Golden Core Recognition Program honors efforts on behalf of CS. Computer 2002, 29, 103. [Google Scholar]
- Fuhr, T.; Gilbert, H.; Reinhard, J.R.; Videau, M. A Forgery Attack on the Candidate LTE Integrity Algorithm 128-EIA3 (Updated Version). 8 December 2010. Available online: https://eprint.iacr.org/2010/618 (accessed on 26 January 2025).
- Liu, F.; Isobe, T.; Meier, W.; Sakamoto, K. Weak keys in reduced AEGIS and Tiaoxin. IACR Trans. Symmetric Cryptol. 2021, 2021, 104–139. [Google Scholar] [CrossRef]
- Biham, E.; Shamir, A.; Cryptol, J. Differential cryptanalysis. In Differential Cryptanalysis of the Data Encryption Standard; Springer: New York, NY, USA, 2011; pp. 332–336. [Google Scholar]
- Li, Y.; Lin, H.; Bi, X.; Huo, S.; Han, Y. MILP-based differential cryptanalysis on full-round shadow. J. Inf. Secur. Appl. 2024, 81, 103696. [Google Scholar] [CrossRef]






| The Number of Multiplications | The Number of XOR Operations | |
|---|---|---|
| m = 2 | ||
| m = 4 |
| Bytes | GHASH | NMH-MAC | ||
|---|---|---|---|---|
| LOL-MINI | LOL-DOUBLE | LOL-MINI | LOL-DOUBLE | |
| 32 | 5.08 | 3.71 | 5.59 | 4.44 |
| 64 | 9.70 | 7.26 | 9.63 | 7.75 |
| 96 | 11.97 | 9.11 | 12.81 | 10.50 |
| 128 | 15.88 | 12.03 | 15.27 | 12.68 |
| 160 | 16.69 | 12.94 | 17.33 | 14.48 |
| 192 | 20.05 | 15.55 | 18.96 | 15.95 |
| 224 | 20.25 | 15.90 | 20.36 | 17.24 |
| 256 | 23.05 | 18.18 | 21.56 | 18.24 |
| 1024 | 36.05 | 29.77 | 30.83 | 27.45 |
| 2048 | 39.71 | 33.19 | 33.49 | 30.01 |
| 4096 | 41.71 | 35.25 | 34.52 | 31.44 |
| 8192 | 42.90 | 36.39 | 35.55 | 32.22 |
| 16,384 | 43.42 | 36.96 | 35.48 | 33.16 |
| Basic Operation | LOL-MINI then GHASH | MLOL |
|---|---|---|
| R function (math.) | ||
| 128-bit specific XOR | ||
| 0 |
| Data Length (Bytes) | Computational Complexity Difference |
|---|---|
| 32 | |
| 64 | |
| 96 | |
| 128 | |
| 160 | |
| 192 | |
| 224 | |
| 256 | |
| 1024 | |
| 2048 | |
| 4096 | |
| 8192 | |
| 16384 |
| Bytes | MLOL (Gbps) | LOL-MINI then GHASH (Mbps) |
|---|---|---|
| 32 | 2.618 | 2035.708 |
| 64 | 3.091 | 4049.903 |
| 96 | 4.171 | 6740.899 |
| 128 | 4.076 | 8821.297 |
| 160 | 4.984 | 9043.705 |
| 192 | 6.500 | 9643.268 |
| 224 | 6.950 | 9806.630 |
| 256 | 7.186 | 10,706.156 |
| 1024 | 10.539 | 15,750.597 |
| Rounds | N | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 3 | 33 | 33 | 33 | 33 | 33 | 33 |
| 2 | 39 | 69 | 162 | 161 | 161 | 161 | 161 | 417 |
| 3 | 235 | 329 | 353 | 289 | 289 | 289 | 289 | 673 |
| 4 | 495 | 647 | 736 | 417 | 417 | 417 | 417 | 801 |
| 5 | 808 | 992 | 896 | 545 | 545 | 545 | 801 | 929 |
| 6 | 1152 | 1152 | 1024 | 673 | 673 | 929 | 1057 | 1057 |
| 7 | 1280 | 1280 | 1152 | 801 | 1057 | 1185 | 1185 | 1185 |
| 8 | 1408 | 1408 | 1280 | 1184 | 1312 | 1312 | 1312 | 1312 |
| 9 | 1408 | 1408 | 1408 | 1408 | 1408 | 1408 | 1408 | 1408 |
| Time | Operation | Variables | Relations | Complexity |
|---|---|---|---|---|
| t | Guess Determine | |||
| t + 1 | Guess Determine Determine Determine Determine | |||
| t + 2 | Guess Determine Determine Determine Determine |
| Linear equations | 128 × (5T − 2) |
| Quadratic equations | 368 × 4T |
| Equation | 2112T − 256 |
| Linear term | 128 × (8T + 3) |
| Quadratic | (64 × 16) × 4T |
| Item | 5120T + 384 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 0 | 6 | 17 | 34 | 39 | 47 | 51 | 59 | 63 | 67 | 72 | 77 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 0 | 6 | 17 | 34 | 39 | 47 | 51 | 59 | 63 | 67 | 72 | 77 |
| Round | Impossible Differential Differentiator |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 |
| Round | Impossible Differential Differentiator |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Mu, D.; Zhang, W.; Dong, X. Encryption Algorithm MLOL: Security and Efficiency Enhancement Based on the LOL Framework. Cryptography 2025, 9, 18. https://doi.org/10.3390/cryptography9010018
Zhang X, Mu D, Zhang W, Dong X. Encryption Algorithm MLOL: Security and Efficiency Enhancement Based on the LOL Framework. Cryptography. 2025; 9(1):18. https://doi.org/10.3390/cryptography9010018
Chicago/Turabian StyleZhang, Xinyue, Daoguang Mu, Wenzheng Zhang, and Xinfeng Dong. 2025. "Encryption Algorithm MLOL: Security and Efficiency Enhancement Based on the LOL Framework" Cryptography 9, no. 1: 18. https://doi.org/10.3390/cryptography9010018
APA StyleZhang, X., Mu, D., Zhang, W., & Dong, X. (2025). Encryption Algorithm MLOL: Security and Efficiency Enhancement Based on the LOL Framework. Cryptography, 9(1), 18. https://doi.org/10.3390/cryptography9010018






