Improving the Security of the LCB Block Cipher Against Deep Learning-Based Attacks

Abstract

This study presents a robust version of Light Cipher Block (LCB) by addressing the vulnerabilities identified in previous versions. The vulnerabilities in LCB, including a linear S-Box, improper bit shuffling, and subkey reusability, were thoroughly examined. To overcome these weaknesses, a modified version called Secure LCB is introduced, incorporating changes to the P-Box and key generation algorithm. Motivated by Gohr’s work at CRYPTO’19, this paper investigates the use of a neural distinguisher built upon a 1-dimensional convolutional neural network (1-d CNN). The deep learning model is tasked with identifying ciphertexts that have a specific, controlled difference in their inputs, as opposed to those with random input differences. The evaluation of the proposed Secure LCB using the neural distinguisher suggests that the modifications made to LCB have effectively enhanced its resistance against the neural distinguisher’s classification. This highlights the importance of addressing vulnerabilities in cryptographic systems and showcases the potential of machine learning techniques in cryptanalysis.

1. Introduction

The proliferation of Internet of Things (IoT) devices has revolutionized various industries, providing unparalleled connectivity and convenience. However, the widespread deployment of IoT devices has raised significant concerns regarding the security of transmitted data, particularly when sensitive information is involved. To address these concerns, lightweight hash functions, stream ciphers and block ciphers play a crucial role. These cryptographic hash functions are designed to efficiently verify the integrity of data without imposing excessive computational overheads on resource-constrained IoT devices. Lightweight hash functions are tailored to the limited processing capabilities of IoT devices, ensuring that data integrity checks can be performed with minimal resource consumption.

In addition to lightweight hash functions, the security landscape of IoT is further fortified by stream ciphers [1], block ciphers and authenticated encryption schemes [2]. Stream ciphers are instrumental in securing data in motion, as they encrypt data bit by bit or byte by byte, making them suitable for real-time communication and resource-efficient encryption. On the other hand, block ciphers [3,4] excel at encrypting data at rest and provide a robust defense against unauthorized access to stored information. By integrating these cryptographic elements into the fabric of IoT security, the integrity, confidentiality and authenticity of transmitted and stored data can be effectively safeguarded, mitigating the risks associated with the widespread deployment of IoT devices. Due to the lightweight nature of IoT devices such as sensors, RFID tags and smartcards, conventional block cipher schemes, such as AES, which are relatively operation-intensive, are unsuitable for implementation. In contrast to conventional algorithms, lightweight block ciphers [4,5] are typically simpler, with smaller block and key sizes, characterized by the following properties. First, applications operating on resource-constrained devices typically do not demand the encryption of large datasets. Second, potential adversaries confront limitations in both data availability and computational resources, thereby necessitating that lightweight ciphers provide only a moderate level of security. Lastly, lightweight ciphers are predominantly deployed in hardware environments, with limited software platform implementation. Therefore, lightweight block ciphers are well suited for resource-constrained devices with limited components. Encryption algorithms, such as Light Cipher Block (LCB) and others, play a crucial role in ensuring the confidentiality and integrity of IoT communications. LCB was initially introduced as an ultrafast lightweight block cipher specifically designed to cater to the unique requirements of IoT devices [6]. Nevertheless, vulnerabilities in LCB were discovered due to the linearity exhibited in its S-box. The vulnerabilities in the S-box were confirmed through the use of a Differential Distribution Table (DDT) [7]. Consequently, to enhance LCB’s resistance against differential cryptanalysis, the authors of [8] proposed modifications to the S-box and number of rounds of the cipher, hereafter referred to as Chan’s LCB.

Recent advancements in machine learning, particularly in the field of neural networks, have opened up exciting possibilities for bolstering the security of cryptographic systems. This progress is largely attributed to the development of sophisticated neural network architectures such as convolutional neural networks (CNNs), recurrent neural networks (RNNs) and deep learning techniques [9]. These neural networks have proven highly effective in tasks related to cryptography, including encryption and decryption analysis.

One noteworthy application of neural networks in cryptography is the use of neural distinguishers. Neural distinguishers are specialized models trained to discern subtle patterns and vulnerabilities in encrypted data. They operate by learning the statistical properties of ciphertexts generated by cryptographic algorithms, making them valuable tools for both security analysts and potential attackers. By identifying patterns and weaknesses in encrypted data, neural distinguishers contribute to the evaluation and improvement of cryptographic algorithms, thus enhancing overall security.

Specifically, in the context of lightweight block ciphers (LCBs) and Chan’s LCB, neural distinguishers have gained significant attention. Lightweight block ciphers are designed to provide efficient encryption in resource-constrained environments, such as Internet of Things (IoT) devices. Chan’s LCB is a lightweight block cipher known for its compact design and suitability for embedded systems. The use of neural distinguishers with these ciphers involves training neural networks to analyze ciphertexts generated by these ciphers, with the goal of uncovering potential vulnerabilities or patterns that could be exploited by adversaries. This approach not only aids in strengthening the security of LCB and Chan’s LCB, but also informs the broader field of lightweight cryptography.

In summary, recent developments in machine learning, especially neural networks, have brought about exciting prospects for enhancing cryptographic system security. neural distinguishers, in particular, have emerged as a powerful technique for analyzing encrypted data, with a specific focus on lightweight block ciphers like LCB and Chan’s LCB. This synergy between machine learning and cryptography promises to shape the future of secure data transmission and encryption technologies.

This research paper aims to explore the application of neural distinguishers in the context of differential cryptanalysis [10] on an LCB cipher and proposes changes to the cipher to withstand the attack. We analyze the vulnerabilities introduced by the existing versions of the LCB cipher to propose modifications for enhancing its resistance against differential cryptanalysis using a neural distinguisher. By leveraging the power of neural networks, we aim to develop improved encryption schemes capable of withstanding differential cryptanalysis while meeting the stringent resource constraints of IoT environments.

The remainder of this paper is structured as follows: Section 2 provides an overview of the different versions of LCB and existing work performed on them. Section 3 details the proposed modification of the LCB cipher. Section 4 describes our analysis of the LCB family. Section 5 presents our experimental results, evaluating the performance and effectiveness of the proposed cipher using the proposed model. Section 6 concludes the paper.

2. Preliminaries

It is preferred for the ciphers used for IoT-constrained devices to be ultrafast or lightweight or both. The term “ultrafast” implies that the cipher is optimized to perform encryption and decryption operations rapidly, enabling it to meet the real-time processing requirements of applications with stringent timing constraints. The “lightweight” aspect of the cipher refers to its ability to operate with minimal computational and memory resources.

In the realm of IoT-constrained algorithms, the utilization of SPNs (Substitution-Permutation Networks) and Feistel structures [11] offers a multifaceted solution that seamlessly combines resource efficiency, speed, security, adaptability and compatibility. These attributes, working in synergy, empower lightweight and secure cryptographic operations on resource-limited IoT devices, effectively addressing the challenges posed by their constrained nature.

An SPN, or a Substitution-Permutation Network, serves as a fundamental building block for encryption in this context. It employs a block cipher structure that discretely divides the encryption process into multiple rounds. In each of these rounds, the SPN applies careful orchestration of substitution and permutation operations to ensure not only robust security, but also operational efficiency.

Concurrently, the Feistel structure [11] plays an equally pivotal role. This block cipher construction segregates the input into two halves, ushering them through a series of rounds. In these rounds, one-half undergoes mixing with a key-dependent function while also being swapped, contributing to the overall cryptographic strength and resilience demanded by IoT-constrained environments. Together, these architectural elements enhance the cryptographic capabilities of IoT devices while preserving their precious resources.

Differential cryptanalysis [12] is a well-established technique primarily applied to block ciphers [13], as they exhibit susceptibility to this form of attack. Block ciphers function by processing data in fixed-size blocks, and differential analysis exploits the discrepancies in input–output pairs for various plaintext combinations. This method allows attackers to glean insights into the inner workings of the block cipher, potentially leading to the discovery of the secret encryption key. In the context of differential cryptanalysis, one of the essential tools at the disposal of cryptanalysts is the Differential Distribution Table (DDT) [7]. This table plays a crucial role in assessing the transmission properties and cryptographic characteristics of an S-box, which is a critical component of many block ciphers.

A Differential Distribution Table [7] is constructed through a systematic process of documenting all conceivable pairs of input differences and their corresponding output differences, effectively creating a matrix of feedback information. Within this matrix, each cell records the frequency with which a particular input–output difference pair occurs. The analysis of the DDT provides valuable insights into the behavior of the S-box, helping to identify any discernible patterns or anomalies that deviate from random behavior. Detecting significant discrepancies, frequently recurring input–output pairs or unusual differentials can be indicative of vulnerabilities within the S-box, which could then be exploited by attackers. In essence, a DDT serves as a critical tool for cryptanalysts in their efforts to understand, evaluate and potentially compromise the security of block ciphers through differential cryptanalysis.

2.1. Light Cipher Block (LCB)

Light Cipher Block is an ultrafast lightweight block cipher designed for resource-constrained IoT security applications [6]. LCB combines the SPN design with the Feistel structure. This cipher operates on a block size of 32 bits and performs encryption for 10 rounds using a 16-bit subkey.

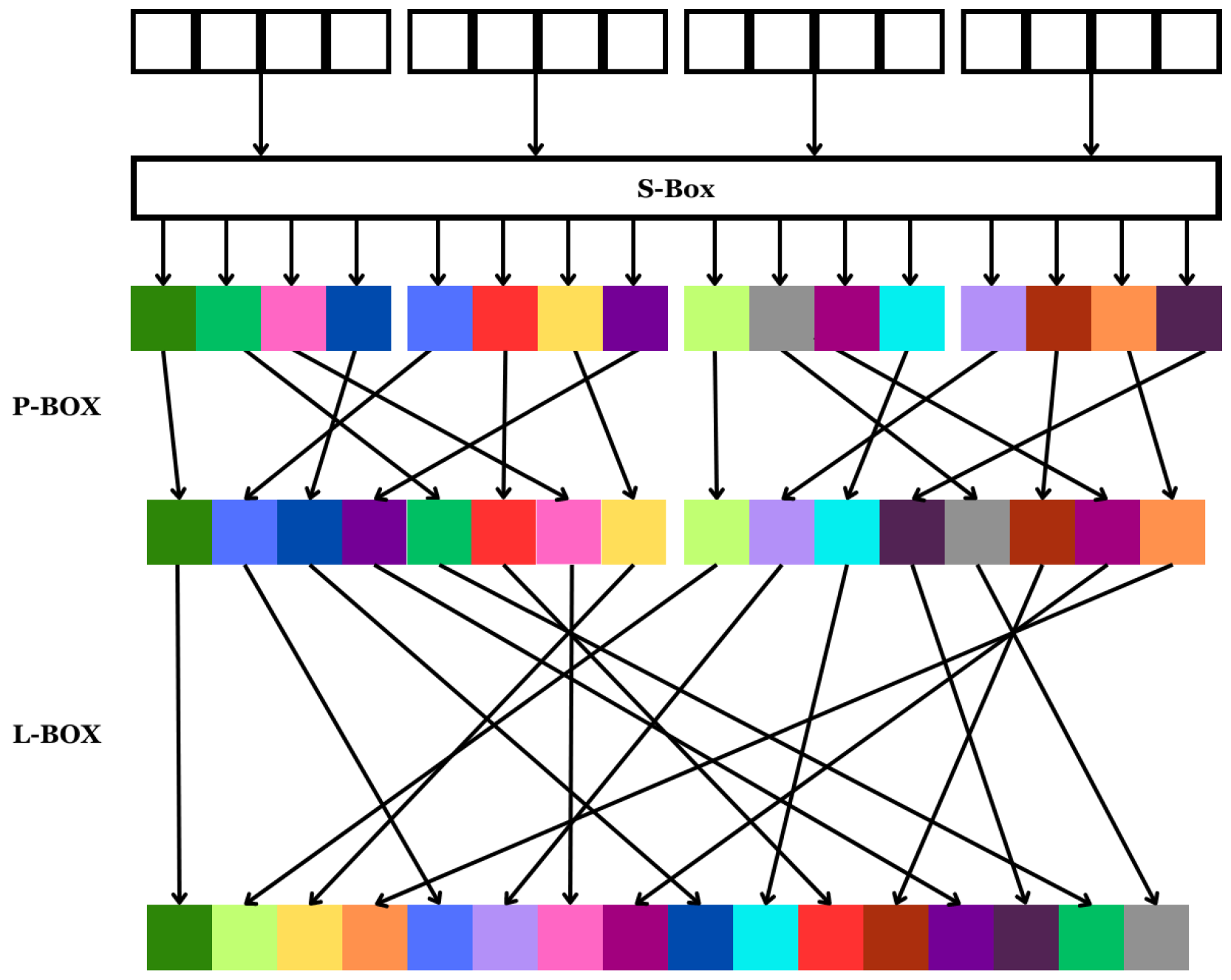
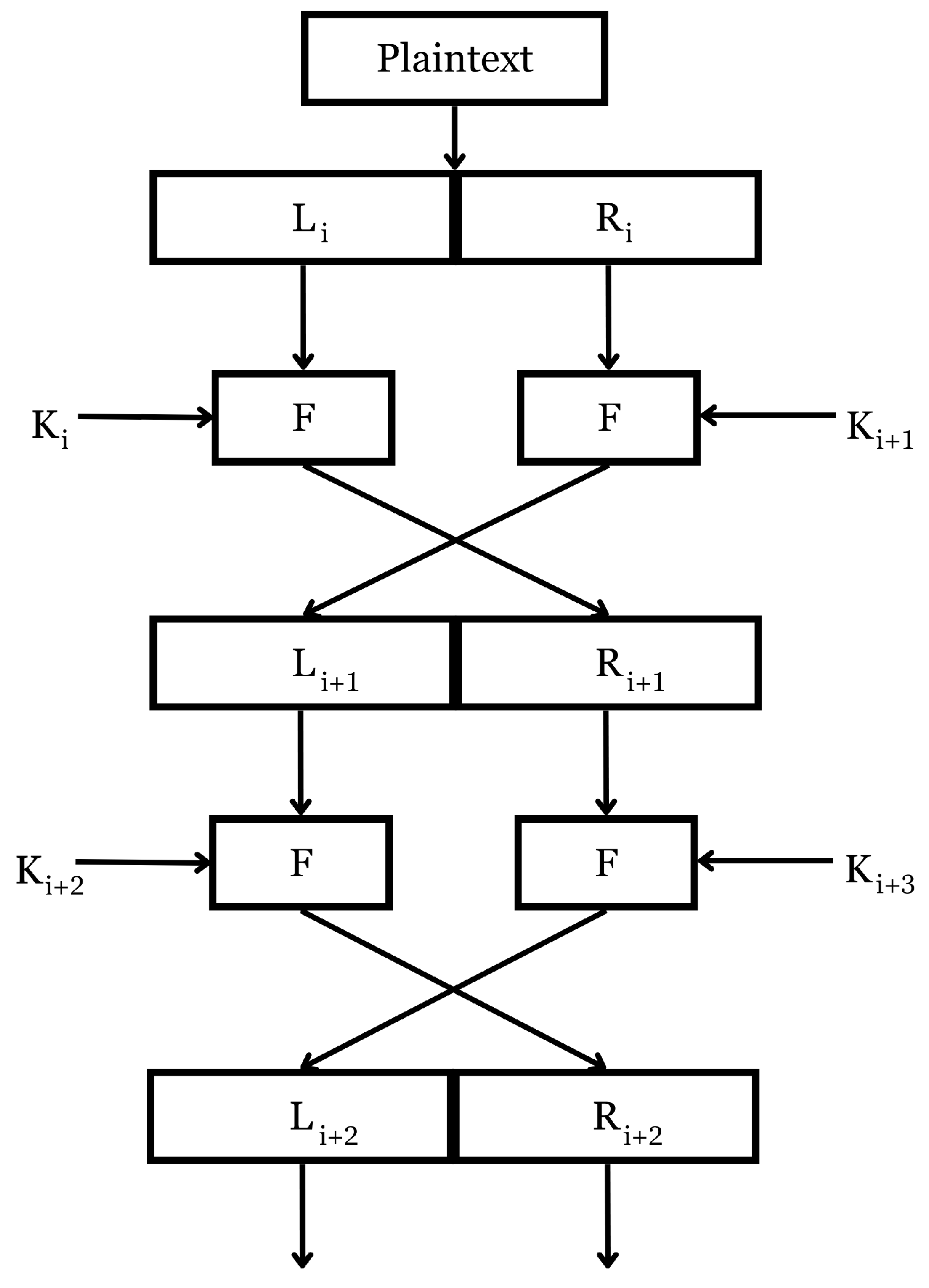
In each round, the plaintext, which has a size of 32 bits, is divided into two equal halves of 16 bits each, namely $L_i$ and $R_i$. These halves then undergo processing through a round function named the F-Block. The F-Block consists of a 16-bit L-box (Linear Box), 8-bit P-boxes (Permutation Box) and 4-bit S-boxes. After processing through their relevant F-Blocks, $L_i$ and $R_i$ are swapped.

The key generation mechanism is straightforward. The 64-bit master key is split into four parts of 16 bits each: $K_1$, $K_2$, $K_3$ and $K_4$. These subkeys are sequentially fed to the output given by the round function during encryption. The same subkeys are used for the process of encryption and the process of decryption.

The process of encryption for two consecutive rounds can be summed up as follows:

$$L_i=L\left(P\left(S\left(R_{i-1}\right)\right)\right)\oplus K_j$$

(1)

$$R_i=L\left(P\left(S\left(L_{i-1}\right)\right)\right)\oplus K_{j+1}$$

(2)

$$L_{i+1}=L\left(P\left(S\left(R_i\right)\right)\right)\oplus K_{j+2}$$

(3)

$$R_{i+1}=L\left(P\left(S\left(L_i\right)\right)\right)\oplus K_{j+3}$$

(4)

where, i = {1, 3, 5, 7, 9} and j = {0}. The S-box used in LCB takes an input of 4 bits and gives an output of 4 bits and is entirely linear [6]. The S-box, represented in the form of a hexadecimal, is described in

Table 1. S-Box.

x	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
S(x)	0	4	1	5	2	6	3	7	8	C	9	D	A	E	B	F

.

The P-box used in the cipher is an 8-bit permutation. It takes two sets of 4-bit outputs denoted as l[ ] and m[ ] from the S-box. The P-box produces an 8-bit output, denoted as n[ ]. The P-box can be represented as in

Table 2. P-Box.

x	n[1]	n[2]	n[3]	n[4]	n[5]	n[6]	n[7]	n[8]
P(x)	l[1]	m[1]	l[4]	m[4]	l[2]	m[2]	l[3]	m[3]

.

The L-box used in the cipher is a 16-bit permutation. It takes two sets of 8-bit outputs, denoted as s[ ] and t[ ], from the P-box. The L-box produces a 16-bit output, denoted as u[ ]. The L-box can be represented as in

Table 3. L-Box.

x	u[1]	u[2]	u[3]	u[4]	u[5]	u[6]	u[7]	u[8]
L(x)	s[1]	t[1]	s[8]	t[8]	s[2]	t[2]	s[7]	t[7]
x	u[9]	u[10]	u[11]	u[12]	u[13]	u[14]	u[15]	u[16]
L(x)	s[3]	t[3]	s[6]	t[6]	s[4]	t[4]	s[5]	t[5]

.

The bit lengths of the L-box, P-box and S-box of the cipher are different. The pattern of the bit traversal of an F-function can be represented as shown in Figure 1.

The output from the F-function is XORed with the respective 16-bit subkey. Two rounds of LCB can be depicted as shown in Figure 2.

2.2. Chan’s LCB

In 2023, Chan et al. [8] proposed a differential cryptanalysis on 10 rounds of LCB. To enhance the resilience of the cipher against this attack, the authors suggest several modifications. The S-box used in the cipher should have good cryptographic properties in order to resist attacks like differential cryptanalysis [14]. Hence, one of the suggested modifications is to replace the original S-box with the PRESENT [15] block cipher’s S-box. Another proposed modification is to expand the total number of rounds from 10 to 20.

The PRESENT [15] block cipher’s S-box can be described as in

Table 4. S-Box.

x	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
S(x)	C	5	6	B	9	0	A	D	3	E	F	8	4	7	1	2

.

The S-Box described in the Table 4 has the following properties:

• Balanced;
• Complete;
• Has no fixed points;
• Non-linearity—4;
• Differential uniformity—4;
• Differential branch number—3;
• Boomerang uniformity—16.

2.3. 1-D Convolutional Neural Network

A 1-D CNN is defined as a collection of linear neural networks, with each network corresponding to a filter [16]. Each filter processes a fragment of the input, and this fragment slides across the input data. The size of the fragment is determined by the kernel size, the stride determines the distance between consecutive sub-parts, and the start and end points of the sub-part depend on the padding used [17].

In the machine learning community, three important concepts are widely recognized. Firstly, there are low-level features (e.g., ${\chi }_1$) that are learned by shallow layers of a neural network. These features are directly connected to the data given as input [18]. Secondly, middle-level features (e.g., ${\chi }_2$) are learned by intermediate layers of the network. They serve as a bridge between the features that are low-level and the features that are high-level. Lastly, the features that are high-level (e.g., ${\chi }_3$) are learned by deep layers and are abstract representations that capture information relevant to the prediction label [19].

To summarize, low-level features capture input-related information, high-level features capture abstract information associated with the prediction label, and the features that are middle-level act as a connection between the two [20].

2.4. Neural Distinguisher

The utilization of neural distinguishers to perform differential cryptanalysis on ciphers is experiencing a rapid increase. At CRYPTO’19, Gohr presented the first ever neural distinguisher based on a plaintext difference constraint, marking a significant milestone in this field [21]. This neural distinguisher aims to differentiate between two classes of ciphertext pairs, denoted as ($C_0$, $C_1$). The first class consists of real pairs with the label Y = 1, which correspond to plaintext pairs with a specific difference $\Delta P$. The second class consists of random pairs with the label Y = 0, which correspond to plaintext pairs with a random difference [17]. The main components of the neural distinguisher are as follows:

• Block 1: This block consists of a 1-D CNN with 1 as its kernel size, followed by batch normalization and the ReLU activation function.
• Block 2-i: This block consists of ten layers, each of which consists of two 1-D CNNs using a kernel size of 3. Each 1-D CNN is followed by batch normalization and the ReLU activation function.
• Block 3: This is a non-linear classification block consisting of three perceptron layers. Between these layers, there are two batch normalization and ReLU functions. The final layer uses a sigmoid function.

3. Proposed Work

This research begins with a comprehensive vulnerability analysis of existing versions of LCB and identifying its weaknesses. We first look at LCB as described in Section 2.1. As pointed out in [8], the LCB cipher proposed in [6] is highly vulnerable due to its linear S-Box. This vulnerability is confirmed by the DDT (Differential Distribution Table) of the S-Box, which is presented in

Table 5. Differential Distribution Table of S-box.

	0	1	2	3	4	5	6	7	8	9	a	b	c	d	e	f
0	16	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	0	0	0	4	0	0	0	4	0	4	0	0	0	4	0	0
2	0	0	0	2	0	4	2	0	0	0	2	0	2	2	2	0
3	0	2	0	2	2	0	4	2	0	0	2	2	0	0	0	0
4	0	0	0	0	0	4	2	2	0	2	2	0	2	0	2	0
5	0	2	0	0	2	0	0	0	0	2	2	2	4	2	0	0
6	0	0	2	0	0	0	2	0	2	0	0	4	2	0	0	4
7	0	4	2	0	0	0	2	0	2	0	0	0	2	0	0	4
8	0	0	0	2	0	0	0	2	0	2	0	4	0	2	0	4
9	0	0	2	0	4	0	2	0	2	0	0	0	2	0	4	4
a	0	0	2	2	0	4	0	0	2	0	2	0	0	2	2	2
b	0	2	0	0	2	0	0	0	4	2	2	2	0	2	0	0
c	0	0	2	0	0	4	0	2	2	2	2	0	0	0	2	2
d	0	2	4	2	2	0	0	2	0	0	2	2	0	0	0	0
e	0	0	2	2	0	0	2	2	2	2	0	0	2	2	0	0
f	0	4	0	0	4	0	0	0	0	0	0	0	0	4	4	4

.

Another vulnerability observed in the cipher is related to the improper shuffling of the first bit positions of the round inputs $L_i$ and $R_i$. Despite going through the F-function, these bit positions do not change properly, and, as depicted in Figure 1, after 10 rounds, the bits return to their original positions, even though $L_i$ and $R_i$ are swapped for bit shuffling.

The final vulnerability is found in the key generation algorithm of the cipher. As mentioned earlier, the key generation involves dividing a 64-bit string into four parts of 16 bits each. The problem with this approach is the reuse of the subkeys for all rounds without any transformation.

Next, we take a look at Chan’s LCB as described in Section 2.2. As highlighted in [8], certain changes have been proposed for the cipher, including modifications to the S-Box and the number of rounds. This paper claims that these alterations render the cipher more robust, making it a modified version of LCB.

However, one vulnerability that still persists in this version of LCB is the key generation process. Additionally, the number of rounds has been increased to 20, with the repetition of keys 10 times to complete the full round of the cipher.

Another vulnerability that has been observed is the shuffling occurring in the P-box. It is suggested that the shuffling should exhibit a more random nature.

With all of these vulnerabilities in mind, we have proposed a modified version called Secure LCB, incorporating the changes to the P-Box and key generation algorithm.

3.1. Secure LCB

This proposed version of LCB, called Secure LCB, addresses the vulnerabilities mentioned in Section 3. First, we modify the P-Box used in the cipher by replacing it with the one shown in

Table 6. Modified P-Box.

x	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
P(x)	7	D	1	8	B	E	2	5	4	A	F	0	3	6	9	C

. This new P-box is specifically designed to address the insufficient shuffling in the P-box. This improves the security by increasing the complexity of the cipher’s structure, thereby making it more resistant to cryptanalytic attacks. This improves the security by increasing the complexity of the cipher’s structure, thereby making it more resistant to cryptanalytic attacks (see Appendix A).

Next, we make changes to the key generation process of the cipher. The new key generation involves a 64-bit key, which is then divided into four parts of 16 bits each: $K_1$, $K_2$, $K_3$ and $K_4$. These keys are sequentially processed through the F-function for each round, and the resulting keys are used for encryption in each round. The key generation process is depicted in Figure 3.

The pseudocode of the key generation algorithm can be given as in Algorithm 1.

Algorithm 1 Proposed key generation algorithm

Require: Generate a 64-bit key

Input: Random 64-bit key

Output: 64-bit key generated using F-function

1: Split the key into ${K_1}^1$, ${K_2}^1$, ${K_3}^1$, ${K_4}^1$   2: Initialize $L_i$, $R_i$, j         3: for each round i from 1 to 10 do   4:       Split ${K_j}^i$ into $L_i$ and $R_i$   5:       $L_{next}=F-function\left(L_i\right)$   6:       $R_{next}=F-function\left(R_i\right)$   7:       ${K_j}^{i+1}$ = CONCATENATE $L_{next}$, $R_{next}$   8:       $j=j+1$   9:       if j = 4 then  10:                  j = 0  11:      end if  12: end for  13: End

Secure LCB retains its 32-bit block size and operates over 20 rounds of encryption using an unique 16-bit subkey for every round. In each round, the plaintext which is of size, 32-bit is divided into 2 equal halves of 16 bits each, namely $L_i$ and $R_i$. These halves then undergo processing through a round function named F-Block. The F-Block consists of a 16-bit L-box (Linear Box), 8-bit P-boxes and 4-bit S-boxes. After processing through their relevant F-Blocks, $L_i$ and $R_i$ are swapped. The Comparison of LCB, Chen’s LCB, and Secure LCB can be see in

Table 7. Comparison of all versions of LCB.

Feature	LCB	Chen’s LCB	Secure LCB
Purpose	Designed for resource- constrained IoT security applications	Improves resistance against differential cryptanalysis	Addresses vulnerabilities and strengthens security further
Design	Combines SPN design with Feistel structure	Replaces the S-Box	Introduces new P-box and advanced key generation
Block Size	32 bits	32 bits	32 bits
Rounds	10 rounds	Increased to 20 rounds for enhanced security	Retains 20 rounds but with improved key management and P-box
Key Features	Uses a basic S-box and P-box structur.	Replaces S-box with PRESENT cipher’s S-box for better cryptographic properties	Modifies P-box (as in Table 6) and uses a new key generation algorithm
Key Generation	Simplistic 16-bit subkeys for each round	Same approach but applied to additional rounds	Uses $K_1$, $K_2$, $K_3$ and $K_4$, processed through F-function for each round
Security	Vulnerable to differential cryptanalysis	Improved resilience but still retains some vulnerabilities	Resistant to both linear and differential attacks

.

The robustness of the cipher is then evaluated using the proposed neural Distinguisher to see how strongly the cipher withstands the attack.

3.2. Proposed Neural Distinguisher Model

Inspired by Gohr’s work presented in CRYPTO’19 [21] and the possibilities of machine learning in the field of cryptanalysis, we present a neural distinguisher model based on 1-D CNN. The model accurately classifies ciphertexts with a specific input difference with ciphertexts with random input differences. The model consists of three blocks, each with specific layer configurations.

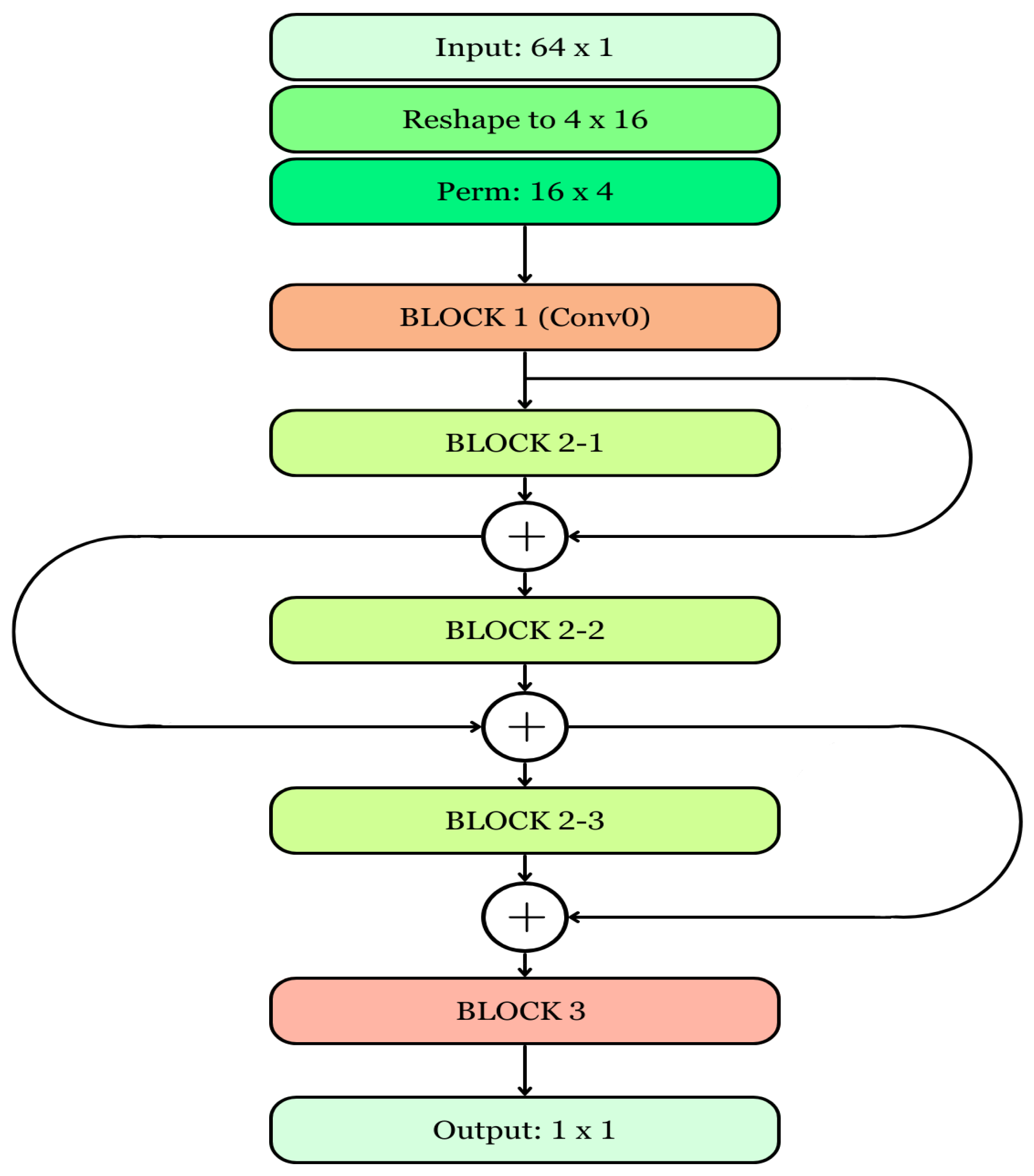
• Block 1: The first block comprises a single 1-D convolutional layer with a kernel size of 1 and 32 filters. Padding is set to 1, followed by batch normalization and a ReLU activation function, as shown in Figure 4.
• Block 2: The second block consists of three layers, where each layer includes two 1-D convolutional layers with a kernel size of 3. After each convolutional layer, batch normalization and ReLU activation are applied. Furthermore, the second layer incorporates a dropout layer at a rate of 0.5, as shown in Figure 4.
• Block 3: In the ultimate classification block, which is non-linear, there are three perceptron layers backed by two batch normalization layers, ReLU activation and dropout layers, and a rate of 0.5 is implemented. The final perceptron layer adopts a sigmoid activation function to enable discernment, as depicted in Figure 4.

For an overview of the model’s mechanics, the initial input shape is 64 × 1, which later undergoes reshaping into a size of 4 × 16. The reshaped input is further transformed into 16 × 4 using the permute function. This input, when passed through BLOCK 1, reshapes the output to 16 × 32. This output is then passed as an input through Block 2, producing an output with dimensions of 16 × 32. This output is finally reshaped to 512 × 1 before being fed to the Multi-Layer Perceptron (MLP).

In the MLP, the first perceptron layer transforms the output from 512 × 1 to 64 × 1. The second perceptron layer maintains the shape as 64 × 1. Finally, the last perceptron layer transforms the output from 64 × 1 to 1 × 1.

This model is utilized for distinguishing ciphertexts with a fixed input difference from ciphertexts with random input differences in the Light Cipher Block (LCB). The flow of the model is depicted in Figure 5.

The hyper-parameters used in training the model are as below:

• Training dataset size: ${10}^7$;
• Validation dataset size: ${10}^6$;
• Depth: 3;
• Total number of epochs: 30;
• Optimizer: SGD (Stochastic Gradient Descent);
• Loss function: binary classification;
• Learning rate: cyclic, ranging from 0.000019 to 0.00004 for every 10 epochs;
• Regularization parameter: 0.00007;
• Batch size: 2000.

4. Analysis of LCB Family with a Specific Controlled Input Difference

In this section, we analyze Secure LCB with the proposed neural distinguisher. All the vulnerabilities present in the earlier versions of LCB were addressed in Secure LCB. To define its security, we perform the same experiments on all the versions of the cipher and compare the results. The experiments are divided into three parts, where we first use LCB, then Chan’s LCB and, finally, Secure LCB.

4.1. Experiment 1

This experiment utilizes the LCB cipher and the previously described neural distinguisher in Section 2 to distinguish pairs of ciphertexts with a specific input difference from pairs of ciphertexts with random input differences. We generate ${10}^7$ pairs of ciphertexts for training the model and ${10}^6$ pairs of ciphertexts for testing the model. The ciphertexts are generated with randomly generated unique plaintexts and keys. The pseudocode of the data generation algorithm can be given as in Algorithm 2.

Algorithm 2 Dataset Generation

Require: $diff\left[0\right]$, $diff\left[1\right]$ - Arrays representing differences.

Output: X - Array of pairs of ciphertexts in binary format.

1: $plaintext\leftarrow$ Generate array of 32-bit random unsigned integers   2: Split Plaintext into their respective 16-bit Left and 16-bit Right Parts:   3:        $plain0l\leftarrow (plaintext\gg 16)\&0xffff$                 ▹ Left part   4:        $plain0r\leftarrow plaintext\&0xffff$                    ▹ Right part   5: Introduce Difference in Plaintext parts:   6:        $plain1l\leftarrow plain0l\oplus diff\left[0\right]$   7:        $plain1r\leftarrow plain0r\oplus diff\left[1\right]$   8: Encryption:   9:        Encrypt $plain0l$ and $plain0r$ and store the results in $ctdata0l$ and $ctdata0r$  10:       Encrypt $plain1l$ and $plain1r$ and store the results in $ctdata1l$ and $ctdata1r$  11: Generation of ciphertext pairs:  12: $ctdata\leftarrow$ Combine $ctdata0l$, $ctdata0r$, $ctdata1l$, and $ctdata1r$  13: $X\leftarrow$ Convert the array $ctdata$ to binary

Considering the vulnerabilities detailed in Section 2.1, we undertook an assessment of the neural distinguisher’s effectiveness on this version of LCB. The steps are as described below.

Step 1: The experiment begins by generating the dataset. Two input difference arrays, diff[0] and diff[1], are used to create pairs of plaintexts. A random 32-bit unsigned integer is generated as the plaintext, and it is then split into two 16-bit parts: plain0l and plain0r. The differences diff[0] and diff[1] are introduced by XORing them with the respective left and right parts, resulting in plain1l and plain1r.

Step 2: Encryption is performed on the original and modified plaintexts. Both plain0l and plain0r are encrypted to generate ciphertexts ctdata0l and ctdata0r, while plain1l and plain1r are encrypted to produce ctdata1l and ctdata1r. These ciphertexts are combined to form a single array of ciphertexts, which is then converted into a binary format to create the dataset X.

Step 3: This step involves using the generated pairs of ciphertexts for training and testing the neural distinguisher model. A training dataset of ${10}^7$ pairs and a testing dataset of ${10}^6$ pairs are used, with the labels Y = 1 for pairs originating from plaintexts with a specific difference and Y = 0 for pairs generated from random plaintexts.

Step 4: The model is tested 20 times using different testing datasets.

Step 5: This step involves evaluating the neural distinguisher’s ability to distinguish ciphertext pairs originating from specific input differences.

Our goal was to predict pairs of ciphertexts originating from a specific input difference.

The input difference for the 10th round was taken from the differential trial conducted on LCB [21].

In this experiment, the obtained training accuracy and testing accuracy are 0.9778 and 0.9658, respectively.

4.2. Experiment 2

In this experiment, we utilize Chan’s LCB cipher in conjunction with the neural distinguisher.

As described in Section 2.2, with these vulnerabilities in mind, we provide Chan’s LCB as the input to the neural distinguisher to determine the prediction values and ascertain whether a pair of ciphertexts belongs to the class with a specific input difference or not. The dataset for testing and training was generated with random plaintexts and keys with sizes of ${10}^6$ and ${10}^7$, respectively. The pseudocode of the data generation algorithm is shown in Algorithm 2. The testing on the model was performed 20 times with different testing datasets.

The input difference for the 20th round was taken from the differential trial conducted on Chan’s LCB [21].

The steps for the experiment to identify the differential trail using the neural distinguisher for the cipher Chan’s LCB is described below.

Step 1: The experiment begins by generating the dataset. Two input difference arrays, diff[0] and diff[1], are used to create pairs of plaintexts. A random 32-bit unsigned integer is generated as the plaintext, and it is then split into two 16-bit parts: plain0l and plain0r. The differences diff[0] and diff[1] are introduced by XORing them with the respective left and right parts, resulting in plain1l and plain1r.

Step 2: Encryption is performed on the original and modified plaintexts. Both plain0l and plain0r are encrypted to generate ciphertexts ctdata0l and ctdata0r, while plain1l and plain1r are encrypted to produce ctdata1l and ctdata1r. These ciphertexts are combined to form a single array of ciphertexts, which is then converted into a binary format to create the dataset X.

Step 3: This step involves using the generated pairs of ciphertexts for training and testing the neural distinguisher model. A training dataset of ${10}^7$ pairs and a testing dataset of ${10}^6$ pairs are used, with the labels Y = 1 for pairs originating from plaintexts with a specific difference and Y = 0 for pairs generated from random plaintexts.

Step 4: The model is tested using the input difference taken from the differential trail conducted on Chan’s LCB [21].

Step 5: This step involves evaluating the neural distinguisher’s ability to distinguish ciphertext pairs originating from specific input differences. In this experiment, the obtained training accuracy and testing accuracy are 0.9522 and 0.9137, respectively.

4.3. Experiment 3

In this experiment, we use Secure LCB to generate sets of ciphertext pairs that share a fixed difference in input. Plaintext pairs with sizes of ${10}^7$ and ${10}^6$ are generated randomly but are unique in nature. These pairs are then encrypted with random keys using Secure LCB to generate pairs of ciphertexts. The pseudocode of the data generation algorithm is shown in Algorithm 2. These pairs are then subsequently fed into the neural distinguisher to evaluate its ability to identify any potential vulnerabilities posed by our modifications.

The input difference was determined with the help of a tool named AutoND [22]. The tool uses an evolutionary algorithm to find the optimal difference for a given algorithm. We trained and tested the model with the top difference obtained from AutoND as well as 26 different random differences.

The steps of the experiment are as described below.

Step 1: The experiment begins by generating the dataset. Two sets of plaintext pairs with sizes of ${10}^7$ and ${10}^6$ are created randomly but with unique values. These pairs are then split and encrypted using Secure LCB with randomly generated keys to produce the corresponding ciphertext pairs.

Step 2: The generated ciphertext pairs are fed into the neural distinguisher. The model is trained and tested on the dataset to evaluate its ability to distinguish between ciphertexts originating from plaintexts with a specific input difference and random differences.

Step 3: The input difference for the experiment is selected using AutoND [22], which utilizes an evolutionary algorithm to identify the optimal difference. The model is tested using the top difference from AutoND as well as 26 different random differences.

Step 4: To ensure the randomness of the ciphertexts generated by Secure LCB, the dataset is subjected to NIST statistical tests [23]. This helps verify the security of the generated bitstreams.

Step 5: The model is evaluated for its ability to detect any vulnerabilities in the Secure LCB encryption scheme based on its ability to distinguish between ciphertexts with specific input differences and those with random differences.

In this experiment, the obtained training accuracy and testing accuracy are 0.4999 and 0.4990, respectively.

Any cipher is said to be secure if the ciphertext generated by the cipher is random in nature [24]. To check for randomness in the dataset generated by Secure LCB, the dataset was passed through NIST statistical tests [23]. We generated bitstreams of ${10}^6$ by using Secure LCB in counter mode (CTR).

5. Results

The results obtained from the experiments in Section 4 are presented in

Table 8. Results of the experiments performed on LCB family with a specific controlled input difference.

Sl No.	Cipher	Difference	Rounds	Training Accuracy	Validation Accuracy	Testing Accuracy	TPR	TNR
1	LCB	0, 836F	10	0.9824	0.9258	0.9658	1	0.9321
2	Chan’s LCB	0, 836F	20	0.9865	0.9653	0.9137	0.8267	0.9999
3	Secure LCB	0020, 0	20	0.5003	0.5002	0.4996	0.4472	0.5514

.

The training and validation values of Secure LCB for random input differences are shown in

Table 9. Results of Secure LCB with random input difference.

Sl. No.	Input Difference	Training Accuracy	Validation Accuracy
1	836F, 9271	0.5002	0.5005
2	0040, 0	0.5001	0.5001
3	700F, 0	0.5001	0.5010
4	0, F009	0.5002	0.4998
5	0020, 0	0.5003	0.5002
6	D372, 0	0.5002	0.4999
7	0, D1E5	0.5001	0.4998
8	8D32, EFAC	0.4999	0.5000
9	A29B, F134	0.5002	0.5004
10	0090, 0040	0.5002	0.5001
11	A1F6, 0	0.5004	0.5003
12	0, 836F	0.5005	0.5003
13	957C, 0	0.5002	0.4999
14	0, B563	0.5003	0.4997
15	0, 0030	0.5001	0.5001
16	0, 0070	0.5002	0.4997
17	000D, 0	0.5001	0.4999
18	000F, 0	0.5001	0.4993
19	0090, 0	0.4999	0.5001
20	00F0, 0	0.5001	0.5001
21	0, 0090	0.5001	0.5003
22	7009, 0	0.5000	0.5009
23	0, 00F0	0.5001	0.5001
24	0, 0009	0.4999	0.5001
25	0790, 0	0.5001	0.5003
26	0, 2D08	0.4999	0.4999

.

As seen from these findings, the original version of LCB records high levels of accuracy during the training and testing phases. However, this poses a significant threat as it suggests that it is prone to differential attacks.

Furthermore, an evaluation was carried out on Chan’s LCB [8], but it was were found to be insufficient at reinforcing resilience against said attacks. Despite some level of reduction observed within its accuracy rates, such adjustments did not adequately enhance its status as being secure against differential attacks.

Consequently, concluding remarks were drawn based on addressing all vulnerabilities discovered within both LCB and Chan’s LCB, which resulted in a sharp decline with an accuracy rate of only 50%. This indicates that the model could only randomly guess between inputs, demonstrating that Secure LCB is resistant to differential attacks using a neural distinguisher.

Additionally, from the NIST Statistical tests [23] of Secure LCB, we can observe that Secure LCB passes all the tests of NIST. The NIST results are tabulated in the

Table 10. Results from NIST statistical test on Secure LCB.

Sl No.	Statistical Test	p-Value	Pass
1	Frequency	0.407091	1/1
2	Block Frequency	0.407091	1/1
3	Cumulative Sums	0.804337	2/2
4	Runs	0.534146	1/1
5	Longest Run	0.253551	1/1
6	Rank	0.804337	1/1
7	FFT	0.148094	1/1
8	Non-Overlapping Template	0.976060	148/148
9	Overlapping Template	0.671779	1/1
10	Universal	0.407091	1/1
11	Approximate Entropy	0.534146	1/1
12	Random Excursion	0.788728	8/8
13	Random Excursion Variant	0.788728	18/18
14	Serial	0.911413	2/2
15	Linear Complexity	0.534146	1/1

.

6. Conclusions

To summarize, the experiments carried out with the neural distinguisher model on various versions of LCB have yielded valuable insights into both the cipher’s weaknesses and the efficiency of using this model to differentiate ciphertexts with specific input differences.

Through testing, training and validation, we observed that the original version of LCB exhibited higher accuracy rates, indicating its proneness to attacks. Though modifications implemented in Chan’s LCB version—such as changes to the S-Box and increased rounds—showed some improvement by lowering distinguisher accuracy rates, they could not achieve a robust level of security.

In contrast, Secure LCB addressed previously identified vulnerabilities, leading to noticeable reductions in training and validation accuracy levels. The proposed modifications, such as replacing the P-box for improved bit shuffling and changing the key generation algorithm, resulted in significant improvements, with accuracy converging towards 0.5.

Additionally, the NIST statistical tests suggest that the dataset from Secure LCB does pass all the tests, meeting the requirements of randomness in the data.

Overall, these experiments underline the potential of machine learning techniques, such as the neural distinguisher model, in analyzing and identifying weaknesses in cryptographic ciphers, thereby contributing to the development of more secure encryption algorithms.