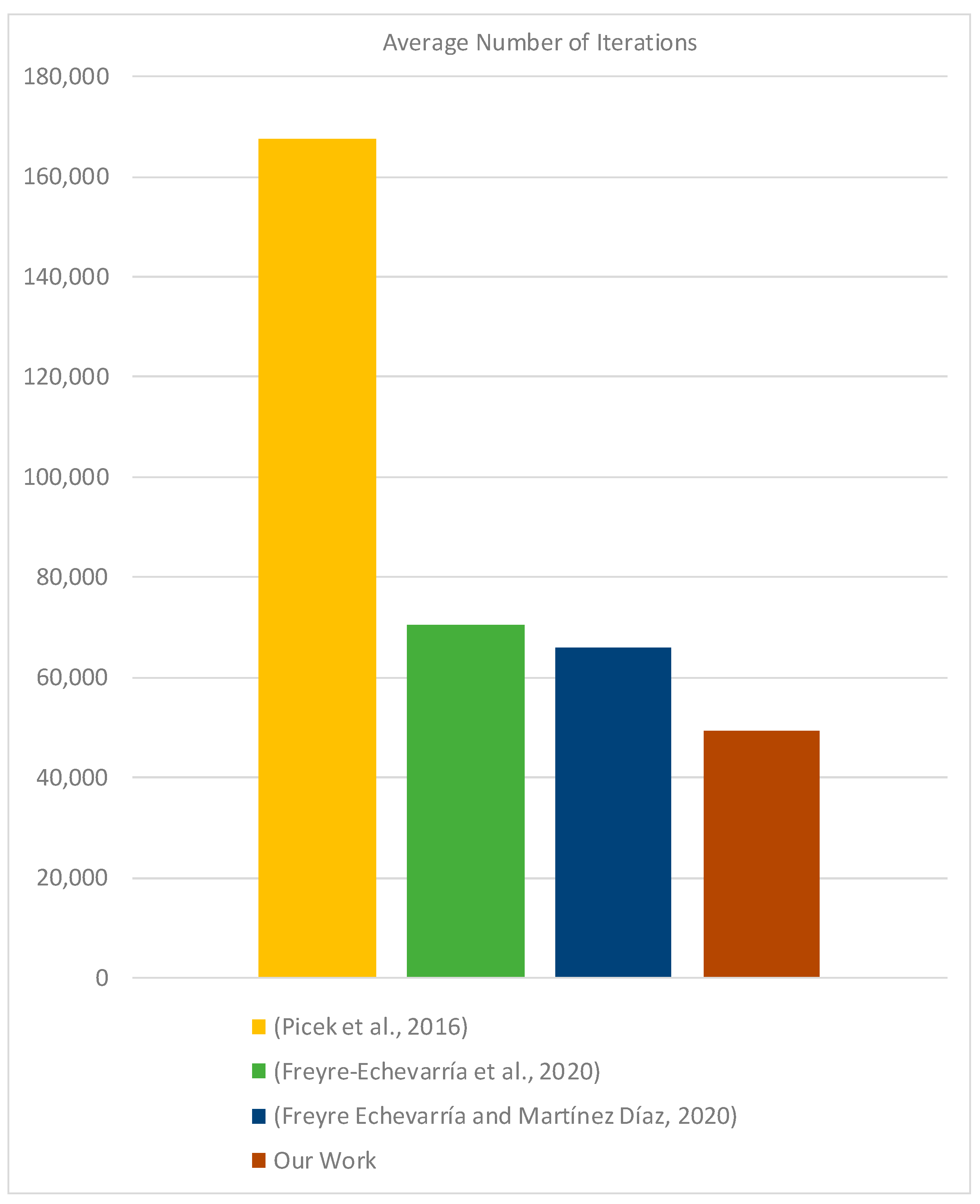Enhancing Smart Communication Security: A Novel Cost Function for Efficient S-Box Generation in Symmetric Key Cryptography

Abstract

In the realm of smart communication systems, where the ubiquity of 5G/6G networks and IoT applications demands robust data confidentiality, the cryptographic integrity of block and stream cipher mechanisms plays a pivotal role. This paper focuses on the enhancement of cryptographic strength in these systems through an innovative approach to generating substitution boxes (S-boxes), which are integral in achieving confusion and diffusion properties in substitution–permutation networks. These properties are critical in thwarting statistical, differential, linear, and other forms of cryptanalysis, and are equally vital in pseudorandom number generation and cryptographic hashing algorithms. The paper addresses the challenge of rapidly producing random S-boxes with desired cryptographic attributes, a task notably arduous given the complexity of existing generation algorithms. We delve into the hill climbing algorithm, exploring various cost functions and their impact on computational complexity for generating S-boxes with a target nonlinearity of 104. Our contribution lies in proposing a new cost function that markedly reduces the generation complexity, bringing down the iteration count to under 50,000 for achieving the desired S-box. This advancement is particularly significant in the context of smart communication environments, where the balance between security and performance is paramount.

1. Introduction

The deployment of secret key encryption algorithms, encompassing both block and stream ciphers, is pivotal across a myriad of information security frameworks [1,2]. These algorithms not only form the backbone of Internet and telecommunication network security but also play a crucial role in safeguarding voluminous data repositories [3,4]. Given their extensive application, the development of advanced encryption ciphers that balance a high throughput with robust cryptographic security emerges as a critical endeavor [5,6].

Contemporary cipher design philosophies are increasingly gravitating towards the substitution–permutation network (SPN) paradigm [7,8]. This approach leverages cryptographic primitives, specifically substitutions and permutations, to achieve the essential security properties of confusion and diffusion [9]. Such attributes are instrumental in thwarting a range of cryptanalytic attacks, including statistical, differential, and linear methodologies. Notably, the integration of substitutions, or S-boxes, injects a layer of nonlinearity between plaintext and ciphertext, thereby enhancing the confusion aspect. To counteract algebraic cryptanalysis, it is imperative for S-boxes to exhibit randomness, eschewing simplistic algebraic frameworks akin to those observed in the Advanced Encryption Standard (AES) cipher’s S-box [10,11].

A cost function in cryptographic systems is a mathematical tool used to evaluate the ‘cost’ or ‘efficacy’ of a given cryptographic operation, typically in terms of its resistance to various attacks or its ability to achieve desired properties like nonlinearity and randomness. The generation of cryptographically robust random substitutions presents a significant computational challenge, traditionally addressed through local search algorithms like the hill climbing algorithm, simulated annealing, and genetic algorithms [12,13,14]. These iterative methods navigate towards an optimal solution by adjusting their state based on specific cost functions, with the search concluding upon reaching a predefined condition, such as solution discovery or an iteration cap.

This study introduces an innovative cost function aimed at streamlining the creation of highly nonlinear random S-boxes. By applying a modified hill climbing algorithm and conducting exhaustive generation experiments, we demonstrate a marked reduction in search complexity. Our findings indicate that, to achieve S-boxes with a nonlinearity score of 104, fewer than 50,000 iterations are required, a significant improvement over previous benchmarks.

Main Contributions

The main contributions of this paper are as follows:

• The introduction of a novel cost function designed to reduce the complexity in generating highly nonlinear S-boxes;
• The implementation and validation of a modified hill climbing algorithm that efficiently navigates the solution space to optimize S-box configurations;
• A comprehensive experimental analysis that demonstrates a substantial reduction in the number of iterations needed to achieve optimal nonlinearity, surpassing existing methods in efficiency and effectiveness;
• The provision of a detailed comparative study that benchmarks the performance of the new method against traditional approaches, highlighting its advantages in real-world cryptographic applications.

These contributions significantly advance the field of cryptographic research by offering more efficient tools for developing secure encryption systems, particularly in environments demanding high standards of data protection and security performance.

The paper is organized as follows: Section 2 reviews the literature relevant to our research. Section 3 delineates methods pertinent to our study, alongside a discussion on established cost function forms. In Section 4, we unveil a novel cost function formulation, which undergoes comprehensive testing in Section 5 through a series of generation experiments employing a hill climbing algorithm with varied cost function parameters. These experiments aim to identify the optimal parameter set that minimizes the number of iterations needed for S-box generation. The implications of our experimental outcomes are explored in Section 6. Finally, Section 7 summarizes our research findings and outlines the conclusions drawn from our work.

2. State of the Art

The quest for generating highly nonlinear substitutions has been a focal point of research within the cryptographic community, with several scholars exploring various local optimization algorithms. Notably, the exploration of the Hill Climbing algorithm has been documented extensively, as seen in studies [12,15]. Similarly, the efficacy of the Local Search Algorithm has been scrutinized in works [13,16], while the principles of Simulated Annealing have been dissected in [17,18,19,20]. Furthermore, the application of the Genetic Algorithm in this context has been elaborated upon in [21,22,23], among others.

These methodologies are distinguished by their reliance on diverse cost functions, with Clark’s cost functions emerging as a particularly prominent and extensively studied tool. Rooted in the Walsh-Hadamard Spectra (WHS), Clark’s cost function was initially introduced in [17], with subsequent analyses and modifications presented in [13,22,24,25]. This cost function has garnered widespread attention due to its foundational role in evaluating the cryptographic robustness of S-boxes.

In a notable advancement, Picek et al. [13] introduced an innovative cost function that demonstrated superior efficiency for certain algorithms when juxtaposed with the WHS-based approach. This development underscored the ongoing evolution of cost function design in enhancing the generation of nonlinear substitutions.

Further contributing to this field, Freyre-Echevarría et al. [12,24] proposed the Walsh-Hadamard Cost Function (WCF) function, a novel cost function predicated on the content analysis of the Walsh-Hadamard spectrum. This function has proven to be particularly adept at facilitating the rapid formation of random bijective 8-bit S-boxes. Remarkably, the Hill Climbing algorithm, when applied in conjunction with the WCF function, has achieved unprecedented efficiency. For instance, the generation of S-boxes with a nonlinearity of 104 required, on average, in excess of 65,000 iterations, setting a new benchmark for this domain.

In our study in [26] delve into the optimization of the Hill Climbing algorithm for the efficient generation of S-boxes, crucial for modern symmetric ciphers. Another our pivotal contribution in [27], explores the simulated annealing algorithm enhanced by a novel cost function based on the Walsh–Hadamard spectrum. In [28] introduce an innovative cost function that revolutionizes the hill-climbing algorithm’s efficiency in generating S-boxes. Lastly, our work [29], presents an optimized simulated annealing approach. By leveraging a multithreaded implementation and introducing refined exit criteria, their method exhibits a 30–40% improvement in generating highly nonlinear S-boxes, showcasing the potential for enhanced cryptographic security through computational efficiency.

Building upon these foundational works, our study introduces a cost function that significantly reduces the iteration count required by the Hill Climbing algorithm to approximately 50,000. This reduction not only represents a substantial improvement over existing methods but also highlights the potential for further optimization in the generation of cryptographically secure S-boxes.

3. Background

The relentless evolution of digital communication systems has underscored the paramount importance of robust cryptographic mechanisms to safeguard data integrity, confidentiality, and authenticity. Among the myriad components that constitute the cryptographic infrastructure, Substitution boxes (S-boxes) play a pivotal role, particularly in the realm of symmetric key cryptography [9]. These nonlinear transformation functions are instrumental in thwarting linear and differential cryptanalysis, thereby fortifying the cipher against various attack vectors.

S-boxes are designed to introduce confusion into the cipher, a concept articulated by Claude Shannon [30] to describe the process of making the relationship between the plaintext, ciphertext, and key as complex and as hidden as possible. By substituting input bits with output bits in a non-linear fashion, S-boxes disrupt the statistical structure of the plaintext, which is crucial for the security of block ciphers like the AES [31] and the Data Encryption Standard (DES) [1].

The design and optimization of S-boxes have been subjects of intense research since the inception of digital cryptography. Early S-boxes were often manually designed or derived from mathematical functions with desirable properties, such as the DES S-boxes [1]. However, with advancements in cryptanalysis [11,32], the focus shifted towards algorithmically generated S-boxes that could meet stringent cryptographic criteria, including high nonlinearity, low correlation immunity, and resistance to differential and linear cryptanalysis [7,33,34].

The quest for optimal S-boxes has led to the exploration of various computational techniques, ranging from Boolean function theory and algebraic constructions to heuristic and metaheuristic algorithms. Each approach aims to balance the trade-offs between cryptographic strength, computational efficiency, and implementation complexity.

Among the spectrum of strategies for S-box generation, heuristic methods have gained prominence due to their ability to navigate vast search spaces for optimal or near-optimal solutions. Algorithms such as Genetic Algorithms (GAs) [21,22,23], Simulated Annealing (SA) [17,18], and Hill Climbing [12,15,35] have been extensively applied to generate S-boxes that fulfill specific cryptographic criteria. These methods, characterized by their iterative search processes and flexibility in handling complex optimization problems, offer a dynamic approach to S-box design, contrasting with the static nature of algebraic and combinatorial constructions [36,37].

Central to the effectiveness of heuristic algorithms in generating S-boxes is the design of appropriate cost functions [12,13,24]. These functions evaluate the cryptographic suitability of candidate S-boxes based on predefined criteria, guiding the search algorithm towards optimal solutions. The complexity of defining such cost functions lies in encapsulating the multifaceted requirements of cryptographic robustness, including nonlinearity, diffusion properties, and resistance to known cryptanalytic attacks, into a quantifiable metric.

Thus, the background of S-box generation encapsulates a rich tapestry of cryptographic theory, algorithmic innovation, and the perpetual arms race between cipher design and cryptanalysis. As digital communication systems continue to evolve, the demand for more sophisticated cryptographic primitives, including S-boxes, will undoubtedly increase. The ongoing research and development in this field not only contribute to the theoretical underpinnings of cryptography but also have profound implications for the security of information in the digital age.

4. Methods

An S-box, by its fundamental definition, represents a nonlinear substitution mapping from an $n$-bit input space to an $m$-bit output space, denoted as $S:{\{0,1\}}^n\to {\{0,1\}}^m$. This mapping is typically articulated through a set of co-ordinate Boolean functions

$$F(x)=(f_1,f_2,\dots ,f_m),$$

where each function $f_i(x_1,x_2,\dots ,x_n)=y_i$ contributes to the transformation process [38]. For the purposes of this discussion, we focus on 8-bit bijective substitutions, implying that $n=m=8$.

The primary cryptographic metric of interest for an S-box is its nonlinearity, $N(S)$, which is quantified using the formula [38]:

$$N(S)=\underset{v\in {\{0,1\}}^m\backslash {\left\{0\right\}}^m}{\min }\{N(v\cdot F(x))\}=\frac{1}{2}(2^8-WH{T}_{\max })$$

(1)

where $WH{T}_{\max }$ is the maximum absolute value of the Walsh–Hadamard transform (WHT) across all non-zero vectors $v$ and $u$, defined as:

$$WH{T}_{\max }=\underset{v,u\in {\{0,1\}}^m\backslash {\left\{0\right\}}^m}{\max }\left|WHT(v\cdot F(x),u)\right|$$

and the WHT itself is calculated by:

$$WHT(f(x),u)={\displaystyle \sum _{x\in {\{0,1\}}^n}{(-1)}^{f(x)\oplus u\cdot x}}$$

(2)

This formulation underscores the role of the Walsh–Hadamard transformation in determining the nonlinearity of an S-box, with the aim of maximizing $N(S)$ by optimizing the WHT coefficients.

In the quest for efficient generation of random S-boxes, several cost functions have been proposed and evaluated. The Walsh–Hadamard Spectrum (WHS) cost function, one of the earliest and most extensively studied, leverages the WHT coefficients and is defined as [21]:

$$WHS={\displaystyle \sum _{v\in {\{0,1\}}^m}{\displaystyle \sum _{u\in {\{0,1\}}^n}{\left||WHT(v\cdot F(x),u)|-X\right|}^R}}$$

(3)

where $X$ and $R$ are parameters selected to minimize the number of search iterations. Despite its widespread application, generating an 8-bit bijective substitution with a nonlinearity of 104 using the WHS function can be computationally intensive, requiring an average of 3.8 million iterations.

Picek et al. introduced an alternative cost function that focuses solely on the positions of non-zero WHT coefficients, significantly enhancing efficiency. This cost function, denoted as PCF, is computed as [13]:

$$PCF={\displaystyle \sum _{i=1}^N{2}^{-i}H{(S)}_{k-i}}$$

(4)

where $H(S)$ is a vector representing the magnitude of WHT coefficients at positions corresponding to multiples of 4, and $k$ is the highest position with a non-zero value. This approach has demonstrated a marked improvement in efficiency, reducing the iteration count to 167,451 for generating S-boxes with $N(S)=104$ [13].

The most recent advancement in cost function design is the WCF function, which has shown exceptional efficacy in combination with the hill climbing algorithm, necessitating only about 65,000 iterations to generate random S-boxes with $N(S)=104$. The WCF function is formulated as [12,24]:

$$WCF={\displaystyle \sum _{v\in {\{0,1\}}^m}{\displaystyle \sum _{u\in {\{0,1\}}^n}{\displaystyle \prod _{z\in C}\left||WHT(v\cdot F(x),u)|-z\right|}}}$$

(5)

where $C=\left\{0,4,\dots ,32\right\}$ is a set of predetermined constants. This innovative approach represents the current state of the art in S-box generation, offering a significant reduction in computational effort while maintaining or enhancing cryptographic robustness [12,24].

5. Novel Cost Function

In our pursuit of refining the generation of S-boxes, a critical component in symmetric cryptography, we have developed a new cost function that significantly improves upon the efficiency and effectiveness of this process. This novel cost function is the culmination of an extensive analysis of the WHT coefficients’ distribution for randomly generated S-boxes. Our research has illuminated the paramount importance of focusing on the extreme values of these coefficients, given their direct impact on the nonlinearity of S-boxes, a crucial metric for cryptographic strength.

The novel cost function is predicated on the observation that the nonlinearity of an S-box is intricately linked to the extremities of the WHT coefficient values. In cryptographic applications, it is these extreme values that must be minimized to enhance the S-box’s resistance to various forms of cryptanalysis. Our approach, therefore, zeroes in on these coefficients, aiming to reduce their magnitude in each iteration of the optimization algorithm. Concurrently, this function encourages the aggregation of other coefficients towards the median of the distribution, thereby systematically elevating the S-box’s nonlinearity with each algorithmic pass.

To operationalize this concept, the novel cost function assigns a dynamic weighting to each spectral coefficient, inversely related to its distance from zero. This weighting scheme is designed to diminish the influence of coefficients closer to the distribution’s center, focusing the optimization effort on the reduction of the most extreme coefficients. This methodological choice is encapsulated in our function, where coefficients within a certain range are effectively neutralized, and the impact of a coefficient’s value escalates with its positional extremity in the distribution.

A similar approach to weighting is observed in existing cost functions; however, our novel cost function introduces a hybrid model that selectively considers only those coefficients exceeding a specific threshold value, $X$, aligning with the criterion $\left|WHT\right|>X$.

This selective consideration is further refined by adjusting the thresholded values by $X$ and a factor of 4, ensuring a consistent and orderly progression of the spectral coefficients’ values. The strategic weighting of these coefficients is achieved by elevating their adjusted magnitudes to a specified power, $R$, thereby fine-tuning the function’s sensitivity to the extremities of the WHT spectrum.

Formally, the novel cost function is defined as:

$$NCFS={\displaystyle \sum _{b=1}^{255}{\displaystyle \sum _{i=0}^{255}{\left(\frac{|WHT[b,i]|-X}{4}\right)}^R}},$$

(6)

where $\left|WHT[b,i]\right|>X$.

This definition underscores our function’s innovative approach to S-box optimization, prioritizing the reduction of extreme WHT coefficients while systematically enhancing the nonlinearity of the S-box. The parameters $X$ and $R$ play a critical role in this process, offering a lever to adjust the function’s focus and efficiency in generating cryptographically robust substitutions.

6. Implementation of the Hill Climbing Algorithm in S-Box Generation

In our research, we have adopted the hill climbing algorithm as the cornerstone search method for generating highly nonlinear bijective S-boxes, a pivotal component in enhancing the cryptographic strength of symmetric ciphers. This section elaborates on the tailored version of the hill climbing algorithm utilized in our study, including modifications and optimizations introduced to refine the search process.

6.1. Algorithmic Framework

The hill climbing algorithm, a heuristic search technique, is renowned for its simplicity and efficiency in navigating large search spaces to find optimal solutions. It iteratively improves the solution by making local changes, akin to climbing a hill until a peak (optimal solution) is reached. In the context of our research, the algorithm starts with an initial randomly generated bijective substitution, denoted as $S_0$, and iteratively modifies it to enhance its nonlinearity, guided by a novel cost function.

The procedural essence of our adapted hill climbing algorithm is encapsulated in Algorithm 1, with pseudocode provided in the appendix of reference [12]:

Algorithm 1: Optimization of Substitution for Cryptographic Applications

Input: Parameters N1, N2, N3 Output: Optimized Substitution S 1. Initialization:  S0 ← GenerateRandomBijectiveSubstitution()  S ← S0  n ← 0 2. While not Termination(S, n):  a. S1 ← GenerateNewSubstitution(S)  b. If Evaluate(S1) ≤ Evaluate(S):   i. S ← S1   ii. n ← 0  c. Else:   i. n ← n + 1  d. Decrement N1 3. Termination(S, n):  return (n ≥ N2) OR (Evaluate(S) ≥ N3) OR (N1 ≤ 0) 4. GenerateNewSubstitution(S):  i, j ← SelectTwoDistinctPositions()  return Swap(S, i, j) 5. Evaluate(S):  return ComputeCostFunction(S) 6. Result:  return S

The pseudocode provided delineates a structured algorithmic approach for optimizing cryptographic substitutions. The process begins with the Initialization step, where a random bijective substitution S0 is generated, setting the stage for subsequent operations. This initial substitution serves as the starting point for the optimization cycle, with S representing the current best-known substitution and n serving as the iteration counter.

In the Iterative Optimization step, the core of the algorithm is executed repeatedly under a conditional loop, governed by defined termination criteria. Each iteration involves generating a new substitution S1 by randomly selecting two distinct positions in the current substitution S and swapping their outputs. The new substitution is then evaluated using a designated cost function, and, if it demonstrates an equal or reduced cost compared to S, it replaces S as the current optimal solution, and the iteration counter n is reset. If S1 results in an increased cost, n is incremented, signifying a continued search for a better substitution.

The Termination Criteria ensure the algorithm halts under three conditions: reaching a preset limit of iterations, experiencing a set number of consecutive iterations without improvement, or achieving a target nonlinearity value for the substitution. This multifaceted stopping mechanism ensures efficiency while preventing the process from running indefinitely.

Upon satisfying any termination condition, the Result step returns the optimized substitution S, marking the end of the algorithm. This output represents the best substitution found within the given constraints and iterations, optimized for the specified cryptographic application.

This pseudocode illustrates a systematic approach to cryptographic optimization, embodying principles of algorithm design that prioritize both effectiveness and computational efficiency. The explicit detailing of operations such as substitution generation and evaluation within iterative cycles underscores the algorithm’s practical applicability to real-world cryptographic challenges.

6.2. Enhancements and Customizations

Our implementation introduces several enhancements to the standard hill climbing algorithm to specifically address the challenges of S-box generation:

• Dynamic Termination Criteria: By incorporating multiple stopping conditions, we ensure a balanced approach that prevents premature convergence while allowing for the sufficient exploration of the search space.
• Cost Function Optimization: The novel cost function $NCFS$ plays a crucial role in guiding the search towards highly nonlinear S-boxes, effectively evaluating the cryptographic suitability of each candidate substitution.

Thus, the adapted hill climbing algorithm, with its emphasis on local optimization and guided by a purpose-designed cost function, proves to be an effective tool for generating S-boxes with desired cryptographic properties. This approach not only demonstrates the algorithm’s adaptability to specific cryptographic objectives but also underscores the importance of tailored heuristic search techniques in the field of cryptography. Through this methodical application, we achieve significant advancements in the efficiency and effectiveness of S-box generation, contributing to the broader goal of securing smart communications.

7. Results

In our quest to ascertain the optimal settings for the parameters $X$ and $R$ within the novel cost function, we embarked on a comprehensive analysis to understand their impact on the efficiency of the search process. This efficiency was quantitatively measured by the number of iterations required by the search algorithm to converge to a solution.

For the purpose of this evaluation, we employed the hill climbing algorithm as our primary search technique. The algorithm initiates with a randomly generated bijective substitution, and iterates until a predefined total number of iterations is reached. To enhance the robustness of our search process, we integrated two additional termination criteria:

• The occurrence of a maximum number of consecutive iterations without any improvement in the cost function;
• The attainment of a target nonlinearity value for the substitution, as determined by Formula (1).

At each iteration, the algorithm modifies the current substitution, thereby generating a new S-box. The novel cost function, as defined by Formula (6), is then applied to evaluate the newly generated S-box. If the cost function’s value does not exhibit an increase, the new S-box is considered an improvement and is adopted as the current best result.

The parameters $X$ and $R$ were varied within the following ranges to ensure a thorough exploration of the parameter space:

• $X$ ranged from −32 to 32, with increments of 4;
• $R$ ranged from 5 to 18, with increments of 1.

To mitigate the effects of randomness and ensure the reliability of our findings, we conducted 100 iterations of the hill climbing algorithm for each unique pair of $X$ and $R$ parameters.

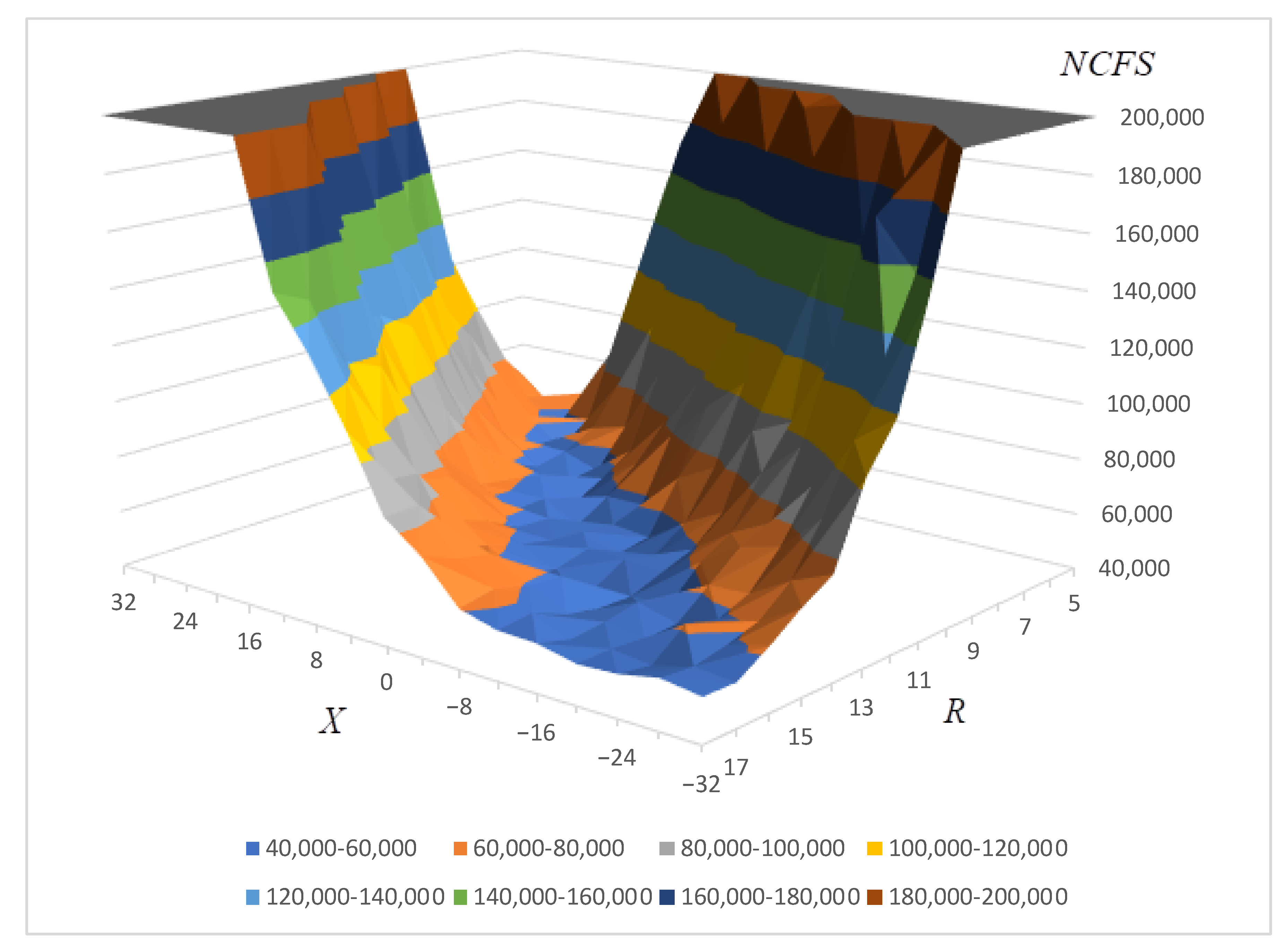
The outcomes of our investigation, focusing on the average number of search iterations required, are depicted in Figure 1. This visualization provides a clear representation of how varying $X$ and $R$ influences the search efficiency.

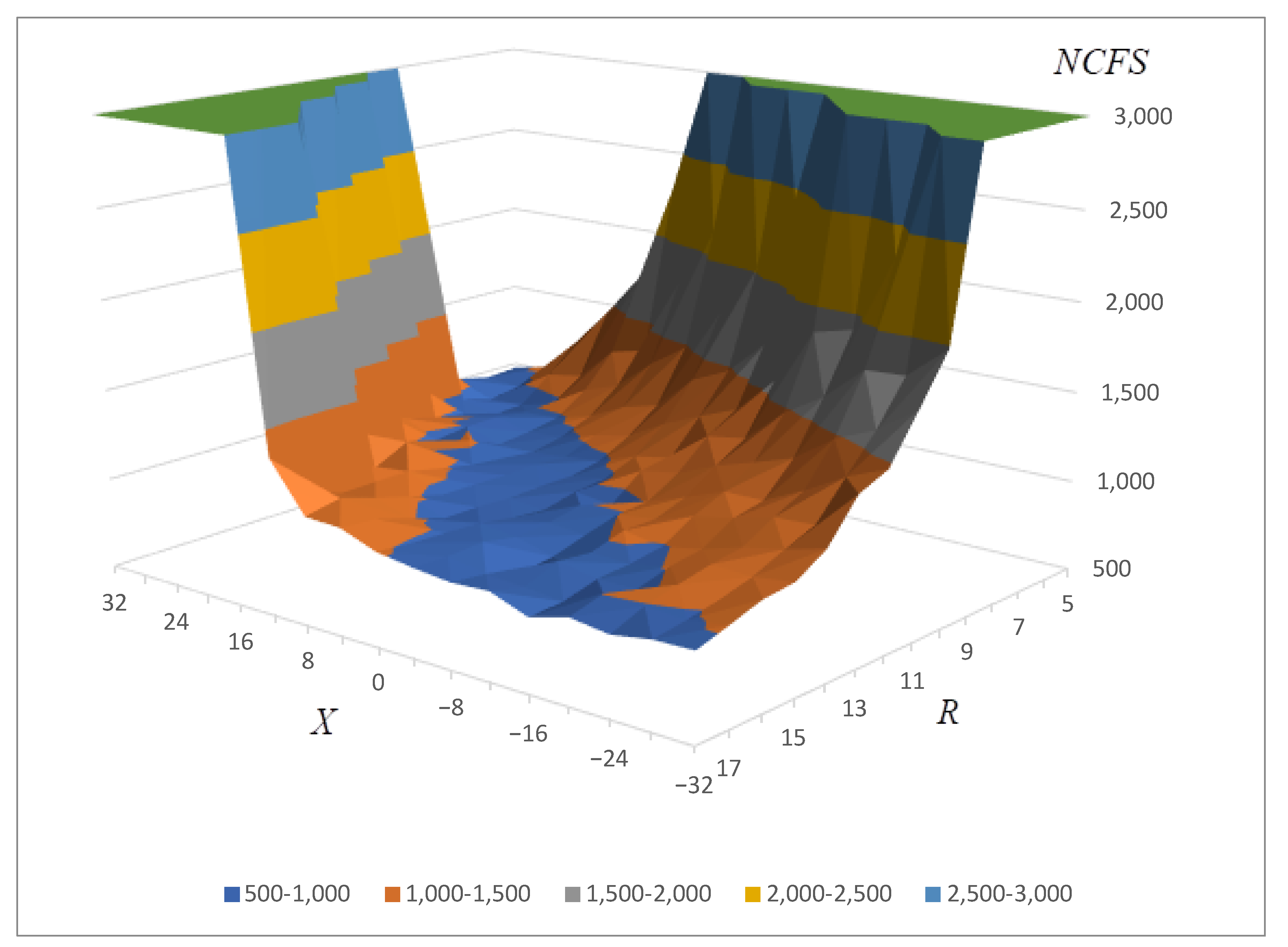
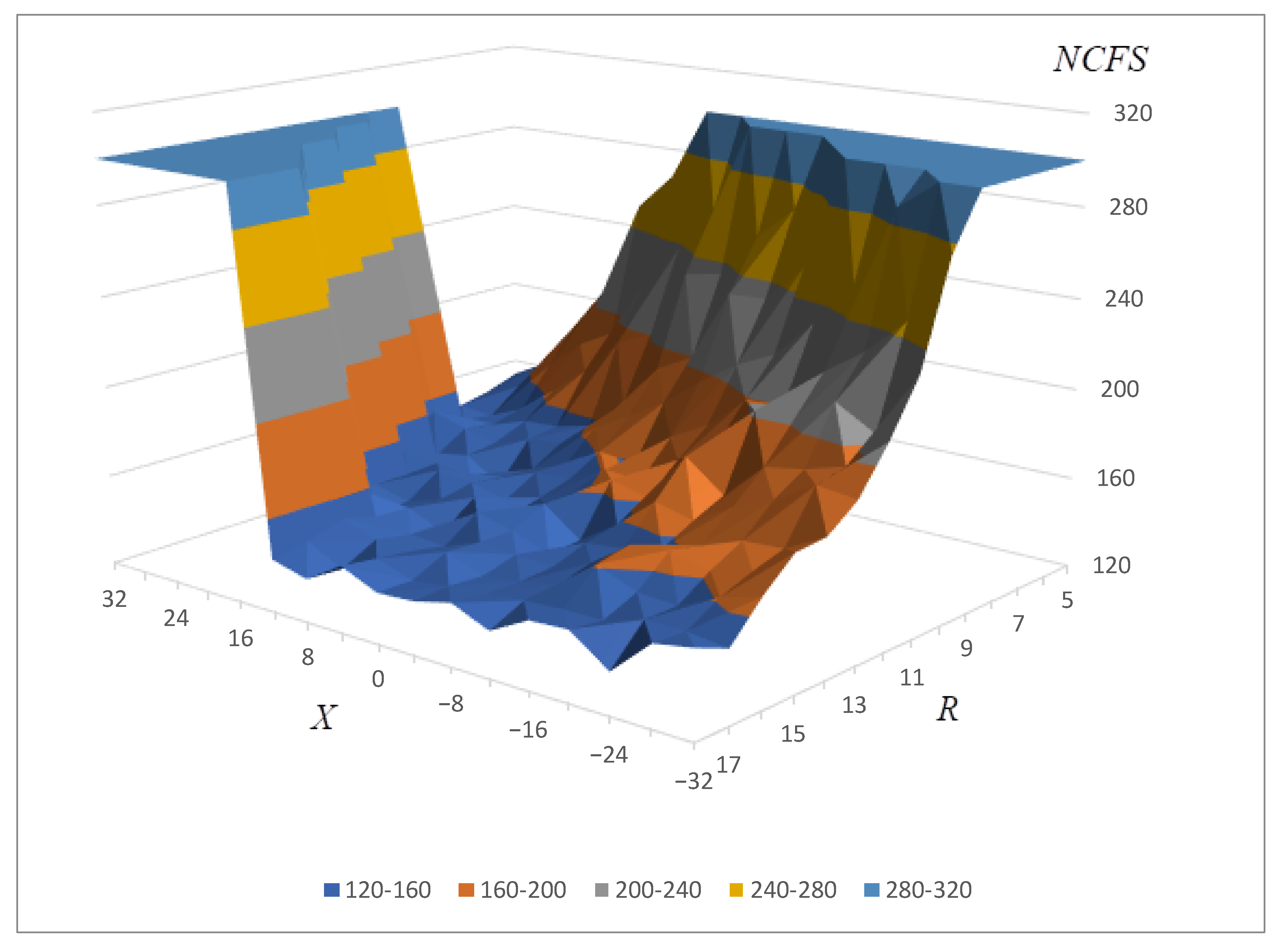
Moreover, to gain deeper insights into the algorithm’s performance across different nonlinearity thresholds, we meticulously recorded the iteration counts necessary to achieve nonlinearity levels of 100 and 102 for each successful run (i.e., runs where an S-box with a nonlinearity of 104 was generated). The aggregated data for these specific nonlinearity benchmarks are presented in Figure 2 and Figure 3, respectively.

This structured approach to parameter evaluation not only underscores the significance of the novel cost function in optimizing the search process but also illuminates the intricate relationship between the parameters $X$ and $R$ and the algorithm’s overall efficiency. Through this analysis, we aim to provide a foundational understanding that can guide future efforts in the generation of cryptographically robust S-boxes.

In Discussion, we provide a detailed comparison of the results shown in Figure 1, Figure 2 and Figure 3 with those from the existing literature. This comparison is aimed at demonstrating the advancements our approach offers over previous methods. Notably, the comparative analysis highlights significant improvements in key performance metrics, which are summarized in

Table 1. Comparison of study results.

Study Reference	Generation Method	Cost Function and Parameters	Average Number of Iterations
[21]	Genetic and Tree	$\mathrm{WHS},X=21$ and $R=7$ in (3)	3,239,000
[13]	Genetic and Tree	$\mathrm{PCF},N=10$ in (4)	167,451
[12]	Hill Climbing	WCF, in (5)	70,596
[24]	Hill Climbing	WCF, in (5)	65,933
Our Work	Hill Climbing	$\mathrm{Novel}\mathrm{Cos}\mathrm{t}\mathrm{Function},X=-8$ and $R=14$ in (6)	49,399

and visually represented in the Figure 4.

8. Discussion

The experimental outcomes underscore the remarkable efficiency of the novel cost function in accelerating the generation of S-boxes. Notably, the function demonstrates a broad spectrum of $X$ and $R$ parameter values that facilitate rapid substitution generation. For instance, setting $R=14$ and $X=-8$ yielded an average search algorithm iteration count of 49,399 for generating bijective S-boxes with a nonlinearity of 104. This performance significantly surpasses that of the previously utilized WCF function, which required over 65,000 iterations, as reported in prior studies. The experimental data reveal that nearly any $X$ value can be effectively paired with an appropriate $R$ weight to expedite the S-box discovery process. An intriguing pattern emerged, suggesting an empirical relationship between $X$ and $R$, expressible as follows: $X=48-4\cdot R$. This heuristic provides a practical guideline for selecting optimal $X$ and $R$ pairings, streamlining the parameterization process. A further analysis identified a specific domain, $R=12\pm 3$, within which the average iteration count reaches its nadir. Deviations from this optimal $R$ range result in increased iteration counts, indicating a localized minimum in the search efficiency landscape. Our findings also highlight the robustness of the novel cost function, with a 100% success rate in generating bijective S-boxes with $N(S)=104$ under the guideline $X=48-4\cdot R$, across the tested parameter space. Notably, as $R$ increases, the range of $X$ values yielding optimal performance broadens, underscoring the function’s adaptability. The paramount efficiency was observed with $X=-8$ and $R=14$, where the hill climbing algorithm averaged 49,399 iterations to generate S-boxes with $N(S)=104$, marking a significant improvement over existing methods.

To contextualize these advancements, a comparative analysis was conducted against the best-known results in the field, as summarized in Table 1.

The Figure 4 graphically represents the data from Table 1, showcasing a reduction in the average number of iterations required by our algorithm compared to existing methods. This visual aid serves to emphasize the enhancements our approach brings to the optimization process in cryptographic applications.

This comparative framework elucidates the substantial efficiency gains afforded by the novel cost function, showcasing a reduction in the average number of iterations by over 20% relative to the prior best-known result.

9. Future Research Directions and Potential Applications

The advancements presented in this study, particularly the development of a novel cost function for optimizing S-box generation, lay the groundwork for a range of future research opportunities and practical applications in the field of cryptography and beyond. This section outlines prospective directions for further investigation and the potential integration of our findings into real-world cryptographic systems.

9.1. Future Research Directions

• Algorithmic Enhancements: Future studies could explore the integration of our novel cost function with other heuristic search algorithms, such as genetic algorithms, simulated annealing, or particle swarm optimization. Comparing the efficiency and effectiveness of these algorithms in generating S-boxes could yield valuable insights into their relative merits and limitations.
• Cost Function Refinement: While our cost function has demonstrated significant improvements in S-box generation, there remains scope for further refinement. Investigating alternative formulations or incorporating additional cryptographic criteria could enhance its utility and applicability.
• Cryptanalysis Resistance Analysis: An in-depth analysis of the resistance of the generated S-boxes against advanced cryptanalytic attacks, including differential and linear cryptanalysis, would provide a more comprehensive understanding of their cryptographic robustness.
• Application to Other Cryptographic Primitives: Extending the application of the novel cost function to the optimization of other cryptographic primitives, such as permutation boxes (P-boxes) or key schedule algorithms, could further contribute to the development of secure cryptographic systems.
• Machine-Learning Approaches: Employing machine-learning techniques to predict optimal parameter settings for the cost function based on the characteristics of the target cryptographic application could streamline the S-box generation process and enhance its adaptability.

9.2. Potential Applications

• Symmetric Key Cryptography: The primary application of our research findings is in the design and optimization of symmetric key ciphers, where the generated S-boxes can be directly employed to enhance the security and efficiency of encryption algorithms.
• Secure Communication Protocols: In the realm of secure communications, especially in environments requiring stringent security measures such as military or financial systems, the optimized S-boxes can be integrated into communication protocols to safeguard against interception and unauthorized access.
• Internet of Things (IoT) Security: As IoT devices become increasingly prevalent, ensuring their security is paramount. The lightweight and efficient S-boxes generated using our approach could be particularly beneficial in resource-constrained IoT environments, providing robust encryption without compromising performance.
• Blockchain and Cryptocurrency: The cryptographic strength of blockchain technology and cryptocurrency relies heavily on the underlying encryption mechanisms. Implementing our optimized S-boxes could enhance the security of blockchain-based applications and transactions.
• Digital Rights Management (DRM): In DRM systems, protecting digital content from unauthorized use is crucial. The S-boxes generated through our methodology could be applied to DRM encryption schemes to ensure content security while minimizing computational overhead.

The exploration of future research directions and the identification of potential applications underscore the broad impact and versatility of our study’s contributions. By continuing to build on the foundation laid by this research, the cryptographic community can advance towards the development of more secure, efficient, and adaptable cryptographic solutions, catering to the evolving security needs of modern digital systems.

10. Conclusions

This study introduced a novel cost function designed to optimize the generation of bijective S-boxes with enhanced nonlinearity, a critical attribute for the cryptographic strength of symmetric ciphers. Through a comprehensive evaluation, we demonstrated that our proposed cost function significantly outperforms existing methods in terms of efficiency, as evidenced by the reduced number of iterations required to achieve S-boxes with a nonlinearity of 104.

Our findings reveal a broad spectrum of parameter values for $X$ and $R$ where the generation process is notably expedited. Specifically, the parameter combination of $R=14$ and $X=-8$ emerged as optimal, necessitating an average of 49,399 iterations, which represents a substantial improvement over the previously established benchmark of more than 65,000 iterations using the WCF function. This efficiency gain underscores the effectiveness of our cost function in facilitating faster and more reliable S-box generation.

Further analysis led to the empirical derivation of a formula, $X=48-4\cdot R$, which serves as a guideline for selecting the most advantageous ratios of $X$ and $R$. This formula not only simplifies the parameter selection process but also highlights the specific domain of $R=12\pm 3$ as yielding the minimum average number of iterations. Deviations from this range result in an increase in the iteration count, emphasizing the critical nature of parameter tuning.

Moreover, our research confirms that adhering to the derived parameter relationship significantly enhances the probability of generating S-boxes with the desired nonlinearity of 104 to 100%, within the tested parameter space. This outcome illustrates the robustness of our approach and its potential applicability in cryptographic systems.

In comparison with existing methods, our work marks a notable advancement in the field of symmetric key cryptography. The reduction in the average number of iterations by more than 20% compared to the best-known results not only demonstrates the superiority of our novel cost function but also contributes to the ongoing efforts to strengthen cryptographic mechanisms.

Table 1 encapsulates the comparative analysis of our method against existing techniques, highlighting the efficiency and effectiveness of our approach in generating nonlinear substitutions with a nonlinearity of 104. This comparison underscores the significant contribution of our work to the cryptographic community, offering a more efficient pathway to secure cipher design.

In conclusion, the development and validation of our novel cost function represent a significant stride towards enhancing the efficiency of S-box generation processes. This advancement holds promising implications for the field of cryptography, potentially leading to the development of more secure and efficient cryptographic systems. Future research will aim to further refine this cost function and explore its applicability to other cryptographic primitives, thereby broadening the scope of its impact on the security domain.