1. Introduction
Secure computation, also known as secure multiparty computation (MPC), refers to the process of computing a joint function on private inputs from multiple parties in a way that ensures the privacy and security of the inputs. This feature enables parties to collaborate in a privacy-preserving way and provides an ideal solution to many scenarios where privacy and security are paramount, such as financial transactionsSt. Alban-Anlage 66, CH-4052 Basel, Switzerland [
1] and voting systems [
2].
Besides the well-known scenarios mentioned above, there is an increasing demand for privacy-preserving applications. For instance, in secure neural network inference, model providers avoid revealing their meticulously trained network models, and the clients avoid leaking their sensitive input data [
3]. An increased interest in secure medical data sharing is being witnessed as well [
4].
However, realizing general-purpose MPC is not easy. Among the few candidates in the literature, garbled circuit (GC) is a promising choice. First proposed by Andrew Yao in 1986 [
5], GC is a cryptographic technique with a constant round complexity. GC offers several advantages over other competitors: compared with fully homomorphic encryption (FHE) [
6], GC is free from prohibitive computational overhead and can be executed much faster; in comparison with secret sharing [
7], GC protects the privacy of intermediate values, preventing information about private inputs from being revealed by intermediate results.
Meanwhile, this powerful technique also has its limitations. In this protocol, the target computation is represented by a Boolean circuit and subsequently transformed into a GC—essentially a network of encrypted tables—for execution. The requirement that the encrypted tables shall be transmitted among parties results in an excessive amount of data communication. Considering that modern application scenarios are typically large-scale and usually have low latency and high energy efficiency requirements, garbling cost becomes a major concern.
To make the protocol more efficient, researchers have proposed various solutions, which generally fall into two categories. One focuses on proposing better garbling schemes, because a smarter way to garble each logic gate can reduce the number of cipher texts in each encrypted table. To name a few,
Free-XOR points out that, by making use of the algebraic property of XOR operations, garbling XOR gates can be free from resulting in any encrypted tables [
8].
Half-gate shows that any two-input nonlinear logic operation, such as AND2, can be garbled using two cipher texts, i.e., a two-entry encrypted table [
9].
Garbling gadget proposes that the garbling cost of any
m-input symmetric logic gate is no more than
m, suggesting that large-fanin-sized logic gates might be more garbling-cost-efficient nonlinearity providers than AND2 [
10].
The other technical direction to which this work belongs is to optimally synthesize the Boolean circuit that implements the target computation. Since XOR gates and inverters are free of garbling cost (by adopting the free-XOR scheme), this is widely regarded as a
multiplicative complexity (MC)
reduction problem: implement the target Boolean function over the basis of {AND, XOR, NOT}, i.e., as an
XOR-AND graph (XAG), then minimize the number of two-input ANDs (AND2s) in the XAG through manipulating logic. Great success has been achieved: Both Songhori et al. and Riazi et al. base their works on establishing a customized library and exploiting standard logic synthesis tools to conduct library binding [
11,
12]; Testa et al. create a logic synthesis toolbox, which leverages existing logic optimization techniques in a hybrid manner [
13]; Liu et al. focuses on detecting the ANDs in a network that can be replaced by XNORs without changing the network’s functionality [
14].
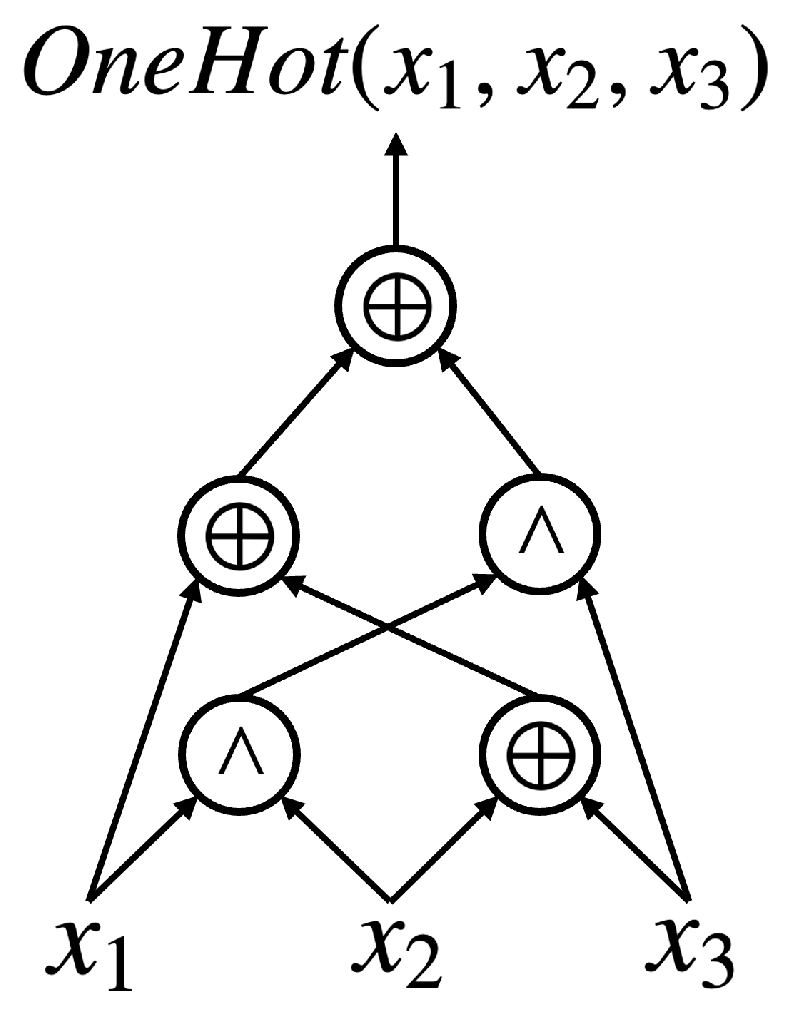
For the first time, we raise the following question: “Is there a kind of logic representation more cipher-text-efficient than XAGs?” Aiming at finding garbling-cost-efficient logic primitives, our exploration started with a systematic study of the properties of three-input symmetric logic gates. Noticing that OneHots, whose truth table is
(in this paper, truth tables are represented in hexadecimal as a bit-string by default, and the most significant bit is on the left-hand side), can provide nonlinearity with more cipher-text efficiency than AND2s, a new logic representation,
XOR-OneHot graph (X1G), is proposed (this manuscript is an extension and summary of the authors’ (Yu, M., De Micheli, G.) previous works [
15,
16]. This work provides more detailed explanations of our techniques and involves a newly proposed logic optimization flow for X1Gs, which consists of three X1G optimization algorithms proposed for the first time). To unleash the efficiency of OneHots, powerful and agile logic optimization algorithms are elaborated, which together make up a customized optimization flow for X1Gs. All our proposed Boolean techniques are developed on top of the most advanced garbling schemes, which distinguishes this work from any existing effort made by the logic synthesis community.
This paper is organized as follows.
Section 2 and
Section 3 provide the preliminaries, respectively, for the aspects of cryptographic protocol and logic synthesis. In
Section 4, the cipher-text efficiency of different logic primitives in providing nonlinearity is analyzed; as a result, X1G is proposed as an ideal logic representation for low-cost GC generation. Based on studying the properties of OneHot operations, a mapping algorithm that bridges existing research on MC reduction and the new proposal of adopting X1Gs are proposed in
Section 5. In
Section 6, we propose a novelly formulated exact synthesis algorithm that can agilely synthesize optimal X1Gs for small-scale Boolean functions. By exploiting the exact synthesis algorithm, along with the Boolean function classification technique, a database of garbling cost-optimal X1G implementations for six-variable Boolean functions is generated. In
Section 7, several heuristic logic optimization algorithms tailored for X1Gs are dedicated, which form an optimization flow that offers high-quality X1G implementations for practical functions. Experimental results on evaluating the performance of (a) the exact synthesis algorithm and (b) the logic optimization flow are presented in
Section 8. In
Section 9, we discuss the potential influence of the runtime overhead of logic synthesis on system performance, which highlights the prospect of X1G-optimization-based low-cost GC generation techniques.
Section 10 concludes this paper.
3. Logic Synthesis
Logic synthesis generally refers to the process of converting a high-level description of a circuit into a lower-level representation, such as a gate-level netlist. It plays an important role in modern electronic design automation (EDA) flows, as it optimizes the designs of integrated circuits for a specified cost criterion. The goal is typically, but not limited to, optimizing area, delay, power consumption, etc.
In logic synthesis, a Boolean circuit is typically abstracted into a logic network for compact representation. A logic network, essentially a directed acyclic graph (DAG), allows efficient applications of graph-based optimization algorithms to manipulate designs.
3.1. Exact Synthesis
Exact Synthesis refers to the task of finding the provably optimum way to represent Boolean functions using allowed types of primitives. The definition of optimum depends on the cost criterion of the synthesis problem.
The exploration of how to efficiently solve an exact synthesis problem has a long history [
21]. In recent years, thanks to the remarkable progress that has been achieved in developing performant
Boolean satisfiability (SAT) solvers, formulating an exact synthesis problem as a SAT problem has become mainstream [
22]. But even for the same exact synthesis problem, depending on the way it is formulated, the difficulty of solving it may vary a lot [
23].
Exact synthesis problems are intractable, as determined by their intrinsic complexity [
24]. Thus, the application of exact synthesis techniques is restricted to small-scale functions. While a high-quality formulation can mitigate the limitation to some extent, the weak scalability of exact synthesis techniques is insurmountable to overcome in principle.
3.2. Peephole Optimization
Most logic synthesis techniques are heuristic, because the target logic networks are usually of large scale and complex, making it infeasible to find the optimum solution in a reasonable time. A large portion of successful heuristics can be categorized as
peephole optimizations. This refers to divide-and-conquer-like strategies, i.e., partitioning a network into subnetworks to break down the problem into a series of amenable ones. Such a partition commonly relies on the concept of
cuts [
25].
3.2.1. Cuts
A cut in a logic network is identified by its root, which is a node, and its leaves, which are a collection of nodes. A feasible set of leaves shall meet two properties: (a) there is at least one leaf on any path from a primary input to the root; (b) all the leaves are on at least one such path.
A cut is recognized as
k-feasible if its number of leaves does not exceed
k. Given a specified
k, the process of finding all the
k-feasible cuts in the target network is known as
cut enumeration [
26].
3.2.2. Logic Rewriting
Logic rewriting refers to the idea of optimizing a logic network by greedily replacing each part of the network, i.e., each cut, with the optimum, or optimal, implementation of the local function of this cut.
The optimization effect of a logic rewriting algorithm highly depends on the selection of k, as k determines the allowed number of leaves of each cut. A larger k allows the process to get closer to the global optimum—to take an extreme example, when k achieves the input size of the network, a logic rewriting algorithm then reduces to the exact synthesis problem of finding the optimum implementation for the function of each primary output. Certainly, due to scalability concerns, it is impossible to set k to be unreasonably large. Configuring k to four or five is common practice.
How the optimum implementations of each cut are obtained is another factor that distinguishes different variants of logic rewriting algorithms. Existing algorithms fall into the categories of finding the optimum implementation of each encountered cut by either (a) invoking an exact synthesis solver on the fly [
15], or (b) referring to a prepared database of optimum implementations of small-scale Boolean functions. The intrinsic complexity of exact synthesis problems determines that (b) typically supports the selection of a larger
k than (a) does.
Based on the functional completeness of the database, (b) can be further divided into two genres: the (i)
Boolean-mining-based functionally incomplete one [
27] and the (ii) functionally complete one [
28]. Boolean mining requires that the Boolean functions that occur in practice be collected before entering the logic optimization procedure; Considering the privacy-preserving property of secure computation, such a premise is likely invalid. Thus, we recognize (i) as inapplicable to our case. In practice, (ii) is usually applied along with
Boolean function classification techniques, since the number of logic functions increases double exponentially with input size.
3.3. Algebraic Rewriting
Algebraic optimization methods consider logic functions as objects of some algebra (not necessarily Boolean algebra) and consider algebra-specific manipulations to optimize them. While such abstractions disregard certain Boolean properties, this simplification leads to fast algorithms that scale well to large logic networks.
In algebraic rewriting, lightweight local transformations based on algebraic axioms are iteratively applied to reshape large logic networks, aiming to optimize a predefined cost function, such as the total area or delay. This technique is especially powerful in near-homogeneous logic networks, i.e., logic representations that allow few types of logic primitives. This is because such networks tend to be more structured, and hence, the eligibility of small portions of logic for algebraic transformations can be efficiently evaluated with less computational overhead.
3.4. Don’t-Cares-Based Optimization
In logic synthesis,
don’t care (DC) refers to a condition for which the output of a logic function or circuit is not specified or does not matter. A DC condition typically arises from the interconnections of logic gates in a logic network, due to the existence of reconvergent paths [
29]. According to the exact cause, DC conditions can be classified into
satisfiability don’t cares (SDCs) and
observability don’t cares (ODCs): The former refers to the input patterns that are never produced under any primary input assignments. The latter refers to the input patterns whose output, if flipped, would not make a difference to any primary output.
DCs bring flexibility into implementing Boolean functions. Therefore, DCs are often used to simplify the design and optimize the resulting logic circuit [
14]. However, finding DCs typically suffers from complex computation. In the last few decades, a technical change from using
binary decision diagrams (BDDs) to using SAT solvers as the tool to compute DC has been witnessed [
30].
3.5. Boolean Function Classification
Boolean function classification is the process of categorizing Boolean functions into different classes based on various characteristics and properties of the functions. For example, since input negation, input permutation, and output negation do not change the combinational complexity of a Boolean function, the so-called
NPN classification [
31] is widely adopted in Boolean function analysis.
In some applications, such as cryptography,
spectral classification provides a powerful tool to classify Boolean functions, because spectral operations preserve algebraic properties [
32]. Based on an n-variable Boolean function
f(
, ⋯,
, ⋯,
, ⋯,
), the five spectral operations are as follows:
Swap two variables: .
Complement a variable: , where “¬” indicates negation.
Complement the function: .
Translational operation: .
Disjoint translational operation: .
Two Boolean functions,
f and
g, are defined as
spectrally equivalent if there is a series of spectral operations
=
, ⋯,
that satisfy
3.6. Multiplicative Complexity
Depending on the context, multiplicative complexity (MC) can refer to the feature of either a Boolean function or an XAG implementation of a function. To avoid ambiguity, we distinguish the two cases as functional MC and structural MC.
Given a Boolean function, its functional MC is the minimum number of AND2s sufficient to implement it over the basis {AND2, XOR2, NOT} (i.e., as an XAG) [
33]. Functional MC commonly serves as an indicator of the nonlinearity of a function. Thus, finding the functional MC of an arbitrary Boolean function correlates with research fields other than cryptography as well. Though receiving wide attention, it is an intractable problem [
34]. So far, the functional MC of any logic function with no more than 6 inputs is known [
35]. Most ongoing research on functional MC focuses on Boolean functions that either have certain features, such as symmetry [
36], or appear frequently in certain applications, such as the interval checking function [
37].
By contrast, structural MC is a feature of an XAG: it refers to the number of AND2s in this logic network. Indeed, a Boolean function’s functional MC lower bounds the structural MC of any XAG implementing this function. Regarding structural MC, a well-known logic synthesis problem, the MC reduction problem asks, “Given an XAG implementation of the target Boolean function (whose functional MC is typically unknown), how does one reduce the number of AND2s in it as much as possible by manipulating logic synthesis techniques?” Free-XOR connects the task of synthesizing practical GCs to the MC reduction problem—in an XAG, AND2 is the only type of logic primitive whose garbling requires cipher texts. Therefore, any progress in addressing the MC reduction problem contributes to the synthesis of lower-cost GCs.
5. Mapping XAGs to X1Gs Following Algebraic Rewriting Rules
To improve the practicality of the GC protocol, previous efforts made by the logic synthesis community focus exclusively on implementing the target function as an XAG and optimizing the network in the sense of reducing its structural MC. Thus, it is desired to elaborate an algorithm that maps an XAG to an X1G, which makes it possible to make full use of existing research and benefit from the cipher-text efficiency of OneHots at the same time.
5.1. An Algebraic-Rewriting-Based Mapping Approach
Equation (
1) suggests replacing each pair of two adjacent AND2s with one OneHot and two XORs. Each application of this rule saves two cipher texts. But, it should be noted that this rewriting rule does not apply to any pair of adjacent AND2s: Given a pair of AND2s
a and
b, while
a is a fanin of
b, it is unwise to directly apply Equation (
1) to get rid of
a and
b, as long as the fanout size of
a is larger than one. This is because the logic function at node
a is at the same time contributing to elsewhere in the logic network, and removing it would compromise the correct functionality of the network. Therefore, it is important to make sure that the algebraic rewriting is only applied to the pairs of AND2s without such concerns. To rule out this problem, we adopt the
covering algorithm proposed in [
39] as a preprocessing on the starting point XAG, which groups those AND2s that can be merged into one AND node with a larger fanin size.
For each AND2 that cannot be paired with another AND2, applying Equation (
2) allows substituting each AND2 with a OneHot, with the amount of required cipher texts unchanged.
As described before, the
covering function in line 1 in Algorithm 1 stands for the covering algorithm in [
39]. Algorithm 1 allows mapping an already highly optimized XAG into an X1G of potentially further lower garbling cost. Furthermore, it has a linear time complexity and is algebraic-rewriting-based, which jointly guarantees an almost negligible runtime.
| Algorithm 1: Mapping an XAG to an X1G by applying algebraic rewriting |
![Cryptography 07 00061 i001]() |
5.2. Limitations
Algorithm 1 serves as a runtime-friendly way to bridge existing research on MC reduction and the proposal of adopting OneHot as a cipher-text-efficient logic primitive. However, it is further noticed that relying on algebraic-rewriting-based mapping can direct us to suboptimality.
When judging the quality of an XAG implementation of the target function that is to be garbled, the number of AND2s in the network is the sole criterion, i.e., every AND2 is of equal cost in the context of MC reduction. This situation changes after OneHots are brought into the scope. When mapping an XAG into an X1G following Algorithm 1, depending on whether an AND2 can be paired with another, either Equation (
1) or (
2) would be applied to replace all AND2s using OneHots and XORs. However, Equation (
1) is the only rule that contributes to a lower garbling cost. In that sense, pairable AND2s, to which Equation (
1) is applicable, are preferable to separated AND2s. This change in criterion explains the limitations of synthesizing X1Gs by applying Algorithm 1 to map the structural-MC-optimal XAGs optimized by previous works into X1Gs.
An example is given by the task of synthesizing the cipher-text-optimal X1G implementation for a 5-variable Boolean function, whose truth table is (when emphasizing the pursuit of fewer cipher texts, we regard the synthesized logic networks as cipher-text/garbling-cost-optimal, instead of optimum because, although we proved that OneHot serves as a more cipher-text-efficient logic primitive than AND2, its optimum remains an open question). It is one of the representatives of all 48 spectral-equivalent classes for 5-variable Boolean functions and has a known functional MC of three.
The optimality of the XAG implementation in
Figure 3a is witnessed by the fact that its structural MC is three, equal to the functional MC of the logic function. Applying Algorithm 1 to it, however, cannot bring us the optimal X1G representation in
Figure 3b—such an application would result in an X1G with three OneHots, whose garbling cost is six cipher texts, which is 50% worse than the optimal. Indeed, the expected XAG that can be mapped into the optimal X1G turns out to be the one with two pairs of adjacent AND2s in it. The structural MC of such an XAG is four, higher than the lower bound determined by the functional MC of the target function.
That being said, to generate the cipher-text-optimal X1G implementation for a given function through applying the algebraic-rewriting-based mapping to its XAG implementation, the optimality of the starting point XAG should be taken care of by paying attention to (a) the number of AND2s and (b) their connectivities. A mapping starting from the XAGs that are optimized with structural MC adopted exclusively as the optimization goal in previous research can end up with suboptimality. Not only the amount but the environment of the AND2s also affects the quality of the X1Gs that the XAGs would be mapped into.
6. Agilely Synthesizing Optimal X1G Implementations for Small-Scale Functions
This section aims to formulate an exact synthesis problem of synthesizing the “truly” optimal XAG implementations for the given logic functions, which render optimal X1G implementations after applying Algorithm 1. The optimality is achieved by formulating both these two features regarding the usage of AND2s as the optimization objective of the exact synthesis.
Due to the limited scalability of exact synthesis, the approach is not applicable to Boolean functions of large scales for concerns of practicality. However, experimental evaluations witnessed that we managed to formulate the problem in such an efficient way that the optimal implementations are successfully synthesized for all 150,357 representative Boolean functions of 6-variable spectral-equivalent classes. These implementations of small functions can be used as building blocks for obtaining high-quality X1G implementations for practical functions.
6.1. AND Fence
We propose the concept of
AND fence to effectively extract the information of our interest from a given XAG. Inspired by
Boolean fences proposed in [
23], which refers to the topology of a whole logic network, we propose AND fences to exclusively describe the usage of AND2s in XAGs.
The procedure for obtaining the AND fence consists of the following: (1) Apply the
covering algorithm to classify AND2s in the network into groups. Each group of AND2s forms an AND tree. The cardinality of the
i-th group is denoted as
, then
. (2) The cardinalities of all
d AND2 groups form the AND fence
of the network, i.e.,
The uniqueness of the AND fence of an XAG is ensured by ordering the AND2 groups by the network topology.
Intuitively, the structural MC of an XAG can be easily learned from its AND fence, as
More to the point, an XAG’s AND fence contains all information required to calculate the garbling cost of the X1G that the XAG would map into, as
6.2. Abstract XAG
The formulated exact synthesis problem of synthesizing the cipher-text-optimal XAGs relies on a type of logic representation, named
abstract XAG. In [
35], the researchers simplified the network description from the original XAG to a more general form. First referred to as abstract XAG in [
40], this logic representation distinguishes from XAG from the following perspectives: (1) Fanin sizes of XORs are allowed to be arbitrary (each XOR node is therefore called an
XOR cloud). (2) Each fanin of any XOR cloud is either a primary input or an AND2 belonging to a lower logical level. (3) Fanins of any AND2 are XOR clouds. (4) Primary outputs are XOR clouds.
To make this representation compatible with the AND fence, we generalize it by allowing the fanin size of AND nodes to be more than two. Since a group of AND2s with a cardinality of c can be concisely represented as ()-input AND, on top of the generalized abstract XAG, it is intuitive to both (a) extract the AND fence of a generalized abstract XAG and (b) construct a network topology of a generalized abstract XAG that meets a given AND fence. To avoid ambiguity, we hereinafter refer abstract XAG to our generalized representation.
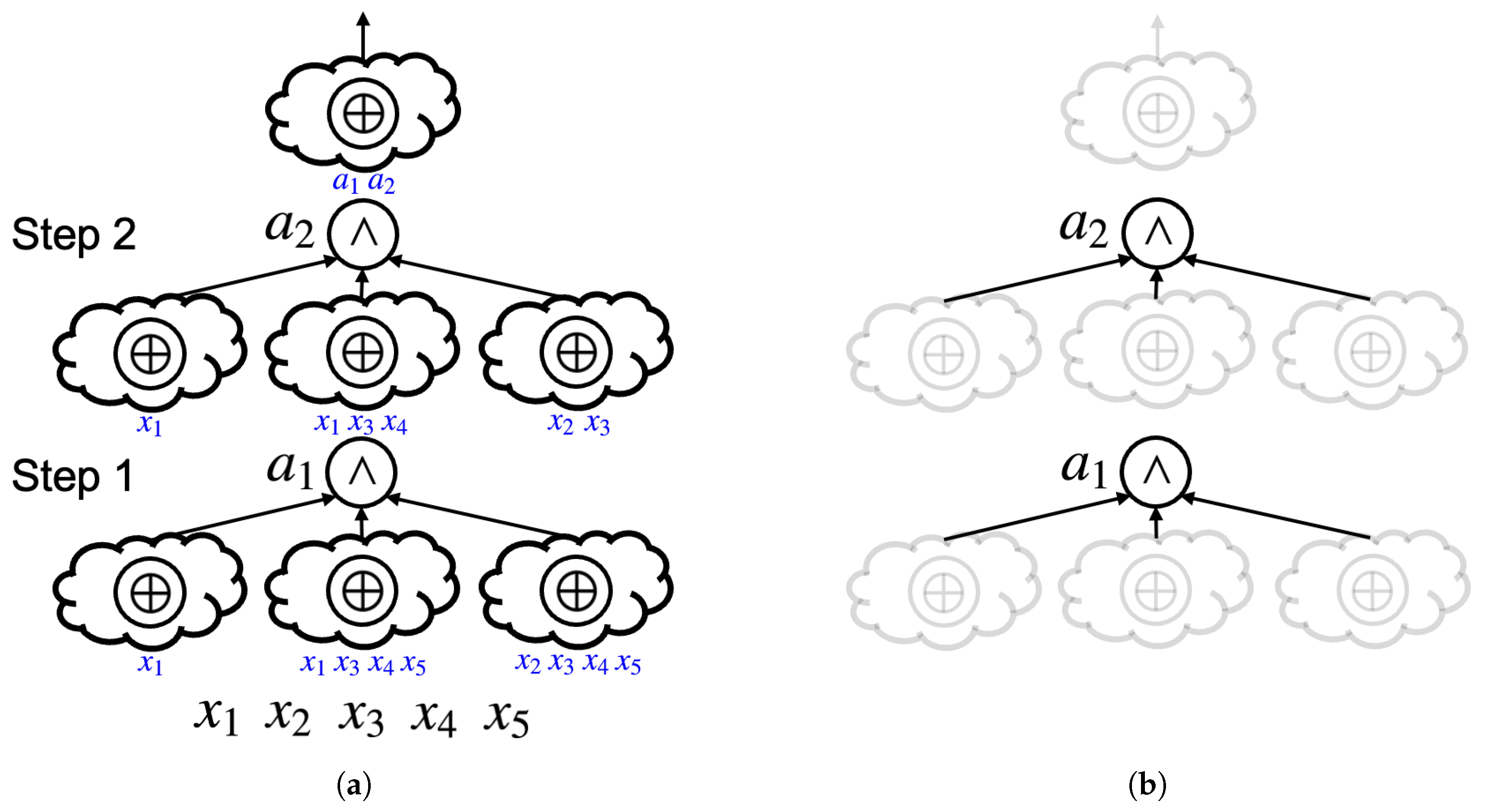
Figure 4a provides an abstract XAG implementation of the Boolean function we saw before. The number of
steps in an abstract XAG is defined as the number of ANDs in it. For conciseness, instead of using arrows, the blue texts under each XOR cloud denote the fanins of that XOR cloud. By focusing on the ANDs in the abstract XAG, the AND fence is easily extracted (
Figure 4b), whose numerical representation is
, as both
and
, the first-step and second-step ANDs, are three-input, indicating that the cardinalities of the two corresponding groups of AND2s are both two.
6.3. Exactly Synthesizing Garbling-Cost-Optimal X1Gs
Utilizing AND fences and abstract XAGs, an exact algorithm to synthesize garbling-cost-optimal X1G implementations is elaborated.
6.3.1. Formulating an Exact Synthesis Problem
We formulate the exact synthesis problem of synthesizing the optimal XAG implementation for a given Boolean function as follows. Given a target AND fence, an incomplete abstract XAG is constructed, as the fanin connectivities of all XOR clouds are missing. A SAT solver is used to find if there is a way to configure the fanins of the XOR clouds so that the resulting abstract XAG implements the target function. The optimality of the synthesized abstract XAG is guaranteed by enumerating all candidates of AND fences in a garbling-cost-ascending manner. In other words, the formulated exact synthesis problem is composed of a series of instances, each of which explores the possibility of using a certain AND fence to implement the function.
The formulation relies on a library of AND fences. Indeed, the completeness of the library contributes directly to the optimality of the synthesized logic networks.
We start by addressing its simpler variant: “When targeting a certain structural MC, how many AND fences are there?” This is the reverse of calculating the structural MC of an AND fence (Equation (
5)), and it is essentially a
positive integer partition problem, a classic problem in number theory and combinatorics. Especially, the permutation of numerically different elements matters in our case, e.g., if
,
and
are two different AND fences. The algorithm proposed in [
41] is adapted to our implementation.
It is known that the functional MC of up to six-variable Boolean functions is upper-bounded by six [
35]. Therefore, by, respectively, figuring out the AND fence candidates with the structural MC ranging from one to six, all AND fences of interest are taken into consideration. There turns out to be 63 AND fence candidates in total in the library.
Algorithm 2 illustrates how the optimal abstract XAG implementation of a function is agilely synthesized. The synthesis procedure consists of solving a series of exact synthesis instances. Making use of a function’s functional MC, the synthesis procedure is accelerated by skipping the instances where the involved AND fences are not able to provide sufficient structural MC (line 4).
| Algorithm 2: Agilely Synthesizing Optimal Abstract XAG using AND Fences |
![Cryptography 07 00061 i002]() |
The abstract XAG in
Figure 4a is exactly the one found by the proposed approach, with
given as the target Boolean function.
6.3.2. Effects of Suboptimality on XOR Counts
By decomposing the XOR clouds into XOR2s, an abstract XAG is converted into an XAG. How to conduct the decomposition is not trivial, as a naïve decomposition can result in functionally equivalent XOR2s, i.e., redundant logic in the resulting XAGs, as well as the X1Gs that the XAGs would map onto. Even if the decomposition is handled in an optimal manner, the resulting number of XOR2s is commonly beyond the minimal, as no efforts have been made to constrain the fanin size of the XOR clouds when synthesizing the optimal abstract XAG implementations.
While the pursuit of the minimal XOR2 count can be taken into consideration by introducing extra constraints to the exact synthesis problem, we recognize such an investigation as unwarranted for two reasons: (a) The garbling cost of an XAG does not depend on the number of XOR2s in it, as determined by the application of Free-XOR. (b) A significant advantage of the proposed exact synthesis problem formulation stems from the relaxation of XOR counts, which considerably increases the number of solutions in the search space and speeds up the problem-solving process.
By further applying Algorithm 1 to the XAGs that the synthesized abstract XAGs decompose into, the optimal X1G implementations are obtained. In this way, the limitation of directly applying Algorithm 1 to the structural-MC-optimal XAGs, which is introduced in
Section 5.2, is overcome.
6.4. Database Generation
Despite the agility of the proposed formulation, due to the exponential complexity of exact synthesis problems, it is impractical to apply the method to exactly synthesize the X1G implementation for large-scale functions. To benefit from the formulation, we make use of it to build a functionally complete database, which contains the optimal X1G implementations of 6-input logic functions. The database later facilitates a database-driven logic rewriting algorithm, which plays a crucial role in our logic optimization flow for the X1G implementations of large-scale functions.
There are 6-input logic functions, and synthesizing the optimal X1G implementations for all of them is not a trivial task, even with the help of the agile formulation. By classifying Boolean functions, the number of functions to consider can be significantly reduced.
When choosing which classification approach to adopt, two factors are taken into consideration: (a) The functions classified into the same category should share the same cost. (b) When there is more than one option that meets (a), the one resulting in fewer classes is better. We recognize the spectral classification as a natural fit to our case.
As introduced in
Section 3.5, for any two spectral-equivalent Boolean functions
f and
g, there exists a series of spectral operations
that converts
f to
g. The reverse process of
, which converts
g to
f, is denoted by
. The reasonability of generating the database by adopting spectral classification is evidenced by the following theorem:
Theorem 1. Assume the garbling-cost-optimal X1G implementation of function f is available, denoted as . Then, by applying to , the obtained X1G is a garbling-cost-optimal X1G implementation of function g.
Proof. If is not a garbling-cost-optimal X1G implementation of the function g, there exists an X1G that also implements function g but requires fewer OneHots than . By applying to , another implementation of function f, , can be obtained. Since applying spectral-equivalent operations never changes the number of OneHots in an X1G, there are fewer OneHots in than in , indicating that is not a garbling-cost-optimal X1G implementation of the function f, which leads to a contradiction. □
Thanks to the adoption of spectral classification, there are only 150,357 equivalent classes for all 6-input Boolean functions. For each class, a representative function is assigned following [
42]. For the representative function of each class, the proposed approach is exploited to efficiently synthesize its optimal X1G implementation. In this way, a 150,357-entry database of the garbling-cost-optimal X1G implementations for 6-input Boolean functions is generated. The database facilitates a performant logic rewriting algorithm, which is introduced in the following section.
7. A Logic Optimization Flow for X1Gs
To synthesize X1G implementations for practical functions, a flow consisting of three logic optimization algorithms is elaborated (
Figure 5).
The XAGs optimized by existing MC reduction techniques are adopted as the input to the flow. By applying algebraic-rewriting-based mapping (Algorithm 1), the XAGs are at first naïvely mapped onto X1Gs. Then, a database-driven logic rewriting algorithm is applied repetitively to the networks, until no gain in #OneHots reduction is observed. As postprocessing, which does not change the network topologies any more, a don’t-care-based optimization approach and algebraic rewriting (Equation (
3)) are exploited to further reduce the garbling cost.
7.1. Database-Driven Logic Rewriting
Algorithm 3 describes our database-driven logic rewriting algorithm.
For each node
n in the network, a set of cuts rooted in it, denoted as
cuts(
n), are computed following the cut enumeration algorithm proposed in [
26] (line 4). As soon as a part of the logic network is rewritten, cut enumeration shall be conducted dynamically.
For the logic cone highlighted by each cut C ∈ cuts(n), using the prepared database, its optimal implementation can be constructed with negligible runtime overhead. Algorithm 3 is elaborated in such a greedy manner that the cut C′ ∈ cuts(n) that leads to the most significant reduction in local cost is to be committed (line 11, 12). Redundant nodes resulting from the rewritten operation are then removed (line 13).
If, for any node in the network, the cuts rooted in it are investigated, Algorithm 3 is terminated.
| Algorithm 3: Database-driven logic rewriting |
![Cryptography 07 00061 i003]() |
7.2. Don’t-Care-Based OneHot Reduction
The truth tables of a OneHot gate and an XOR3 gate are, respectively, and (represented in binary for intuitive comparison). In other words, the two types of gates are functionally distinguishable only by the input pattern . This observation enlightens the possibility of exploiting DC conditions to replace some OneHots in an X1G with XOR3s, without affecting the functionality of the entire logic network. While both SDCs and ODCs can be utilized for logic optimization, we investigated the former in this work.
In Algorithm 4, the logic network is first converted into a logically equivalent
conjunctive normal form (CNF) formula
P, following the well-known Tseitin encoding [
43] (line 1). For each OneHot node
n, another CNF formula
P′ is constructed by adding extra clauses to
P (line 5; “∧” denotes conjunction)—these clauses specify the input signals of node
n to be constant ones. A SAT solver is then invoked to figure out if there is a set of variable assignments that satisfies
P′. If not, it means that no primary input combination can produce pattern
as the input of node
n, indicating such a OneHot node is functionally indistinguishable from an XOR3 node with the same input. Hence, the logic network can be optimized by replacing
n with an XOR3 node (line 7).
| Algorithm 4: Don’t-care-based logic optimization for X1G |
![Cryptography 07 00061 i004]() |
8. Experimental Results
Here, we report the experimental evaluations of the effectiveness of (a) the exact synthesis formulation for agilely synthesizing cipher-text-optimal X1G implementations of small-scale functions, proposed in
Section 6, and (b) the logic optimization flow for improving the X1G implementations of practical functions.
All experiments are conducted on an Apple M1 Max chip with 32 GB memory.
8.1. Evaluation on the Exact Synthesis Formulation
In [
15], an exact synthesis algorithm is proposed to exactly synthesize optimal X1G implementation. The algorithm is at the core of the widely welcomed
single selection variable (SSV)-based, area-oriented SAT encoding [
22]. In addition, the heuristic of using functional MC to guide the targeted numbers of OneHots and XORs is integrated. We adopt this exact synthesis algorithm (hereinafter referred to as
baseline) as the object of comparison in order to provide a convincing comparison.
In this experiment, the benchmark consists of all representative functions of the 48 spectral-equivalent classes for five-variable Boolean functions. The exact synthesis solver is implemented by exploiting the C++ reasoning library
bill (available at
https://github.com/lsils/bill), with
Glucose (available at
https://www.labri.fr/perso/lsimon/research/glucose/) adopted as the underneath SAT solver. The conflict limit for the SAT solver is set to 100,000.
As can be learned from
Table 2, among the 48 target functions, the baseline algorithm failed to find any solution for five of them, while ours managed to synthesize X1G implementations for all of them. For seven functions, the solutions found by the baseline algorithm are suboptimal, as ours found solutions using fewer OneHots. This is evidenced by the total numbers of OneHots (column Accumulated #OneHots in
Table 2) in the 43 solutions found, respectively, by the two approaches. These observations imply the infeasibility of relying on the baseline algorithm to generate a high-quality database for six-variable Boolean functions: while the algorithm is designed to be exact, in practice, even a reasonable conflict limit may divert it from the optimum.
In general, the X1G implementations synthesized following the proposed exact synthesis algorithm (Algorithm 2) always require fewer OneHots, together with an on-average 33.67× faster synthesis procedure. By capturing the significant characteristic of this practical GC generation problem in which XORs are free of garbling cost, Algorithm 2 smartly removes the constraint on XOR count in order to increase the number of solutions in the search space and make it possible for the SAT solver to find a solution efficiently.
8.2. Evaluation on the X1G Optimization Flow
In this experiment, three benchmark suites of different properties are involved to provide a comprehensive evaluation: the EPFL (available at
https://github.com/lsils/benchmarks), the cryptographic (available at
https://homes.esat.kuleuven.be/~nsmart/MPC/), and the MPC benchmark suites [
12]. The EPFL benchmark suite consists of two kinds of combinational circuits, arithmetic ones and random/control ones. The cryptographic benchmark suite involves block ciphers and other cryptographic functions. The MPC benchmark suite brings into scope popular MPC tasks, such as the secure auction and stable matching problems.
The garbling costs (i.e., #cipher-texts) of the X1Gs optimized by applying the proposed flow are compared with the state of the art, which is collected from three works in the literature [
12,
13,
14], as none of them dominate the others in all of the benchmark suites involved. Since XAG is the adopted logic representation in these three works, the corresponding garbling costs are calculated as
#AND2s, where #AND2s denotes the number of AND2s in the structural-MC-optimal XAG implementations reported in the state of the art. These XAG implementations are adopted as the inputs to the proposed flow. As garbling a OneHot gate also requires two cipher texts (
Table 1), the same cost as garbling an AND2, the garbling cost of an X1G is calculated as
#OneHots.
As for implementation details, all logic optimization algorithms involved in the proposed flow are implemented on top of the C++ logic network library
mockturtle (available at
https://github.com/lsils/mockturtle). In the implementation of the database-driven logic rewriting algorithm, we empirically set the maximum number of spectral operations allowed for matching (applying to the
spectral_canonicalization function in line 17 of Algorithm 3) to be 100,000. For practical purposes, if the local function of a cut cannot be matched to any of the representatives within this limitation, such a cut is regarded as an unqualified candidate to operate rewriting. The SAT-based SDC computation in Algorithm 4 is implemented exploiting the C++ exact synthesis library
percy (available at
https://github.com/lsils/percy), with
MiniSAT [
44] adopted as the SAT solver. To avoid an excessive runtime cost in SDC computation, the solving of each SAT instance (line 6 of Algorithm 4) is bounded by a conflict limitation of 100,000. For the same reason, for benchmarks with more than 30,000 nodes, the DC-based optimization stage is bypassed.
In
Table 3, we report the garbling costs after applying each stage of the optimization flow (#cipher-texts), the reductions in garbling costs achieved by applying the whole flow (red), and the overall runtime (Time). Due to the distinguishing features of the two kinds of benchmarks involved in the EPFL benchmark suite, we calculated the geometric means separately.
An interesting observation is that, by simply applying the mapping algorithm (Algorithm 1), a 2.41% reduction and an 11.90% reduction in garbling cost are achieved for the arithmetic circuits and random/control circuits, respectively. This finding evidences OneHot’s superior cipher-text efficiency in providing nonlinearity compared with AND2. Although not included in the table due to space limitations, it is thrilling that this considerable reduction is obtained with an almost negligible runtime overhead. The most time-consuming case happens to the log2 benchmark, which takes 0.48 s. Among all the random/control circuits, none of them require more than 0.10 s to finish.
Based on a more careful profile of the effectiveness of the logic optimization flow, logic rewriting (Algorithm 3) and mapping (Algorithm 1), respectively, contribute to 32.64% and 62.77% of the reduction in garbling costs, using 84.23% and 0.07% of the runtime. While the contribution made by DC-based optimization (Algorithm 4) and algebraic rewriting (Equation (
3)) seems rather trivial, their roles in the flow are indeed crucial, as they managed to seize the optimization opportunities missed by the high-effort logic rewriting stage.
Through case studies on
Adder,
Barrel shifter, and
Decoder, it is recognized that no reduction in #cipher-texts was achieved by the proposed flow because of benchmark features. Since the AND2s in the three starting point XAGs are separated, all OneHots in the three resulting X1Gs hold the feature described by Equation (
2) and are unable to offer nonlinearity in a cipher-text-efficient manner. Therefore, the effectiveness of the proposed flow can vary from function to function, which is also learned from the evaluation results for the other two benchmark suites.
Observations from the experimental results in
Table 3 and
Table 4 are consistent in general.
It turns out that, for all functions in the MPC benchmark suite, the application of the algebraic rewriting rule did not lead to any reduction in garbling cost. Interestingly enough, for MD5 in the cryptographic benchmark suite, the algebraic rewriting stage is the only one that achieved a lower garbling cost, even though it was by merely 0.01%. This fact demonstrates the unique role of each optimization approach involved in the proposed flow.
The least reduction in garbling cost is achieved for the MPC benchmark suite. This is likely explained by the following two facts: (a) an analysis of the benchmarks shows that AND2s are generally located far from each other; (b) with the experience of specialists, the benchmarks are designed to be garbling-cost-friendly, leaving little room for optimization.
9. Discussion
The experimental results in the previous section reveal the trade-off between the efforts in logic optimization and the runtime overhead of applying logic optimization algorithms. Considering this trade-off, X1G optimization algorithms/flows of different flavors are desired according to the target application scenario.
Optimally synthesizing Boolean circuits on the spot in an application-by-application manner can be time-consuming and may become a bottleneck of system performance. Under such circumstances, lightweight X1G optimization algorithms/flows that strike a balance between quality and speed are a suitable choice. According to our evaluation results, the mapping algorithm (Algorithm 1) and the algebraic rewriting rule (Equation (
3)) provide such a solution.
Conversely, for frequent functions in secure computation, such as the MPC benchmark suite involved in the experimental evaluation, their X1G implementations can be optimally synthesized in advance and made publicly available. In this situation, high-effort logic algorithms, such as the logic rewriting algorithm (Algorithm 3) and the don’t-care-based optimization algorithm (Algorithm 4), are preferable, since there is an unlimited time budget and exploiting any opportunities to reduce garbling cost is the priority. Notice that open-source optimized Boolean circuit implementations would not lead to any compromise in privacy, given that the security of the GC protocol comes from the encrypted tables that are created in the GC generation stage.
In future work, customized logic optimization algorithms supporting X1Gs can be designed in an application-scenario-aware manner, so as to meet the variant requirements of emerging MPC tasks.
10. Conclusions
Improving the efficiency of garbled circuits is more urgent than ever before to meet the rapidly increasing application requirements of MPC. Existing efforts made by the logic synthesis community focus intensively and exclusively on addressing the MC reduction problem, which is based on the premise of adopting XAGs as the logic representation for the target computation to be garbled. However, there is a lack of formal proof of the superiority of using XAGs as the underlying logic representation for the task of low-cost GC generation. Based on a thorough study of cipher texts’ efficiency for logic gates, we propose here, for the first time, a more efficient logic representation based on X1Gs for generating efficient GCs. To support this claim, we showed (a) a novel exact synthesis algorithm to agilely synthesize the garbling-cost-optimal X1G implementations for small-scale functions and (b) a logic optimization flow for X1Gs, scalable to practical functions, that consists of a series of customized X1G optimization algorithms and that achieves high-quality X1G implementations. Comprehensive experimental evaluations for public benchmark suites evidenced the effectiveness of our proposals: compared with the state of the art, for the EPFL arithmetic, the EPFL random/control, the cryptographic, and the MPC benchmark suites, adopting X1Gs as the logic representation and applying our elaborated logic optimization algorithms jointly led to 7.34%, 26.14%, 13.51%, and 4.34% reductions, respectively, in garbling costs, with reasonable runtime overheads. This work offers a new perspective for low-cost GC generation and enables practical high-performance secure computation.