Abstract
This research paper presents a novel digital color image encryption approach that ensures high-level security while remaining simple and efficient. The proposed method utilizes a composite key r and x of 128-bits to create a small in-dimension private key (a chaotic map), which is then resized to match the color matrix dimension. The proposed method is uncomplicated and can be applied to any image without any modification. Image quality, sensitivity analysis, security analysis, correlation analysis, quality analysis, speed analysis, and attack robustness analysis are conducted to prove the efficiency and security aspects of the proposed method. The speed analysis shows that the proposed method improves the performance of image cryptography by minimizing encryption–decryption time and maximizing the throughput of the process of color cryptography. The results demonstrate that the proposed method provides better throughput than existing methods. Overall, this research paper provides a new approach to digital color image encryption that is highly secure, efficient, and applicable to various images.
Keywords:
cryptography; private key; chaotic logistic map; chaotic logistic map key; chaotic parameter; MSE; PSNR; CC; throughput 1. Introduction
Encrypting digital images is an important security measure that can help protect the confidentiality and integrity of sensitive information. When digital images are transmitted over the internet or stored on a device, they are vulnerable to interception and unauthorized access. Encryption can help prevent unauthorized access to these images by making the data unreadable without the proper decryption key [1,2,3].
Encrypting digital images can help protect against data tampering or alteration as well. With encryption, if someone tries to modify the encrypted data, the decryption process will fail, alerting the recipient that the data have tampered with [4,5].
In many industries, such as healthcare, finance, and legal services, images often contain sensitive personal information, such as medical records, financial statements, or legal documents. Encrypting these images can help ensure this information remains confidential and secure [5,6,7].
Overall, encrypting digital images is an important security measure that can help to protect sensitive information and prevent unauthorized access to data [8,9,10,11,12].
Color digital images are among social media’s most popular digital data types. Their ubiquity is due to several reasons, the most important of which are [9,10,11,12,13,14]:
- Ease of obtaining a digital color image because of the diversity of the sources it provides and the diversity of the equipment that generates it.
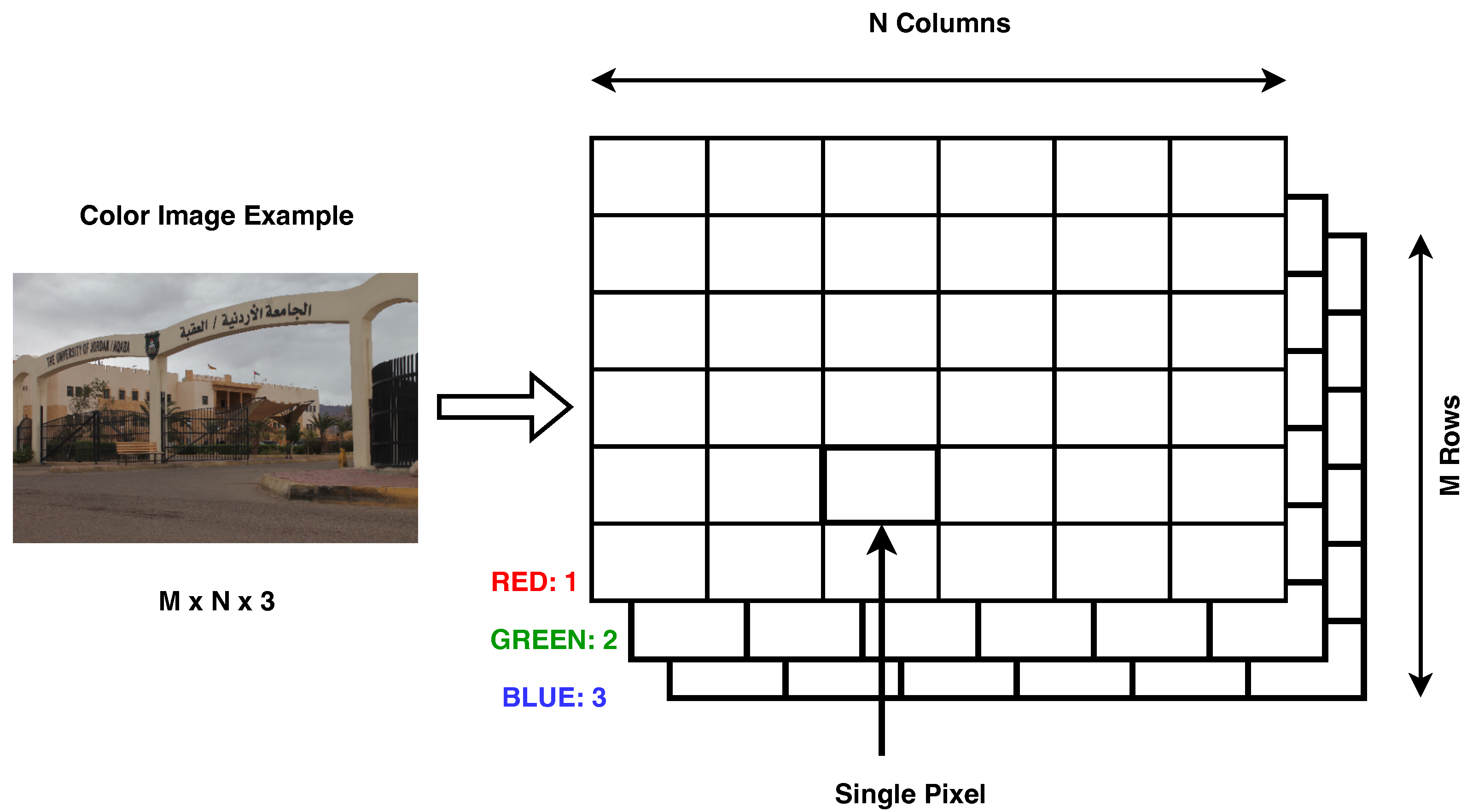
- The digital image can be processed easily because it is presented as a matrix with three dimensions, which consist of a two-dimensional matrix for each of the primary colors (red, green, and blue), as shown in Figure 1.
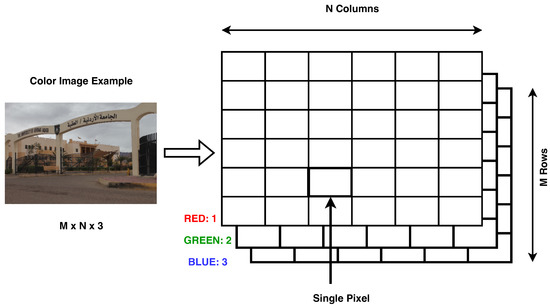 Figure 1. 3D Matrix Color Image.
Figure 1. 3D Matrix Color Image. - Ease of dealing with the matrix of each color, ease of extracting each color from the three colors matrices, and ease of re-combining these matrices to produce the colored image.
- Using the digital revolution in many vital applications, especially engineering, medical, and data security and protection applications.
In this context, the topic of private key cryptography for digital color image encryption is of great importance and relevance, as shown in Figure 2 [15,16,17].

Figure 2.
Image Cryptography.
Digital color image encryption refers to the process of converting a color image into an unreadable format by using mathematical algorithms to protect its confidentiality during transmission and storage. With the proliferation of digital media and the increasing amount of sensitive information being transmitted online, digital image encryption has become an essential component of data security. The encryption process involves using a secret key known only to the sender and receiver, which is used to transform the image into a cipher that is unintelligible to anyone else. Decryption is performed by applying the same key in reverse, which converts the cipher back into the original image [16,17,18].
The importance of digital color image encryption is clear when considering the sensitive nature of many types of visual data, such as medical images, financial documents, and legal records. Without encryption, these images could be intercepted or accessed by unauthorized individuals, potentially leading to identity theft, financial fraud, or other malicious activity. Encrypting images maintains this information’s confidentiality, ensuring that only the intended recipient can access the data. This is especially important in today’s digital age, where data breaches and cyberattacks have become increasingly common. As such, digital image encryption is a critical tool in protecting the privacy and security of digital assets and is essential for maintaining trust in online transactions and communications [19,20].
The Mean Squared Error (MSE), Peak Signal-to-Noise Ratio (PSNR), and Correlation Coefficient (CC) are commonly used metrics in image processing and analysis. These metrics can be used to measure the quality and accuracy of image encryption techniques [2,3].
MSE is a metric used to measure the difference between two images. It is calculated as the average of the two images’ squared differences between corresponding pixels. A lower MSE value indicates a better match between the original and decrypted image. MSE is often used in image encryption to evaluate the level of distortion introduced during encryption and decryption [12,14].
PSNR is another commonly used metric in image processing. It is calculated as the ratio of the maximum possible power of a signal to the power of the noise that corrupts the signal. PSNR is often used in image encryption to evaluate the level of noise introduced during encryption and decryption. A higher PSNR value indicates less noise and better quality of the decrypted image [19,20].
CC is a metric used to measure the degree of similarity between two images. It measures the linear relationship between the two images, where a value of 1 indicates a perfect positive correlation, −1 indicates a perfect negative correlation, and 0 indicates no correlation. CC is often used in image encryption to evaluate the level of similarity between the original and encrypted image. A higher CC value indicates better similarity between the original and decrypted image [2,8].
In image encryption, MSE, PSNR, and CC can be used to evaluate the quality and effectiveness of different encryption techniques. For example, a good encryption technique should have a low MSE value, high PSNR value, and high CC value. These metrics can be used to optimize encryption parameters and to compare the performance of different encryption algorithms [12,19].
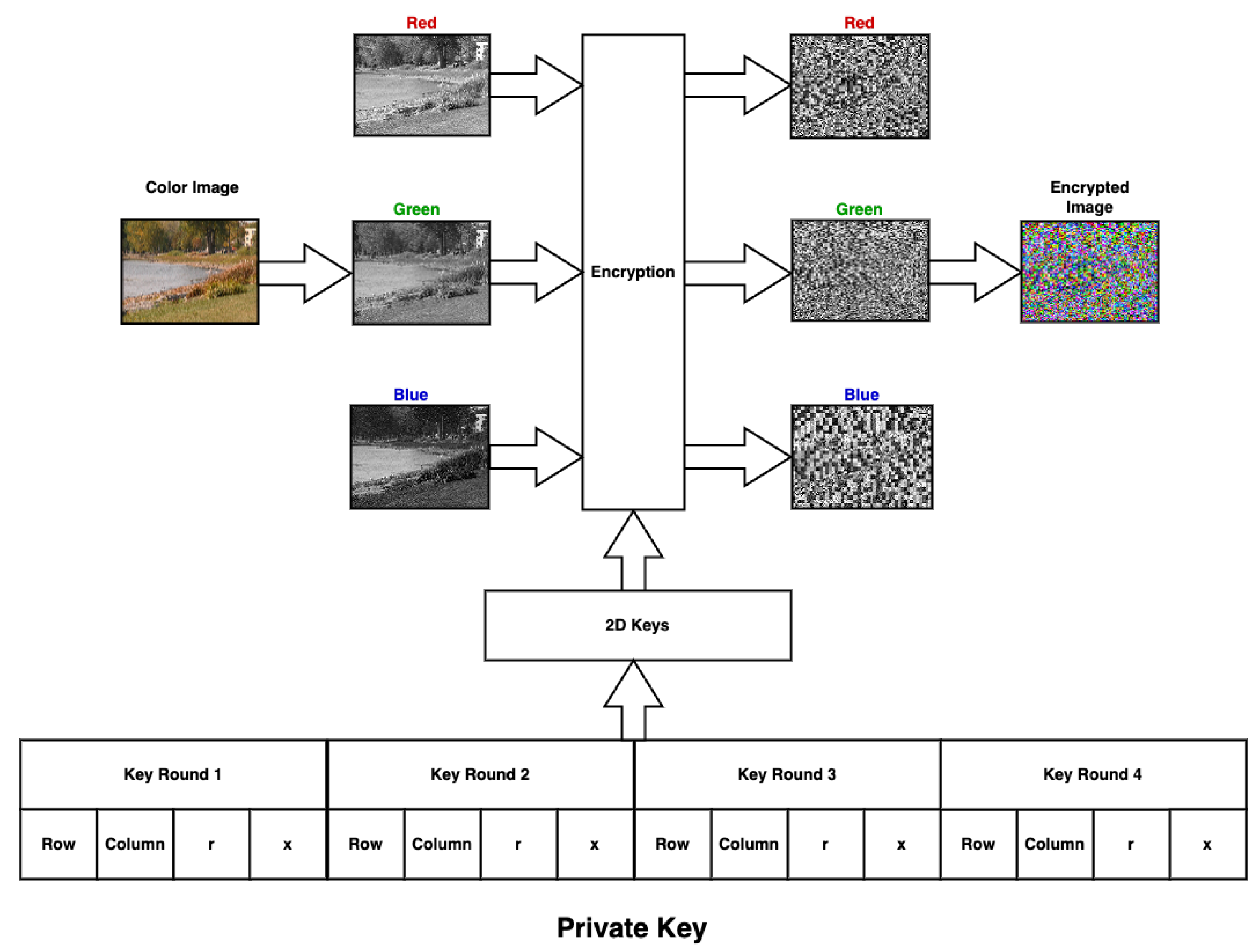
The proposed approach in this research paper presents a novel digital color image encryption method that uses enhanced 2D chaotic logistic maps to generate a complex private key. The generated key has a large space, making hacking or guessing impossible. The method is simple and is applicable to any image without any modification. Furthermore, the proposed method has been tested for its efficiency aspects; the results show that it can improve the performance of image cryptography by minimizing encryption–decryption time and maximizing the throughput of the process of color cryptography. This research is important, as it provides a practical solution to address the security concerns surrounding the confidentiality of digital color images, which is critical in fields such as medical imaging, national security, and commerce.
The proposed method for digital image encryption using chaotic logistic maps aims to achieve the following objectives: first, to develop efficient, high-level security, and simple digital image encryption method that can work with any size of an image without any modifications; second, to study and evaluate the performance of the proposed method in terms of throughput and compare its results with the state-of-the-art methods; third, to devise an encryption method that is sensitive to initial conditions and robust against various attacks, and conduct an extensive analysis of the proposed method in terms of security, quality, sensitivity, and speed; and finally, to investigate the potential of using chaotic logistic maps in digital image cryptography and the effect on the performance and time requirements.
2. Related Work
There have been many cryptographic algorithms, including those based on encryption standard methods such as Data Encryption Standard (DES), Triple Data Encryption Standard (3DES), Advanced Encryption Standard (AES), and Blow Fish (BF) [21,22,23,24].
These methods use a fixed-length Private Key (PK), fixed-length block size, and fixed number of rounds to accomplish the encryption and decryption phases. While all of these methods are based on encryption standards that provide good values of quality parameters, they have low speed and can only be used to encrypt/decrypt data with small size, such as messages and text files [22,23,24,25].
In [26], the authors evaluated several different encryption techniques, finding that the DES, 3DES, AES, and BF methods produced throughputs of 7988, 2683, 5326, and 10,176 bytes per second, respectively. However, due to their small size, these rates are not suitable for encrypting or decrypting data with larger size such as digital color images.
Because there is a necessity to deal with massive data sizes and protect these data, chaos-based algorithms for encryption are heavily used. They provide high security, good throughput, sizeable key space, randomness, and sensitivity to initial conditions, all of which make them a great candidate for encryption algorithms [20].
Chaos theory and logistic maps have become widely used in image encryption thanks to their ability to generate complex and unpredictable patterns. This section reviews several of the latest works that have used chaos theory and logistic maps in image encryption [19,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]. The use of chaos theory and logistic maps is described in detail in Section 3.
In [38], the authors proposed a novel encryption method for 3D point and mesh data in fog computing using chaotic maps. The proposed method utilizes the chaotic dynamics of a chaotic map to generate a sequence of pseudo-random numbers, which is then used as the encryption key. The method was applied to 3D point and mesh data and tested for encryption quality, time complexity, and resistance against attacks. Their experimental results showed that the proposed method provides a high level of encryption security with low time complexity, making it suitable for edge computing applications.
In [19], the authors proposed a color image encryption algorithm that is both provably secure and fast. The algorithm utilizes a combination of substitution boxes (S-boxes) and hyperchaotic maps to generate the encryption key and perform the encryption process. The S-boxes are used to substitute the pixel values of the input image, while the hyperchaotic maps generate the sequence of pseudo-random numbers used as the encryption key. The proposed algorithm can be applied in various fields, such as secure image transmission and storage, video surveillance, and medical imaging, ensuring data confidentiality and integrity.
In [27], the authors introduced a method based on the chaotic map model, realizing improved throughput and reaching 0.1691 M bytes per second, while in [44] the introduced method achieved a throughput equal to 0.71 Mbyte per second. In [28], the authors made performance comparisons between chaotic and non-chaotic methods of data cryptography; a comparison of the results is shown in Table 1.

Table 1.
Performance comparisons of different cryptographic methods [28].
In [39], the authors proposed an image encryption algorithm based on a logistic map. The algorithm uses the logistic map to generate a sequence of pseudo-random numbers, which is used as the encryption key to scramble the pixel values of the input image. The algorithm’s implementation is computationally efficient, making it suitable for resource-constrained devices in real-time applications.
In [40], the authors introduced a technique for encrypting images that utilizes chaotic and logistic maps in three dimensions. The method they proposed involves using both a 3D chaotic map and a logistic map to produce two chaotic sequences that mix and spread out the image.
In [41,43], the authors proposed an image encryption scheme based on a chaotic map and a logistic map. The proposed schemes use a chaotic map to generate a key stream and a logistic map to generate a sequence of substitution boxes that are used to encrypt the images.
In [42], the authors presented a chaotic image encryption algorithm based on a fractional-order chaotic map and a logistic map. The proposed algorithm uses a fractional-order chaotic map to generate a chaotic sequence and a logistic map to generate a pseudo-random permutation matrix that is used to scramble the image.
In [29], the authors presented a method for encrypting images using a cosine transform-based chaotic system. The proposed system employs a four-dimensional chaotic map to create a secret key and a logistic map to generate a random sequence, which is then combined with the image using a cosine transform. The resulting encrypted image resists various attacks, including statistical analysis attacks and differential attacks. The authors evaluated the performance of the proposed method using several metrics and compared it with other encryption methods. In [30], the authors introduced an image encryption technique based on a chaotic system that uses cosine transformations. In contrast, another paper [31] presented a new image encryption algorithm combining chaotic maps and dynamic function generation. In [32], the authors suggested a DNA encoding and chaotic system-based algorithm for encrypting multiple images, while in [33] the authors proposed a multiple-image encryption technique using bit-plane decomposition and chaotic maps. These methods all produce good results while offering varying speeds, as shown in Table 2.

Table 2.
Performance comparisons of the methods in [29,30,31,32,33].
In conclusion, chaos theory and logistic maps have been extensively used in image encryption thanks to their ability to generate complex and unpredictable patterns. The latest research in this field shows that combining different chaotic maps and logistic maps can improve the security and robustness of image encryption algorithms.
3. The Proposed Method
This paper introduces a method of image cryptography that is able to meet all the requirements of data cryptography, in particular the following [45,46]:
- The private key must be complicated to guess; in addition, it must provide sufficient key space (KS) in order to make the hacking process difficult and provide a high degree of image protection.
- The private key must be sensitive even to very slight changes in order to ensure that any change in the key when decrypting leads to the generation of a bad image, allowing any changes to be accurately considered an attempt to hack the key. Furthermore, the encryption process must change the image to become incomprehensible and useless, while the decryption process must produce an image that is entirely identical to the original image.
- The method must generate high quality parameter values during the encryption–decryption process. An image’s level of damage and subsequent restoration can be evaluated by calculating its MSE, PSNR, and/or CC; these measures of quality can be determined by comparing two images, and can be calculated using Equations (1)–(3) [47,48,49].where m is the number of rows in the cover image, n is the number of columns in the cover image, is the pixel value of the original image, and is the pixel value of the sent image.where is the maximum signal value that exists in the original (“known to be good”) image.where is the correlation coefficient, is the value of the first message, is the mean of X, is the value of the second message, is the mean of Y, and n is the total number of pixels in the image.
- In the encryption phase, the MSE must be very high and the PSNR must be very low, while in the decryption phase the MSE must be zero and thePSNR must be infinite. A good image encryption algorithm should aim to produce an encrypted image that has low correlation with the original image in order to ensure that the encrypted image is highly distorted and difficult to recover without the decryption key.
- The method must minimize both the encryption and decryption times and maximize the encryption and decryption throughput in terms of bytes encrypted or decrypted per second.
- The method should be easy to use and able to process any image without causing any change in the processes implemented by the method.
A chaotic logistic map is a one-dimensional function that can be modified to be two-dimensional for application to a 2D key, as we show later in the paper. The proposed method uses a 2D chaotic key generated using a chaotic logistic map model following Equation (4). The chaotic logistic map key (CLMK) is generated using the model parameters r and x. Equation (4) is used to generate the chaotic logistic map, with the generated numbers being susceptible to the selected initial values of r and x.
The chaotic logistic map (CLM) function is calculated using Equation (4) [50].
Here, the first parameter of the logistic function, denoted as , varies between 0 and 1, while the second parameter, denoted as r, varies between 0 and 4. The behavior of the logistic function depends on the value chosen for r. Specifically, when r is within certain ranges, the logistic function generates different output types. For instance, if r is between 0 and 1, the output consists of fixed and stable values near zero, while if r is between 1 and 3 the output consists if fixed and stable values near ((). The output consists of periodic attractors if r is between 3 and 3.57, while if r is between 3.57 and 4 the output is chaotic [28,29,30,31].
Based on applying the CLM model using the parameters r and x, the R and C parameters are used to set the dimension of the key. Equation (5) describes how the 2D CLM map is generated:
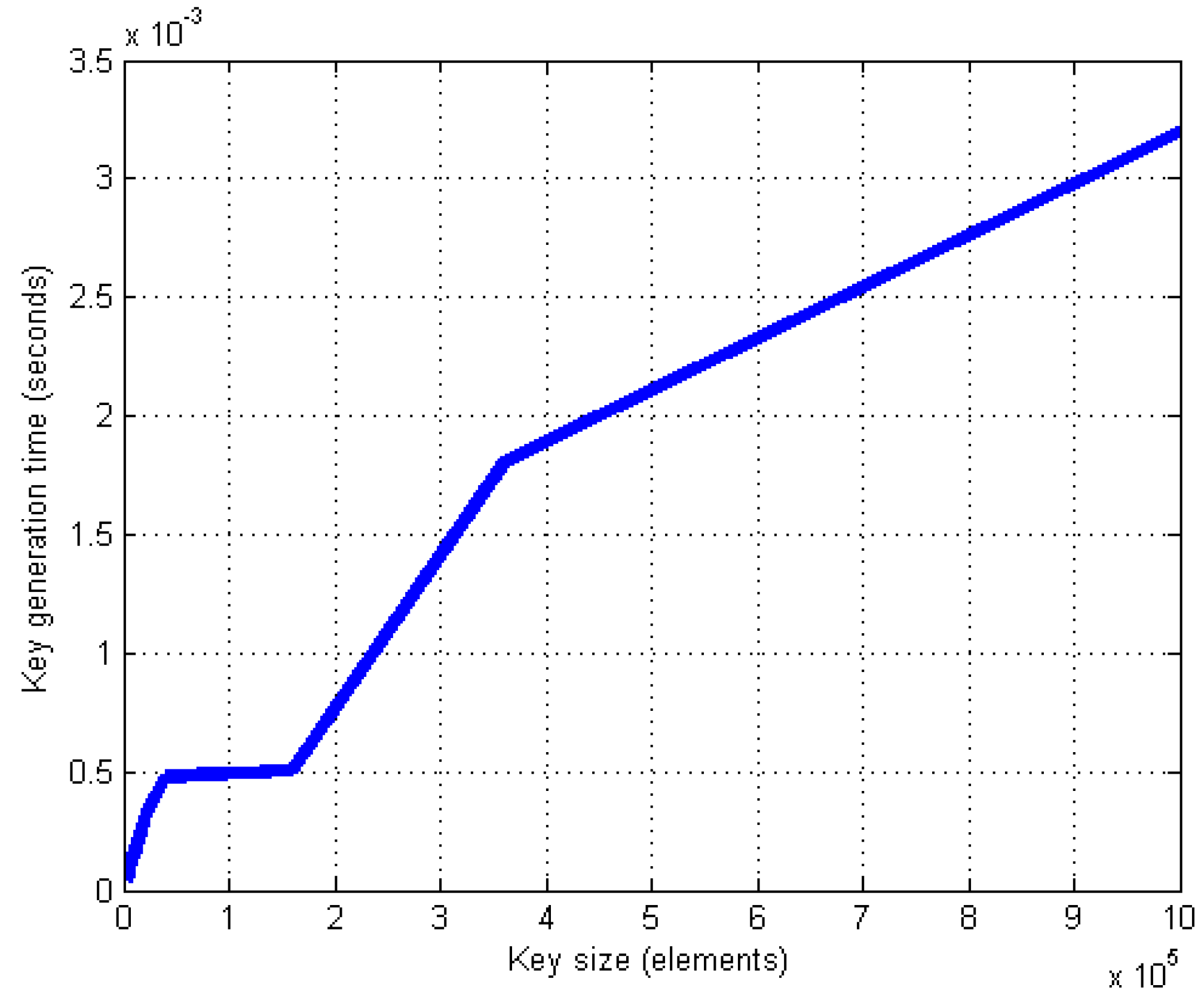
where is a 2D map of size , is the row index, and is the column index. The 2D chaotic key requires varying times for generation depending on the key size. Table 3 shows the time required to generate a 2D CLM key with various sizes.

Table 3.
Required time to generate 2D chaotic logistic key.
The 2D chaotic key, Table 3, shows the required time to generate a 2D CLM key of various sizes.
From Table 3, it can be seen that increasing the number of elements in the key increases the generation time (see Figure 3). For a vast size, the generation time grows rapidly, and the efficiency of cryptography is negatively affected. To overcome this problem, a key with a smaller size can be used; such a key must be resized to match the size of the color matrix, as shown in Figure 4.
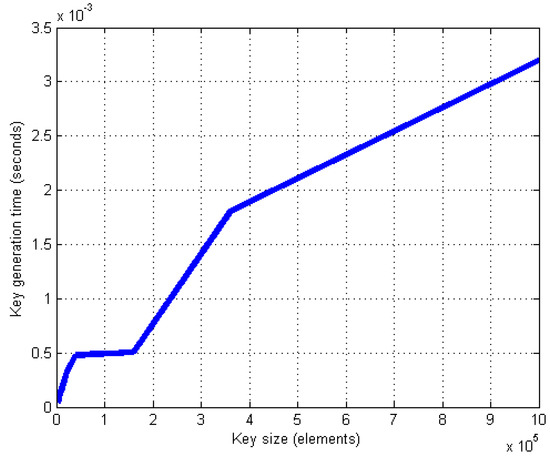
Figure 3.
Time to generate chaotic logistic key.
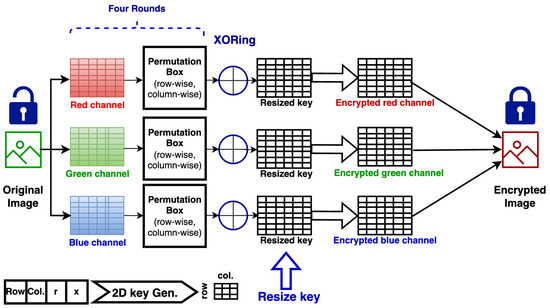
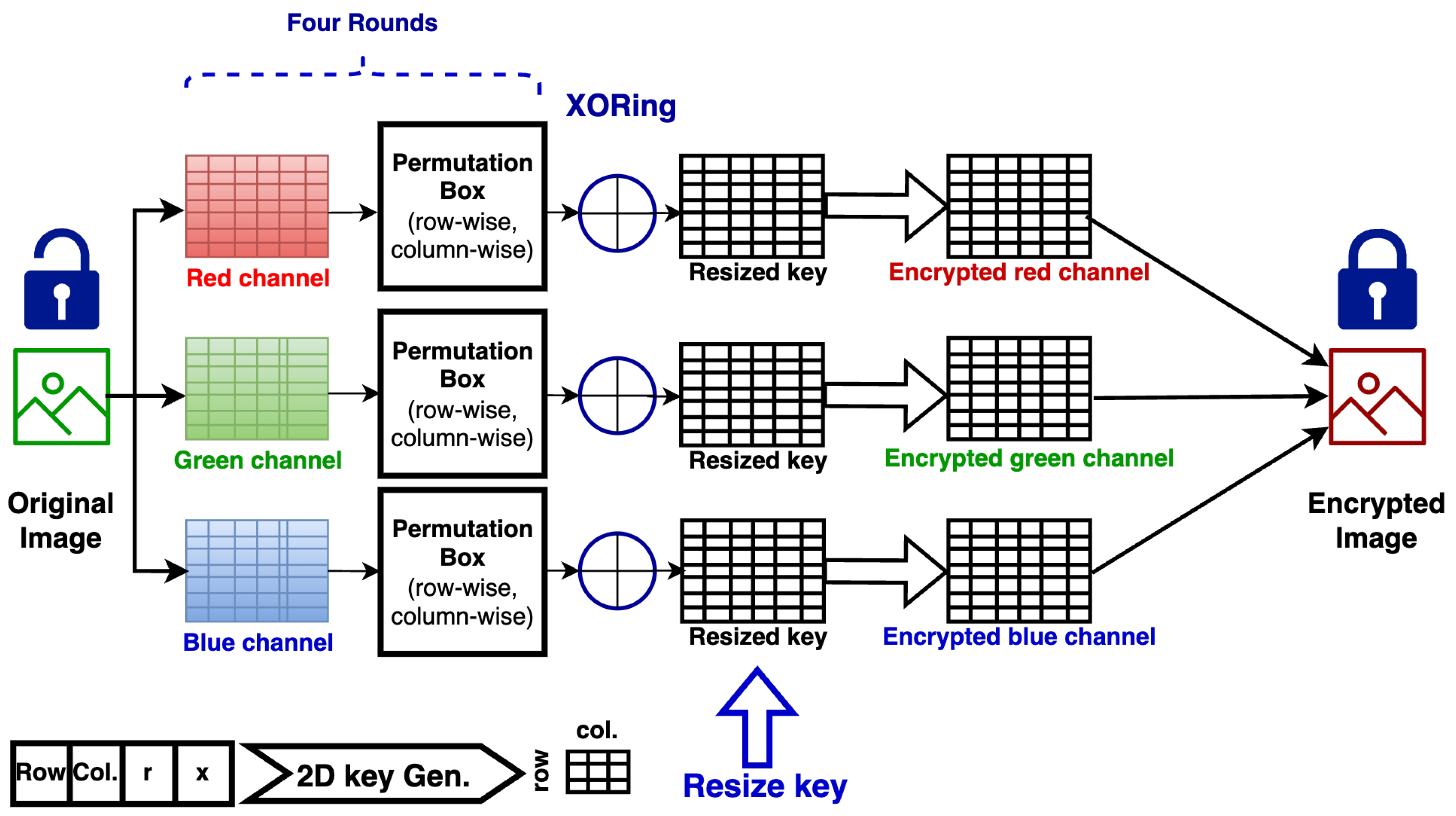
Figure 4.
The proposed method.
Figure 4 depicts the proposed encryption method, which is a private key consisting of four parameters used to generate the 2D logistic key; the parameters are the number of rows and columns in the generated 2D logistic key and the chaotic parameters r and x. The plaintext image to be encrypted is split into three different matrices, one for each color channel. After that, the matrix passes through a permutation box that shuffles the matrix row- and column-wise. The generated 2D logistic key is then resized to match the size of each color matrix, then they are XORed together; this is considered one round and then repeated for four rounds. Each round has a unique private key. Finally, the three matrices are combined together to form the encrypted image.
The encryption phase of the proposed method can be implemented by applying Algorithm 1 (see Figure 5).
| Algorithm 1 Encryption Process. |
| Inputs: Color image to be encrypted, Private Key Output: Encrypted image Process
|
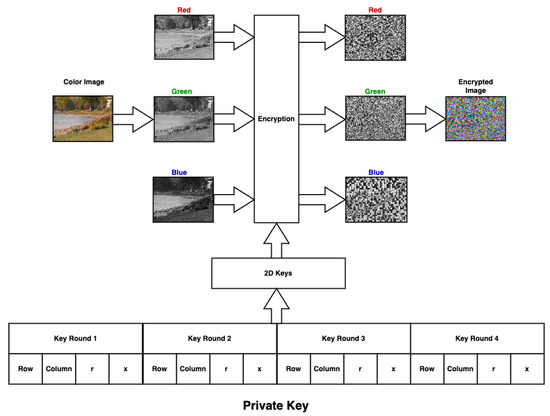
Figure 5.
The proposed encryption phase.
The decryption phase of the proposed method can be implemented by applying Algorithm 2 (see Figure 6).
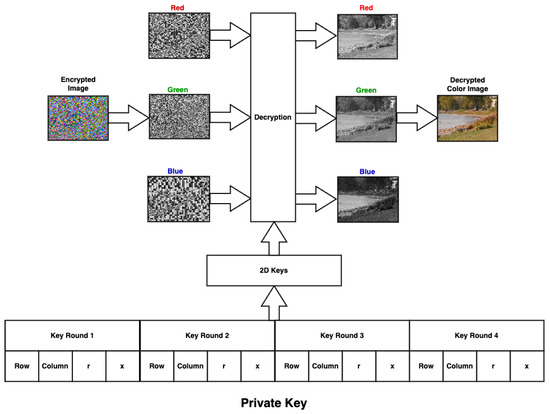
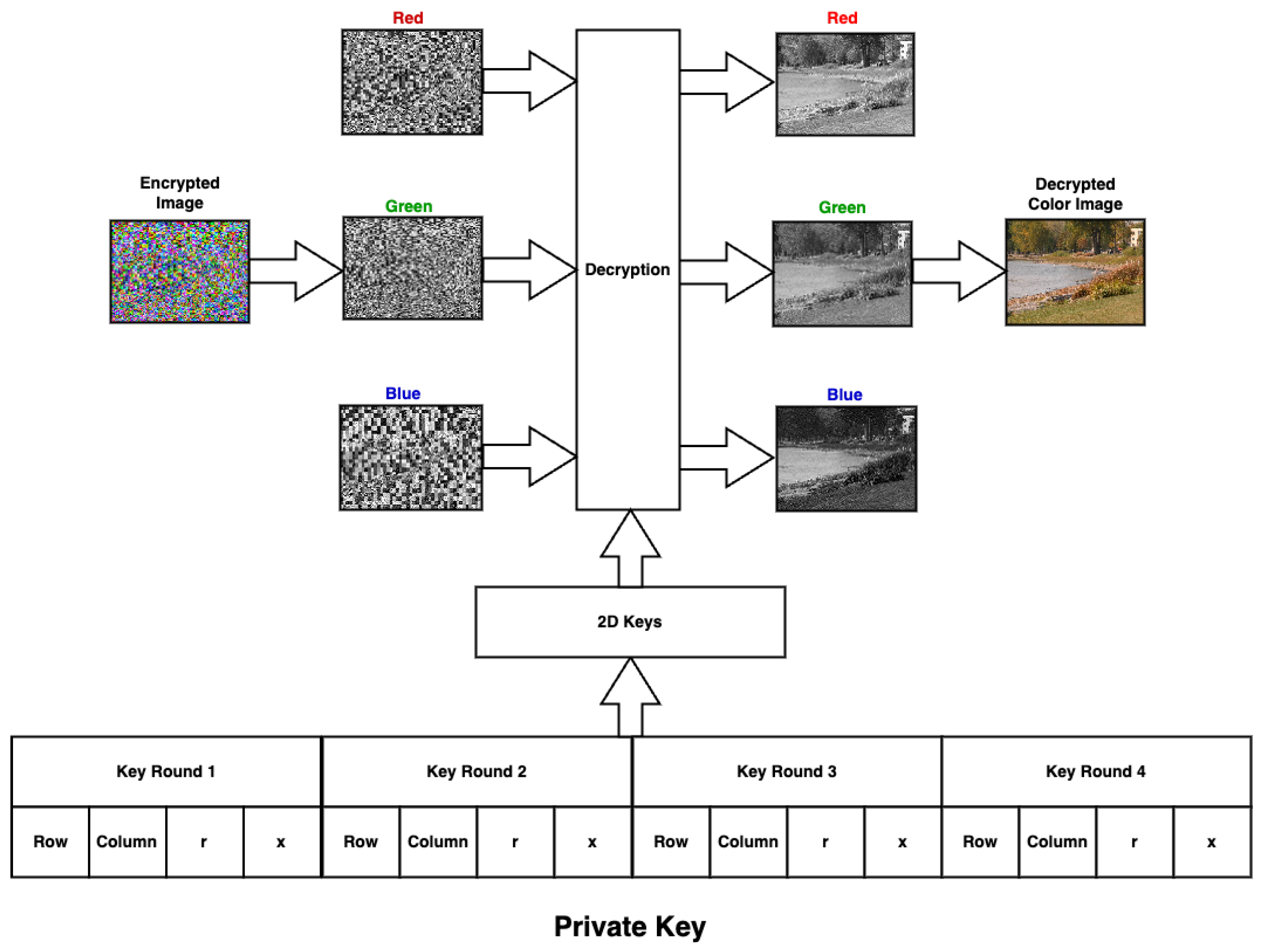

Figure 6.
The proposed decryption Phase.
Figure 6.
The proposed decryption Phase.

| Algorithm 2 Decryption Process. |
| Inputs: Encrypted color image, Private Key. Output: Decrypted image Process
|
4. Implementation and Results
To test the proposed method, we applied a proposed encryption–decryption approach to random images from a standard image dataset. The selected images were encrypted and decrypted using the proposed method in order to conduct a performance assessment and to ensure that the results can be reproduced by other researchers. The analysis involved comparing the source (original), encrypted, and decrypted images using their plots and histograms.
We utilized the Kodak Lossless True Color Image Suite to evaluate the effectiveness of our proposed encryption approach. We accessed the dataset from [51], which provided a diverse range of high-quality images to test our algorithm’s performance. Overall, the Kodak dataset provides a standardized platform to evaluate the robustness and security of an image encryption approach, and can ensure that our proposed approach is reliable and effective. The pictures in this dataset are lossless actual-color (24 bits per pixel, known as "full color") images.
Figure 7, Figure 8 and Figure 9 illustrate the generated outputs from the code execution. These figures represent the plots and histograms of the source image file, encrypted image file, and decrypted image file, respectively.
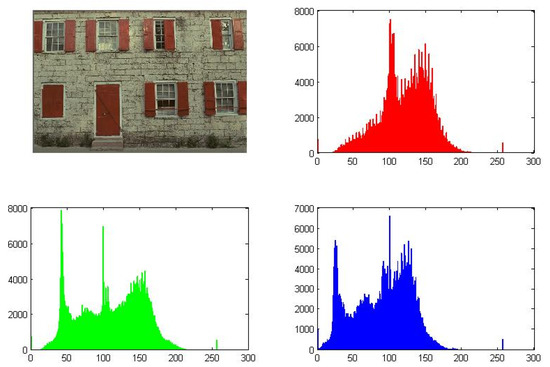
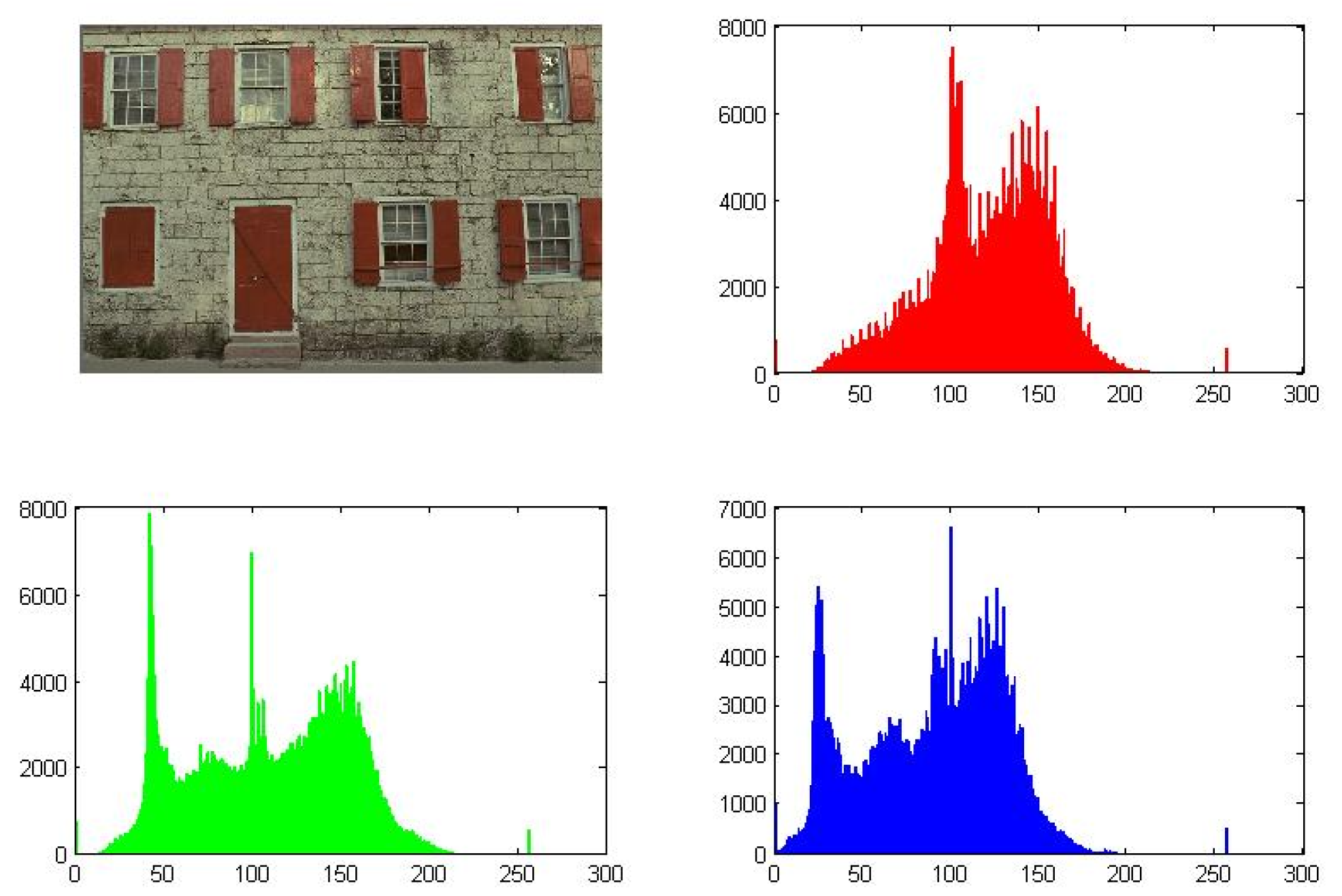
Figure 7.
Source image and its histograms for each channel (example).
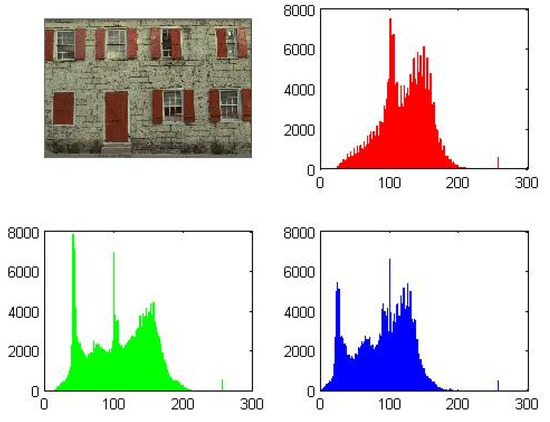
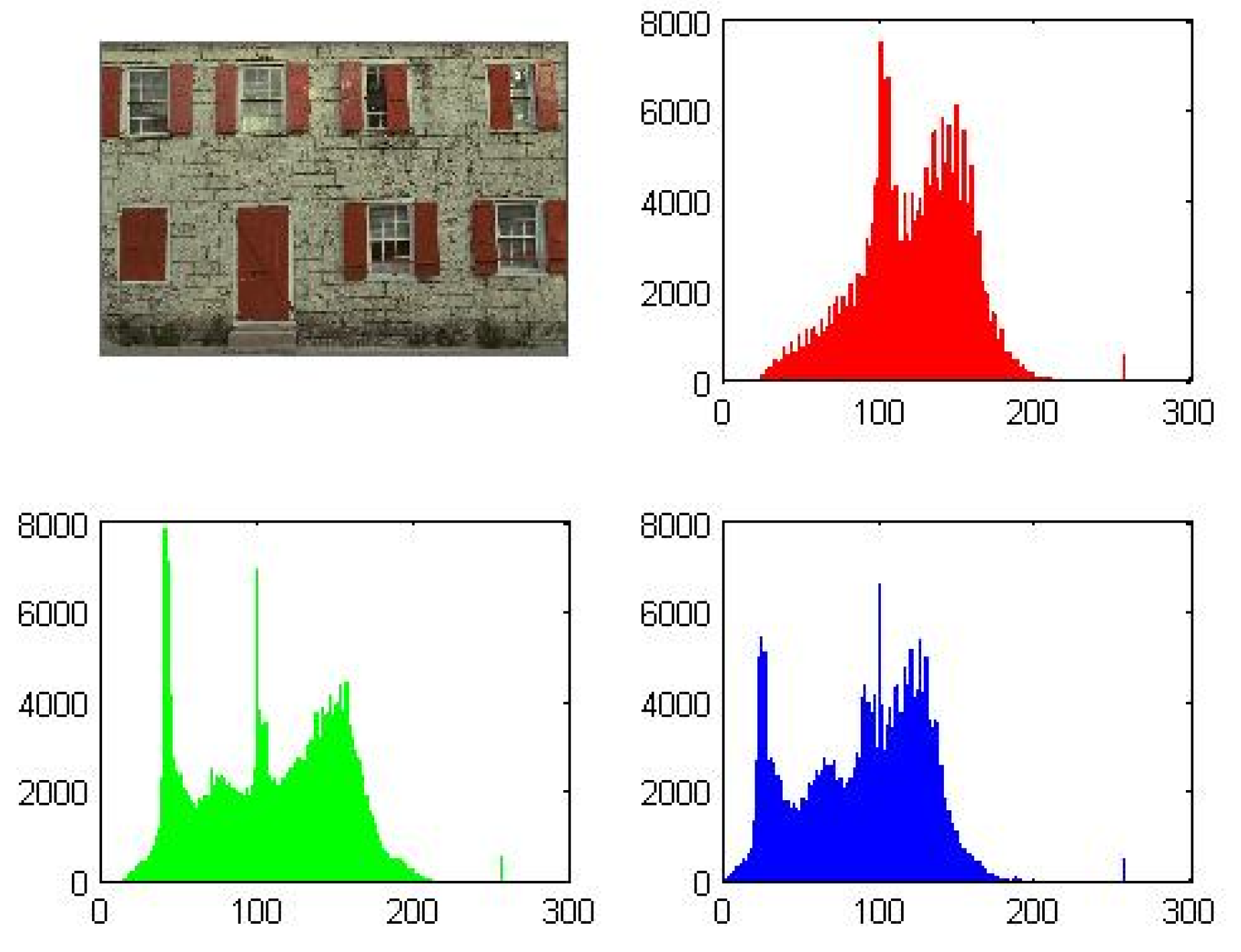
Figure 8.
Decrypted image and its histograms for each channel (example).
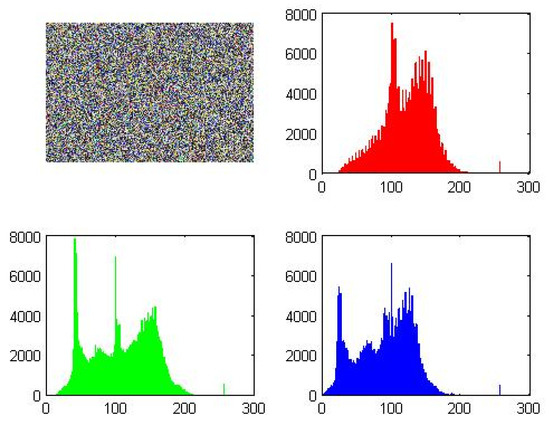
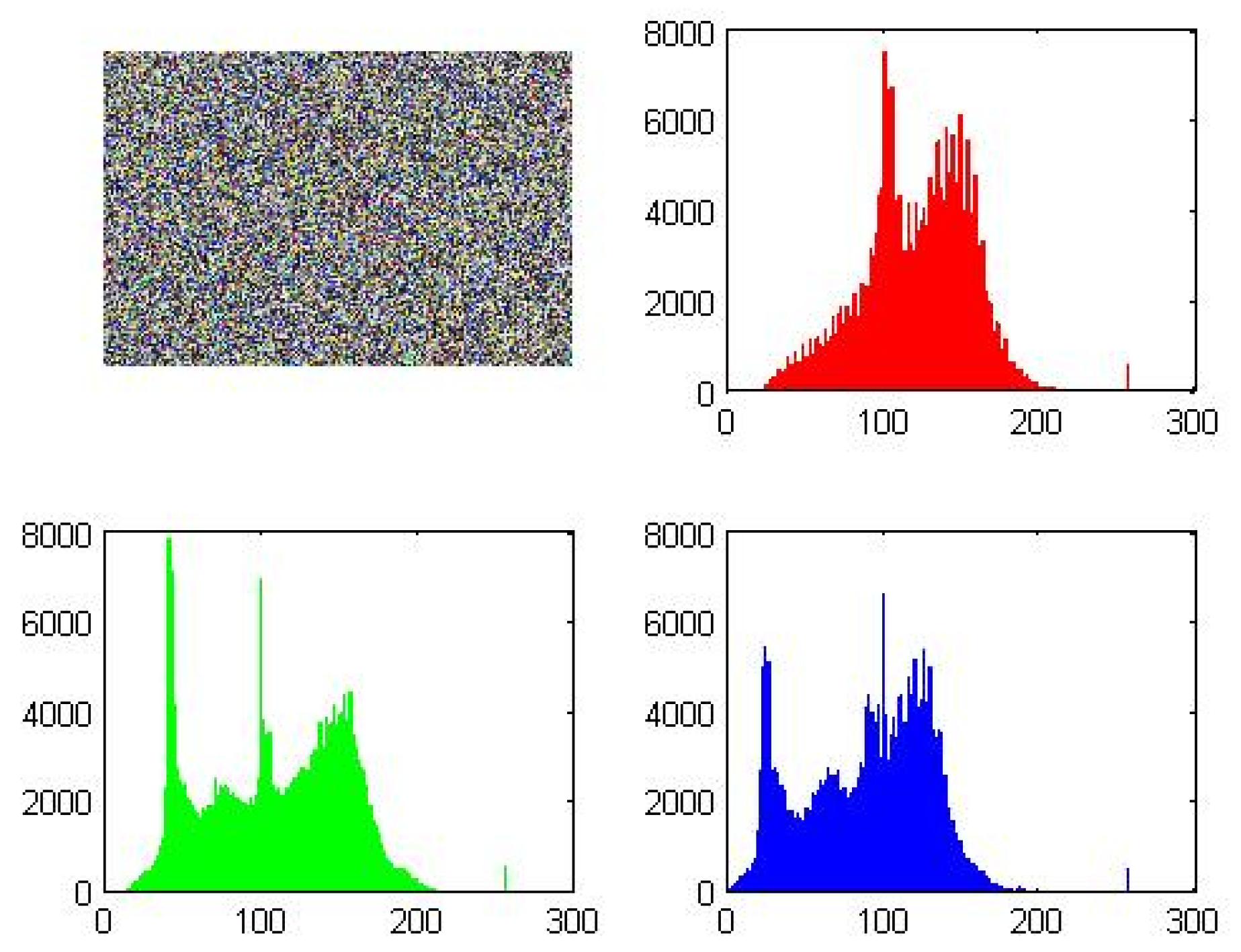
Figure 9.
Encrypted image and its histograms for each channel (example).
A successful encryption process can be observed by comparing Figure 7 (source image) with Figure 9 (encrypted image). The significant differences in their plots indicate that the encryption is effective and that it would be very challenging to restore the original image from the encrypted one either partially or wholly.
On the other hand, the similarity between the source image file (Figure 7) and the decrypted image file (Figure 8) demonstrates the effectiveness of the decryption process. This means that the original image can be accurately recovered after decryption, ensuring the integrity of the image data.
Multiple images from the Kodak dataset were selected and tested to further validate the proposed encryption–decryption approach in order to provide a comprehensive evaluation of the method’s performance across different types of images. This approach allows researchers to assess the robustness and reliability of the encryption–decryption process in various scenarios, ensuring the method’s applicability in real-world applications.
The obtained experimental results are studied and analyzed in the following subsections, with several types of analyses performed in order to demonstrate the enhancements achieved by the proposed method.
4.1. Image Quality
A number of different metrics can be used to assess a security method’s resistance to differential attack. Among these are the Unified Average Changing Intensity (UACI), which can be calculated using Equation (6) (where M and N are the dimension of the two images to compare I and K) and the Number of Pixels Change Rate (NPCR), for which the mathematical formula is shown in Equation (7):
where
The obtained values for various metrics in Table 4 are very close to the results reported in [38], demonstrating the robustness of the proposed method against differential attacks. Our results indicate that a minor change in the original image makes a maximum difference in the encrypted image. This feature leads to the diffusion property, indicating immunity to ciphertext-only attacks.

Table 4.
Image quality measurements.
The Structural Similarity Index Measure (SSIM), computed using Equation (8), is a metric utilized to evaluate the quality of an image after decryption and to gauge the resemblance between the original and encrypted images. The SSIM index ranges from −1 to 1 as a decimal value, with 1 signifying complete similarity, 0 denoting no similarity, and −1 representing perfect anti-correlation.
where is the pixel sample mean of image x, is the pixel sample mean of image y, is the variance of image x, is the variance of image y, is the covariance of image x and image y, , are two variables used to stabilize division with a weak denominator, and L is the dynamic range of the pixel-value (); here, by default and .
4.2. Sensitivity Analysis
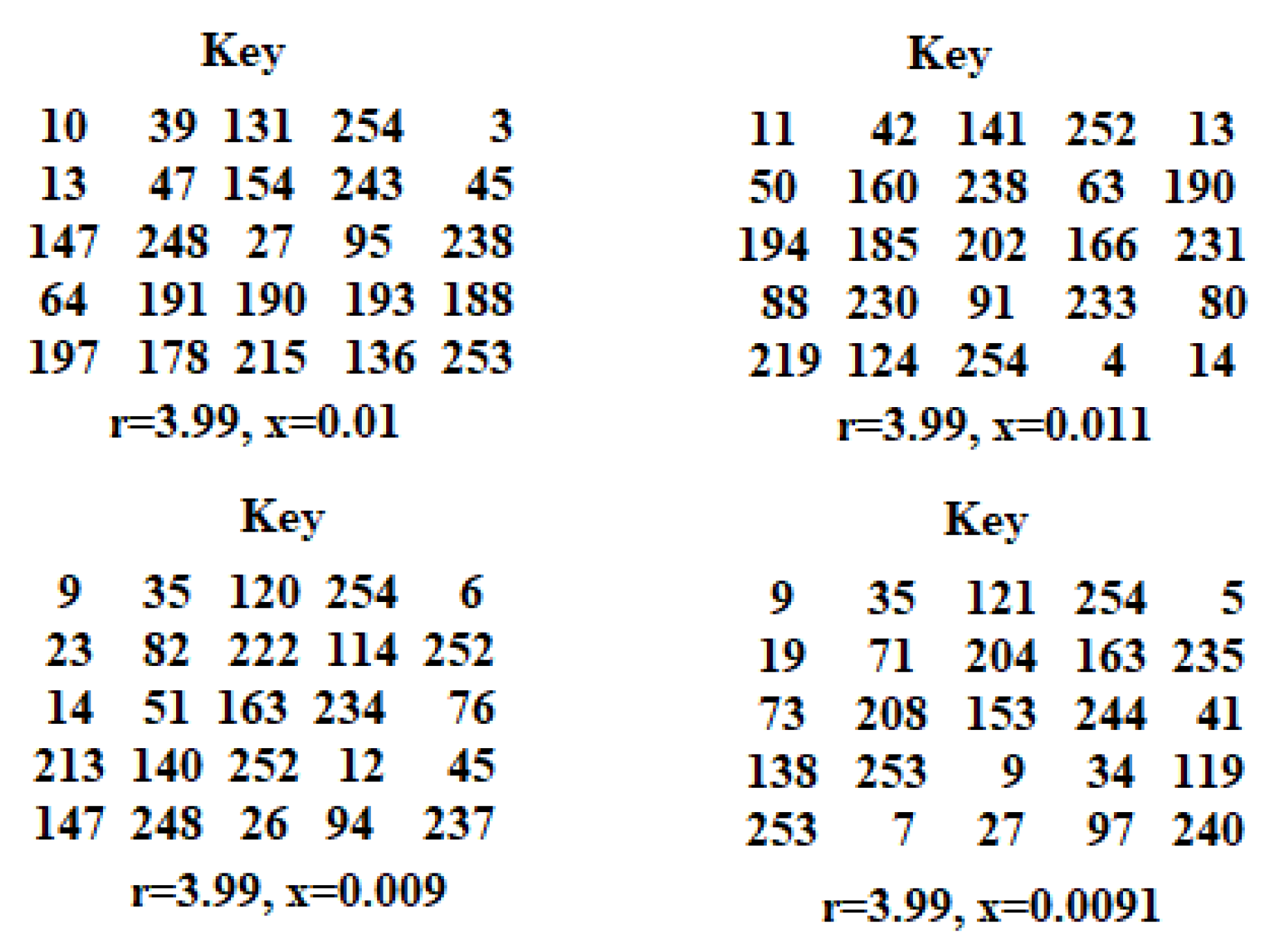
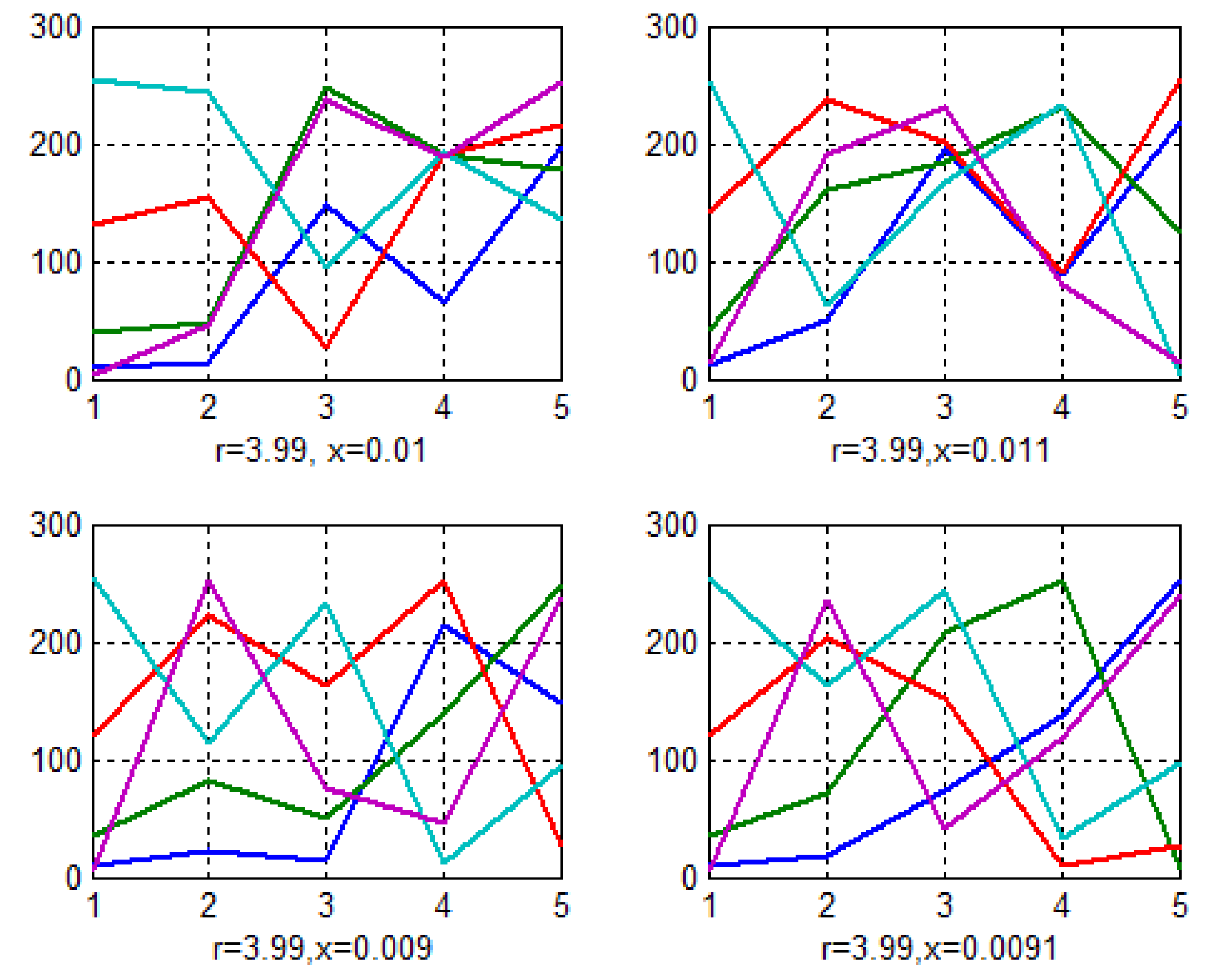
The private key is composed of four elements, and even a slight alteration in one or more of these elements results in the creation of a new key. Utilizing this new key during the decryption process yields a corrupted decrypted image, which indicates that any modifications to the private key can be viewed as a hacking attempt. An identical private key must be employed for both the encryption and decryption phases. Figure 10 and Figure 11 display the 2D key’s contents when using varying parameter values; minor changes in the chaotic parameters r and x generate keys with distinct values.
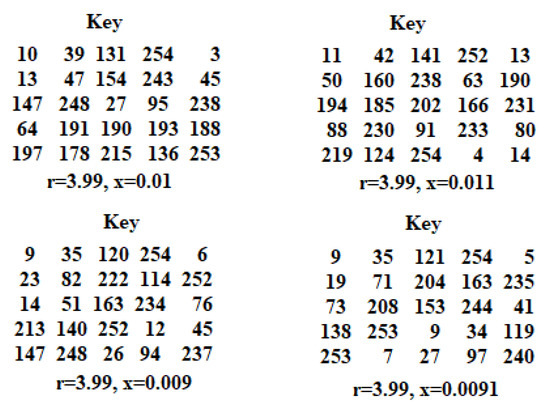
Figure 10.
Key generation samples.
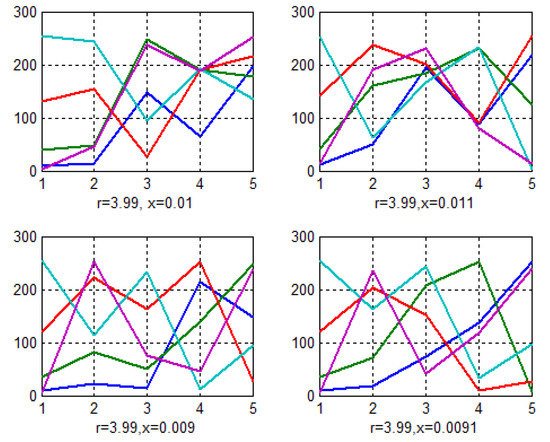
Figure 11.
Different keys generated when changing parameter values.
For an ideal match between the input image and the decrypted image, the quality parameters should be MSE = 0 and PSNR = infinite. Table 5 demonstrates the values of these parameters when slight alterations are made to the private key during the decryption stage.

Table 5.
Using different private keys in the decryption phase.
In Figure 12, the image has been encrypted using a selected private key and the encrypted image has been decrypted using another private key; the resulting decrypted image is a corrupted and damaged image. In this case, the errors in the private key during the decryption phase are considered a hacking attempt that results in a damaged image file being produced. This experiment proves the sensitivity of the proposed method to its initial conditions, as any minor change in the key results in a corrupted image.

Figure 12.
Encryption and decryption using different private keys.
4.3. Security Analysis
In this research, the r and x parameters of the chaotic map, described in Section 3, determine the key. Thus, in a brute-force attack the main parameters are determined by the sizes of r and x.
Here, r and x use a double data type, which has the structure shown below.
| 1 Bit | 11 bits | 52 bits |
| Sign | Exponent | Mantissa |
Thus, x may use up to 52 bits for its values, resulting in a total of different values. However, to obtain the desired chaotic characteristic, the value for r has to be between 3.57 to 4 [52]. Thus, the number of different values for r when using 52 bits is determined by the formula
Using this value for r and 64-bits for x, we have . With this, we can assume that any hacking attempt will be conducting using a brute-force approach.
Table 6 shows the performance results. It can be seen that the method throughput can be increased by increasing the image size and using moderate values for R and C. Here, we can minimize the times required to generate each color private key.

Table 6.
Encryption time and throughput for the selected images.
As seen in Table 6, it takes approximately 4.3714 s on average to generate the chaotic map from r and x and perform either encryption or decryption. Assuming that a hacker has a more powerful machine capable of doing this in 1s and that the average number of attempts is half the search space, brute-force hacking would require
Thus, the average time (in centuries) required to obtain one key would be
Having a computer 1000 times faster or computing on 1000 computers in parallel would reduce the time to centuries.
Additionally, because a slight change in the key brings about drastic changes in the cryptogram or the plain image, using an AI algorithm dependent on “getting closer” to the desired image during decryption is of little value.
4.4. Correlation Analysis
The Correlation Coefficient (CC) calculated between two datasets can be used to measure the strength of rapprochement between them. If the CC between image 1 and image 2 is equal to one, then we can say that image 2 is identical (equal) to image 1. The selected images were encrypted and decrypted using the proposed method and the CC was calculated; the results show that the CC between the input image and the decrypted image is always zero. The CC between the input image and the encrypted one is always minimal, indicating that the encryption phase destroys the input image. Table 7 shows the calculated CC between the input image and the encrypted image using the proposed method; it can be seen that the CC values between the input and encrypted images are very small, which indicates that there is no rapprochement between them.

Table 7.
Obtained correlation coefficients.
Calculating the CC determines the level of correlation between two files, and the correlation coefficient is always in the range [−1, 1]. Values between [0.7–1] are considered strong correlation (gray values from the source files are similar to gray values from the encrypted file), values between [0.3–0.7] are considered medium correlation, and values between [0–0.3] are considered weak correlation. Figure 13 shows a sample output, where the calculated CC value between two image files expresses the dependency between their corresponding gray values.

Figure 13.
CC for encrypted and decrypted images.
4.5. Quality Analysis
The above image was encrypted and decrypted using various lengths of rows and columns for the 2D key. Table 8 shows the MSE and PSNR quality parameters.

Table 8.
MSE and PSNR results (between the source and encrypted images).
Figure 14 shows a sample output. A suitable image cryptography method should maximize the MSE value in the encryption phase while minimizing the value of PSNR; conversely, in the decryption phase the MSE should be minimized and the PSNR should be maximized.

Figure 14.
Sample output.
From Table 8, it can be seen that the obtained values for MSE and PSNR are acceptable and that the proposed method satisfies the requirement of providing suitable quality parameters during the encryption and decryption phases. In the decryption phase, the MSE is always zero, while the PSNR is always infinite.
The private keys shown in Table 9 were used in four rounds of encryption and the selected images in the Kodak dataset were treated using the proposed method. The obtained results for MSE and PSNR are shown in Table 10.

Table 9.
Encryption key used in the four rounds.

Table 10.
Obtained MSE and PSNR between the selected images and the encrypted images.
The results provided in Table 10 demonstrate that the proposed method achieves excellent quality parameters.
4.6. Speed Analysis
To perform a speed analysis, it is necessary to measure the encryption–decryption time. Total encryption time includes the following times needed to accomplish the proposed method encryption/decryption phase: time to shuffle the rows, time to shuffle the columns, time to generate a 2D key, time required for key resizing, and time required to apply XORing (encryption/decryption). Furthermore, all of these steps must be repeated four times. The image “sampleMerry_0055_Lasalle.jpg” was encrypted using the proposed method and private keys with various R and C values. Table 11 shows the obtained results.

Table 11.
Encryption time and throughput for various private key sizes.
From Table 11, we can draw the following conclusions:
- Increasing R and C increases the time required to generate the keys.
- As the values of R and C increase, the time required for encryption increases slightly, suggesting that moderate values of R and C should be selected in order to optimize the efficiency of the proposed method to match the large size of the images in the dataset.
Table 12 compares the average throughput of our proposed method (Table 6) to the state-of-the-art methods discussed in Section 2. It can be seen that our method results in an enhancement of up to 2.14 times compared to other chaotic approaches, and that its throughput is very close to the other methods.

Table 12.
Throughput enhancement.
4.7. Attack Robustness Analysis
This subsection discusses the robustness of the proposed method against various attacks. For instance, in occlusion attacks parts of the transmitted data may be tampered with, becoming either hidden or overridden during transmission. Various percentages of occlusion were tested, with the obtained results listed in Table 13; the numbers in Table 13 show the degradation of various quality measurements as the occlusion percentage increases. From Figure 15 and Figure 16, it is clear that while decrypted images with 6.25%, 25%, and 50% occlusion of the encrypted images are distorted, they remain perceptible to the human eye, while decrypted images with 75% occlusion of the encrypted image are not recoverable. This indicates that our proposed method can withstand up to 50% occlusion attacks.

Table 13.
Occlusion attack analysis.

Figure 15.
Low occlusion values.

Figure 16.
High occlusion values.
Another common type of attack is a chosen-plaintext attack, in which the attacker has the ability to choose plaintext images and access their corresponding encrypted ciphertext images. This is considered a very dangerous attack.
In [53], the authors discussed a chosen-plaintext attack on an image encryption scheme that uses a modified permutation–diffusion structure. The authors first introduced the encryption scheme and its architecture, which involves permutation and diffusion phases. The authors then proposed a chosen-plaintext attack on the encryption scheme involving the attacker choosing specific plaintext images and analyzing the corresponding ciphertext images produced by the encryption scheme. Through a series of mathematical analyses, the authors showed that the encryption scheme is vulnerable to this attack and that the secret key used in the scheme can be easily recovered by the attacker. In the same study, the authors presented experimental results to support their analysis, demonstrating that the proposed attack effectively breaks the encryption scheme. They further discussed the limitations of the encryption scheme and suggested possible modifications that to enhance its security. They suggested that a robust image encryption technique should incorporate than one round; in our proposed method we used four rounds of permutation, making the proposed approach robust against chosen-plaintext attacks.
5. Conclusions
In this paper, we have evaluated a new method for color images file cryptography. The proposed cryptographic algorithm uses a chaotic logistic map model to generate two complicated secret keys for encryption and decryption. A chaotic logistic map model is used to generate the 2D key by adding the matrix dimensions R and C to the model. The pseudo-random numbers generated for the chaotic map were tested and found to have acceptable values comparable to those in the related literature. Various image files were tested and several types of analysis were performed, showing that the proposed method can provide a high level of security. The chaotic logistic map derived from the private key has a complicated structure that is sensitive to minor key component changes. In addition, it provides a huge key space, thereby decreasing the possibility of key hacking. A speed analysis showed that the proposed method can provide increased image cryptography performance by minimizing the encryption–decryption time and maximizing the throughput of the color cryptography process. The results obtained in this study show that the provided throughput is better than that provided by existing chaotic methods.
Author Contributions
Conceptualization, M.A.-F., Z.A., C.O. and O.A.; Formal analysis, M.A.-F., A.A.-H., I.A. and Z.A.; Methodology, M.A.-F., Z.A., C.O. and A.A.-H.; software, M.A.-F., A.A.-H., O.A. and K.A.; Supervision, Z.A., C.O. and M.A.-F.; Writing—original draft, M.A.-F., A.A.-H. and K.A.; Writing—review and editing, C.O., M.A.-F., A.A.-H., I.A. and Z.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 3DES | Triple Data Encryption Standard |
| AES | Advanced Encryption Standard |
| BF | Blow Fish |
| CC | Correlation Coefficient |
| CLM | Chaotic Logistic Map |
| CLMK | Chaotic Logistic Map Key |
| DES | Data Encryption Standard |
| KS | Key Space |
| MSE | Mean Square Error |
| NPCR | Number of Pixels Change Rate |
| PK | Private Key |
| PSNR | Peak Signal to Noise Ratio |
| SSIM | Structural Similarity Index Measure |
| UACI | Unified Average Changing Intensity |
References
- Arora, H.; Soni, G.K.; Kushwaha, R.K.; Prasoon, P. Digital Image Security Based on the Hybrid Model of Image Hiding and Encryption. In Proceedings of the 2021 6th International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 8–10 July 2021; pp. 1153–1157. [Google Scholar]
- Abu-Faraj, M.; Al-Hyari, A.; Alqadi, Z. A Complex Matrix Private Key to Enhance the Security Level of Image Cryptography. Symmetry 2022, 14, 664. [Google Scholar] [CrossRef]
- Abu-Faraj, M.; Aldebei, K.; Alqadi, Z. Simple, Efficient, Highly Secure, and Multiple Purposed Method on Data Cryptography. Trait. Signal 2022, 39, 173–178. [Google Scholar] [CrossRef]
- Wang, S.; Li, W.; Wang, F. Web-scale multidimensional visualization of big spatial data to support earth sciences—A case study with visualizing climate simulation data. Informatics 2017, 4, 17. [Google Scholar] [CrossRef]
- Fonseca, L.M.G.; Namikawa, L.M.; Castejon, E.F. Digital image processing in remote sensing. In Proceedings of the 2009 Tutorials of the XXII Brazilian Symposium on Computer Graphics and Image Processing, Rio de Janeiro, Brazil, 11–15 October 2009; pp. 59–71. [Google Scholar]
- Abu-Faraj, M.; Zubi, M. Analysis and implementation of kidney stones detection by applying segmentation techniques on computerized tomography scans. Ital. J. Appl. Math. 2020, 43, 590–602. [Google Scholar]
- Ge, Y.; Liu, P.; Ni, Y.; Chen, J.; Yang, J.; Su, T.; Zhang, H.; Guo, J.; Zheng, H.; Li, Z.; et al. Enhancing the X-ray differential phase contrast image quality with deep learning technique. IEEE Trans. Biomed. Eng. 2020, 68, 1751–1758. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, C.Y.; Wang, H.J. Enhancing image quality in Visual Cryptography with colors. In Proceedings of the 2012 International Conference on Information Security and Intelligent Control, Yunlin, Taiwan, 14–16 August 2012; pp. 103–106. [Google Scholar]
- Rasras, R.J.; Abuzalata, M.; Alqadi, Z.; Al-Azzeh, J.; Jaber, Q. Comparative Analysis of Color Image Encryption-Decryption Methods Based on Matrix Manipulation. Int. J. Comput. Sci. Mob. Comput. 2019, 8, 14–26. [Google Scholar]
- Pujari, V.G.; Khot, S.R.; Mane, K.T. Enhanced visual cryptography scheme for secret image retrieval using average filter. In Proceedings of the 2014 IEEE Global Conference on Wireless Computing & Networking (GCWCN), Lonavala, India, 22–24 December 2014; pp. 88–91. [Google Scholar]
- Ibrahim, D.; Ahmed, K.; Abdallah, M.; Ali, A.A. A New Chaotic-Based RGB Image Encryption Technique Using a Nonlinear Rotational 16 × 16 DNA Playfair Matrix. Cryptography 2022, 6, 28. [Google Scholar] [CrossRef]
- Abu-Faraj, M.; Al-Hyari, A.; Al-Taharwa, I.; Al-Ahmad, B.; Alqadi, Z. CASDC: A Cryptographically Secure Data System Based on Two Private Key Images. IEEE Access 2022, 10, 126304–126314. [Google Scholar] [CrossRef]
- Ioannidou, I.; Sklavos, N. On General Data Protection Regulation Vulnerabilities and Privacy Issues, for Wearable Devices and Fitness Tracking Applications. Cryptography 2021, 5, 29. [Google Scholar] [CrossRef]
- Abu-Faraj, M.; Al-Hyari, A.; Aldebei, K.; Alqadi, Z.; Al-Ahmad, B. Rotation Left Digits to Enhance the Security Level of Message Blocks Cryptography. IEEE Access 2022, 10, 69388–69397. [Google Scholar] [CrossRef]
- Stallings, W. Cryptography and Network Security, 4th ed.; Pearson Education: Bengaluru, India, 2006. [Google Scholar]
- Abu-Faraj, M.; Al-Hyari, A.; Al-taharwa, I.; Alqadi, Z.; Ali, B. Increasing the Security of Transmitted Text Messages Using Chaotic Key and Image Key Cryptography. Int. J. Data Netw. Sci. 2023, 7, 809–820. [Google Scholar] [CrossRef]
- Abu-Faraj, M.; Al-Hyari, A.; Al-Ahmad, B.; Alqadi, Z.; Ali, B.; Alhaj, A. Building a Secure Image Cryptography System using Parallel Processing and Complicated Dynamic Length Private Key. Appl. Math. Inf. Sci. (AMIS) 2022, 16, 1017–1026. [Google Scholar] [CrossRef]
- Khan, A.; Chefranov, A.; Demirel, H. Image-Level Structure Recognition Using Image Features, Templates, and Ensemble of Classifiers. Symmetry 2020, 12, 1072. [Google Scholar] [CrossRef]
- Abduljabbar, Z.A.; Abduljaleel, I.Q.; Ma, J.; Sibahee, M.A.A.; Nyangaresi, V.O.; Honi, D.G.; Abdulsada, A.I.; Jiao, X. Provably Secure and Fast Color Image Encryption Algorithm Based on S-Boxes and Hyperchaotic Map. IEEE Access 2022, 10, 26257–26270. [Google Scholar] [CrossRef]
- Chaudhary, N.; Shahi, T.B.; Neupane, A. Secure Image Encryption Using Chaotic, Hybrid Chaotic and Block Cipher Approach. J. Imaging 2022, 8, 167. [Google Scholar] [CrossRef] [PubMed]
- Elminaam, D.S.A.; Kader, H.M.A.; Hadhoud, M.M. Performance evaluation of symmetric encryption algorithms. IJCSNS Int. J. Comput. Sci. Netw. Secur. 2008, 8, 280–286. [Google Scholar]
- Singh, S.P.; Maini, R. Comparison of data encryption algorithms. Int. J. Comput. Sci. Commun. 2011, 2, 125–127. [Google Scholar]
- Singh, G.; Kumar, A.; Sandha, K. A study of new trends in Blowfish algorithm. Int. J. Eng. Res. Appl. 2011, 1, 321–326. [Google Scholar]
- Labao, A.; Adorna, H. A CCA-PKE Secure-Cryptosystem Resilient to Randomness Reset and Secret-Key Leakage. Cryptography 2022, 6, 2. [Google Scholar] [CrossRef]
- Agrawal, M.; Mishra, P. A comparative survey on symmetric key encryption techniques. Int. J. Comput. Sci. Eng. 2012, 4, 877. [Google Scholar]
- Nadeem, A.; Javed, M.Y. A performance comparison of data encryption algorithms. In Proceedings of the 2005 International Conference on Information and Communication Technologies, Las Vegas, NV, USA, 4–6 April 2005; pp. 84–89. [Google Scholar]
- Elmanfaloty, R.A.; Abou-Bakr, E. An image encryption scheme using a 1D chaotic double section skew tent map. Complexity 2020, 2020, 7647421. [Google Scholar] [CrossRef]
- Kumar, B.; Karthikka, P.; Dhivya, N.; Gopalakrishnan, T. A performance comparison of encryption algorithms for digital images. Int. J. Eng. Res. Technol. 2014, 3, 2169–2174. [Google Scholar]
- Heucheun Yepdia, L.M.; Tiedeu, A.; Kom, G. A robust and fast image encryption scheme based on a mixing technique. Secur. Commun. Netw. 2021, 2021, 6615708. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y.; Huang, H. Cosine-transform-based chaotic system for image encryption. Inf. Sci. 2019, 480, 403–419. [Google Scholar] [CrossRef]
- Asgari-Chenaghlu, M.; Balafar, M.A.; Feizi-Derakhshi, M.R. A novel image encryption algorithm based on polynomial combination of chaotic maps and dynamic function generation. Signal Process. 2019, 157, 1–13. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X. Multiple-image encryption algorithm based on DNA encoding and chaotic system. Multimed. Tools Appl. 2019, 78, 7841–7869. [Google Scholar] [CrossRef]
- Tang, Z.; Song, J.; Zhang, X.; Sun, R. Multiple-image encryption with bit-plane decomposition and chaotic maps. Opt. Lasers Eng. 2016, 80, 1–11. [Google Scholar] [CrossRef]
- Nita, S.L.; Mihailescu, M.I.; Pau, V.C. Security and Cryptographic Challenges for Authentication Based on Biometrics Data. Cryptography 2018, 2, 39. [Google Scholar] [CrossRef]
- Naseer, Y.; Shah, T.; Shah, D.; Hussain, S. A Novel Algorithm of Constructing Highly Nonlinear S-p-boxes. Cryptography 2019, 3, 6. [Google Scholar] [CrossRef]
- Cowper, N.; Shaw, H.; Thayer, D. Chaotic Quantum Key Distribution. Cryptography 2020, 4, 24. [Google Scholar] [CrossRef]
- Abu Taha, M.; Hamidouche, W.; Sidaty, N.; Viitanen, M.; Vanne, J.; El Assad, S.; Deforges, O. Privacy Protection in Real Time HEVC Standard Using Chaotic System. Cryptography 2020, 4, 18. [Google Scholar] [CrossRef]
- Raghunandan, K.R.; Dodmane, R.; Bhavya, K.; Rao, N.S.K.; Sahu, A.K. Chaotic-Map Based Encryption for 3D Point and 3D Mesh Fog Data in Edge Computing. IEEE Access 2023, 11, 3545–3554. [Google Scholar] [CrossRef]
- Li, R.; Liu, Q.; Liu, L. Novel image encryption algorithm based on improved logistic map. IET Image Process. 2019, 13, 125–134. [Google Scholar] [CrossRef]
- Del Rey, A.M.; He, P.; Sun, K.; Zhu, C. A Novel Image Encryption Algorithm Based on the Delayed Maps and Permutation-Confusion-Diffusion Architecture. Secur. Commun. Netw. 2021, 2021, 6679288. [Google Scholar] [CrossRef]
- Liu, L.; Hao, S.; Lin, J.; Wang, Z.; Hu, X.; Miao, S. Image block encryption algorithm based on chaotic maps. IET Signal Process. 2018, 12, 22–30. [Google Scholar] [CrossRef]
- Wu, X.; Yu, S.; Gao, L. A chaotic image encryption algorithm based on fractional-order chaotic map and logistic map. Nonlinear Dyn. 2018, 92, 1301–1316. [Google Scholar]
- Zhang, Y.; Zhang, Y.; Zhou, X.; Huang, H. A novel image encryption algorithm based on logistic map. Nonlinear Dyn. 2021, 103, 27–44. [Google Scholar]
- Vijayalakshmi, C.; Lavanya, L.; Navya, C. A Hybrid Encryption Algorithm Based On AES and RSA. Int. J. Innov. Res. Comput. Commun. Eng. 2016, 4, 909–917. [Google Scholar]
- Zhang, L.; Yuan, X.; Wang, K.; Zhang, D. Multiple-image encryption mechanism based on ghost imaging and public key cryptography. IEEE Photonics J. 2019, 11, 1–14. [Google Scholar] [CrossRef]
- Gao, W.; Yang, L.; Zhang, D.; Liu, X. Quantum Identity-Based Encryption from the Learning with Errors Problem. Cryptography 2022, 6, 9. [Google Scholar] [CrossRef]
- Salunke, S.; Ahuja, B.; Hashmi, M.F.; Marriboyina, V.; Bokde, N.D. 5D Gauss Map Perspective to Image Encryption with Transfer Learning Validation. Appl. Sci. 2022, 12, 5321. [Google Scholar] [CrossRef]
- Alexan, W.; ElBeltagy, M.; Aboshousha, A. RGB Image Encryption through Cellular Automata, S-Box and the Lorenz System. Symmetry 2022, 14, 443. [Google Scholar] [CrossRef]
- Pourasad, Y.; Cavallaro, F. A novel image processing approach to enhancement and compression of X-ray images. Int. J. Environ. Res. Public Health 2021, 18, 6724. [Google Scholar] [CrossRef] [PubMed]
- Msekh, Z.A.; Hreshee, S.S. Implementation of a chaos-based symmetric text encryption using Arduino microcontrollers. In Proceedings of the Journal of Physics: Conference Series, Quebec City, QC, Canada, 15 June 2021; Volume 1963, p. 012086. [Google Scholar]
- Franzen, R. Kodak Lossless True Color Image Suite. 1999, Volume 4. Available online: http://r0k.us/graphics/kodak (accessed on 10 December 2022).
- Zhu, S.; Wang, G.; Zhu, C. A Secure and Fast Image Encryption Scheme Based on Double Chaotic S-Boxes. Entropy 2019, 21, 790. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, L.Y.; Wang, J.; Zhang, Y.; Wong, K.w. Chosen-plaintext attack of an image encryption scheme based on modified Permutation–Diffusion structure. Nonlinear Dyn. 2016, 84, 2241–2250. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).