Abstract
This paper describes three methods of creating a subliminal channel in visual cryptography that are defined for a (2,2) sharing scheme. They work by hiding additional covert information besides the original encrypted image. The first channel is revealed when the user folds the share along the specific axis. The second channel encodes subpixels on the basis of the encrypted message bits. It is designed to hide a wide range of data types. The third channel may be applied to a single share or multiple shares and is revealed when the proper parts of the shares are stacked. Fold and overlapping algorithms are adequate for printed shares, but the encryption method is only suitable for digital shares. The capacity of these methods ranges from half of the image size to the whole image size. The presented algorithms work on black-and-white images but are expandable to color visual cryptography. They may find applications in steganography and other data-hiding techniques. The created subliminal channels do not interfere with regular images that may still be revealed by stacking the shares. In short, this article introduces subliminal channels in visual cryptography, presents three algorithms for both binary and colorful images, shows examples of use with the results obtained, and discusses features of each method.
1. Introduction
Subliminal channels are covert methods of communication used in the normal transmission of data to hide additional information. They are usually implemented in digital signature algorithms [1]. The idea of covert channels in cryptography takes advantage of data redundancy (providing space for secret data) and randomization (messages with and without hidden data are indistinguishable from the perspective of an external observer).
There are other fields in which subliminal channels may also be present. Visual cryptography is a technique of image encryption that works by creating meaningless shares that should be combined to recover the message [2]. From this perspective, it may be considered a secret-sharing method [3]. However, in visual cryptography, the “decryption” stage may be performed without using a computer, just by stacking the shares. This is because the human visual system perceives the mixture of white and black pixels as a gray level.
Multiple extensions of visual cryptography have been proposed. Some of them allow the shares to contain false information instead of random noise [4,5,6]. Then, the real secret image may be recovered when all required parts are stacked together. Less often, visual cryptography algorithms focus on color images [7,8,9], in which case the image is decomposed and each component is processed separately. Usually, extending the scheme to color images does not require computing power to recover the secret data. These methods may find applications in encrypting financial data, biometric verification, medical imaging etc. [10].
This article introduces subliminal channels to visual cryptography. It presents three different approaches to concealing additional secret data in regular visual cryptography schemes (Section 4). Later, it shows examples of decoding both overt and covert data (Section 5). Furthermore, the article discusses features of the presented algorithms, their security, and some additional topics (Section 6). Finally, as another added value, exemplary implementations are given in the Appendix A.
2. Literature Review
Subliminal channels in visual cryptography can hardly be found in the literature. There are, however, a few examples of such research. These methods use base 6 because there are six fundamental blocks. For instance, a secret message may be hidden in a share with the use of codewords from the codebook [11]. The subliminal image may be binary, gray, or colorful. In another technique of data hiding, extracting private data from shares requires certain computation [12]. The authors also proposed a modification of covert data positions in shares to improve security.
Moreover, some works discuss related topics, such as combining visual cryptography with the least significant bit technique, known from steganography [13]. With this approach, it is possible to obtain a capacity of eight bits/pixel. This method allows to conceal additional data to be hidden, but in a different manner than subliminal channels.
As can be seen, the topic is not widely studied at this moment. Therefore, it is a promising research area that encourages new discoveries and the development of creative solutions.
3. Motivations and Contributions
The main motivation of this paper is to raise awareness of subliminal channels in visual cryptography and to show possible variants of such methods. This objective consists of a few steps: defining the model, inventing algorithms, conducting tests, and summarizing obtained results.
The paper describes three ways of creating a subliminal channel in existing algorithms of visual cryptography. It also shows how to extend these techniques to colorful images. When possible, the results of decoding overt and covert data are presented visually. Interesting features, advantages, limitations, and security issues are discussed as well. As an additional contribution, all implementations are available as free software under the GNU General Public License.
4. Materials and Methods
4.1. Background
The basic visual cryptography method encrypts a binary image by creating two meaningless shares. Both of them are required to recover secret data; therefore, it is called the (2,2) threshold scheme. When shares are generated, each pixel is replaced by a block of subpixels, as presented in Table 1. For white pixels, the same random block is chosen for both shares; for black pixels, the opposite subpixels are selected.

Table 1.
Result of stacking subpixels in the (2,2) visual sharing scheme [13].
According to visual cryptography rules, subpixels should resemble random noise. This is why they contain both white and black pixels. In this way, the user with only one share is not able to reveal any information about the secret [2]. However, it is consequently not possible to obtain pure white pixels in the resulting image. After stacking, black pixels are entirely black, but white pixels are perceived by the human vision system as gray. In most cases, it suffices to read the secret information.
The presented (2,2) threshold scheme finds application in encrypting binary images. To visually encrypt grayscale images, we need to transform them into binary first. A popular method is thresholding—the easiest algorithm that sets all pixels above the threshold to white and the rest to black. Despite its simplicity, it has serious drawbacks, including the fact that the image loses most of its details. A better option is to use a dithering technique [14]. This technique simulates gradients through the use of dots, which may vary in size, shape, or spacing. The differences between these approaches are presented in Figure 1.

Figure 1.
Differences between halftoning techniques: (a) Original image. (b) Thresholding method. (c) Dithering method.
Visual cryptography may also be extended to color images. Generally, digital images are represented in an additive RGB model. In visual cryptography, a subtractive CMY model is used because the colors are mixed when the shares are stacked. Before encrypting, the components are extracted and transformed into halftone images [7].
The first method of visual cryptography for color images produces three color shares (cyan, magenta, yellow) and one mask with white and black pixels. The subpixel blocks in the mask are chosen randomly and used as a base for color shares. When the pixel in a color component is not zero, the subpixels of the color share should be opposite to the mask. When the pixel is zero, the subpixels are identical to the mask. A summary of this algorithm is presented in Table 2.

Table 2.
Stacking subpixels in visual color sharing scheme [7].
Another method separately encrypts each color component. The resulting six shares, consisting of white and color pixels, are temporary. They are later combined (one of each color) to create final shares [7]. This algorithm generates two colorful shares that may be stacked to reveal the secret image.
4.2. Model
In a regular secret-sharing scheme, we have generation and reconstruction phases. During generation, the algorithm takes as input a secret image and creates two (or more) meaningless shares. Later, these shares may be stacked to recover the hidden secret. Reconstruction algorithm accepts shares at input and returns recovered images.
However, with a subliminal channel, the model changes a little. The presented system is now designed for data hiding; therefore, the algorithms serve for embedding and extracting. The embedding algorithm takes secret data as another argument. Optionally, some parameters may be passed, for example, the offset of a covert image. The extracting algorithm recovers the hidden message from shares. The model is presented in Figure 2 with a subliminal channel marked with a dotted line.
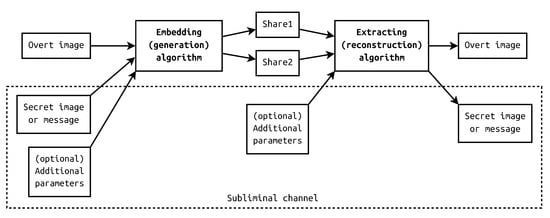
Figure 2.
Model of a subliminal channel in visual cryptography.
4.3. Fold Method
The fold method creates a subliminal channel over a single share. This share is a part of normal visual sharing scheme, and at the same time it also carries secret information. To reveal the covert image, the user needs to know the direction and an offset of the fold line. When the share is folded, subpixels from one side overlie subpixels from another side, as presented in Figure 3.
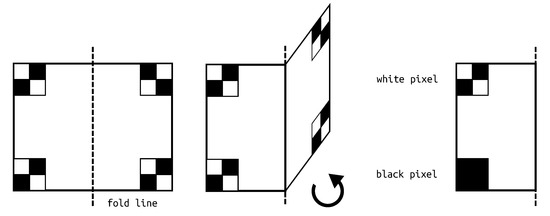
Figure 3.
Scheme of fold method.
The main aspect of the fold method is that subpixels behind the fold line are flipped horizontally or vertically, depending of the fold line direction. This must be taken into consideration during share generation, as depicted in the hiding algorithm (Algorithm 1). At the beginning, the secret image is encrypted into two temporary shares. They are later pasted into the first share of the regular image. In the basic version, the first temporary share is placed in the top left corner. Depending on the fold direction, the second temporary share is placed left from the top-right corner or at the top above the bottom-left corner. Later, the remaining blocks of subpixels in the first regular share are chosen randomly. Subpixels of the second regular share are the same for white pixels and the opposite for black pixels (the ¬ symbol denotes inverse operation, i.e., white pixels become black and vice versa). Obviously, the fold line must be chosen so that the secret image fits the share and the maximum dimensions of the secret image are half of the regular picture.
| Algorithm 1:Share generation with fold subliminal channel |
 |
The algorithm may be modified to put the secret image in a location other than the top-left corner of the share. This may easily be changed by adding an offset to the place of the secret image share, but it has not been shown in Algorithm 1 for reasons of clarity.
The created shares may be stacked to reveal the regular image. The subliminal channel is hidden in the first share (which may be folded to recover the secret image). The advantage of this method is that the recovery is possible with and without a computer.
Fold method can be extended to color-visual cryptography. In the technique with a mask and three color shares, the secret binary image may be hidden in the mask, and color shares are generated normally. In the technique with colorful shares, color components of the secret image are encrypted, and the shares are pasted into suitable regular color shares; later, regular shares are combined identically as in basic method.
4.4. Encryption Method
Another idea of subliminal channel in visual cryptography uses an encryption algorithm. This method is adequate for any data, especially text messages, binary images, and grayscale images. First, the data to be hidden should be encrypted. Then, subpixels are divided into two groups on the basis of the value of their top left pixel. In each iteration, a proper group is chosen depending on the current bit of encrypted data. From this group, a random subpixel block is chosen. Algorithm 2 presents how to create shares with this technique.
| Algorithm 2:Share generation with encryption subliminal channel |
 |
Besides the existing subliminal channel, resulting shares may be stacked normally to reveal the regular image. The limitation of this method is that it requires a computer to recover the secret because the message must be decrypted.
Algorithm 2 is also adequate for concealing binary images. The hidden image should be of the same size as the container. At the beginning, the secret image is encrypted. Then, subpixels are chosen so that their top-left pixel is equal to the current bit of the encrypted data. Additionally, the algorithm may also be extended to the first method of color visual cryptography. Encrypted messages should be encoded in subpixels of the mask, and the remaining color shares are generated without changes.
4.5. Overlapping Method
The overlapping approach to creating subliminal channels in visual cryptography may use a single share or multiple shares. In the first version, shares of the secret image are placed in the same regular share; in the second version, each secret share is embedded in an individual regular share. These methods are shown in Algorithms 3 and 4. The main difference is that with multiple shares, some parts of the second share are ready earlier.
In the presented algorithms, shares of the secret image are placed in the top-left and bottom-right corners. This is to keep the methods simple and to help readers understand them easier. It is possible to choose other parts of the regular share to be used as a container for secret data. Then, to recover the hidden image, the user should know the offset of both parts. During generation, the secret shares are pasted with desired offset instead of in corners.
The overlapping method assumes that when stacked normally, hidden shares cannot overlap. In other words, the secret image cannot be bigger than half of the regular image. The information from the subliminal channel may be recovered with a computer but also when shares are printed on slides. When the covert channel is distributed among shares, they should be stacked with a desired offset. When the channel is present in a single share, the slide may be cut with scissors and its parts stacked together (of course, it is advisable to copy the slide beforehand in order to not lose the possibility of recovering the regular image).
| Algorithm 3:Share generation with overlapping subliminal channel (version for a single share) |
 |
The overlapping method is also adequate for color visual cryptography. The method with a mask and color components may be used for creating a subliminal channel inside the mask. In such a case, a secret binary image is embedded with single overlapping. Unfortunately, this approach is inconvenient for color covert pictures because too many images need to be stacked. The second method with colorful shares is good for both versions of overlapping. Then, each component of a color image is encrypted separately and hidden in the corresponding regular share.
| Algorithm 4:Share generation with overlapping subliminal channel (version for multiple shares) |
 |
5. Results
The experiments we conducted used images from Figure 4 unless stated otherwise.

Figure 4.
Images used in tests (dimensions of peppers: , dimensions of smile: ).
5.1. Fold Method
Figure 5 presents regular shares and the result of their stacking. Figure 6 presents how the secret image is revealed when the share with the subliminal channel is folded. The fold line has been chosen exactly in the middle of the regular share.

Figure 5.
Regular shares and regular image generated with fold method.

Figure 6.
Hidden image revealed in the fold method (vertical and horizontal fold).
Figure 7 shows the results of applying fold method in the color-visual cryptography. Secret binary image has been hidden inside a mask. The fold direction is horizontal, and the line is in the middle of the share. The second method of visual cryptography was used to create a subliminal channel with a color image within. The result is presented in Figure 8.

Figure 7.
Fold method in color visual cryptography: C, M, Y color shares, a mask, stacking result and revealed secret binary image.

Figure 8.
Fold method in color visual cryptography: colorful shares, stacking result, and revealed secret color image.
5.2. Encryption Method
The encryption method has been tested for a text message and for an encrypted binary image. In the first case, lorem ipsum text of a maximum possible length was encrypted and hidden in halftone and color pepper images. The subpixels depend on the ciphertext, as presented in Table 3.

Table 3.
Encrypted message hidden in subpixels.
The result of hiding the encrypted binary image may be presented visually. Figure 9 shows regular shares and the result of their stacking, but also secret binary image recovered from the first share. This time, another secret image (Lena) was used because the smile picture is smaller than the cover image. This method allows an encrypted binary image of the same size as the carrier to be concealed.

Figure 9.
Regular shares, stacking result, and binary image revealed and decrypted with encryption method.
5.3. Overlapping Method
Figure 10 shows shares created with overlapping method and the result of their stacking. Subliminal channel for a single share is presented in Figure 11 in which secret parts are in opposite corners. Another subliminal channel is shown in Figure 12 in which two shares are overlapped to reveal the secret image.

Figure 10.
Regular shares and regular image generated with the overlapping method.

Figure 11.
Subliminal channel in a share with cut corners and result of their stacking.

Figure 12.
Shares with subliminal channel overlapped to reveal hidden image.
An overlapping method may also be applied to color visual cryptography. For the algorithm with a mask and three components, the result is almost identical as in Figure 11, so it will be omitted. For the algorithm with colorful shares, the results are presented in Figure 13 (single share) and Figure 14 (multiple shares). This time, a smaller image of peppers was used for the testing, and the secret shares therefore seem larger.

Figure 13.
Subliminal channel in a colorful share with cut parts and the result of their stacking.

Figure 14.
Colorful shares with subliminal channel overlapped to reveal hidden color image.
6. Discussion
Fold and overlapping methods are designed to create subliminal channels that may be recovered with printed shares. Revealing secret data is very easy if the user knows the key (overlapping offset or location and direction of the fold line), as it comes down to folding the share or stacking its parts. The maximum size of the hidden image is half of the regular image, because parts of shares with subliminal channel do not overlap. These methods may also be used with a computer, but then they have one limitation. In a (2,2) sharing scheme, white pixels are represented with the same subpixel block in both shares. This means that some fragments of shares (or even parts of a single share) will be identical. This is hard to observe with the naked eye but may be detected programmatically. In other schemes with more than two shares and different matrices, this problem does not exist.
On the other hand, the encryption method may only be applied with a computer. The advantage of this approach is that it provides maximum security. As a reminder, subpixels in visual cryptography should resemble random noise. This is satisfied when the message is encrypted. The output of the encryption algorithm has roughly the same number of 0 and 1, and their distribution is random. Additionally, the cardinalities of and from Algorithm 2 are equal; therefore, each subpixel block in a resulting share is present with an equal probability of .
Below, it is explained why randomization is needed in visual cryptography and what happens when the secret image is not encrypted. Suppose that we hid a binary image in a share by choosing subpixels with the top-left pixel equal to a current pixel of the secret image. Then, the hidden image may be revealed just by putting a template with holes on the share, which is presented in Figure 15. Unfortunately, the outline of the secret image is visible in the share, especially long lines of the hat. A lack of randomization is therefore detectable even by the human vision system.

Figure 15.
Unencrypted image hidden in a share: (a) Secret image revealed with a template.
(b) Outline of the image visible in the share.
Another example shows how encryption may be used incorrectly. In a binary image, we may conceal (image size) bits in total. Suppose the user wants to increase the capacity by using two upper pixels of each subpixel block instead of only the upper left. In an encrypted message pair, (0,0), (0,1), (1,0), and (1,1) are present with a probability of . However, the subpixel set has six elements: (0,0) is represented by one block  , (0,1) by two blocks
, (0,1) by two blocks  , (1,0) by two blocks
, (1,0) by two blocks  , and (1,1) by one block
, and (1,1) by one block  . This means that horizontal subpixel blocks would be overrepresented in a share. This may not be noticeable, but the statistical anomaly is possible to detect and may arouse suspicion.
. This means that horizontal subpixel blocks would be overrepresented in a share. This may not be noticeable, but the statistical anomaly is possible to detect and may arouse suspicion.
 , (0,1) by two blocks
, (0,1) by two blocks  , (1,0) by two blocks
, (1,0) by two blocks  , and (1,1) by one block
, and (1,1) by one block  . This means that horizontal subpixel blocks would be overrepresented in a share. This may not be noticeable, but the statistical anomaly is possible to detect and may arouse suspicion.
. This means that horizontal subpixel blocks would be overrepresented in a share. This may not be noticeable, but the statistical anomaly is possible to detect and may arouse suspicion.Sometimes, instead of using encryption, the user may want to apply pixel permutation [15]. This is performed by mixing pixels but without changing their values. The permutation technique gives randomization, but is good only when the numbers of white and black pixels are comparable. To recover the secret image, a reverse permutation should be applied.
Subliminal channels in visual cryptography show various levels of resistance to attacks. For example, the encryption method requires exact images to successfully decrypt the covert image. However, fold and overlapping techniques are based on the human vision system during decoding, so they provide robustness to some attacks. Below, results of adding random noise to shares are presented. The tests were conducted for images disturbed by 1%, 2%, 5%, 10%, and 15%. Figure 16 shows how the fold method is affected by adding more noise, and Figure 17 shows the same for the overlapping method. It may be seen that with a higher level of noise, both peppers and the smile become less clear. This attack does not seem very practical because a disturbance of the hidden image also degrades the quality of the regular image.
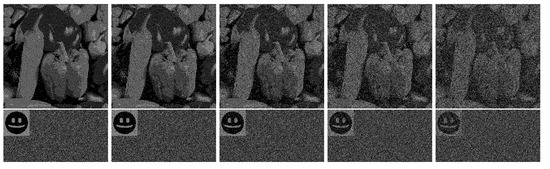
Figure 16.
Robustness of the fold technique to noise attack (overt and covert images).
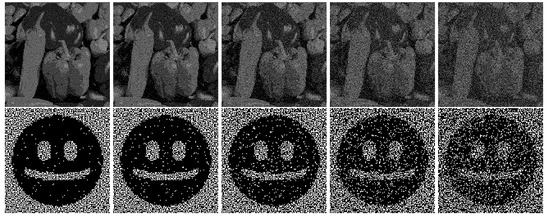
Figure 17.
Robustness of the overlapping technique to noise attack (overt and covert images).
Visual cryptography is in general not resistant to occlusion attacks. When some areas of the share are missing or covered, the overt image may only be decoded partially. This affects the subliminal channel if the secret image is placed in areas that were attacked.
Adding a subliminal channel to visual cryptography is associated with performing more operations during share generation. In fold and overlapping methods, secret shares are created at the beginning and pasted into a regular share. Then, in each iteration, we check if the current fragment of the regular share is a part of the secret share or not. A single check doubles the operations performed in the most nested loop. However, the presented algorithms may be implemented in another way; for example, in the overlapping method, instead of checking whether something belongs to the secret share, we may use separate loops for areas that are only associated with the regular share—to the right of the secret share, bottom etc. In this case, we obtain better performance at the expense of code complexity and readability. The tests have also shown that the encryption method has the best performance. This is because the encryption step is performed only once at the beginning, and the next operations are almost identical as in a standard scheme, apart from selecting a subpixel block from a different group. Furthermore, the important factor is the CPU support for AES encryption, which (according to manufacturer documentation) accelerates the performance of AES by 3 to 10× over a complete software implementation. AES was used in both versions of the algorithm, and image encryption turned out to be about 10% slower than text encryption because of the required conversion to bytes.
When compared to other methods, subliminal channels in visual cryptography show varied advantages. In standard visual cryptography, we may divide and encode a single binary image. Introducing a subliminal channel allows additional information to be concealed, which may be, depending on the selected approach, an image or any digital data. This hidden message is not visible with the naked eye, so it is suitable for steganographic purposes. In the literature, subliminal channels in visual cryptography are rarely present, but some mentions may be found in [11,12,13]. These methods generally require additional computations to reveal hidden data (except one method from [12]). On the other hand, two algorithms described in this paper allow the secret message to be recovered just by stacking shares, which proves their effectiveness. The third algorithm, which does require computational power for decryption, has another important strength of generality, as it may conceal any type of data (comparing to texts or images proposed in references). To sum up the benefits of presented subliminal channels, all of them are ready to use not only with black and white, but also with color images. This gives a lot of possible carriers and extends applicability.
7. Conclusions
This article presents three methods of creating a subliminal channel in visual cryptography. Fold and overlapping techniques are designed for printed shares. They are easy to use and do not require computing power. The encryption technique needs a computer but gives a high level of security offered by a strong encryption algorithm. It may process various types of data, including (but not limited to) text and images. The methods described also work with color-visual cryptography algorithms. The results show that the recovered images are clearly visible, and at the same time, shares still resemble random noise. This is crucial in implementing the subliminal channel, because it should be invisible during normal use. Adding secret data does not affect regular images, so the scheme is practical and may be implemented in existing systems. Another important aspect is available capacity. With the encryption method, we are able to embed a secret message of the same size as the regular image. The remaining channels offer up to half of the carrier size. In terms of robustness, fold and overlapping techniques show reasonable resistance to noise attack. The tests revealed that introduced disturbance affects not only hidden data, but also the regular image. However, both pictures are still possible to recognize, so to destroy hidden message, the attacker has to damage the regular image as well. Encryption method is vulnerable to attacks but instead is characterized by high security.
There are multiple directions of future research in this field. For example, it would be interesting to provide a physical implementation of the solutions presented and test their effectiveness. There may be more ways of data hiding than the three described, and they are still waiting to be discovered. Additionally, new channels may be invented for algorithms that use a larger number of shares. These methods use different matrices, and potential ideas should consider their subpixels’ configuration and scheme parameters. Subliminal channels may also be created in extended algorithms of visual cryptography. In such cases, shares contain irrelevant information, so these techniques may focus on fake channels that reveal false information when stacked improperly. Finally, the further development of data hiding in color visual cryptography is possible, as this topic is rarely discussed.
Subliminal channels are a great way of covert communication in an insecure environment. They find application in, for example, steganography [16], to hide secret data without suspicion. Normally, visual cryptography is used for image protection [17], and when saving computing resources is important [18,19]. This research shows another perspective and invites scientists to share new ideas of secret communication in visual cryptography.
Author Contributions
K.K.: conceptualization, methodology, software, investigation, resources, writing—original draft preparation, visualization; M.R.O.: validation, investigation, writing—review and editing, supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The USC-SIPI Image Database (a large collection of standard test images) https://sipi.usc.edu/database/database.php?volume=misc (accessed on 12 September 2022) contains “pepper” image used in this study.
Acknowledgments
We would like to thank Piotr Wiśniewski for tips on the permutation technique. Research project supported by program "Excellence initiative–research university" for the AGH University of Science and Technology.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RGB | red, green, blue |
| CMY | cyan, magenta, yellow |
Appendix A. Exemplary Implementations
| # GPLv3 https://www.gnu.org/licenses/gpl-3.0.html |
| import os |
| import numpy as np |
| subpixels = [ |
| np.array([[0,0],[1,1]]), |
| np.array([[0,1],[0,1]]), |
| np.array([[0,1],[1,0]]), |
| np.array([[1,1],[0,0]]), |
| np.array([[1,0],[1,0]]), |
| np.array([[1,0],[0,1]]) |
| ] |
| # standard (2,2) visual secret sharing scheme for binary images |
| def create_shares(img): |
| # empty shares |
| shares = [np.zeros((img.shape[0] * 2, img.shape[1] * 2), dtype=np.uint8 |
| ) for _ in range(2)] |
| # create shares |
| r = os.urandom(img.shape[0] * img.shape[1]) |
| for i in range(img.shape[0]): |
| for j in range(img.shape[1]): |
| shares[0][2*i:2*i+2,2*j:2*j+2] = subpixels[r[i*img.shape[1]+j] % 6] |
| if img[i,j] == 255: |
| shares[1][2*i:2*i+2,2*j:2*j+2] = shares[0][2*i:2*i+2,2*j:2*j+2] |
| else: |
| shares[1][2*i:2*i+2,2*j:2*j+2] = (shares[0][2*i:2*i+2,2*j:2*j+2] |
| + 1) % 2 |
| return shares |
| # fold subliminal channel |
| def fold(regular_img, secret_img, fdir, fold): |
| # check dimensions |
| if 2 * secret_img.shape[0] > regular_img.shape[0] or 2 * secret_img. |
| shape[1] > regular_img.shape[1]: |
| raise Exception(f’The shape of the secret image {secret_img.shape} |
| cannot exceed half of the regular image {regular_img.shape}!’) |
| # check fold line placing |
| if not fdir and (fold < 2 * secret_img.shape[0] or fold > 2 * |
| regular_img.shape[0] // 2): |
| raise Exception(f’The secret image could not be recovered with shapes |
| {regular_img.shape} (regular), {secret_img.shape} (secret) and |
| horizontal fold line on {fold}!’) |
| elif fdir and (fold < 2 * secret_img.shape[1] or fold > 2 * regular_img |
| .shape[1] // 2): |
| raise Exception(f’The secret image could not be recovered with shapes |
| {regular_img.shape} (regular), {secret_img.shape} (secret) and |
| vertical fold line on {fold}!’) |
| # empty shares for the regular image |
| shares = [np.zeros((regular_img.shape[0] * 2, regular_img.shape[1] * 2) |
| , dtype=np.uint8) for _ in range(2)] |
| # create shares for the secret image |
| secret_shares = create_shares(secret_img) |
| # paste secret shares |
| shares[0][:2*secret_img.shape[0],:2*secret_img.shape[1]] = |
| secret_shares[0] |
| if not fdir: |
| shares[0][2*fold-2*secret_img.shape[0]:2*fold,:2*secret_img.shape[1]] |
| = np.flipud(secret_shares[1]) |
| else: |
| shares[0][:2*secret_img.shape[0],2*fold-2*secret_img.shape[1]:2*fold] |
| = np.fliplr(secret_shares[1]) |
| # create regular shares |
| r = os.urandom(regular_img.shape[0] * regular_img.shape[1]) |
| for i in range(regular_img.shape[0]): |
| for j in range(regular_img.shape[1]): |
| # fit subpixels of share2 for existing parts of share1 |
| if np.any(shares[0][2*i:2*i+2,2*j:2*j+2]): |
| if regular_img[i,j] == 255: |
| shares[1][2*i:2*i+2,2*j:2*j+2] = shares[0][2*i:2*i+2,2*j:2*j+2] |
| else: |
| shares[1][2*i:2*i+2,2*j:2*j+2] = (shares[0][2*i:2*i+2,2*j:2*j |
| +2] + 1) % 2 |
| # for unused parts create shares normally |
| else: |
| shares[0][2*i:2*i+2,2*j:2*j+2] = subpixels[r[i*regular_img.shape |
| [1]+j] % 6 |
| if regular_img[i,j] == 255: |
| shares[1][2*i:2*i+2,2*j:2*j+2] = shares[0][2*i:2*i+2,2*j:2*j+2] |
| else: |
| shares[1][2*i:2*i+2,2*j:2*j+2] = (shares[0][2*i:2*i+2,2*j:2*j |
| +2] + 1) % 2 |
| return shares |
| # encryption subliminal channel with a text (negative) |
| def encryption_text(regular_img, message, iv, key): |
| if len(message) * 8 > regular_img.shape[0] * regular_img.shape[1]: |
| raise Exception(f’The message is too long ({len(message) * 8} bits), |
| the capacity is {regular_img.shape[0] * regular_img.shape[1]} |
| bits!’) |
| from cryptography.hazmat.primitives.ciphers import Cipher, algorithms, |
| modes |
| message += b"x00" |
| if len(message) % 16 != 0: |
| message += bytes(16-(len(message) % 16)) |
| # encrypt secret message |
| cipher = Cipher(algorithms.AES(key), modes.CBC(iv)) |
| encryptor = cipher.encryptor() |
| ct = encryptor.update(message) + encryptor.finalize() |
| # create shares |
| shares = [np.zeros((regular_img.shape[0] * 2, regular_img.shape[1] * 2) |
| , dtype=np.uint8) for _ in range(2)] |
| r = os.urandom(regular_img.shape[0] * regular_img.shape[1]) |
| l = 0 |
| for i in range(regular_img.shape[0]): |
| for j in range(regular_img.shape[1]): |
| if l < len(ct)*8: |
| bit = (ct[l//8] >> (7–(l%8))) & 1 |
| shares[0][2*i:2*i+2,2*j:2*j+2] = subpixels[(r[l] % 3) + 3*bit] |
| if regular_img[i][j] == 255: |
| shares[1][2*i:2*i+2,2*j:2*j+2] = shares[0][2*i:2*i+2,2*j:2*j+2] |
| else: |
| shares[1][2*i:2*i+2,2*j:2*j+2] = (shares[0][2*i:2*i+2,2*j:2*j |
| +2] + 1) % 2 |
| l += 1 |
| else: |
| shares[0][2*i:2*i+2,2*j:2*j+2] = subpixels[r[i*regular_img.shape |
| [1]+j] % 6] |
| if regular_img[i,j] == 255: |
| shares[1][2*i:2*i+2,2*j:2*j+2] = shares[0][2*i:2*i+2,2*j:2*j+2] |
| else: |
| shares[1][2*i:2*i+2,2*j:2*j+2] = (shares[0][2*i:2*i+2,2*j:2*j |
| +2] + 1) % 2 |
| return shares |
| # encryption subliminal channel with a binary image (negative) |
| def encryption(regular_img, secret_img, iv, key): |
| if secret_img.shape[0] != regular_img.shape[0] or secret_img.shape[1] |
| != regular_img.shape[1]: |
| raise Exception(f’The shapes of secret and regular images should be |
| equal, are: {secret_img.shape} and {regular_img.shape}!’) |
| from cryptography.hazmat.primitives.ciphers import Cipher, algorithms, |
| modes |
| from functools import reduce |
| # create secret message |
| secret_img = secret_img.flatten() // 255 |
| secret = bytes([reduce(lambda x,y: (x << 1) + y, secret_img[8*i:8*i+8]) |
| for i in range(len(secret_img)//8)]) |
| if len(secret) % 16 != 0: |
| secret += bytes(16-(len(secret) % 16)) |
| # encrypt secret message |
| cipher = Cipher(algorithms.AES(key), modes.CBC(iv)) |
| encryptor = cipher.encryptor() |
| ct = encryptor.update(secret) + encryptor.finalize() |
| # create shares |
| shares = [np.zeros((regular_img.shape[0] * 2, regular_img.shape[1] * 2) |
| , dtype=np.uint8) for _ in range(2)] |
| r = os.urandom(regular_img.shape[0] * regular_img.shape[1]) |
| l = 0 |
| for i in range(regular_img.shape[0]): |
| for j in range(regular_img.shape[1]): |
| bit = (ct[l//8] >> (7-(l%8))) & 1 |
| shares[0][2*i:2*i+2,2*j:2*j+2] = subpixels[(r[l] % 3) + 3*bit] |
| if regular_img[i][j] == 255: |
| shares[1][2*i:2*i+2,2*j:2*j+2] = shares[0][2*i:2*i+2,2*j:2*j+2] |
| else: |
| shares[1][2*i:2*i+2,2*j:2*j+2] = (shares[0][2*i:2*i+2,2*j:2*j+2] |
| + 1) % 2 |
| l += 1 |
| return shares |
| # overlapping subliminal channel without offset (single image) |
| def overlapping1(regular_img, secret_img): |
| # check dimensions |
| if 2 * secret_img.shape[0] > regular_img.shape[0] or 2 * secret_img. |
| shape[1] > regular_img.shape[1]: |
| raise Exception(f’The shape of the secret image {secret_img.shape} |
| cannot exceed half of the regular image {regular_img.shape}!’) |
| # empty shares for the regular image |
| shares = [np.zeros((regular_img.shape[0] * 2, regular_img.shape[1] * 2) |
| , dtype=np.uint8) for _ in range(2)] |
| # create shares for the secret image |
| secret_shares = create_shares(secret_img) |
| # paste secret shares in corners |
| shares[0][:secret_shares[0].shape[0],:secret_shares[0].shape[1]] = |
| secret_shares[0] |
| shares[0][-secret_shares[1].shape[0]:,-secret_shares[1].shape[1]:] = |
| secret_shares[1] |
| # create regular shares |
| r = os.urandom(regular_img.shape[0] * regular_img.shape[1]) |
| for i in range(regular_img.shape[0]): |
| for j in range(regular_img.shape[1]): |
| # fit subpixels of share2 for existing parts of share1 |
| if np.any(shares[0][2*i:2*i+2,2*j:2*j+2]): |
| if regular_img[i,j] == 255: |
| shares[1][2*i:2*i+2,2*j:2*j+2] = shares[0][2*i:2*i+2,2*j:2*j+2] |
| else: |
| shares[1][2*i:2*i+2,2*j:2*j+2] = (shares[0][2*i:2*i+2,2*j:2*j |
| +2] + 1) % 2 |
| # for unused parts create shares normally |
| else: |
| shares[0][2*i:2*i+2,2*j:2*j+2] = subpixels[r[i*regular_img.shape |
| [1]+j] % 6] |
| if regular_img[i,j] == 255: |
| shares[1][2*i:2*i+2,2*j:2*j+2] = shares[0][2*i:2*i+2,2*j:2*j+2] |
| else: |
| shares[1][2*i:2*i+2,2*j:2*j+2] = (shares[0][2*i:2*i+2,2*j:2*j |
| +2] + 1) % 2 |
| return shares |
| # overlapping subliminal channel without offset (two images) |
| def overlapping2(regular_img, secret_img): |
| # check dimensions |
| if 2 * secret_img.shape[0] > regular_img.shape[0] or 2 * secret_img. |
| shape[1] > regular_img.shape[1]: |
| raise Exception(f’The shape of the secret image {secret_img.shape} |
| cannot exceed half of the regular image {regular_img.shape}!’) |
| # empty shares for the regular image |
| shares = [np.zeros((regular_img.shape[0] * 2, regular_img.shape[1] * 2) |
| , dtype=np.uint8) for _ in range(2)] |
| # create shares for the secret image |
| secret_shares = create_shares(secret_img) |
| # paste secret shares in corners |
| shares[0][:secret_shares[0].shape[0],:secret_shares[0].shape[1]] = |
| secret_shares[0] |
| shares[1][-secret_shares[1].shape[0]:,-secret_shares[1].shape[1]:] = |
| secret_shares[1] |
| # create regular shares |
| r = os.urandom(regular_img.shape[0] * regular_img.shape[1]) |
| for i in range(regular_img.shape[0]): |
| for j in range(regular_img.shape[1]): |
| # fit subpixels of share2 for existing parts of share1 |
| if np.any(shares[0][2*i:2*i+2,2*j:2*j+2]): |
| if regular_img[i,j] == 255: |
| shares[1][2*i:2*i+2,2*j:2*j+2] = shares[0][2*i:2*i+2,2*j:2*j+2] |
| else: |
| shares[1][2*i:2*i+2,2*j:2*j+2] = (shares[0][2*i:2*i+2,2*j:2*j |
| +2] + 1) % 2 |
| # fit subpixels of share1 for existing parts of share2 |
| elif np.any(shares[1][2*i:2*i+2,2*j:2*j+2]): |
| if regular_img[i,j] == 255: |
| shares[0][2*i:2*i+2,2*j:2*j+2] = shares[1][2*i:2*i+2,2*j:2*j+2] |
| else: |
| shares[0][2*i:2*i+2,2*j:2*j+2] = (shares[1][2*i:2*i+2,2*j:2*j |
| +2] + 1) % 2 |
| # for unused parts create shares normally |
| else: |
| shares[0][2*i:2*i+2,2*j:2*j+2] = subpixels[r[i*regular_img.shape |
| [1]+j] % 6] |
| if regular_img[i,j] == 255: |
| shares[1][2*i:2*i+2,2*j:2*j+2] = shares[0][2*i:2*i+2,2*j:2*j+2] |
| else: |
| shares[1][2*i:2*i+2,2*j:2*j+2] = (shares[0][2*i:2*i+2,2*j:2*j |
| +2] + 1) % 2 |
| return shares |
References
- Simmons, G.J. The subliminal channel and digital signature. In Proceedings of the Eurocrypt 84 Workshop on Advances in Cryptology: Theory and Application of Cryptographic Techniques, Lecture Notes in Computer Science, Paris, France, 9–11 April 1984; Volume 209, pp. 364–378. [Google Scholar]
- Naor, M.; Shamir, A. Visual Cryptography. Advances in Cryptology–EUROCRYPT ’94, Proceedings; Springer: Perugia, Italy, 1994; Volume 950, pp. 1–12. [Google Scholar]
- Shamir, A. How to Share a Secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Yourmaran, R.; Adler, A.; Miri, A. An Improved Visual Cryptography Scheme For Secret Hiding. In Proceedings of the 23rd Biennial Symposium on Communications, Kingston, ON, Canada, 30 May–1 June 2006; pp. 340–343. [Google Scholar]
- Rao, Y.S.; Sukonkina, Y.; Bhagwati, C.; Singh, U.K. Fingerprint based authentication application using visual cryptography methods. In Proceedings of the TENCON 2008—2008 IEEE Region 10 Conference, Hyderabad, India, 19–21 November 2008; pp. 1–5. [Google Scholar]
- Ateniese, G.; Blundo, C.; De Santis, A.; Stinson, D.R. Extended capabilities for visual cryptography. Theor. Comput. Sci. 2001, 250, 143–161. [Google Scholar] [CrossRef]
- Hou, Y.C. Visual cryptography for color images. Pattern Recognit. 2003, 36, 1619–1629. [Google Scholar] [CrossRef]
- De Prisco, R.; De Santis, A. Color visual cryptography schemes for black and white secret images. Theor. Comput. Sci. 2013, 510, 62–86. [Google Scholar] [CrossRef]
- Verheul, E.; van Tilborg, H. Constructions and Properties of k out of n visual secret sharing schemes. Des. Codes Cryptogr. 1997, 11, 179–196. [Google Scholar] [CrossRef]
- Weir, J.P. Visual Cryptography and Its Applications; BookBoon: London, UK, 2012. [Google Scholar]
- Chen, T.; Wu, C.S.; Lee, W.B. A Novel Subliminal Channel Found in Visual Cryptography and Its Application to Image Hiding. In Proceedings of the Third International Conference on Intelligent Information Hiding and Multimedia Signal Processing (IIH-MSP 2007), Kaohsiung, Taiwan, 26–28 November 2007. [Google Scholar]
- Fang, W.P.; Lin, J.C. Visual cryptography with extra ability of hiding confidential data. J. Electron. Imaging 2006, 15, 023020. [Google Scholar] [CrossRef][Green Version]
- Chang, C.C.; Chuang, J.C.; Lin, P.Y. Sharing a secret two-tone image in two gray-level images. In Proceedings of the 11th International Conference on Parallel and Distributed Systems, Fukuoka, Japan, 20–22 July 2005; Volume 2, pp. 300–304. [Google Scholar]
- Crocker, L.D.; Boulay, P.; Morra, M. Digital Halftoning. Computer Lab and Reference Library, June 1991. Available online: https://gist.githubusercontent.com/tcoppex/d6d2f3dad05a806a6068b860750c8895/raw/437843dba782af9dcce89838c0b48b38644fbb5f/DHALF.TXT (accessed on 30 March 2022).
- Koptyra, K.; Ogiela, M.R. Key generation for multi-secret steganography. In Proceedings of the 2nd International Conference on Information Science and Security (ICISS), Seoul, Korea, 14–16 December 2015; pp. 1–4. [Google Scholar]
- Koptyra, K.; Ogiela, M.R. Steganography in IoT: Information Hiding with APDS-9960 Proximity and Gestures Sensor. Sensors 2022, 22, 2612. [Google Scholar] [CrossRef] [PubMed]
- Castiglione, A.; Santis, A.D.; Pizzolante, R.; Castiglione, A.; Loia, V.; Palmieri, F. On the Protection of fMRI Images in Multi-domain Environments. In Proceedings of the 29th International Conference on Advanced Information Networking and Applications, Gwangju, Korea, 24–27 March 2015; pp. 476–481. [Google Scholar] [CrossRef]
- Pizzolante, R.; Carpentieri, B.; Castiglione, A.; Castiglione, A.; Palmieri, F. Text Compression and Encryption through Smart Devices for Mobile Communication. In Proceedings of the Seventh International Conference on Innovative Mobile and Internet Services in Ubiquitous Computing, Taichung, Taiwan, 3–5 July 2013; pp. 672–677. [Google Scholar] [CrossRef]
- Albano, P.; Bruno, A.; Carpentieri, B.; Castiglione, A.; Castiglione, A.; Palmieri, F.; Pizzolante, R.; You, I. A Secure Distributed Video Surveillance System Based on Portable Devices. In Multidisciplinary Research and Practice for Information Systems; CD-ARES 2012, Lecture Notes in Computer Science; Quirchmayr, G., Basl, J., You, I., Xu, L., Weippl, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7465. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).




























































