Designing a Practical Code-Based Signature Scheme from Zero-Knowledge Proofs with Trusted Setup
Abstract
:1. Introduction
Our Contribution
2. Preliminaries
| a | a scalar |
| a vector | |
| a matrix | |
| a function or algorithm | |
| a protocol | |
| the identity matrix | |
| a security parameter | |
| the set of integers |
2.1. Coding Theory
2.2. Technical Tools
- I. Setup: the helper takes a random seed as input, generates some auxiliary information , then sends the former to the prover and the latter to the verifier.
- II. Commitment: the prover uses , in addition to his secret , to create a commitment and sends it to the verifier.
- III. Challenge: the verifier selects a random challenge from the challenge space and sends it to the prover.
- IV. Response: the prover computes a response using (in addition to his previous information), and sends it to the verifier.
- V. Verification: the verifier checks the correctness of , then checks that this was correctly formed using , and accepts or rejects accordingly.
- Completeness: if all parties follow the protocol correctly, the verifier always accepts.
- 2-Special Soundness: given an adversary that outputs two valid transcripts and with , it is possible to extract a valid secret . Note that this is not necessarily the one held by the prover, but could in principle be any witness for the relation .
- Special Honest-Verifier Zero-Knowledge: there exists a probabilistic polynomial-time simulator algorithm that is capable, on input , to output a transcript which is computationally indistinguishable from one obtained via an honest execution of the protocol.
3. The New Scheme
3.1. Security
| Algorithm 1: Our Proposed Sigma Protocol with Helper |
Public Data Parameters , a full-rank matrix and a commitment function . Private Key A vector . Public Key The syndrome . I. Setup () Input: Uniform random . 1. Generate and from . 2. For all : i. Generate randomness from . ii. Compute . 3. Set . II. Commitment () Input: and . 1. Regenerate and from . 2. Determine isometry such that . 3. Generate randomness . 4. Compute . III. Challenge () Input: - 1. Sample uniform random . 2. Set . IV. Response () Input: and . 1. Regenerate from . 2. Compute . 3. Set . V. Verification () Input: and . 1. Compute . 2. Check that and that is an isometry. 3. Check that . 4. Output 1 (accept) if both checks are successful, or 0 (reject) otherwise. |
3.2. Removing the Helper
| Algorithm 2: Generic Transformation to Transform Sigma Protocol with Helper into a Zero-Knowledge Proof |
Public Data, Private Key, Public Key Same as in Figure 1. I. Commitment (Prover) Input: Public data and private key. 1. For all : i. Sample uniform random . ii. Compute . iii. Compute . 2. Send and to verifier. II. Challenge (Verifier) Input: - 1. Sample uniform random index . 2. Sample uniform random challenge . 3. Set . III. Response (Prover) Input: and . 1. Compute . 3. Send and to verifier. IV. Verification (Verifier) Input: and . 1. For all : i. Compute . ii. Check that this is equal to . 2. Set if all checks are successful, and otherwise. 3. Compute . 4. Output . |
3.3. Obtaining a Signature Scheme
| Algorithm 3: The Fiat–Shamir Transformation |
Public Data, Private Key, Public Key Same as in , plus a collision-resistant hash function . I. Signature (Signer) Input: Public data, private key and message . 1. Generate commitment as in . 2. Compute challenge . 3. Produce response as in . 4. Output signature . II. Verification (Verifier) Input: Public data, public key, message and signature . 1. Parse as . 2. Compute challenge . 3. Perform verification as in . 4. Accept or reject accordingly. |
4. Communication Cost and Optimizations
- N copies of the auxiliary information , each consisting of q hash values.
- N copies of the commitment , each consisting of a single hash value.
- The index I and the challenge z, respectively an integer and a field element.
- The protocol response , consisting of two -bit randomness strings, an isometry, and a length-n vector with elements in .
- The seeds , each a -bit string.
4.1. Protocol Commitments
4.2. Auxiliary Information
4.3. Seeds
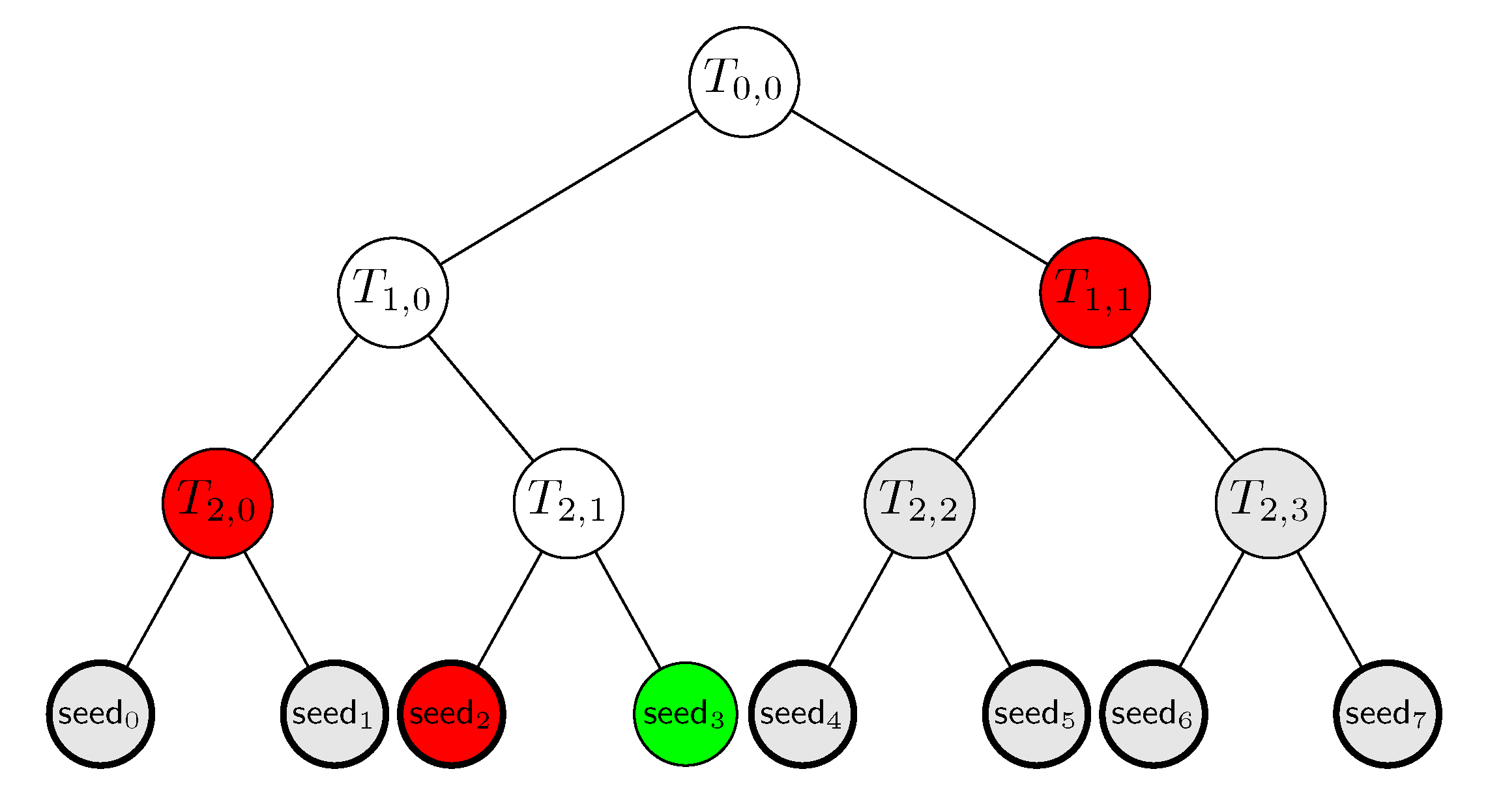
4.4. Executions
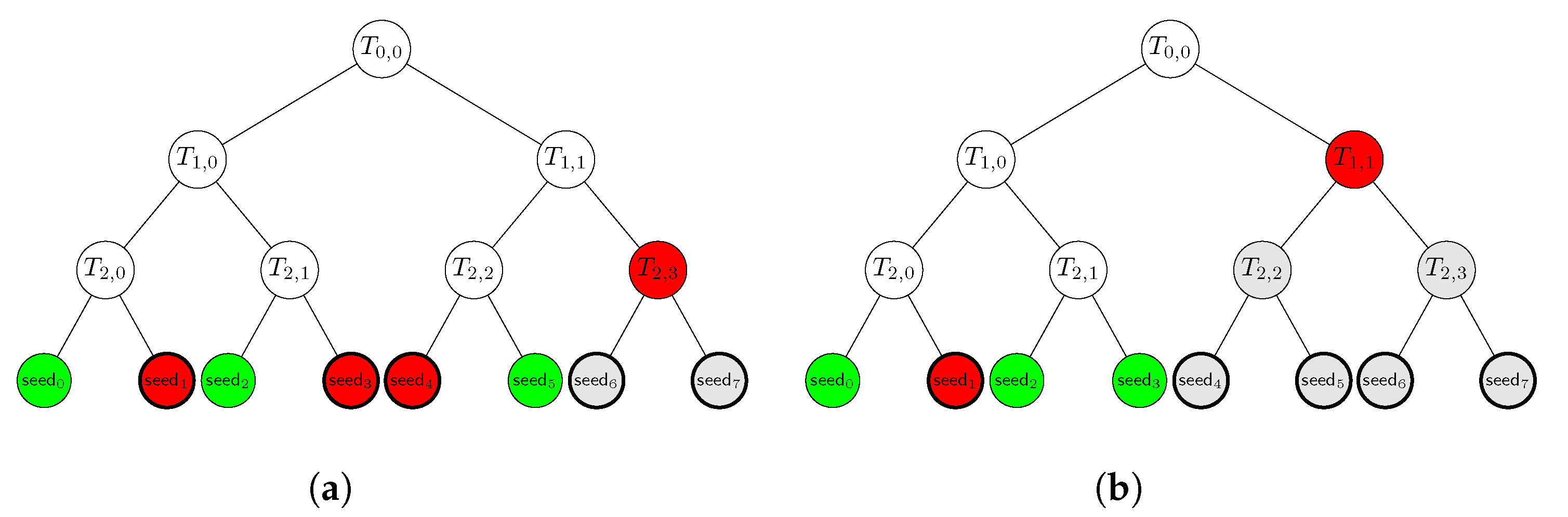
5. Practical Considerations
| Algorithm 4: The Optimized Zero-Knowledge Proof |
Public Data Parameters , a full-rank matrix , a commitment function and a collision-resistant hash function . Private Key A vector . Public Key The syndrome . I. Commitment (Prover) Input: and . 1. Sample uniform random . 2. Compute . 3. For all : i. Compute . ii. Build tree and call its root. 4. Compute . 5. For all : i. Compute . 6. Build tree and call its root. 7. Send h and to verifier. II. Challenge (Verifier) Input: - 1. Sample uniform random with . 2. For all : i. Sample uniform random . 3. Set . III. Response (Prover) Input: and . 1. For all : i. Compute . 2. Send and to verifier. IV. Verification (Verifier) Input: and . 1. For all : i. Compute . ii. Compute . iii. Compute . iv. Check that this is equal to . 2. Set if all checks are successful, and otherwise. 3. For all : i. Compute . ii. Compute . 4. For all : i. Recover from . ii. Compute . iii. Build tree and call its root. 5. Compute 6. Set if and otherwise. 7. Output . |
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shor, P. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM J. Comput. 1997, 26, 1484–1509. [Google Scholar] [CrossRef] [Green Version]
- McEliece, R. A Public-Key Cryptosystem Based On Algebraic Coding Theory. Deep Space Netw. Prog. Rep. 1978, 44, 114–116. [Google Scholar]
- Albrecht, M.R.; Bernstein, D.J.; Chou, T.; Cid, C.; Gilcher, J.; Lange, T.; Maram, V.; von Maurich, I.; Misoczki, R.; Niederhagen, R.; et al. Classic McEliece: Conservative Code-Based Cryptography. In NIST Post-Quantum Standardization, 3rd Round; 2021; Available online: https://www.hyperelliptic.org/tanja/vortraege/mceliece-round-3.pdf (accessed on 9 December 2021).
- 2017. NIST Call for Standardization. Available online: https://csrc.nist.gov/Projects/Post-Quantum-Cryptography (accessed on 9 December 2021).
- Melchor, C.A.; Aragon, N.; Bettaieb, S.; Bidoux, L.; Blazy, O.; Bos, J.; Deneuville, J.C.; Arnaud Dion, I.S.; Gaborit, P.; Lacan, J.; et al. HQC: Hamming Quasi-Cyclic. In NIST Post-Quantum Standardization, 3rd Round; 2021; Available online: https://pqc-hqc.org/doc/hqc-specification_2021-06-06.pdf (accessed on 9 December 2021).
- Aragon, N.; Barreto, P.S.L.M.; Bettaieb, S.; Bidoux, L.; Blazy, O.; Deneuville, J.C.; Gaborit, P.; Gueron, S.; Güneysu, T.; Melchor, C.A.; et al. BIKE: Bit Flipping Key Encapsulation. In NIST Post-Quantum Standardization, 3rd Round; 2021; Available online: https://bikesuite.org/files/v4.2/BIKE_Spec.2021.07.26.1.pdf (accessed on 9 December 2021).
- 2021. NIST Status Update. Available online: https://csrc.nist.gov/Presentations/2021/status-update-on-the-3rd-round (accessed on 9 December 2021).
- Stern, J. A new identification scheme based on syndrome decoding. In Advances in Cryptology—CRYPTO’ 93; Stinson, D.R., Ed.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 13–21. [Google Scholar]
- Fiat, A.; Shamir, A. How to prove yourself: Practical solutions to identification and signature problems. In CRYPTO; Springer: Berlin/Heidelberg, Germany, 1986; pp. 186–194. [Google Scholar]
- Véron, P. Improved identification schemes based on error-correcting codes. Appl. Algebra Eng. Commun. Comput. 1997, 8, 57–69. [Google Scholar] [CrossRef] [Green Version]
- Gaborit, P.; Girault, M. Lightweight code-based identification and signature. In Proceedings of the 2007 IEEE International Symposium on Information Theory, Nice, France, 24–29 June 2007; pp. 191–195. [Google Scholar]
- Cayrel, P.L.; Véron, P.; El Yousfi Alaoui, S.M. A zero-knowledge identification scheme based on the q-ary syndrome decoding problem. In Selected Areas in Cryptography; Springer: Berlin/Heidelberg, Germany, 2011; pp. 171–186. [Google Scholar]
- Courtois, N.T.; Finiasz, M.; Sendrier, N. How to Achieve a McEliece-Based Digital Signature Scheme. Lect. Notes Comput. Sci. 2001, 2248, 157–174. [Google Scholar]
- Debris-Alazard, T.; Sendrier, N.; Tillich, J.P. Wave: A new family of trapdoor one-way preimage sampleable functions based on codes. In ASIACRYPT; Springer: Berlin/Heidelberg, Germany, 2019; pp. 21–51. [Google Scholar]
- Biasse, J.F.; Micheli, G.; Persichetti, E.; Santini, P. LESS is More: Code-Based Signatures Without Syndromes. In AFRICACRYPT; Nitaj, A., Youssef, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 45–65. [Google Scholar]
- Barenghi, A.; Biasse, J.F.; Persichetti, E.; Santini, P. LESS-FM: Fine-tuning Signatures from a Code-based Cryptographic Group Action. PQCrypto 2021, 2021, 23–43. [Google Scholar]
- Beullens, W. Not Enough LESS: An Improved Algorithm for Solving Code Equivalence Problems over . In Proceedings of the International Conference on Selected Areas in Cryptography, Halifax, NS, Canada, 21–23 October 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 387–403. [Google Scholar]
- Gaborit, P.; Ruatta, O.; Schrek, J.; Zémor, G. RankSign: An efficient signature algorithm based on the rank metric. In International Workshop on Post-Quantum Cryptography; Springer: Berlin/Heidelberg, Germany, 2014; pp. 88–107. [Google Scholar]
- Aragon, N.; Blazy, O.; Gaborit, P.; Hauteville, A.; Zémor, G. Durandal: A Rank Metric Based Signature Scheme. In Advances in Cryptology–EUROCRYPT 2019; Ishai, Y., Rijmen, V., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 728–758. [Google Scholar]
- Baldi, M.; Battaglioni, M.; Chiaraluce, F.; Horlemann-Trautmann, A.L.; Persichetti, E.; Santini, P.; Weger, V. A new path to code-based signatures via identification schemes with restricted errors. arXiv 2020, arXiv:2008.06403. [Google Scholar]
- Debris-Alazard, T.; Tillich, J.P. Two attacks on rank metric code-based schemes: RankSign and an IBE scheme. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Brisbane, Australia, 2–6 December 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 62–92. [Google Scholar]
- Bardet, M.; Briaud, P. An algebraic approach to the Rank Support Learning problem. arXiv 2021, arXiv:2103.03558. [Google Scholar]
- Katz, J.; Kolesnikov, V.; Wang, X. Improved non-interactive zero knowledge with applications to post-quantum signatures. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, Toronto, ON, Canada, 15–19 October 2018; pp. 525–537. [Google Scholar]
- Beullens, W. Sigma Protocols for MQ, PKP and SIS, and Fishy Signature Schemes. Eurocrypt 2020, 12107, 183–211. [Google Scholar]
- Berlekamp, E.; McEliece, R.; van Tilborg, H. On the inherent intractability of certain coding problems (Corresp.). IEEE Trans. Inf. Theory 1978, 24, 384–386. [Google Scholar] [CrossRef]
- Barg, S. Some new NP-complete coding problems. Probl. Peredachi Informatsii 1994, 30, 23–28. [Google Scholar]
- Beullens, W. Sigma protocols for MQ, PKP and SIS, and fishy signature schemes. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 10–14 May 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 183–211. [Google Scholar]
- Abdalla, M.; An, J.H.; Bellare, M.; Namprempre, C. From identification to signatures via the Fiat-Shamir transform: Minimizing assumptions for security and forward-security. In EUROCRYPT; Springer: Berlin/Heidelberg, Germany, 2002; pp. 418–433. [Google Scholar]
- Kiltz, E.; Lyubashevsky, V.; Schaffner, C. A concrete treatment of Fiat-Shamir signatures in the quantum random-oracle model. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Tel Aviv, Israel, 29 April–3 May 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 552–586. [Google Scholar]
- Don, J.; Fehr, S.; Majenz, C.; Schaffner, C. Security of the Fiat-Shamir Transformation in the Quantum Random-Oracle Model. In CRYPTO; Springer: Cham, Switzerland, 2019; pp. 356–383. [Google Scholar]
- Liu, Q.; Zhandry, M. Revisiting Post-quantum Fiat-Shamir. In Advances in Cryptology-CRYPTO 2019; Springer: Cham, Switzerland, 2019; pp. 326–355. [Google Scholar]
- Unruh, D. Computationally binding quantum commitments. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Vienna, Austria, 8–12 May 2016; pp. 497–527. [Google Scholar]
- Fehr, S. Classical proofs for the quantum collapsing property of classical hash functions. In Proceedings of the Theory of Cryptography Conference, Panaji, India, 11–14 November 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 315–338. [Google Scholar]
- Beullens, W.; Katsumata, S.; Pintore, F. Calamari and Falafl: Logarithmic (linkable) ring signatures from isogenies and lattices. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Daejeon-gu, Korea, 7–11 December 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 464–492. [Google Scholar]
- Prange, E. The use of information sets in decoding cyclic codes. IRE Trans. Inf. Theory 1962, 8, 5–9. [Google Scholar] [CrossRef]
- Peters, C. Information-set decoding for linear codes over . In International Workshop on Post-Quantum Cryptography; Springer: Berlin/Heidelberg, Germany, 2010; pp. 81–94. [Google Scholar]
- Bellini, E.; Caullery, F.; Gaborit, P.; Manzano, M.; Mateu, V. Improved Veron Identification and Signature Schemes in the Rank Metric. In Proceedings of the 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019; pp. 1872–1876. [Google Scholar]
- Lyubashevsky, V. Fiat-Shamir with Aborts: Applications to Lattice and Factoring-Based Signatures. In ASIACRYPT; Springer: Berlin/Heidelberg, Germany, 2009; pp. 598–616. [Google Scholar]
- Bardet, M.; Briaud, P.; Bros, M.; Gaborit, P.; Neiger, V.; Ruatta, O.; Tillich, J.P. An algebraic attack on rank metric code-based cryptosystems. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 10–14 May 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 64–93. [Google Scholar]
- Bardet, M.; Bros, M.; Cabarcas, D.; Gaborit, P.; Perlner, R.; Smith-Tone, D.; Tillich, J.P.; Verbel, J. Improvements of Algebraic Attacks for solving the Rank Decoding and MinRank problems. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Daejeon-gu, Korea, 7–11 December 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 507–536. [Google Scholar]
- Feneuil, T.; Joux, A.; Rivain, M. Shared Permutation for Syndrome Decoding: New Zero-Knowledge Protocol and Code-Based Signature. Cryptology ePrint Archive: Report 2021/1576. Available online: https://eprint.iacr.org/2021/1576 (accessed on 9 December 2021).
- Gueron, S.; Persichetti, E.; Santini, P. Designing a Practical Code-Based Signature Scheme from Zero-Knowledge Proofs with Trusted Setup. Cryptology ePrint Archive: Report 2021/1020. Available online: https://eprint.iacr.org/2021/1020 (accessed on 9 December 2021).
| M | s | q | n | k | w | Pk Size (B) | Signature Size (kB) |
|---|---|---|---|---|---|---|---|
| 512 | 23 | 128 | 220 | 101 | 90 | 104.2 | 24.6 |
| 1024 | 19 | 256 | 207 | 93 | 90 | 114 | 22.2 |
| 2048 | 16 | 512 | 196 | 92 | 84 | 117 | 20.2 |
| 4096 | 14 | 1024 | 187 | 90 | 80 | 121.3 | 19.5 |
| Scheme | Security Level | Public Data | Public Key | Sig. | PK + Sig. | Security Assumption |
|---|---|---|---|---|---|---|
| Stern | 80 | 18.43 | 0.048 | 113.57 | 113.62 | Low-weight Hamming |
| Veron | 80 | 18.43 | 0.096 | 109.06 | 109.16 | Low-weight Hamming |
| CVE | 80 | 5.18 | 0.072 | 66.44 | 66.54 | Low-weight Hamming |
| Wave | 128 | - | 3205 | 1.04 | 3206.04 | High-weight Hamming |
| cRVDC | 125 | 0.050 | 0.15 | 22.48 | 22.63 | Low-weight Rank |
| Durandal-I | 128 | 307.31 | 15.24 | 4.06 | 19.3 | Low-weight Rank |
| Durandal-II | 128 | 419.78 | 18.60 | 5.01 | 23.61 | Low-weight Rank |
| LESS-FM-I | 128 | 9.78 | 9.78 | 15.2 | 24.97 | Linear Equivalence |
| LESS-FM-II | 128 | 13.71 | 205.74 | 5.25 | 210.99 | Permutation Equivalence |
| LESS-FM-III | 128 | 11.57 | 11.57 | 10.39 | 21.96 | Permutation Equivalence |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gueron, S.; Persichetti, E.; Santini, P. Designing a Practical Code-Based Signature Scheme from Zero-Knowledge Proofs with Trusted Setup. Cryptography 2022, 6, 5. https://doi.org/10.3390/cryptography6010005
Gueron S, Persichetti E, Santini P. Designing a Practical Code-Based Signature Scheme from Zero-Knowledge Proofs with Trusted Setup. Cryptography. 2022; 6(1):5. https://doi.org/10.3390/cryptography6010005
Chicago/Turabian StyleGueron, Shay, Edoardo Persichetti, and Paolo Santini. 2022. "Designing a Practical Code-Based Signature Scheme from Zero-Knowledge Proofs with Trusted Setup" Cryptography 6, no. 1: 5. https://doi.org/10.3390/cryptography6010005
APA StyleGueron, S., Persichetti, E., & Santini, P. (2022). Designing a Practical Code-Based Signature Scheme from Zero-Knowledge Proofs with Trusted Setup. Cryptography, 6(1), 5. https://doi.org/10.3390/cryptography6010005







