Abstract
This paper formalises the security of programmable secure computation focusing on simplifying security proofs of new algorithms for existing computation frameworks. Security of the frameworks is usually well established but the security proofs of the algorithms are often more intuitive than rigorous. This work specifies a transformation from the usual hybrid execution model to an abstract model that is closer to the intuition. We establish various preconditions that are satisfied by natural secure computation frameworks and protocols, thus showing that mostly the intuitive proofs suffice. More elaborate protocols might still need additional proof details.
1. Introduction
Over the years of secure multiparty computation (MPC) research many different frameworks [1,2,3,4,5,6,7] and applications [8,9,10,11,12,13] have been developed. Among the applications, some are tailored for a specific framework, others are more general and simply assume some underlying computation capabilities. Especially, when developing a new application or algorithm for MPC, it would be best if we had standard notions to use to specify the requirements (types of functionalities, data types and security assumptions) that the algorithm has on the MPC frameworks. This would give basis for the applicability of the algorithm as well as the security proof of the algorithm.
The security proofs and claims of the programmable MPC frameworks are usually well documented and follow the best practices of universally composable security [14]. Therefore, we are given guarantees that everything from protocol inputs until protocol outputs remains secure independently of the context where the protocol is being used. However, the standard set of operations in MPC frameworks is quite small, essentially supporting linear combinations, multiplication, giving inputs and getting outputs. In addition, these frameworks are often specified as one monolithic secure functionality, for example, arithmetic black box (ABB) [15]. ABB is essentially a representation of a secure computer where you can put values and give computation commands.
It is a separate task to build all other necessary algorithms and building blocks in order to achieve bigger applications like secure machine learning. Building full-fledged applications, like the equality check in Algorithm 1, that do not release intermediate values, is straightforward to model in ABB. In this case, you can give this code as commands to the ABB that would give out the desired outcome. However, note that instead of the shared values, the inputs would be private inputs of the participants. If the ABB is secure, then the output z is computed securely and, for example, if the ABB operates on finite fields, then this protocol is also correct. Formally, there is no good way to add primitive operations inside the ABB as there is no access to the internal representation of the intermediate data. Whenever a new operation is added, we should formally prove the security of the whole ABB. Still, ABB is the best abstraction to define quite generic new primitives for secure computation, for real-world uses see [16,17].
Many algorithms can be sped up by releasing intermediate values. For example, consider the sorting algorithm in Algorithm 2 where the comparison result b is published in the middle of the algorithm and elements are ordered based on this. The value b can be seen as given out from the ABB and then a new command can be given to reorder the values as necessary. In addition, there is no way in ABB to actually return the intermediate representation of the secure values and . Therefore, the effect of such a protocol is such that there are intermediate representations of m and k inside the ABB but the order and its use is defined by the follow up commands sent to the ABB. In this case, the security of the ABB is not necessarily sufficient to give security guarantees. Additional reasoning must be carried out, as the published values and actions based on them happen outside of the ABB.
| Algorithm 1 Equality Check |
| Input: Two shared values and Output: 0 if , non-zero value otherwise Generate a shared random non-zero value . Compute . Publish as z. return z |
Our view of secure computation adds an explicit way to consider such choices and published values as well as to consider each operation such as comparison or addition individually, not just as one functionality. In short, our goal is to define an abstract execution environment for secure protocols where the only details that are relevant for the security analysis are necessary. These details are those that can be easily seen from algorithms written down in pseudocode like our two examples. One considers secure values , different computations can be carried out with them and a special focus is on the published values x. For example, if some comparison-based sorting algorithm is defined similarly to Algorithm 2, then special care should be taken to analyse what the published values can leak. For example, they may leak something about the number of equal values in the input.
| Algorithm 2 Two-element Comparison-Based Sorting |
| Input: Two shared values and Output: Return fresh shares of x and y so that larger is the first Shuffle and to learn , where . Compute private comparison , where if . Publish as b. return if else |
From the viewpoint of building secure computation algorithms, it is easier to think of secure functionalities for individual protocols, like addition, multiplication, comparison, equality checks or bit decomposition. Essentially, if we had such small secure protocols then any algorithm described as using them could immediately be implemented in any concrete instantiations of these protocols while the composition theorem guarantees the security of the algorithm. Therefore, we have a conflict of interest between the frameworks that are specified as secure computational units versus the algorithm development that benefits from considering primitive operations of the computational unit individually. Either the security proofs of the concrete algorithms are very generic and refer more to intuition (e.g., that only published values should be analysed) or the algorithm is proven secure with respect to some fixed MPC framework, e.g., [18,19,20]. In the first case, we lose the rigour and good security definitions given by detailed security proofs. In the second, we are not exploring the full setting where this algorithm could be applicable and the proofs should be done again when implemented with different basic primitives and protection schemes.
Studying the separate arithmetic protocols as individual secure components is fairly straightforward for the cases of passive security that operate without private setup parameters. For example, earlier protocol development [21,22,23] focused their proofs on a fixed representation of the secure values and simply stated that the protocols are more generally applicable in practice. However, for frameworks using private setup parameters like shared keys in their operation, the monolithic functionality is a natural and nicer choice. Essentially, the monolithic functionality allows hiding the setup inside the protocol and using common flavours of composable security. If we would like to consider monolithic functionalities by their components, then we would need to take the joint state of the components into account. This could be achieved, for example, by using the joint-state UC framework [24] for the security proofs.
If we use a secure computation functionality as a starting point for defining a new algorithm, then we can base the algorithm on the ideal functionality of the framework. Therefore, the proof of the algorithm is in a hybrid model assuming interactions with the specification of the underlying computation functionality. The resulting hybrid model is usually still more complex than desired. A malicious adversary could possibly change the scheduling of subprotocols, create unplanned subprotocol instances, alter intermediate values or cause significant local computations. Most proofs first analyse the security in the abstract setting where shares are treated as non-malleable secure storage and focus on analysing only the values that are explicitly revealed.
We rigorously formalise the abstract execution model and study under which conditions the abstract and the full hybrid model are equivalent. We first establish the foundations of specifying secure computation environments and the security of both their computation protocols and secure storage in Section 2. We call the combination of the storage and the protocols the secure protection domain. Second, we study how to extend the protection domain with a new protocol. Third, we show how such security proofs can be done in an abstract setting when making some natural assumptions about the protection domain and the protocol. In doing this, we formalise the intuition that in most algorithms only the values that are public or malleable need proper discussion in a security proof. The abstract model and all relevant conditions are derived in Section 3. We specify the abstract model in a sequence of steps that each simplify some aspect of the hybrid model. In Section 4, we summarise the abstract execution model as well as the conditions under which it can be used. In addition, we explore why these conditions are satisfied by most programmable secure computation frameworks and primitive protocols. For protection domains, we specify the properties that have to be met in order for the storage to be secure and flexible enough to allow secure computation. In addition, we define a canonical form for reasonable functionalities defining the primitive operations for secure computation. Essentially, we assume that all functionalities are such that their output depends on the input values and not on the format of the protection. The storage allows for some homomorphic modifications but does not reveal information about the stored values. We also study the properties of the secure computation protocols that can realise these functionalities. Overall, we note that as long as some parties in the computation remain honest, they should also have control over which computations can be executed with the private values. Therefore, the adversarial actions are quite limited as long as the protocols are able to deal with malformed inputs and have reasonable semantics.
2. Materials and Methods
Modelling MPC protocols as asynchronous distributed system requires many low-level details that cannot be neglected in the definitions and proofs. We define a visual representation for the reactive simulatability framework (RSIM) [25,26,27] to visualise the main insight and sketch how the arguments can be fleshed out to complete proofs. RSIM is one formalisation for composable security, thus showing security according to their definitions guarantees security in overall contexts where the protocol might be used.
In this section, we describe the RSIM framework and our visual notation for it. Second, we discuss general privacy definitions based on observational equivalence and different models for security and composition. Third, we establish the meta theorem showing what we have to prove in the following to establish that the proofs in the abstract model are sufficient for the security in the hybrid execution model. Finally, we describe the secure protection domains and the core assumptions that we make regarding them and their execution environments.
2.1. Asynchronous Systems and Visual Notation
This section describes the core of the RSIM model for adaptive adversaries where a system is described by a fixed set of machines, for more details see in [25,26,27]. An asynchronous distributed system in RSIM consists of machines that we denote as boxes and communication buffers denoted by bullets. All machines communicate with outside world through ports. We denote input ports as white () and output ports as grey ().
Standard buffers have three ports: input, output and clocking. In our notation, these ports are never drawn, as they are always used to connect ports of the machines. Instead, we denote a buffer as an arrow with a bullet ( 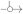 ). We extend this model by adding buffers which leak information to the machine that clocks it. These can be used to ensure that the adversary learns some meta information about the messages, such as the subprotocol instance that receives the message. For visual clarity, we omit these details and use an arrow with a dotted bullet (
). We extend this model by adding buffers which leak information to the machine that clocks it. These can be used to ensure that the adversary learns some meta information about the messages, such as the subprotocol instance that receives the message. For visual clarity, we omit these details and use an arrow with a dotted bullet (  ) for the leaky buffer. We use a dedicated notation for sender-clocked (
) for the leaky buffer. We use a dedicated notation for sender-clocked (  ) and receiver-clocked (
) and receiver-clocked (  ) buffers and omit port squares if they are deducible from context. By default all buffers are clocked by the adversary. The notation is illustrated in Figure 1. A message written to the input port of a buffer is appended to an internal queue of messages . A leaky buffer also has a corresponding queue of leaks that is kept in sync. Leaks can be fetched using a dedicated port, thus the clocking machine must have at least one input port to receive the leakage. The full construction of it can be found in Appendix A. An input to standard clocking port causes to be removed from the queue and written to the output port. An empty output is written to the output if the input is out of range.
) buffers and omit port squares if they are deducible from context. By default all buffers are clocked by the adversary. The notation is illustrated in Figure 1. A message written to the input port of a buffer is appended to an internal queue of messages . A leaky buffer also has a corresponding queue of leaks that is kept in sync. Leaks can be fetched using a dedicated port, thus the clocking machine must have at least one input port to receive the leakage. The full construction of it can be found in Appendix A. An input to standard clocking port causes to be removed from the queue and written to the output port. An empty output is written to the output if the input is out of range.
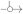 ). We extend this model by adding buffers which leak information to the machine that clocks it. These can be used to ensure that the adversary learns some meta information about the messages, such as the subprotocol instance that receives the message. For visual clarity, we omit these details and use an arrow with a dotted bullet (
). We extend this model by adding buffers which leak information to the machine that clocks it. These can be used to ensure that the adversary learns some meta information about the messages, such as the subprotocol instance that receives the message. For visual clarity, we omit these details and use an arrow with a dotted bullet (  ) for the leaky buffer. We use a dedicated notation for sender-clocked (
) for the leaky buffer. We use a dedicated notation for sender-clocked (  ) and receiver-clocked (
) and receiver-clocked (  ) buffers and omit port squares if they are deducible from context. By default all buffers are clocked by the adversary. The notation is illustrated in Figure 1. A message written to the input port of a buffer is appended to an internal queue of messages . A leaky buffer also has a corresponding queue of leaks that is kept in sync. Leaks can be fetched using a dedicated port, thus the clocking machine must have at least one input port to receive the leakage. The full construction of it can be found in Appendix A. An input to standard clocking port causes to be removed from the queue and written to the output port. An empty output is written to the output if the input is out of range.
) buffers and omit port squares if they are deducible from context. By default all buffers are clocked by the adversary. The notation is illustrated in Figure 1. A message written to the input port of a buffer is appended to an internal queue of messages . A leaky buffer also has a corresponding queue of leaks that is kept in sync. Leaks can be fetched using a dedicated port, thus the clocking machine must have at least one input port to receive the leakage. The full construction of it can be found in Appendix A. An input to standard clocking port causes to be removed from the queue and written to the output port. An empty output is written to the output if the input is out of range.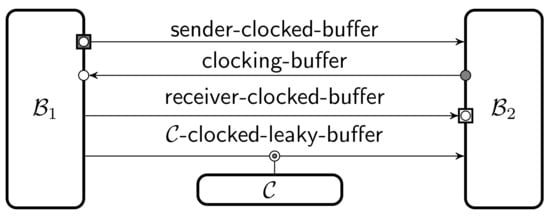
Figure 1.
Notation for machines and communicating through various buffers with clocking the leaky buffer.
Input–output behaviour of a machine is determined by a state update function , where is the state space and is the product of the domains of all input ports and is the product of the domains of all output ports including clocking ports. All domains must contain an empty output . A machine can clock at most one buffer and thus only one clocking output can be non-empty. Execution rules also assure that one and only one input is non-empty when the machine is invoked except the main scheduler that can be invoked with empty inputs. As a result, a machine can clock only a single sender-clocked buffer and leaks cannot reach the clocker without explicit polling.
One machine is declared as the master scheduler that manages all undefined execution timings. In our setting, this machine is always either the adversary or the simulator. At the start of computations, the master scheduler is invoked. The scheduler will write to its output ports and clocks one buffer to start the chain of state transformations. When a machine writes a message to an output port, it is absorbed by the buffer and control goes back to the machine. When a message is written to a clocking port, the corresponding buffer releases a specified message and the control goes to the receiver. When a machine stops execution without clocking anything, the control goes to the master scheduler. The execution stops when the master scheduler reaches an end state and becomes inactive.
A collection is a finite set of machines and buffers. It is closed if all its buffers are connected to ports and vice versa. A free connector is a connector that has one end attached to a buffer in a collection while the other end is not attached to any machine in the collection. Similarly, a free port is a port that belongs to a machine in a collection and is not connected to any buffer. An extended collection does not have free ports and a reduced collection does not have free connectors.
Collections and have matching interfaces if collections can be merged by joining free port and connector pairs while respecting restrictions posed by destination labels as well as ensuring there are no two ports expecting the same connection. Let the shorthand denote the resulting collection. Notation emphasises that is a distributed subroutine that matches structural restrictions posed by calling it out. We also use a shorthand for to emphasise that is the outer environment although the concept is inherently symmetric. In this setting, the interface of can be partitioned into two sets according to the target collection. We refer to these as sub-interfaces.
We visualise the interface of an extended collection as a dashed border surrounding its machines and buffers. Free connectors must reach a right port type on a border. For clarity, we label these interface ports by the names of their host machine, e.g., which buffers must be connected to the adversary or environment .
2.2. Security through Observational Equivalence
Collections and have identical interfaces if there exists a one-to-one mapping between interface elements that respects port types and destination labels. A distinguisher is a reduced collection that has a matching interface and has a dedicated machine with two end states 0 and 1. Let denote the end state of when the collection stops. Then, the strongest equivalence form known as perfect observational equivalence , which means that for any valid distinguisher . Perfect observational equivalence indicates that and realise the same functionality modulo implementation details that are encapsulated by the collection border. Perfect observational equivalence is unattainable for cryptographic constructions as the security inherently emerges from the asymmetry between honest and corrupted parties.
Let be a collection that models a protocol. Then, the interface naturally splits into two sub-interfaces. A service interface specifies how to call out the protocol. An adversarial interface exposes protocol weaknesses to the adversary. The set of adversaries is compatible with and if is a well-defined and closed collection for any . Note that the definition allows collections where and are communicating. Similarly we can define a set of compatible environments .
Definition 1
(Security). Let and be collections with an identical service interface and let be the set of compatible environments. Let be the set of compatible adversaries. Then, is as secure as if there exists a function such that for all .
Let denote that is as secure as . The notation is justified as the relation is reflexive and transitive for appropriate sets of adversaries. The corresponding equivalence relation captures protocols with similar security properties. Maximal elements over the relation identify maximally secure protocols, also known as ideal implementations.
This definition allows us to specify a wide spectrum of security definitions [28,29,30,31]. We can consider only nonuniform polynomial adversaries or different corruption models, for example, choose between static vs adaptive adversary, or semi-honest vs. active security [32,33]. The protocol determines the set of unavoidable attacks. By tweaking the implementation of , we can model fairness [34,35], selective failure (abort) [36,37] and security against covert adversaries [38]. The exact definition of plausible environments determines how and where the protocol can be used securely. Restrictions on the correspondence define various flavours of black-box [39] and white-box security [40,41] or specify tightness requirements like polynomial and superpolynomial simulation [42,43]. Restrictions to and usually fix the model of corruption while constraints on place restrictions on the protocol scheduling.
Theorem 1
(Secure two-system composition). Assume that we have three collections , , such that collections and are well-defined and have an identical service interface. Let be the subset of compatible environments and let be a natural construction . Then, the construction proves that for the set of environments is also a proof for for the set of environments .
The theorem is particularly useful when the set of plausible environments and adversaries is closed, i.e., and . As security is commonly defined against nonuniform polynomial-time adversaries the second constraint is trivially satisfied. The first constraint is satisfied when environments consist of all sequential compositions of poly-time subprotocols. The resulting sequential composition theorems [29,30,44] play a central role in cryptography. Alternatively, we can consider the set of all concurrent compositions of poly-time subprotocols. The resulting security notion is known as universal composability (UC) and has many flavours [14,25,45,46,47,48,49,50] which differ in minor details. Most formalisations assume that machines and connections between them remain unaltered during the execution while Canetti’s second formalisation of universal composability [51] allows dynamic reconfiguration of the environment. We consider an extension of the RSIM model [25,27] which has leaky buffers for proper modelling of secure communication channels. The resulting adaptive-adversary RSIM is very close to the simplified version of UC (SUC) that was defined to characterise MPC protocols [52]. Our formalisation of MPC in RSIM gives us more flexibility to split protocols into components to modularise the proofs and transformations.
2.3. Soundness and Completeness Theorems
Our main contribution is a description of an abstract execution model which hides all irrelevant technical details while the security proof in this model remains sound and complete. That is, a proof in the abstract model exists if and only if it exists in the original execution model. In other words, the abstract model is both sound and complete and, therefore, a suitable replacement for the hybrid execution model. Here, soundness means that a proof in the abstract setting means that there is also a proof in the original execution model. Completeness, on the other hand, specifies that if there is a proof in the original model, then there is also a proof in the abstract model.
Let and be the protocols of interest, and let and be their counterparts in the abstract execution model. Let and denote the set of environments for original and abstract execution models. Let and denote the set of plausible adversaries. To show that security proofs in the abstract model are sound and complete, we define three explicit constructions and their semi-inverses
which satisfy the following three pairs of equivalence relations
Note that constructions (1) together with equivalence relations (2)–(4) define a commutative square in Figure 2 with the equivalence guarantees for individual elements where for brevity pairs , and are defined through up or down arrows depending on the direction of traversal. As a result, the existence of implies the existence of , and vice versa.
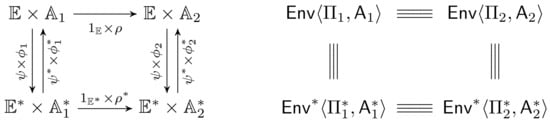
Figure 2.
Equivalence guarantees and their relations to and .
Theorem 2.
Proof.
For the proof, we simply trace the equivalence square depicted in Figure 2.
Soundness. Assume that there exists such that
The claim follows as we can define and the transitivity of equivalence relation proves the equivalence .
Completeness Assume that there exists such that
The claim follows as we can define and the transitivity of equivalence relation proves . □
In many cases, the security definitions limit the resource consumption of the parties, e.g., the adversaries are polynomial, in such cases have to keep these restrictions. We apply this theorem to show that we can hide the vast majority of technical details when analysing the security of a compound protocol. We split the construction into four major blocks. In Section 3.1, we show that certain attack techniques do not help the adversary when the protocol satisfies natural requirements to message scheduling. Thus, we can consider only a subset of adversaries, i.e., we partition and and choose a canonical representative for each class. As a result, the environment remains the same during the abstraction and , are also identity functions.
In Section 3.2, we separate state from protocol participants and replace message passing with a shared memory. Again the environment remains the same but now and . As a result, we need to explicitly define and . In Section 3.3, we expose the internals of ideal functionalities to further simplify the memory model and remove the share representation. We again explicitly define and . In Section 3.4, we define the abstract model by simplifying the environment to a simple representative class of environments. Fortunately, we can define and so that observational equivalence guarantees
hold and the last pair of equivalence relations () follows directly.
2.4. Programmable Multiparty Computation
Most platforms for multiparty computations, see, e.g., in [1,2,4], consist of a secure storage and a system of primitive protocols operating on top of the storage. As a result, one can safely combine primitive instructions to implement any algorithm, thus we call such frameworks programmable. In this section, we formalise building blocks and show how one can extend existing secure computation instruction set with new primitives. Our work falls into a long list of MPC formalisations [14,25,29,52,53,54] where we are focused on specifying programmable secure computation. First, we discuss the storage properties, then we formalise two flavours of computations of the secure computation engine and define protection domains as our abstraction of a secure computation framework. For protection domains, we discuss their security and the natural conditions for environments and adversaries that we expect in our following security analysis.
2.4.1. Security of Distributed Storage Domains
A modular design of multiparty computation protocols requires the ability to store intermediate values. A secure storage can be built on top of different primitives, such as secret sharing, encryption, commitments, trusted hardware or a combination of different schemes. We develop the formalism for secret sharing, however, the abstract description for storing and retrieving values is universal. A secure storage domain is defined by two algorithms and which can use parameters from shared setup . A machine distributes an input into shares. A machine converts shares back to the original value or returns a special failure symbol ⊥. Throughout the paper, we explicitly assume that the behaviour of and does not depend on previous queries.
An adversarial structure defines which subsets of parties can be corrupted without losing security properties. We define privacy and integrity properties for secure storage through observational equivalence. Our definitions are generalisations of privacy and recoverability of secret sharing schemes [55] and are tailored toward the concrete application of secret sharing as a storage domain.
Intuitively, a storage is hiding if no information about the stored value leaks from shares captured by the adversary. However, there are three subtle issues: First, the outcomes of and could leak information about private parameters or other shared values. Second, in security proofs we often want to simulate shares for some values and use the remaining shares without changes. Third, we need to specify what happens when the adversary corrupts more parties than expected. Formally, we define the hiding property through two collections and that have identical layout, see Figure 3a. Machines and are for storing values and the corresponding shares. The state of is a one-dimensional array . The state of consists of a two-dimensional array for shares and a one-dimensional array that specifies how the shares will be generated.
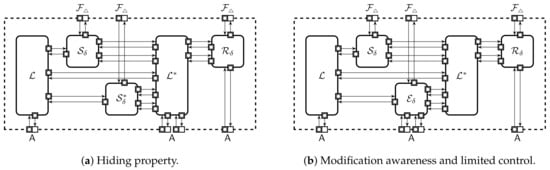
Figure 3.
Configurations defining security properties of a storage domain.
An adversary can adaptively specify the values of and , but each location can only be set once. The adversary can also read and write shares of corrupted parties . A static adversary must send the list of corrupted parties to before any value is shared while an adaptive adversary can issue corruption calls at any moment. When is queried and the location is uninitialised, initiates an update cycle. The machine always asks to share the value using in collection . In collection , the value is shared only if . If , then asks a share simulator to create the share . A share simulator is an efficient and potentially stateful machine, which can query values from only after the set of corrupted parties does not belong into . Finally, can place a reconstruction order for . The machine sends to if . Otherwise, first asks to share the value and then forwards the shares to . In both cases sends the output back to .
Definition 2
(Hiding storage). A storage domain δ is perfectly hiding if no adversary can distinguish configurations and . A storage domain δ is hiding for if the advantage is negligible for any adversary from .
Many secret sharing schemes do not use private setup parameters. As a result, different sharings are independent from each other and it is sufficient to prove simulatability of a single sharing. In case of adaptive corruption, the secret sharing scheme must be efficiently patchable [56] as the simulator must progressively disclose shares of an unknown value. The existence of trusted setup allows to achieve integrity even for honest minority. However, now different shares are correlated with each other due to shared setup parameters and we cannot reduce hiding to simpler security notions. In this case, we assume that uses the setup parameters of the corrupted parties.
Note that the hiding property does not guarantee privacy throughout the entire period of computations. Instead, each storage domain can define to specify which parties can be corrupted while still maintaining privacy. For instance, the adversary who corrupts learns its local state which is a separate trivial storage domain. Values in the public domain become visible as soon as the adversary corrupts some participant.
As the adversary can always change shares under its control, security of a compound protocol relies on the integrity of stored values. Robust secret sharing guarantees that values cannot be altered while verifiable secret sharing allows to detect corrupted values. Modification awareness for a storage domain is defined through an efficient extractor machine and an efficient operation . Let be the original secret sharing where is the share of , and let be its adversarial modification and A the set of corrupted parties. Then, the extractor gets together with the setup parameters of A as an input and has to output a difference such that . We denote reconstruction failures by ⊥ and we expect that the modification operator is such that and for any a in the value domain. Modification function generalises the observation that in many MPC protocols adversarial modifications result in additive changes to the value [57].
Intuitively, a storage domain is modification aware if there exists a good extractor machine which cannot be fooled by an adversary. The success of an adversary is defined through a collection that also contains machines and , see Figure 3b. A two-dimensional array forms the entire state of . As before, an adversary can adaptively specify the values of but each value can be set only once. The adversary has the power to corrupt parties and read and modify the shares of corrupted parties by interacting with . The extractor just forwards communication between and . Queries to uninitialised locations lead to the same update cycle as in , i.e., generates shares from . During a share update query additionally computes the difference and sends a pair to . As a response, updates the value and gives control back to . Each sharing in can be updated by at most once. The limit on modifications attempts eliminates trivial attacks where the adversary first invalidates its shares and then changes them back to original values. For many storage schemes this causes to fail as is stateless and has no knowledge of the previous modification or share values, thus it has to assume that for any . The adversary can also place reconstruction orders for . Given such an order sends to who sends the output back to . The adversary wins the game if the outcome of differs from and the set of corrupted parties is in .
Definition 3
(Modification awareness). A storage domain δ is modification aware against a class of adversaries if the advantage against the modification game is negligible for any .
For robust secret sharing, the extractor always outputs the neutral element of the modification operator because the adversary cannot affect the shared value. Local storage is robust by definition as the adversary cannot alter local state before corrupting the party and after corruption the definition poses no restrictions to modifications. Extractor for verifiable secret sharing can output ⊥ or the neutral element because the adversary can either invalidate the shared value or create a different sharing of the same value. Therefore, for most cases the potential changes to the value are quite limited.
On the other hand, modification awareness does not guarantee that the adversary can efficiently find a share modification for any potential change of the value. A two-way extractor can handle such requests. The success of an adversary against the two-way extractor is defined through a collection that has the same layout as in Figure 3b. An adversary can adaptively initialise and update the values of . For the update, has to provide to . As a response sets , sends to . Given from , the extractor first fetches from and computes new shares for the corrupted parties such that . Finally, sends to and returns the control to . returns control to . The rest of the collection specification is identical to . As before, must issue a reconstruction order for a location at the end of the game. The adversary breaks the two-way extractor if the outcome of differs from and the set of corrupted parties A is in .
Definition 4
(Limited control). A class of adversaries has a limited control over a storage domain δ if the advantage in the collection is negligible for any adversary from the class.
2.4.2. Canonical Description of Ideal Functionalities
An idealised computation can be formalised in many different ways. We consider a decomposable functionality working on the data representation of the given protection domain and using the setup from the protection domain. In general, inputs and outputs of an ideal functionality may belong to several storage domains, e.g., some of them may be secret shared while the others are local variables. The entire computational process can be split into rounds where each round consists of three phases: reconstruction, computation and sharing as in Figure 4. Machines and are functionalities for sharing and reconstruction which internally execute functionalities and of individual storage domains and is a combined setup procedure. Machine gathers inputs and interacts with to reconstruct the values. These values are passed to that evaluates a stateful function and sends outputs to together with a storage domain for each output. interacts with to share outputs. If the reconstruction fails then also outputs ⊥ and the storage domain has to have a way to generate shares of ⊥. Most notably, there must be a canonical way to create shares of ⊥ for verifiable secret sharing. Note that it is always possible to define functionalities that ignore some input and where such condition may not be necessary. However, if the input is used in the computation of the functionality then a malformed input can only result in a malformed output, otherwise the functionality leaks information or introduces selective failures. The adversary can interact with through and . Machines and can coordinate their actions through a receiver-clocked buffer between and . Note that , and all receive setup parameters, however there is an important distinction that we expect only and to get the private parameters of different parties and only learns any public parameters. The latter is necessary to correctly define because public parameters might, for example, specify the modulus for all computations.
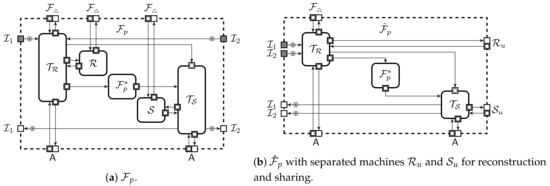
Figure 4.
Internal structure of a two-party functionalities.
The corruption mode for is defined through a communication between , and . All responses to must be computable from the inputs and outputs of the protocol instance and the setup parameters received by . For robust protocols, is disconnected from . For fair protocols, can send only abort signals to but gets no information from . For protocols without fairness the adversary could see corrupted parties outputs before deciding to abort. After abort, all parties get shares of ⊥ as output. Protocol instances inside are distinguished by instance tags sent by protocol participants . All protocol instances are run concurrently and independently.
Definition 5
(Canonical ideal functionality). An ideal functionality has a standard corruption mode if all outputs are generated by and the adversary cannot learn anything about the shares of honest parties other than revealed by the published values. Functionality is in canonical form if it is a collection of , , , and with the internal structure specified above, has a standard corruption mode, and always outputs ⊥ if any input is ⊥.
2.4.3. Canonical Description of Local Functionalities
Ideal functionalities define operations computed together with other parties. Each party may also perform local operations with their shares. In principle, all kinds of local operations are possible. However, usually the storage domain defines a set of meaningful operations where the local operations are also meaningful operations on the shared values. For example, local linear operations are possible for linear sharing schemes. By definition, the output share of the local functionality depends only on the input shares of this party and, therefore, local functionalities cannot be described as canonical ideal functionalities.
Definition 6
(Meaningful local operation). A local operation implements a function if for any input where are the values reconstructed from the input shares of and are the values reconstructed from the output shares of .
In the following, we represent local operations as where each is a collection of machines implementing local operations carried out by parties in . We assume that each local operation consist of a single round. More complex local computations can be implemented as a series of local computations.
2.4.4. Security of Protection Domains
A protection domain consists of storage domains and computation protocols . For instance, a secure computation engine in the Arithmetic Black-Box model [15] is a specific protection domain with no explicit access to the stored values. Protection domain is also a refinement of a standard MPC deployment model [11] which divides participants into input, result and computing parties.
Let be the canonical ideal functionalities that the protection domain should implement. We will simplify the ideal functionalities by joining their sharing and reconstruction components. More formally, let be a machine that has k port pairs for reconstruction. A query to p-th pair is sent internally to that is part of the ideal functionality and the reply is routed back to the corresponding output port. Let be analogous extension of the machine . Note that and have only a single port pair for . Let be a collection we obtain by removing components and from as depicted in Figure 4b. Then, the ideal functionality for the protection domain is defined through a collection where only use public parameters. Let the corresponding extended collection be denoted as . The collection is observationally equivalent to provided that the trusted setup sends the same input parameters for all .
Definition 7.
A protection domain has modular representation if collections and are observationally equivalent.
As a next step we need to specify the class of reasonable environments. A typical compound protocol in an MPC platform take shares as input and produces shares as output. The latter causes subtle issues. Note that a universally composable protocol must remain secure even if the adversary knows all inputs, while a verifiable secret sharing could be secure only if the adversary knows only a limited set of inputs. Consequently, universal composability is unachievable as the adversary can alter shared values without detection. However, these protocols do not run in a generic environment, and therefore we should also study their security in a more restricted setting where we separate the outside environment and the other computations that happen in the protection domain. This allows us to make reasonable assumptions about the visibility of the output shares. In the most general case, the best we can achieve if we have any shared setup, is joint-state universal composability [24] while joint-state sequential composition is the absolute minimum.
We define the set of plausible environments through a cartesian product where is the trusted setup and specifies all plausible compound protocols and environments in which might be executed. The inner environment specifies computations done in the MPC framework while is an outer environment representing the rest of the world in which the compound protocol should preserve security.
Definition 8.
A list of protocols with a shared setup is secure protection domain if for any and provided that is a well-defined closed collection.
The signature of a protection domain determines what can be computed with the protection domain and what restrictions must be met to preserve security. The actual security guarantees are specified in terms of plausible adversaries and which depend on the environment. Each protection domain also specifies an adversary structure which lists all sets of parties that the adversary can corrupt if we want to keep security guarantees. The adversary structure is limited by the secure storage domains of the protection domain and the security properties of the individual protocols in the protection domain. The corruption mode specifies the type of tolerated adversaries ranging from static semi-honest to adaptive malicious adversaries.
2.4.5. Secure Extension of Protection Domains
To modularise proofs, a protection domain is often defined through a minimal set of protocols that implement ideal functionalities . After that each new primitive is added by defining a protocol and proving its security. To establish basic security, we need to prove . Such proofs usually follow the two phase strategy where one proves
The first step follows directly from the security definition of a protection domain. Thus, the main bulk of the proof must be carried out in the hybrid execution model where real protocol implementations are replaced with .
To show validity of the extension, we must analyse the extended protection domain when using the ideal implementation . For that we have to analyse compound protocols . It is easy to restructure these compound protocols into observationally equivalent collections . For example, can be obtained by joining and on Figure 5. Formally, the list of protocols may not be a secure protection domain as each protocol occurs twice. It is easy to see that a secure protection domain is securely extendable provided that each protocol instance is independent of the other instances of the same protocol. The next theorem describes under which conditions the second proof stage can be generalised.
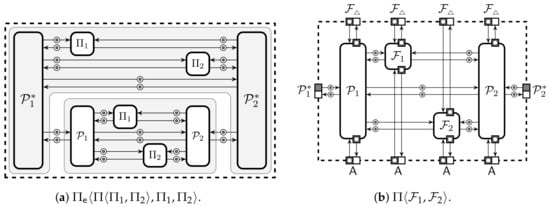
Figure 5.
Protection domain extension with protocols and ideal functionalities where is carried out by and is carried out by .
Definition 9.
Protocols with shared setup are a securely extendable protection domain if the list of protocols with is also a secure protection domain.
Theorem 3.
Let be a securely extendable protection domain with a shared setup . Let be as secure as an ideal functionality . Then, is a secure protection domain for compound protocols provided that is a secure protection domain for the set of compound protocols .
Proof.
Let us fix a target signature for the extended domain, and let be a compound protocol. Let be the set of adversaries against . As we can restructure the compound protocol into observationally equivalent form , we can replace all protocols with ideal implementations and we need to show
for environments and adversaries . By pushing into we obtain a compound protocol that interfaces only with , and . Indeed, the construction just removes interface boundaries between and , and nothing else changes. By the assumptions is a valid compound protocol for and thus over the environments
The latter completes the proof as we can push out of the compound protocol to obtain . □
In other words, it is sufficient to analyse the security of against adversaries implicitly defined by the definition of securely extendable protection domains with respect to compound protocols and environments .
2.4.6. Restrictions to Environments and Adversaries
It is usually impossible to prove for canonical if leaks the joint state to the environment . In particular, no shares can pass the service interface between and nor can send outputs that depend on the private setup parameters. We can force this constraint structurally by including dedicated protocols into the protection domain which allow parties to securely share and reconstruct values, i.e., they are are equivalent to securely applying and to inputs and outputs.
Let us consider the inner environment that shares the state with . Note that the inner environment can carry out the same actions as the protocol , thus we prefer this notation to clearly distinguish it from that represents also the rest of the world and all actions possible there. In the following, compatible with means that is the full environment against the protocol . Due to nesting, the same physical entity is represented by different machines in different collections, such as and in Figure 5. In principle, a protocol participant can communicate with many machines from the inner environment . However, simple physical considerations suggest that each protocol node should have only one parent node that provides inputs to and receives its outputs. By duplicating protocols we can always reach a configuration where communicates only with a single parent node . We consider only such inner environments that satisfy this restriction. In addition, we assume that the state of is such that it allows to restore all computations that have occurred before it was corrupted (e.g., inputs and random choices are stored).
Definition 10
(Generic adversary). We call the class of adversaries against a protocol Π and the inner environment generic if the only restrictions on the adversary are the port compatibility with the protocol Π, the inner environment and the environment .
A real-world adversary corrupts physical hardware or administrators, thus it is natural to assume that it will corrupt all machines hosted by it. Therefore, we assume that either all machines representing a party are corrupted or none are. Sometimes many logical protocol participants are represented by one physical party and in such cases it is also reasonable to assume that they are also all corrupted together.
Definition 11
(Coherent adversary). A coherent adversary always corrupts and simultaneously, i.e., sends a corruption call to immediately after responds to a corruption call, or vice versa.
Lemma 1.
Any generic adversary can be extended to a coherent adversary provided that adversary structures for and Π are compatible.
3. Results
In this section, we show the required transformations from the hybrid protocol to the abstract execution model. We show that any hybrid protocol satisfying some conditions can be translated to the abstract setting and vice versa. Therefore, we fulfil the requirements of Theorem 2 by defining the , , and their semi-inverses and showing that the protocol designer only has to define in the abstract execution model. We consider the protocol as a subprotocol of representing the rest of the computations in the protection domain and the outer environment using and controlling the protection domain. The combination of and forms the class of environments against this protocol .
We define the transformation to the abstract model in small steps in order to make it clear where the different conditions come from and to make it easier to argue the correctness of these transformations. In Section 3.1, we show that it is sufficient to limit adversarial capabilities. In Section 3.2, we modify the protocol description and adversary to use a shared memory and limit adversarial actions to only modifications of real protocol messages. In Section 3.3, we show how to remove share representation and only give the adversary the access allowed by the limited control property of the storage domain. Finally, in Section 3.4 we arrive at the abstract execution model.
3.1. Minimal Requirements to Message Scheduling
In the following, we show that under certain natural restrictions about the protocol the adversaries ability to influence the execution is rather limited. All attacks can be accomplished by only modifying the state of corrupted parties while keeping them running. This is the first substantial step towards abstract model, as these attacks preserve the structure of computations. In term of the soundness theorem we define a universal construction that achieves
where is the set of protocols that use and is the set of environments where the protocol is intended to run, meaning they contain the outer environment and the inner environment . The main result in shown in Theorem 4.
3.1.1. Basics of Protocol Execution
The formal description of a participant of is quite complicated, as it must be able to execute several instances of the protocol in parallel and correctly handle corruption queries from the adversary . To simplify matters, we represent the participant as a collection of two machines and , where interprets the original protocol without modifications and models the effects of corruption by switching communication between the adversary and other machines.
The corresponding collection is depicted in Figure 6 together with the numbering of port pairs and machine names connecting to them. The zeroth port pair between and is for communicating with the adversary. Next k port pairs between and are for calling out subprotocols. The last port pair between and is for communicating with the inner environment . All these ports are directly matched with port-pairs between and the corresponding external machines. Note that all our buffers come in pairs, thus we also use the shorthand to specify the pair, where is outgoing from and is incoming to the party. This notation can be enhanced with additional indices if it is important to consider many parties or ideal functionalities at once.
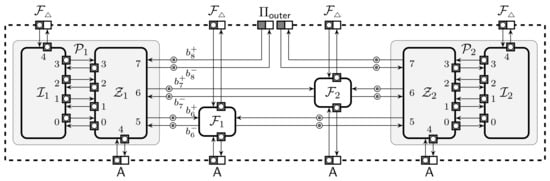
Figure 6.
Internal structure of a two-party protocol calling out two protocols and .
When is in the honest state it mediates communication between the matching ports. Every time receives a message, it writes the respective message and also clocks the messages to . When receiving a message from it also gives control back to after writing the message to the output port. When is corrupted, then can order to write a message to any of its output ports and all messages arriving to the input ports of are forwarded to . Additionally, can issue a special message to to receive the internal state of . Each message sent between and is a triple where specifies the instance of the protocol and the instance of the sub-protocol called by . Similarly, a message sent between and is triple where specifies the instance of the protocol and the instance of calling it.
3.1.2. Tight Message Scheduling
The structure of subprotocols determines what the adversary can do with ingoing and outgoing messages. For example, consider a protocol where submits several inputs without any reply from . Then, the adversary can trivially reorder inputs by delaying messages. Although sequence numbers can be added to fix the intended order of messages, we still cannot guarantee the arrival of . Only a reply to after the ℓ-th input stops the flow of inputs which the adversary can reorder. Therefore, sending one-by-one has no theoretical benefit over a single message . In practice one could still stream these as individual messages but it does not affect the theoretical communication model. The same argument invalidates the utility of piecewise release of outputs. As a result, neither nor should send a new message before they get a reply from their respondent. A reply in a protocol fixes time-point in a protocol after which an input or an output is committed and can not be changed.
A protocol might include a party without consent by sending outputs before it has sent inputs. In practical protocol constructions, we always know when is going to participate in a protocol, and thus we can always assume that all parties provide an input before receiving any outputs. The following definition summarises minimal requirements for protocol constructions to be secure against network delays. Communication patterns of such protocols may still depend on inputs or outputs. For example, a party can submit an unbounded number of inputs that depend on previous replies.
Definition 12
(Tight message scheduling). An ideal functionality has a tight message scheduling if and cannot send two consecutive messages to their recipients. Additionally, must send the first message before receiving anything from and both and must know when the other stops sending messages for a given protocol instance.
3.1.3. Robustness against Malformed Inputs
As a corrupted party can arbitrarily deviate from a protocol specification, we must relate its messages with the state progression in the honest protocol run. For that we show that a corrupted party can always run the interpreter honestly and deliver all messages from ideal functionalities to the interpreter instantly.
Definition 13
(Semi-simplistic adversary). An adversary is semi-simplistic if it fulfils the following conditions for corrupted .
- (a)
- The adversary clocks any outgoing buffer and any incoming buffer connected to an honest party only when all incoming buffers connected to corrupted parties are empty.
- (b)
- Upon receiving a message from that comes from , the adversary immediately orders to forward it to without changes.
- (c)
- The adversary can send arbitrary messages to on behalf of .
- (d)
- The adversary can fetch the state of .
- (e)
- The adversary gives no other orders to .
Conditions (a)–(b) formalise instant message delivery which preserves the order of messages: if receives before then must receive before . Furthermore, corrupted parties receive messages earlier than honest parties. Conditions (c)–(e) guarantee that the adversary can not directly manipulate the state of , thus is running honestly.
Lemma 2.
For any adversary, , there exists an equivalent semi-simplistic adversary . The overhead in computational complexity can be arbitrary.
Proof.
Adversarial behaviour. When a party, , is not corrupted just does whatever does. Whenever corrupts , the new adversary also corrupts and sends the Reveal message to get the internal state of . After that, can internally simulate the interpreter by initialising it with the state. Let denote the corresponding virtual interpreter. Whenever gets an incoming message destined to the interpreter, it forwards it to without changes. If sends back a reply, deletes it. If does not send a reply, then control still goes to when stops. After that, passes the original message to . Whenever wants to send a message to , sends it to . If sends back a reply, forwards it to . If wants to send a message to other parties forwards it to . As a result, all incoming messages reach without changes and right after being received by while the sends out exactly the same messages as .
Modified clocking. To guarantee that can always empty a buffer , we must do another modification. First, the adversary can keep the buffer empty by clocking it immediately when writes to it for corrupted . This fulfils the conditions (a)–(b). The timing of might change but we only need to preserve the behaviour of . For that, stores the messages and internally simulates buffers to .
Complexity. The overhead in the computational complexity consists of copying and running the interpreter. The state of the must be copied and its further actions as must be simulated. Simulated interpretation comes with at most a polynomial slowdown as the state is of polynomial size. As incoming messages of are potentially altered by the actions of , the interpreter is not guaranteed to terminate. Therefore, we can give no overhead bound in this construction. Nevertheless, is semi-simplistic. □
Adversarial actions may lead to unexpected inputs, thus the interpreter is not guaranteed to terminate. Overall, there are three possibilities to overload the interpreter. First, they may get unexpected messages from ideal functionalities or the environment. The interpreter should be able to ignore such messages. Second, the adversary might be able to trick the environment or an ideal functionality to send overly long inputs to the interpreter. These attacks are harmless as long as the interpreter knows the maximal input length and ignores the rest. Third, the adversary might trick the interpreter to do expensive local computations. This is a serious concern unless the amount of local computations is bounded.
Definition 14
(Robustness against malformed inputs). A protocol is robust against malformed inputs if the running time of the interpreter is polynomial for all semi-simplistic adversaries.
Corollary 1.
If a protocol is robust against malformed inputs, then semi-simplistic and generic adversaries are equivalent to each other.
Proof.
The robustness guarantees that the construction introduced in Lemma 2 has a polynomial overhead. Each time invokes , it is guaranteed to stop and pass the control back to . As the number of times invokes is bounded by the running time of , the total running time of can be only polynomial times bigger than the running time of . In addition, any semi-simplistic adversary is also a generic adversary. □
3.1.4. Security against Rushed Execution
A semi-simplistic adversary may create messages that are dropped by recipients as they are not ready to process them. Let a tuple denote the event where writes a message to the output port p, and let denote the event where the recipient writes a reply to its output port. Note that for semi-simplistic adversaries the interpreters are always running honestly.
Definition 15
(Input and output signature). Let the input signature for a particular round of computations in canonical ideal functionality (Definition 5) be the set of parties that must provide inputs before forwards recovered inputs to , and let the output signature be the set of parties that receive output shares from .
Definition 16.
We say that a round of computation is rushed if the ideal functionality executes the computation before some interpreter in the input signature has computed its input to this round. A protocol is secure against rushed execution for the set of environments if no semi-simplistic adversary from the class of adversaries can rush a round of computation.
The explicit limitations on the set of adversaries is necessary, as there may be a gap between protocols that unbounded adversaries can rush vs. polynomial time adversaries. Usually, one considers only polynomial-time adversaries. Security against rushing allows us to avoid situations where semi-simplistic adversaries desynchronise a protocol by sending out messages way earlier than the event takes place.
Definition 17
(Lazy adversary). A semi-simplistic adversary is lazy if it always waits for signal from to clock a message out of the buffer and it always clocks at most one message with right tags per signal.
Lemma 3.
Assume that ideal functionalities and protocol Π have tight scheduling. If a protocol Π is secure against rushed execution, then semi-simplistic adversary can be converted to equivalent lazy semi-simplistic adversary.
Proof.
Assume that all ideal functionalities have unlimited buffering. Let be a modified adversary that internally runs the original adversary and monitors what messages are written to outgoing buffers and when they are clocked. This allows to catch all events where tries to clock a message out of a buffer before the interpreter has produced the event . For these events, catches the clocking signal and forwards it as soon as the event occurs. Note that thanks to tight scheduling the tags and the port uniquely determine the buffer and the message of the protocol and it is clear which message can be clocked.
Such delays have no effect on execution. If nobody submits its input after the event , then we have a prohibited a rushing event. As we have security against rushing, still waits for inputs when clocks . If never clocks a message, then the event never occurs, and thus security against rushing guarantees that the corresponding round of computation is never completed or this party was not in the input signature. Consequently, the overall execution does not change.
In the general case, might keep after a delay while its dropped in the original run. The reverse is not possible as no messages can take the place of delayed because tightness ensures has only one outstanding message for instance of . As knows all messages sent and received by , tight message scheduling guarantees that knows which rounds of computations are completed or pending. Therefore, can efficiently compute whether a message will be dropped or not. Thus, we can always convert to the lazy adversary that never clocks a message that is dropped.
Note that the the communication between and is similar, except that is in the role of the (with tight scheduling), and we can only convert the adversary to lazy clocking if is secure against rushing. Otherwise, for a coherent adversary, we know that adversary can only create messages to the buffers between the corrupted party in and . Therefore, delays can affect only corrupted buffers and without lessening of generality we can assume that instead the adversary could perform the follow up actions of the corrupted party in without really clocking this message. □
Theorem 4.
If a protocol is robust against malformed inputs and is secure against rushed execution, then lazy semi-simplistic and generic adversaries are equivalent to each other.
Proof.
From Corollary 1, we know that generic adversaries are equivalent with semi-simplistic adversaries. Lemma 3 proves that any semi-simplistic adversary can be transformed to a lazy semi-simplistic adversary. In turn, each lazy semi-simplistic adversary is also a semi-simplistic adversary. □
Theorem 5
(Characterisation of rushing). A semi-simplistic adversary can rush a round of computation π for a functionality with tight scheduling only if one of the following holds for a corrupted in the input signature.
- (a)
- The round π is not in the program code of the interpreter .
- (b)
- The interpreter needs an input from to submit an input to π.
- (c)
- The interpreter needs an output from a round of computation to submit an input to π and is executed concurrently or after π.
Proof.
Let a party be in the input signature of a rushed round of computation such that its interpreter computes the input for the round after is completed and let be the corresponding outgoing buffer. As does not proceed without the input from , the input had to be present in . For honest parties, only can create such inputs. Consequently, must have been corrupted before the input to was clocked.
There are two options why the interpreter cannot produce input before this clocking event. First, the program code of never computes inputs for , i.e., is not scheduled. Second, must be waiting for a message m to arrive through some incoming buffer before it can compute the input to . For semi-simplistic adversaries, the buffer is always emptied before clocking of . Thus, the input m must be created by another round of computation or inputs from that is still incomplete. □
The possibility of (b) can be eliminated by the design of or . We can include Byzantine agreements in to make sure that no honest party starts before necessary inputs are received from , or we can restrict to give inputs in a manner that all parties who execute receive inputs in one go. Let be the canonical ideal functionality for . Then, we can analyse if the adversary can rush in using Theorem 5. If rushing is impossible, then all corrupted parties in round are guaranteed to get input from before executing and we need to exclude only possibilities of (a) and (c).
The majority of all multiparty computation protocols operate with values that are secret shared among all participants. Consequently, no computation round can be rushed if the protocol consists of sequential execution of subprotocols and some party is honest. In particular, if a protocol description is symmetric for all parties and input functionalities are also symmetric, then dependencies between rounds of computation are the same for all parties and no round is computed without the inputs from honest parties.
3.2. Shared Memory and Simplistic Adversaries
Lazy semi-simplistic adversaries are quite restricted, as they clock messages to according to protocol specification. Still, they can send out more messages than are finally clocked. We define a shared memory model where such attacks can be carried out by modifying a limited set of memory locations and call this the simplistic adversary. In more formal terms, we define a ⋈-operator that acts on protocols and their components together with a universal construction and its semi-inverse that achieves
where is the set of protocols satisfying the above restrictions which use in black-box way and is the set of compatible environments. The first part constructing the memory model and simplistic adversary are shown in Theorems 6 and 7 through a ⋄-operator. This is extended to memory alignment in Theorem 8.
3.2.1. Interpreter Specification
The changes to the memory model alter the interpreters as well as the communication patterns. The interpreter in is a universal random access machine with two special communication instructions DmaCall and Send. All instances of share a program . The internal state of is a three-dimensional array where t specifies a protocol instance, a storage domain and ℓ a memory location. A protocol instance t can access only its slice . Initially, the state is empty and there are no active protocol instances. launches a new protocol instance by sending a special triple denoted as Init to . Upon initialisation, launches a new protocol instance with the input m of type and stores as the instance of the parent protocol.
An instruction DmaCall initiates a query–response round where the vector specifies the memory locations to be assembled into a tuple m and specifies to which locations the elements of a response tuple are stored. The respondent and its protocol instance is fixed by the port number p and the instance tag t. The instruction is not complete until the response comes. An instruction Send initiates analogous communication without response.
Tags and encode the instance of a caller and a callee in all triplets . Therefore, the outcome of DmaCall and Send instructions depends on the port p. As ports are meant for subprotocols, outgoing messages must be in the form where is the current protocol instance and fixes the instance of a subprotocol.
The remaining instructions formalise a type safe memory manipulation and conditional jumps. Conditional jumps in the program can occur only on public or local variables. A special local storage domain is used for storing the state of the instruction interpreter including program counters and memory locations of incomplete DmaCall instructions. This state can be quite complex for interpreter types that concurrently execute several protocol instructions.
Definition 18.
A program is well-formed if the following holds.
- (a)
- Each memory location can be assigned only once.
- (b)
- No instruction can read a memory location before it is initialised.
- (c)
- A new message with tag is never written to the output port p to before reading a message with tag from the input port p from .
- (d)
- For instructionsDmaCallandSend, no other program instruction can read memory locations in the vector α and write the memory location β.
Note that after the location has been used as an input to some ideal functionality, only and are allowed to read it and only writes the return location . For conceptual clarity and brevity, we consider only well-formed programs. Well-formedness is largely a property of the concrete implementation of the protocol, hence we may also address it as the protocol with well-formed implementation.
3.2.2. Shared Memory Model for Communication
Replacing message passing with shared memory allows us to merge individual states of interpreters into consolidated memory and limits the adversary to only work with messages sent by . Let be a stateless interpreter, is a collection of parts of interpreters that deal with protocol inputs and outputs, and is a memory machine for storing the internal state of . We introduce to make some follow-up steps of the transformation clearer later on. contains the input–output modules of each interpreter in the protocol. When gives an input to then it writes it to memory and clocks the notification to . When receives output from then it reads it from memory, writes it to buffer to and gives control back to . Let be modified ideal functionalities with access to the shared memory as depicted in Figure 7.
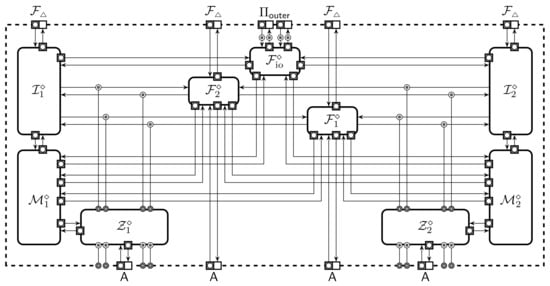
Figure 7.
Decomposed interpreters for protocol calling out protocols and .
The memory stores the state of as a three-dimensional array . Each buffer pair can be used to access and modify . Given an input Fetch, returns . Given an input Set, updates the state by setting and replies . For convenience, there are also commands for block reads and writes. The communication between and goes through the exchange of memory locations. The interpreter translates DmaCall into a message , where is the caller instance, specifies the locations of message components and locations for the reply. Send instructions are translated into triples . A recipient or queries to assemble the message m and processes the resulting triple as in the original setting. When a reply is generated then all elements are stored to memory locations and a special message is sent back. Upon receiving Init for and protection domain , writes components of an input m to some default memory locations and sends Init to .
The machine simulates the original execution of the protocol to . For that, must simulate a missing machine and buffers between and . Let the buffers connecting to be and analogously to between and . can communicate with and clock buffers and but can not access before adversary issues a corruption call. modifies only the memory locations of incomplete DmaCall and Send calls. Define as an extended collection consisting of machines , together with all buffers attached to the machines. Let the corresponding adversarial construction be defined as a reduced collection consisting of .
Theorem 6.
Let Π be the protocol with a well-formed implementation and let be the set of compatible environments. Then,
where and is the set of compatible lazy semi-simplistic adversaries.
Proof sketch.
Let us define another extended collection that consists of machines together with all attached buffers. We get a trivial equivalence for any and . Therefore, it is sufficient to prove that for any and that meet the restrictions. Although collections and are quite different there is a natural matching between machines and their internal states. Initially, the internal states of and coincide. The same is true for the interpreters and although their internal state is stored in different locations. Therefore, we can run the standard bisimulation argument and show that the actions of or cannot diverge execution to non-equivalent states.
First, define that achieves the goal by ignoring memory access restrictions. As contains the entire state of , can internally replicate all computations of and fetch all messages sent by from . Therefore, can perfectly simulate and the buffers and provided that states of and and and have not diverged yet. However, note that only the messages from and responses to corrupted parties are required to be accessed from the memory, thus the same can easily also satisfy memory access restrictions.
As is lazy semi-simplistic, we know that creates a message before reads the corresponding input. Therefore, translates DmaCall and Send instructions before must fetch the corresponding input from the memory. Property (a) of a well-formed program guarantees that can swap the values in the locations just before it clocks the address tuple to . Property (d) guarantees that the change does not alter further actions of . Consequently, we can guarantee that and always get the same inputs and thus the executions of the ideal functionalities in the two worlds give the same results. Therefore, also and get the same results from the ideal functionalities and the simulation done by is perfect. □
To show the full equivalence of the two execution models, we need to define a class of simplistic adversaries against and that are produced by and then define semi-inverse of with the right properties.
Definition 19
(Simplistic adversary). An adversary is simplistic if it satisfies the following.
- (a)
- The adversary clocks any outgoing buffer and any incoming buffer to an honest party only when all incoming buffers to corrupted parties are empty.
- (b)
- The adversary can modify the state of the corrupted party only in the locations α of pendingDmaCallandSendinstructions. These changes are done before the corresponding tuple is clocked to and each value is modified at most once.
Corollary 2.
For any lazy semi-simplistic adversary and for any well-formed implementation of Π, the construction is simplistic adversary.
Proof.
The way alters memory just before clocking in the proof of Theorem 6 guarantees that the property (b) of simplistic adversary is satisfied. The clocking rules for are analogous the semi-simplistic adversary A and are therefore satisfied as preserves clocking with respect to the matched buffers in the two configuration. □
We specify the semi-inverse through simulator machines that go between and . The simulator translates clocking signals, provides read only access to the state of and translates memory writes to actual protocol messages. As before, let be the reduced collection consisting of .
Theorem 7.
Let be the protocol with a well-formed implementation and let be the set of compatible environments. Then,
where and is the set of simplistic adversaries compatible with the protocol and the environment. The resulting adversary is lazy and semi-simplistic.
Proof sketch.
Let us define another extended collection that consists of machines together with all buffers attached to the machines. Then, it is sufficient to prove that the equivalence holds for any and as by construction.
We can use the same natural matching between machines and their internal states as in Theorem 6. Equivalence is obvious when does not corrupt . The machine just forwards all clocking signals and the equivalence follows from the construction of and . To fetch a value , the machine sends Reveal message to and forwards the response. After a first Reveal, call is corrupted and will instantly forward the communication from to .
When issues memory modification instructions, can locally store all altered values . As the adversary is simplistic, it alters only memory locations related to DmaCall and Send instructions. Let tuples and denote the outcomes of and for these instructions. Then, by construction can clock a tuple only after is written to . Moreover, does not change values in the location after is clocked to . By property (d) of a well-formed implementation, these changes alter only the corresponding message assembled by and nothing more. Therefore, must always check whether has altered any of the locations . If there are no changes, clocks the message to . If there are changes orders to write a message to . After that can clock and ignore the original message . As a result, and get the same message at the same time and equivalence is preserved. As is simplistic then the clocking and modification rules carry over and the resulting adversary is lazy semi-simplistic adversary. □
3.2.3. Memory Alignment and Protocol Specification
Let a global state be a four-dimensional array that combines the states of all machines . More precisely, let for parties in the storage domain and for parties outside the domain . For brevity, let denote a tuple .
Definition 20
(Memory-alignment). A well-formed protocol uses an ideal functionality in memory-aligned manner if each individual input is reconstructed from and each output is shared to . This restriction must hold regardless of adversarial behaviour.
Note that memory-aligned usage is not a property of a protocol. It easy to define implementations where memory locations are not aligned in subprotocol calls. However, simple incremental addressing is enough to achieve memory alignment for all ideal functionalities when there are no local operations. Local operations without restrictions can easily break the alignment if some parties carry them out and others do not. However, alignment could be achieved by giving a dedicated memory region to local computation outputs that are not inputs to some ideal functionality.
However, from now we will treat local operations explicitly as external components rather than internal affairs of the interpreter. We represent local operations reading and writing to as fragmented functionalities where each is a collections of machines implementing local operations. Formally, we need a new interpreter and memory machine that have additional sender-clocked port pairs for communicating with . To initiate an operation, sends a tuple of locations to which performs the computation and gives control back . As before, determines the locations of inputs and the locations of outputs in the state of .
We add a sender-clocked buffer pair between and as local computations may utilise setup parameters of the respective party . As a result, all local operations can be pushed out from to and without changing the overall execution as shown in Figure 8.
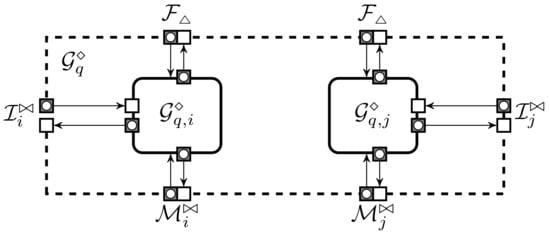
Figure 8.
Encapsulation of local computations involving two parties.
Definition 21
(Canonical protocol). Let , , denote ideal functionalities used in a well-formed protocol. A protocol specification is in a canonical form if
- (a)
- all conditional jumps are based on local values,
- (b)
- the remaining local operations are implemented with and
- (c)
- all ideal functionalities are used in memory-aligned manner.
These conditions must hold regardless of the adversarial behaviour.
Similarly to the previous cases, any well-formed protocol can also be represented in the canonical form. Note that in canonical protocol specification, the interpreter can be isolated from the trusted setup as it runs no computations on its own. A canonical protocol specifications guarantees that operates with aligned memory locations. Therefore, the entire collection of memory modules can be replaced by a single memory module with the same set of port pairs that keeps the internal state to answer all queries. To reconstruct an input or store an output, always addresses a block .
This allows us to define a collection that meets the specification of by replacing and with a machines and which directly communicate with the shared memory . Given an input , the machine fetches , reconstructs the underlying value x and sends it back to . Given an input the machine computes shares for y and writes them to .
To preserve compatibility, we replace and with machines and that consolidate memory locations instead of messages. The machine collects location tuples instead of incoming messages. When all tuples for a particular round of computation have arrived, extracts all unique input locations and reconstructs inputs with the help of . After that it sends output locations to and proceeds as . Whenever wakes up , it first clocks in a message from that contains the output locations and uses to share the outputs. To isolate and from the memory, we add a separate machine between and . This machine manages all cases when or give any values to by receiving the locations from or and retrieving the necessary values itself. For clarity, let us define as a collection of as we push into the adversary in the next step.
Thanks to , can still leak inputs, outputs and their locations, or perform selective aborts based on values. The adversary gets a limited access to the memory through . Note that we are working with the canonical ideal functionalities as specified in Section 2.4.2 which limits and subsequent adversaries to only read the shares of corrupted parties. is defined based on with the difference that it writes the values to and sends only the location information to . Define as an extended collection consisting of machines , ,, with all attached buffers. Let be the reduced collection consisting of and all . Therefore, the new adversary expects memory locations from the ideal functionality and fetches corrupted parties values from the memory .
Theorem 8.
Let be a well-formed protocol specification that is in a canonical form and let be the set of compatible environments. Then,
where and is the set of compatible simplistic adversaries for and for . The resulting adversaries and are simplistic.
Proof.
The buffers between and and adversary are the same in both worlds, and the adversary accesses the same state of the interpreter in and . The differences are the joining to , introducing as separate functionalities and decomposing to , and that also interact with .
All memory addresses are written once by a well-formed protocol, thus the outputs of are never overwritten and the adversary can access them from when needed. In addition, the buffers connecting to and are sender-clocked and therefore this separation is invisible for . Therefore, separating the local functionalities is equivalent to the local functionalities inside where writes all outputs to . As all ideal functionalities are canonical, we can replace all instances of and with and provided that we rewire the memory to .
Adversary is simplistic as it respects the clocking rules of simplistic and the construction did not change the clocking or the modified memory locations. Similarly, transforming to equivalent is straightforward and can be accomplished getting the same values as read from from communication with . □
3.3. Reduction to Abstract Memory Model
Simplistic adversaries are extremely restricted. They can alter a fixed set of memory locations and decide when ideal functionalities and interpreters perform their computations. As a protection domain consists of ideal functionalities which use two universal machines and for reconstruction and sharing, it is straightforward to define an intermediate memory module that stores reconstructed values. With additional simplifications we can restate all operations in terms of and quantify memory modifications in terms of underlying values instead of shares. In more formal terms, we define a *-operator that acts on protocols and their components together with a universal and its semireverse that achieves
where is the set of protocols with canonical specification and is the set of compatible environments. The forward transformation is covered step by step through the whole section and the reverse is summarised in Lemma 12.
3.3.1. Introduction of Abstract Memory
We split the memory of values and shares and introduce a dedicated memory module for the values. The internal state of is a three-dimensional array is such that an entry contains the value corresponding to shares in in at all critical time-steps. Then, we place machines and between and together with a pair of sender-clocked buffers for synchronisation as depicted in Figure 9. Recall that only receive public parameters. Local variables and the state of each party are also stored in . For that we replace the pair of sender clocked buffers between each interpreter and with a corresponding buffer pair between and . allows the adversary can read and write local variables of corrupted parties.
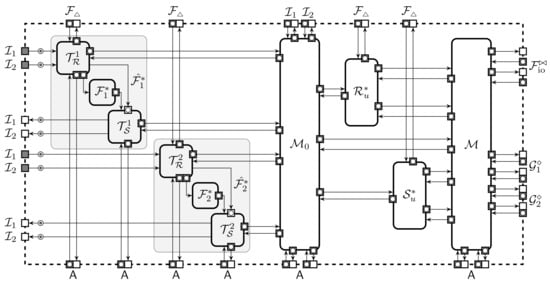
Figure 9.
Separating memory to for values and for shares, .
We synchronise the states of and as follows. When a machine queries a share from a location and is empty or invalid writes Share to the synchronisation buffer. Then, uses to share and gives control back to who uses to complete the query. Whenever is updated writes Update to the synchronisation buffer. After that uses to update and gives control back to . Finally, must write Invalid to the synchronisation buffer when the value of is updated. After this marks the location as invalid and gives control back to . This mechanism guarantees that and give always coherent replies to other machines.
As a result, we can connect directly to instead of and without changing the execution, let this be . When queries , the machine replies . When wants to share a value x to a location , the machine sets and marks the location as invalid. The latter allows us to replace a sub-collection inside without changing the execution outcome. More precisely, let be an extended collection consisting of and let be an extended collection consisting of .
Theorem 9.
Collections and are observationally equivalent for well-formed protocol specification in a canonical form.
Proof.
The substitution does not change communication between the collection and . Therefore, it is sufficient to show that machines run in the same order and provide identical replies to and . The latter is sufficient as communication with other machines in the collection is sender clocked and invisible to outside observers.
In particular, we need to show that when a machine queries its value is same in both collections. Assume that so far all queries have yielded identical results. In , the response to is computed from , while responds . By the construction the value of is invalidated whenever is updated. Consequently, the reply contains the reconstruction of as in .
Assume that the location of a new query is initialised. If was the last machine to update in then it was also the last to update in . Therefore, contains the correct value. By the construction, the update marked the location as invalid and thus the reply yields shares generated by . For other machines, the memory cells are updated identically in both collections. If is uninitialised in , then no machine has updated this location. Thus, could not have initialised nor could any other machine have initialised in . □
3.3.2. Extended Modification-Awareness
As the adversary can modify shares of corrupted parties and therefore change the values in . Here, we study under which assumptions the adversary can update itself after modifying shares . The concept of modification awareness (Definition 3) is meant to tackle this, but some interactions in the computations are not captured by the definition. We can apply the extractor from the modification awareness in our current setting but its success is not necessarily the same.
We define a collection where we place the extractor between , and as in Figure 10. The extractor which forwards messages between to and simultaneously extracts changes corresponding to share modifications. These modifications are sent to who updates the state accordingly. A slightly modified machine does not invalidate a location when the extractor alters the location .
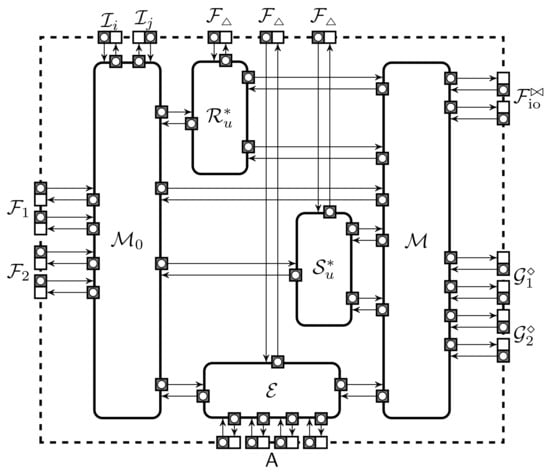
Figure 10.
Separating a value modification module from , collection .
Definition 22.
An adversarial modification of is oblique if the extractor fails to correctly update the value of .
Theorem 10.
Collections and are observationally equivalent for an environment adversary pair provided that the extraction failure is negligible.
Proof.
As the machine forwards the communication between and without modification, the states of the configurations can diverge only if the values of differ when replies to some query. It is straightforward to see that the latter occurs only if the extraction fails for . □
Definition 23.
Local operation is transparent if any modification of output shares can be effectively converted to a modification of inputs and oblique modification goes to oblique modification.
Common local operations—copying and linear combination—do not contribute to extraction failures as they are reversible and thus oblique modifications can be back-propagated. To bind the probability of extraction failures, we need to reason about the environment and protocol together as oblique changes may enter the protocol through inputs. For instance, in verifiable storage domains, an adversary can corrupt a parent party in and invalidate its input shares for . As knows the original shares, it can modify invalid shares to the originals inside . The resulting modification is oblique. By definition, holds ⊥ in that location meaning that the modification function always results in ⊥ independently of the extractor outcome.
Non-canonical ideal functionalities are a potential source of oblique modifications. For example, consider a weird flavour of non-fair computations where the adversary learns the output shares of honest parties before it can invalidate some of them. To create an oblique modification, the adversary can later corrupt a party with invalidated share and replace it with the original. Unconventional local functionalities can also create oblique modifications simply by invalidating the input shares. As the adversary knows the original shares, it can create oblique modification by restoring the valid share.
Lemma 4.
Assume that all local operations are transparent and ideal functionalities are in a canonical form. Assume that generates all protocol inputs for domain δ and the inputs of are determined by the adversary. Then, the probability of extraction failures in a well-formed program is negligible for simplistic adversaries provided that every storage domain is modification aware.
Proof.
Let be a simplistic adversary that with probability creates an extraction failure in storage domain in some protocol instance. Then, we can define a new adversary against modification awareness of storage domain (see Figure 3b).
First, note that the adversary can perfectly simulate and , as it has direct access to (inputting values through and reading from through ) and in the modification game and can run the trusted setup for all other domains. As a consequence, can perfectly simulate protocol inputs and ideal functionalities . The simulation of the protocol is straightforward, as the flow of the interpreters depends only on local values and new local values can be created by ideal functionalities or local operations. As learns the entire output of for protection domains , the shares of can be directly computed. The requested shares of can be computed by backtracking all dependencies to shares generated by and then redoing all local operations.
Next, we add back-propagation of modified shares for the domain . By definition, a simplistic adversary can modify only the inputs of ideal functionalities. If a modification is generated by then this modification can be used to win the modification game. If the modification is computed by a local functionality then due to transparency, can always back-propagate a change to a change of one input of and an oblique change is guaranteed to remain oblique. This process can be repeated until reaches a protocol input or an output of ideal functionality . These are potential challenge shares generated by .
Each input modification leads to a modification of a potential challenge. The total number of such modifications is bounded by the number of inputs to ideal functionalities that have domain . Let the corresponding number be n. As we cannot check which modification is oblique, must set one of them randomly as the challenge modification when it generates the shares. As a result, succeeds in modification awareness game with probability . The claim follows as is negligible whenever is negligible. □
Corollary 3.
If all local operations are transparent, ideal functionalities are in a canonical form and the environment is simulatable; then, the probability of extraction failures in a well-formed program with modification aware storage domain is negligible for simplistic adversaries.
Proof.
The proof of Lemma 4 can be generalised to a class of environments that can be simulated in the modification awareness game. Simulation means running the environment analogously to the protocol as part of the modification game. Therefore, we require the assumption that does not leak the setup parameters or joint state. In addition, in such simulation we can notice the modifications to inputs of done in that could be oblique. Such modifications can be used or propagated similarly to the actions with values of in Lemma 4. □
3.3.3. Meaningful Local Operations
Local operations cause another state update procedure where the information flows from the machine to . Meaningful local operations (Definition 6) produce such output shares that the state can be updated from itself. Note that a value in is read-only by . An adversary can obliviously update by sending differences to through . The canonical protocol description guarantees that reads only after the location has been initialised. Thus, if a local operation initialises then it is always completed before the read of .
This allows us to define a new collection where machines update the state instead of . Each interacts with interpreters and the abstract memory and receives public parameters from . For that we slightly modify the behaviour of , and . Whenever calls it also calls after it gets the control back. The machine immediately checks if the operation has been computed in or if there are enough inputs in to complete the local operation in . If all inputs are present and the operation has not been executed yet, then reads inputs from , computes the outputs according to and writes it to . Modified does not invalidate a location when the functionality alters the location but otherwise behaves as before.
Theorem 11.
Collections and are observationally equivalent provided that a well-formed protocol specification is in a canonical form and all local operations are meaningful and implement some deterministic functionality.
Proof.
Modifications to the collection do not change the order of machine activations. Indeed, changes in eliminate only a ping-pong interaction between and . Changes in inject a ping-pong interaction between and . As the communication in these interactions is sender-clocked the other machines can distinguish collections only based on the states of and . Clearly, modifications do not change the state of as long as responses to queries and remain same in both collections. Therefore, it is sufficient to consider only the responses to queries .
Only an ideal functionality (or ) can query . Therefore, it is sufficient to consider when updates , as otherwise both collections behave identically. For well-formed programs, the value is never fetched by before all interpreters have defined their shares. Although may depend on several local operations we know that all of them complete by that time. As the adversary never overwrites inputs of local computations, we can inductively prove that the update chain gives the the same result for as the reconstruction step in . □
The result can be generalised to meaningful non-deterministic local functionalities. First, all inputs to must have a correct distribution, or otherwise we cannot apply the definition. Second, the inputs of local functionalities with non-deterministic outputs must be independent. For instance, if the local functionality is deterministic and we re-run the same shares we get the same output while gives two independent outputs.
3.3.4. Isolation of Protocol Outputs
By construction all protocol outputs are obtained by releasing shares of type even if outputs are locally private values. As a next step, we modify the construction so that all output shares are generated anew by . This a major prerequisite for isolating the adversary from the memory . We define a new collection in Figure 11 where is replaced by to construct inputs and to create outputs. always gives control back to that called it. writes the value to as soon as sufficient shares have been received and always forwards the signal to the party whose input was clocked to it. All these added buffers are sender clocked. Send instructions from are forwarded only to . The behaviour of is different from . The machine keeps a special cache of published values which is initially empty. For each input Send or DmaCall from , it extracts all locations of output shares. If a triple , the machine fetches the corresponding value from , computes the shares and stores them into . If , then it uses the shares in .
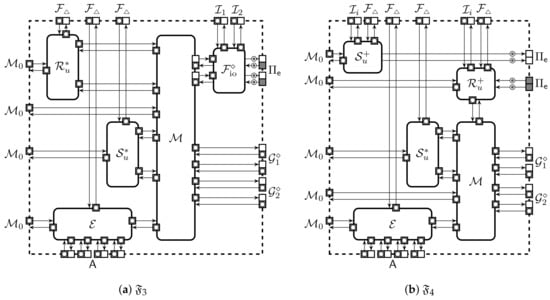
Figure 11.
Memory models for input–output isolation.
Definition 24.
A protocol environment pair is in an output-isolated configuration for a class of adversaries and resource consumption constraints if there is a construction ϕ such that for and the construction ϕ satisfies resource constraints. A protocol Π is output-isolated if this property holds for any environment.
Any protocol where all outputs are returned by deterministic (e.g., local values) or where no shared outputs are returned are output isolated. The value is guaranteed to have the same distribution as when outputs are computed by an ideal functionality. However, the behaviour of may still reveal the discrepancy. For instance, may decide whether to abort or continue based on the output shares of honest parties if can reveal them to . The latter creates a discrepancy that is impossible to resolve in . It is also an explicit weakness of a protocol. Any protocol can be converted to output-isolated protocol by resharing outputs before returning them. Hence, almost all functionalities used in practice can be implemented with isolated outputs.
Lemma 5.
A canonical well-formed protocol specification is output-isolated for coherent adversaries if all outputs are computed by some ideal functionalities with standard corruption mode, output shares are not used further in computations and they are immediately returned as outputs.
Proof.
It is straightforward to see that in processes inputs identically to in . Therefore, we need to consider only the output generation. In , output generation starts when writes its output to . At some point, the adversary clocks the corresponding message from to some . writes DmaCall or Send message to push its share of to , and fetches the corresponding part of . By construction, is created by from . In , sends DmaCall or Send message to , which uses instead of to create the output. By construction, and have the same distribution. However, there is a discrepancy between and protocol output.
Note that only can observe the discrepancy, as honest parties do not use output shares in further computations. Coherent has also corrupted the parent node in the inner environment and thus can fetch shares from the outputs sent to . For that, we must guarantee that the outputs arrive earlier than wants to read the i-th share of . The latter is straightforward as the output shares are published as soon as they become available for and can always clock the output to . □
Lemma 6.
Any protocol is output-isolated for the class of environments that do not use randomised output shares at all.
Proof.
Note that the changes introduced by alter only output shares given to the environment and only for non-deterministic . As a result, the adversary can compute the protocol outputs based on the state of corrupted party instead of the actual protocol output reaching the parent node . This hides the discrepancy between and , as these shares are never used in any other protocol. □
Lemma 7.
Any protocol where output shares have the same distribution as freshly generated shares is output-isolated for the class of adversaries that do not access the protocol state at all.
Proof.
By assumption all protocol outputs are identically distributed in and . As the adversary learns nothing about the protocol state it cannot detect the discrepancy, nor can the adversary alter the protocol execution as it cannot alter the protocol state. □
Theorem 12.
Let be a canonical ideal functionality that does not leak shares to adversary and let Π be a protocol that is as secure as for a class of environments and adversaries . Then, Π is also output-isolated for the same classes of adversaries and environments.
Proof.
Let be an adversary against the original protocol and environment pair , and let be the construction that proves the security of the protocol. Then, is an ideal adversary that defines protocol inputs and receives protocol outputs in . As the adversary does not learn values from the ideal functionality , its interface is compatible with . By definition, is equivalent to for all adversaries that behave honestly. Indeed, if an adversary does not corrupt parties then cannot also corrupt parties. The same must be true for the adversary . Although corrupts some parties and alters their inputs, these parties remain honest in the protocol. As a result, . The claim follows as satisfies the assumptions of Lemma 7. □
A protocol is secure if any adversary can be converted to an adversary against ideal implementation. Therefore, all adversaries against can be modified to adversaries that do not read the shares of the outputs from at all. That means that output-isolation is necessary for security in general. The intuition is that since these shares are updated during outputting and not used in the protocol then reading them is only relevant in . Thus, in the following we only consider such adversaries.
3.3.5. Complete Memory Isolation
The transformation defining protocol output isolation in the previous section cuts the last link between the memory and the environment . Only the actions of the adversary can now depend on all local computations and ideal functionalities only use . Thus, honest execution does not require and in this section we show how can simulate for hiding storage domains. Therefore, we will completely remove from the protocol description.
First, we minimise the number of memory locations accessed by . Memory locations can be divided into three classes: protocol inputs, outputs of ideal functionalities and outputs of local computations. A coherent adversary can always extract protocol inputs from the parent node when the latter submits them to . Simulation of local computations is straightforward provided that we know the inputs of . Only the outputs of ideal functionalities must be fetched from the memory . In the following, we consider the details of constructing the adversary that only reads these values written by ideal functionalities from and does not touch other memory locations.
Let be the class of adversaries that only read the outputs of from . More formally, let be the new adversary that internally runs and clones interpreters to answer adversarial queries about corrupted shares of . To reconstruct the state of a newly corrupted party , has to redo all the computations done by so far. For that, must get all protocol inputs submitted by . We use the assumption that the state of contains enough information for to repeat all computations and thus the input extraction becomes trivial. The adversary must also access local variables and outcomes of random choices of stored in . The output shares of are queried from as usual. As a result, can rerun a clone of to recreate the state of . In addition to the real values from , uses the inputs known to it to fill the simulated memory with protocol inputs and local computation outputs that can access.
Lemma 8.
Assume that we can rerun all computations for any corrupted parent node. Then, for any coherent simplistic adversary .
Proof.
By construction of from , we can just repeat all computations as necessary and only read the outputs of . □
Clearly, the outcome of depends only on the locations that are read by the adversary which are the outputs of ideal functionalities . As these locations are directly updated by , we can remove the remaining update mechanisms for protocol inputs and local operations. Let be a simplified collection where does not update and is not connected to it. Interpreters activate only , and machines are removed. Note that while the shares are not read, the adversary can still do modifications to all inputs of ideal functionalities and the outputs returned to . Therefore, we disconnect from and join it to so that can supply it with the values that it recomputes that should be in memory . Let the new adversary combining and be and the respective class of adversaries is such that they submit direct coherent modifications to and .
Lemma 9.
For any defined as above we have .
Proof.
By definition, reads only outputs of from and these are not affected by the changes as these are written after executes. Nothing other than values in are affected by the transformation to . Note that the extractor still sees valid shares and works in the same manner as before but is just considered to be part of the adversary. □
To shield completely from , we use the simulator from the hiding property definition (Definition 2) and assume the adversary does not read the output shares as discussed for output-isolation. Let be the adversary that runs internally but uses simulators for each protection domain instead of values in . We denote by the class of limited control adversaries (Definition 4) that do not interact with .
Lemma 10.
Let be an environment that uses storage domains without private parameters. Then, for any limited control adversaries and as defined above using and not reading the output memory locations.
Proof.
W.l.o.g. we can consider only the case where the protocol uses only one storage domain as there are no parameters that might be shared by domains. Define an adversary against hiding games so that the first hiding game is equivalent to and the second to . First, note that needs to internally simulate all computations of . As does not use storage domains with private variables, can internally evaluate and for any storage domain and recreate all computations inside . Second, note that machines , , , form a subcollection that interacts with through the machine . The adversary can clock some buffers inside and interact with and . After simulating , the adversary can produce all inputs to the protocol .
For the outputs of ideal functionality , the adversary interacts with the hiding game. It corrupts locations when issues corruption calls. When an ideal functionality wants to write x to , remaps a location to and set by interacting with . It also sets to mark that the values is inside the protocol scope. In one game this does not affect the outcome but in the second this means that all shares will be simulated. When queries corrupted shares of , the adversary fetches corresponding shares from .
The first hiding game is equivalent to as the shares are generated by . When is in the second game then the shares of the protocol are simulated because and the second game is equivalent to the definition of . Most importantly, note that the adversary modifying the memory locations does not affect the interaction with the hiding game. always simulates the computations to learn the new value in that it can put into in the game. succeeds thanks to that gives the coherent modification of the value together with the share modification to and . Note that in case uses the extractor, this proof also covers the case where the hiding property is somehow invalidated by the extraction. □
The same proof can be generalised to storage domains with private setup parameters if the environment can be simulated inside the hiding games, meaning that all sharing operations inside the environment are carried out inside the hiding game with . As before, this is possible if the does not reveal setup parameters that would invalidate the hiding property. For the adversary , the memory has become meaningless, thus define the limited control execution model from by removing connections between and , including . This setup is shown in Figure 12.
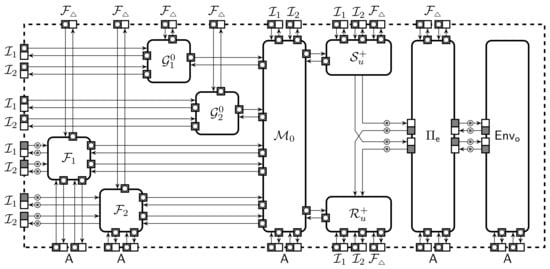
Figure 12.
Limited control execution model for two-party protocols.
Lemma 11.
Then for any .
Proof.
Trivial as does not communicate with the memory or . □
Corollary 4.
Any coherent adversary against the hybrid model can be transformed to an equivalent coherent limited control adversary against the same protocol in for hiding and modification aware storage domains and for well-formed protocols that are in a canonical form and use meaningful transparent local operations.
Proof.
We work with a coherent adversary which works well as a generic adversary (Lemma 1). In Lemma 2 and Corollary 1, we show that if a protocol is robust against malformed inputs then any generic adversary is equivalent to semi-simplistic adversary. In Lemma 3 and Theorem 4, we show equivalence of semi-simplistic and lazy semi-simplistic adversary if all functionalities have tight scheduling and the protocol is secure against rushing. In Theorem 6 and Corollary 2 we conclude that it is sufficient to consider only simplistic adversaries when running well-formed programs. We then show that we can separate the value and share memories (Theorems 8 and 9), limit their interactions (Theorems 10 and 11). Assuming output isolation we continue the simplifications in Lemmas 8–10 to move from real shares to simulated shares. Finally, in Lemma 11 we conclude that it suffices to consider the limited control execution model. □
3.3.6. From Limited Control to the Hybrid Model
Lemma 12.
Any coherent limited control adversary against can be transformed to an equivalent coherent simplistic adversary against the same protocol in for storage domains with limited control and negligible extraction failure, and for well-formed protocols that are in a canonical form and use meaningful transparent local operations.
Proof.
Theorems 8, 10 and 11 guarantee that , , and are observationally equivalent for any adversary for well-formed protocol specification in a canonical form, using meaningful local functionalities and storage with negligible extraction failure. However, for to we modified the adversary and have to consider how any coherent adversary against can be transformed to a simplistic coherent adversary against .
Consider the adaptor machine that connects to the abstract adversary that only interacts with and does clocking. If the protocol in it is using a storage domain with limited access, then all modifications to the values can be translated to the values of the shares in in . Note that by definition the new adversary against reads only the values that are modified from the memory and only uses them to compute the modification. If the extraction has negligible failure then the values in are the same in and after this change. The added memory and changed interaction with do not change the view of the adversary or the values returned to . □
Corollary 5.
For all coherent limited control adversaries against the protocol in there exists a hybrid adversary such that if the protocols are secure against rushing and malformed inputs, have well-formed specification, are in a canonical form, use meaningful local operations for deterministic functionalities, use storage domains with limited access and negligible extraction failure.
Proof.
Semi-simplistic and lazy semi-simplistic adversary is equivalent to the generic adversary as shown in Corollary 1 and Theorem 4 for protocols secure against rushing. Simplistic adversaries can be transformed to equivalent lazy semi-simplistic adversaries for the same well-formed protocol in the respective protocol description as shown in Theorem 7. Theorem 8 shows that storing values in in aligned manner can be reversed to any memory layout and can be merged to the interpreters. Lemma 12 shows that any limited control adversary can be transformed to equivalent simplistic adversary for the canonical protocol. Therefore, we have shown that any limited control adversary can be transformed to an equivalent adversary in the hybrid protocol. □
3.4. Abstract Model
Results from previous sections allow us to consider an execution model where the environment interacts with a system consisting of interpreters , a semi-protected memory module , a library of idealised functionalities and for local and global operations and modules and for storing and fetching values from the memory . The environment for the protocol in question consists of the rest of the computation represented by and outer representing the rest of the world as in Figure 12. The left-hand side of the figure is completely stated in terms of abstract memory and public parameters whereas the right-hand side, especially is still a complex network of nodes exchanging shares.
In Appendix C, we discuss further means to simplify the collection for many cases where the adversary does not really need individual buffers to clock each input and output of . For example, this is allowed in the usual case where the order and execution of is sequential within one protocol instance. These simplifications would also carry over to the abstract execution model.
3.4.1. Abstract Execution Environment
Consider a restricted class of environments where the inner environment is trivial, i.e., parent parties just forward inputs and outputs between and the protocol that we are considering. Each instance of runs only a single instance of . All inputs provided by are first shared in using for the protection domain where these values are and then reconstructed by in . The output of is reconstructed by the relevant reconstruction functionality in before it reaches . Therefore, the main component of is and is almost invisible.
For adversaries that do not read the state of corrupted parent nodes , we can simplify to as depicted in Figure 13. Machines and handle protocol inputs and outputs. Buffers between and allow instant sharing of their states. In , interacts with only when it executes DmaCall or Send instructions. As there is only one instance of for each instance of , we modify the interpreter in so that it would send a message to . As the buffer is clocked by the adversary, the interpreter does not lose control and can carry out as usual. By definition the interpreter expects an input from to launch a new protocol instance or as a reply to a DmaCall instruction. In , the machine sends the corresponding inputs. No changes are made to that still submits and receives plain values.
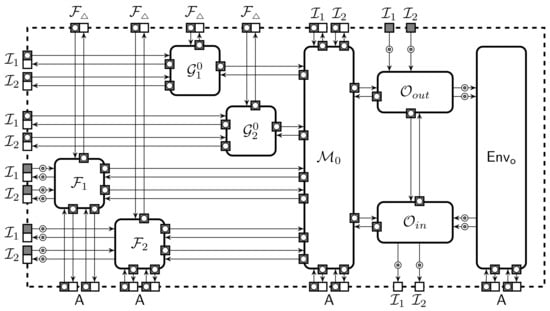
Figure 13.
Abstract execution model for two-party protocols, .
Machines and simulate the inner environment with instant clocking. The machine collects incoming instructions and forwards DmaCall to who immediately gives the control back. After that treats the instruction as a message from and simulates the reactions of and . When releases some values , then fetches them from the memory and sends to . The machine simulates the actions of , and . Based on the inputs from , it knows what messages interpreters expect and thus can assign correct memory locations to all messages sent to . When some message arrives to , writes corresponding values to and forwards the response of to the correct interpreter. Fast clocking inside the simulation guarantees that creates responses no later than in , and writes the outputs to as soon as all release instructions have arrived. As the adversary clocks the buffer, can reorder and delay protocol inputs exactly the same way as in .
Lemma 13.
Let be the class of adversaries against the collection that do not observe the state of corrupted parent nodes. Let be the class of adversaries against and be the protocol. Then there exist transformations ϕ and such that
where is the restricted environment in and is the corresponding environment in that contain the same .
Proof.
First, convert the adversary against to the adversary against . W.l.o.g. we can assume that the original adversary immediately clocks buffers from to as this alters only in which order values will be reconstructed. The adversary can correct the ordering and timing by clocking the leaky buffer between and . For the same reason, we can assume that immediately clocks buffers from to .
As adversary clocks buffers from to instead of buffers from to and buffers from to instead of buffers from to then machines and carry out a perfect simulation. The claim follows as the transformation is reversible. □
In practical deployments, protocol inputs may come from different input parties. However, as we cannot rule out coalitions between input parties, we must include the class into the set of potential environment . Consequently, we have established that protocol can be secure only if it is secure in the abstract execution model defined as follows.
Definition 25.
Abstract execution environment for a protocol is defined as the collection of , and in . Let denote the set of all abstract environments.
Abstract execution environment is very close to the minimal attack model. The adversary gets setup information of the corrupted parties and learns the values of protocol inputs and outputs. Adversary can also read and write some values in and interact with ideal functionalities if there is corresponding interface. Finally, the adversary can influence the order of execution by clocking leaky buffers between the interpreters and other machines. Depending on the environment the adversary can learn additional information about protocol inputs and outputs but nothing more.
Definition 26.
An environment class is embeddable into the abstract model for the class of adversaries if there exist transformations and such that
For most protection domains, it is quite easy albeit highly tiresome to prove that relevant environment classes are embeddable into the abstract model. In fact, we have used similar assumptions in Section 3.3 as the simulatability of the .
For embedding, we need to push all interactions between and to . The modified adversary internally runs and forwards all queries for to that internally simulates to provide correct responses. If all parameters generated by the setup are public, then can just redo all computations in . There is a small caveat as learns protocol outputs when all parties have sent them to . Thus, must simulate initial shares of corrupted parties without knowing the secrets. The latter implies that storage domains for the protocol outputs must be hiding.
Similar simulation is possible for protocols with private setup parameters as long as can simulate interactions with knowing only protocol outputs and public parameters generated by . In particular, note that the generic inner environment is a protocol for which all inputs are generated by inside and in and all outputs are processed by when given to and when given to . By placing the same restrictions to as to we can carry put exactly the same simplification operations as we did to arrive to from . As modification extractor and share simulator use only the public and corrupted parties parameters, the modified environment does not need parameters it cannot get.
3.4.2. Security in the Abstract Model
Throughout the paper we have transformed the initial protocol to the same protocol in the abstract execution environment. We call the abstraction of .
Definition 27
(Security in the abstract world). Let and be protocols and and their abstractions. Let and be the abstractions of classes of adversaries and against original protocols. Then, is as secure as in the abstract model if there exists a function such that for all and .
By definition, security can be defined with respect to any other protocol . In practice, our goal is to prove that the protocol is as secure as some canonical ideal functionality . The simplifications from hybrid execution model to the abstract model can be applied to all protocols . Similarly, they could be done for for the protocol that only calls once per instance and returns all results to . Note that is output-isolated and the transformation is allowed as long as satisfies the rules we have set for the canonical ideal functionalities inside the protection domain.
In the context of Section 2.3, our current transformations define and the same can be applied to adversaries against . Therefore, in order to prove that is as secure as we can use for both and . In order to prove that is as secure as we would need a similar transformation . However, note that for coherent adversaries the functionality is equivalent to , the details of this can be found in Appendix B. The main intuition is that has also the machines of the parties but coherent adversary corrupts them coherently with the parties in and does not gain any access that it does not have to just the machine. Hence, combining the equivalence of and with forms the required transformation . It remains to argue that the security in the abstract model indeed suffices for the security in the hybrid execution model. The following theorem achieves this by putting the results of this paper into the relevant context.
Theorem 13.
Let be ideal functionality and Π is a protocol constructed on top of a hybrid protection domain with canonical (Definition 5) with tight scheduling (Definition 12), meaningful (Definition 6) and transparent (Definition 23) local functionalities. The storage domains in the protection domain are hiding (Definition 2), modification-aware (Definition 3) and have limited control (Definition 4). If the protocol Π satisfies all abstraction assumptions:
- is well-formed (Definition 18) and in a canonical form (Definition 21),
- is robust against malformed inputs (Definition 14),
- is secure against rushing (Definition 16),
- is output-isolated (Definition 24)
and the environment class is embeddable into for the class of adversaries and then security in the abstract model is necessary and sufficient for security in the hybrid model.
Proof.
Necessity. Trivial that just forwards the inputs and outputs to and from and has to be a valid protocol. Therefore, is a valid class of adversaries against as they are formed by the trivial and a generic adversary in . If then by security definition, the protocol must be secure against among all other environments and from Corollary 4 the protocol running with environment in in the hybrid model can be transformed to the abstract model.
Sufficiency. Sufficiency in the abstract model results from the reversability of the series of transformations we have made from the hybrid to the abstract world. If all environments of interest are embeddable, then we can apply Lemma 13 showing equivalence of the abstract execution model and the limited control model. The rest of the sufficiency follows from Corollary 5 showing that we can move from limited control model to the hybrid model. Hence, in total a security proof in the abstract model can be translated to a security argument of the same protocol in the hybrid model. □
4. Discussion
With the transformations in Section 3 we have established the required transformations , and from Section 2.3 and shown their semi-inverses. Therefore, we have shown the abstract execution model and that it suffices to prove security in the abstract model when making a series of assumptions about the protection domain and the protocol.
On the side of the protection domain, we assume that all ideal functionalities are in a canonical form (Definition 5) and have tight scheduling (Definition 12), local functionalities are meaningful (Definition 6) and transparent (Definition 23), secure storage domains are hiding (Definition 2), modification-aware (Definition 3) and have limited control (Definition 4). These are mostly reasonable properties, however, they should be explicitly shown for the protection domain (the framework for programmable MPC) that is used. On the other hand, one can simply assume these properties as the requirements of their new algorithm for secure computation. If no other preconditions are made, then the algorithm can be securely implemented on any framework meeting these requirements. However, note that often it is reasonable to make additional requirements for the protection domain, for example, to specify the data types for which the algorithm works.
On the protocol side, we assume that it is well-formed (Definition 18) and in a canonical form (Definition 21), robust against malformed inputs (Definition 14), secure against rushing (Definition 16) and output-isolated (Definition 24). We have argued that some of these are natural or easily achievable requirements of the protocol or the concrete protocol implementation. Security against rushing is achievable for protocols where some honest party is always included in the subprotocols (Theorem 5). The main open question is the output isolation, which we have shown to hold for several special cases but for some protocols this property should be proven in addition to the security proof in the abstract model. Nevertheless, we have shown that secure protocols are output isolated (Theorem 12), thus such a proof must exist for all protocols both in order to use our framework as well as to prove security at all. In addition, most primitive functionalities return outputs as soon as they are computed and are therefore always output-isolated (Lemma 5).
We can consider the proposed sorting algorithm in Algorithm 2 as a concrete example of these properties and their use. This algorithm assumes that we have a protection domain that can shuffle values, compute comparisons and publish values. We expect all these to be represented as some canonical ideal functionalities. A common way to read this protocol is that parties execute these operations together. We also expect that the parties only start the computations once they have the input values and that they only write the outputs of the computations to the derived variables. In addition, they continue with the next instruction only when they have completed the previous one. Therefore, when reading this protocol description we already assume it to be executed so that it is well-formed. It is also in a canonical form because the conditional decision in the output is done based on a public value and we can assume that the implementation assures that the memory is aligned. We do not usually think of robustness against malformed inputs, however, we indirectly assume that the inputs are correct and all errors from incorrect formats are handled by the computation implementation outside the algorithm itself. In secure multiparty computation, we are concerned with cases where some participant is honest, thus we also achieve security against rushing when executing this algorithm. The main problem with this algorithm is output isolation. It is not immediately clear that it is output isolated since the values and are computed several steps before they are returned. Hence, we should either modify the algorithm to include a step to re-randomise the secure representation of the values right before returning them or prove output-isolation independently.
The abstract model is quite restricted, the adversary can manage the timing of the ideal functionalities used by the protocol as well as the input and output timing of . In addition, the adversary has access to the corrupted parties values in and other access depending on the storage domain. For reasonable schemes, either we consider a passive adversary that does not modify or we use a robust or verifiable scheme that ensures that the adversary has limited control over the shared values as long as the set of corrupted parties satisfies the bounds set by the storage domain. Therefore, this satisfies the part of the intuition that in security proofs of the protocol, the focus should be on the values that are made available to any party and can therefore also be seen by the adversary corrupting that party. Note that this also means that, in fact, the part of the protocol that needs to be analysed is the semantics of the published values and not really the cryptographic properties of the secure computation framework where the protocol is executed. One could say that we are left with security proofs without any cryptography.
If the protocol has one round, e.g., it receives some inputs and then gives outputs and finishes its work like common for protocols implementing arithmetic operations, then they are usually output-isolated. If, in addition, the execution of subprotocols in one instance of the protocol has sequential scheduling then the adversary can not alter the order in which the values are published. Therefore, being able to simulate all visible values is sufficient. Note that most protocols for secure computation fall into this category and, therefore, the intuitive proofs are easy to carry to formal proofs. However, if the scheduling is concurrent or there are many rounds, then at the very least the values should be simulated within the rounds in which they are computed and their order may depend on the scheduling. More details might be required depending on the model.
Author Contributions
Conceptualisation, S.L. and P.P.-R.; Methodology, S.L. and P.P.-R.; Writing—original draft, S.L. and P.P.-R.; Writing—review and editing, S.L. and P.P.-R. Both authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Estonian Centre of Excellence in IT (EXCITE) and by the Estonian Personal Research Grants PRG49 and PRG920.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MDPI | Multidisciplinary Digital Publishing Institute |
| MPC | Secure multiparty computation |
| ABB | Arithmetic black box |
| RSIM | Reactive simulatability |
| UC | Universal composability |
| Secret sharing of value x | |
| Environment | |
| Class of environments | |
| Adversary | |
| Class of adversaries | |
| Protocol | |
| Inner environment representing computations in the secure computation framework | |
| Class of protocols | |
| Protocol participant i | |
| Code interpreter of | |
| Corruption manager for | |
| Secure setup functionality | |
| Ideal functionality | |
| Ideal functionality of a protection domain | |
| Input–output functionality | |
| Local functionality p for | |
| Local functionality on values | |
| Secret sharing functionality | |
| Reconstruction functionality | |
| Machine inside that manages timing of | |
| Machine inside that manages timing of | |
| Machine inside that manages access to | |
| Extractor | |
| Storage of values in a storage domain | |
| Storage of shares in a storage domain | |
| Memory | |
| Memory holding only values | |
| Internal state of the protocol participant | |
| Global state combining of all participants | |
| State kept in | |
| m | Protocol message |
| Transformations of the adversary | |
| Transformations of the environment | |
| Transformation defined in the security proof | |
| Storage domain called | |
| Adversary structure for storage domain | |
| Modification operator in storage domain | |
| ⊥ | Failure symbol denoting invalid values |
| Configuration i |
Appendix A. Buffers Leaking Message Annotations
We specify leaky buffers using standard RSIM components. The hearth of the construction is a tag leaking machine and three buffers for input, output and leakage, see Figure A1. The machine accepts pairs of strings as inputs. When receives from the buffer , the pair is written to an output buffer and the annotation t is written to the sender-clocked buffer . There are two ports for clocking the leaky buffer. The first port determines when the annotation arrives to . The second port controls when and in which order message pairs are written to the port .
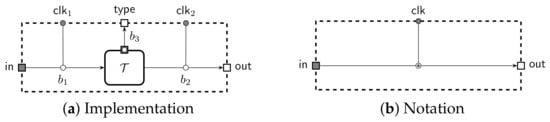
Figure A1.
Collection implementing a leaky buffer and the corresponding notation.
Appendix B. Two Ways to Specify Ideal Functionalities
Two equivalent ways to depict ideal functionality are given in Figure A2. Commonly, one specifies the ideal functionality as a single machine . Alternatively, we can specify the ideal functionality as a special case of the hybrid protocol execution from Section 3.1.1 with just one ideal functionality The environment provides inputs to parties who forward these directly to . Whenever sends a message to , it forwards it to the environment. Let and denote the these alternative configurations.
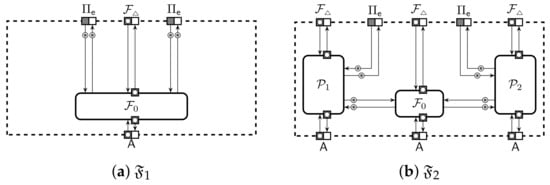
Figure A2.
Two alternatives for specifying ideal functionality.
Lemma A1.
For coherent adversaries configurations and in Figure A2 are equivalent.
Proof.
In both configurations, gets exactly the same inputs including tags and the adversary controls when receives its inputs. However, the message travels through two leaky buffers in the configuration instead of one in . Adaptation of an adversary from to is straightforward. The new adversary clocks buffers between and as soon as possible and then clocks buffers to the same as .
It is straightforward to simulate clocking for in . However, in there is no way to corrupt the party directly in . For coherent adversary corrupting in also means corrupting in , hence any modifications can be done in in . □
Appendix C. Combined Interpreter with Simplified Clocking
The new memory-isolated model makes many clocking signals redundant. Adversarial control over buffer clocking is necessary only if this allows to control the execution order for the protocols or provides a time slot to carry out adversarial actions. Therefore, we simplify the model further by replacing all interpreters with a joint interpreter that combines some buffers. The simplest construction is such where the interpreter is just a collection of interpreters . For most protocol specifications, this model can be further simplified to the configuration depicted in the left of Figure A3 and most sequential protocol specifications to the configuration depicted on the right.
As the original contains modules and which combine and broadcast DmaCall-s and potentially interact with the adversary, we can extract machines and which only combine or broadcast DmaCall-s. We push these into the interpreter . The use of sender clocked buffers forces us to add dummy buffers for passing control from to and from to . However, the corresponding changes are straightforward and guarantee equivalence for passive adversaries who ignore leaks.
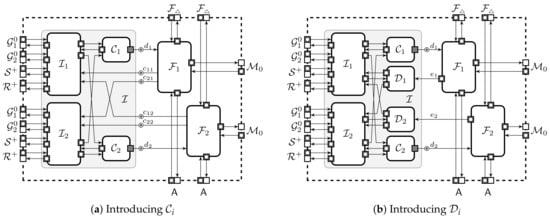
Figure A3.
Joining the interpreters by merging outgoing and incoming buffers.
In many cases, the adversary can simulate the leaks of and mimic the effect of multiple clockings with a single buffer. The adversary must always know what is the next DmaCall when receives an input and when inside is going to start a new round of computations. This is clearly true for sequential protocol implementations, but it also holds for many concurrent implementations. We can introduce if we additionally show that the outcome of the execution cannot be influenced by clockings of . This is evident for sequential protocol implementations, as only a single subprotocol instance is active at all times and thus delays in clockings just pause the protocol execution.
References
- Bogdanov, D.; Laur, S.; Willemson, J. Sharemind: A Framework for Fast Privacy-Preserving Computations. In Lecture Notes in Computer Science, Proceedings of the Computer Security—ESORICS 2008, 13th European Symposium on Research in Computer Security, Málaga, Spain, 6–8 October 2008; Jajodia, S., López, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5283, pp. 192–206. [Google Scholar] [CrossRef] [Green Version]
- Damgård, I.; Pastro, V.; Smart, N.P.; Zakarias, S. Multiparty Computation from Somewhat Homomorphic Encryption. In Lecture Notes in Computer Science, Proceedings of the Advances in Cryptology—CRYPTO 2012—32nd Annual Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2012; Safavi-Naini, R., Canetti, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7417, pp. 643–662. [Google Scholar] [CrossRef] [Green Version]
- Bogdanov, D. Sharemind: Programmable Secure Computations with Practical Applications. Ph.D. Thesis, University of Tartu, Tartu, Estonia, 2013. [Google Scholar]
- Demmler, D.; Schneider, T.; Zohner, M. ABY—A Framework for Efficient Mixed-Protocol Secure Two-Party Computation. In Proceedings of the 22nd Annual Network and Distributed System Security Symposium, NDSS 2015, San Diego, CA, USA, 8–11 February 2015. [Google Scholar]
- Alexandra Institute. FRESCO—A Framework for Efficient Secure Computation. Available online: http://github.com/aicis/fresco (accessed on 20 August 2021).
- KU Leuven. SCALE-MAMBA Software. Available online: https://github.com/KULeuven-COSIC/SCALE-MAMBA (accessed on 20 August 2021).
- Keller, M. MP-SPDZ: A Versatile Framework for Multi-Party Computation. In Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security—CCS’20, Virtual Event, 9–13 November 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 1575–1590. [Google Scholar] [CrossRef]
- Bogetoft, P.; Christensen, D.L.; Damgård, I.; Geisler, M.; Jakobsen, T.P.; Krøigaard, M.; Nielsen, J.D.; Nielsen, J.B.; Nielsen, K.; Pagter, J.; et al. Secure Multiparty Computation Goes Live. In Lecture Notes in Computer Science, Proceedings of the Financial Cryptography and Data Security, 13th International Conference, FC 2009, Accra Beach, Barbados, 23–26 February 2009; Revised Selected Papers; Dingledine, R., Golle, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5628, pp. 325–343. [Google Scholar] [CrossRef] [Green Version]
- Mohassel, P.; Zhang, Y. SecureML: A System for Scalable Privacy-Preserving Machine Learning. In Proceedings of the 2017 IEEE Symposium on Security and Privacy, SP 2017, San Jose, CA, USA, 22–26 May 2017; pp. 19–38. [Google Scholar] [CrossRef]
- Bogdanov, D.; Kamm, L.; Kubo, B.; Rebane, R.; Sokk, V.; Talviste, R. Students and Taxes: A Privacy-Preserving Study Using Secure Computation. PoPETs 2016, 2016, 117–135. [Google Scholar] [CrossRef] [Green Version]
- Archer, D.W.; Bogdanov, D.; Lindell, Y.; Kamm, L.; Nielsen, K.; Pagter, J.I.; Smart, N.P.; Wright, R.N. From Keys to Databases—Real-World Applications of Secure Multi-Party Computation. Comput. J. 2018, 61, 1749–1771. [Google Scholar] [CrossRef] [Green Version]
- Mohassel, P.; Rindal, P. ABY3: A Mixed Protocol Framework for Machine Learning. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, CCS 2018, Toronto, ON, Canada, 15–19 October 2018; Lie, D., Mannan, M., Backes, M., Wang, X., Eds.; ACM: New York, NY, USA, 2018; pp. 35–52. [Google Scholar] [CrossRef]
- Laud, P.; Pankova, A. Privacy-preserving record linkage in large databases using secure multiparty computation. BMC Med. Genom. 2018, 11, 35–55. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Canetti, R. Universally Composable Security: A New Paradigm for Cryptographic Protocols. In Proceedings of the 42nd Annual Symposium on Foundations of Computer Science, FOCS 2001, Las Vegas, NV, USA, 14–17 October 2001; pp. 136–145. [Google Scholar] [CrossRef] [Green Version]
- Damgård, I.; Nielsen, J.B. Universally Composable Efficient Multiparty Computation from Threshold Homomorphic Encryption. In Lecture Notes in Computer Science, Proceedings of the Advances in Cryptology—CRYPTO 2003, 23rd Annual International Cryptology Conference, Santa Barbara, CA, USA, 17–21 August 2003; Boneh, D., Ed.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2729, pp. 247–264. [Google Scholar] [CrossRef] [Green Version]
- Lipmaa, H.; Toft, T. Secure Equality and Greater-Than Tests with Sublinear Online Complexity. In Lecture Notes in Computer Science, Proceedings of the Automata, Languages, and Programming—40th International Colloquium, ICALP 2013, Riga, Latvia, 8–12 July 2013; Fomin, F.V., Freivalds, R., Kwiatkowska, M.Z., Peleg, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7966, pp. 645–656. [Google Scholar] [CrossRef]
- Escudero, D.; Ghosh, S.; Keller, M.; Rachuri, R.; Scholl, P. Improved Primitives for MPC over Mixed Arithmetic-Binary Circuits. In Lecture Notes in Computer Science, Proceedings of the Advances in Cryptology—CRYPTO 2020—40th Annual International Cryptology Conference, CRYPTO 2020, Santa Barbara, CA, USA, 17–21 August 2020; Micciancio, D., Ristenpart, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; Volume 12171, pp. 823–852. [Google Scholar] [CrossRef]
- Damgård, I.; Escudero, D.; Frederiksen, T.K.; Keller, M.; Scholl, P.; Volgushev, N. New Primitives for Actively-Secure MPC over Rings with Applications to Private Machine Learning. In Proceedings of the 2019 IEEE Symposium on Security and Privacy, SP 2019, San Francisco, CA, USA, 19–23 May 2019; pp. 1102–1120. [Google Scholar] [CrossRef]
- Kamm, L.; Willemson, J. Secure Floating-Point Arithmetic and Private Satellite Collision Analysis. Int. J. Inf. Secur. 2015, 14, 531–548. [Google Scholar] [CrossRef] [Green Version]
- Veugen, T.; Abspoel, M. Secure integer division with a private divisor. Proc. Priv. Enhancing Technol. 2021, 2021, 339–349. [Google Scholar] [CrossRef]
- Catrina, O.; de Hoogh, S. Improved Primitives for Secure Multiparty Integer Computation. In Lecture Notes in Computer Science, Proceedings of the Security and Cryptography for Networks, 7th International Conference, SCN 2010, Amalfi, Italy, 13–15 September 2010; Garay, J.A., Prisco, R.D., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6280, pp. 182–199. [Google Scholar] [CrossRef]
- Nishide, T.; Ohta, K. Multiparty Computation for Interval, Equality, and Comparison Without Bit-Decomposition Protocol. In Lecture Notes in Computer Science, Proceedings of the Public Key Cryptography—PKC 2007, 10th International Conference on Practice and Theory in Public-Key Cryptography, Beijing, China, 16–20 April 2007; Okamoto, T., Wang, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4450, pp. 343–360. [Google Scholar] [CrossRef] [Green Version]
- Damgård, I.; Fitzi, M.; Kiltz, E.; Nielsen, J.B.; Toft, T. Unconditionally Secure Constant-Rounds Multi-party Computation for Equality, Comparison, Bits and Exponentiation. In Lecture Notes in Computer Science, Proceedings of the Theory of Cryptography, Third Theory of Cryptography Conference, TCC 2006, New York, NY, USA, 4–7 March 2006; Halevi, S., Rabin, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3876, pp. 285–304. [Google Scholar] [CrossRef] [Green Version]
- Canetti, R.; Rabin, T. Universal Composition with Joint State. In Lecture Notes in Computer Science, Proceedings of the Advances in Cryptology—CRYPTO 2003, 23rd Annual International Cryptology Conference, Santa Barbara, CA, USA, 17–21 August 2003; Boneh, D., Ed.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2729, pp. 265–281. [Google Scholar] [CrossRef] [Green Version]
- Pfitzmann, B.; Waidner, M. A Model for Asynchronous Reactive Systems and its Application to Secure Message Transmission. In Proceedings of the 2001 IEEE Symposium on Security and Privacy—SP’01, Oakland, CA, USA, 14–16 May 2001; pp. 184–200. [Google Scholar]
- Backes, M.; Pfitzmann, B.; Waidner, M. A General Composition Theorem for Secure Reactive Systems. In Lecture Notes in Computer Science, Proceedings of the Theory of Cryptography, First Theory of Cryptography Conference, TCC 2004, Cambridge, MA, USA, 19–21 February 2004; Naor, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 2951, pp. 336–354. [Google Scholar] [CrossRef] [Green Version]
- Backes, M.; Pfitzmann, B.; Waidner, M. The reactive simulatability (RSIM) framework for asynchronous systems. Inf. Comput. 2007, 205, 1685–1720. [Google Scholar] [CrossRef] [Green Version]
- Goldreich, O. The Foundations of Cryptography—Volume 2: Basic Applications; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Canetti, R. Security and Composition of Multiparty Cryptographic Protocols. J. Cryptol. 2000, 13, 143–202. [Google Scholar] [CrossRef]
- Micali, S.; Rogaway, P. Secure Computation (Abstract). In Lecture Notes in Computer Science, Proceedings of the Advances in Cryptology—CRYPTO’91, 11th Annual International Cryptology Conference, Santa Barbara, CA, USA, 11–15 August 1991; Feigenbaum, J., Ed.; Springer: Berlin/Heidelberg, Germany, 1991; Volume 576, pp. 392–404. [Google Scholar] [CrossRef] [Green Version]
- Beaver, D. Secure Multiparty Protocols and Zero-Knowledge Proof Systems Tolerating a Faulty Minority. J. Cryptol. 1991, 4, 75–122. [Google Scholar] [CrossRef]
- Canetti, R.; Feige, U.; Goldreich, O.; Naor, M. Adaptively Secure Multi-Party Computation. In Proceedings of the Twenty-Eighth Annual ACM Symposium on the Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; Miller, G.L., Ed.; ACM: New York, NY, USA, 1996; pp. 639–648. [Google Scholar] [CrossRef]
- Zikas, V.; Hauser, S.; Maurer, U.M. Realistic Failures in Secure Multi-party Computation. In Lecture Notes in Computer Science, Proceedings of the Theory of Cryptography, 6th Theory of Cryptography Conference, TCC 2009, San Francisco, CA, USA, 15–17 March 2009; Reingold, O., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5444, pp. 274–293. [Google Scholar] [CrossRef] [Green Version]
- Gordon, S.D.; Katz, J. Complete Fairness in Multi-party Computation without an Honest Majority. In Lecture Notes in Computer Science, Proceedings of the Theory of Cryptography, 6th Theory of Cryptography Conference, TCC 2009, San Francisco, CA, USA, 15–17 March 2009; Reingold, O., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5444, pp. 19–35. [Google Scholar] [CrossRef] [Green Version]
- Cohen, R.; Lindell, Y. Fairness Versus Guaranteed Output Delivery in Secure Multiparty Computation. J. Cryptol. 2017, 30, 1157–1186. [Google Scholar] [CrossRef]
- Kiraz, M.; Schoenmakers, B. A protocol issue for the malicious case of Yao’s garbled circuit construction. In Proceedings of the 27th Symposium on Information Theory in the Benelux, Noordwijk, The Netherlands, 8–9 June 2006; pp. 283–290. [Google Scholar]
- Mohassel, P.; Franklin, M.K. Efficiency Tradeoffs for Malicious Two-Party Computation. In Lecture Notes in Computer Science, Proceedings of the Public Key Cryptography—PKC 2006, 9th International Conference on Theory and Practice of Public-Key Cryptography, New York, NY, USA, 24–26 April 2006; Yung, M., Dodis, Y., Kiayias, A., Malkin, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3958, pp. 458–473. [Google Scholar] [CrossRef] [Green Version]
- Aumann, Y.; Lindell, Y. Security Against Covert Adversaries: Efficient Protocols for Realistic Adversaries. In Lecture Notes in Computer Science, Proceedings of the Theory of Cryptography, 4th Theory of Cryptography Conference, TCC 2007, Amsterdam, The Netherlands, 21–24 February 2007; Vadhan, S.P., Ed.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4392, pp. 137–156. [Google Scholar] [CrossRef] [Green Version]
- Küsters, R.; Datta, A.; Mitchell, J.C.; Ramanathan, A. On the Relationships between Notions of Simulation-Based Security. J. Cryptol. 2008, 21, 492–546. [Google Scholar] [CrossRef]
- Goyal, V.; Gupta, D.; Sahai, A. Concurrent Secure Computation via Non-Black Box Simulation. In Lecture Notes in Computer Science, Proceedings of the Advances in Cryptology—CRYPTO 2015—35th Annual Cryptology Conference, Santa Barbara, CA, USA, 16–20 August 2015; Gennaro, R., Robshaw, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9216, pp. 23–42. [Google Scholar] [CrossRef]
- Kiyoshima, S. Non-black-box Simulation in the Fully Concurrent Setting, Revisited. J. Cryptol. 2019, 32, 393–434. [Google Scholar] [CrossRef]
- Pass, R. Simulation in Quasi-Polynomial Time, and Its Application to Protocol Composition. In Lecture Notes in Computer Science, Proceedings of the Advances in Cryptology—EUROCRYPT 2003, International Conference on the Theory and Applications of Cryptographic Techniques, Warsaw, Poland, 4–8 May 2003; Biham, E., Ed.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2656, pp. 160–176. [Google Scholar] [CrossRef] [Green Version]
- Barak, B.; Sahai, A. How To Play Almost Any Mental Game Over The Net—Concurrent Composition via Super-Polynomial Simulation. In Proceedings of the 46th Annual IEEE Symposium on Foundations of Computer Science (FOCS 2005), Pittsburgh, PA, USA, 23–25 October 2005; pp. 543–552. [Google Scholar] [CrossRef]
- Oren, Y. On the Cunning Power of Cheating Verifiers: Some Observations about Zero Knowledge Proofs (Extended Abstract). In Proceedings of the 28th Annual Symposium on Foundations of Computer Science, Los Angeles, CA, USA, 27–29 October 1987; pp. 462–471. [Google Scholar] [CrossRef]
- Canetti, R. Universally Composable Security: A New Paradigm for Cryptographic Protocols. Cryptology ePrint Archive, Report 2000/067. 2000. Available online: https://eprint.iacr.org/2000/067 (accessed on 20 August 2021).
- Maurer, U.; Renner, R. Abstract Cryptography. In Proceedings of the Innovations in Computer Science—ICS 2011, Beijing, China, 7–9 January 2011; Chazelle, B., Ed.; Tsinghua University Press: Beijing, China, 2011; pp. 1–21. [Google Scholar]
- Küsters, R. Simulation-Based Security with Inexhaustible Interactive Turing Machines. In Proceedings of the 19th IEEE Computer Security Foundations Workshop, (CSFW-19 2006), Venice, Italy, 5–7 July 2006; pp. 309–320. [Google Scholar] [CrossRef]
- Hofheinz, D.; Shoup, V. GNUC: A New Universal Composability Framework. J. Cryptol. 2015, 28, 423–508. [Google Scholar] [CrossRef] [Green Version]
- Böhl, F.; Unruh, D. Symbolic universal composability. J. Comput. Secur. 2016, 24, 1–38. [Google Scholar] [CrossRef]
- Camenisch, J.; Krenn, S.; Küsters, R.; Rausch, D. iUC: Flexible Universal Composability Made Simple. In Lecture Notes in Computer Science, Proceedings of the Advances in Cryptology—ASIACRYPT 2019—25th International Conference on the Theory and Application of Cryptology and Information Security, Kobe, Japan, 8–12 December 2019; Galbraith, S.D., Moriai, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 11923, pp. 191–221. [Google Scholar] [CrossRef]
- Barak, B.; Canetti, R.; Lindell, Y.; Pass, R.; Rabin, T. Secure Computation Without Authentication. In Lecture Notes in Computer Science, Proceedings of the Advances in Cryptology—CRYPTO 2005: 25th Annual International Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2005; Shoup, V., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3621, pp. 361–377. [Google Scholar] [CrossRef] [Green Version]
- Canetti, R.; Cohen, A.; Lindell, Y. A Simpler Variant of Universally Composable Security for Standard Multiparty Computation. In Lecture Notes in Computer Science, Proceedings of the Advances in Cryptology—CRYPTO 2015—35th Annual Cryptology Conference, Santa Barbara, CA, USA, 16–20 August 2015; Gennaro, R., Robshaw, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9216, pp. 3–22. [Google Scholar] [CrossRef] [Green Version]
- Yao, A.C. Protocols for Secure Computations (Extended Abstract). In Proceedings of the 23rd Annual Symposium on Foundations of Computer Science, Chicago, IL, USA, 3–5 November 1982; pp. 160–164. [Google Scholar] [CrossRef]
- Beaver, D. Foundations of Secure Interactive Computing. In Lecture Notes in Computer Science, Proceedings of the Advances in Cryptology—CRYPTO’91, 11th Annual International Cryptology Conference, Santa Barbara, CA, USA, 11–15 August 1991; Feigenbaum, J., Ed.; Springer: Berlin/Heidelberg, Germany, 1991; Volume 576, pp. 377–391. [Google Scholar] [CrossRef] [Green Version]
- Bellare, M.; Rogaway, P. Robust Computational Secret Sharing and a Unified Account of Classical Secret-Sharing Goals. In Proceedings of the 14th ACM Conference on Computer and Communications Security—CCS’07, Alexandria, VA, USA, 2 November–31 October 2007; Association for Computing Machinery: New York, NY, USA, 2007; pp. 172–184. [Google Scholar] [CrossRef] [Green Version]
- Damgård, I.; Nielsen, J.B. Adaptive versus static security in the UC model. In Proceedings of the International Conference on Provable Security, Hong Kong, China, 9–10 October 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 10–28. [Google Scholar]
- Genkin, D.; Ishai, Y.; Prabhakaran, M.; Sahai, A.; Tromer, E. Circuits resilient to additive attacks with applications to secure computation. In Proceedings of the Symposium on Theory of Computing, STOC 2014, New York, NY, USA, 31 May–3 June 2014; Shmoys, D.B., Ed.; ACM: New York, NY, USA, 2014; pp. 495–504. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).