Hardware Performance Evaluation of Authenticated Encryption SAEAES with Threshold Implementation
Abstract
1. Introduction
1.1. Purpose and Approach
1.2. Contributions
- (I)
- Identification of design challenges in extending AES implementation to SAEAES (Section 4) Our design is based on the 3-share and uniform TI of AES using the generalized changing of the guards [27]. We identify that the mode of operation enforces the byte order, making the conventional row-oriented serialization inefficient [23]. Also, the mode of operation should preserve the secret key that the on-the-fly key schedule overwrites.
- (II)
- Column-oriented AES implementation (Section 5.2) We propose a new AES circuit architecture that uses the column-oriented data serialization to address the aforementioned incompatibility with the row-oriented serialization.
- (III)
- The first SAEAES implementation with threshold implementation (Section 5) We show the first TI of SAEAES that uses the column-oriented serialization and the 3-share and uniform AES S-box. The design has an independent key store for preserving the secret key until the next AES call.
- (IV)
- Improved TI of key array (Section 5.5) We show the concrete realization of the key array for TI that reduces the register size by 216 bits or 32% from the original design [27].
- (V)
- Performance evaluation and comparison (Section 6) We synthesize our design using a standard cell library to evaluate its circuit area in GE (gate equivalents). We show that our design uses 18,288 GE with TI composed of AES (14,256 GE, 78%), the key store (3422 GE, 19%), and the mode of operation (610 GE, 3%). Compared with the conventional SAEB-GIFT implementation that uses 6229 GE [13], the SAEAES implementation is roughly three times larger. We identify that the non-linear key schedule and the extended states for satisfying uniformity as the major factors for this difference.
1.3. Organization
2. SAEAES
2.1. Authenticated Encryption
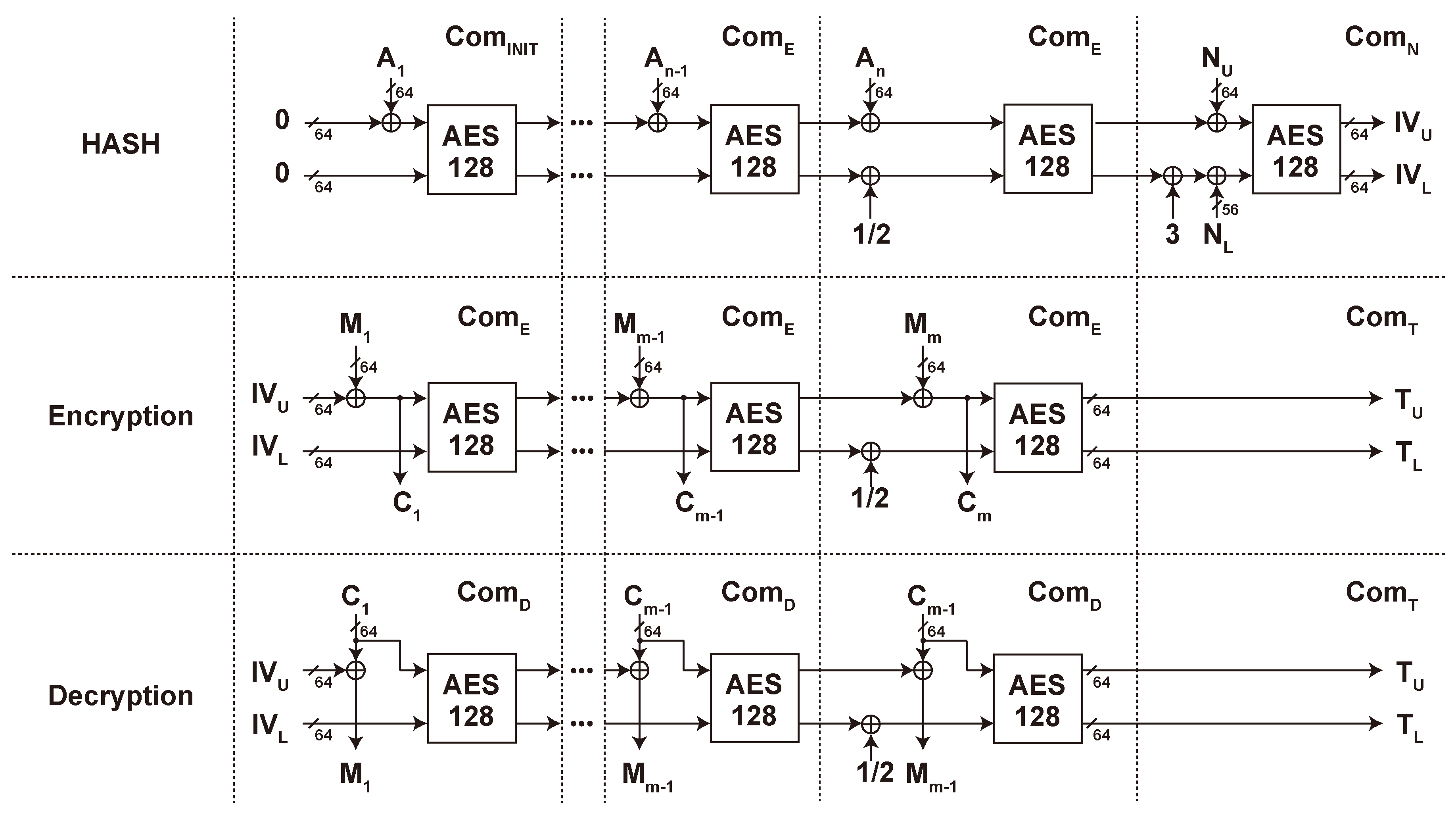
2.2. SAEAES and its Algorithm
- (1)
- Minimum state size No extra memory in addition to AES, which reduces the register size in hardware implementation.
- (2)
- Inverse free No need for AES decryption. This reduces the cost of implementing inverse AES operations and overhead for selectors or conditional branches.
- (3)
- XOR only The extra operation in addition to AES is XOR only, which is more efficient than other options, such as multiplication in AES-GCM.
- (4)
- Online The message and ciphertext blocks are scanned only once. There is no need for a buffer storing the blocks until the second scan.
- (5)
- Efficient handling of repeated associated data SAEAES can skip shortcut some operations for several Encryption/Decryption with the same (i.e., repeated) associated data.
2.3. Hardware Implementations of SAEAES
3. Threshold Implementation of AES
3.1. Side-Channel Attack and Countermeasure
3.2. Threshold Implementation
- (1)
- Non-completeness The sharing is non-complete if each of , , and receives only a proper subset of the input share . The sharing given by Equation (1) satisfies non-completeness because , , and do not accept , , and , respectively.
- (2)
- Correctness The sharing is correct if it represents the original function f, i.e., .
- (3)
- Uniformity The sharing is said to satisfy uniformity if it preserves the uniform distribution: a uniform sharing generates a uniformly distributed output share given a uniformly distributed input share. The uniform distribution of the input share is the necessary condition for the TI’s security. With uniformity, we can feed the output share to the next sharing thereby enabling cascaded connection between sharings.
3.2.1. Composing a Sharing for a Target Function
3.2.2. Lack of Uniformity and Refreshing
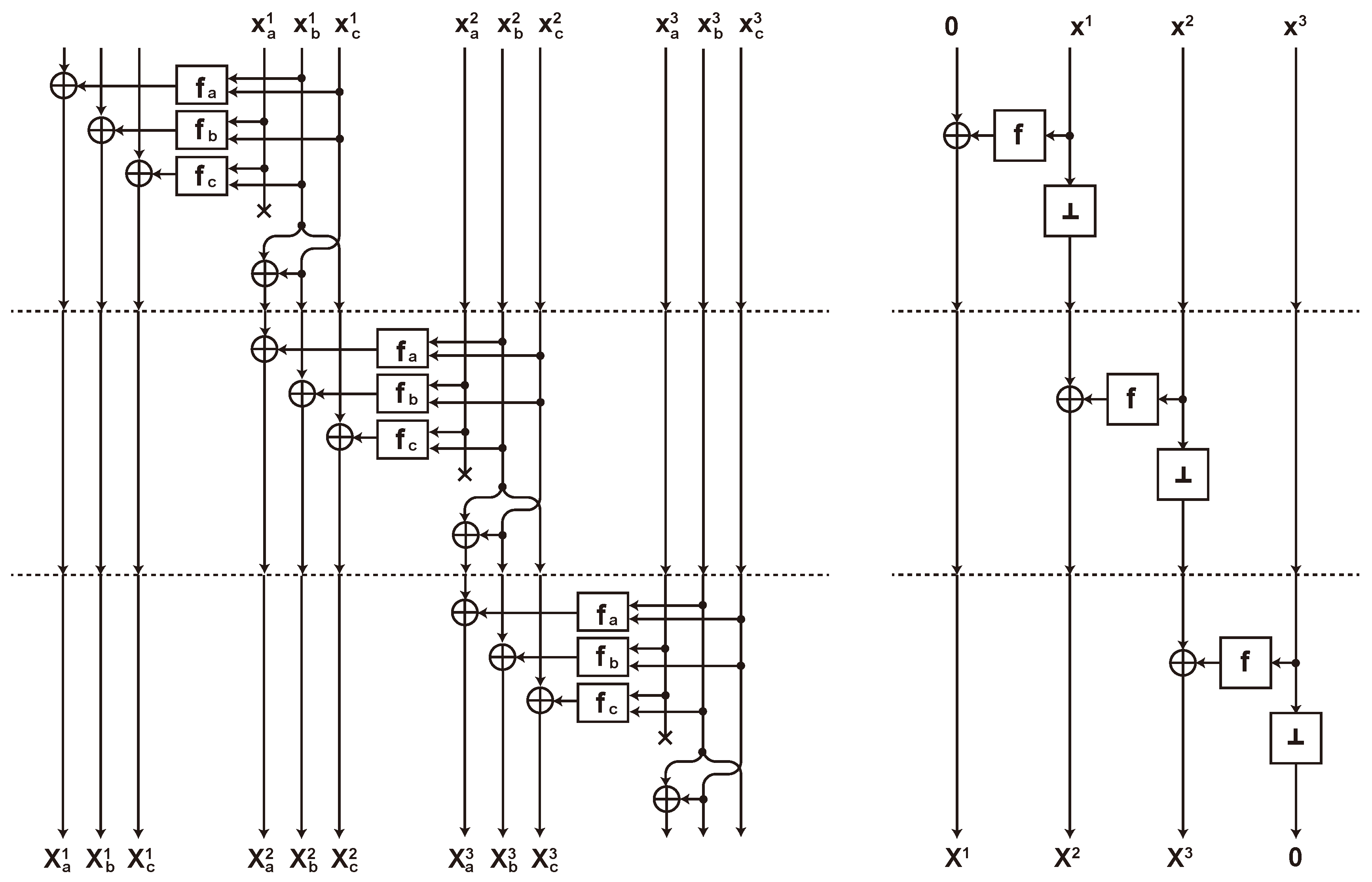
3.3. Changing of the Guards
4. Design Challenges
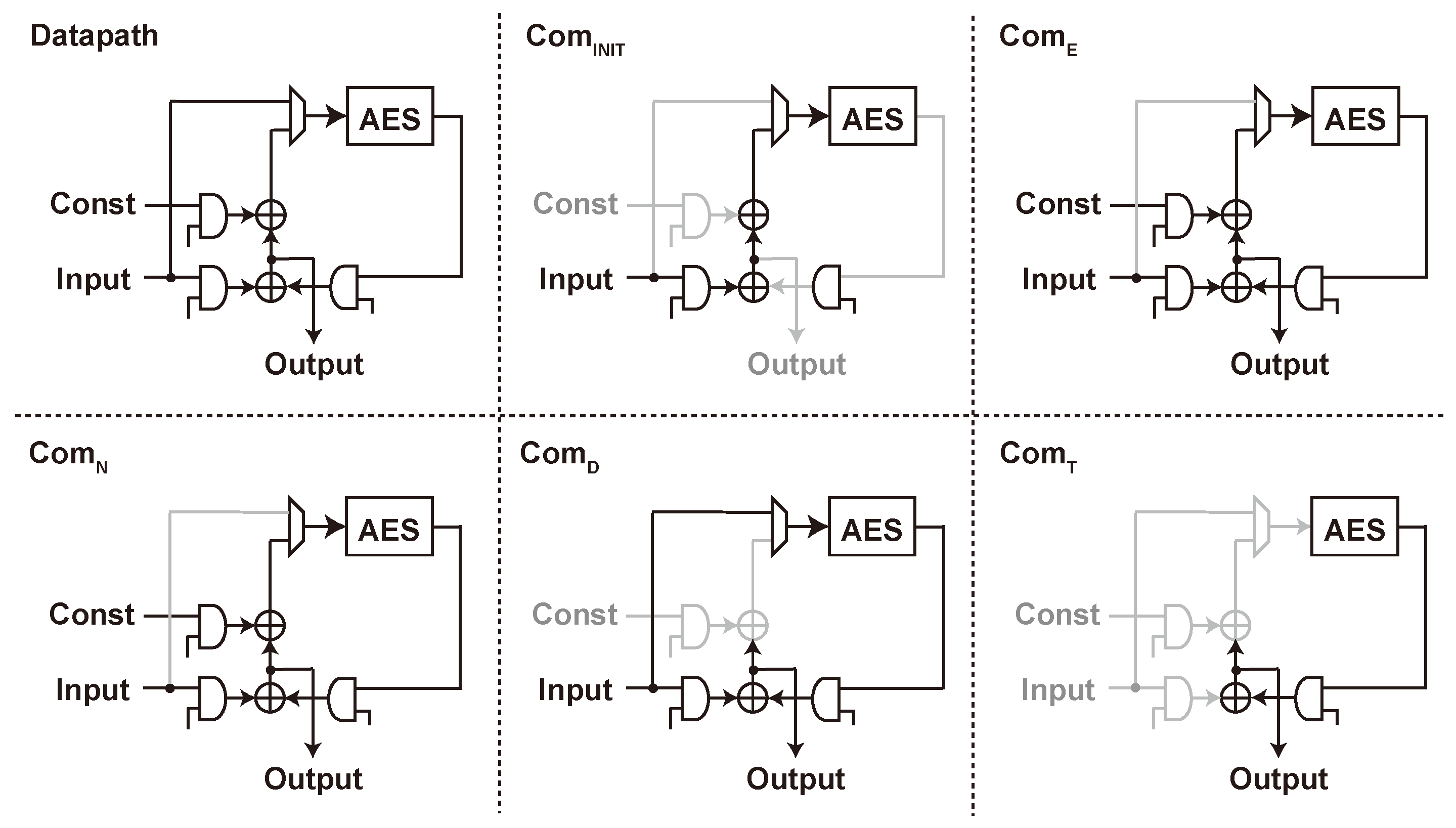
4.1. Byte Order and Serialization
4.2. On-The-Fly Key Schedule
4.3. Scan Flip Flop and Clock Gating
5. Proposed Design
5.1. Design Policy
5.2. Column-Oriented Serialization
5.2.1. State Array
5.2.2. Key Array
5.2.3. Comparing Row-Oriented and Column-Oriented Arrays
5.3. AES Implementation
5.4. SAEAES Implementation
5.5. Threshold Implementation
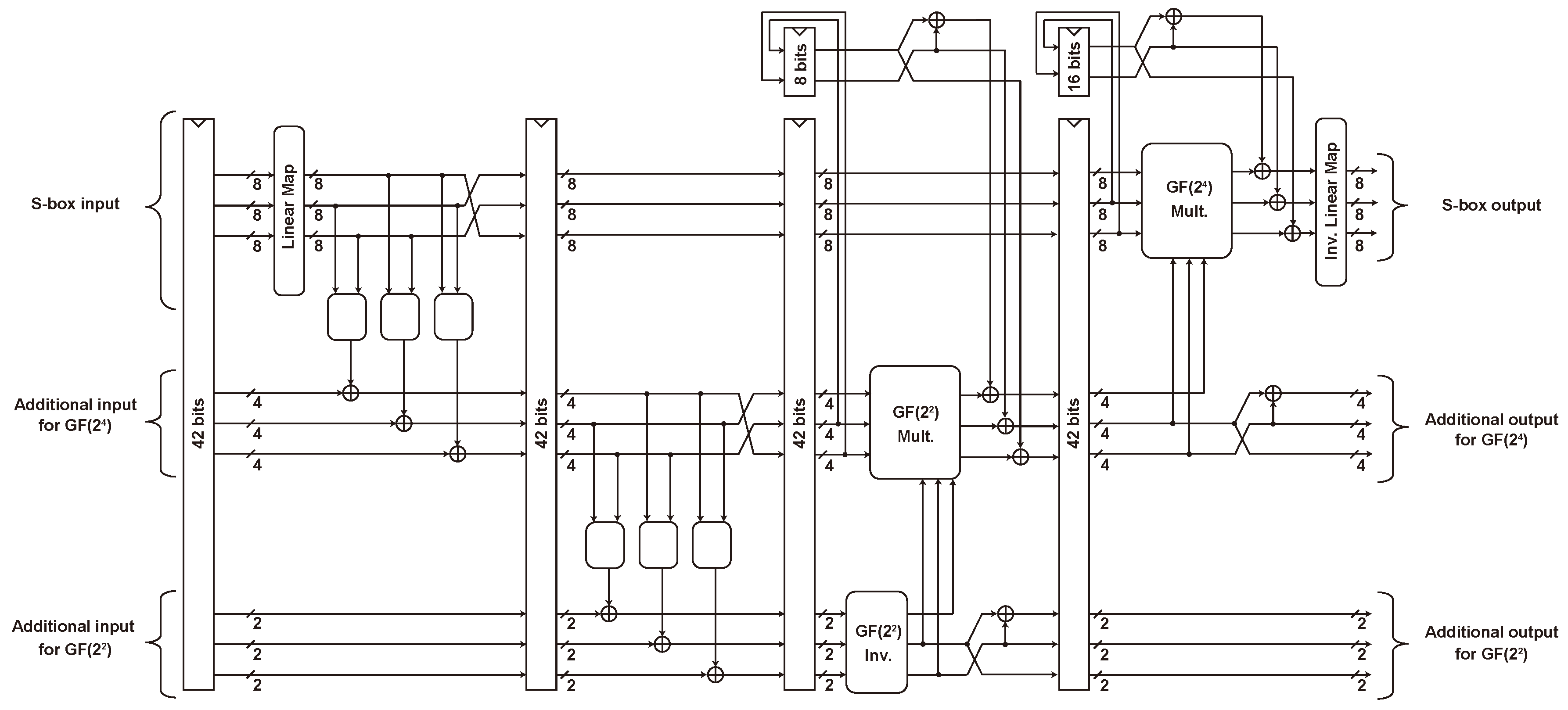
5.5.1. S-box
5.5.2. State Array
5.5.3. Key Array and Key Store
6. Evaluation
6.1. Performance Evaluation
6.2. Comparison with SAEB-GIFT and Other AEADs
6.2.1. Key Store
6.2.2. Non-Linear Key Schedule
6.2.3. S-Box
6.2.4. Other AEADs
7. Conclusions
Funding
Conflicts of Interest
References
- Bogdanov, A.; Knudsen, L.R.; Leander, G.; Paar, C.; Poschmann, A.; Robshaw, M.J.B.; Seurin, Y.; Vikkelsoe, C. PRESENT: An Ultra-Lightweight Block Cipher. In Cryptographic Hardware and Embedded Systems—CHES 2007, Proceedings of the 9th International Workshop, Vienna, Austria, 10–13 September 2007; Paillier, P., Verbauwhede, I., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4727, pp. 450–466. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology (NIST). Submission Requirements and Evaluation Criteria for the Lightweight Cryptography Standardization Process. 2018. Available online: https://csrc.nist.gov/Projects/lightweight-cryptography (accessed on 7 August 2020).
- Kocher, P.C.; Jaffe, J.; Jun, B. Differential Power Analysis. In Advances in Cryptology—CRYPTO ’99, Proceedings of the 19th Annual International Cryptology Conference, Santa Barbara, CA, USA, 15–19 August 1999; Wiener, M.J., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1666, pp. 388–397. [Google Scholar] [CrossRef]
- Mangard, S.; Oswald, E.; Popp, T. Power Analysis Attacks—Revealing the Secrets of Smart Cards; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Sönmez, M. On the NIST Lightweight Cryptography Standardization. In Proceedings of the 23rd Workshop on Elliptic Curve Cryptography (ECC 2019), Bochum, Germany, 2–4 December 2019. [Google Scholar]
- Nikova, S.; Rechberger, C.; Rijmen, V. Threshold Implementations Against Side-Channel Attacks and Glitches. In Information and Communications Security, Proceedings of the 8th International Conference, ICICS 2006, Raleigh, NC, USA, 4–7 December 2006; Ning, P., Qing, S., Li, N., Eds.; Lecture Notes in Computer, Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4307, pp. 529–545. [Google Scholar] [CrossRef]
- Ishai, Y.; Sahai, A.; Wagner, D.A. Private Circuits: Securing Hardware against Probing Attacks. In Advances in Cryptology—CRYPTO 2003, Proceedings of the 23rd Annual International Cryptology Conference, Santa Barbara, CA, USA, 17–21 August 2003; Boneh, D., Ed.; Lecture Notes in Computer, Science; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2729, pp. 463–481. [Google Scholar] [CrossRef]
- Groß, H.; Wenger, E.; Dobraunig, C.; Ehrenhöfer, C. Suit up!—Made-to-Measure Hardware Implementations of ASCON. In Proceedings of the 2015 Euromicro Conference on Digital System Design, Funchal, Portugal, 26–28 August 2015; pp. 645–652. [Google Scholar]
- Arribas, V.; Nikova, S.; Rijmen, V. Guards in Action: First-Order SCA Secure Implementations of Ketje Without Additional Randomness. In Proceedings of the 21st Euromicro Conference on Digital System Design (DSD), Prague, Czech Republic, 29–31 August 2018; pp. 492–499. [Google Scholar]
- Caforio, A.; Balli, F.; Banik, S. Energy Analysis of Lightweight AEAD Circuits. Cryptology ePrint Archive, Report 2020/607. 2020. Available online: https://eprint.iacr.org/2020/607 (accessed on 7 August 2020).
- Beyne, T.; Bilgin, B. Uniform First-Order Threshold Implementations. In Proceedings of the International Conference on Selected Areas in Cryptography, Ottawa, ON, Canada, 10–12 August 2016; Springer: Cham, Switzerland, 2016; Volume 10532, pp. 79–98. [Google Scholar]
- Gao, S.; Roy, A.; Oswald, E. Constructing TI-Friendly Substitution Boxes Using Shift-Invariant Permutations. In Topics in Cryptology—CT-RSA 2019, Proceedings of the The Cryptographers’ Track at the RSA Conference 2019, San Francisco, CA, USA, 4–8 March 2019, LNCS; Springer: Berlin/Heidelberg, Germany, 2019; Volume 11405, pp. 433–452. [Google Scholar]
- Naito, Y.; Sugawara, T. Lightweight Authenticated Encryption Mode of Operation for Tweakable Block Ciphers. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2020, 2020, 66–94. [Google Scholar] [CrossRef]
- Naito, Y.; Sasaki, Y.; Sugawara, T. Lightweight Authenticated Encryption Mode Suitable for Threshold Implementation. In Advances in Cryptology—EUROCRYPT 2020, Proceedings of the 39th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, 10–14 May 2020; Canteaut, A., Ishai, Y., Eds.; Part II; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2020; Volume 12106, pp. 705–735. [Google Scholar] [CrossRef]
- Naito, Y.; Matsui, M.; Sugawara, T.; Suzuki, D. SAEB: A Lightweight Blockcipher-Based AEAD Mode of Operation. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2018, 2018, 192–217. [Google Scholar]
- National Institute of Standards and Technology (NIST). Federal Information Processing Standards Publication 197: ADVANCED ENCRYPTION STANDARD (AES); National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 2001.
- Gueron, S.; Jha, A.; Nandi, M. COMET: COunter Mode Encryption with Authentication Tag. 2019. Available online: https://csrc.nist.gov/CSRC/media/Projects/lightweight-cryptography/documents/round-2/spec-doc-rnd2/comet-spec-round2.pdf (accessed on 7 August 2020).
- Chakraborty, B.; Nandi, M. MixFeed. 2019. Available online: https://csrc.nist.gov/CSRC/media/Projects/lightweight-cryptography/documents/round-2/spec-doc-rnd2/mixFeed-spec-round2.pdf (accessed on 7 August 2020).
- Naito, Y.; Matsui, M.; Sakai, Y.; Suzuki, D.; Sakiyama, K.; Sugawara, T. SAEAES. 2019. Available online: https://csrc.nist.gov/CSRC/media/Projects/lightweight-cryptography/documents/round-2/spec-doc-rnd2/SAEAES-spec-round2.pdf (accessed on 7 August 2020).
- Banik, S.; Pandey, S.K.; Peyrin, T.; Sasaki, Y.; Sim, S.M.; Todo, Y. GIFT:A Small Present—Towards Reaching the Limit of Lightweight Encryption. In Proceedings of the Cryptographic Hardware and Embedded Systems (CHES), LNCS, Taipei, Taiwan, 25–28 September 2017; Springer: Berlin/Heidelberg, Germany, 2017; Volume 10529, pp. 321–345. [Google Scholar]
- Beierle, C.; Jean, J.; Kölbl, S.; Leander, G.; Moradi, A.; Peyrin, T.; Sasaki, Y.; Sasdrich, P.; Sim, S.M. The SKINNY Family of Block Ciphers and Its Low-Latency Variant MANTIS. In Advances in Cryptology—CRYPTO 2016, Proceedings of the 36th Annual International Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2016; Robshaw, M., Katz, J., Eds.; Part, II; Lecture Notes in Computer, Science; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9815, pp. 123–153. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology (NIST). Announcing the ADVANCED ENCRYPTION STANDARD (AES). FIPS PUB 197. 2001. Available online: https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.197.pdf (accessed on 7 August 2020).
- Moradi, A.; Poschmann, A.; Ling, S.; Paar, C.; Wang, H. Pushing the Limits: A Very Compact and a Threshold Implementation of AES. In Advances in Cryptology—EUROCRYPT 2011, Proceedings of the 30th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Tallinn, Estonia, 15–19 May 2011; Paterson, K.G., Ed.; Lecture Notes in Computer, Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6632, pp. 69–88. [Google Scholar] [CrossRef]
- Bilgin, B.; Gierlichs, B.; Nikova, S.; Nikov, V.; Rijmen, V. Trade-Offs for Threshold Implementations Illustrated on AES. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2015, 34, 1188–1200. [Google Scholar] [CrossRef]
- Ueno, R.; Homma, N.; Aoki, T. Toward More Efficient DPA-Resistant AES Hardware Architecture Based on Threshold Implementation. In Constructive Side-Channel Analysis and Secure Design, Proceedings of the 8th International Workshop, COSADE 2017, Paris, France, 13–14 April 2017; Guilley, S., Ed.; Revised Selected, Papers; Lecture Notes in Computer, Science; Springer: Berlin/Heidelberg, Germany, 2017; Volume 10348, pp. 50–64. [Google Scholar] [CrossRef]
- Daemen, J. Changing of the Guards: A Simple and Efficient Method for Achieving Uniformity in Threshold Sharing. In Cryptographic Hardware and Embedded Systems—CHES 2017, Proceedings of the 19th International Conference, Taipei, Taiwan, 25–28 September 2017; Fischer, W., Homma, N., Eds.; Lecture Notes in Computer, Science; Springer: Berlin/Heidelberg, Germany, 2017; Volume 10529, pp. 137–153. [Google Scholar] [CrossRef]
- Sugawara, T. 3-Share Threshold Implementation of AES S-box without Fresh Randomness. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2019, 2019, 123–145. [Google Scholar] [CrossRef]
- Balli, F.; Caforio, A.; Banik, S. Low-latency Meets Low-Area: An Improved Bit-Sliding Technique for AES, SKINNY and GIFT. Cryptology ePrint Archive, Report 2020/608. 2020. Available online: https://eprint.iacr.org/2020/608 (accessed on 7 August 2020).
- Dworkin, M. Special Publication 800-38D: Recommendation for Block Cipher Modes of Operation: Galois/Counter Mode (GCM) and GMAC; National Institute of Standards & Technology: Boulder, CO, USA, 2017.
- Salowey, J.; Choudhury, A.; McGrew, D. RFC5288: AES Galois Counter Mode (GCM) Cipher Suites for TLS; Internet Engineering Task Force: Fremont, CA, USA, 2008. [Google Scholar]
- Nikova, S.; Rijmen, V.; Schläffer, M. Secure Hardware Implementation of Nonlinear Functions in the Presence of Glitches. J. Cryptol. 2011, 24, 292–321. [Google Scholar] [CrossRef]
- Wegener, F.; Moradi, A. A First-Order SCA Resistant AES Without Fresh Randomness. In Constructive Side-Channel Analysis and Secure Design, Proceedings of the 9th International Workshop, COSADE 2018, Singapore, 23–24 April 2018; Springer: Cham, Seitzerland, 2018; pp. 245–262. [Google Scholar] [CrossRef]
- Rezvani, B.; Diehl, W. Hardware Implementations of NIST Lightweight Cryptographic Candidates: A First Look. IACR Cryptol. ePrint Arch. 2019, 2019, 824. [Google Scholar]
- Canright, D. A Very Compact S-Box for AES. In Cryptographic Hardware and Embedded Systems—CHES 2005, Proceedings of the 7th International Workshop, Edinburgh, UK, 29 August–1 September 2005; Rao, J.R., Sunar, B., Eds.; Lecture Notes in Computer, Science; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3659, pp. 441–455. [Google Scholar] [CrossRef]
- NanGate. NanGate FreePDK45 Open Cell Library. Available online: https://si2.org/open-cell-library (accessed on 7 August 2020).
- Oshida, H.; Ueno, R.; Homma, N.; Aoki, T. On Masked Galois-Field Multiplication for Authenticated Encryption Resistant to Side Channel Analysis. In Constructive Side-Channel Analysis and Secure Design, Proceedings of the 9th International Workshop, COSADE 2018, Singapore, 23–24 April 2018; Springer: Cham, Seitzerland, 2018; pp. 44–57. [Google Scholar] [CrossRef]
- Poschmann, A.; Moradi, A.; Khoo, K.; Lim, C.; Wang, H.; Ling, S. Side-Channel Resistant Crypto for Less than 2300 GE. J. Cryptol. 2011, 24, 322–345. [Google Scholar] [CrossRef]




| Cycle | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| column-oriented | — | — | — | — | — | — | — | — | ||||||||
| row-oriented | — | — | — | — | — | — | — | — |
| Cycle | State Array | Key Array |
|---|---|---|
| 1 | S-box lookup | Output |
| ⋮ | ⋮ | ⋮ |
| 16 | S-box lookup | Output |
| 17 | Pipeline Latency | S-box lookup |
| 18 | Pipeline Latency | S-box lookup |
| 19 | Pipeline Latency | S-box lookup |
| 20 | Pipeline Latency | S-box lookup |
| 21 | ShiftRows | Pipeline Latency |
| 22 | ShiftRows | Pipeline Latency |
| 23 | ShiftRows | Pipeline Latency |
| 24 | MixColumns | Pipeline Latency |
| 25 | MixColumns | — |
| 26 | MixColumns | — |
| 27 | MixColumns | — |
| Identifier | Target | Diagram | Orientation | Primitive | Area [GE] |
|---|---|---|---|---|---|
| (SR) | State Array | Figure 4-left | Row | Scan FF | 1219 |
| (SC) | State Array | Figure 5-left | Column | FF with enable | 1388 |
| (KR) | Key Array | Figure 4-right | Row | Scan FF | 1075 |
| (KC) | Key Array | Figure 5-right | Column | FF with enable | 1067 |
| Command | Description |
|---|---|
| Absorbing 64-bit data block in Hash and Encryption | |
| A special case of without a feedback | |
| Absorbing a 120-bit nonce at the end of Hash | |
| Absorbing a 64-bit ciphertext block in Decryption | |
| Output the entire 128-bit state as a tag |
| Component | Unprotected [bits] | TI [bits] |
|---|---|---|
| Total | 416 | 2208 |
| State array | 128 | 672 |
| Key array | 128 | 456 |
| Key store | 128 | 456 |
| S-box | 32 | 192 |
| Identifier | Component | Unprotected [GE] | TI [GE] |
|---|---|---|---|
| (C1) | Total | 4690 | 18,288 |
| (C2) | Total/Key Store | 961 | 2877 |
| (C3) | Total/Shift Register 18×4 | — | 545 |
| (C4) | Total/AES | 3423 | 14,256 |
| (C5) | Total/AES/Key Array | 1067 | 3222 |
| (C6) | Total/AES/State Array | 1373 | 6553 |
| (C7) | Total/AES/S-box | 533 | 3218 |
| (C8) | Total/AES/Shift Register 18×4 | — | 545 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sugawara, T. Hardware Performance Evaluation of Authenticated Encryption SAEAES with Threshold Implementation. Cryptography 2020, 4, 23. https://doi.org/10.3390/cryptography4030023
Sugawara T. Hardware Performance Evaluation of Authenticated Encryption SAEAES with Threshold Implementation. Cryptography. 2020; 4(3):23. https://doi.org/10.3390/cryptography4030023
Chicago/Turabian StyleSugawara, Takeshi. 2020. "Hardware Performance Evaluation of Authenticated Encryption SAEAES with Threshold Implementation" Cryptography 4, no. 3: 23. https://doi.org/10.3390/cryptography4030023
APA StyleSugawara, T. (2020). Hardware Performance Evaluation of Authenticated Encryption SAEAES with Threshold Implementation. Cryptography, 4(3), 23. https://doi.org/10.3390/cryptography4030023





