Security Analysis of Lightweight IoT Cipher: Chaskey
Abstract
1. Introduction
2. Related Work
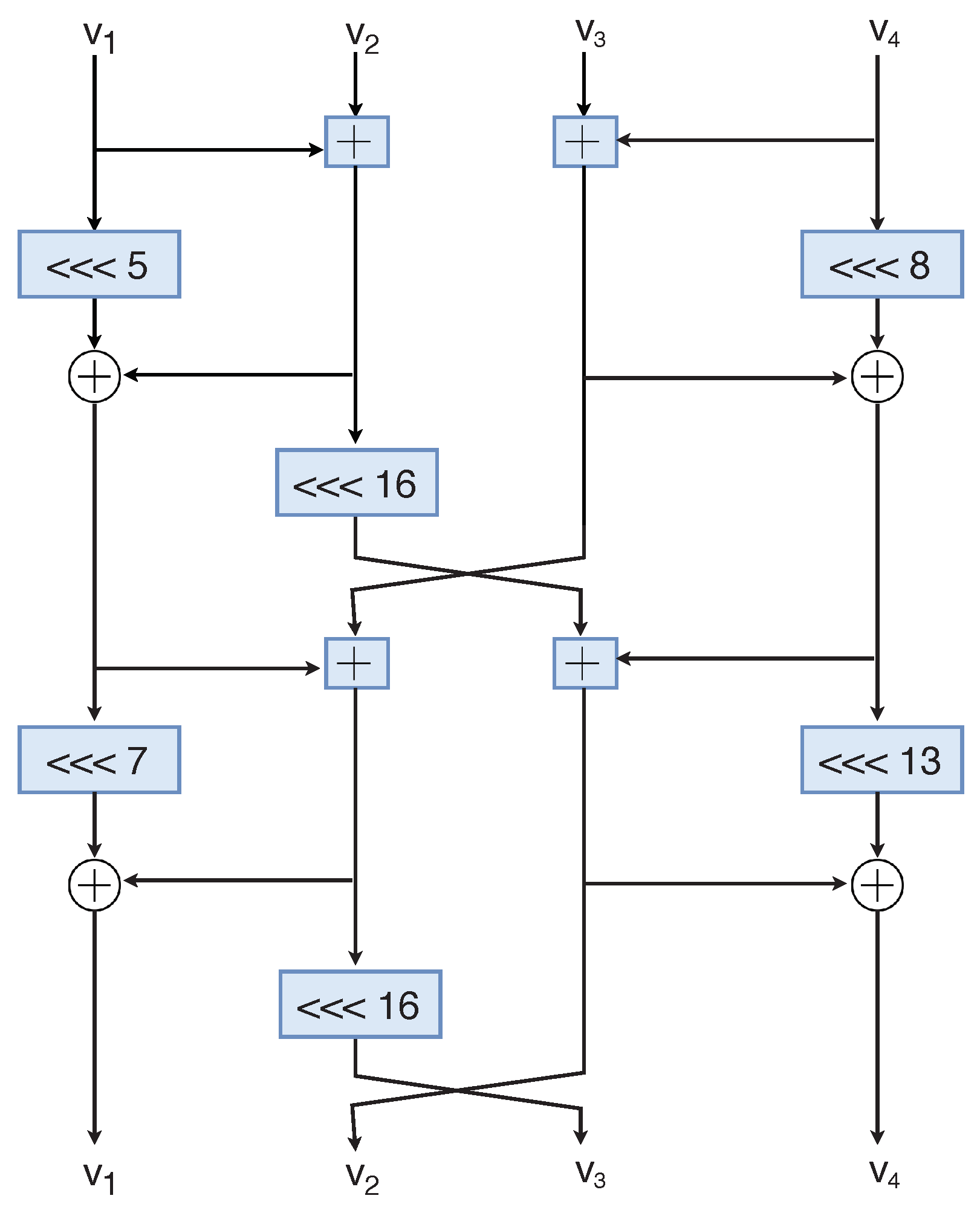
3. Description of Chaskey
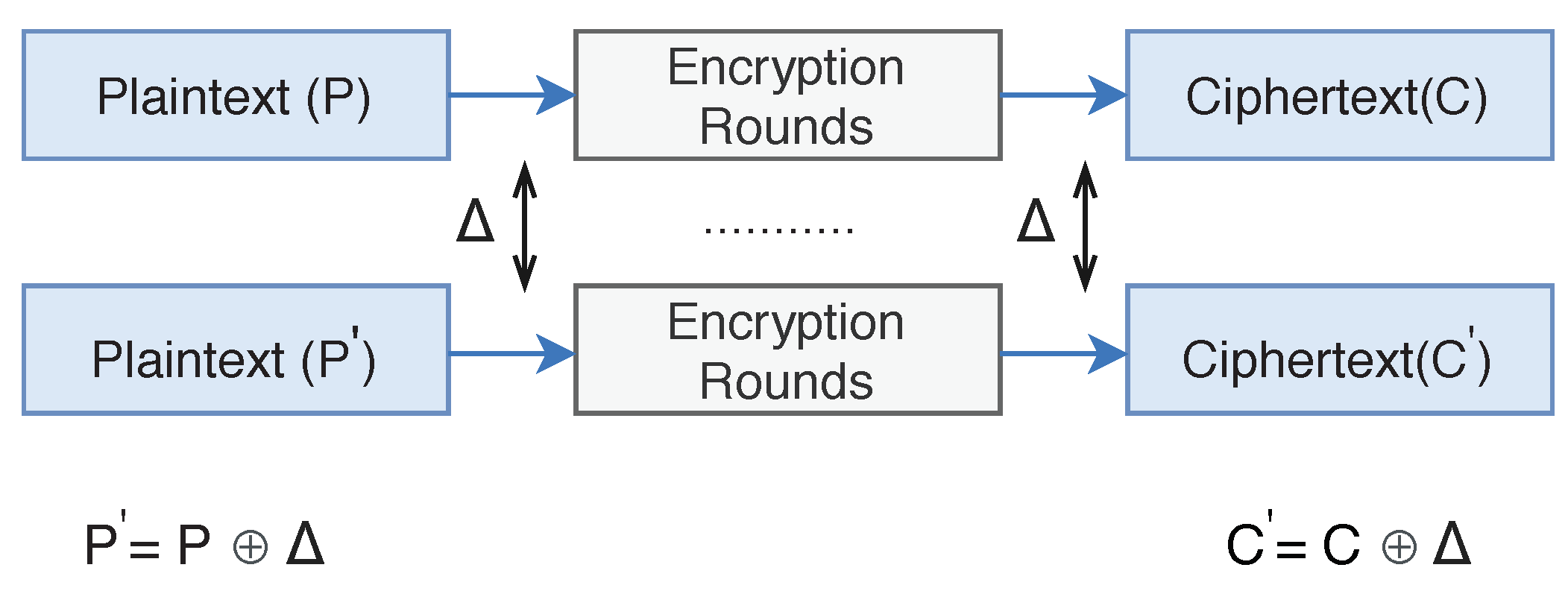
4. Differential Cryptanalysis
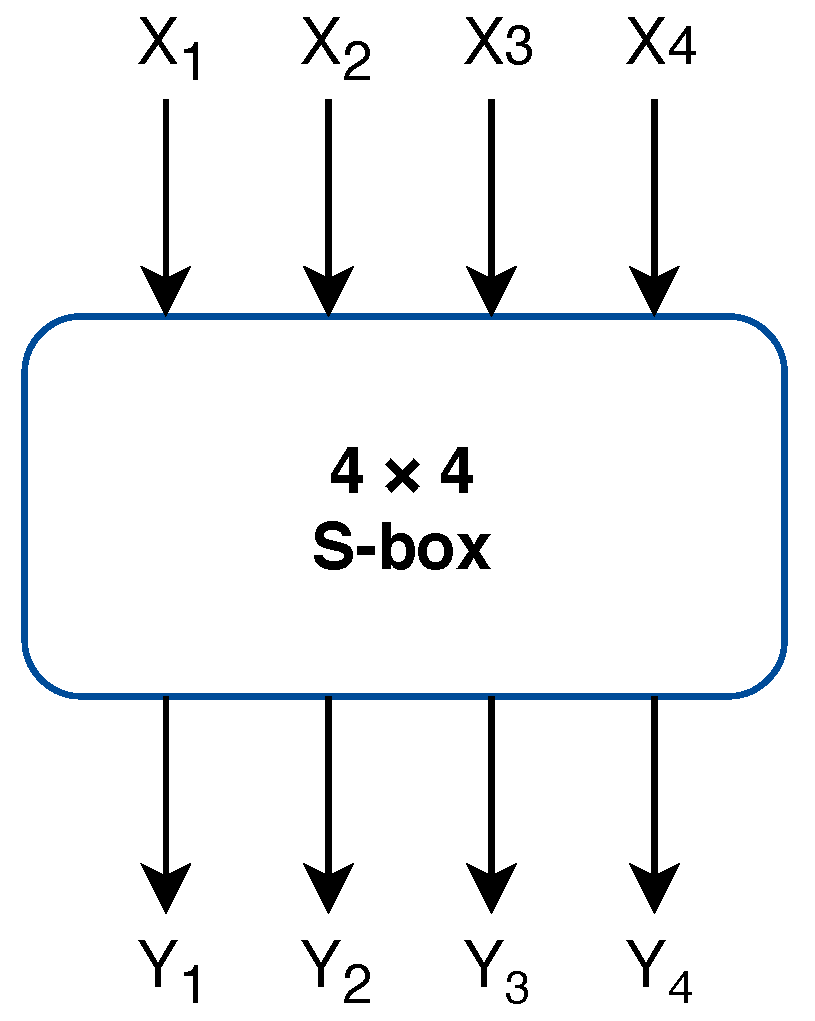
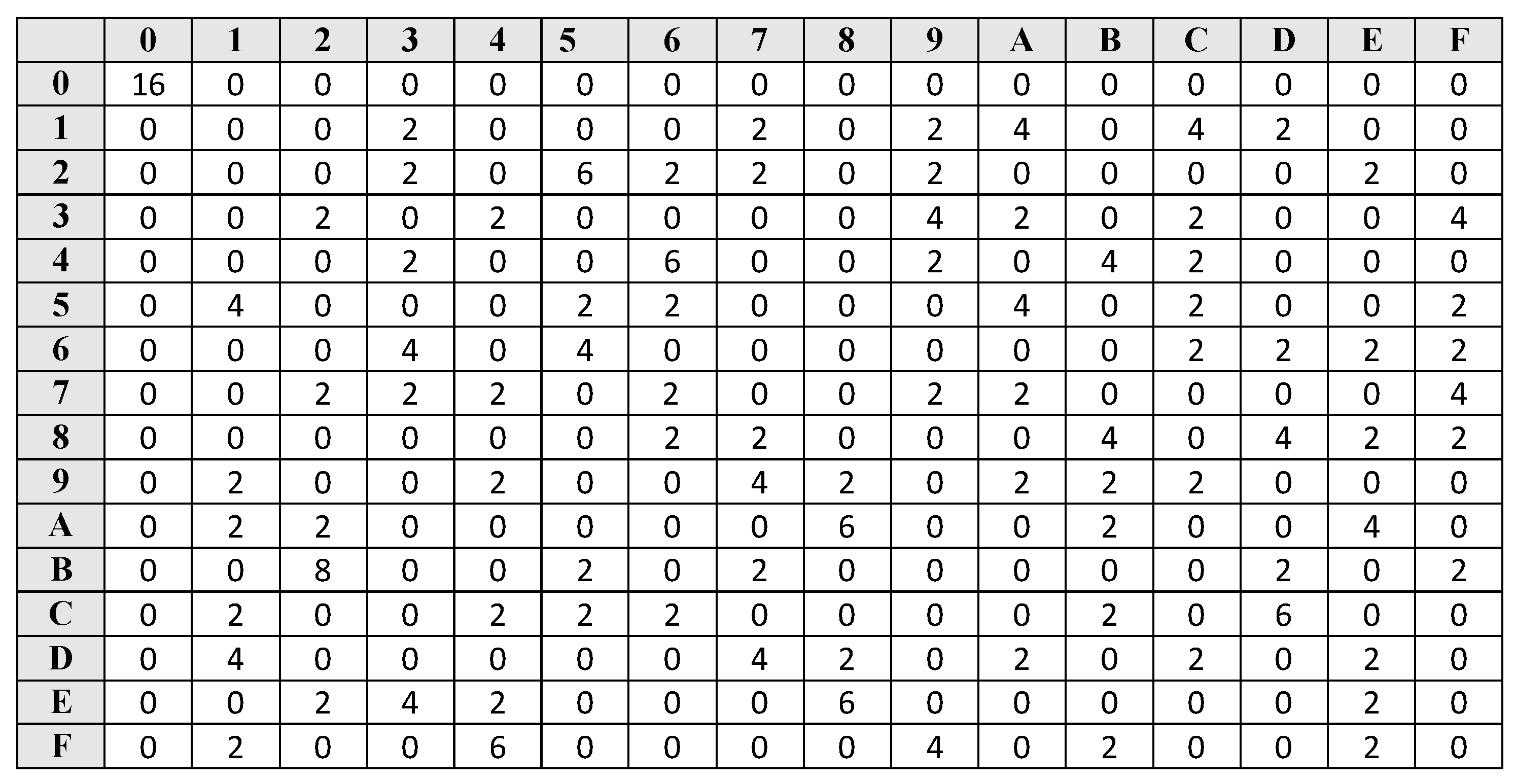
5. Calculating Differential Probabilities
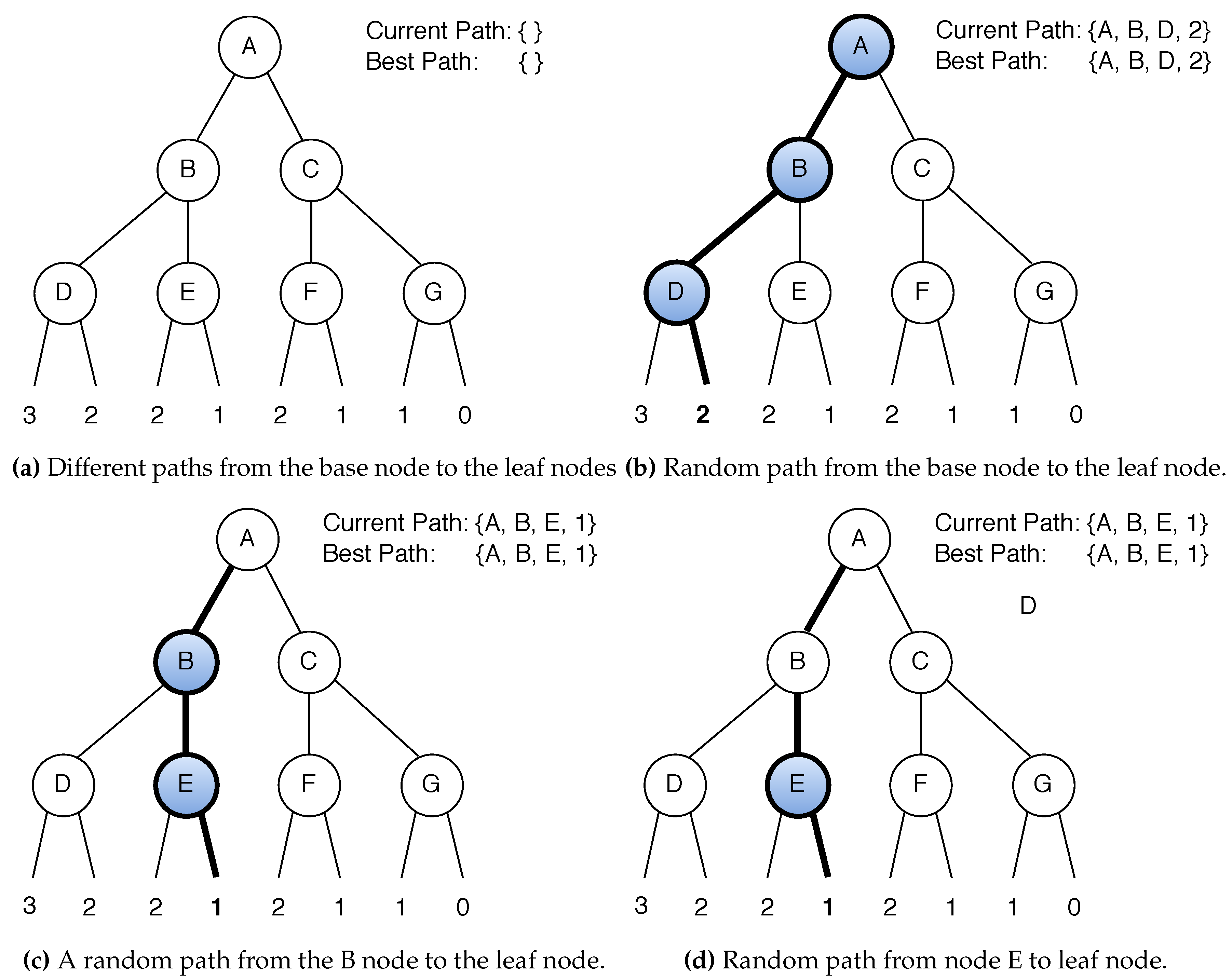
6. Heuristic Tool Used to Find Differential Path
7. Pseudocode of Heuristic Tool
| Algorithm 1 Random move to find differential path |
| 1: function RANDOM-PATH () |
| 2: while do |
| 3: if ( and ) ∈ pDDT then |
| 4: output and weight is added to the path and weight list, respectively |
| 5: Similarly, do for other two modular operations |
| 6: else |
| 7: |
| 8: |
| 9: |
| 10: |
| 11: Add , and , |
| 12: to the weight and path list, respectively |
| 13: Similarly, do for other two modular operations |
| 14: end if |
| 15: end while |
| 16: return |
| 17: end function |
| Algorithm 2 Recursive Nested Heuristic function |
| function Nested-Heuristic() |
| while do |
| ) |
| if ( then |
| end if |
| Follow and go to the next round |
| if then |
| NESTED-HEURISTIC () |
| end if |
| end while |
| end function |
8. Results
9. Conclusions
Funding
Conflicts of Interest
References
- Shimizu, A.; Miyaguchi, S. Fast Data Encipherment Algorithm FEAL. In Proceedings of the Advances in Cryptology—EUROCRYPT’87, Workshop on the Theory and Application of of Cryptographic Techniques, Amsterdam, The Netherlands, 13–15 April 1987; Chaum, D., Price, W.L., Eds.; Springer: Berlin/Heidelberg, Germany, 1987; Volume 304, pp. 267–278. [Google Scholar] [CrossRef]
- Matsui, M.; Yamagishi, A. A New Method for Known Plaintext Attack of FEAL Cipher. In Proceedings of the Advances in Cryptology—EUROCRYPT’92, Workshop on the Theory and Application of of Cryptographic Techniques, Balatonfüred, Hungary, 24–28 May 1992; Rueppel, R.A., Ed.; Springer: Berlin/Heidelberg, Germany, 1992; Volume 658, pp. 81–91. [Google Scholar] [CrossRef]
- Biham, E.; Shamir, A. Differential Cryptanalysis of DES-like Cryptosystems. In Proceedings of the Advances in Cryptology—CRYPTO’90, 10th Annual International Cryptology Conference, Santa Barbara, CA, USA, 11–15 August 1990; pp. 2–21. [Google Scholar] [CrossRef]
- Wang, X.; Yu, H. How to Break MD5 and Other Hash Functions. In Proceedings of the Advances in Cryptology—EUROCRYPT 2005, 24th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Aarhus, Denmark, 22–26 May 2005; Cramer, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3494, pp. 19–35. [Google Scholar] [CrossRef]
- Biryukov, A.; Velichkov, V. Automatic Search for Differential Trails in ARX Ciphers. In Proceedings of the Topics in Cryptology—CT-RSA 2014, San Francisco, CA, USA, 25–28 February 2014; Benaloh, J., Ed.; Springer International Publishing: Cham, Switzerland, 2014; pp. 227–250. [Google Scholar]
- Mouha, N.; Mennink, B.; Van Herrewege, A.; Watanabe, D.; Preneel, B.; Verbauwhede, I. Chaskey: An Efficient MAC Algorithm for 32-bit Microcontrollers. In Proceedings of the Selected Areas in Cryptography—SAC 2014, Montreal, QC, Canada, 14–15 August 2014; Joux, A., Youssef, A., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 306–323. [Google Scholar]
- Leurent, G. Improved Differential-Linear Cryptanalysis of 7-Round Chaskey with Partitioning. In Proceedings of the Advances in Cryptology—EUROCRYPT 2016, Vienna, Austria, 8–12 May 2016; Fischlin, M., Coron, J.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 344–371. [Google Scholar]
- Kraleva, L.; Ashur, T.; Rijmen, V. Rotational Cryptanalysis on MAC Algorithm Chaskey. IACR Cryptol. ePrint Arch. 2020, 2020, 538. [Google Scholar]
- Dwivedi, A.D.; Morawiecki, P.; Srivastava, G. Differential Cryptanalysis of Round-Reduced SPECK Suitable for Internet of Things Devices. IEEE Access 2019, 7, 16476–16486. [Google Scholar] [CrossRef]
- Dhar, D.A.; Morawiecki, P.; Wójtowicz, S. Finding Differential Paths in ARX Ciphers through Nested Monte-Carlo Search. Int. J. Electron. Telecommun. 2018, 64, 147–150. [Google Scholar] [CrossRef]
- Dwivedi, A.D.; Srivastava, G. Differential Cryptanalysis of Round-Reduced LEA. IEEE Access 2018, 6, 79105–79113. [Google Scholar] [CrossRef]
- Dobraunig, C.; Eichlseder, M.; Mendel, F. Heuristic Tool for Linear Cryptanalysis with Applications to CAESAR Candidates. In Proceedings of the Advances in Cryptology—ASIACRYPT 2015, Auckland, New Zealand, 29 November–3 December 2015; Iwata, T., Cheon, J.H., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 490–509. [Google Scholar]
- Lipmaa, H.; Moriai, S. Efficient Algorithms for Computing Differential Properties of Addition. In Fast Software Encryption; Matsui, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 336–350. [Google Scholar]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Dwivedi, A.D. Security Analysis of Lightweight IoT Cipher: Chaskey. Available online: https://github.com/ashudhar7/Chaskeydifferential (accessed on 4 August 2020).


| Threshold Probability | Elements in pDDT |
|---|---|
| 0.1 | 3,951,388 |
| 0.07 | 3,951,388 |
| 0.06 | 167,065,948 |
| 0.01 | ≥72,589,325,174 |
| Round | Block1 | Block2 | Block3 | Block4 | |
|---|---|---|---|---|---|
| 1 | 0x00000008 | 0x00000008 | 0x00008181 | 0x00000081 | −7 |
| 2 | 0x00000000 | 0x00000000 | 0x80000000 | 0x00000000 | 0 |
| 3 | 0x80000000 | 0x80000000 | 0x00008000 | 0x80001000 | −9 |
| 4 | 0x80009810 | 0x80109080 | 0x90108000 | 0x92008082 | −27 |
| 5 | 0x03964a02 | 0x0a008200 | 0x0a020213 | 0x1a428252 | −60 |
| weight | −103 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dwivedi, A.D. Security Analysis of Lightweight IoT Cipher: Chaskey. Cryptography 2020, 4, 22. https://doi.org/10.3390/cryptography4030022
Dwivedi AD. Security Analysis of Lightweight IoT Cipher: Chaskey. Cryptography. 2020; 4(3):22. https://doi.org/10.3390/cryptography4030022
Chicago/Turabian StyleDwivedi, Ashutosh Dhar. 2020. "Security Analysis of Lightweight IoT Cipher: Chaskey" Cryptography 4, no. 3: 22. https://doi.org/10.3390/cryptography4030022
APA StyleDwivedi, A. D. (2020). Security Analysis of Lightweight IoT Cipher: Chaskey. Cryptography, 4(3), 22. https://doi.org/10.3390/cryptography4030022





