I2PA: An Efficient ABC for IoT
Abstract
1. Introduction
2. Related Works
3. Mathematic Background
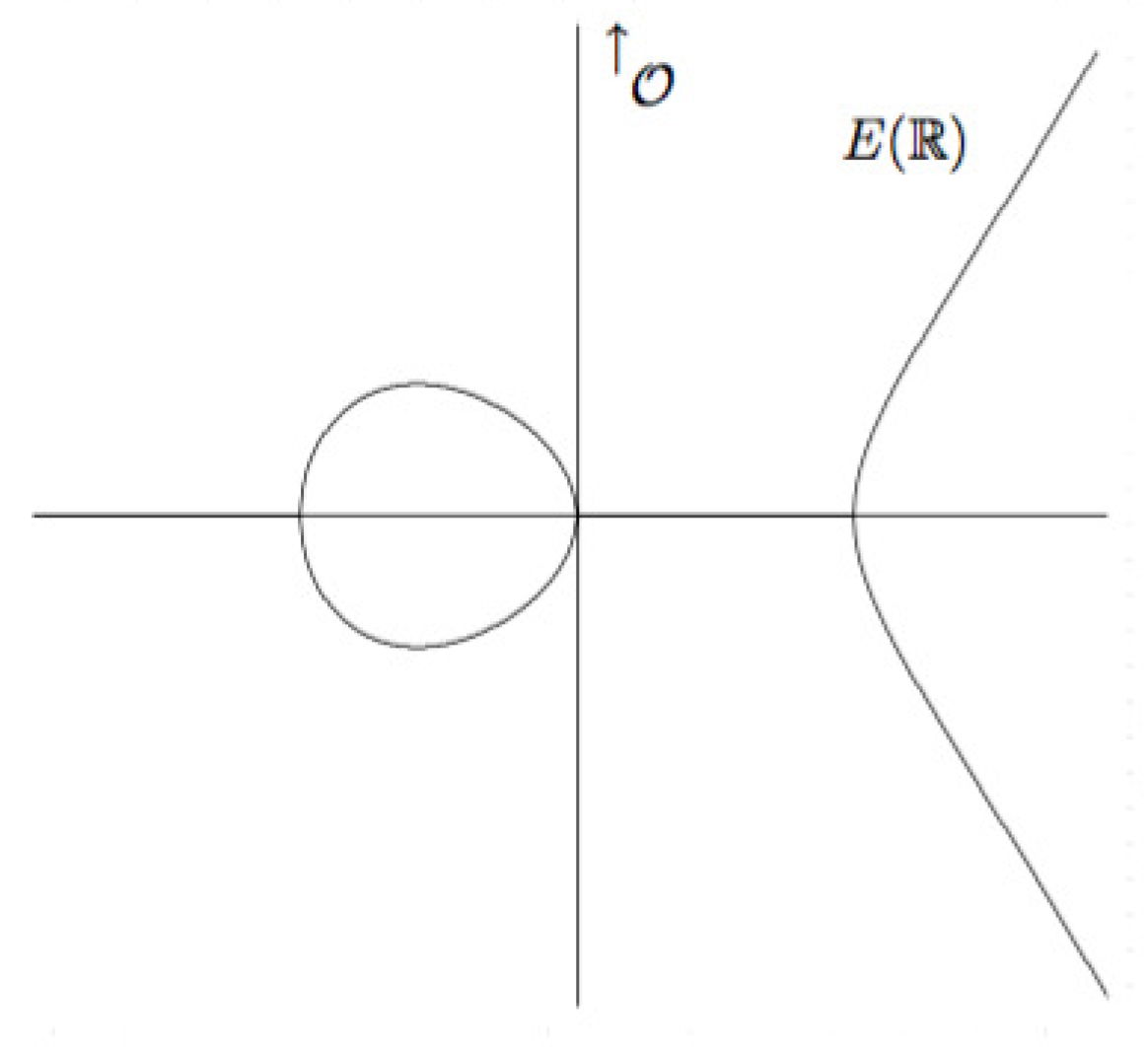
3.1. Definition
- When the equation can be simplified to , where a, b .
- When and , the equation can be simplified to , where a, b . This curve is said to be non-supersingular. If , the equation can be simplified to , where a, b, c . This curve is said to be supersingular.
- When and the equation can be simplified to , where a, b . This curve is said to be non-supersingular. If , the equation can be simplified to . This curve is said to be supersingular.
3.2. Edwards’ Curves
- If d is a non-square in , the addition law is complete. This ensures that denominators are never zero.
- The addition law is strongly unified, i.e., it can also be used for doubling.
- The point (0,1) is the neutral element.
- The point (0,−1) has order 2.
- The points (±1,0) have order 4.
- The inverse of is .
3.3. Elliptic Curve Discrete Logarithm Problem (ECDLP)
4. Definition
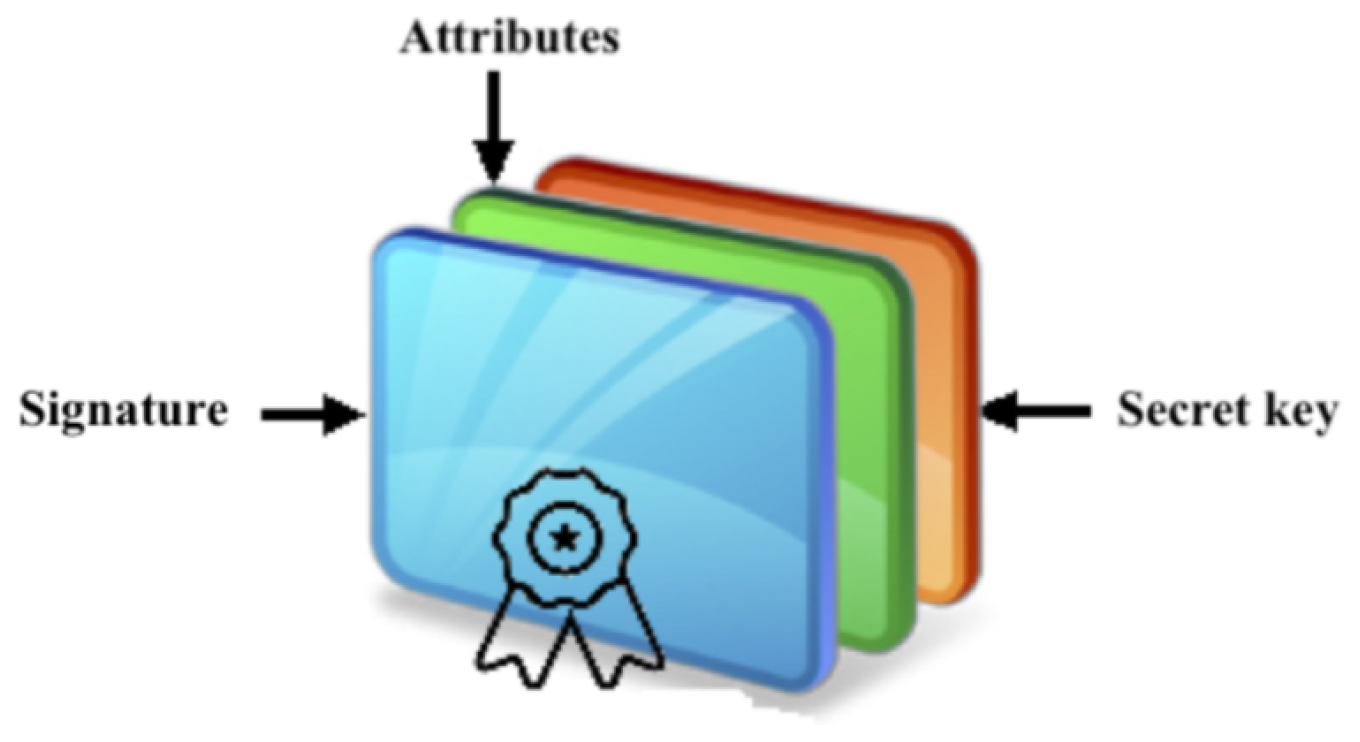
4.1. Attribute
4.2. Credential
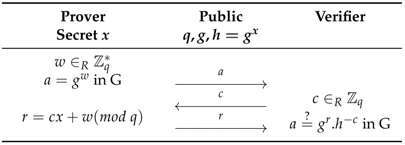
4.3. Zero-Knowledge Proofs
4.4. Blind Signing
4.5. Blindness
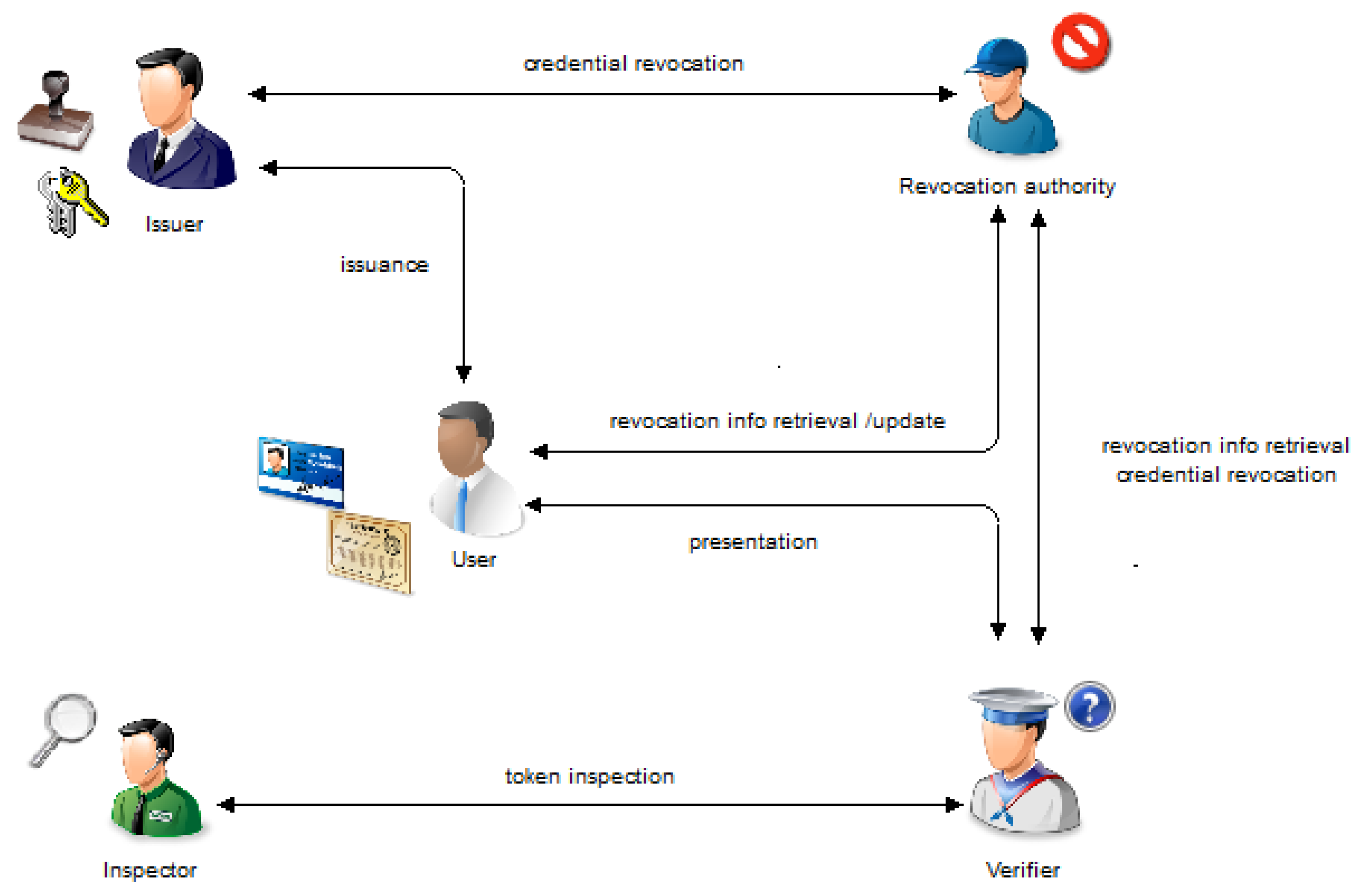
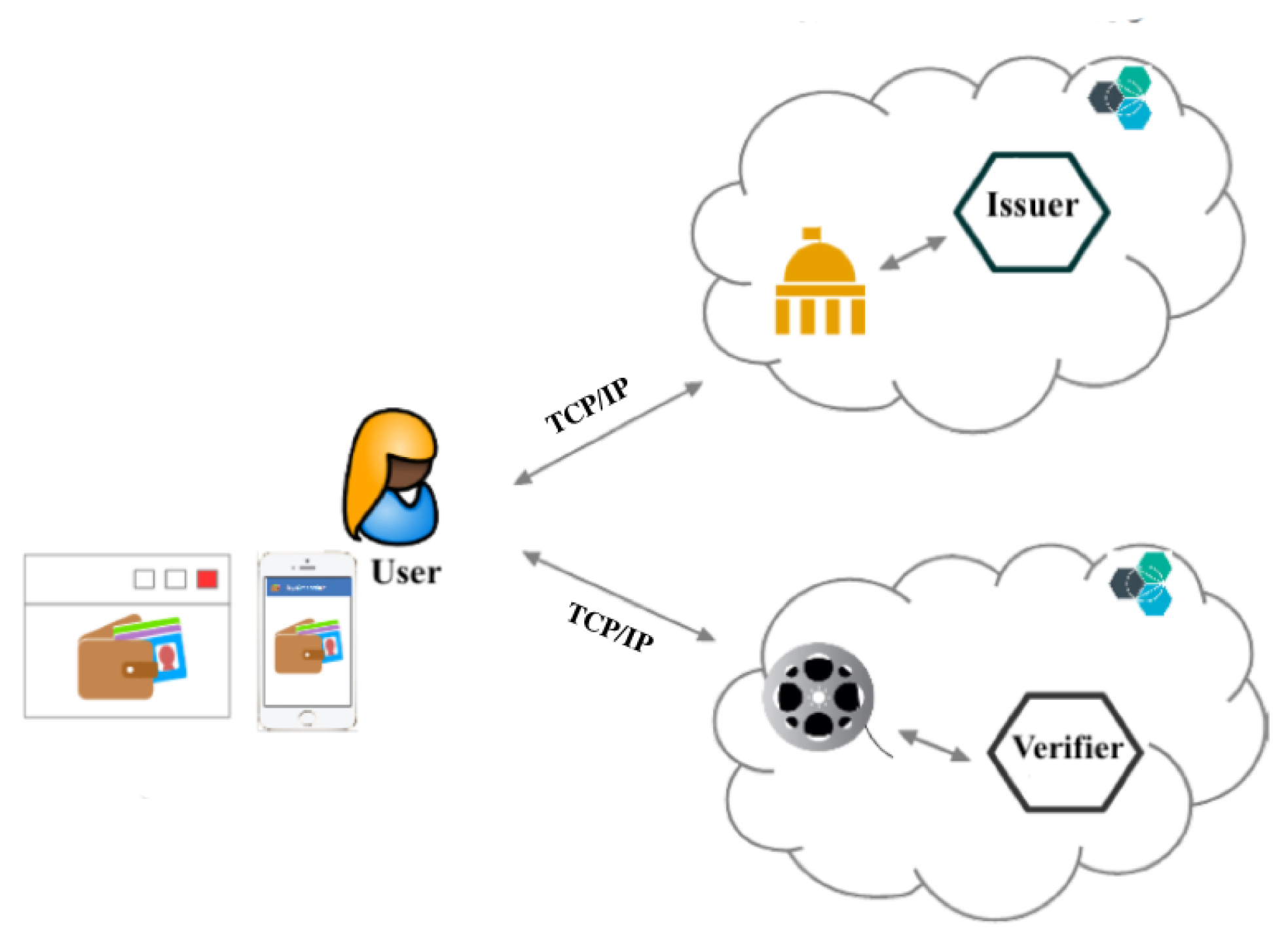
5. Architecture
- Set-up: Performed to output system’s parameters.
- Issuance: An interactive protocol between users and issuer. By issuing a credential to a user, the issuer guarantees the correctness of attributes contained in the credential.
- Presentation: An interactive protocol in which a user reveals or proves to a verifier possession of some attributes or claims about attributes. This phase is also known as verification.
- Inspection: Provides conditional anonymity. It enables a trusted party, the so-called inspector, to revoke, in some conditions, anonymity of cheating provers.
- Revocation: Ends the validity of credentials whenever necessary.
- Authenticity: feature that guarantees that an ABC cannot be modified.
- Non-transferability: feature that prevents the user from transferring her ABC to another user.
- Minimal information: feature that guarantees that during the verification protocols no other information is revealed to the verifier beyond the disclosed attributes, and the corresponding issuer, etc.
- Multi-show unlinkability: feature that guarantees that different presentations of a given ABC cannot be linked.
- Issuance unlinkability: feature which guarantees that the presentation of an ABC cannot be linked to its issuance.
- Selective disclosure: Allows a user to prove only a subset of attributes to a verifier.
- Carry-over attributes: Enables users to carry over some attributes from an existing ABC into a new one without disclosing them to the issuer.
- Predicate proof: Allows logical operators to be applied on attributes without disclosing them.
- Proof of holdership: A cryptographic evidence for proving ownership of ABC.
- Unforgeability: feature that guarantees that no malicious third party can forge a valid ABC.
- Etc.
6. Contribution
6.1. Set-Up
- k: a security parameter.
- p: a prime number that defines the field .
- E: an elliptic curve defined over .
- : a base point of prime order q.
- : issuer’s secret key.
- : issuer’s public key.
- : a hash function defined as follow:
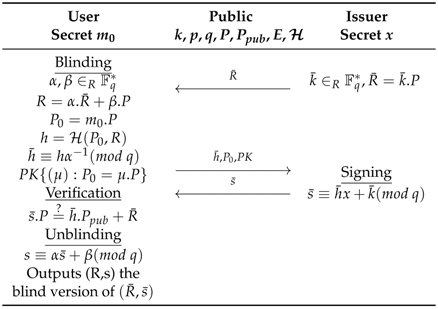
6.2. Issuance
6.3. Signature on a Single Message
- Blinding: The issuer generates a random integer , computes the resulting point and sends it to the user. The latter generates random factors and , blinds her document, and sends it to the issuer.
- Singing: The issuer signs the blinded document with his secret key x by computing and sends the blinded and signed document to the user.
- Unblinding: The user unblinds the blinded and signed document with her blind factors and without invalidating it.
- Set-up: receives the problem and should find such that . It chooses a hash function which behaves like a random oracle, sets and sends the public parameters to expecting it forges a credential. and start playing the game of chosen message attack [38].
- Hashing oracle: starts by initializing an empty database. When sends for hashing, checks whether or not that message has already been sent. If so, it picks from the database and returns it as a response to that query, otherwise it picks , stores the couple in the database and returns as a response to that query.
- Issuing oracle: When queries the issuing oracle for the message , first checks whether has already been queried for issuance. If so, it aborts and the game is stopped (Event 1) [38], otherwise, it computes (where denotes the hashing oracle), picks , computes and sends to as response to its issuing query. As we can see, the algorithm is valid since .
- Forging step: Finally, outputs a forged signature on message with . It computes and extracts z as solution of the DLP.
- Probability analysis: The simulation fails if queries the same message for issuance (Event 1). This happens with probability at most . Hence, the simulation is successful with probability at least (provable by recurrence reasoning). The tuple is a valid credential with probability at least [39] and guesses it correctly with probability at least [39]. Finally, the overall successful probability is [39]. The time complexity of the algorithm is since the issuing oracle computes at most scalar multiplications.
6.4. Verification
6.5. Randomized Version
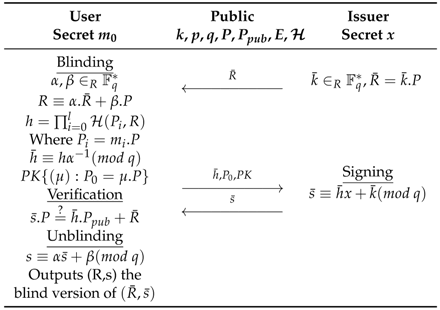
6.6. Signature on a Block of Messages
6.7. Selective Disclosure
7. Complexity Analysis
- : Scalar multiplication over EC
- : Point adding over EC
7.1. Operations over the Curve Comparison
7.2. Memory Usage Comparison
- T: Total of variables needed in this phase
- P: Total of variables to be stored permanently in this phase
7.3. Feature Comparison
- : Fully supported
- ⊘: Partially supported
- ×: Not supported
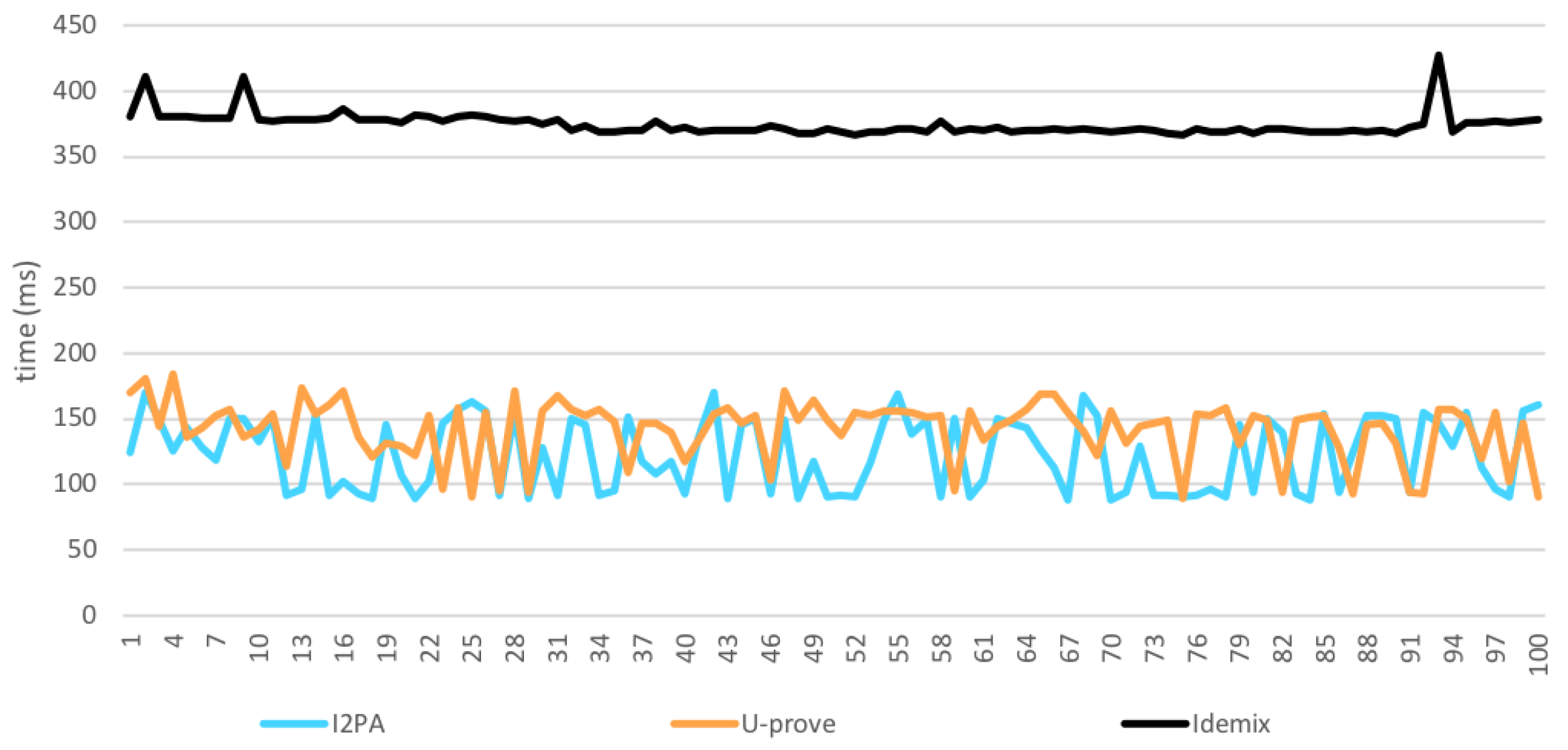
8. Performance Evaluation
8.1. Hardware Set-up
- Model Pi 3 B+
- 1 Go of SDRAM LPDDR2
- A 64-bit quad core processor clocked at 1.4 GHz
- Raspbian operating system.
- Dual Band 2.4 GHz and 5GHz IEEE 802.11. b/g/n/AC Wireless LAN
- Enhanced Ethernet performance over USB 2.0 (maximum throughput of 300 Mbps).
- model TECNO SPARK KB7j
- RAM 2 GB
- ROM 16 GB
- CPU 2.0 GH*4
- Battery 3500 mAh
- Memory 16 GB
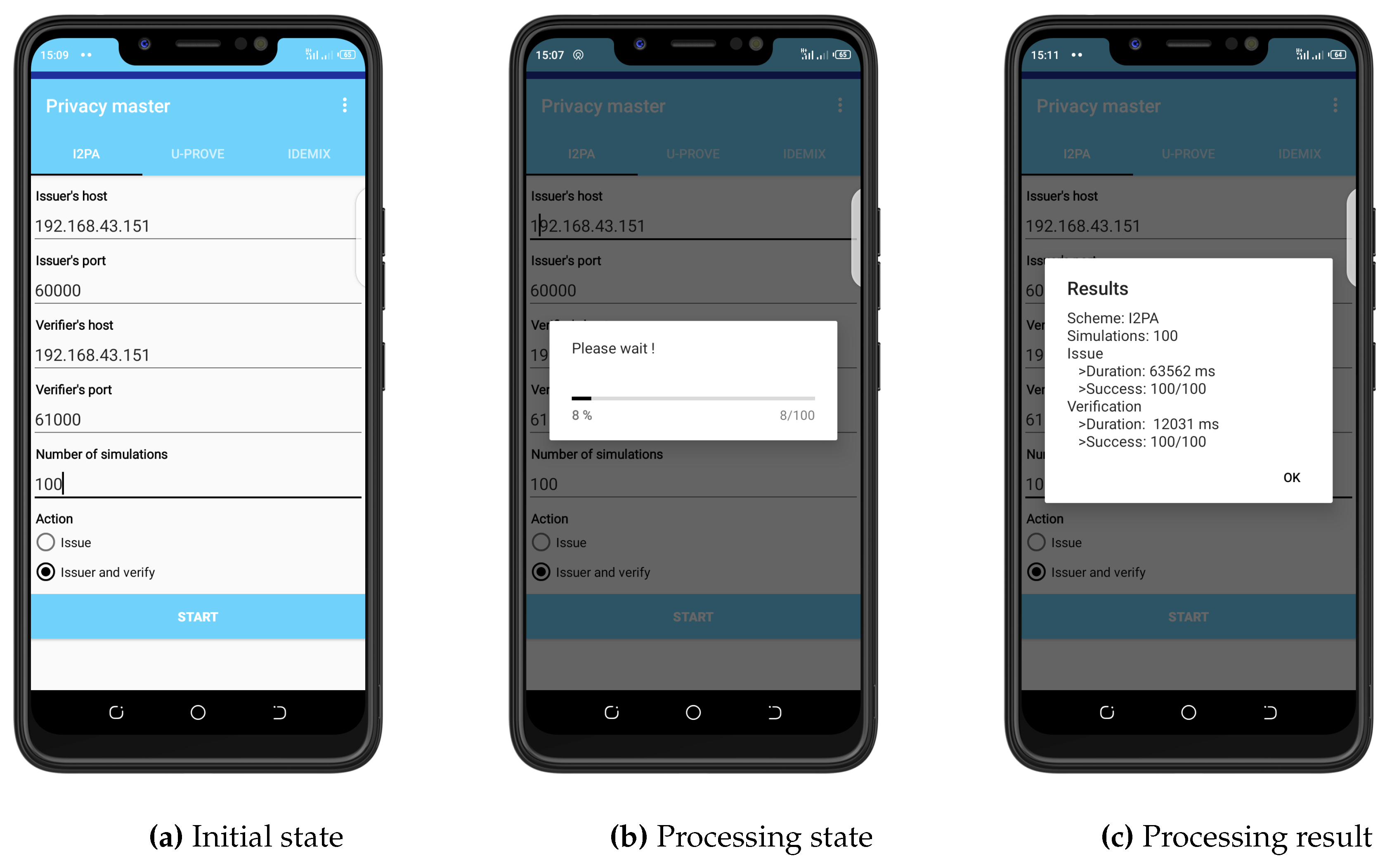
8.2. Software Set-up
8.3. Curve and Parameters
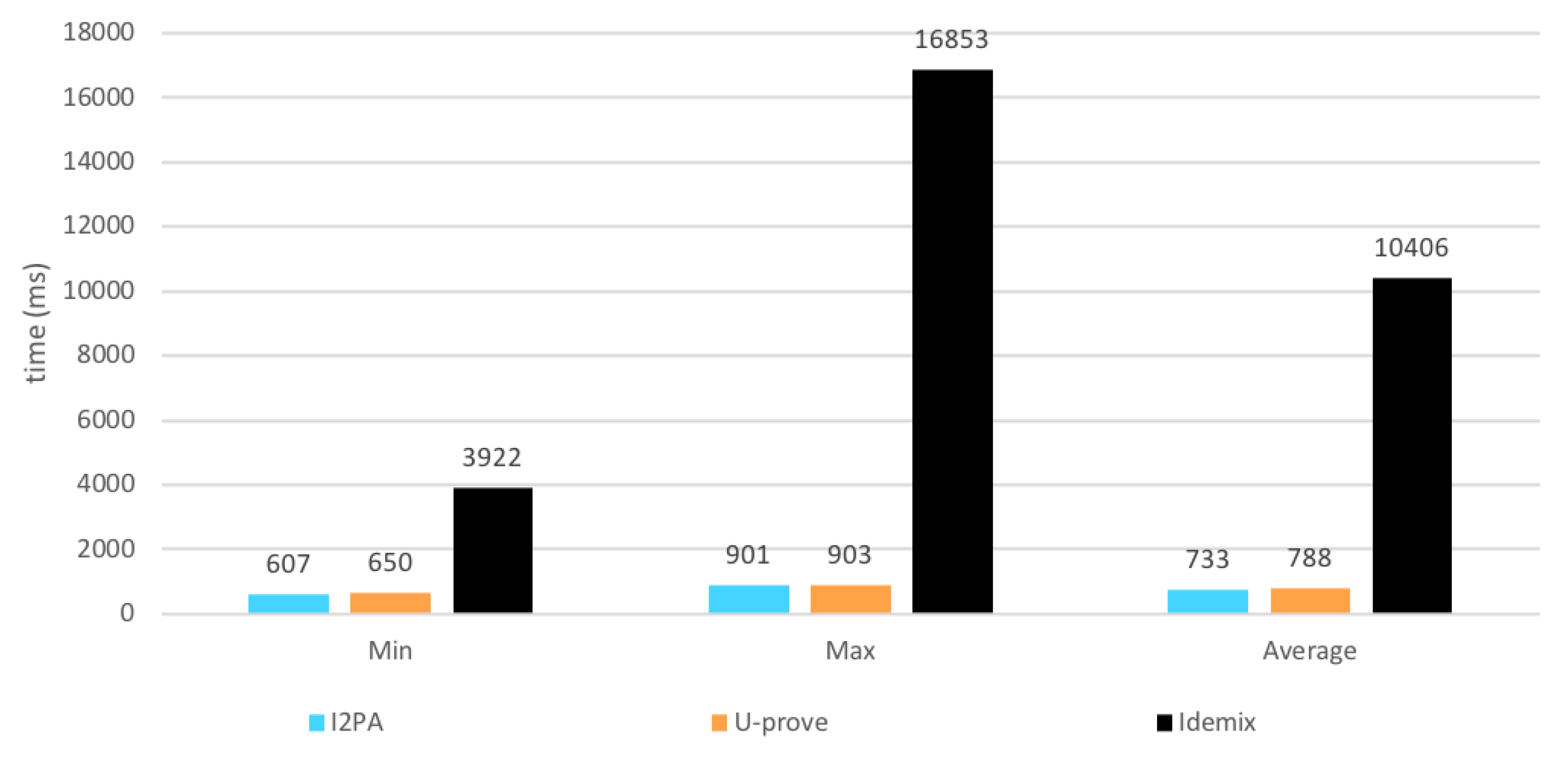
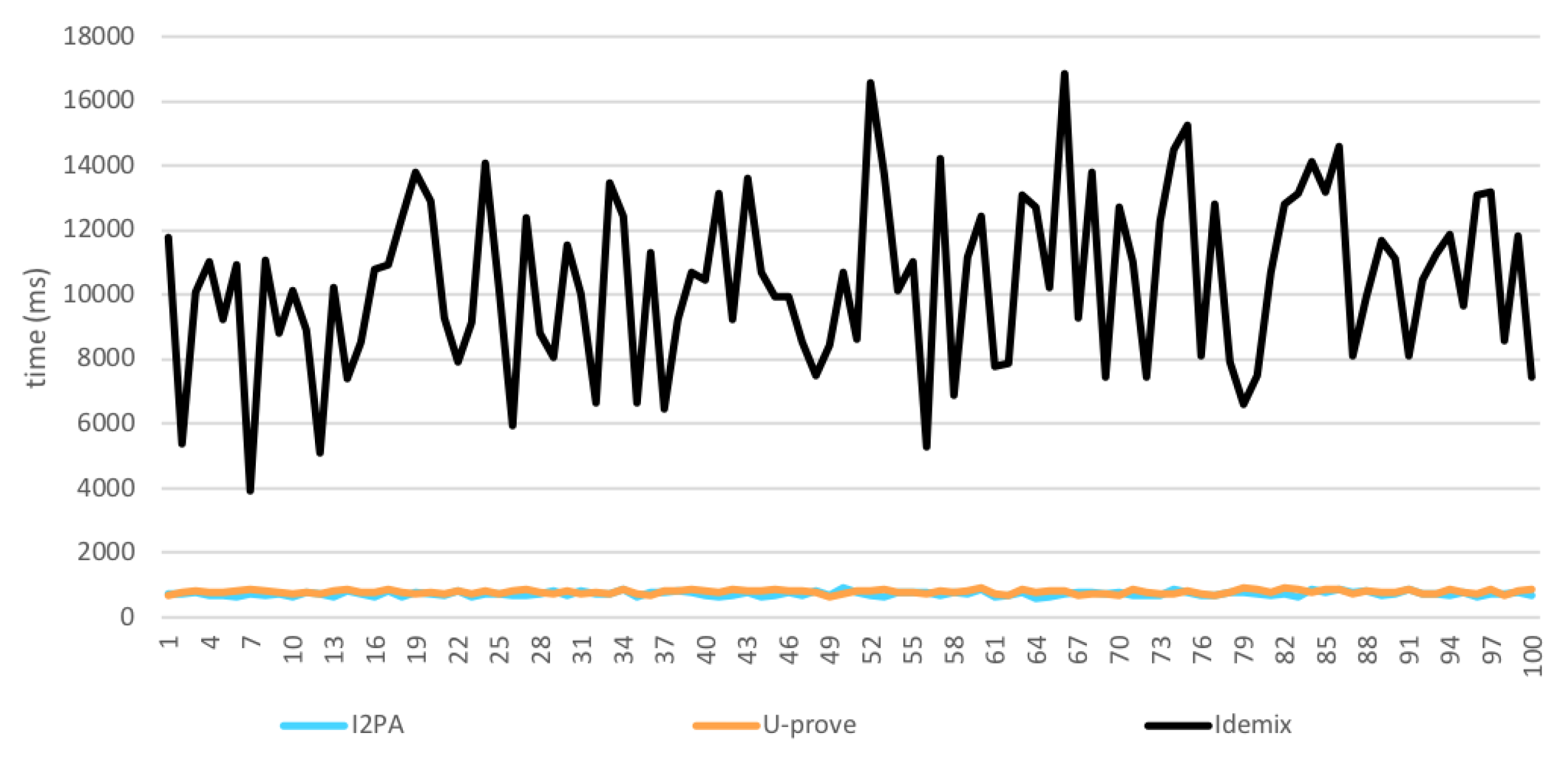
8.4. Issuance
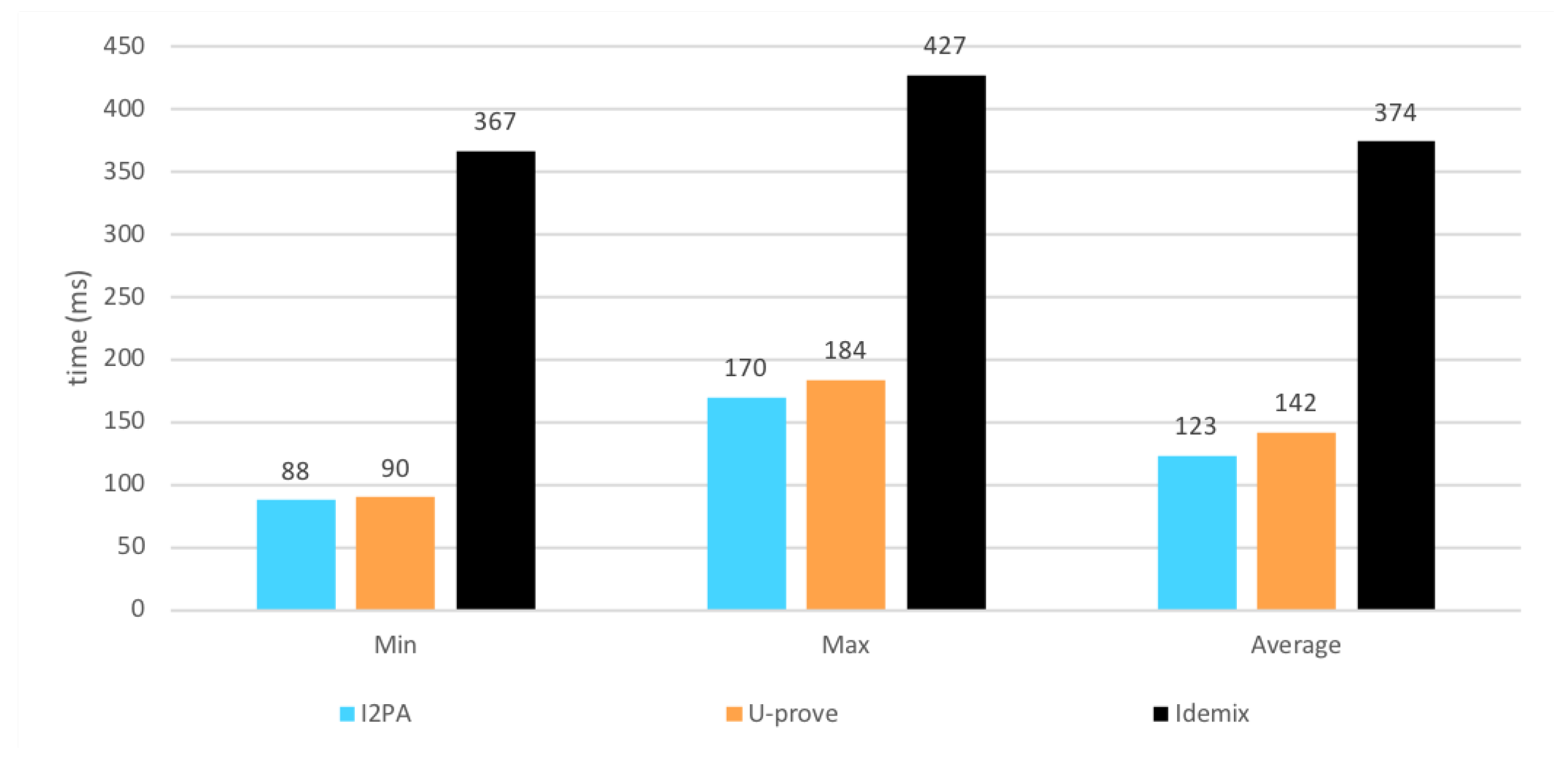
8.5. Verification
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Miranda, J.; Mäkitalo, N.; Garcia-Alonso, J.; Berrocal, J.; Mikkonen, T.; Canal, C.; Murillo, J.M. From the Internet of Things to the Internet of People. IEEE Internet Comput. 2015, 19, 40–47. [Google Scholar] [CrossRef]
- Bradley, J.; Barbier, J.; Handler, D. L’internet of Everything, un Potentiel de 14,4 Trillions de Dollars. Available online: https://www.cisco.com/web/FR/tomorrow-starts-here/pdf/ioe_economy_report_fr.pdf (accessed on 12 March 2018).
- Mbaye, A.; Ciss, A.A.; Niang, O. A Lightweight Identification Protocol for Embedded Devices. arXiv 2014, arXiv:1408.5945. [Google Scholar]
- Alpar, G.; Hoepman, J.H. A secure channel for attribute-based credentials: [Short paper]. In Proceedings of the 2013 ACM Workshop on Digital Identity Management, Berlin, Germany, 8 November 2013; pp. 13–18. [Google Scholar] [CrossRef]
- Camenisch, J.; Van Herreweghen, E. Design and implementation of the idemix anonymous credential system. In Proceedings of the 9th ACM Conference on Computer and Communications Security, Washington, DC, USA, 18–22 November 2002; pp. 21–30. [Google Scholar]
- Paquin, C.; Zaverucha, G. U-Prove Cryptographic Specification v1.1; Technical Report; Microsoft Corporation: Redmond, WA, USA, 2011. [Google Scholar]
- Vullers, P.; Alpár, G. Efficient selective disclosure on smart cards using idemix. In IFIP Working Conference on Policies and Research in Identity Management; Springer: Berlin/Heidelberg, Germany, 2013; pp. 53–67. [Google Scholar]
- Alpár, G.; Batina, L.; Lueks, W. Designated attribute-based proofs for RFID applications. In International Workshop on Radio Frequency Identification: Security and Privacy Issues; Springer: Berlin/Heidelberg, Germany, 2012; pp. 59–75. [Google Scholar]
- Sinha, R.; Srivastava, H.K.; Gupta, S. Performance based comparison study of RSA and elliptic curve cryptography. Int. J. Sci. Eng. Res. 2013, 4, 720–725. [Google Scholar]
- Bernal Bernabe, J.; Hernandez-Ramos, J.L.; Skarmeta Gomez, A.F. Holistic privacy-preserving identity management system for the internet of things. Mob. Inf. Syst. 2017, 2017, 6384186. [Google Scholar] [CrossRef]
- Persiano, G.; Visconti, I. An Efficient and Usable Multi-show Non-transferable Anonymous Credential System. In Financial Cryptography; Springer: Berlin/Heidelberg, Germany, 2004; pp. 196–211. [Google Scholar] [CrossRef]
- About IRMA. Available online: https://privacybydesign.foundation/irma-en/ (accessed on 3 March 2018).
- Liu, Z.; Seo, H.; Xu, Q. Performance evaluation of twisted Edwards-form elliptic curve cryptography for wireless sensor nodes. Secur. Commun. Netw. 2015, 8, 3301–3310. [Google Scholar] [CrossRef]
- De Fuentes, J.; González-Manzano, L.; Serna-Olvera, J.; Veseli, F. Assessment of attribute-based credentials for privacy-preserving road traffic services in smart cities. Person. Ubiquitous Comput. 2017, 21, 869–891. [Google Scholar] [CrossRef][Green Version]
- Lueks, W.; Alpár, G.; Hoepman, J.H.; Vullers, P. Fast revocation of attribute-based credentials for both users and verifiers. Comput. Secur. 2017, 67, 308–323. [Google Scholar] [CrossRef]
- de Fuentes, J.M.; Gonzalez-Manzano, L.; Solanas, A.; Veseli, F. Attribute-Based Credentials for Privacy-Aware Smart Health Services in IoT-Based Smart Cities. Computer 2018, 51, 44–53. [Google Scholar] [CrossRef]
- Hajny, J.; Dzurenda, P.; Malina, L. Attribute-based credentials with cryptographic collusion prevention. Secur. Commun. Netw. 2015, 8, 3836–3846. [Google Scholar] [CrossRef]
- Camenisch, J.; Lysyanskaya, A. An efficient system for non-transferable anonymous credentials with optional anonymity revocation. In International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 2001; pp. 93–118. [Google Scholar]
- Brands, S.A. Rethinking Public Key Infrastructures and Digital Certificates: Building in Privacy; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Camenisch, J.; Lysyanskaya, A. Signature schemes and anonymous credentials from bilinear maps. In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 2004; pp. 56–72. [Google Scholar]
- Alpár, G. Attribute-Based Identity Management : Bridging the Cryptographic Design of ABCs with the Real World. Available online: https://repository.ubn.ru.nl/bitstream/handle/2066/135177/135177.pdf (accessed on 16 september 2018).
- Hanzlik, L.; Kluczniak, K. A short paper on how to improve U-Prove using self-blindable certificates. In International Conference on Financial Cryptography and Data Security; Springer: Berlin/Heidelberg, Germany, 2014; pp. 273–282. [Google Scholar]
- Dzurenda, P.; Hajny, J.; Malina, L.; Ricci, S. Anonymous Credentials with Practical Revocation using Elliptic Curves. In Proceedings of the 14th International Joint Conference on e-Business and Telecommunications—Volume 6: SECRYPT, Madrid, Spain, 24–26 July 2017; pp. 534–539. [Google Scholar] [CrossRef]
- Hajny, J.; Dzurenda, P.; Malina, L. Privacy-PAC: Privacy-Enhanced Physical Access Control. In Proceedings of the 13th Workshop on Privacy in the Electronic Society, Scottsdale, AZ, USA, 3 November 2014; pp. 93–96. [Google Scholar] [CrossRef]
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Miller, V.S. Use of elliptic curves in cryptography. In Conference on the Theory and Application of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 1985; pp. 417–426. [Google Scholar]
- Hu, X.; Zheng, X.; Zhang, S.; Li, W.; Cai, S.; Xiong, X. A High-Performance Elliptic Curve Cryptographic Processor of SM2 over GF(p). Electronics 2019, 8, 431. [Google Scholar] [CrossRef]
- Hu, X.; Zheng, X.; Zhang, S.; Cai, S.; Xiong, X. A Low Hardware Consumption Elliptic Curve Cryptographic Architecture over GF(p) in Embedded Application. Electronics 2018, 7, 104. [Google Scholar] [CrossRef]
- Lara-Nino, C.A.; Diaz-Perez, A.; Morales-Sandoval, M. Energy/Area-Efficient Scalar Multiplication with Binary Edwards Curves for the IoT. Sensors 2019, 19, 720. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Seo, H. IoT-NUMS: Evaluating NUMS elliptic curve cryptography for IoT platforms. IEEE Trans. Inf. Forensics Secur. 2018, 14, 720–729. [Google Scholar] [CrossRef]
- Chatzigiannakis, I.; Vitaletti, A.; Pyrgelis, A. A privacy-preserving smart parking system using an IoT elliptic curve based security platform. Comput. Commun. 2016, 89, 165–177. [Google Scholar] [CrossRef]
- Aziz Ciss, A. Trends in Elliptic Curves Cryptography. IMHOTEP Afr. J. Pure Appl. Math. 2015, 2, 1–12. [Google Scholar]
- Bernstein, D.J.; Lange, T. Faster addition and doubling on elliptic curves. In International Conference on the Theory and Application of Cryptology and Information Security; Springer: Berlin/Heidelberg, Germany, 2007; pp. 29–50. [Google Scholar]
- Bernstein, D.J.; Birkner, P.; Joye, M.; Lange, T.; Peters, C. Twisted edwards curves. In International Conference on Cryptology in Africa; Springer: Berlin/Heidelberg, Germany, 2008; pp. 389–405. [Google Scholar]
- Hisil, H.; Wong, K.K.H.; Carter, G.; Dawson, E. Twisted Edwards curves revisited. In International Conference on the Theory and Application of Cryptology and Information Security; Springer: Berlin/Heidelberg, Germany, 2008; pp. 326–343. [Google Scholar]
- Goldwasser, S.; Micali, S.; Rackoff, C. The Knowledge Complexity of Interactive Proof-Systems (Extended Abstract). In Proceedings of the 17th Annual ACM Symposium on Theory of Computing, Providence, RI, USA, 6–8 May 1985; pp. 291–304. [Google Scholar] [CrossRef]
- Qu, H.; Shang, P.; Lin, X.J.; Sun, L. Cryptanalysis of A Privacy-Preserving Smart Metering Scheme Using Linkable Anonymous Credential. IACR Cryptol. ePrint Arch. 2015, 2015, 1066. [Google Scholar]
- Hülsing, A. Digital Signature Schemes and the Random Oracle Model. Available online: https://www.win.tue.nl/applied_crypto/2016/20161115_ROM_Signatures.pdf (accessed on 24 February 2019).
- Liu, J.K.; Baek, J.; Zhou, J.; Yang, Y.; Wong, J.W. Efficient online/offline identity-based signature for wireless sensor network. Int. J. Inf. Secur. 2010, 9, 287–296. [Google Scholar] [CrossRef]
- Jansma, N.; Arrendondo, B. Performance Comparison of Elliptic Curve and RSA Digital Signatures. Available online: http://www.nicj.net/files/performance_comparison_of_elliptic_curve_and_rsa_digital_signatures.pdf (accessed on 24 February 2019).
- Camenisch, J. Direct Anonymous Attestation Explained; Technical Report; IBM Research: Yorktown Heights/Albany, NY, USA, 2007. [Google Scholar]
- Alpar, G. Cryptography Fact Sheet about Idemix’s Basic Proof Techniques. Available online: https://privacybydesign.foundation/pdf/idemix_overview.pdf (accessed on 24 February 2018).
- ALPAR, G. U-PROVE CRYPTOGRAPHY. Available online: http://www.cs.ru.nl/ gergely/objects/u-prove.pdf (accessed on 24 February 2018).
- El Housni, Y. Edwards Curves; Working Paper or Preprint; HAL Id: hal-01942759; HAL: Paris, France, 2018. [Google Scholar]
- Josefsson, S.; Liusvaara, I. Edwards-Curve Digital Signature Algorithm (EdDSA); Technical Report; RFC, 2017; Volumle: 8032, pp. 1–60. Available online: http://www.rfc-editor.org/info/rfc8032 (accessed on 21 June 2019).

| 0.32 | 0.32 | 0.32 |
| (a) | (b) | (c) |
| Prover | Public | Verifier |
|---|---|---|
| Secret | ||
| Keeps secret | ||
| Prover | Public | Verifier |
|---|---|---|
| Secret | ||
| Prover | Public | Verifier |
|---|---|---|
| Secret | ||
| Protocol | U-prove | I2PA | ecHM12 |
|---|---|---|---|
| Issuance | |||
| Verification |
| Protocol | Idemix | U-prove | I2PA |
|---|---|---|---|
| User | T: n + 6 | T: n + 9 | T: n + 9 |
| P: n + 4 | P: n + 4 | P: n + 4 | |
| Issuer | T: n + 9 | T: 2n + 8 | T: 10 |
| P: n + 4 | P: 2n + 6 | P: 7 |
| Protocol | Idemix | U-prove | I2PA |
|---|---|---|---|
| fully blind signature | ⊘ | ✔ | ✔ |
| Selective disclosure | ✔ | ✔ | ✔ |
| Randomization | ✔ | × | ✔ |
| Untraceability | ✔ | ⊘ | ✔ |
| Unlinkability | ✔ | ✔ | ✔ |
| Unforgeability | ✔ | ✔ | ✔ |
| small keys size | × | ✔ | ✔ |
| Bandwidth saving | × | ✔ | ✔ |
| small devices efficiency | × | ✔ | ✔ |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sene, I.; Ciss, A.A.; Niang, O. I2PA: An Efficient ABC for IoT. Cryptography 2019, 3, 16. https://doi.org/10.3390/cryptography3020016
Sene I, Ciss AA, Niang O. I2PA: An Efficient ABC for IoT. Cryptography. 2019; 3(2):16. https://doi.org/10.3390/cryptography3020016
Chicago/Turabian StyleSene, Ibou, Abdoul Aziz Ciss, and Oumar Niang. 2019. "I2PA: An Efficient ABC for IoT" Cryptography 3, no. 2: 16. https://doi.org/10.3390/cryptography3020016
APA StyleSene, I., Ciss, A. A., & Niang, O. (2019). I2PA: An Efficient ABC for IoT. Cryptography, 3(2), 16. https://doi.org/10.3390/cryptography3020016





