2.1. PUF Architectures and Soft Data
A wide range of PUF architectures have been proposed since the initial papers on PUFs were published [
10,
11]. The source of entropy (randomness) for the PUF is chip-to-chip and within-die process variations that occur between and within chips during production. The PUF architecture defines the mechanism that is used to measure small signal variations introduced by process variations effects. In some cases, the measurement process leverages the existing architectural features of the chip, for example, the SRAM PUF measures its entropy source, that is, the state of the individual SRAM cells, by simply applying power to the SRAM array [
12]. For most PUFs, however, circuit components need to be added to the chip, for example, the RO PUF requires a set of MUXs and counters to select and measure the frequencies associated with elements in the array of ROs [
10]. In another example, the HELP PUF adds a launch-capture clocking mechanism to precisely time the delays of combinational logic paths [
7,
8].
For PUF architectures that measure and digitize the signal behavior associated with the entropy source, the digitized values provide additional information that can be leveraged in strong challenge-response-pair (CRP) forms of authentication. The digitized values represent the magnitude of the signal behavior, for example, RO frequency or path delay and are often used as input to mathematical processes defined by the PUF architecture. The goal of the mathematical operations is to isolate and amplify the random differences that occur among multiple copies of the individual circuit components. The digitized values are eventually converted to a bit and used in the response of the CRP. We refer to the digitized values as soft data.
Of the PUF architectures that create soft data (the RO and HELP PUFs are just two examples), the conversion to bits can be accomplished in a variety of ways. For example, the RO PUF typically selects a pair of ROs and then computes a difference by subtracting the soft data associated with the two ROs. The sign of the difference can then be used to generate a bit, with, for example, negative differences producing a ‘0’ and positive differences producing a ‘1’. The HELP PUF also computes differences among pairings of path delays and uses a modulus operation to assign a ‘0’ or ‘1’ to the differences.
2.2. Error Correction and Avoidance Methods
Nearly all PUF architecture need to deal with bit-flip errors, which are differences in the response bitstring that occur when the response is regenerated. Bit-flip errors are most probable when the magnitude of the difference between a pair of soft data values is close to zero. In these cases, regeneration of the bitstring, which takes place later in the field and under potentially adverse environmental conditions, can result in bits flipping from ‘0’ to ‘1’ or vice versa. Although authentication protocols can be designed to be tolerant to a small number of bit-flip errors, the number of bit-flip errors that can occur is too large in most PUF architectures to guarantee that authentication works correctly when regeneration is carried out in harsh environments.
To deal with this issue, nearly all PUF architectures define an error correction or error avoidance method to improve reliability during regeneration. Error correction is the more popular of the two reliability-enhancing methods. Error correction typically processes the PUF response bits into a final response bitstring using algorithms based on linear block codes [
13] or Bose-Chaudhuri-Hochquenghen (BCH) codes [
14]. However, nearly all of the error correction schemes ignore the magnitude of the difference in the soft data and use all of the PUF response bits to construct a smaller but reproducible bitstring response, including bits that have a high probability of changing value.
Error avoidance schemes, on the other hand, integrate a thresholding method that skips bits that are deemed unreliable. The reliability of a bit is often directly related to the soft data associated with the bit and in particular, the distance of the soft data value to the bit-flip line. The bit-flip line is defined by the PUF architecture as a soft threshold between ‘0’ or a ‘1’. Unlike error correction methods, error avoidance methods can only be used with PUF architectures that produce soft data values, for example, the RO [
10], metal resistance [
15], NVM [
16] and HELP [
8,
17,
18] PUFs are some examples. Notable exceptions here are memory-based PUFs, including SRAM, DRAM, FF and latch-based PUFs, which as originally proposed, are not capable to producing soft data.
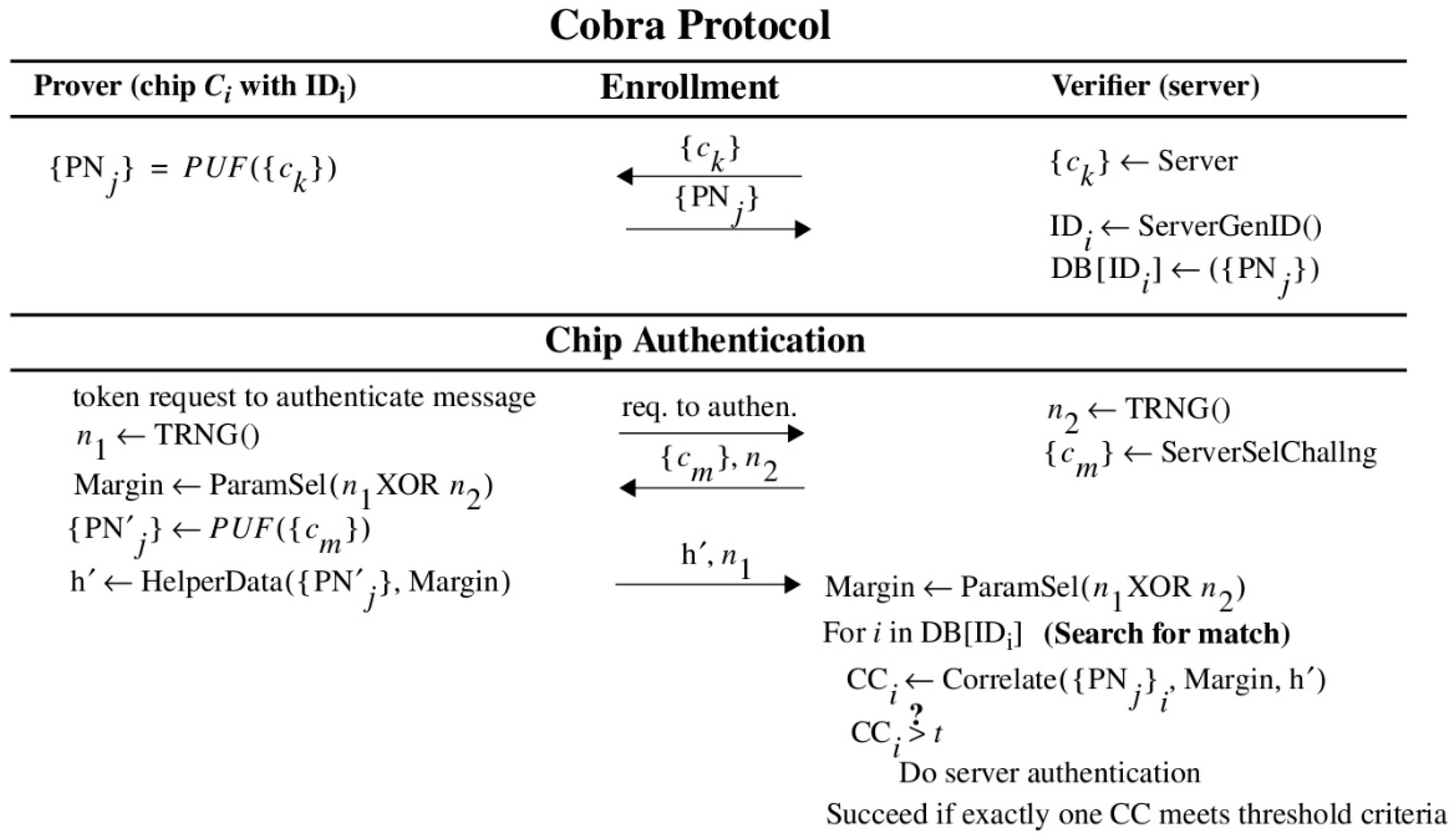
In typical usage scenarios, an enrollment phase is carried out in which challenges are applied to the PUF in a secure facility and response bitstrings are generated for the first time. In addition to the response bitstring, PUF architectures that use either error correction or error avoidance methods also produce Helper Data. Helper Data is typically maintained in the secure facility and transmitted to the fielded device later during regeneration to enable the PUF to precisely reproduce the response bitstring. The form of the generated Helper Data varies dramatically depending on the error correction or avoidance method employed. A key contribution of the method proposed here relates to Helper Data and in particular to Helper Data that is generated by error avoidance methods. The next two subsections discuss a simple error avoidance scheme used by the HELP PUF as well as features of the generated Helper Data that are leveraged in the proposed Cobra protocol.
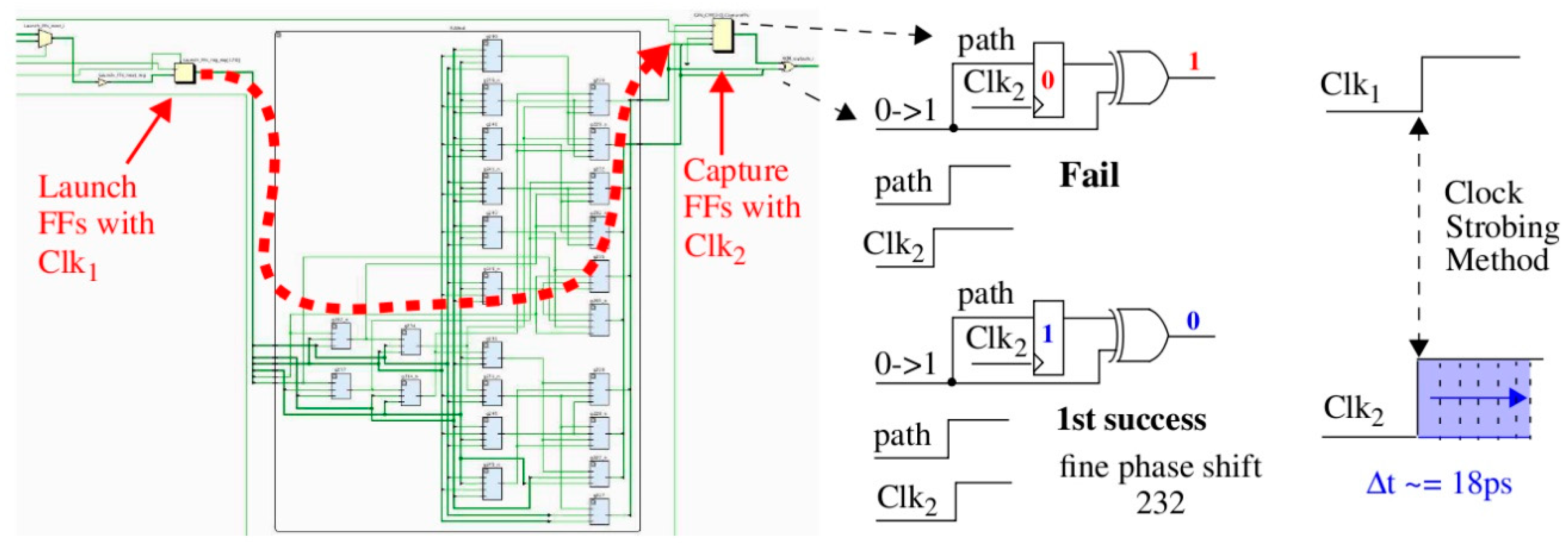
2.3. HELP PUF
To better exemplify the principles of the proposed technology, we use the HELP PUF architecture and data collected from a set of Zynq FPGAs in the illustrative examples that follow [
17,
18]. HELP uses a launch-capture technique to obtain accurate digital timing values of path delays through a combinational logic block. The combinational logic block for a full adder is shown in
Figure 1 but any functional unit can be used (the combinational logic from one column of the Advanced Encryption Standard is used in [
7,
8,
17,
18] and for the experimental results presented in
Section 4). Logic signal transitions are launched from the Launch FFs shown on the left using Clk
1 and captured in the Capture FFs shown on the right using Clk
2.
The digital clock manager (DCM) on the FPGA is used to create the clocks, with dynamic fine phase shift enabled for Clk
2. Dynamic fine phase shift allows a state machine running in the programmable logic (PL) of the FPGA to increment the phase shift by increments of 18 ps (see right side of
Figure 1). A path through the full adder is timed by repeatedly applying a 2-vector sequence to the Launch FFs until the signal propagating along the highlighted path is successfully captured in the Capture FF. A successful capture occurs in this example when the ‘0’ produced from the first vector V
1 of the 2-vector sequence is overwritten by the ‘1’ produced by V
2 (see center portion of
Figure 1). When this occurs, the current fine phase shift value, which is an integer typically between 100 and 500, is recorded by HELP as the digitized timing value for this path. These timing values represents the soft data associated with HELP.
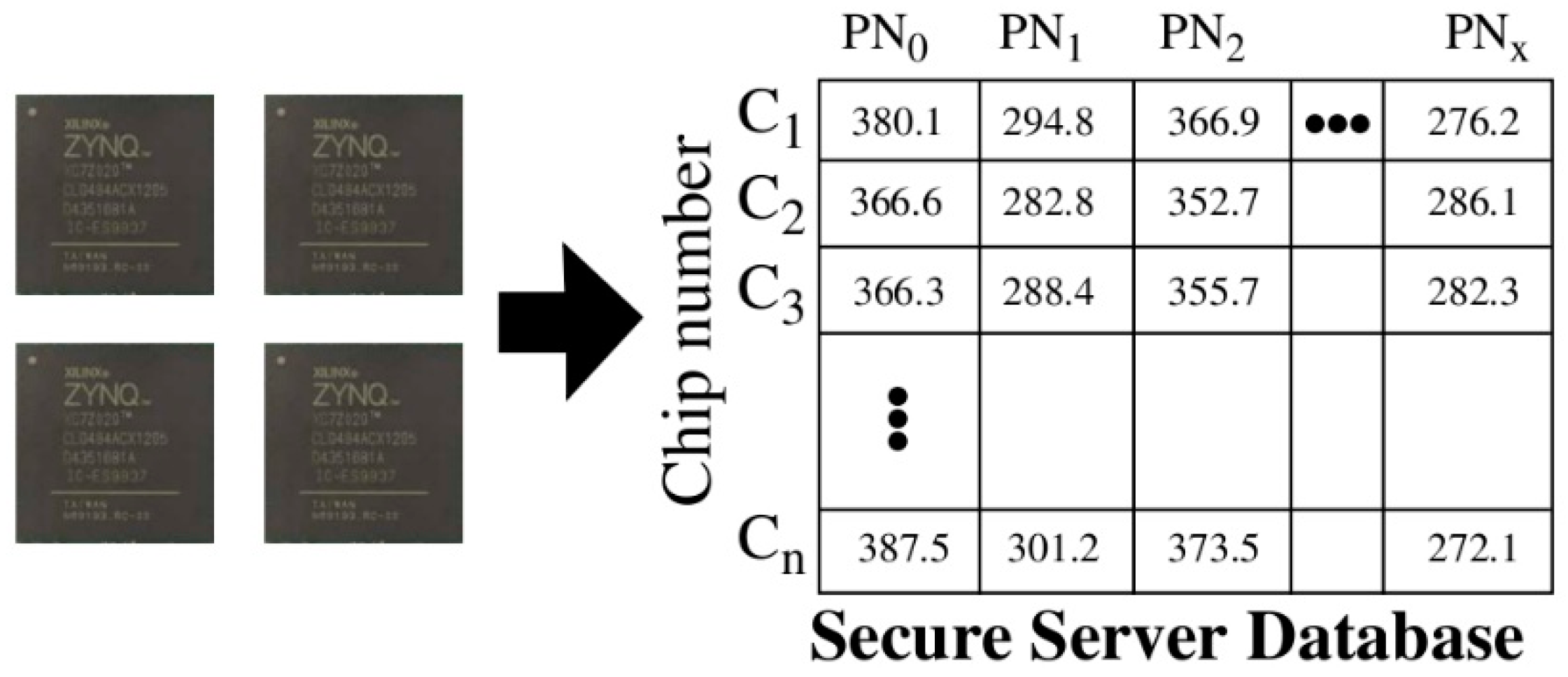
During enrollment, a set of timing values, called
PUF Numbers or
PN, for each chip are stored in the rows of a secure database as shown in
Figure 2. This data is consulted by the secure server to authenticate these chips after they are deployed in fielded systems. The storage of soft data on the server, in contrast to response bitstrings, is the first of several significant differences that exist between Cobra and the PUF-based protocols proposed by others [
1,
2,
3,
4,
5,
6].
As indicated above, the proposed Cobra protocol leverages Helper Data to carry out authentication. The Helper Data is derived from the PNs stored in the secure database on the server and from an instance of HELP that is programmed into the programmable logic of an FPGA, which represents the fielded chip. The entropy that is associated with each chip is captured by the PN stored in the server database. An adversary carrying out machine learning attacks against the protocol would attempt to learn the timing information stored in the database by reverse-engineering the bitstring responses that are exchanged openly over the network. Once learned, the adversary can then impersonate the chip. Therefore, it is vital that the relationship between the PN and the response bitstring be obscured and remain hidden to make this task difficult or impossible for the adversary.
2.4. Helper Data Generation Using an Error Avoidance Technique
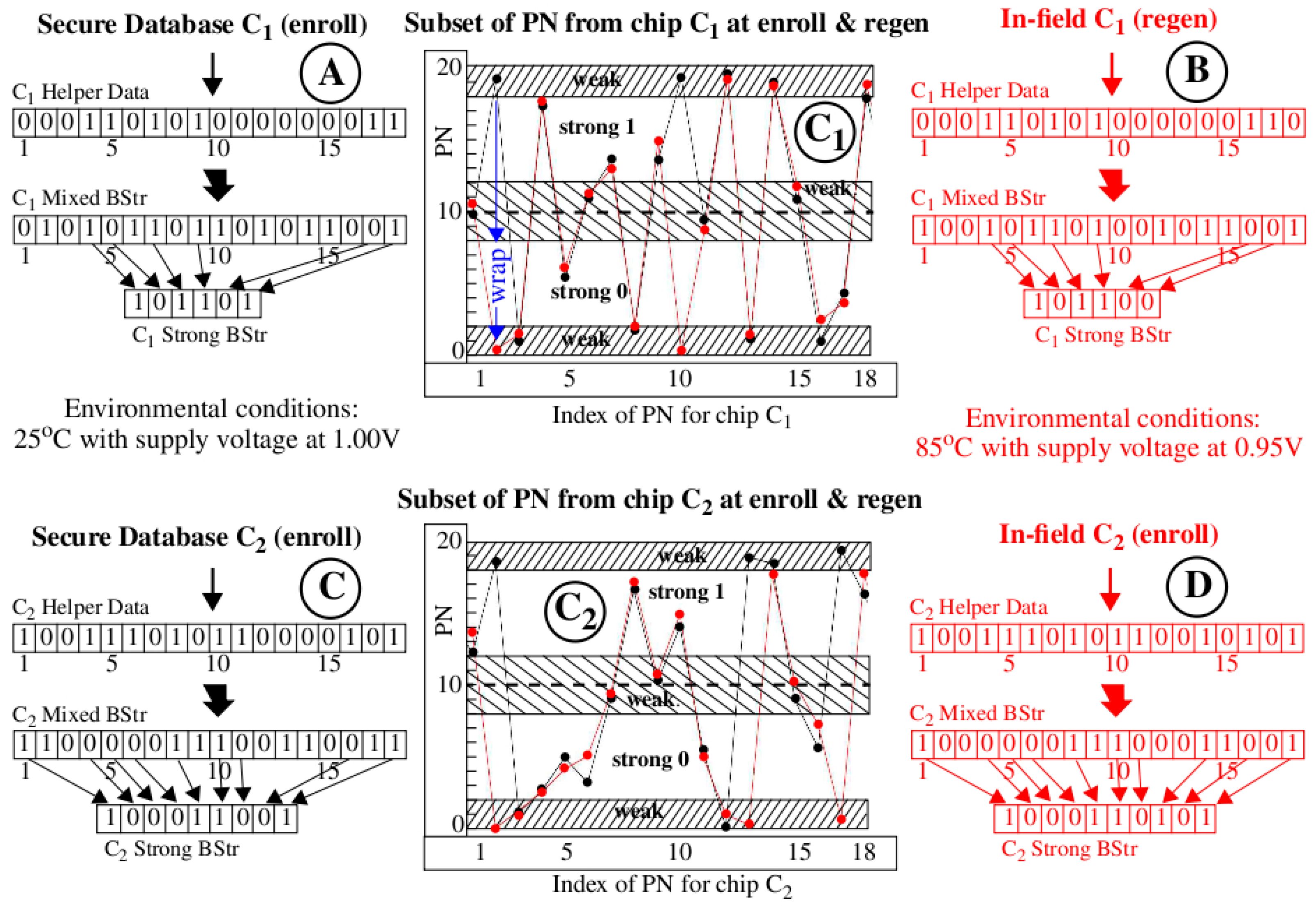
The illustration presented in
Figure 3 shows how bitstrings and Helper Data are generated using an error avoidance scheme called Margining, as a precursor to our discussion on the proposed Helper Data correlation method. The graphs labeled with “C
1” and “C
2” (in large circles) in the center of the figure plot a set of 18 PN (timing values) along the x-axis for two chips C
1 (top) and C
2 (bottom), with the black curves depicting PN obtained from the secure server database and the red curves depicting PN generated on-the-fly by these chips during regeneration in the field. The environmental conditions for data collected during enrollment and stored in the secure database are specified as 25 °C under nominal supply voltage conditions (1.00 V) while to fielded chips are subjected to high temperature (85 °C) and low supply voltage conditions (−5% or 0.95 V). The data shown are actual measurements obtained from two Zynq FPGAs used in our experiments.
The HELP PUF converts the PN into a bitstring by applying the following algorithm. First, a pseudo-random number generator selects pairs of PN and creates differences. A temperature-voltage compensation method called TVComp is then applied to the differences to compensate the measured timing values for changes introduced by environmental conditions (we omit the details of these operations [
19] here to focus the discussion on the proposed correlation technique). Finally, a modulus operation is applied to the compensated differences to remove path length bias effects. The modulus operation is defined in the standard way as returning the positive remainder after dividing by the modulus. The value of the modulus is one of several parameters to the HELP algorithm. The graphs shown in
Figure 3 use a modulus of 20, which is reflected as the maximum value given on the y-axis.
The TVComp process implemented within HELP is very effective at compensating the chip regenerated PN (red values) but is not ideal. The red data points are vertically offset above and below the black (enrollment) data points because of uncompensated temperature-voltage noise (TVNoise). An interesting example labeled ‘wrap’ is shown for the 2nd data point in the upper “C1” graph where TVNoise has caused the point to ‘wrap’ from the enrollment value near 20 back around to a value near 0 during regeneration. Despite these anomalies, the black and red curves in each graph track very closely, that is, they are correlated. In contrast, the black curves from both graphs (for C1 and C2) are not correlated. This key observation serves as the basis for the innovation proposed within the Cobra protocol.
As mentioned earlier, the error avoidance scheme implemented within HELP is called Margining. The Margining scheme skips soft data values (PN in our example) for cases in which the probability of a bit-flip error is large. These highly probable bit-flip regions are labeled “weak” in the center graphs of
Figure 3 and are located adjacent to the bit-flip lines at 0, 10 and 20. In other words, PN that are within a distance of 2.0 of these bit-flip lines have the highest probability of changing value. For example, the PN labeled “wrap” represents a bit-flip error which is introduced by TVNoise. PN that are located in the “weak” regions are assigned ‘0’ in the Helper Data bitstring. For example, the “C
1 Helper Data” bitstrings in the region labeled with the circled “A” in the figure begins with “000,” which reflects that the status of the first 3 PN in the black curve of graph “C
1”. In contrast, the 4th bit is ‘1’ because the PN at position 4 in graph “C
1” falls within the “strong 1” region.
The “C
1 Mixed BStr” in region “A” of
Figure 3 records the bit value associated with each of the 18 PN, with PN < 10.0 assigned ‘0’ and those ≥10.0 assigned ‘1’. This response bitstring corresponds one-to-one to the “C
1 Helper Data” bitstring and contains both strong and weak bits. The “C
1 Strong BStr” is constructed from the “C
1 Mixed BStr” by selecting only those bits identified as strong in the “C
1 Helper Data” bitstring. The region labeled “B” shows the corresponding bitstrings generated using the red (regeneration) data points from graph “C
1”. The graphs and annotations labeled “C
2,” “C” and “D” are completely analogous to “C
1”, “A” and “B” except the PN and bitstrings are derived from second chip C
2.
The HELP authentication protocol from Reference [
7] proposes a DualHelperData scheme in which both the Helper Data and Strong BStr are exchanged between the server modeled on the left side of
Figure 3 and the fielded chips modeled on the right side. As discussed earlier, exposing the Strong BStr to the adversary enables model-building attacks where the adversary attempts to reverse engineer the PN stored in the secure database using machine learning (ML) algorithms. Although attempts to model-build HELP have not been successful (see [
20]), the exposure of the response bitstrings (Strong BStr) still represents a vulnerability that enables ML attacks. If it becomes possible to construct an ML attack that is able to deduce the relationships among the PN, then the response bitstrings to other challenges can be predicted and the chip impersonated.
2.5. Proof-of-Concept: Helper Data Correlation
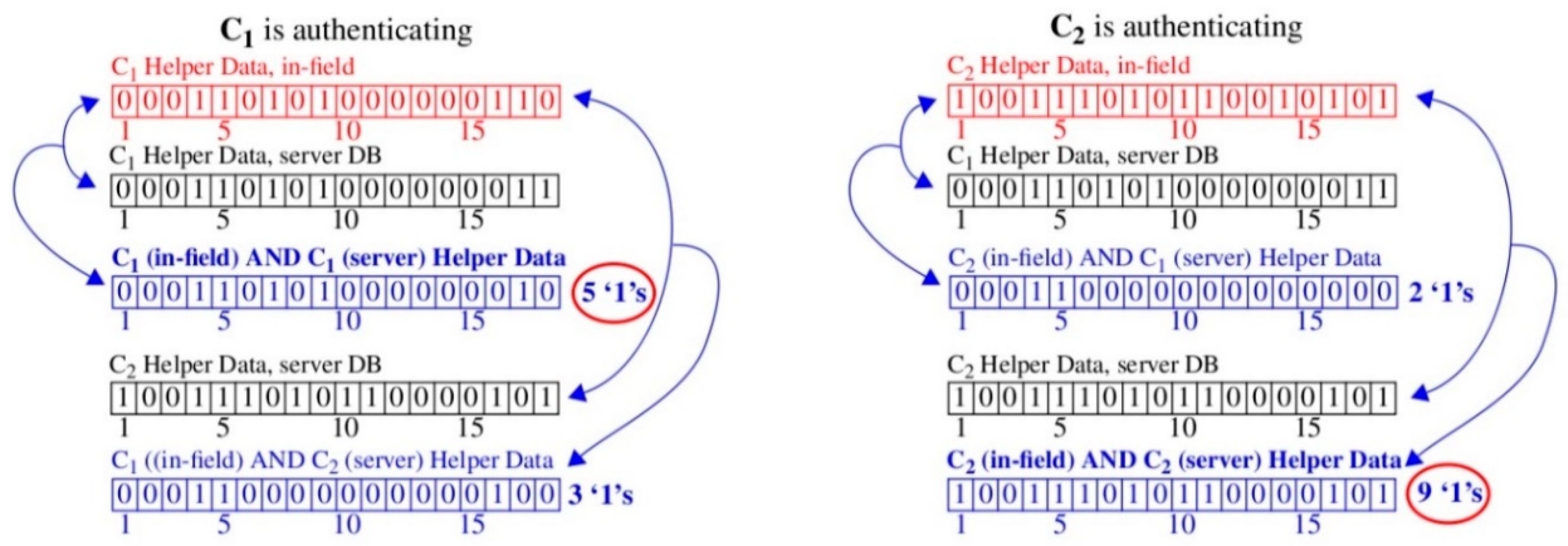
As a mitigation strategy, we propose an alternative authentication protocol that exchanges only the Helper Data bitstrings. Authentication is carried out in Cobra by correlating the Helper Data bitstrings generated using the enrollment data on the server with the Helper Data bitstring generated on-the-fly by the chip. The simplest correlation strategy is to compute a new bitstring by bitwise AND’ing the Helper Data bitstrings from the server and chip and then counting the number of ‘1’s in the AND’ed version. We refer to the number of ‘1’s as the correlation coefficient (CC) because it reflects the level of similarity that exists (among the ‘1’s) between the two Helper Data bitstrings.
As an example, the left column of
Figure 4 shows an authentication attempt by chip C
1 while the right column shows an attempt by chip C
2. The top-most red-colored bitstrings in each column are the Helper Data bitstrings transmitted by the chips to the server. For each Helper Data bitstring received during authentication, the server carries out an exhaustive search operation using the PN stored its secure database. It constructs the black-colored Helper Data bitstrings in each column using the technique described in
Figure 3 (in fact, the bitstrings shown here are identical to those shown in
Figure 3).
For each Helper Data bitstring it constructs, the server bitwise AND’s it with the received chip’s Helper Data bitstring. For example, the AND’ed versions are labeled “C
1 (in-field) AND C
1 (server) Helper Data” and “C
1 (in-field) AND C
2 (server) Helper Data” in the left column of
Figure 4. As discussed, the bitwise AND operation is a form of correlation that acts to preserve more ‘1’s in cases where the bitstrings are similar. The CCs (number of ‘1’s) are reported to the right of AND’ed Helper Data bitstrings. The results for both authentication attempts show higher correlation for cases where the server-generated Helper Data bitstring is derived using PN collected earlier during enrollment from the same chip. In other words, the authenticating chip is correctly identified to the server using only the information provided by the CC.
This example uses only a small number of 18 PN from the larger set of 2048 that are produced by each iteration of the HELP algorithm [
7]. The results shown in
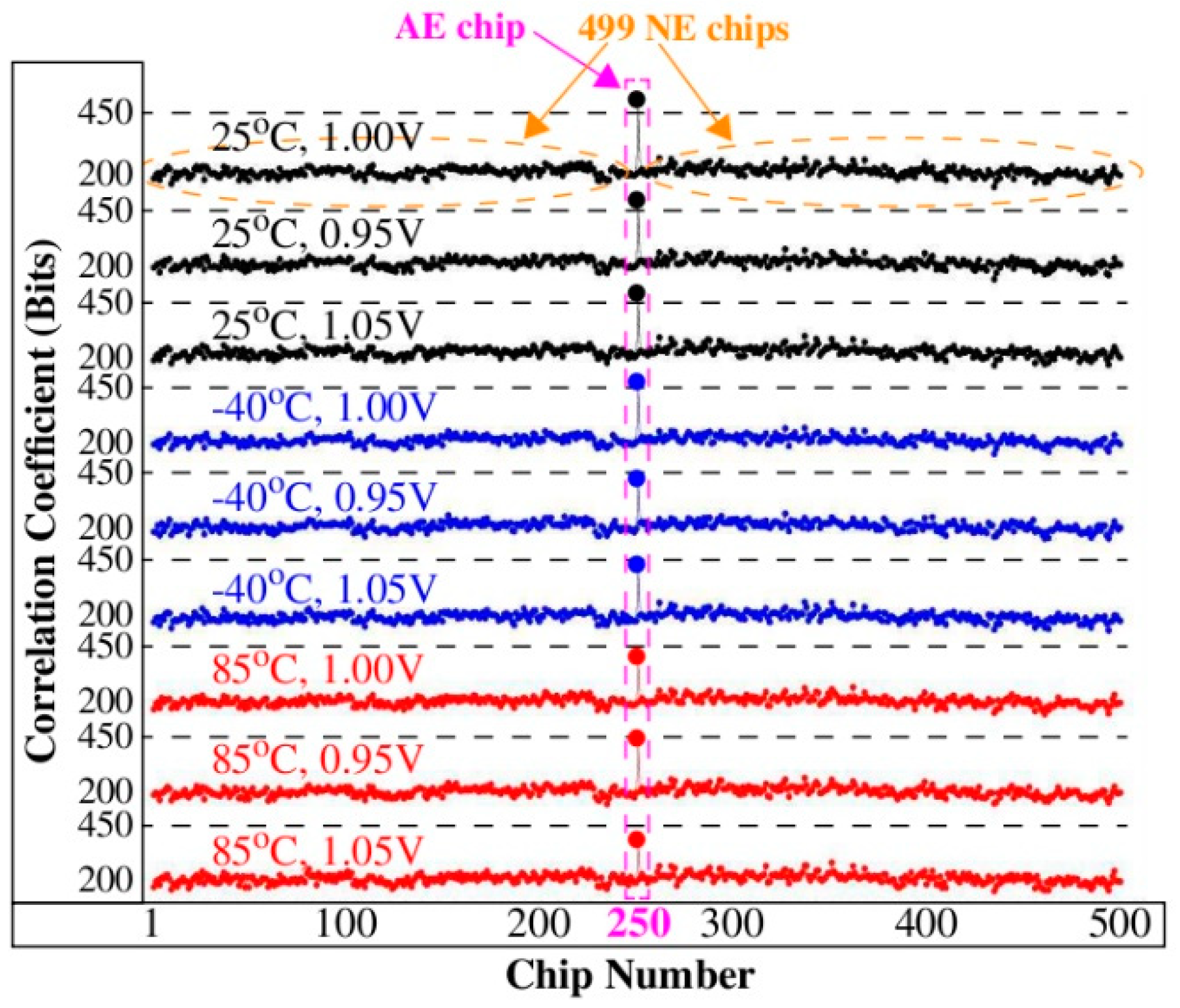
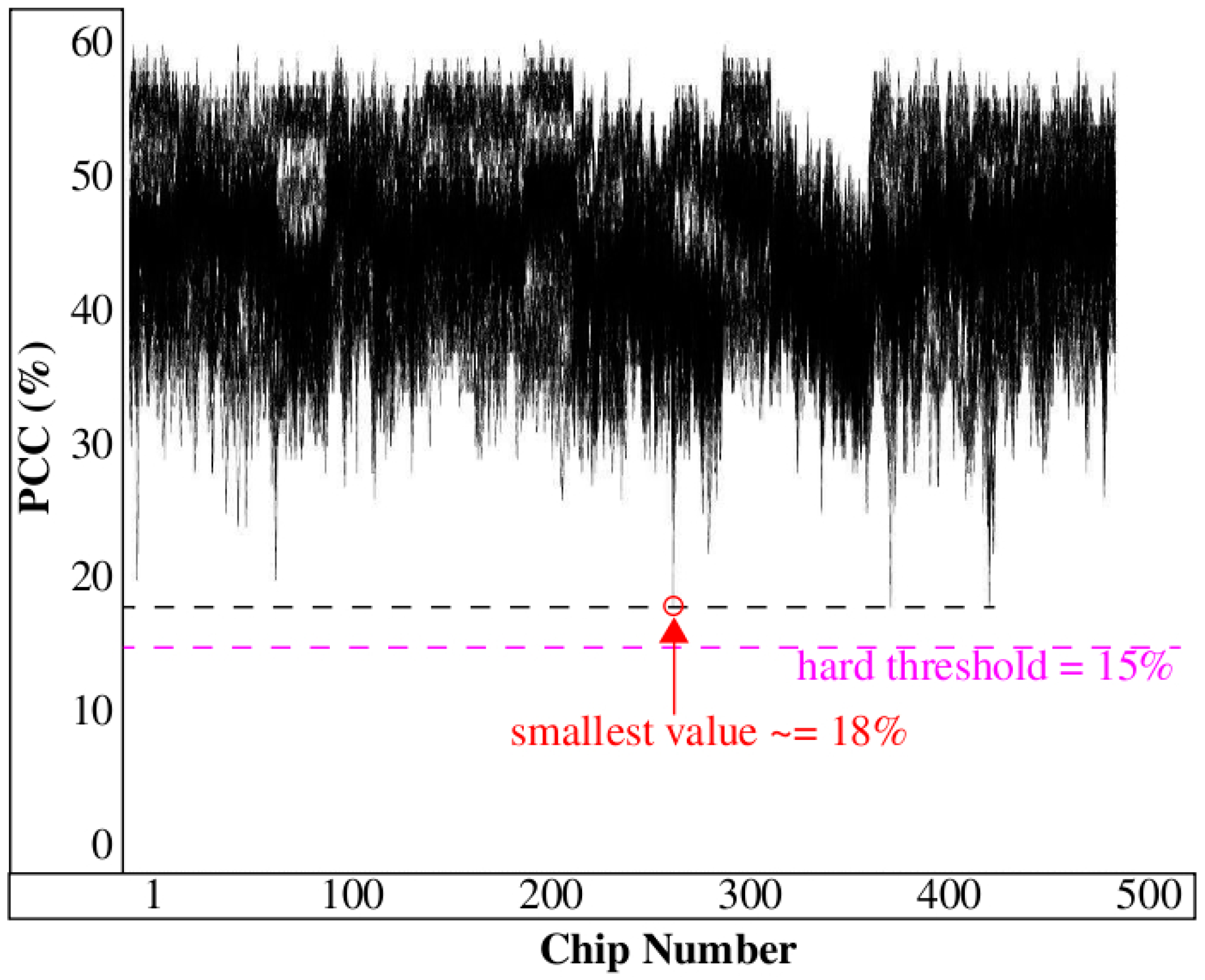
Figure 5 expand the example illustration to the full length bitstrings and to PN collected across 9 TV corners using 500 Xilinx Zynq FPGAs. Each of the 9 curves plots the CCs for the 500 chips along the x-axis. The authenticating chip is labeled C
250 and is highlighted in the center region of the figure.
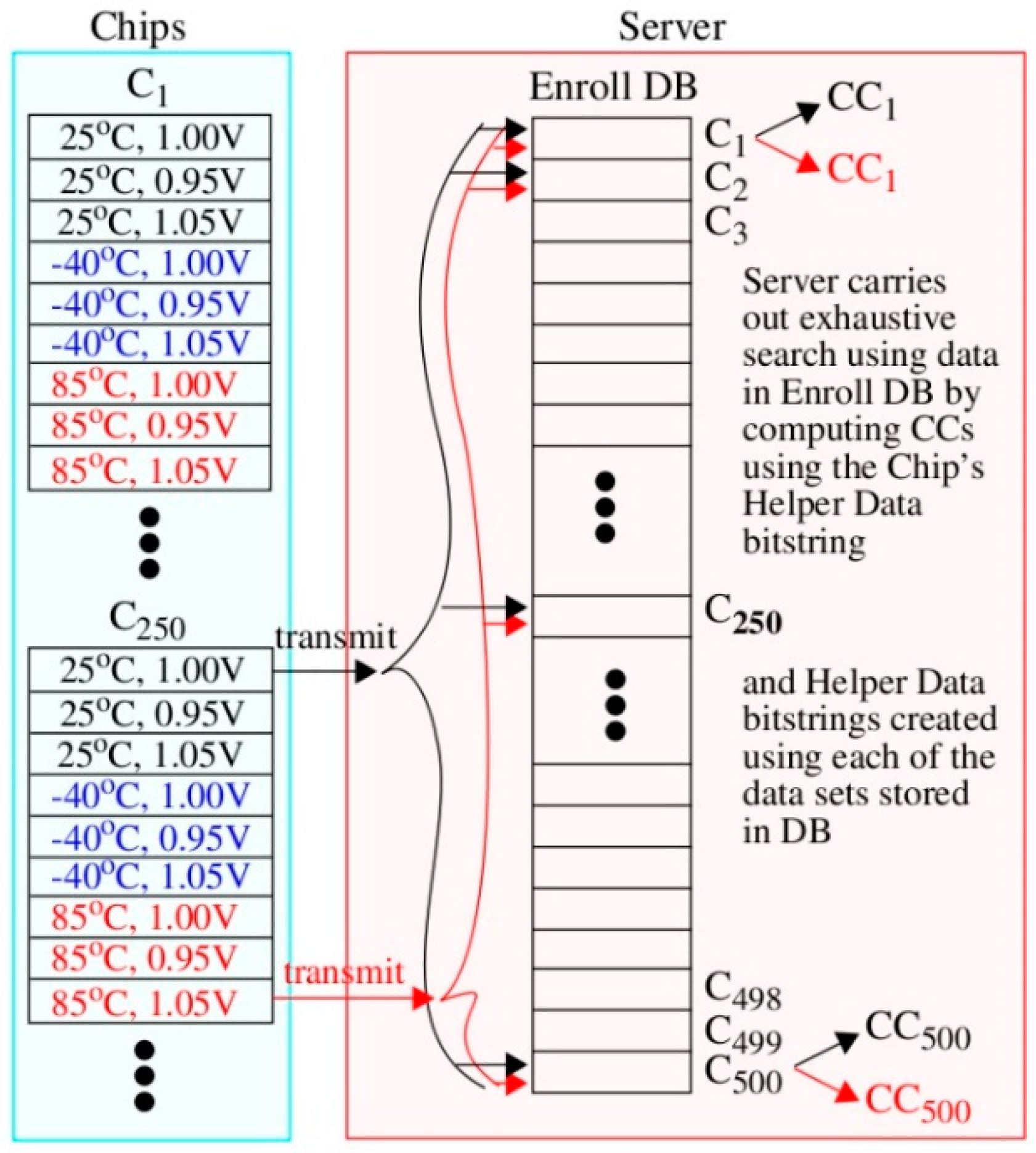
The graphic illustration given in
Figure 6 shows how the curves in
Figure 5 are constructed. Here, the chip’s Helper Data bitstring on the left, regenerated under 25 °C, 1.00 V, is transmitted to the server on the right. A second authentication request is also shown in red where the chip in this case is regenerating Helper Data with environmental conditions set to −40 °C, 1.05 V. The server carries out an exhaustive search using data stored in the Enroll DB separately for each of these two authentication attempts and computes a set of 500 CCs. The CCs are plotted along the x-axis in
Figure 5 as the top-most and bottom-most curves. A similar process is carried out to construct the CCs for the remaining 7 curves in
Figure 5 but using PN from the other TV corners.
The CCs in
Figure 5 for C
250 (referred to as the authentic-enrolled (
AE) chip) vary from more than 450 bits in the top curve to approx. 380 bits in the bottom curve. Although the correlation is weakened when the chip is exposed to harsh environmental conditions, it still remains high with respect to the CCs produced by the remaining 499 chips (referred to as non-authentic-enrolled (
NE) chips) from the DB. The largest value associated with a NE chip is approx. 260. The large margin between the AE and NE CCs suggests that it should be possible for the server to define a threshold to distinguish successful authentications from unsuccessful authentications with very high probability, for example, any value between 260 and 380 works in this example.
Note that our analysis considers only AE and NE authentication attempts. Two other possibilities include non-authentic-not-enrolled (
NN) and non-authentic-counterfeit (
NC) authentication attempts. Modeling NN authentication attempts is trivially accomplished by removing their data from the Enroll DB. It follows that attempts to authenticate by chips with no data in the Enroll DB would produce CCs similar to those produced for the 499 NE CCs shown in
Figure 5. Modeling NC authentication attempts is difficult without employing some type of machine learning algorithm if in fact an attack model can be devised. We leave this non-trivial task for future work.
We emphasize here that under the AND correlation scheme, it is possible for adversaries to construct Helper Data bitstrings with all ‘1s’, which guarantees a large number of matches. However, large CCs would occur for ALL data sets in the secure DB, which, in turn, would be flagged by the server and result in a failed authentication attempt. This is true because the server allows only one CC to be above the threshold in order for an authentication attempt to be classified as successful.