Measurement of Charge and Refractive Indices in Optically Trapped and Ionized Living Cells
Abstract
1. Introduction
2. Methods
2.1. Cell Culture and Treatment
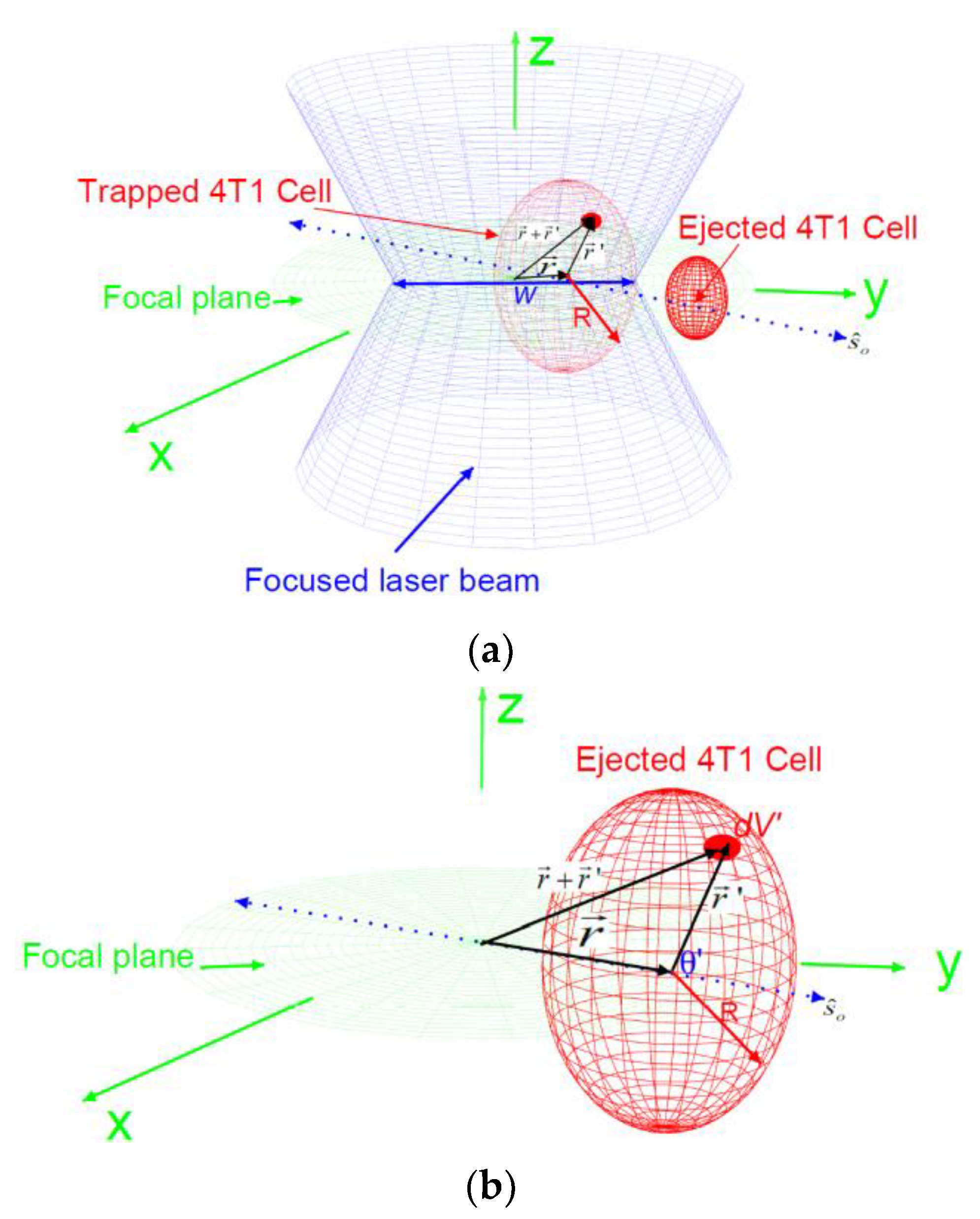
2.2. Laser Trap Set-Up
2.3. The Forces
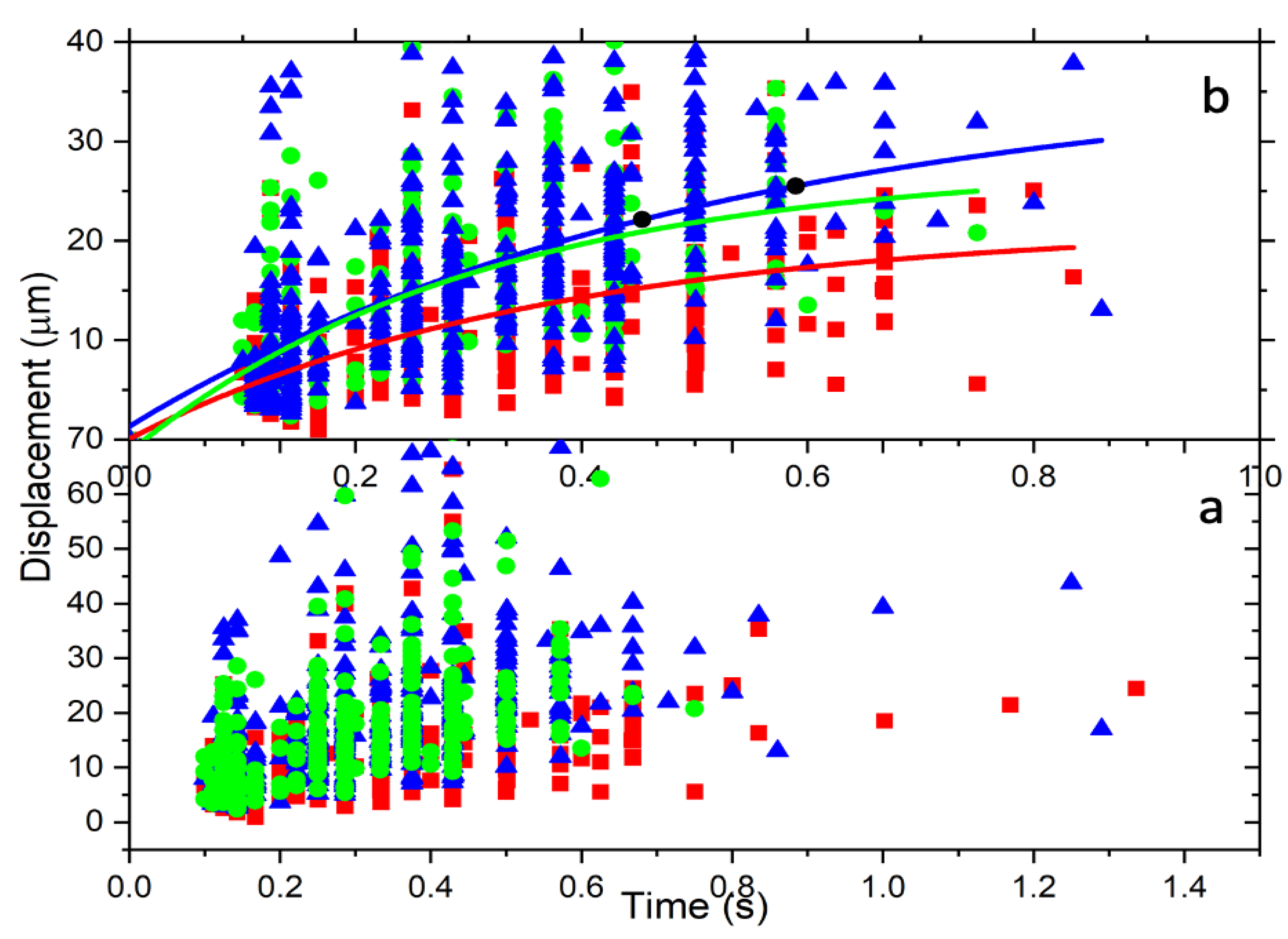
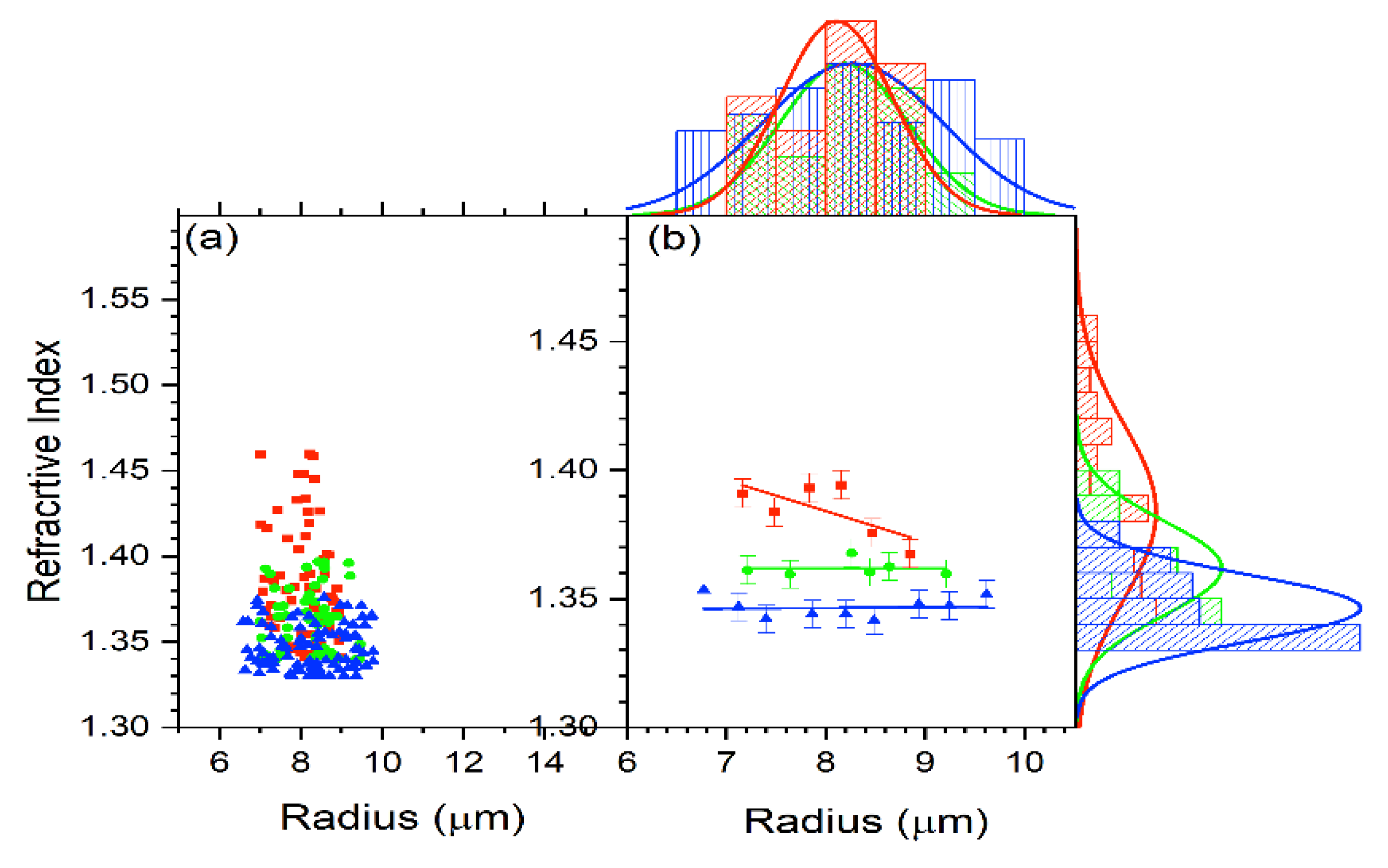
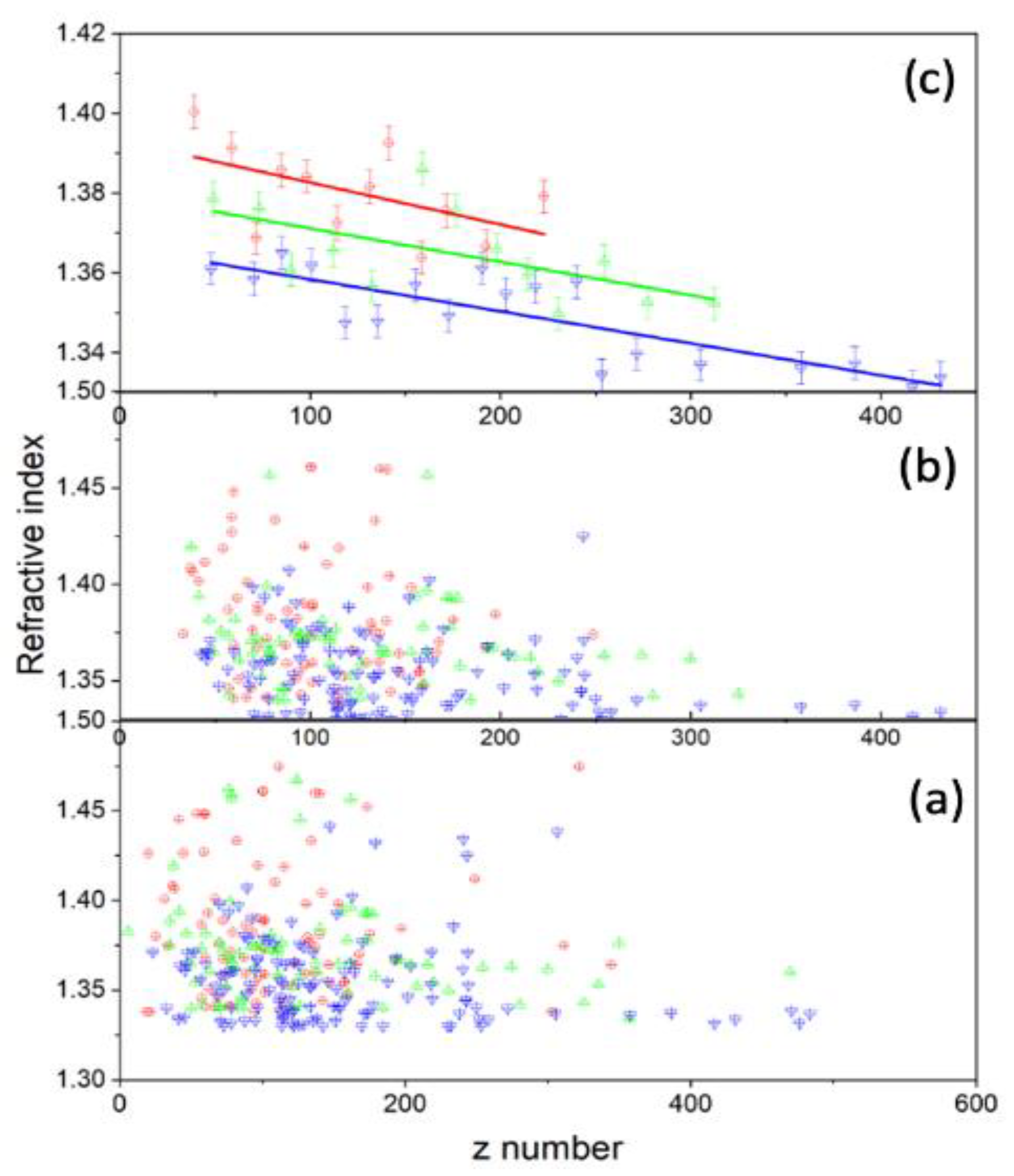
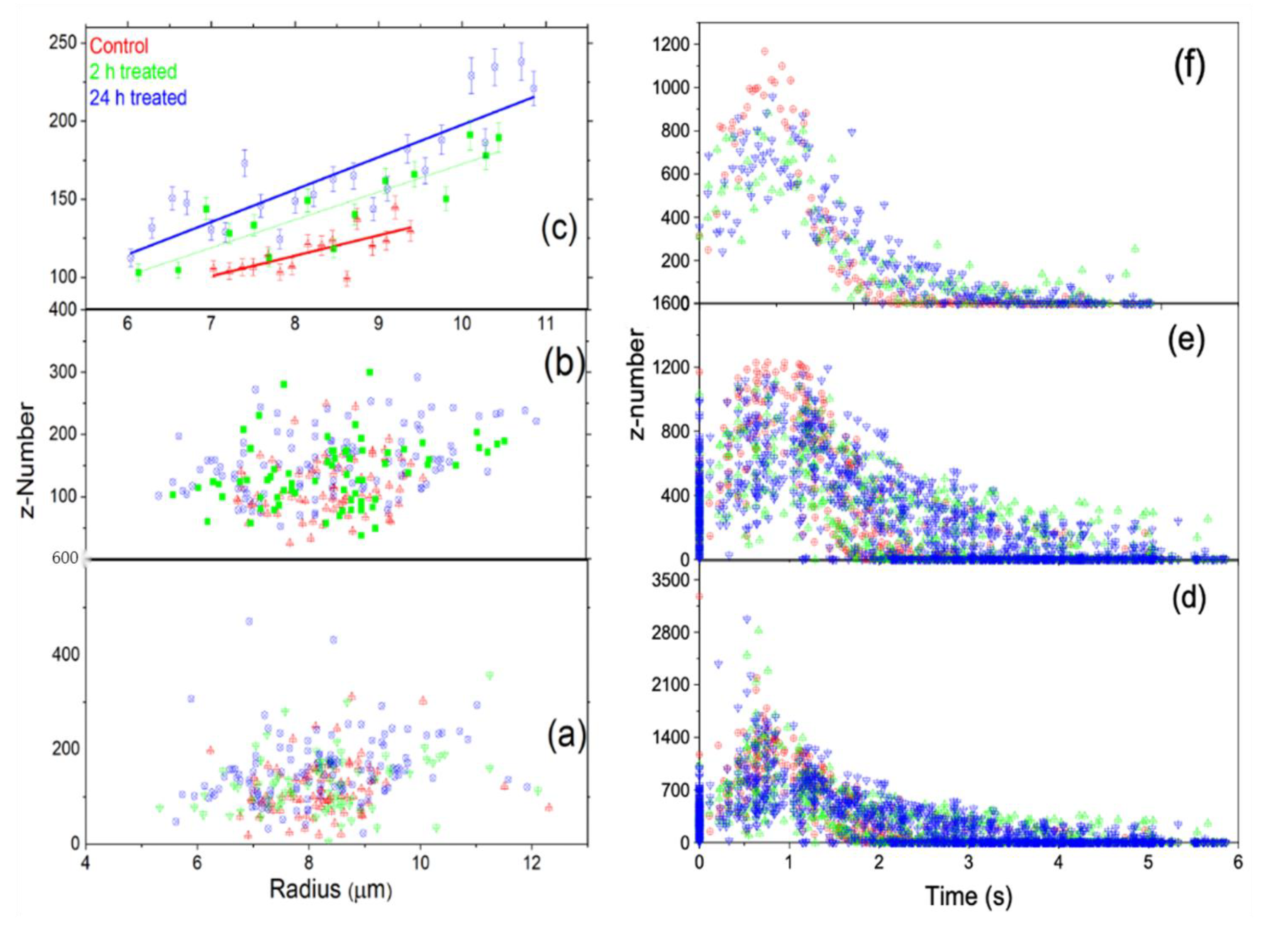
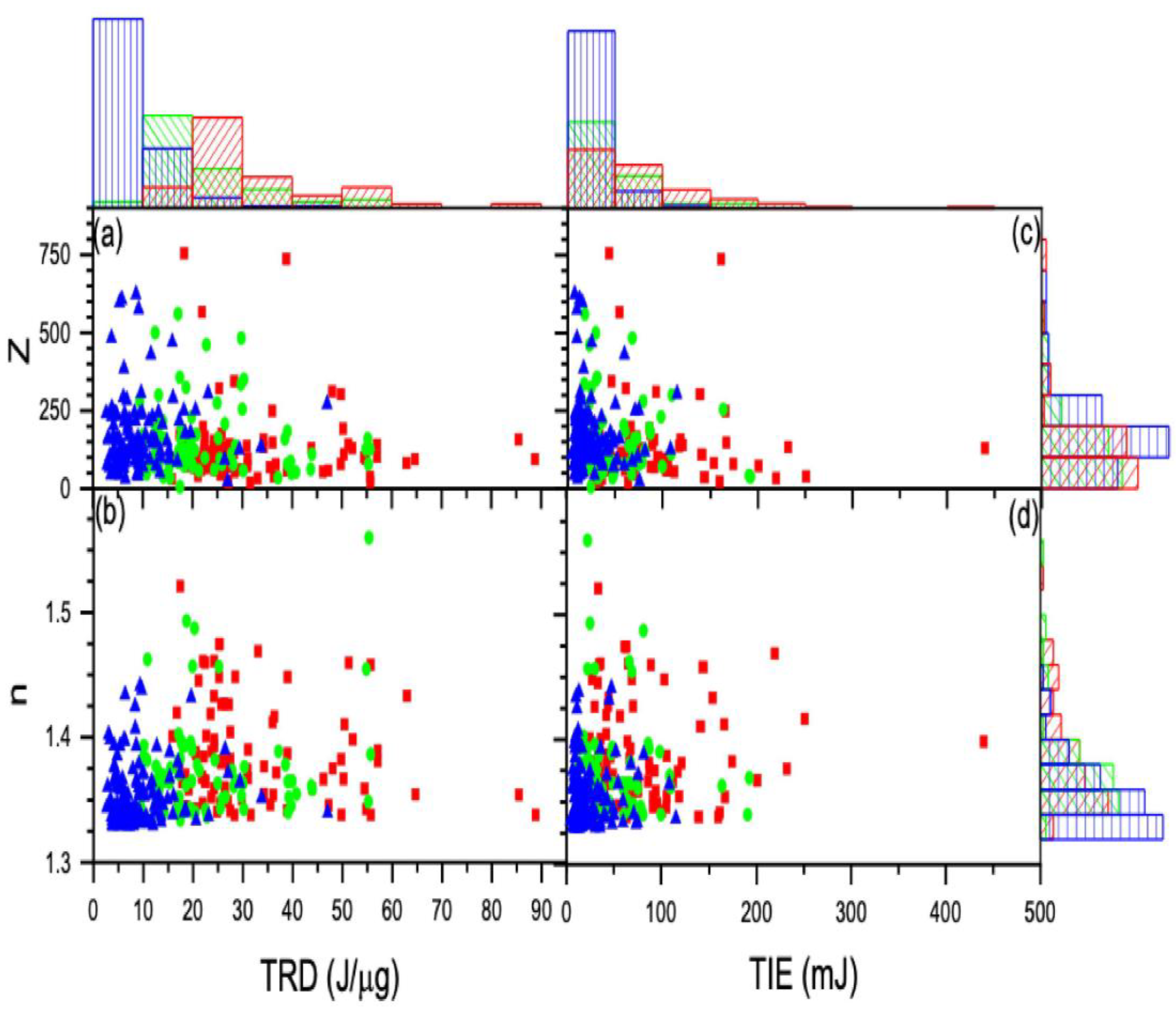
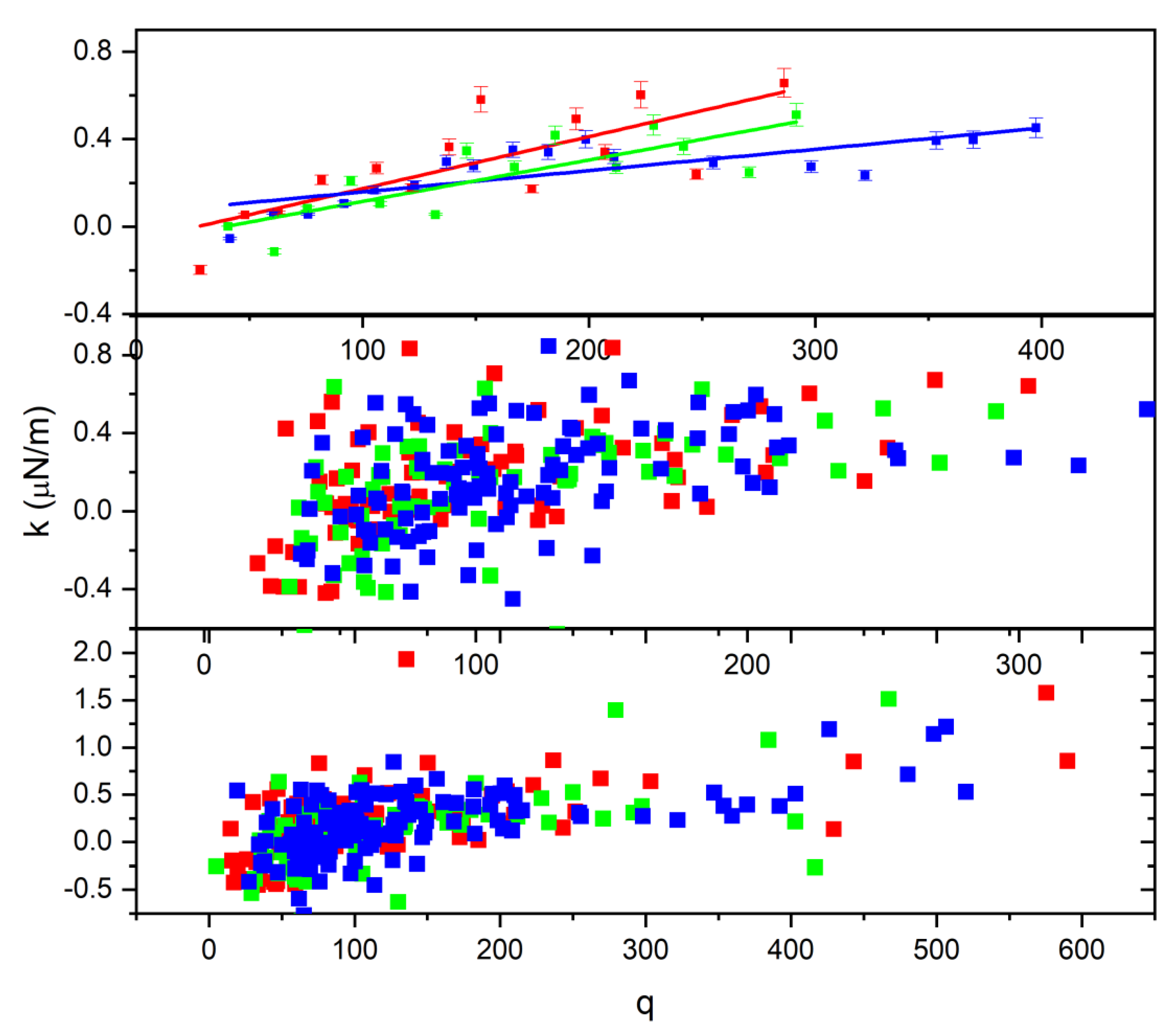
3. Results and Discussion
3.1. Reduced Method
3.1.1. First Approach
3.1.2. Second Approach
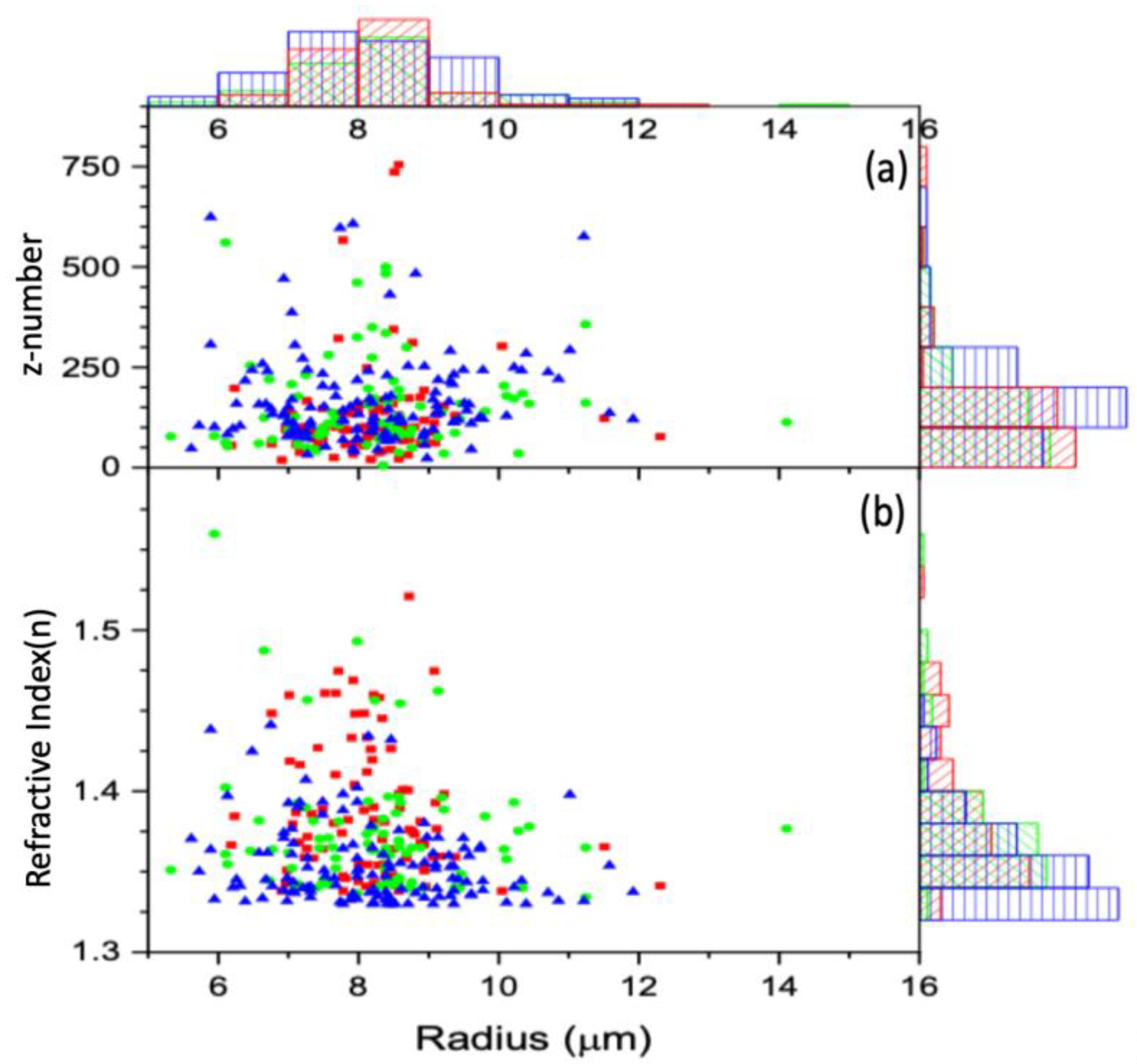
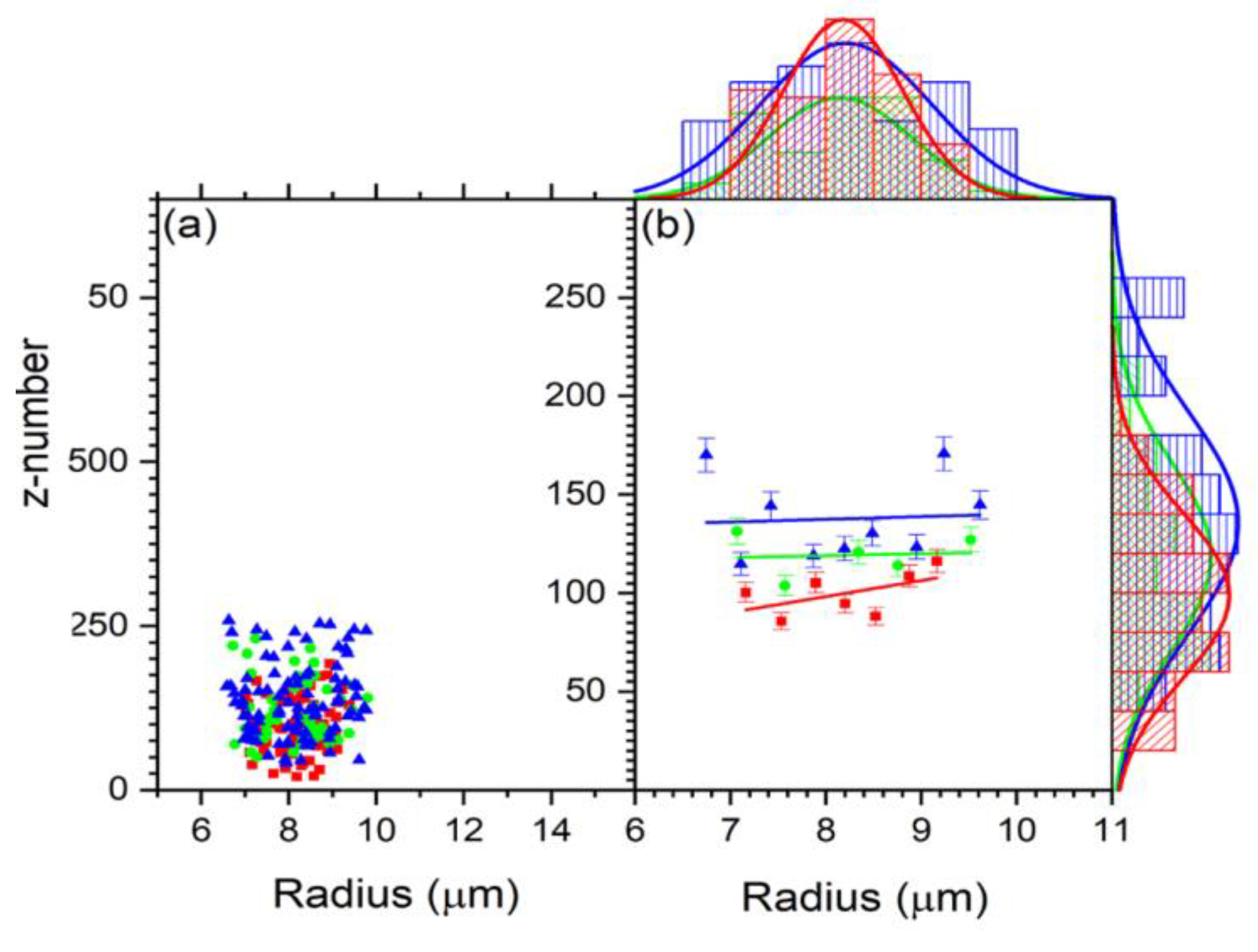
3.2. Radiation Effect on the Cell Charge and Refracted Index
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Statement of Significance
References
- World Health Organization. Global Health Observatory; World Health Organization: Geneva, Switzerland, 2018; Available online: http://www.Who.int/gho/database/en/ (accessed on 21 June 2018).
- Bray, F.; Ferlay, J.; Soerjomataram, I.; Siegel, R.L.; Torre, L.A.; Jemal, A. Global cancer statistics 2018: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2018, 68, 394–424. [Google Scholar] [CrossRef]
- Baskar, R.; Lee, K.A.; Yeo, R.; Yeoh, K.W. Cancer and radiation therapy: Current advances and future directions. Int. J. Med. Sci. 2012, 9, 193–199. [Google Scholar] [CrossRef]
- Liauw, S.L.; Connell, P.P.; Weichselbaum, R.R. New paradigms and future challenges in radiation oncology: An update of biological targets and technology. Sci. Transl. Med. 2013, 5, sr2–sr173. [Google Scholar] [CrossRef]
- Lane, R.J.; Khin, N.Y.; Pavlakis, N.; Hugh, T.J.; Clarke, S.J.; Magnussen, J.; Rogan, C.; Flekser, R.L. Challenges in chemotherapy delivery: Comparison of standard chemotherapy delivery to locoregional vascular mass fluid transfer. Future Oncol. 2018, 14, 647–663. [Google Scholar] [CrossRef]
- Wang, L.; Correa, C.R.; Zhao, L.; Hayman, J.; Kalemkerian, G.P.; Lyons, S.; Cease, K.; Brenner, D.; Kong, F.-M. The effect of radiation dose and chemotherapy on overall survival in 237 patients with stage III non–small-cell lung cancer. Int. J. Radiat. Oncol. Biol. Phys. 2009, 73, 1383–1390. [Google Scholar] [CrossRef][Green Version]
- Begg, A.C.; Stewart, F.A.; Vens, C. Strategies to improve radiotherapy with targeted drugs. Nat. Rev. Cancer 2011, 11, 239–253. [Google Scholar] [CrossRef]
- Maingon, P.; Govaerts, A.S.; Rivera, S.; Vens, C.; Shash, E.; Grégoire, V. New challenge of developing combined radio-drug therapy. Chin. Clin. Oncol. 2004, 3, 10–21037. [Google Scholar]
- Yoo, G.S.; Park, W.; Yu, J.I.; Choi, D.H.; Kim, Y.-J.; Shin, K.H.; Wee, C.W.; Kim, K.; Park, K.R.; Kim, Y.B.; et al. Comparison of breast conserving surgery followed by radiation therapy with mastectomy alone for pathologic N1 breast cancer patients in the era of anthracycline plus taxane-based chemotherapy: A multicenter retrospective study (KROG 1418). Cancer Res. Treat. Off. J. Korean Cancer Assoc. 2019, 51, 1041. [Google Scholar] [CrossRef]
- Nguyen, P.T.; Abbosh, A.; Crozier, S. Three-dimensional microwave hyperthermia for breast cancer treatment in a realistic environment using particle swarm optimization. IEEE Trans. Biomed. Eng. 2016, 64, 1335–1344. [Google Scholar] [CrossRef]
- Ami, N.; Sato, H.; Hayakawa, Y. Paclitaxel-induced hypothermia and hypoperfusion increase breast cancer metastasis and angiogenesis in mice. Oncol. Lett. 2018, 15, 2330–2334. [Google Scholar] [CrossRef]
- Norouzi, H.; Khoshgard, K.; Akbarzadeh, F. In vitro outlook of gold nanoparticles in photo-thermal therapy: A literature review. Lasers Med. Sci. 2018, 33, 917–926. [Google Scholar] [CrossRef]
- Rastinehad, A.R.; Anastos, H.; Wajswol, E.; Winoker, J.S.; Sfakianos, J.P.; Doppalapudi, S.K.; Carrick, M.R.; Knauer, C.J.; Taouli, B.; Lewis, S.C.; et al. Gold nanoshell-localized photothermal ablation of prostate tumors in a clinical pilot device study. Proc. Natl. Acad. Sci. USA 2019, 116, 18590–18596. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, J. Current status and future directions of cancer immunotherapy. J. Cancer 2018, 9, 1773–1781. [Google Scholar] [CrossRef]
- Pulaski, B.A.; Ostrand-Rosenberg, S. Mouse 4T1 breast tumor model. Curr. Protoc. Immunol. 2000, 39, 20–22. [Google Scholar] [CrossRef]
- Yan, S.; Tianen, Y. A study of the radiosensitive effects on mammary carcinoma in mice by Chinese medicine (Salvia plus Astragalus) and aspirin. Chin. J. Cancer Res. 1989, 1, 54–59. [Google Scholar] [CrossRef]
- Zhang, P.; Cui, Z.; Liu, Y.; Wang, D.; Liu, N.; Yoshikawa, M. Quality evaluation of traditional Chinese drug toad venom from different origins through a simultaneous determination of bufogenins and indole alkaloids by HPLC. Chem. Pharm. Bull. 2005, 53, 1582–1586. [Google Scholar] [CrossRef]
- Gao, Y.; Huang, R.; Gong, Y.; Park, H.S.; Wen, Q.; Almosnid, N.M.; Chippada-Venkata, U.D.; Hosain, N.A.; Vick, E.; Farone, A.; et al. The antidiabetic compound 2-dodecyl-6-methoxycyclohexa-2, 5-diene-1, 4-dione, isolated from Averrhoa carambola L., demonstrates significant antitumor potential against human breast cancer cells. Oncotarget 2015, 6, 24304. [Google Scholar] [CrossRef]
- Chen, C.; Nong, Z.; Xie, Q.; He, J.; Cai, W.; Tang, X.; Chen, X.; Huang, R.; Gao, Y. 2-Dodecyl-6-methoxycyclohexa-2, 5-diene-1, 4-dione inhibits the growth and metastasis of breast carcinoma in mice. Sci. Rep. 2017, 7, 6704. [Google Scholar] [CrossRef]
- Muhammed, E.; Chen, L.; Gao, Y.; Erenso, D. Chemo-treated 4T1 breast cancer cells radiation response measured by single and multiple cell ionization using infrared laser trap. Sci. Rep. 2019, 9, 17547. [Google Scholar] [CrossRef]
- Muhammed, E.; Cooper, J.; Devito, D.; Mushi, R.; del Pilar Aguinaga, M.; Erenso, D.; Crogman, H. Elastic property of sickle cell anemia and sickle cell trait red blood cells. J. Biomed. Opt. 2021, 26, 096502. [Google Scholar] [CrossRef]
- Kelley, M.; Gao, Y.; Erenso, D. Single cell ionization by a laser trap: A preliminary study in measuring radiation dose and charge in BT20 breast carcinoma cells. Biomed. Opt. Express 2016, 7, 3438–3448. [Google Scholar] [CrossRef] [PubMed]
- Kelley, M.; Cooper, J.; Devito, D.; Mushi, R.; del Pilar Aguinaga, M.; Erenso, D.B. Laser trap ionization for identification of human erythrocytes with variable hemoglobin quantitation. J. Biomed. Opt. 2018, 23, 055005. [Google Scholar] [CrossRef] [PubMed]
- Pasquerilla, M.; Kelley, M.; Mushi, R.; Aguinaga, M.D.P.; Erenso, D. Laser trapping ionization of single human red blood cell. Biomed. Phys. Eng. Express 2018, 4, 045020. [Google Scholar] [CrossRef]
- Liu, P.Y.; Chin, L.K.; Ser, W.; Chen, H.F.; Hsieh, C.M.; Lee, C.H.; Sung, K.B.; Ayi, T.C.; Yap, P.H.; Liedberg, B.; et al. Cell refractive index for cell biology and disease diagnosis: Past, present and future. Lab Chip 2016, 16, 634–644. [Google Scholar] [CrossRef]
- Parvin, T.; Ahmed, K.; Alatwi, A.M.; Rashed, A.N.Z. Differential optical absorption spectroscopy-based refractive index sensor for cancer cell detection. Opt. Rev. 2021, 28, 134–143. [Google Scholar] [CrossRef]
- Balcioglu, H.E.; van de Water, B.; Danen, E.H. Tumor-induced remote ECM network orientation steers angiogenesis. Sci. Rep. 2016, 6, 22580. [Google Scholar] [CrossRef]
- Yu, Y.F.; Kanna, V.; Bourouina, T.; Ng, S.H.; Yap, P.H.; Liu, A.Q. An on-chip glass sphere resonator for label-free detection. In Proceedings of the 2010 IEEE 23rd International Conference on Micro Electro Mechanical Systems (MEMS), Hong Kong, China, 24–28 January 2010; pp. 831–834. [Google Scholar]
- Lim, C.T.; Dao, M.; Suresh, S.; Sow, C.H.; Chew, K.T. Large deformation of living cells using laser traps. Acta Mater. 2004, 52, 1837–1845. [Google Scholar] [CrossRef]
- Huang, J.; Wang, L.; Liu, B.; Wan, S.; Xue, Q. In vitro evaluation of the tribological response of Mo-doped graphite-like carbon film in different biological media. ACS Appl. Mater. Interfaces 2015, 7, 2772–2783. [Google Scholar] [CrossRef]
- Grover, W.H.; Bryan, A.K.; Diez-Silva, M.; Suresh, S.; Higgins, J.M.; Manalis, S.R. Measuring single-cell density. Proc. Natl. Acad. Sci. USA 2011, 108, 10992–10996. [Google Scholar] [CrossRef]
- Zhao, Y.; Lai, H.S.S.; Zhang, G.; Lee, G.B.; Li, W.J. Measurement of single leukemia cell’s density and mass using optically induced electric field in a microfluidics chip. Biomicrofluidics 2015, 9, 022406. [Google Scholar] [CrossRef]
- Baniyash, M.; Netanel, T.; Witz, I.P. Differences in cell density associated with differences in lung-colonizing ability of B16 melanoma cells. Cancer Res. 1981, 41, 433–437. [Google Scholar] [PubMed]
- Pakhomov, A.G.; Miklavcic, D.; Markov, M.S. Advanced Electroporation Techniques in Biology and Medicine; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Hercules, W.A.; Lindesay, J.; Coble, A.; Schmukler, R. Electroporation of biological cells embedded in a polycarbonate filter. arXiv 2003, arXiv:physics/0308015. [Google Scholar] [CrossRef]
- Jordan, C.A.; Neumann, E.; Sowers, A.E. (Eds.) Electroporation and Electrofusion in Cell Biology; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Chang, D. (Ed.) Guide to Electroporation and Electrofusion; Academic Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Almessiere, M.; Slimani, Y.; Güngüneş, H.; Korkmaz, A.D.; Trukhanov, S.; Guner, S.; Alahmari, F.; Baykal, A. Correlation between chemical composition, electrical, magnetic and microwave properties in Dy-substituted Ni-Cu-Zn ferrites. Mater. Sci. Eng. 2021, 270, 115202. [Google Scholar] [CrossRef]
- Kabbur, S.M.; Waghmare, S.D.; Nadargi, D.Y.; Sartale, S.D.; Kambale, R.C.; Ghodake, U.R.; Suryavanshi, S.S. Magnetic interactions and electrical properties of Tb3+ substituted NiCuZn ferrites. J. Magn. Magn. Mater. 2019, 473, 99–108. [Google Scholar] [CrossRef]
- Goangul, M.S.; Stewart, W.C.; Erenso, D.; Crogman, H.T. The radiation response measurement of a single and multiple cell ionization of neuroblastoma cells by infrared laser trap. J. Radiat. Res. 2022, rrac082. [Google Scholar] [CrossRef]
- Itatani, J.; Zeidler, D.; Levesque, J.; Spanner, M.; Villeneuve, D.M.; Corkum, P.B. Controlling high harmonic generation with molecular wave packets. Phys. Rev. Lett. 2005, 94, 123902. [Google Scholar] [CrossRef]
- Miklavčič, D.; Pavšelj, N.; Hart, F.X. Electric properties of tissues. In Wiley Encyclopedia of Biomedical Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; Volume 1, pp. 3578–3589. [Google Scholar]
- Stogryn, A.L.E.X.; Desargant, G. The dielectric properties of brine in sea ice at microwave frequencies. IEEE Trans. Antennas Propag. 1985, 33, 523–532. [Google Scholar] [CrossRef]
- Kapil, K.M.; Gilbert, M.K. Effect of the Oscillating Electric Field Due to the Oscillating Electric Dipole on Raman Lines. East Eur. J. Phys. 2019, 4, 47–57. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muhammed, E.; Erenso, D.B.; Gao, Y.; Chen, L.; Kelley, M.; Vazquez, C.; Gale, M.; Nichols, C.; Crogman, H.T. Measurement of Charge and Refractive Indices in Optically Trapped and Ionized Living Cells. Tomography 2023, 9, 70-88. https://doi.org/10.3390/tomography9010007
Muhammed E, Erenso DB, Gao Y, Chen L, Kelley M, Vazquez C, Gale M, Nichols C, Crogman HT. Measurement of Charge and Refractive Indices in Optically Trapped and Ionized Living Cells. Tomography. 2023; 9(1):70-88. https://doi.org/10.3390/tomography9010007
Chicago/Turabian StyleMuhammed, Endris, Daniel B. Erenso, Ying Gao, Li Chen, Michele Kelley, Carina Vazquez, Mitchell Gale, Cody Nichols, and Horace T. Crogman. 2023. "Measurement of Charge and Refractive Indices in Optically Trapped and Ionized Living Cells" Tomography 9, no. 1: 70-88. https://doi.org/10.3390/tomography9010007
APA StyleMuhammed, E., Erenso, D. B., Gao, Y., Chen, L., Kelley, M., Vazquez, C., Gale, M., Nichols, C., & Crogman, H. T. (2023). Measurement of Charge and Refractive Indices in Optically Trapped and Ionized Living Cells. Tomography, 9(1), 70-88. https://doi.org/10.3390/tomography9010007





