Ultrashort Echo Time Double Echo Steady-State MRI for Quantitative Conductivity Mapping in the Knee: A Feasibility Study
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
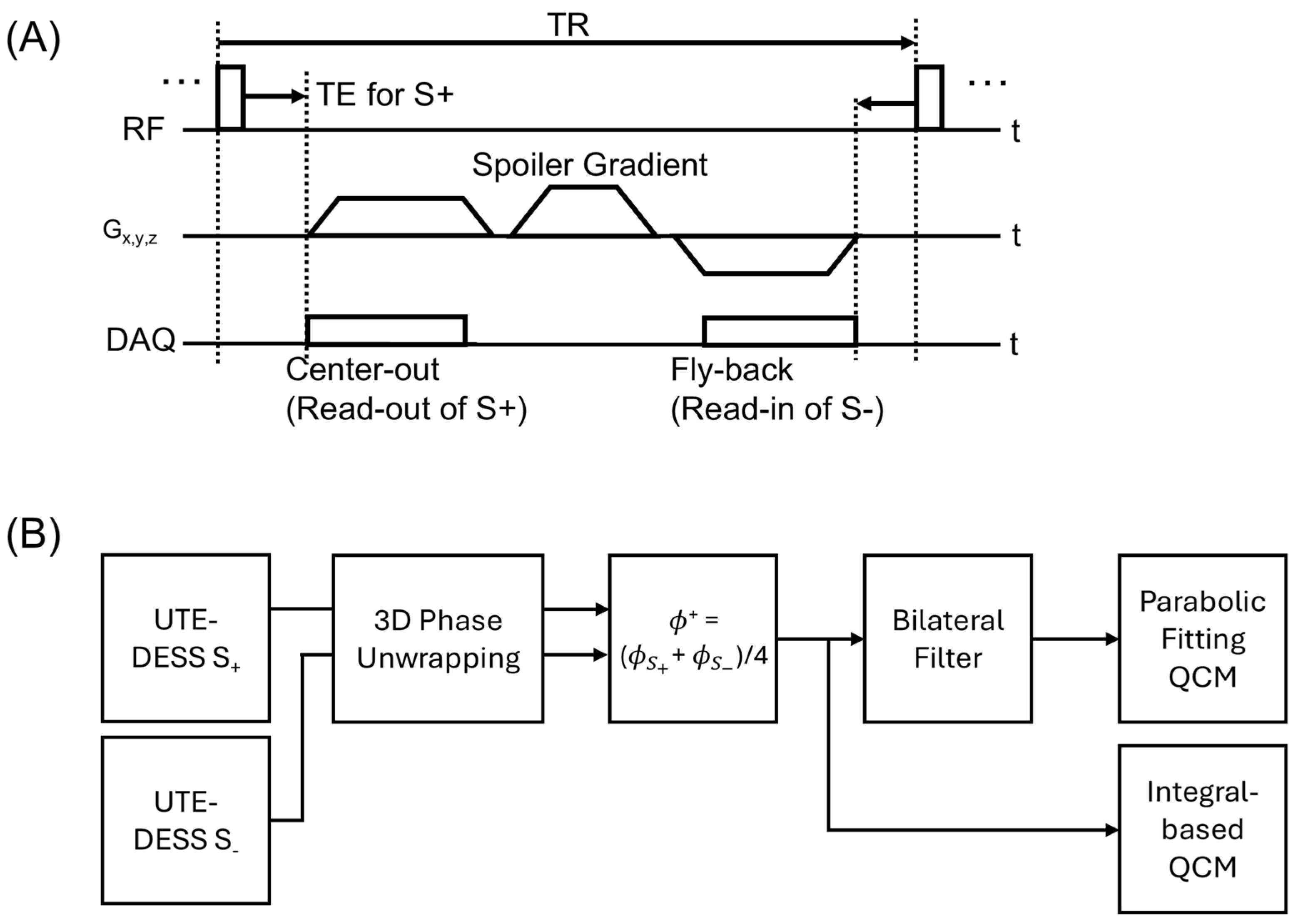
2.1. QCM
- Bilateral filtering: A bilateral filter with degree of smoothing of 3 and spatial sigma of 1 was used to reduce spatial noise in .
- Sliding window: Data were retrieved using a sliding kernel of size 8 × 8 × 8 mm3.
- Outlier removal based on signal intensity: Voxels with intensity differing by more than 20% from the mean were removed.
- Parabolic fitting: Local curvature was estimated using the 3D second-order polynomial.
2.2. UTE-QCM Using UTE-DESS
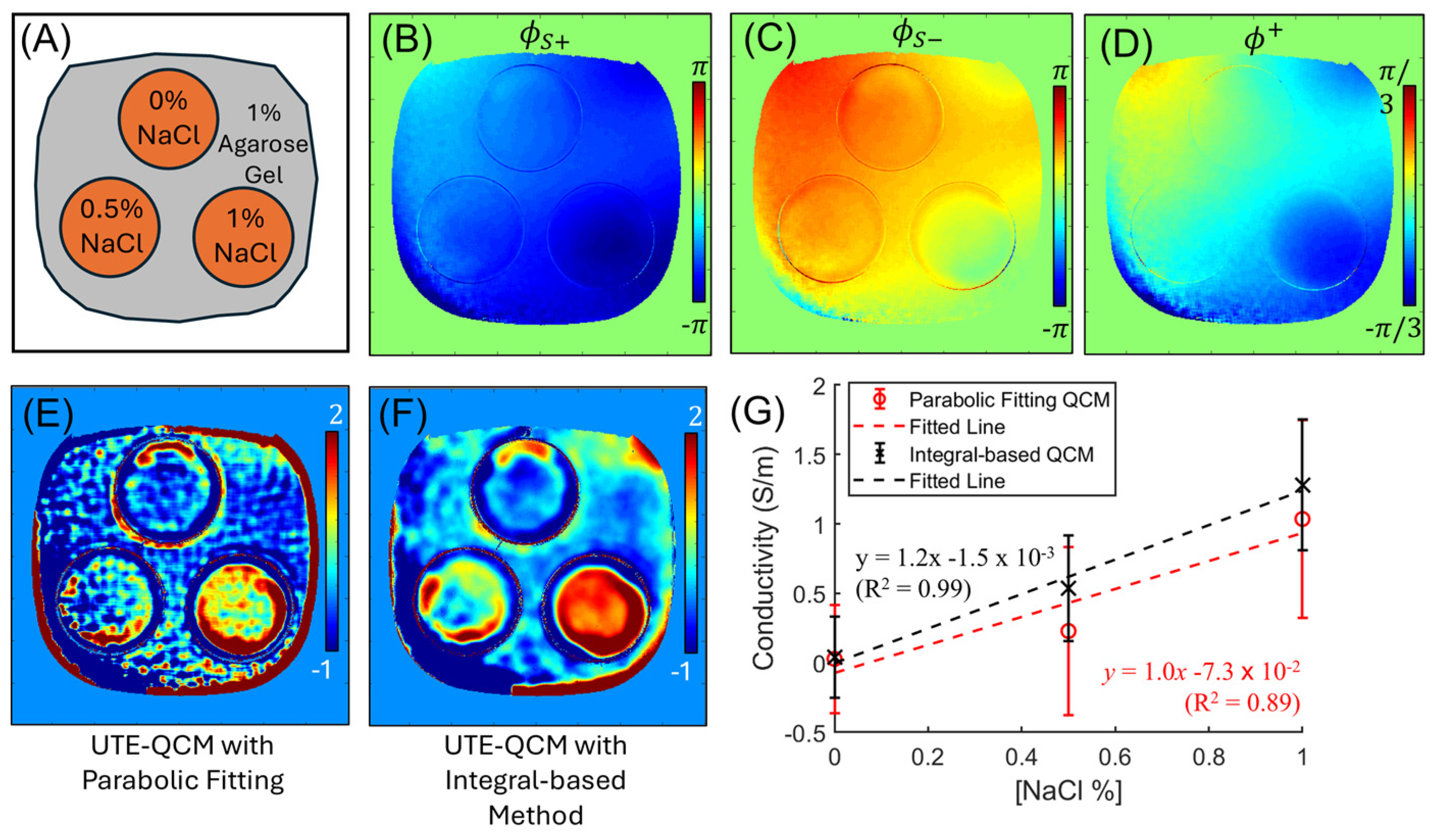
2.3. Experimental Setup
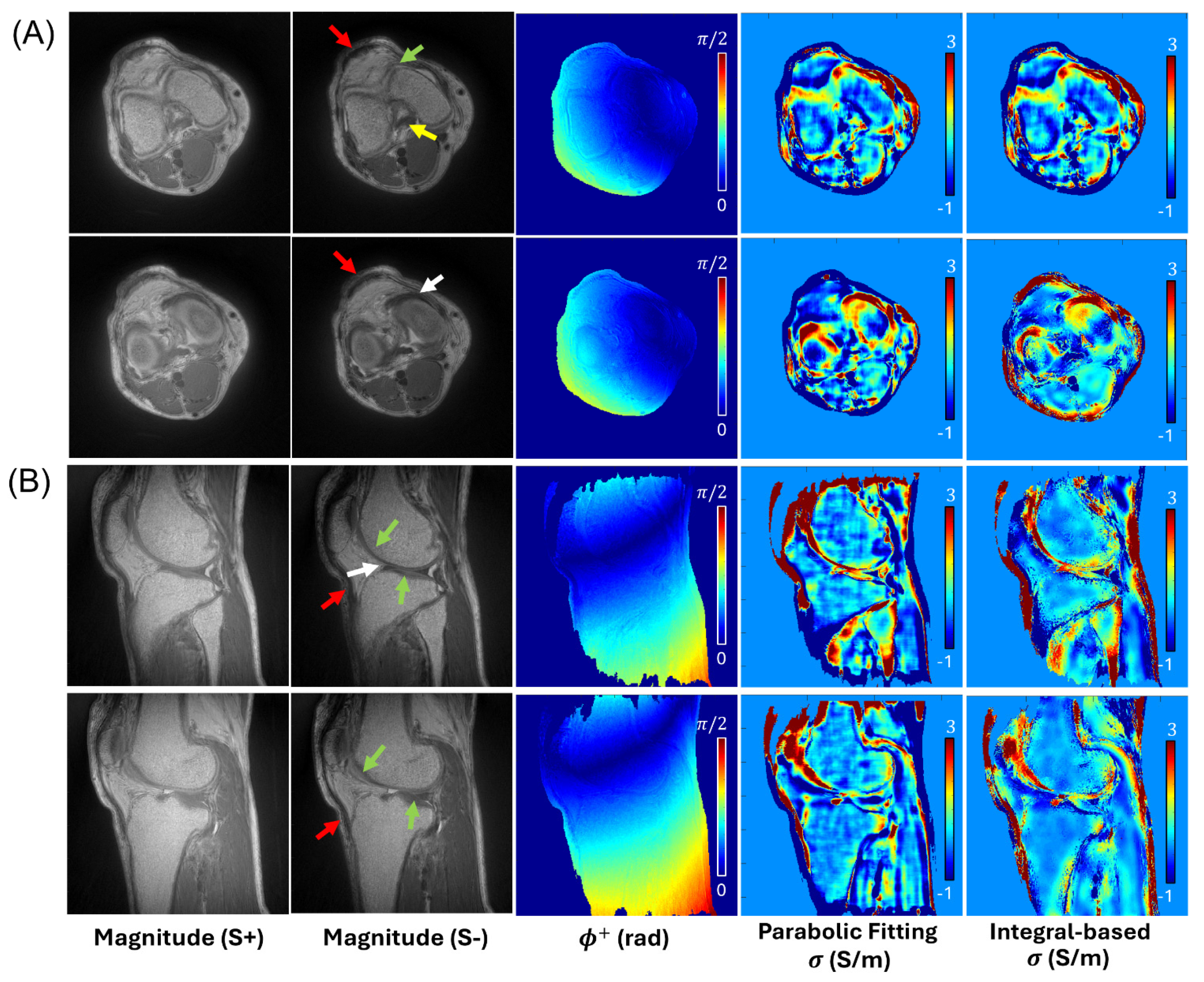
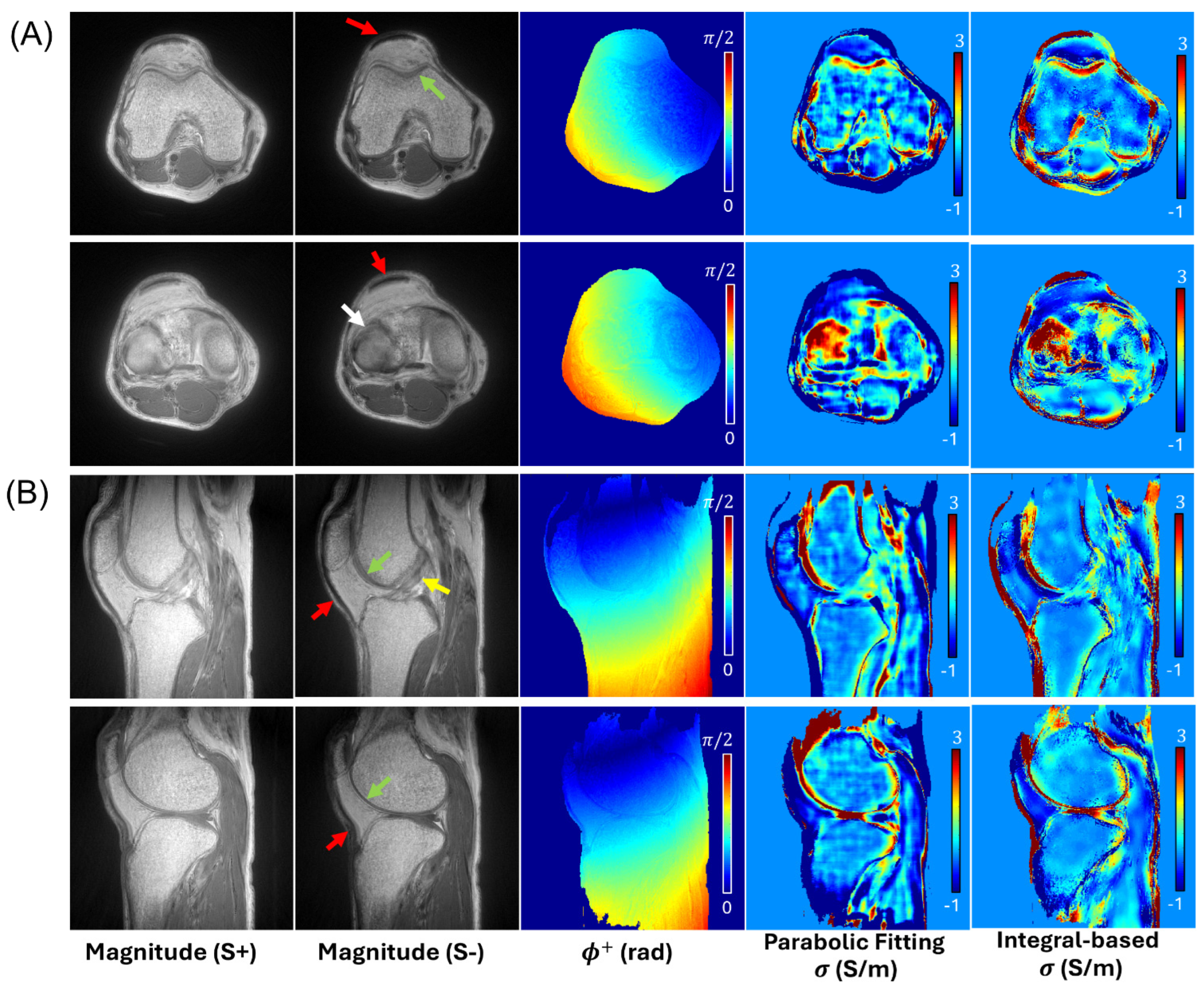
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UTE-QCM | Ultrashort Echo Time Quantitative Conductivity Mapping |
| MSK | Musculoskeletal |
| UTE-DESS | Ultrashort Echo Time Double Echo Steady-State |
| B1+ | Transmit Radiofrequency Field |
| QCM | Quantitative Conductivity Mapping |
| MRI | Magnetic Resonance Imaging |
| GAG | Glycosaminoglycan |
| FCD | Fixed Charge Density |
| 23Na | Sodium-23 |
| RF | Radiofrequency |
| 1H | Proton |
| SNR | Signal-To-Noise Ratio |
| SSFP | Steady-State Free Precession |
| UTE | Ultrashort Echo Time |
| S+/S− | Positive and Negative DESS Echoes |
| NaCl | Sodium Chloride |
| TE | Echo Time |
| TR | Repetition Time |
| FOV | Field of View |
| rBW | Readout Bandwidth |
References
- Latikka, J.A.; Hyttinen, J.A.; Kuurne, T.A.; Eskola, H.J.; Malmivuo, J.A. The Conductivity of Brain Tissues: Comparison of Results in Vivo and in Vitro Measurements. In Proceedings of the 2001 Conference Proceedings of the 23rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Istanbul, Turkey, 25–28 October 2001; IEEE: New York, NY, USA, 2001; Volume 1, pp. 910–912. [Google Scholar]
- Haacke, E.M.; Petropoulos, L.S.; Nilges, E.W.; Wu, D.H. Extraction of Conductivity and Permittivity Using Magnetic Resonance Imaging. Phys. Med. Biol. 1991, 36, 723–734. [Google Scholar] [CrossRef]
- Kim, D.-H.; Chauhan, M.; Kim, M.-O.; Jeong, W.C.; Kim, H.J.; Sersa, I.; Kwon, O.I.; Woo, E.J. Frequency-Dependent Conductivity Contrast for Tissue Characterization Using a Dual-Frequency Range Conductivity Mapping Magnetic Resonance Method. IEEE Trans. Med. Imaging 2015, 34, 507–513. [Google Scholar] [CrossRef] [PubMed]
- Voigt, T.; Katscher, U.; Doessel, O. Quantitative Conductivity and Permittivity Imaging of the Human Brain Using Electric Properties Tomography. Magn. Reson. Med. 2011, 66, 456–466. [Google Scholar] [CrossRef] [PubMed]
- Tha, K.K.; Katscher, U.; Yamaguchi, S.; Stehning, C.; Terasaka, S.; Fujima, N.; Kudo, K.; Kazumata, K.; Yamamoto, T.; Van Cauteren, M.; et al. Noninvasive Electrical Conductivity Measurement by MRI: A Test of Its Validity and the Electrical Conductivity Characteristics of Glioma. Eur. Radiol. 2018, 28, 348–355. [Google Scholar] [CrossRef] [PubMed]
- Liao, Y.; Oros-Peusquens, A.M.; Lindemeyer, J.; Lechea, N.; Weiß-Lucas, C.; Langen, K.J.; Shah, N.J. An MR Technique for Simultaneous Quantitative Imaging of Water Content, Conductivity and Susceptibility, with Application to Brain Tumours Using a 3T Hybrid MR-PET Scanner. Sci. Rep. 2019, 9, 88. [Google Scholar] [CrossRef]
- Ropella, K.M.; Noll, D.C. A Regularized, Model-Based Approach to Phase-Based Conductivity Mapping Using MRI. Magn. Reson. Med. 2017, 78, 2011–2021. [Google Scholar] [CrossRef]
- Van Lier, A.L.H.M.W.; Raaijmakers, A.; Voigt, T.; Lagendijk, J.J.W.; Luijten, P.R.; Katscher, U.; Van Den Berg, C.A.T. Electrical Properties Tomography in the Human Brain at 1.5, 3, and 7T: A Comparison Study. Magn. Reson. Med. 2014, 71, 354–363. [Google Scholar] [CrossRef]
- Shin, J.; Kim, M.J.; Lee, J.; Nam, Y.; Kim, M.; Choi, N.; Kim, S.; Kim, D.-H. Initial Study on in Vivo Conductivity Mapping of Breast Cancer Using MRI. J. Magn. Reson. Imaging 2015, 42, 371–378. [Google Scholar] [CrossRef]
- Kim, S.Y.; Shin, J.; Kim, D.H.; Kim, M.J.; Kim, E.K.; Moon, H.J.; Yoon, J.H. Correlation between Conductivity and Prognostic Factors in Invasive Breast Cancer Using Magnetic Resonance Electric Properties Tomography (MREPT). Eur. Radiol. 2016, 26, 2317–2326. [Google Scholar] [CrossRef]
- Bangerter, N.K.; Tarbox, G.J.; Taylor, M.D.; Kaggie, J.D. Quantitative Sodium Magnetic Resonance Imaging of Cartilage, Muscle, and Tendon. Quant. Imaging Med. Surg. 2016, 6, 699–714. [Google Scholar] [CrossRef]
- Zbýň, Š.; Mlynárik, V.; Juras, V.; Szomolanyi, P.; Trattnig, S. Evaluation of Cartilage Repair and Osteoarthritis with Sodium MRI. NMR Biomed. 2016, 29, 206–215. [Google Scholar] [CrossRef] [PubMed]
- Zaric, O.; Juras, V.; Szomolanyi, P.; Schreiner, M.; Raudner, M.; Giraudo, C.; Trattnig, S. Frontiers of Sodium MRI Revisited: From Cartilage to Brain Imaging. Magn. Reson. Imaging 2021, 54, 58–75. [Google Scholar] [CrossRef]
- Jang, H.; Ma, Y.; Carl, M.; Jerban, S.; Chang, E.Y.; Du, J. Ultrashort Echo Time Cones Double Echo Steady State (UTE-Cones-DESS) for Rapid Morphological Imaging of Short T2 Tissues. Magn. Reson. Med. 2021, 86, 881–892. [Google Scholar] [CrossRef] [PubMed]
- Chaudhari, A.S.; Sveinsson, B.; Moran, C.J.; McWalter, E.J.; Johnson, E.M.; Zhang, T.; Gold, G.E.; Hargreaves, B.A. Imaging and T2 Relaxometry of Short-T2 Connective Tissues in the Knee Using Ultrashort Echo-Time Double-Echo Steady-State (UTEDESS). Magn. Reson. Med. 2017, 78, 2136–2148. [Google Scholar] [CrossRef]
- Serralles, J.E.C.; Lattanzi, R.; Giannakopoulos, I.I.; Zhang, B.; Ianniello, C.; Cloos, M.A.; Polimeridis, A.G.; White, J.K.; Sodickson, D.K.; Daniel, L. Noninvasive Estimation of Electrical Properties From Magnetic Resonance Measurements via Global Maxwell Tomography and Match Regularization. IEEE Trans. Biomed. Eng. 2020, 67, 3–15. [Google Scholar] [CrossRef]
- Karsa, A.; Shmueli, K. New Approaches for Simultaneous Noise Suppression and Edge Preservation in Quantitative Conductivity Mapping From Low-SNR Data. In Proceedings of the 29th Annual Meeting of ISMRM, Online, 15–20 May 2021; p. 3774. [Google Scholar]
- Liu, J.; Liu, T.; De Rochefort, L.; Ledoux, J.; Khalidov, I.; Chen, W.; Tsiouris, A.J.; Wisnieff, C.; Spincemaille, P.; Prince, M.R.; et al. Morphology Enabled Dipole Inversion for Quantitative Susceptibility Mapping Using Structural Consistency between the Magnitude Image and the Susceptibility Map. NeuroImage 2012, 59, 2560–2568. [Google Scholar] [CrossRef]
- Lee, J.; Shin, J.; Kim, D.H. MR-Based Conductivity Imaging Using Multiple Receiver Coils. Magn. Reson. Med. 2016, 76, 530–539. [Google Scholar] [CrossRef]
- Chang, E.Y.; Du, J.; Statum, S.; Pauli, C.; Chung, C.B. Quantitative Bi-Component T2* Analysis of Histologically Normal Achilles Tendons. Muscles Ligaments Tendons J. 2015, 5, 58–62. [Google Scholar]
- Chang, E.Y.; Du, J.; Chung, C.B. UTE Imaging in the Musculoskeletal System. J. Magn. Reson. Imaging 2015, 41, 870–883. [Google Scholar] [CrossRef]
- Athertya, J.S.; Ma, Y.; Afsahi, A.M.; Lombardi, A.F.; Moazamian, D.; Jerban, S.; Sedaghat, S.; Jang, H. Accelerated Quantitative 3D UTE-Cones Imaging Using Compressed Sensing. Sensors 2022, 22, 7459. [Google Scholar] [CrossRef]
- Jang, H.; Carl, M.; Ma, Y.; Jerban, S.; Guo, T.; Zhao, W.; Chang, E.Y.; Du, J. Fat Suppression for Ultrashort Echo Time Imaging Using a Single-Point Dixon Method. NMR Biomed. 2019, 32, e4069. [Google Scholar] [CrossRef] [PubMed]
- Deligianni, X.; Bär, P.; Scheffler, K.; Trattnig, S.; Bieri, O. Water-Selective Excitation of Short T2 Species with Binomial Pulses. Magn. Reson. Med. 2014, 72, 800–805. [Google Scholar] [CrossRef]
- Hauger, O.; Dumont, E.; Chateil, J.-F.; Moinard, M.; Diard, F. Water Excitation as an Alternative to Fat Saturation in MR Imaging: Preliminary Results in Musculoskeletal Imaging. Radiology 2002, 224, 657–663. [Google Scholar] [CrossRef][Green Version]
- Duc, S.R.; Koch, P.; Schmid, M.R.; Horger, W.; Hodler, J.; Pfirrmann, C.W.A. Diagnosis of Articular Cartilage Abnormalities of the Knee: Prospective Clinical Evaluation of a 3D Water-Excitation True FISP Sequence. Radiology 2007, 243, 475–482. [Google Scholar] [CrossRef]
- Rossmann, C.; Haemmerich, D. Review of Temperature Dependence of Thermal Properties, Dielectric Properties, and Perfusion of Biological Tissues at Hyperthermic and Ablation Temperatures. Crit. Rev. Biomed. Eng. 2014, 42, 467–492. [Google Scholar] [CrossRef]
- Wheaton, A.J.; Borthakur, A.; Shapiro, E.M.; Regatte, R.R.; Akella, S.V.S.; Kneeland, J.B.; Reddy, R. Proteoglycan Loss in Human Knee Cartilage: Quantitation with Sodium MR Imaging—Feasibility Study. Radiology 2004, 231, 900–905. [Google Scholar] [CrossRef]
- Madelin, G.; Lee, J.-S.; Regatte, R.R.; Jerschow, A. Sodium MRI: Methods and Applications. Prog. Nucl. Magn. Reson. Spectrosc. 2014, 79, 14–47. [Google Scholar] [CrossRef] [PubMed]
- Sedaghat, S.; Park, J.; Fu, E.; Liu, F.; Jung, Y.; Jang, H. Effects of Motion in Ultrashort Echo Time Quantitative Susceptibility Mapping for Musculoskeletal Imaging. J. Imaging 2025, 11, 347. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Sedaghat, S.; Park, J.I.; Fu, E.; Jung, Y.; Jang, H. Ultrashort Echo Time Double Echo Steady-State MRI for Quantitative Conductivity Mapping in the Knee: A Feasibility Study. Tomography 2026, 12, 18. https://doi.org/10.3390/tomography12020018
Sedaghat S, Park JI, Fu E, Jung Y, Jang H. Ultrashort Echo Time Double Echo Steady-State MRI for Quantitative Conductivity Mapping in the Knee: A Feasibility Study. Tomography. 2026; 12(2):18. https://doi.org/10.3390/tomography12020018
Chicago/Turabian StyleSedaghat, Sam, Jin Il Park, Eddie Fu, Youngkyoo Jung, and Hyungseok Jang. 2026. "Ultrashort Echo Time Double Echo Steady-State MRI for Quantitative Conductivity Mapping in the Knee: A Feasibility Study" Tomography 12, no. 2: 18. https://doi.org/10.3390/tomography12020018
APA StyleSedaghat, S., Park, J. I., Fu, E., Jung, Y., & Jang, H. (2026). Ultrashort Echo Time Double Echo Steady-State MRI for Quantitative Conductivity Mapping in the Knee: A Feasibility Study. Tomography, 12(2), 18. https://doi.org/10.3390/tomography12020018




