Multifractal Analysis of Choroidal SDOCT Images in the Detection of Retinitis Pigmentosa
Abstract
1. Introduction
- Night blindness (nyctalopia), that is, difficulties with night vision;
- Reduced visual acuity;
- A typical hyperpigmentation of the retina in a “bone spicule” pattern in the mid-periphery, visible by fundoscopy;
- Attenuation of retinal arteries;
- Dysfunction of photoreceptors, distinguishable by electroretinographic abnormalities;
- A peripheral ring scotoma and narrowing of the visual field (detectable by visual field testing).
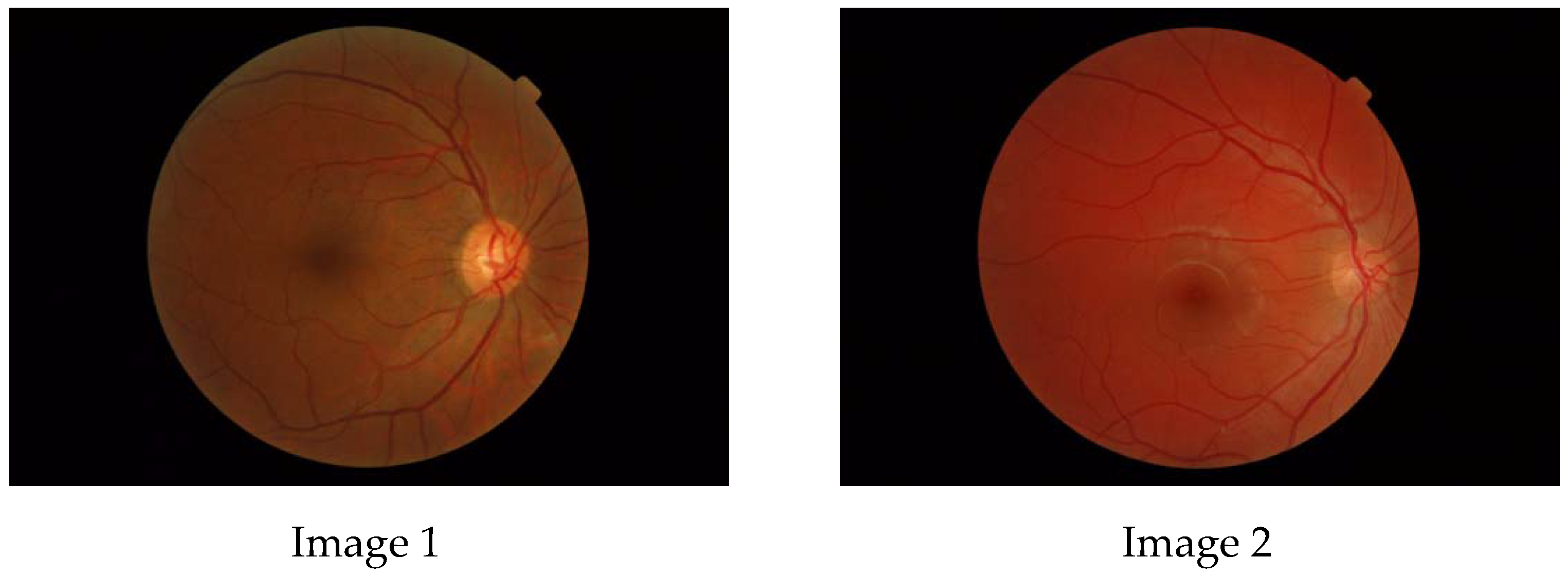
- fundus image photography;
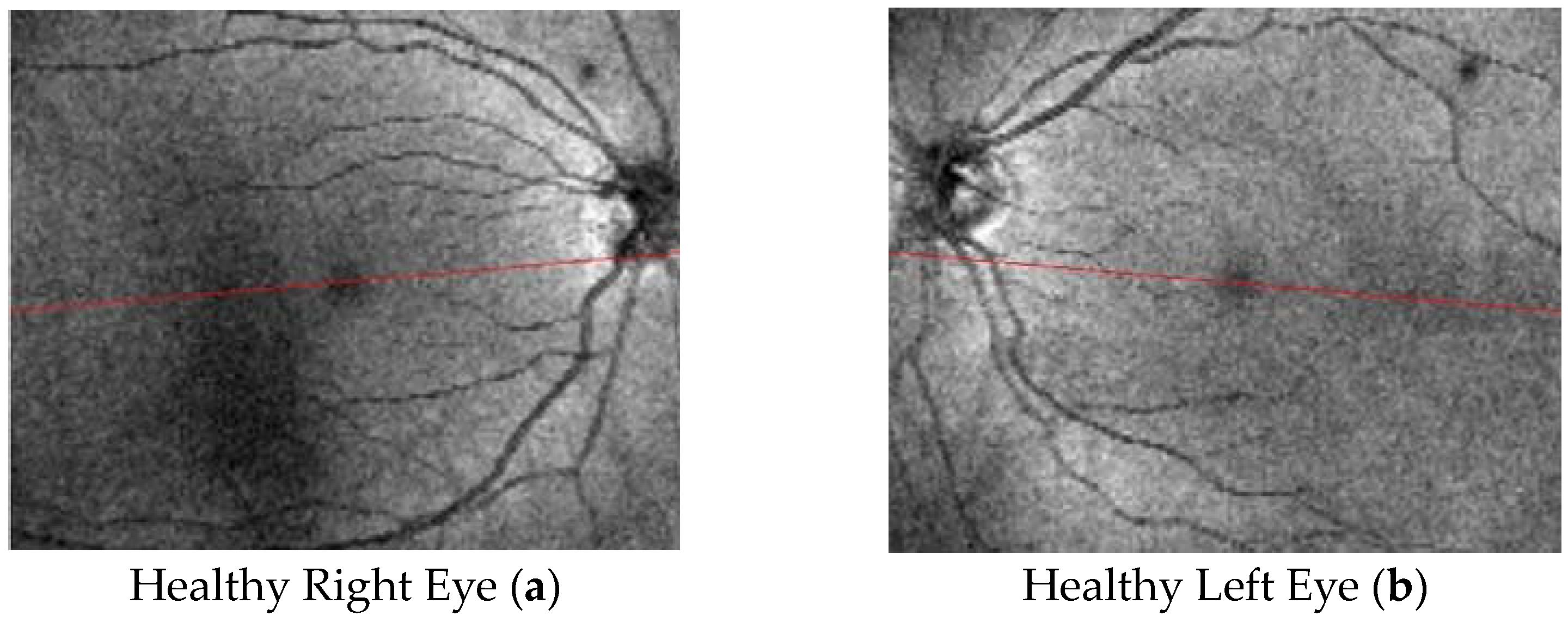
- optical coherence tomography (OCT).
- ○
- OCTA small field, which is limited to the posterior pole (macula and optic discs);
- ○
- OCTA wide field, which allows for the analysis of a larger retinal area.
2. Mathematical Background
2.1. Fractal Dimension
2.2. Multifractals
3. The Algorithms
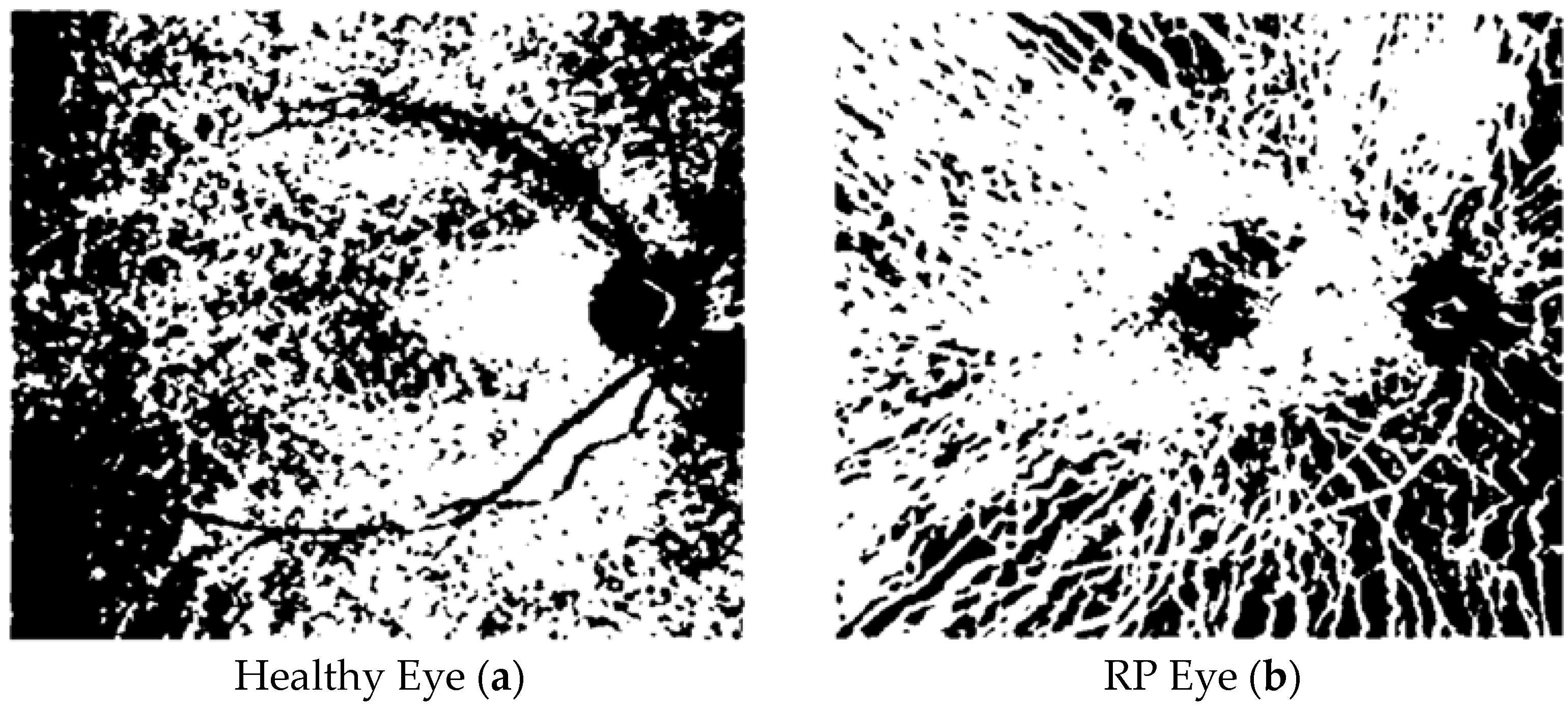
3.1. Computing the Fractal Dimension
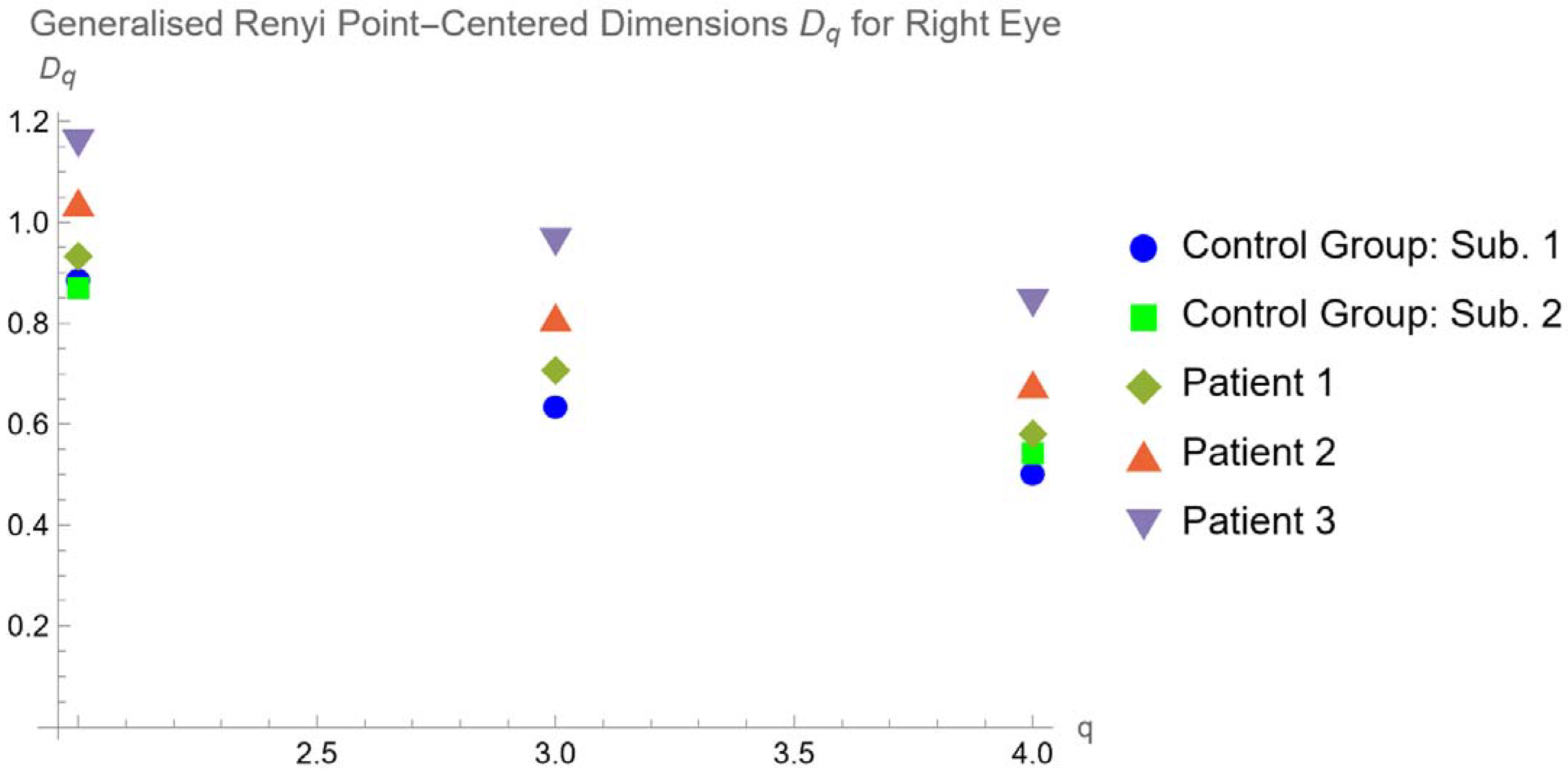
3.2. Computing the Generalized Renyi Point-Centered Dimensions
3.2.1. The Case When
3.2.2. The Case When
4. Results
- A patient with Usher’s disease corresponding to Figure 3a,b of Abdolrahimzadeh et al. [29] and is called “Patient 3”. Usher’s syndrome is a genetic disease characterized by partial or total loss of hearing and vision, due to anomalies of the inner ear and retina, respectively. It is considered the most frequent cause of blindness associated with early-onset deafness and has an estimated prevalence of around one case in 30,000 people. Three types can be distinguished based on the symptoms and age of onset. Type 1 presents with severe deafness from birth and a progressive loss of vision starting from childhood, as well as disorders of balance and orientation in space. Children with this form in fact begin to walk later and may have difficulty riding a bicycle or playing some sports. There are at least 10 genes associated with Usher’s syndrome, all involved in the production of proteins aimed at the processes of vision, hearing, and balance. In all cases, the syndrome is transmitted in an autosomal recessive manner.
4.1. Fractal Dimension
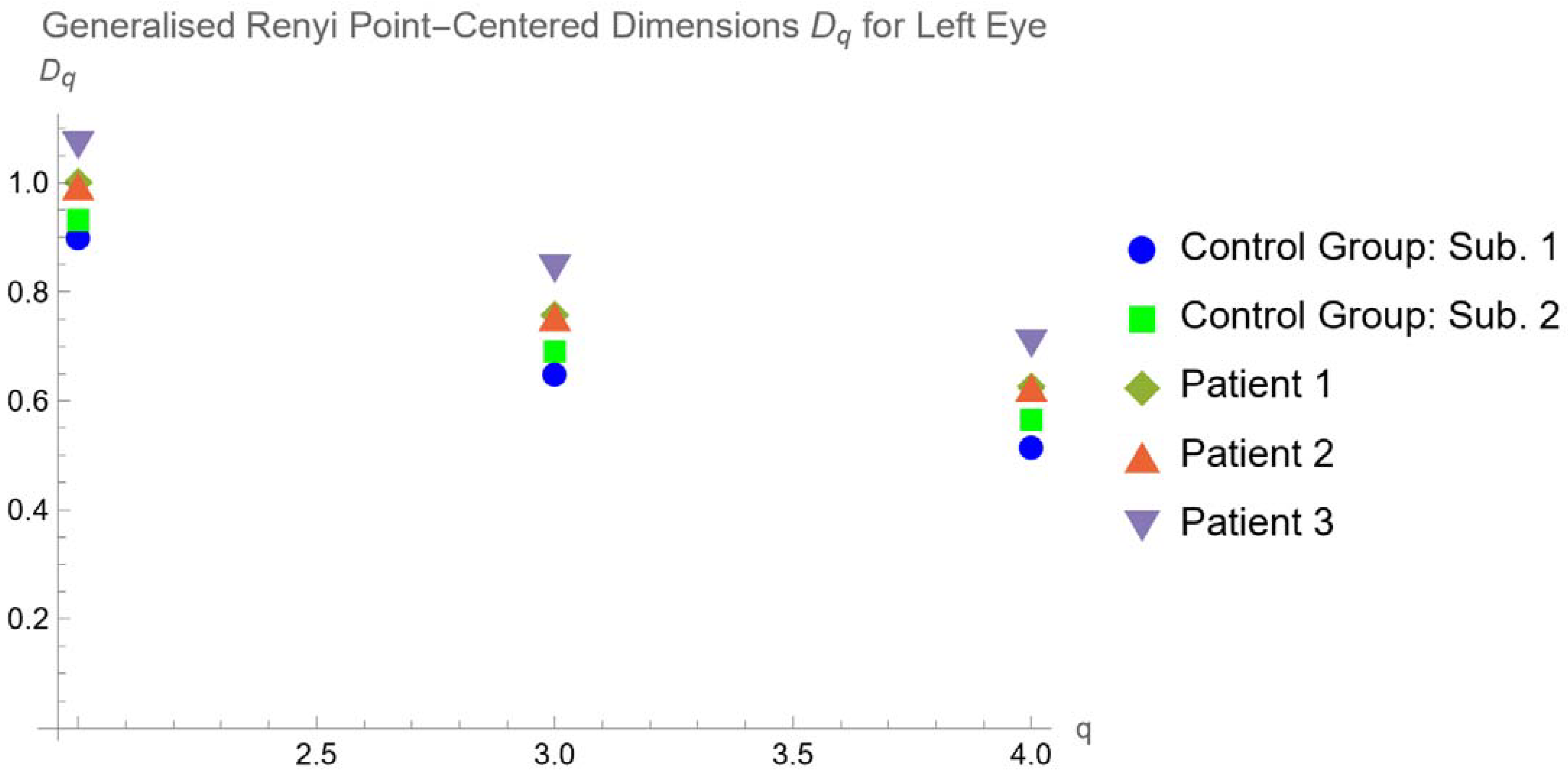
4.2. Generalized Renyi Point-Centered Dimensions
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Verbakel, S.K.; Van Huet, R.; Boon, C.; den Hollander, A.I.; Collin, R.; Klaver, C.; Hoyng, C.B.; Roepman, R.; Klevering, B.J. Nonsyndromic retinitis pigmentosa. Prog. Retin. Eye Res. 2018, 66, 157–186. [Google Scholar] [CrossRef] [PubMed]
- Marigo, V. Programmed cell death in retinal degeneration: Targeting apoptosis in photoreceptors as potential therapy for retinal degeneration. Cell Cycle 2007, 6, 652–655. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, S.; Di Iorio, E.; Barbaro, V.; Ponzin, D.; Sorrentino, F.S.; Parmeggiani, F. Retinitis pigmentosa: Genes and disease mechanisms. Curr. Genom. 2011, 12, 238–249. [Google Scholar]
- Campbell, J.P.; Zhang, M.; Hwang, T.S.; Bailey, S.T.; Wilson, D.J.; Jia, Y.; Huang, D. Detailed Vascular Anatomy of the Human Retina by Projection-Resolved Optical Coherence Tomography Angiography. Sci. Rep. 2017, 7, 42201. [Google Scholar] [CrossRef] [PubMed]
- Family, F.; Masters, B.R.; Platt, D.E. Fractal Pattern Formation in Human Retinal Vessels. Phys. Nonlinear Phenom. 1989, 38, 98–103. [Google Scholar] [CrossRef]
- Decencière, E.; Zhang, X.; Cazuguel, G.; Lay, B.; Cochener, B.; Trone, C.; Gain, P.; Ordonez, R.; Massin, P.; Erginay, A.; et al. Feedback on a publicly distributed database: The Messidor database. Image Anal. Stereol. 2014, 33, 231–234. [Google Scholar] [CrossRef]
- Lakshminarayanan, V.; Raghuram, A.; Myerson, J.; Varadharajan, S. The Fractal Dimension in Retinal Pathology. J. Mod. Opt. 2003, 50, 1701–1703. [Google Scholar] [CrossRef]
- Yu, S.; Lakshminarayanan, V. Fractal Dimension and Retinal Pathology: A Metaanalysis. Appl. Sci. 2021, 11, 2376. [Google Scholar] [CrossRef]
- Mitamura, Y.; Mitamura-Aizawa, S.; Nagasawa, T.; Katome, T.; Eguchi, H.; Naito, T. Diagnostic imaging in patients with retinitis pigmentosa. J. Med. Investig. 2012, 59, 1–11. [Google Scholar] [CrossRef]
- Fujimoto, J.G.; Drexler, W.; Schuman, J.S.; Hitzenberger, C.K. Optical Coherence Tomography (OCT) in ophthalmology: Introduction. Opt. Express 2009, 17, 3978–3979. [Google Scholar] [CrossRef]
- Jauregui, R.; Park, K.S.; Duong, J.K.; Mahajan, V.B.; Tsang, S.H. Quantitative progression of retinitis pigmentosa by optical coherence tomography angiography. Sci. Rep. 2018, 8, 13130. [Google Scholar] [CrossRef] [PubMed]
- Minicucci, F.; Oikonomou, F.D.; De Sanctis, A.A. Fractal dimensional analysis for retinal vascularization images in retinitis pigmentosa: A pilot study. In Chaos, Fractals and Complexity; Springer Proceedings in Complexity; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Spaide, R.F.; Koizumi, H.; Pozzoni, M.C. Enhanced depth imaging spectral-domain optical coherence tomography. Am. J. Ophthalmol. 2008, 146, 496–500. [Google Scholar] [CrossRef] [PubMed]
- Margolis, R.; Spaide, R.F. A pilot study of enhanced depth imaging optical coherence tomography of the choroid in normal eyes. Am. J. Ophthalmol. 2009, 147, 811–815. [Google Scholar] [CrossRef] [PubMed]
- Chhablani, J.; Wong, I.Y.; Kozak, I. Choroidal imaging: A review. Saudi J. Ophthalmol. 2014, 28, 123–128. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Harrison, J.M.; Nateras, O.S.; Chalfin, S.; Duong, T.Q. Decreased retinal-choroidal blood flow in retinitis pigmentosa as measured by MRI. Doc. Ophthalmol. 2013, 126, 187–197. [Google Scholar] [CrossRef] [PubMed]
- Meleppat, R.K.; Zhang, P.; Ju, M.J.; Manna, S.K.K.; Jian, Y.; Pugh, E.N.; Zawadzki, R.J. Directional optical coherence tomography reveals melanin concentration-dependent scattering properties of retinal pigment epithelium. J. Biomed. Opt. 2019, 24, 66011. [Google Scholar] [CrossRef] [PubMed]
- Meleppat, R.K.; Fortenbach, C.R.; Jian, Y.; Martinez, E.S.; Wagner, K.; Modjtahedi, B.S.; Motta, M.J.; Ramamurthy, D.L.; Schwab, I.R.; Zawadzki, R.J. In Vivo Imaging of Retinal and Choroidal Morphology and Vascular Plexuses of Vertebrates Using Swept-Source Optical Coherence Tomography. Transl. Vis. Sci. Technol. 2022, 11, 11. [Google Scholar] [CrossRef]
- Meleppat, R.K.; Ronning, K.E.; Karlen, S.J.; Burns, M.E.; Pugh, E.N., Jr.; Zawadzki, R.J. In vivo multimodal retinal imaging of didease-related pigmentary changes in retinal pigment epithelium. Sci. Rep. 2021, 11, 16252. [Google Scholar] [CrossRef] [PubMed]
- Finzi, A.; Cellini, M.; Strobbe, E.; Campos, E.C. ET-1 plasma levels, choroidal thickness and multifocal electroretinogram in retinitis pigmentosa. Life Sci. 2014, 118, 386–390. [Google Scholar] [CrossRef]
- Strobbe, E.; Cellini, M.; Fresina, M.; Campos, E.C. ET-1 plasma levels, aqueous flare, and choroidal thickness in patients with retinitis pigmentosa. J. Ophthalmol. 2015, 2015, 292615. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Wheeler, J.A. The Fractal Geometry of Nature. Am. J. Phys. 1983, 51, 286–287. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Les Objets Fractals; Flammarion: Paris, France, 1999. [Google Scholar]
- Falconer, K. Fractal Geometry Mathematical Foundations and Applications; John Wiley & Sons: Oxford, UK, 1990. [Google Scholar]
- Barnsley, M.F. Fractals Everywhere, 3rd ed.; Academic Press: San Diego, CA, USA, 1993. [Google Scholar]
- Peitgen, H.-O.; Jürgens, H.; Saupe, D. Chaos and Fractals; Springer: New York, NY, USA, 2004. [Google Scholar]
- Harte, D. Multifractals Theory and Applications; Chapman & Hall/CRC: Boca Raton, FL, USA; London, UK; New York, NY, USA; Washington, DC, USA, 2001. [Google Scholar]
- Reiss, M.A.; Sabathiel, N.; Ahammer, H. Noise dependency of algorithms for calculating fractal dimensions in digital images. Chaos Solitons Fractals 2015, 78, 39–46. [Google Scholar] [CrossRef]
- Abdolrahimzadeh, S.; Di Pippo, M.; Ciancimino, C.; Di Staso, F.; Lotery, A.J. Choroidal vascularity index and choroidal thickness: Potential biomarkers in retinitis pigmentosa. Eye 2023, 37, 1766–1773. [Google Scholar] [CrossRef] [PubMed]


| Image | FD | Confidence (95%) | p-Value | |
|---|---|---|---|---|
| Subject 1 (CG) | 1.557 | 0.999 | 1.510–1.604 | 2.308 × 10−10 |
| Subject 2 (CG) | 1.485 | 1.000 | 1.456–1.514 | 1.838 × 10−11 |
| Patient 1 | 1.167 | 0.997 | 1.096–1.237 | 1.350 × 10−7 |
| Patient 2 | 1.130 | 0.999 | 1.083–1.177 | 2.092 × 10−8 |
| Patient 3 | 0.907 | 0.992 | 0.815–0.998 | 1.758 × 10−6 |
| Image | FD | Confidence (95%) | p-Value | |
|---|---|---|---|---|
| Subject 1 (CG) | 1.307 | 0.989 | 1.172–1.443 | 3.803 × 10−7 |
| Subject 2 (CG) | 1.071 | 0.999 | 1.034–1.108 | 5.337 × 10−10 |
| Patient 1 | 1.055 | 0.996 | 0.981–1.128 | 2.733 × 10−7 |
| Patient 2 | 0.981 | 0.999 | 0.944–1.018 | 1.328 × 10−8 |
| Patient 3 | 1.087 | 0.990 | 0.964–1.211 | 3.172 × 10−6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minicucci, F.; Oikonomou, F.D.; De Sanctis, A.A. Multifractal Analysis of Choroidal SDOCT Images in the Detection of Retinitis Pigmentosa. Tomography 2024, 10, 480-492. https://doi.org/10.3390/tomography10040037
Minicucci F, Oikonomou FD, De Sanctis AA. Multifractal Analysis of Choroidal SDOCT Images in the Detection of Retinitis Pigmentosa. Tomography. 2024; 10(4):480-492. https://doi.org/10.3390/tomography10040037
Chicago/Turabian StyleMinicucci, Francesca, Fotios D. Oikonomou, and Angela A. De Sanctis. 2024. "Multifractal Analysis of Choroidal SDOCT Images in the Detection of Retinitis Pigmentosa" Tomography 10, no. 4: 480-492. https://doi.org/10.3390/tomography10040037
APA StyleMinicucci, F., Oikonomou, F. D., & De Sanctis, A. A. (2024). Multifractal Analysis of Choroidal SDOCT Images in the Detection of Retinitis Pigmentosa. Tomography, 10(4), 480-492. https://doi.org/10.3390/tomography10040037







