The Basics of Evolution Strategies: The Implementation of the Biomimetic Optimization Method in Educational Modules
Abstract
1. Introduction
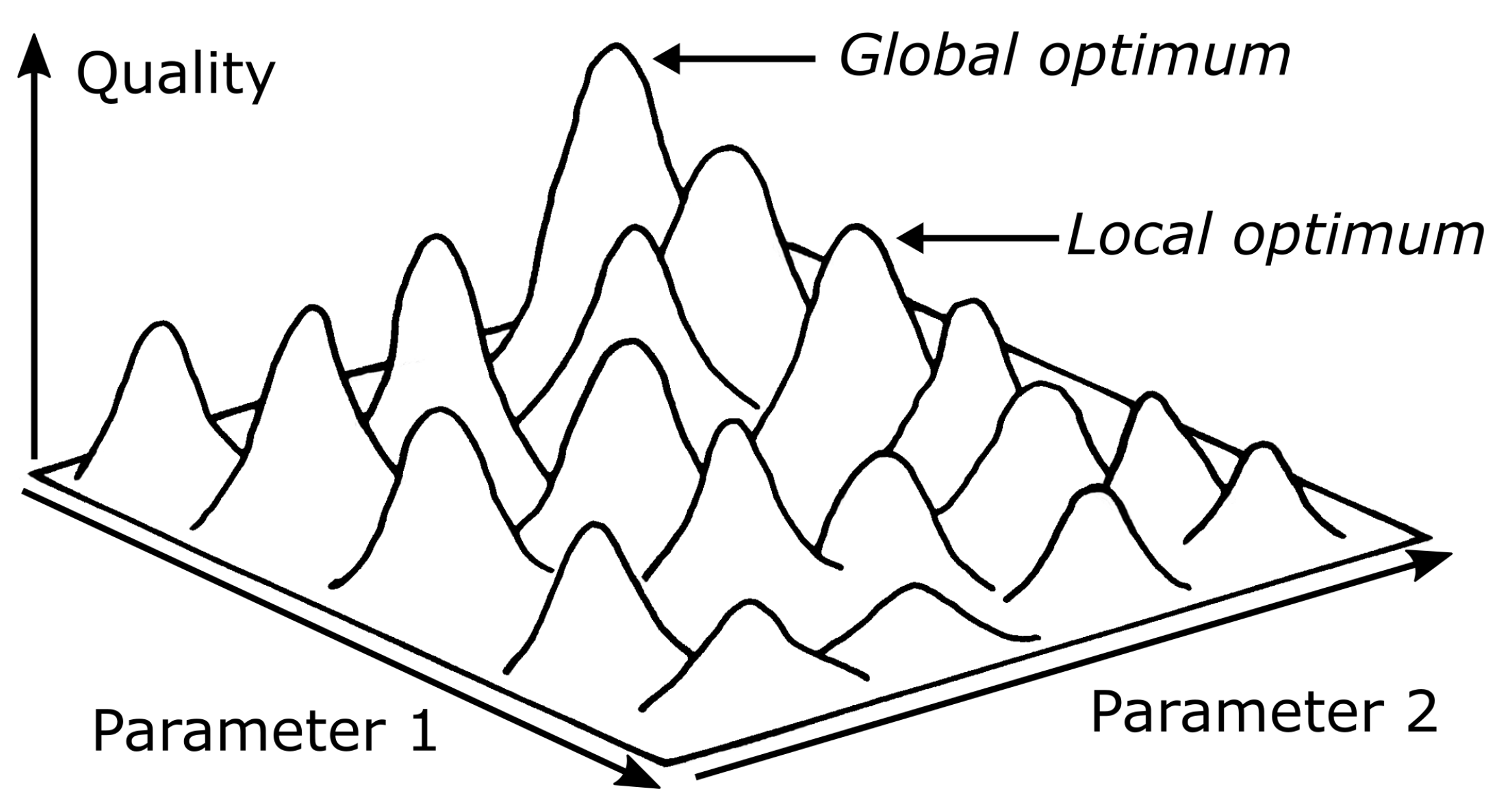
1.1. Concept of Optimization
1.2. Aim of the Project
2. Biological Evolution
2.1. Mutation
2.2. Recombination
2.3. Selection
2.4. Isolation
3. Evolution Strategies
3.1. Evolutionary Algorithms
3.2. Sequences of Operation in ES Symbolized by Playing Cards
- Variable set: To reflect the biological model, the elements of the search space in the ES are not called solution vectors, as usual, but individuals. The object parameters are noted on the data card. The black dots represent a variable column. The variable set symbolizes the genotype of an individual in biology.
- Realization: The zigzag line below a card indicates the realization of the object parameter values noted on it. In biology, the realization of an individual’s genetic information (genotype) forms its appearance or phenotype. In technology, the realization of object parameter values creates either a real technical object or a corresponding computer simulation.
- Population: The variability of a population is symbolized by the different object parameter values of each individual. This is similar to the genotypes in a biological population. A set of cards surrounded by an oval indicates that the cards are in a ballot box.
- Duplication: The double arrow indicates that the information on a data card is to be duplicated and transferred to a second card, resulting in a reproduction of the original individual. If the double arrow refers to a population, the entire record of the population will be copied.
- Mutation: The zigzag arrow on a card indicates that the object parameter values noted on the card will be changed randomly. This change can affect all parameter values or it might be limited to a few pre-determined parameter values by a random process.
- Recombination: Two opposing arrows between individual cards indicate that the numerical values of the individuals are randomly exchanged. Similar to the biological model, the ES distinguishes between dominant and intermediate recombination. In the case of dominant recombination, the value of each individual parameter of the offspring is statistically equally distributed to determine from which parent it is inherited. In the case of intermediate recombination, the offspring simply inherits the geometric mean of the parental values. Contrary to the usual biological model, the ES may not only involve two individuals, but might include several individuals in a recombination.
- Isolation: The enclosure of a population by symbolic barbed wire indicates that the individuals in that population are isolated from the individuals outside the wire and, therefore, information cannot be exchanged between them. However, isolation only makes sense if it is lifted after a certain period of time (cf. Section 2.4). The letter is a measure of the duration of isolation. Whether the population is isolated from other populations for generations, seconds of processor time, or calls of the quality function must be determined in advance [9,16].
- Random choice: A set of cards surrounded by an oval indicates that the cards lie within a ballot box. The arrow with an symbolizes that, depending on the context of the task, one or more cards will be randomly drawn from this ballot box to participate in the generation of the next generation’s offspring. Unless otherwise agreed, the random selection is based on the principle of equal statistical distribution. This means that each parent is equally likely to reproduce, and unlike the biological model, the selection of parents does not depend on the quality of the individuals. In other words, no sexual selection occurs in the ES. When several sets of cards lie within the ballot box, entire populations, rather than individuals, are selected according to this random principle.
- Evaluation: The arrow with the letter Q indicates that the quality of an individual or of a population is recorded. The determination of the quality by means of experimental results, objective calculation, and subjective criteria (cf. Section 3.7) has the advantage that subsequent selection can be performed formally at the information level. The quality Q is inspired by the idea of fitness in biology.
- Selection: The selection process is symbolized by a branching arrow with the letter Q next to it, indicating that the individuals in the ballot box are selected according to their quality Q (cf. Section 3.7). The selected individuals always have better quality values than those that are discarded. If several sets of cards lie within the ballot box, populations are selected according to this principle, not individuals [9,37].
3.3. Basic Version of Evolution Strategy
- 0.
- Initialization: The individuals of the initial population are distributed as evenly as possible in the search space. Therefore, the initial population should be generated stochastically. Each individual represents a possible solution for optimizing the objective function (cf. Equations (1)–(4), and the fitness is calculated for each individual. The population size with individuals remains constant throughout the optimization process.
- 1.
- Recombination: Parents are selected stochastically with a “put-back” option that enables multiple drawing, and then recombined. Intermediate and dominate recombinations are possible (cf. Section 3.4).
- 2.
- Mutation: The offspring is mutated, evaluated, and stored in an intermediate population. Mutation is achieved by adding a mutation step size (cf. Section 3.5 and Section 3.6).
- 3.
- Selection: The iteration steps are repeated times, and then, the best individuals are selected for the next generation. We distinguish between the plus selection and the comma selection (cf. Section 3.4).
- 4.
- Termination: Iteration steps 1 to 3 are repeated until a termination criterion is met, such as the attainment of a specified maximum number of iterations or no further specified improvement of the solutions after several generations.
3.4. Variants of Evolution Strategy
3.5. Evolution Window
3.5.1. Speed of Progress
3.5.2. Mutation Step Size
3.6. Step Size Control
3.6.1. The 1/5 Success Rule
3.6.2. Mutation Step Size Control
3.6.3. Covariance Matrix Adaptation
3.7. Selection Criteria
4. Application of Evolution Strategy in Technology
5. Educational Modules on Evolution Strategy
5.1. Educational Module: Optimization of a Milk Carton
- What is the goal of the optimization?The primary optimization goal is to minimize the material consumption of a milk carton while maintaining the same volume. If, as in this case, glued surfaces and folds are not taken into account, this means that the surface area of the milk carton pack should be minimized (cf. Equation (1)).
- What changes can be made to the optimization object to achieve the optimum?The surface area of a cuboid can be influenced by varying its side lengths (Figure 8).
- How can a variable object be efficiently evaluated?The quality Q of a cuboid can be calculated as , where Q is the surface area and a, b, and c are the side lengths of the milk carton.
- Which constraints limit the optimization?The milk carton should still hold a volume of 1 L ( = 1000 cm3 = 1000 mL). In addition, the side lengths must never become negative or zero ( cm).
- How many input variables does this optimization problem have?This is an optimization problem with two input variables. There will always be offspring violating the constraint = 1000 mL if all three side lengths are varied.
5.2. Educational Modules: Fastest and Shortest Marble Track and Various Marble Track Shapes
- The ES on which the optimization is based must be defined, e.g., –ES with mutative step size control.
- Changing the parental support heights by small random values calculates the support heights of the offspring curves.
- All offspring curves are realized one after the other, and their running times are determined.
- The offspring with the smallest running time becomes the parent of the next generation.
- Steps 2 to 4 are repeated until a predefined termination criterion is met.
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CAM | Covariance Matrix Adaptation | |
| EA | evolution algorithm | |
| EP | evolutionary programming | |
| ES | evolution strategy | |
| GA | genetic algorithms | |
| g | parameter g | |
| h | parameter h | |
| O | offspring | |
| P | parent | |
| Q | quality | |
| z | random factor | |
| (pronounced alpha) | change factor of step size | |
| (pronounced gamma) | time unit of isolation | |
| (pronounced delta) | mutation step size | |
| (pronounced lambda) | number of offspring in a generation | |
| (pronounced mu) | number of parent individuals selected | |
| (pronounced xi) | variation of mutation step size | |
| (pronounced rho) | number of parents involved in recombination | |
| (pronounced chi) | object parameter | |
| (pronounced Omega) | radius of curvature | |
| (pronounced omega) | random drawing from ballot box |
References
- Yang, X.S. Nature-Inspired Optimization Algorithms; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Slowik, A.; Kwasnicka, H. Evolutionary algorithms and their applications to engineering problems. Neural Comput. Appl. 2020, 32, 12363–12379. [Google Scholar] [CrossRef]
- Slowik, A.; Kwasnicka, H. Nature inspired methods and their industry applications—Swarm intelligence algorithms. IEEE Trans. Ind. Inform. 2017, 14, 1004–1015. [Google Scholar] [CrossRef]
- Kvasov, D.E.; Mukhametzhanov, M.S. Metaheuristic vs. deterministic global optimization algorithms: The univariate case. Appl. Math. Comput. 2018, 318, 245–259. [Google Scholar] [CrossRef]
- Sergeyev, Y.D.; Kvasov, D.; Mukhametzhanov, M. On the efficiency of nature-inspired metaheuristics in expensive global optimization with limited budget. Sci. Rep. 2018, 8, 453. [Google Scholar] [CrossRef]
- VDI:6224; Biomimetic Optimization–Application of Evolutionary Algorithms. Standard VDI 6224: Part 1. Verein Deutscher Ingenieure: Beuth, Germany, 2012.
- Hollstein, R. Evolutionäre Algorithmen. In Optimierungsmethoden: Einführung in Die Klassischen, Naturanalogen und Neuronalen Optimierungen; Springer: Berlin/Heidelberg, Germany, 2023; pp. 147–184. Available online: https://link.springer.com/chapter/10.1007/978-3-658-39855-2_12 (accessed on 19 March 2024). (In German)
- Gerdes, I.; Klawonn, F.; Kruse, R. Evolutionäre Algorithmen: Genetische Algorithmen–Strategien und Optimierungsverfahren; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Rechenberg, I. Evolutionsstrategie’94; Frommann-Holzboog: Stuttgart, Germany, 1994. [Google Scholar]
- Schwefel, H.P. Evolution and Optimum Seeking: The Sixth Generation; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1993. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT press: Cambridge, MA, USA, 1992. [Google Scholar]
- Fogel, L.J.; Owens, A.J.; Walsh, M.J. Artificial Intelligence through Simulated Evolution; John Willey & Sons, Inc.: New York, NY, USA, 1966. [Google Scholar]
- Nissen, V. Einführung in Evolutionäre Algorithmen: Optimierung nach dem Vorbild der Evolution; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Sauer, S. Technische Optimierungsverfahren nach dem Vorbild der Natur. Unpublished Staatsexamen Thesis, University of Freiburg, Freiburg, Germany, 2009. (In German). [Google Scholar]
- Yuen, S.; Ezard, T.H.; Sobey, A.J. Epigenetic opportunities for evolutionary computation. R. Soc. Open Sci. 2023, 10, 221256. [Google Scholar] [CrossRef]
- Herdy, M. Beiträge zur Theorie und Anwendung der Evolutionsstrategie; Mensch-und-Buch-Verlag: Berlin, Germany, 2000. [Google Scholar]
- Herdy, M. Application of the Evolutionsstrategie to discrete optimization problems. In Proceedings of the International Conference on Parallel Problem Solving from Nature; Schwefel, H.P., Männer, R., Eds.; Springer: Berlin/Heidelberg, Germany, 1991; pp. 187–192. [Google Scholar] [CrossRef]
- Herdy, M. Self-adaptive Population Size and Stepsize in Combinatorial Optimization Problems: Solving Magic Squares as an Example. In Proceedings of the GECCO 2002: Proceedings of the Bird of a Feather Workshops, Genetic and Evolutionary Computation Conference, New York, NY, USA, 9–13 July 2002; pp. 156–160. [Google Scholar]
- Dudenredaktion. “Optimum”. Available online: https://www.duden.de/rechtschreibung/Optimum (accessed on 18 December 2023).
- Sauer, S.; Herdy, M.; Speck, T.; Speck, O. Evolutionsstrategie: Optimieren nach dem Vorbild der Natur—Interdisziplinäre Arbeitsweise der Biomechanik und Bionik. Prax. Naturwissenschaften Biol. Sch. 2010, 59, 34–41. (In German) [Google Scholar]
- Lambers, H.; Chapin, F.S.; Pons, T.L. Plant Physiological Ecology; Springer: Berlin/Heidelberg, Germany, 2008; Volume 2, pp. 4–6. [Google Scholar]
- Mylo, M.D.; Speck, O. Longevity of System Functions in Biology and Biomimetics: A Matter of Robustness and Resilience. Biomimetics 2023, 8, 173. [Google Scholar] [CrossRef]
- Bauer, G.; Speck, T.; Blömer, J.; Bertling, J.; Speck, O. Insulation capability of the bark of trees with different fire adaptation. J. Mater. Sci. 2010, 45, 5950–5959. [Google Scholar] [CrossRef]
- Speck, O.; Speck, T. Is a Forest Fire a Natural Disaster? Investigating the Fire Tolerance of Various Tree Species—An Educational Module. Biomimetics 2024, 9, 114. [Google Scholar] [CrossRef]
- Darwin, C. On the Origin of Species by Means of Natural Selection; Murray: London, UK, 1859. [Google Scholar]
- Strittmatter, G.; Klonk, S. Lexikon der Biologie “Mutation”. 1999. Available online: https://www.spektrum.de/lexikon/biologie/mutation/44508 (accessed on 21 December 2023).
- Dudenredaktion. “Rekombination”. Available online: https://www.duden.de/rechtschreibung/Rekombination (accessed on 18 December 2023).
- Dudenredaktion. “Combinatio”. Available online: https://www.duden.de/rechtschreibung/Kombination_Verknuepfung (accessed on 22 December 2023).
- Strittmatter, G.; Klonk, S. Lexikon der Biologie “Rekombination”. 1999. Available online: https://www.spektrum.de/lexikon/biologie/rekombination/56162 (accessed on 22 December 2023).
- Dudenredaktion. “Selectio”. Available online: https://www.duden.de/rechtschreibung/Selektion (accessed on 22 December 2023).
- Spencer, H. The Principles of Biology. Vol. I. London: Williams and Norgate. Syst. Synth. Philos. 1864, 2, 444. [Google Scholar]
- Sauer, P.; Kattmann, U. Lexikon der Biologie “Selektion”. 1999. Available online: https://www.spektrum.de/lexikon/biologie/selektion/60907 (accessed on 22 December 2023).
- Lexikonredaktion. Lexikon der Biologie “Isolation”. 1999. Available online: https://www.spektrum.de/lexikon/biologie/isolation/34657 (accessed on 3 January 2024).
- ISO:18458:2015-05; Biomimetics—Terminology, Concepts and Methodology. International Organization for Standardization: Beuth, Germany, 2015.
- Rechenberg, I. Artificial evolution and artificial intelligence. In Machine Learning: Principles and Techniques; Chapmann & Hall, Ltd.: London, UK, 1988; pp. 83–103. [Google Scholar]
- Jacob, C. Illustrating Evolutionary Computation with Mathematica; Morgan Kaufmann: Burlington, MA, USA, 2001. [Google Scholar]
- Rechenberg, I. Evolutionsstrategie. In Optimierung Technischer Systeme nach Prinzipien der Biologischen Evolution; Frommann-Holzboog: Stuttgart, Germany, 1973. [Google Scholar]
- Papula, L. Mathematik für Ingenieure und Naturwissenschaftler Band 3; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Agapie, A. Evolution Strategies under the 1/5 Success Rule. Mathematics 2022, 11, 201. [Google Scholar] [CrossRef]
- Hansen, N. The CMA evolution strategy: A comparing review. In Towards a New Evolutionary Computation: Advances in the Estimation of Distribution Algorithms; Springer: Berlin/Heidelberg, Germany, 2006; pp. 75–102. [Google Scholar]
- Hansen, N.; Gawelczyk, A.; Ostermeier, A. Sizing the population with respect to the local progress in (1,λ)-evolution strategies—A theoretical analysis. In Proceedings of the 1995 IEEE International Conference on Evolutionary Computation, Perth, WA, Australia, 29 November–1 December 1995; Volume 1, p. 80. [Google Scholar]
- Corpus, K.R.M.; Bui, J.C.; Limaye, A.M.; Pant, L.M.; Manthiram, K.; Weber, A.Z.; Bell, A.T. Coupling covariance matrix adaptation with continuum modeling for determination of kinetic parameters associated with electrochemical CO2 reduction. Joule 2023, 7, 1289–1307. [Google Scholar] [CrossRef]
- Herdy, M. Evolutionsstrategie mit subjektiver Selektion zur Optimierung von Kaffeemischungen. Atp Autom. Prax. 1997, 39, 18–24. [Google Scholar]
- Herdy, M. Evolutionsstrategie mit subjektiver Selektion zur Optimierung von Kaffeemischungen. In Industrielle Anwendungen Evolutionärer Algorithmen; Hafner, S., Beiersdörfer, S., Eds.; Oldenbourg Wissenschaftsverlag: Oldenbourg, Germany, 1998; pp. 15–23. [Google Scholar]
- Hasançebi, O. Cost efficiency analyses of steel frameworks for economical design of multi-storey buildings. J. Constr. Steel Res. 2017, 128, 380–396. [Google Scholar] [CrossRef]
- Fadda, E.; Perboli, G.; Squillero, G. Adaptive batteries exploiting on-line steady-state evolution strategy. In Proceedings of the Applications of Evolutionary Computation: 20th European Conference, EvoApplications 2017, Amsterdam, The Netherlands, 19–21 April 2017; Proceedings, Part I 20. Springer: Berlin/Heidelberg, Germany, 2017; pp. 329–341. [Google Scholar] [CrossRef]
- Ogidan, O.S.; Giacomoni, M. Enhancing the performance of a multiobjective evolutionary algorithm for sanitary sewer overflow reduction. J. Water Resour. Plan. Manag. 2017, 143, 04017023. [Google Scholar] [CrossRef]
- Speck, O.; Speck, T. Biomimetics and education in Europe: Challenges, opportunities, and variety. Biomimetics 2021, 6, 49. [Google Scholar] [CrossRef]
- Jacobs, S.; Eggermont, M.; Helms, M.; Wanieck, K. The education pipeline of biomimetics and its challenges. Biomimetics 2022, 7, 93. [Google Scholar] [CrossRef]
- Speck, O.; Sauer, S.; Herdy, M. Optimierung einer Kugelbahn. 2010. Available online: https://www.bionik-online.de/bionik-experimente/evolutionsstrategie/ (accessed on 19 March 2024). (In German).
- Bernoulli, J. Problema novum ad cujus solutionem Mathematici invitantur. Acta Erud. 1696, 18, 551. [Google Scholar]
- Padyala, R. Brachistochrone—The path of quickest descent. Resonance 2019, 24, 201–216. [Google Scholar] [CrossRef]
- Newton, I. De ratione temporis quo grave labitur per rectam data duo puncta conjungentem, ad tempus brevissimum quo, vi gravitatis, transit ab horum uno ad alterum per arcum cycloidis. Philos. Trans. R. Soc. Lond. 1697, 19, 424–425. [Google Scholar]
- Leibniz, G.W. Communicatio suae pariter, duarumque alienarum ad edendum sibi primum a Dn. Jo. Bernoullio, deinde a Dn. Marchione Hospitalio communicatarum solutionum problematis curva celerrimi descensus a Dn. Jo. Bernoullio Geometris publice propositi, una cum solutione sua problematis alterius ab eodem postea propositi. Acta Erud. 1697, 19, 201–205. [Google Scholar]
- Bernoulli, J. Curvatura radii in diaphanis non uniformibus, Solutioque Problematis a se in Actis 1696, p. 269, propositi, de invenienda Linea Brachystochrona, id est, in qua grave a dato puncto ad datum punctum brevissimo tempore decurrit, & de curva Synchrona seu radiorum unda construenda. Acta Erud. 1697, 19, 206–211. [Google Scholar]
- Bernoulli, J. Solutio problematum fraternorum, Peculiari Programmate Cal. Jan. 1697 Groningae, nec non Actorum Lipsmense Jun. & Dec. 1696, & Febr. 1697 propositorium; una cum Propositione reciproca aliorum. Acta Erud. 1697, 19, 211–214. [Google Scholar]
- Marquis de l’Hôpital, G.F.A. Domini Marchionis Hospitalii solutio problematis de linea celerrimi descensus. Acta Erud. 1697, 19, 217–222. [Google Scholar]













| Biological Evolution (Biology) | Evolution Strategy (Technology) | |
|---|---|---|
| Subject | Living being | Object to be optimized |
| Mutation | Random change of genetic information | Random change of input variables (i.e., object parameters) |
| Recombination | Reshuffling of parental genetic material (e.g., meiosis) | New combination of parental object parameters |
| Selection | Selection of those individuals with the best fit to the natural environment | Selection of those individuals that best meet the optimization criterion |
| Result | Adapted organism | Optimized object |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Speck, O.; Speck, T.; Baur, S.; Herdy, M. The Basics of Evolution Strategies: The Implementation of the Biomimetic Optimization Method in Educational Modules. Biomimetics 2024, 9, 439. https://doi.org/10.3390/biomimetics9070439
Speck O, Speck T, Baur S, Herdy M. The Basics of Evolution Strategies: The Implementation of the Biomimetic Optimization Method in Educational Modules. Biomimetics. 2024; 9(7):439. https://doi.org/10.3390/biomimetics9070439
Chicago/Turabian StyleSpeck, Olga, Thomas Speck, Sabine Baur, and Michael Herdy. 2024. "The Basics of Evolution Strategies: The Implementation of the Biomimetic Optimization Method in Educational Modules" Biomimetics 9, no. 7: 439. https://doi.org/10.3390/biomimetics9070439
APA StyleSpeck, O., Speck, T., Baur, S., & Herdy, M. (2024). The Basics of Evolution Strategies: The Implementation of the Biomimetic Optimization Method in Educational Modules. Biomimetics, 9(7), 439. https://doi.org/10.3390/biomimetics9070439










