Aerodynamic Effects of Time-Varying Corrugations on Dragonfly Wings in Flapping Flight
Abstract
1. Introduction
2. Materials and Methods
2.1. The Flapping Motion of the Airfoil
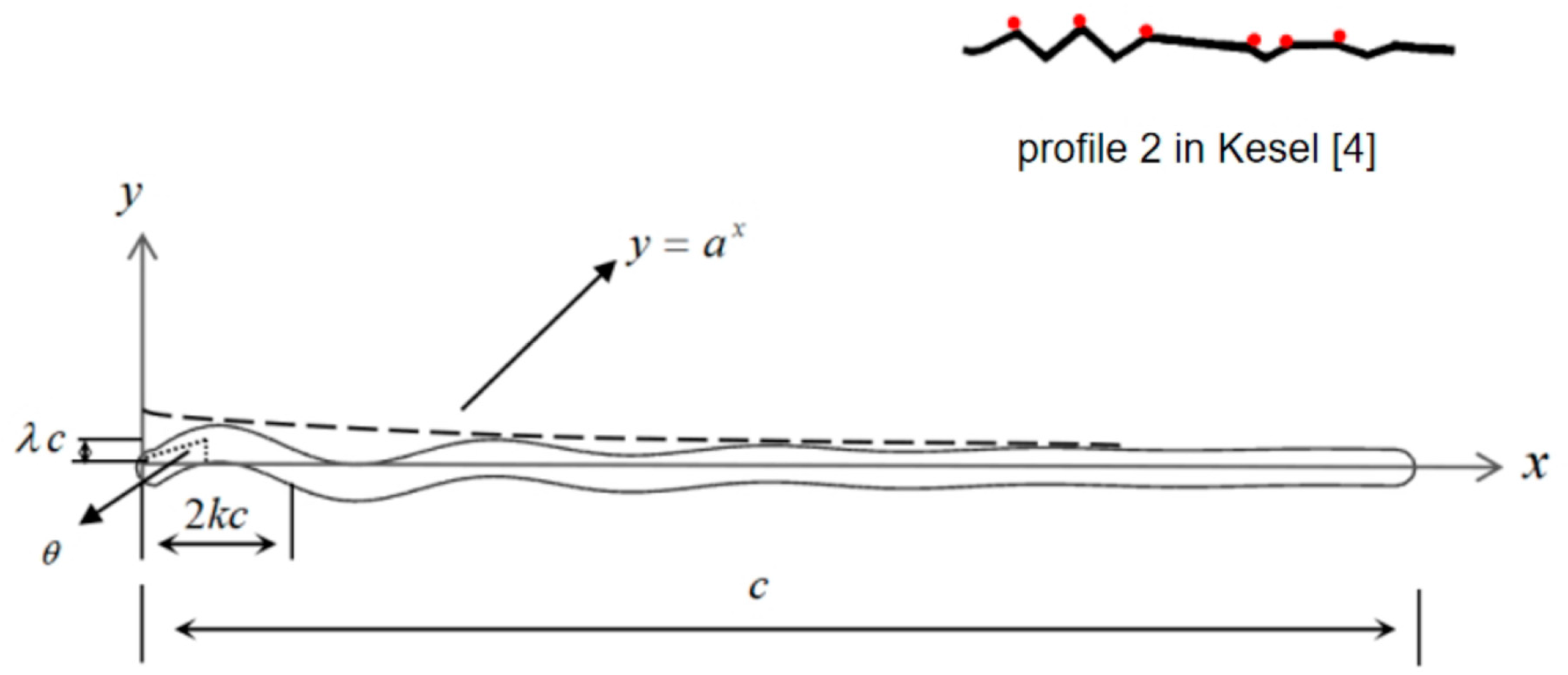
2.2. Two-Dimensional Airfoil with Time-Varying Corrugations
2.3. The Flow Equations and Solution Method
2.4. Parameters in Calculation
3. Results and Discussion
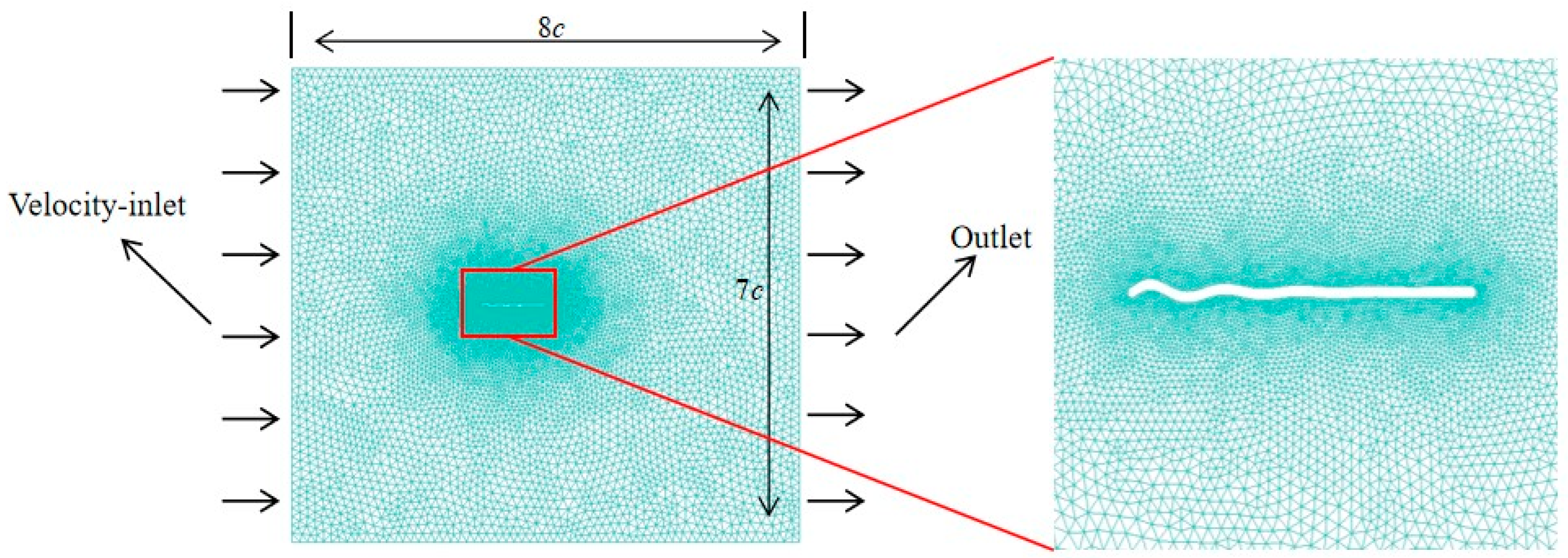
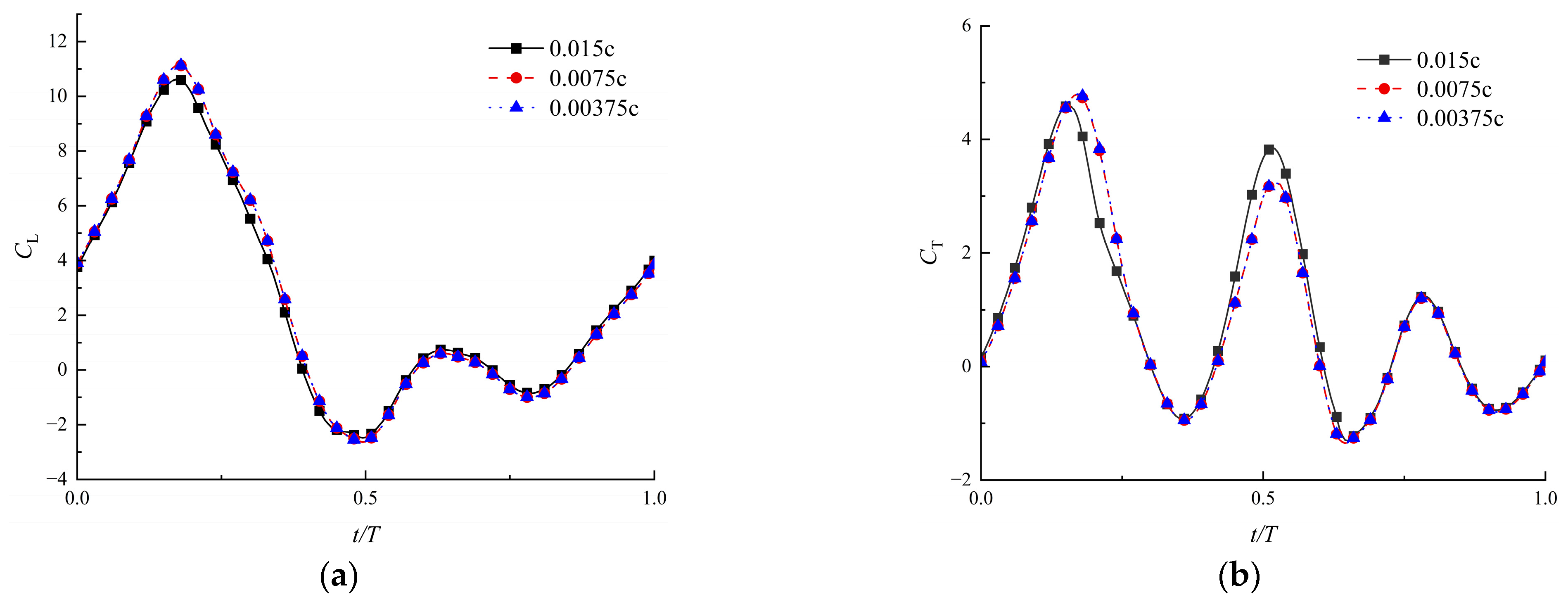
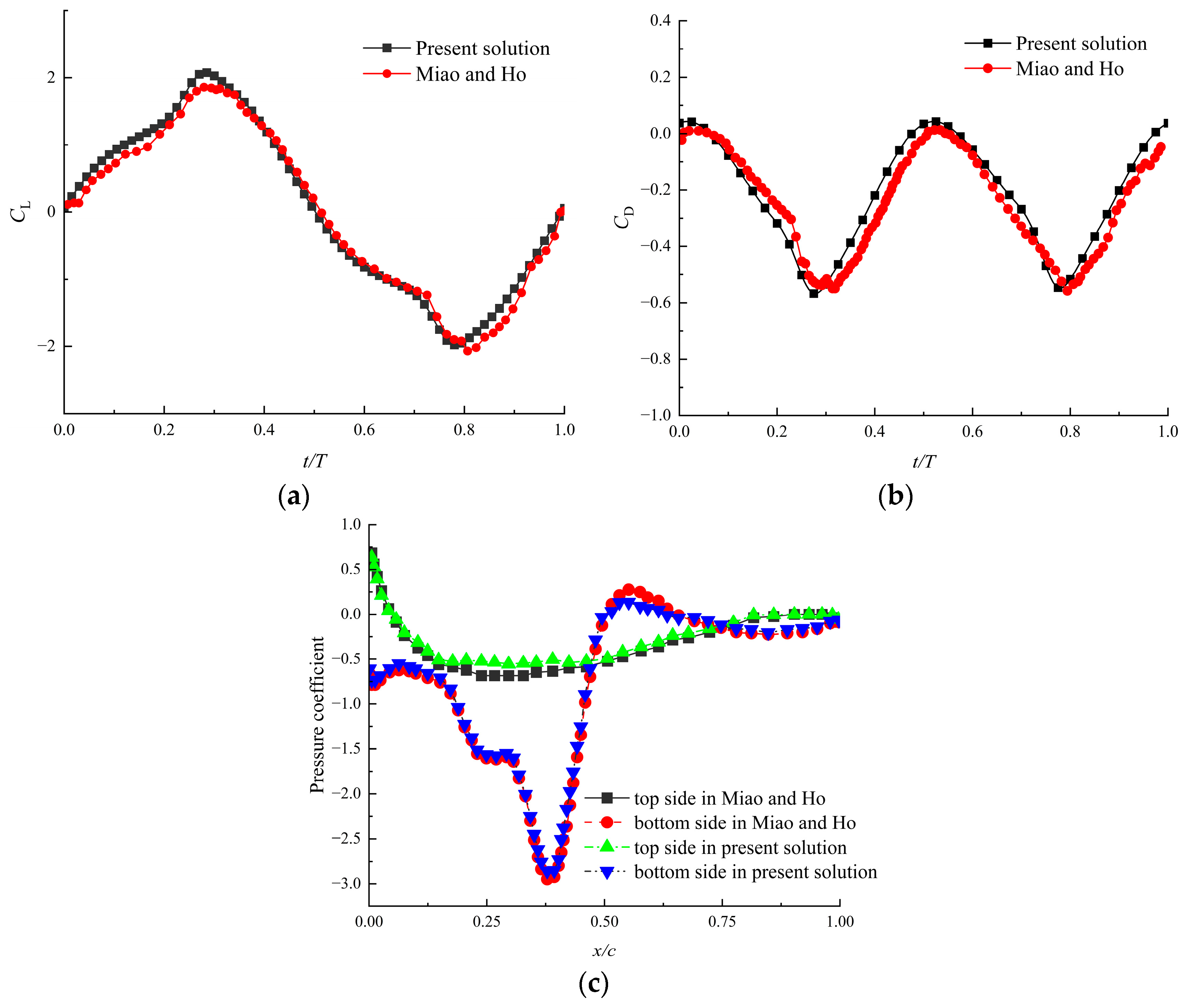
3.1. Grid Sensitivity Test, Time-Step Convergence and Code Validation
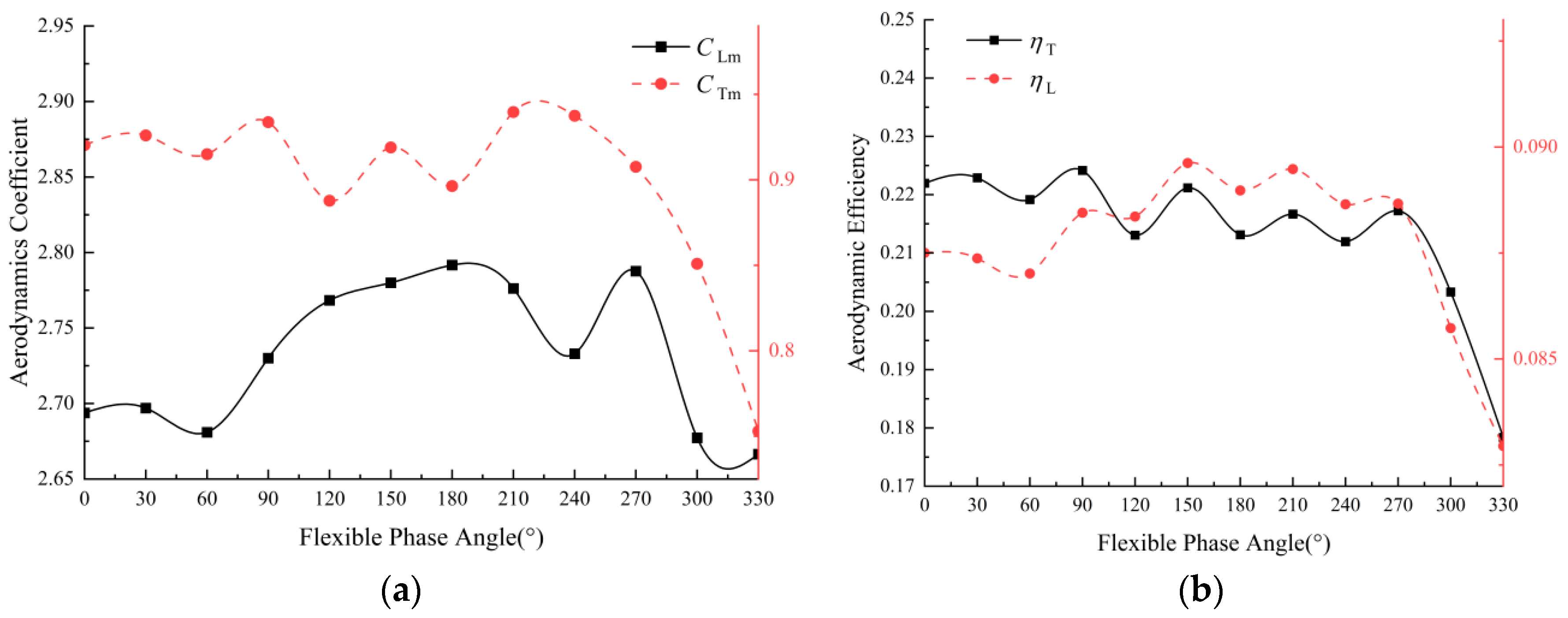
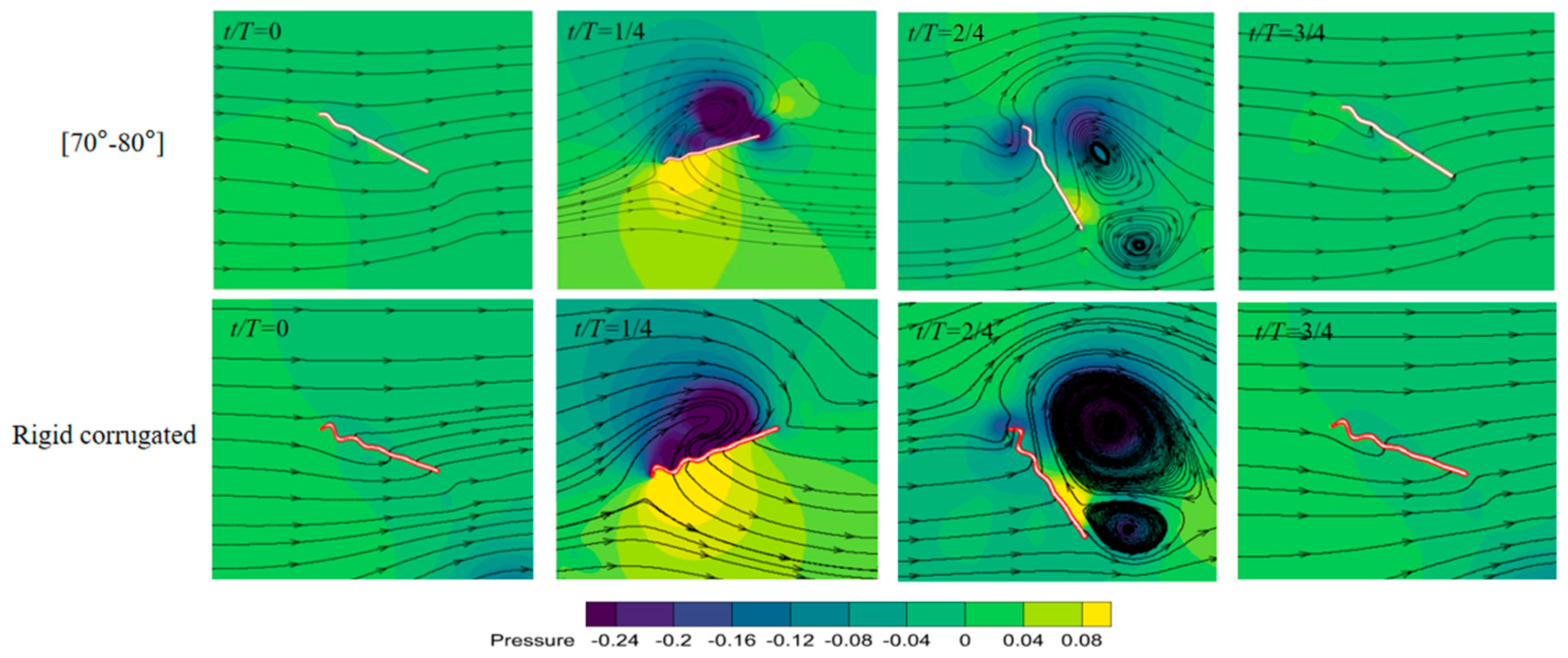
3.2. Effects of Time-Varying Corrugations at Different Phase Angles
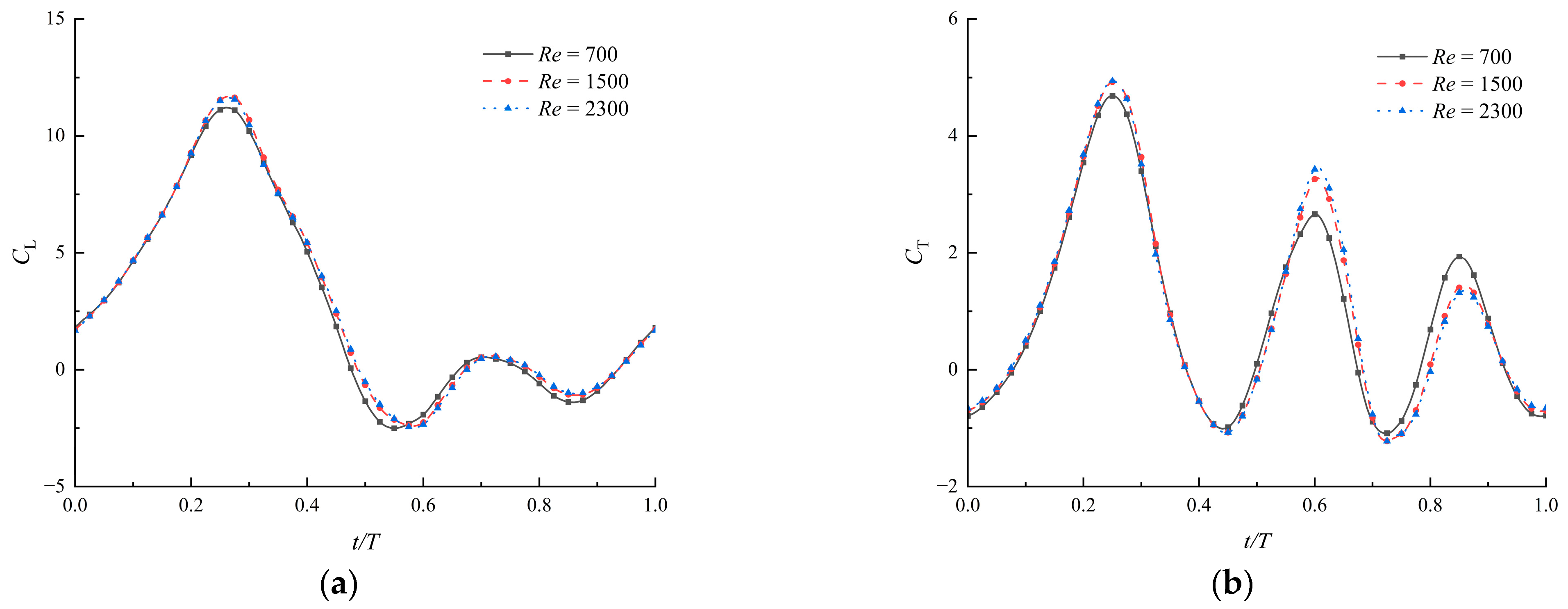
3.3. Effects of Time-Varying Corrugations at Different Reynolds Numbers
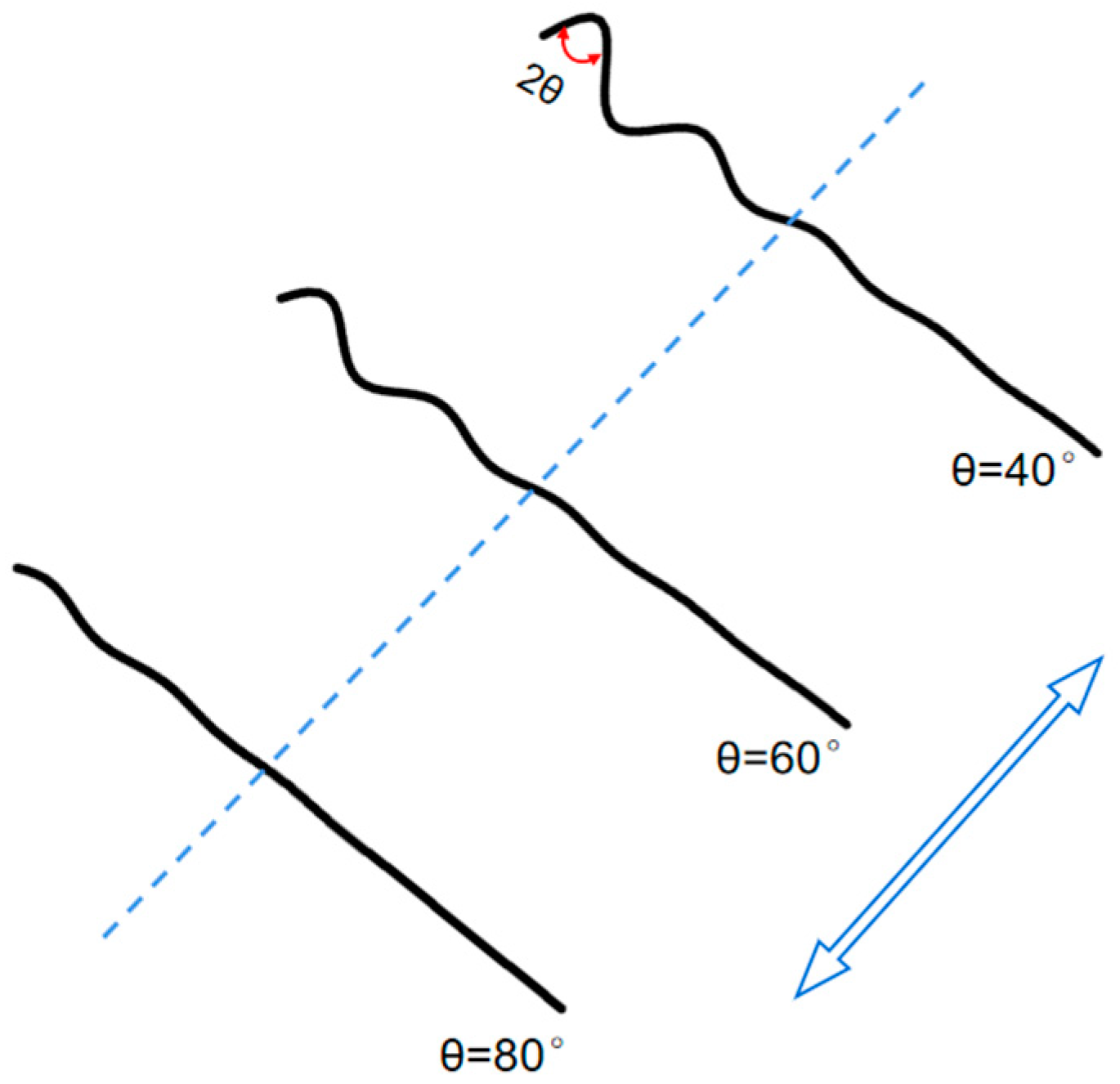
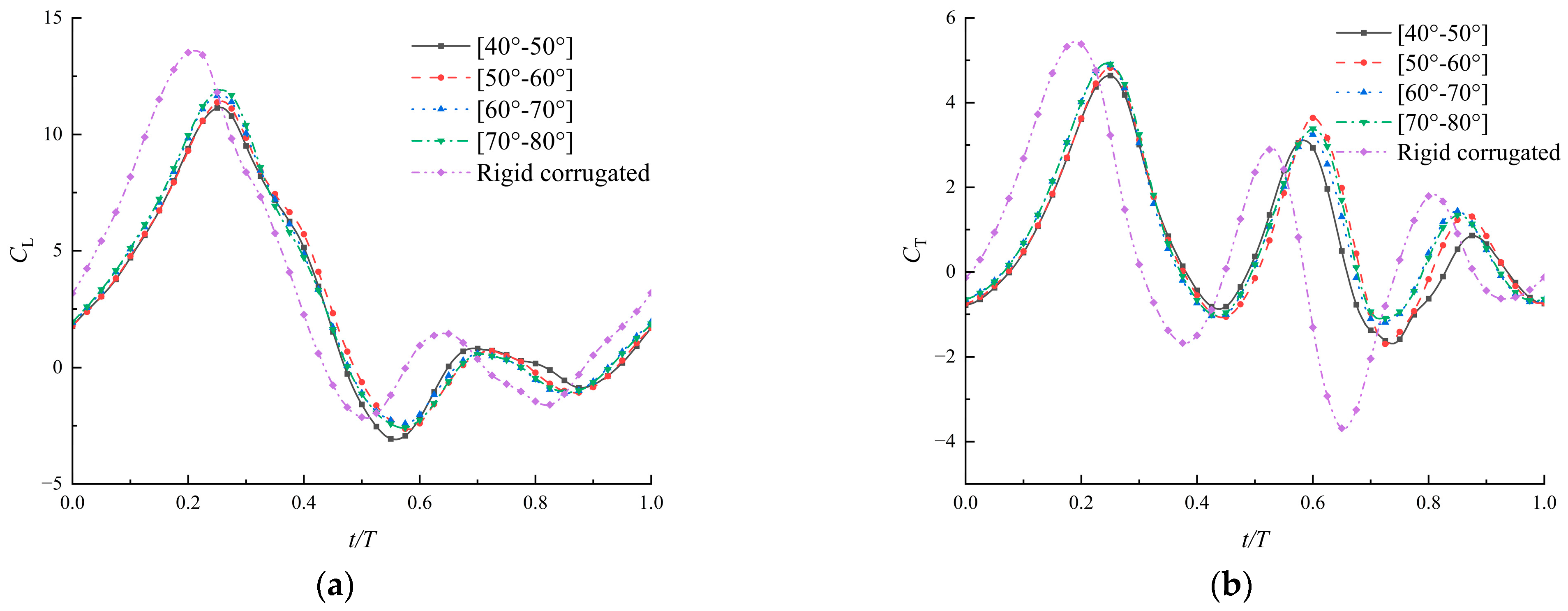
3.4. Effects of Time-Varying Corrugations with Different Angles
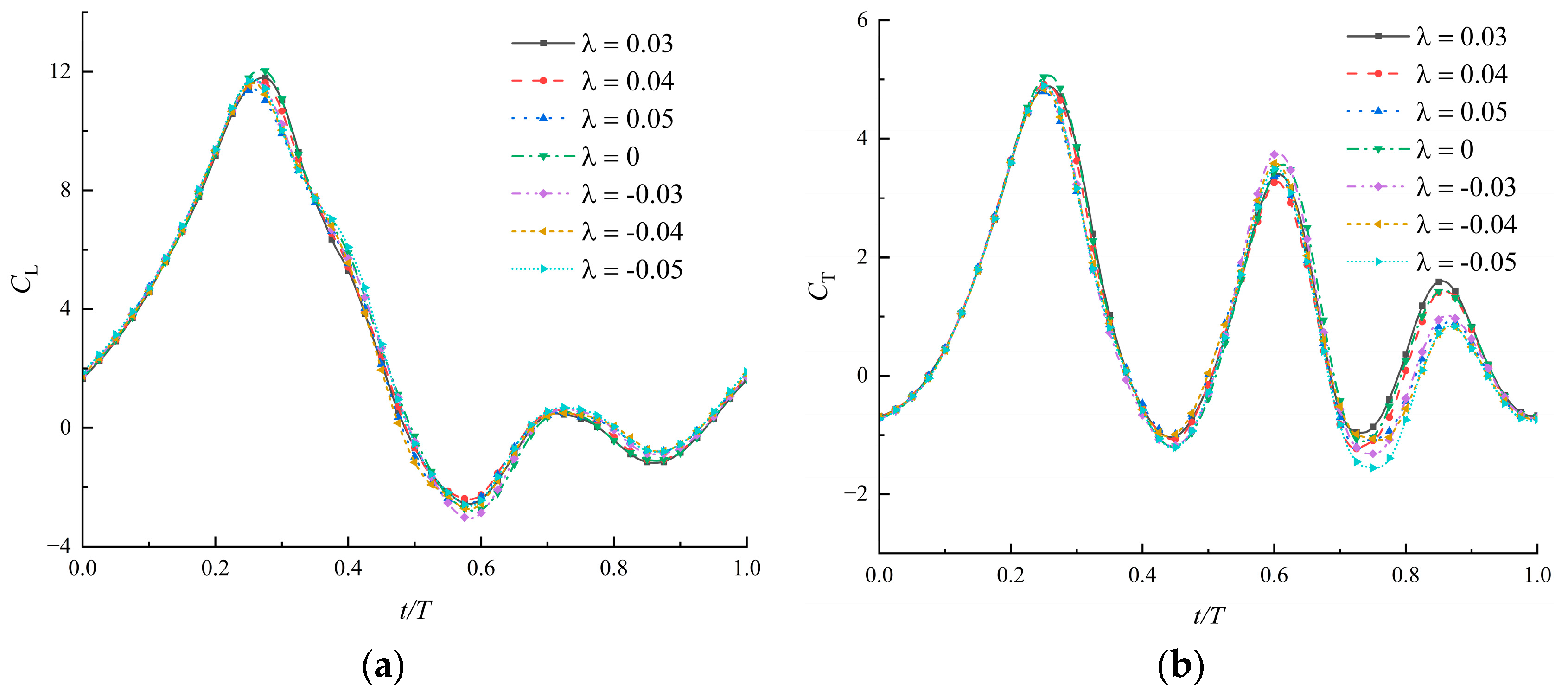
3.5. Effects of Time-Varying Corrugations under Different Heights
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Rees, C.J. Form and function in corrugated insect wings. Nature 1975, 256, 200–203. [Google Scholar] [CrossRef]
- Sunada, S.; Zeng, L.; Kawachi, K. The Relationship Between Dragonfly Wing Structure and Torsional Deformation. J. Theor. Biol. 1998, 193, 39–45. [Google Scholar] [CrossRef]
- Okamoto, M.; Yasuda, K.; Azuma, A. Aerodynamic characteristics of the wings and body of a dragonfly. J. Exp. Biol. 1996, 199, 281–294. [Google Scholar] [CrossRef] [PubMed]
- Kesel, A.B. Aerodynamic characteristics of dragonfly wing sections compared with technical aerofoils. J. Exp. Biol. 2000, 203, 3125–3135. [Google Scholar] [CrossRef] [PubMed]
- Kim, W.-K.; Ko, J.H.; Park, H.C.; Byun, D. Effects of corrugation of the dragonfly wing on gliding performance. J. Theor. Biol. 2009, 260, 523–530. [Google Scholar] [CrossRef] [PubMed]
- Vargas, A.; Mittal, R.; Dong, H. A computational study of the aerodynamic performance of a dragonfly wing section in gliding flight. Bioinspir. Biomim. 2008, 3, 026004. [Google Scholar] [CrossRef] [PubMed]
- Levy, D.-E.; Seifert, A. Parameter study of simplified dragonfly airfoil geometry at Reynolds number of 6000. J. Theor. Biol. 2010, 266, 691–702. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Yin, Y.; Zhong, Z.; Zhao, H. Aerodynamic Performance of Dragonfly Wing with Well-designed Corrugated Section in Gliding Flight. CMES Comput. Model. Eng. Sci. 2015, 109, 285–302. [Google Scholar]
- Narita, Y.; Chiba, K. Aerodynamics on a faithful hindwing model of a migratory dragonfly based on 3D scan data. J. Fluids Struct. 2024, 125, 104080. [Google Scholar] [CrossRef]
- Meng, X.G.; Xu, L.; Sun, M. Aerodynamic effects of corrugation in flapping insect wings in hovering flight. J. Exp. Biol. 2011, 214, 432–444. [Google Scholar] [CrossRef]
- Meng, X.; Sun, M. Aerodynamic Effects of Corrugation in Flapping Insect Wings in Forward Flight. J. Bionic Eng. 2011, 8, 140–150. [Google Scholar] [CrossRef]
- Dao, T.; Loan Au, T.K.; Park, S.H.; Park, H.C. Effect of Wing Corrugation on the Aerodynamic Efficiency of Two-Dimensional Flapping Wings. Appl. Sci. 2020, 10, 7375. [Google Scholar] [CrossRef]
- Xuan, H.; Hu, J.; Yu, Y.; Zhang, J. Aerodynamic effects of bio-inspired corrugated wings on gliding and hovering performances. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 319–329. [Google Scholar] [CrossRef]
- Nguyen, K.; Au, L.T.K.; Phan, H.V.; Park, S.H.; Park, H.C. Effects of wing kinematics, corrugation, and clap-and-fling on aerodynamic efficiency of a hovering insect-inspired flapping-wing micro air vehicle. Aerosp. Sci. Technol. 2021, 118, 106990. [Google Scholar] [CrossRef]
- Wang, Y.; He, X.; He, G.; Wang, Q.; Chen, L.; Liu, X. Aerodynamic performance of the flexibility of corrugated dragonfly wings in flapping flight. Acta Mech. Sin. 2022, 38, 322038. [Google Scholar] [CrossRef]
- Sun, W.; Wang, Y.; He, G.; Wang, Q.; Yu, F.; Song, W. Effects of kinematic parameters and corrugated structure on the aerodynamic performance of flexible dragonfly wings. J. Fluids Struct. 2024, 125, 104058. [Google Scholar] [CrossRef]
- Newman, D.J.S. The Functional Wing Morphology of Some Odonata; University of Exeter: Exeter, UK, 1982. [Google Scholar]
- Gorb, S.N. Serial elastic elements in the damselfly wing: Mobile vein joints contain resilin. Naturwissenschaften 1999, 86, 552–555. [Google Scholar] [CrossRef] [PubMed]
- Donoughe, S.; Crall, J.D.; Merz, R.A.; Combes, S.A. Resilin in dragonfly and damselfly wings and its implications for wing flexibility. J. Morphol. 2011, 272, 1409–1421. [Google Scholar] [CrossRef] [PubMed]
- Appel, E.; Gorb, S.N. Resilin-bearing wing vein joints in the dragonfly Epiophlebia superstes. Bioinspir. Biomim. 2011, 6, 046006. [Google Scholar] [CrossRef]
- Appel, E.; Michels, J.; Gorb, S. Resilin in Insect Flight Systems. Adv. Funct. Mater. 2023, 2215162. [Google Scholar] [CrossRef]
- Andersen, S.O.; Weis-Fogh, T.R. Andersen, S.O.; Weis-Fogh, T.R. A Rubberlike Protein in Arthropod Cuticle. In Advances in Insect Physiology; Beament, J.W.L., Treherne, J.E., Wigglesworth, V.B., Eds.; Academic Press: Cambridge, MA, USA, 1964; pp. 1–65. [Google Scholar]
- Haas, F.; Gorb, S.; Blickhan, R. The function of resilin in beetle wings. Proc. R. Soc. Lond. Ser. B Biol. Sci. 2000, 267, 1375–1381. [Google Scholar] [CrossRef] [PubMed]
- Rajabi, H.; Shafiei, A.; Darvizeh, A.; Gorb, S.N. Resilin microjoints: A smart design strategy to avoid failure in dragonfly wings. Sci. Rep. 2016, 6, 39039. [Google Scholar] [CrossRef] [PubMed]
- Dan, H.; Zhong, Z.; Yin, Y.; Pan, Y.; Zhao, H. The Role of Soft Vein Joints in Dragonfly Flight. J. Bionic Eng. 2017, 14, 738–745. [Google Scholar]
- Norberg, R.A. Hovering flight of the dragonfly Aeschna juncea L., kinematics and aerodynamics. Swim. Fly. Nat. 1975, 2, 763–781. [Google Scholar]
- Wang, Z.J.; Birch, J.M.; Dickinson, M.H. Unsteady forces and flows in low Reynolds number hovering flight: Two-dimensional computations vs robotic wing experiments. J. Exp. Biol. 2004, 207, 449–460. [Google Scholar] [CrossRef] [PubMed]
- Sun, M. Insect flight dynamics: Stability and control. Rev. Mod. Phys. 2014, 86, 615. [Google Scholar] [CrossRef]
- Yang, S.; Liu, C.; Wu, J. Effect of motion trajectory on the aerodynamic performance of a flapping airfoil. J. Fluids Struct. 2017, 75, 213–232. [Google Scholar] [CrossRef]
- Wang, H.; Zeng, L.; Liu, H.; Yin, C. Measuring wing kinematics, flight trajectory and body attitude during forward flight and turning maneuvers in dragonflies. J. Exp. Biol. 2003, 206, 745–757. [Google Scholar] [CrossRef] [PubMed]
- Miao, J.M.; Ho, M.H. Effect of flexure on aerodynamic propulsive efficiency of flapping flexible airfoil. J. Fluids Struct. 2006, 22, 401–419. [Google Scholar] [CrossRef]
- Ashraf, M.A.; Young, J.; Lai, J.C.S. Reynolds number, thickness and camber effects on flapping airfoil propulsion. J. Fluids Struct. 2011, 27, 145–160. [Google Scholar] [CrossRef]




| Re | 700 | 1500 | 2300 |
|---|---|---|---|
| 2.663 | 2.823 | 2.810 | |
| 0.946 | 0.961 | 0.970 | |
| 4.212 | 4.276 | 4.221 | |
| 0.082 | 0.082 | 0.082 | |
| 0.236 | 0.240 | 0.242 |
| [40°–50°] | [50°–60°] | [60°–70°] | [70°–80°] | Rigid Corrugated | |
|---|---|---|---|---|---|
| 2.698 | 2.779 | 2.823 | 2.801 | 3.387 | |
| 0.780 | 0.918 | 0.961 | 1.016 | 0.693 | |
| 4.008 | 4.153 | 4.277 | 4.280 | 5.122 | |
| 0.080 | 0.081 | 0.085 | 0.087 | 0.100 | |
| 0.194 | 0.229 | 0.239 | 0.248 | 0.173 |
| [40°–50°] | [40°–60°] | [40°–70°] | [40°–80°] | |
|---|---|---|---|---|
| 2.698 | 2.730 | 2.774 | 2.734 | |
| 0.780 | 0.962 | 0.924 | 0.926 | |
| 4.008 | 4.137 | 4.213 | 4.188 | |
| 0.080 | 0.080 | 0.081 | 0.082 | |
| 0.194 | 0.230 | 0.240 | 0.230 |
| −0.05 | −0.04 | −0.03 | 0 | 0.03 | 0.04 | 0.05 | |
|---|---|---|---|---|---|---|---|
| 2.958 | 2.790 | 2.827 | 2.888 | 2.756 | 2.823 | 2.790 | |
| 0.808 | 0.901 | 0.912 | 0.971 | 1.046 | 0.961 | 0.905 | |
| 4.276 | 4.114 | 4.260 | 4.419 | 4.272 | 4.276 | 4.088 | |
| 0.082 | 0.083 | 0.084 | 0.085 | 0.083 | 0.082 | 0.082 | |
| 0.202 | 0.225 | 0.227 | 0.257 | 0.261 | 0.240 | 0.225 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, D.; Tan, B.; Shi, B.; Zhong, Z. Aerodynamic Effects of Time-Varying Corrugations on Dragonfly Wings in Flapping Flight. Biomimetics 2024, 9, 433. https://doi.org/10.3390/biomimetics9070433
Hou D, Tan B, Shi B, Zhong Z. Aerodynamic Effects of Time-Varying Corrugations on Dragonfly Wings in Flapping Flight. Biomimetics. 2024; 9(7):433. https://doi.org/10.3390/biomimetics9070433
Chicago/Turabian StyleHou, Dan, Biao Tan, Binghao Shi, and Zheng Zhong. 2024. "Aerodynamic Effects of Time-Varying Corrugations on Dragonfly Wings in Flapping Flight" Biomimetics 9, no. 7: 433. https://doi.org/10.3390/biomimetics9070433
APA StyleHou, D., Tan, B., Shi, B., & Zhong, Z. (2024). Aerodynamic Effects of Time-Varying Corrugations on Dragonfly Wings in Flapping Flight. Biomimetics, 9(7), 433. https://doi.org/10.3390/biomimetics9070433





