Abstract
The concept of Image Phase Congruency (IPC) is deeply rooted in the way the human visual system interprets and processes spatial frequency information. It plays an important role in visual perception, influencing our capacity to identify objects, recognize textures, and decipher spatial relationships in our environments. IPC is robust to changes in lighting, contrast, and other variables that might modify the amplitude of light waves yet leave their relative phase unchanged. This characteristic is vital for perceptual tasks as it ensures the consistent detection of features regardless of fluctuations in illumination or other environmental factors. It can also impact cognitive and emotional responses; cohesive phase information across elements fosters a perception of unity or harmony, while inconsistencies can engender a sense of discord or tension. In this survey, we begin by examining the evidence from biological vision studies suggesting that IPC is employed by the human perceptual system. We proceed to outline the typical mathematical representation and different computational approaches to IPC. We then summarize the extensive applications of IPC in computer vision, including denoise, image quality assessment, feature detection and description, image segmentation, image registration, image fusion, and object detection, among other uses, and illustrate its advantages with a number of examples. Finally, we discuss the current challenges associated with the practical applications of IPC and potential avenues for enhancement.
1. Introduction
Phase congruency is a fundamental concept in signal processing, particularly in image processing and computer vision. It involves the alignment of local phase components in a signal, which is crucial for the detection of image features such as edges, corners, and textures. Image Phase Congruency (IPC) was first introduced by Morrone and Owens in the mid-1980s as a means to mimic the human visual system’s ability to detect features based on phase alignment [1,2]. Since then, IPC has become a widely used tool for various image processing and computer vision tasks.
At its essence, IPC relies on the fact that significant image features coincide with locations where the Fourier components of an image are in phase with each other. This alignment suggests the presence of important features like edges or corners [3]. One of the key advantages of IPC is its ability to analyze images across multiple scales and orientations, enabling the detection of features of varying sizes and shapes. In computer vision, IPC has been proven to be invaluable for feature detection. For example, there have been a large number of traditional edge detection methods that rely on intensity differentiation, such as the Sobel, Canny, or second Derivatives of Gaussian (DoG) operators [4,5,6]. However, these methods can be sensitive to contrast variations and may struggle in complex scenes. Phase congruency offers an alternative that is more robust to these challenges [3,7,8].
Since the publication of Kovesi’s computational method for IPC in the 1990s [3], it has been widely used in a variety of applications in computer vision, ranging from low-level to high-level tasks. These applications include image denoise, image quality assessment, autofocus, image super-resolution, feature detection and description, image segmentation, image registration, image fusion, object detection and recognition, and so on [3,8,9,10,11,12,13,14,15,16,17]. Despite its effectiveness, one major drawback of IPC is its high computational cost, mainly due to its reliance on multi-scale analysis. However, advancements in semiconductor and computer chip technology in recent years have significantly reduced the impact of such computational burden. There has been intensive ongoing research and development to improve and enhance the utilization of IPC [18,19,20,21,22,23,24]. However, as far as we know, there has been no comprehensive review of its advancements since its inception almost four decades ago.
In this comprehensive survey, we explore the origins of IPC in human visual perception, compare its various computational implementations, and examine its diverse applications in both image processing and computer vision. Additionally, we discuss the challenges and potential enhancements needed for IPC to be more widely employed. For sake of clarity and conciseness, we do not distinguish between image processing and computer vision below.
2. Phase Congruency in Biological Perception
2.1. Frequency Analysis in Biological Perception
Human brains interpret and understand sounds, images, and other sensory inputs based on their constituent frequencies. For example, the human ear is sensitive to different frequencies of sound waves, and the brain interprets these frequencies to discern pitch, timbre, and other auditory qualities [25,26,27]. Music perception, in particular, relies heavily on frequency analysis, as melodies, harmonies, and rhythms are all composed of specific frequencies that the brain learns to recognize and appreciate. In the human visual system, it has been convincingly shown that frequency analysis relates to the perception of patterns and textures [28,29,30,31]. For instance, certain visual patterns might be composed of repeating elements that create a particular frequency or rhythm. The visual system is adept at recognizing these patterns and using them to interpret our surroundings. More broadly, frequency analysis in human perception involves the brain’s ability to extract meaningful information from sensory inputs based on their frequency content [27,32]. This process is fundamental to our understanding of and interactions with the world around us.
In the frequency domain, a signal is represented by a spectrum of frequencies, each with its own amplitude and phase. This spectral representation provides valuable insights into the signal’s characteristics. For instance, high-frequency components correspond to fine details, while low-frequency ones represent smoother parts.
2.2. Fourier Transform and Phase Congruency
Fourier transform is a well-established mathematical operation that decomposes a signal into its constituent frequencies. For a given signal, there are theoretically infinite constituent frequencies; thus, in practice, the Fourier transform is essentially an approximation that utilizes the weighted sum of a number of basis functions, each of which represents a constituent frequency [33]. Figure 1 illustrates a 1D pulse function and its approximations with the sum of different numbers of Fourier basis functions. It is obvious that the more basis function terms used, the more accurate the Fourier transform, as is the case in any approximation method. It is less intuitive but graphically conspicuous that at the two jumping steps of the pulse function shown as locations and in Figure 1, the Fourier components and their summations are perfectly aligned, as highlighted with the dashed circles. These two locations are where the phases of the Fourier components are in complete agreement and the signal reaches high phase congruency. This will be mathematically described below.
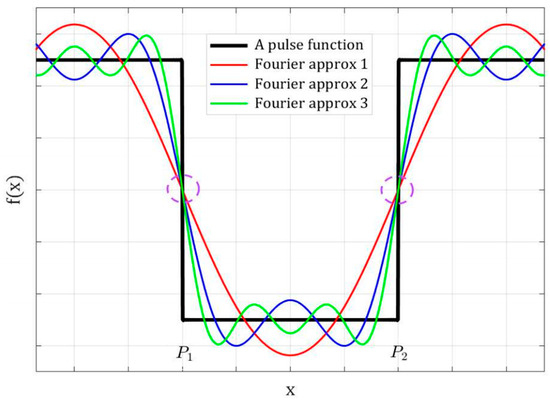
Figure 1.
A pulse function and its approximations by different numbers of Fourier components.
The Fourier transform of a 1D signal is as follows:
where is the Fourier component number, while and are the real and imaginary components of . Its amplitude and phase are as follows:
Phase congruency is defined as follows [2]:
where represents the amplitude of the Fourier component , its local phase at position , and the total number of components. The value of is the amplitude weighted mean local phase of all the Fourier terms at the point under consideration. The term is approximately equal to one minus half of when it is small according to the Taylor expansion. The operation to find the maximum of is equivalent to finding where the weighted variance of local phase is minimal relative to the weighted average local phase.
2.3. Biological Basis of Phase Congruency
As briefly mentioned in Section 2.1, both the human auditory and visual systems utilize frequency analysis for information processing. There are reasons to believe that different sensory systems may share some common operating mechanisms. For example, both vision and hearing employ hierarchical processing models [34,35]. Hermman et al. reported that synchronization of neural activity is more sensitive to regularity imposed by a coherent frequency modulation in sounds compared with the sustained response, which implies the role of phase congruency in some auditory functions [36]. In addition, studies on the patterns of cortical connectivity have found evidence for direct connections between different sensory primary cortices, especially hearing and vision, which suggests that the basis for cross-modal interactions to affect perceptual processing is present at very early stages of sensory processing [37,38]. Nevertheless, in this report we mostly focus on vision-related phase congruency. For structural simplicity, we divide this section into two parts, i.e., spatial phase congruency and temporal phase congruency. Though they are closely related, we mainly discuss the spatial aspect in this report.
2.3.1. Spatial Phase Congruency
Phase congruency was initially proposed in the psychophysical study of visual phenomena. Mach bands are a visual illusion named after the 19th-century Austrian physicist Ernst Mach, who first described the phenomenon. It refers to the illusionary perception of brighter and darker bands along the boundaries where two different intensities meet [39]. That is, when a bright area is adjacent to a dark area, an even brighter band appears to exist along the edge of the bright area, and a darker band along the edge of the dark area, despite the fact that these bands are not physically present in the pattern. The illusion is not caused by differences in the physical intensity of light at the boundaries, but rather by the way the visual system processes these changes. One explanation is that Mach bands arise due to lateral inhibition, a neural process where excited neurons inhibit the activity of neighboring neurons [40]. However, this lateral inhibition theory cannot explain that there are no Mach bands in a square waveform [41]. Inspired by such observations, Morrone et al. demonstrated that phase relationships between Fourier components can explain the physically non-existing structure in their groundbreaking study on an odd and even symmetry visual field model [1]. As shown in Figure 2, there are no contrast variations in the intensity gradients of the step pattern across the stripes, but there are variations in the weighted local phase.
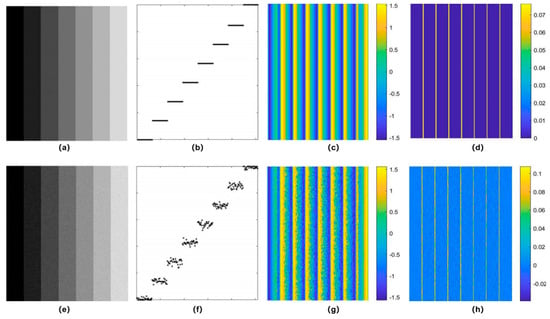
Figure 2.
Mach bands. (a) An ideal step intensity pattern; (b–d) Intensity cross-section, weighted local phase, and horizontal gradients of (a). (e) A step intensity pattern with Gaussian noise. (f–h) Intensity cross-section, weighted local phase, and horizontal gradients of (e).
Burr et al. experimentally showed that the human visual system has phase response-based line and edge detectors, and the receptive fields are symmetric; one class is even-symmetric related to line detectors, the other odd-symmetric [42]. Based on these psychophysical observations, Morrone et al. developed a local energy model such that the local maxima of the local energy functions occur at locations of maximal phase congruency, and two-step simultaneous line and edge detectors based on the model, one step is linear and the other nonlinear [2,43,44,45]. Other researchers made various improvements to this class of local energy model-based feature detectors and also extended to 3D images [46,47].
More recently, physiological studies on primate and human brains provided additional evidence of phase congruency being employed by the visual system. Ringach conducted electrophysiological recording of simple cells in primate primary visual cortex (V1) and found Gabor-like receptive fields with odd-symmetry and even-symmetry [48]. Perna et al. showed sensitivity to phase congruency associated with edges and lines in human V1, but more importantly, they found that only higher-level areas can recognize phase types [49]. Henriksson et al. further employed functional magnetic resonance imaging (fMRI) to look for phase-sensitive neural responses in the human visual cortex and found sensitivity to the phase difference between spatial frequency components in all studied visual areas, all of which showed stronger responses for the stimuli with congruent phase structure [50]. Some results from this study are shown in Figure 3.
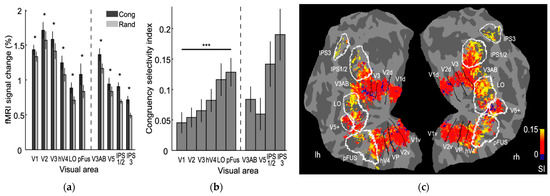
Figure 3.
Results of an fMRI study showing human visual cortex is tuned to phase congruency. (a) Mean fMRI signal changes for the congruent (Cong) and random (Rand) stimulus category blocks shown for regions of interest in various visual areas averaged from both hemispheres across all subjects. Asterisks indicate statistically significant differences between conditions (* p < 0.05); Wilcoxon signed rank test. (b) Congruency selectivity indices for the visual areas (*** p < 0.001). (c) Group-averaged congruency selectivity index maps for left and right hemispheres (reproduced with permission from Henriksson et al. [50]; Copyright 2009 Society for Neuroscience).
Computational studies also indicate that the detection of phase congruency probably involves higher-level visual cortex, even more than V1. For example, a natural image statistics study showed that pooling across multiple frequencies is statistically optimal to utilize the V1 output in V2 [51]. Thompson showed how image higher-order statistics can be modified so that they are sensitive to image phase structure only and that natural images have consistent higher-order statistical properties, differentiating them from random-phase images with the same power spectrum. Thus, it is possible that the sensitivity to relative phase can be determined directly by the higher-order structure of natural scenes [52].
2.3.2. Temporal Phase Congruency
For a significant portion of the time the visual system is experiencing non-static stimuli. In other words, it receives a sequence of images instead of a static one, even if we ignore the microsaccades of the eye [53]. Some experimental evidence suggests that feature tracking may be used by the human visual system [54,55]. Frequency analysis has been widely applied to motion perception. The usage of spatiotemporal filter-based models has been well established; that is, motion detectors can be constructed as spatiotemporal filters [56,57,58]. The transformation of such filters from the frequency space to the space-time space makes them more intuitive, which results in the spatiotemporal receptive field, oriented in space-time [59].
It has been experimentally shown that photoreceptors exploit nonlinear dynamics to selectively enhance and encode local phase congruency of temporal stimuli, and that to mitigate for the inherent sensitivity to noise of the local phase congruency, the photoreceptor nonlinear coding mechanisms are tuned to suppress random phase signals [60]. Another study showed that temporal processing by photoreceptors alone, in the absence of any spatial interactions, improved target detection from cluttered background dramatically, which is also explained by photoreceptor temporal non-linear dynamic models [61]. These findings are consistent with the well-established theory that non-linear processing by the visual system is matched to the statistics of natural scenes [62,63].
Del Viva et al. reported a strong dependency of perception of motion transparency on the relative phase of harmonic components of one-dimensional gratings. A feature-tracking model computing local energy function from a pair of space-time separable front stage filters combined with a battery of directional second stage mechanisms is able to quantitatively emulate the phase congruency dependence illusion and the insensitivity to overall phase [64]. Fleet et al. proposed a method to compute the 2D component velocity from image sequences using the first-order behavior of surfaces of constant local phase, resulting in high-resolution and robust velocity detection in the presence of contrast, scale, orientation, and speed [65].
2.4. Image Phase Congruency and Phase Correlation
A closely related concept arising from Fourier analysis is phase correlation, which involves computing the Fourier transforms of two images and then calculating their cross-power spectrum.
where is the inverse Fourier transform; and are the Fourier transforms for input signals and ; is the Hadamard product; is the conjugate of ; and ( and are the spatial coordinates and frequencies, respectively. The phase correlation contains information about the relative displacement between the two signals. By performing an inverse Fourier transform on the cross-power spectrum, a correlation function is obtained with a peak located at the relative displacement. The position of this peak indicates the relative shift between the two inputs. Phase correlation may be involved in certain perceptual processes, such as temporal correlations and feature integration [66], but studies are very limited, and the topic is not within the scope of this report.
Mathematically, both phase congruency and phase correlation use Fourier analysis to utilize the phase instead of the amplitude of images. Both involve computing Fourier transforms and manipulating phase values to extract meaningful information from signals and share the advantages of being insensitive to illumination and contrast variations, scales, orientations, and noises [3,67]. Phase-based methods’ insensitivities to image contrast play a critical role in many applications, as discussed in later sections. For example, phase congruency and phase correlation both reduce the impact of nonlinear radiometric differences due to nonlinearity in the imaging system, sensor characteristics, atmospheric conditions, or post-processing adjustments, which are frequently encountered in remote sensing and multi-modal image fusion [68].
One important distinction, as their definitions in Equations (3) and (4) illustrate, is that phase congruency reflects the local phase relationship of features within a single signal or image, while phase correlation indicates the spatial relationship between two similar signals or images. Another very important difference is that phase congruency is local, while phase correlation is global. Due to these differences, their applications in computer vision are also very different. Though both have been employed for image registration and motion detection [13,67,69], phase congruency essentially acts as local feature detectors and other feature-based processing is necessary, while phase correlation can directly provide the relative displacement between the two images as a global operator.
3. Computational Implementations of IPC
IPC is difficult to implement as originally defined by Morrone et al. (Equation (3)) [1]. For practical applications, various alternatives have been proposed for IPC since then [3,70,71,72]. The best known and most widely utilized implementation was by Kovesi [3], though it is not necessarily the most efficient one [71].
3.1. Relevant Computational Aspects for IPC Implementation
Fundamentally, IPC is a multiscale technique. Multiscale image analysis typically decomposes an image into multiple components, each corresponding to a different scale [73,74]. The decomposition can be carried out using Fourier transform, wavelet transform, principle or independent component analysis, curvelet transform, etc. [75,76,77,78]. The scales can range from very fine details to broader, more abstract patterns. At each scale, specific techniques are employed to extract relevant features or metrics. The extracted features from multiple scales are then combined or analyzed jointly to gain a comprehensive understanding of the image or dataset. The multiscale approach allows for the capture of both local and global information, enabling a more robust and accurate interpretation of the image. Understanding how IPC handles noise in images is another important computational aspect. Techniques to enhance noise robustness, such as preprocessing steps to reduce noise or post-processing steps to filter out spurious detection, are employed for IPC computation [79].
3.2. IPC Computation from FOURIER and Hilbert Transforms
Vanketash et al. proposed the first computationally friendly approach for IPC based on the finding that the points of maximum phase congruency are equivalent to peaks in the local energy function [70]. Wang et al. presented an implementation of IPC computation using 2D Hilbert transforms [80].
where is the input image without the DC component, while is the Hilbert transform. The phase congruency is directly proportional to the local energy function.
where is the phase congruency, while is the total number of Fourier components. Thus, phase congruency can be calculated by combining Equations (5) and (6).
It becomes clear that phase congruency is independent of the magnitude of the input signal. It is a unitless value within the range . This relationship is graphically illustrated in Figure 4. This is a very important property, as it is insensitive to image illumination and contrast variations. Thus phase congruency has built-in amplitude normalization, which is a strategy widely used in image processing such as normalized cross-correlation and other more sophisticated methods [81,82].
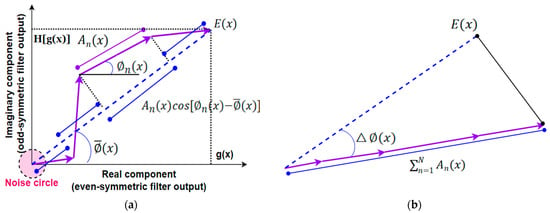
Figure 4.
Graphical illustration of the phase congruency of a signal, its local energy, and the amplitude sum of the Fourier components. (a) Total local energy (dashed blue line) and individual Fourier components as complex vectors (purple arrows) and their relationships. (b) Phase congruency inequality (the sum of the magnitudes of individual Fourier components is greater than or equal to the total local energy, where “equal to” happens if and only if phase angles of all components are perfectly aligned, that is, the average phase deviation is zero).
As the Hilbert transform is a multiplier operation, in the frequency domain it has the effect of shifting the phase of the negative and positive frequency components by and , respectively [83]. Thus, for 2D images, Equation (7) can be easily implemented by discrete Fourier transform.
3.3. IPC Computation from Wavelet Transform
In the mid-1990s, Kosevi proposed to use wavelet transform to compute phase congruency. It was implemented as part of his PhD dissertation [84]. This seminal work and later improvement reached a much wider audience when it was published as journal papers and open-source computer code [3,7]. The majority of the work using IPC for computer vision applications has adopted this approach. To preserve the phase information, linear-phase filters are necessary. As such, non-orthogonal wavelets in even-symmetric and odd-symmetric quadrature pairs are utilized.
where is the input signal, is the quadrature pair of even-symmetric and odd-symmetric filters at a scale , and is the output of the filter pair. More specifically, log-Gabor filters are used (illustrated in Figure 5), and the bandwidths of filters are set to constant at all scales. The corresponding amplitude and phase are as follows:

Figure 5.
Graphical illustrations of log-Gabor filters in the spatial and frequency domains.
The local energy is as follows:
And similar to Equation (7), the phase congruency is expressed as follows:
Computationally, Equation (11) is not stable if the filter outputs are all near zeros, which can be solved by adding a non-zero negligible value. In addition, to take into account noise in real signals and images, a noise compensation is added to the local energy term, which is equivalent to soft thresholding for denoise [85]. It should be noted that the distribution of filter responses should not be too narrow and that a uniform distribution is of particular significance as step discontinuities are common in images. A weighting function is added to devalue phase congruency at locations where the filter response spread is narrow. In addition, at a point of phase congruency, the cosine of the phase deviation should be large and the absolute value of the sine of the phase deviation should be small. Using their difference will increase phase congruency sensitivity. Taking all these factors into consideration, a practical computational definition of phase congruency is augmented as follows:
where is the smallest non-zero value for the computing platform, is the noise threshold, is the weight function, is for positive , 0 is for non-positive , and is the phase deviation function, which is calculated as follows:
For 2D images, Equation (12) can be expanded to the following expression:
where and are the total numbers of orientations and scales, respectively. The spread weighting function in 2D should be separable, and ideally it should be a 2D Gaussian function to minimize its impact on phase.
Obviously, a larger number of orientations and scales can produce more accurate IPC at the cost of more computations. However, today’s computing platforms support highly parallel processing, and if properly handled, the impact on processing speed can be significantly reduced.
3.4. IPC Computation from Monogenic Filters
Felsberg et al. proposed to generalize an analytical signal to two dimensions as a monogenic signal by using the Reisz transform and to use the monogenic filters termed Spherical Quadrature Filters (SQFs) to calculate the phase and orientation of such the signal [72,86]. This approach is more efficient than computing IPC from the wavelet transform described above.
The monogenic signal of an input is calculated as follows:
where and are the convolutional kernels of the Reisz transform. In spherical coordinates, the amplitude, local phase, and local orientation angles can be computed by the following expression:
where and are the local phase and local orientation, respectively. The triplet [ forms a set of monogenic SQFs.
The outputs from the SQFs at two different scales can be used to calculate the cosine of the angle between these vectors by the scalar product and the absolute value of the sine by the magnitude of the cross product. And IPC can be computed as follows:
Wang et al. proposed an alternative implementation for IPC using monogenic filters and experimentally showed that it consumed lower time and smaller memory space than IPC from log-Gabor filters and that SQFs can not only overcome the limitations of log-Gabor filters but also improve the location accuracy and noise robustness with comparable or better performance [87]. It should be noted that Kovesi also adopted monogenic filters in his later computer code implementation [88].
3.5. A unified Formulation for IPC Computations
Forero et al. proposed a unified formulation for IPC from both log-Gabor filters and monogenic filters by expressing it as the product of three different components [71].
where is the weight function based on frequency distribution, the phase congruency quantification function, and the noise compensation. The phase congruency quantification is the raw phase congruency computed as follows:
where is a hyper parameter for sensitivity tuning, and , as illustrated in Figure 4b, is approximated by the phase deviation instead of its cosine in Equation (13). This makes IPC more sensitive to phase deviations.
For IPC from log-Gabor filters, the noise compensation term is as follows:
And for IPC from monogenic filters, the following expression is used:
where is the Heaviside step function [89].
3.6. IPC for 3D Images
Feature detection via the local energy model underlying IPC has been applied to 3D images by using 3D Morlet wavelets [47]. IPC has also been extended to 3D images by using conic spread filters as the weighting function [90]. It has been applied to confocal microscopy, seismic data analysis, and crack detection in materials [90,91,92,93], which will be discussed in more detail in the next section.
4. Applications of Phase Congruency in Low-Level Computer Vision
As illustrated in Figure 6, IPC has been utilized in different ways for various computer vision applications, which can be simplified as three different approaches or some of their combinations, i.e., (1) some of the intermediate results of computing IPC, including the scale-orientation feature maps and/or noise statistics thereof; (2) IPC itself; (3) image features, statistics, or transformations derived from IPC. For computer vision applications, we label them as low-, mid-, and high-level. It should be noted this classification is not rigorous, and they approximately correspond to the operations of image-to-image, image-to-features, and features-to-analysis, respectively. Due to the complexity of computer vision, real applications usually consist of multiple tasks, and some of them may involve different levels of operations. And as expected, IPC applications usually involve employment of other image processing and computer vision techniques. We will discuss each application category in detail in the following sections.
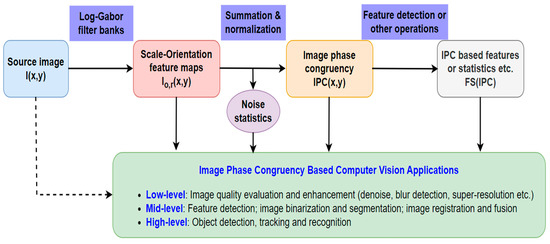
Figure 6.
Illustration of various approaches to IPC applications. IPC statistics are statistical values computed from IPC, such as average, standard deviation, percentile, and entropy, etc.
IPC has been widely adopted in various low-level computer visions, such as image denoise, image quality assessment, autofocus and blur detection, image super-resolution, and so on.
4.1. Image Denoise Using IPC
As noise is ubiquitous in real images, denoise is an essential low-level task in computer vision, usually as the first step of processing. The raw phase congruency, i.e., the phase congruency quantification function (the in Equation (19)), is sensitive to noise. As such, for practical implementation, noise compensation (the in Equation (19)) is utilized as the log-Gabor filters are suitable for noise detection [3]. Moreover, denoise is an inherent step in such IPC computational implementations.
A number of studies also combined IPC with other metrics or incorporated it with existing methods to gain better denoise performance. Huang et al. used the weighted sum of IPC of an input image and its intensity normalized version to detect noise in iris images [94]. Zhu et al. proposed to reduce speckle noise in ultrasound images by incorporating IPC and a feature asymmetry metric into the regularization term of optimization to distinguish features and speckle noise [95]. Luo et al. presented a nonconvex low rank model with IPC and overlapping group sparsity regularization for removing mixed Salt and Pepper noise and random value impulse noise in natural images to preserve local irregular structures [96]. Huang et al. used IPC to replace image gradients in the classic Perona–Malik anisotropic diffusion model to obtain improved edge-preserving noise removal in natural images [97]. Similarly, Gharshallah et al. also constructed a new filter based on a modified anisotropic diffusion combined with the IPC, which is incorporated in the diffusion function to enhance image edges while eliminating noise and texture background for lung CT images [98].
IPC has also been combined with an encoder–decoder neural network to reduce noise in low-resolution ultrasound images [18]. The encoder–decoder structure is also inherently multiscale and matches the characteristics of IPC.
4.2. Image Quality Evaluation Using IPC
The primary objective of Image Quality Evaluation (IQA) is to assess the quality of images by analyzing their characteristics and evaluating their overall quality [99]. There are two primary aspects of image quality, i.e., fidelity and intelligibility. Fidelity refers to the degree of deviation between the evaluated image and a standard or reference image. Intelligibility focuses on the ability of an image to provide information to humans and/or machines. IQA can be categorized as full-reference, reduced-reference, and no-reference methods based on the availability of reference images. There have been a large number of IPC-based image quality metrics proposed in the literature.
4.2.1. Full-Reference IQA
Liu et al. used the cross-correlation between the IPCs of two images to measure the similarity by dividing them into sub-blocks initially. It showed good sensitivity to various distortions such as noise, mean shift, contrast stretching, blur, and compression [100]. Zhang et al. proposed a Feature Similarity Image Quality (FSIM) index for full-reference IQA where IPC acts as the primary feature and the image gradient magnitude as the secondary feature. After obtaining the local quality map, IPC was again used as a weight function to derive a single quality score. Experiments on six benchmark IQA databases showed that FSIM achieved much higher consistency with subjective evaluations than other state-of-the-arts metrics [101,102,103,104,105].
Instead of using IPC as is, other studies made changes to how phase congruency information is employed or computed. Saha et al. utilized phase deviation-sensitive energy features instead of final IPC to form energy maps, which essentially set the noise compensation term in Equation (19) to a constant as noise should not be removed from IQA [106]. Recently, Zhang et al. proposed a symmetric phase congruency metric, which utilized the sign responses of neighboring pixels to find the symmetry phase congruency to evaluate image quality. They experimentally showed this modification is more sensitive to image structures and more robust to noises [107]. Chen et al. went further by replacing the log-Gabor filters in IPC by Gaussian functions and Laplacian of Gaussian signals to reduce the computational cost while improving performance [108].
4.2.2. Reduced-Reference and No-Reference IQA
Liu et al. proposed a reduced-reference IQA model by applying fractal analysis to IPC to extract features to construct a quality metric [9]. Many more studies were carried out on no-reference IQA using IPC.
Hassen et al. suggested a simple sharpness measure where sharpness is identified as strong local phase congruency, which correlates well with subjective quality evaluations [109]. Other researchers have adopted more sophisticated approaches in using IPC for no-reference IQA by applying some additional operations to IPC and/or combining IPC or IPC-based features with other inputs derived from the input image. Li et al. employed the mean and entropy of the IPC of an image and its mean gradient and entropy as inputs to a regression neural network to perform no-reference IQA that does not require training with subjective evaluations [110,111]. Zhao et al. fed the curvelet features of IPC and its local spectral entropy to a Support Vector Machine (SVM) to train an IQA prediction model [112]. Similarly, Miao et al. combined image gradients and the local binary pattern feature of its IPC as inputs for SVM training [113].
IPC based no-reference IQA for hyper-spectral images was also successfully demonstrated by Shao et al. to have excellent correlation with subjective image quality scores; they used IPC to obtain noise and blur characteristics for each single band in the hyper-spectral input [114].
A special-use case of no-reference IQA is for image reconstruction in computational imaging. The cost function for image reconstruction is essentially an image quality metric. The cost functions in computational imaging are usually defined on simple distance metrics [115]. Tian et al. proposed to construct cost functions using IPC for such applications and showed it can improve the quality of reconstructed images in some lensless imaging systems [116]. Figure 7 shows some image examples using the regularized mean square difference and the IPC-based cost function as the optimization objectives, respectively.

Figure 7.
Examples of image reconstruction in lensless imaging by different cost functions. From left to right: ground truth; reconstructed images with regularized mean square difference cost function and IPC-based cost function; Segment Anything Model (SAM) outputs of reconstructed images with regularized mean square difference cost function and with IPC-based cost function. In the last two columns, white boxes indicate failed segmentation in one of two cases, and blue boxes indicate failed segmentation in both cases (the reconstruction method was presented by Tian et al. [116]; SAM was described by Kirillov et al. [117]).
4.3. Autofocus and Blur Detection Using IPC
Autofocus is an import function in cameras and other imaging systems to capture high-quality images. Many digital imaging systems utilize image-based methods to achieve automatic focusing, termed passive autofocus [118]. It involves analyzing key features or contrast of an image to automatically adjust the lens, ensuring that the target is clearly imaged. One of the key issues in passive autofocus is blur detection, that is, how to judge whether an image is focused, which is usually accomplished by focus measures [119]. It should be noted that image blur degrades image quality, and thus some of the IQA methods inherently contain blur detection. In this section, blur detection is considered without taking into account other image quality factors.
Blur can disrupt the phase coherence in images; thus, IPC can be used for blur detection [10]. Tian et al. constructed an IPC-based focus measure and compared it with a number of commonly used focus measures derived from image variance, image gradient, image spectrum, and wavelet band ratio. The IPC-based focus measure is more robust for noisy imaging sensors in varying illuminations and has a great balance of defocus sensitivity and effective range [11], as illustrated in Figure 8. Tawari et al. presented a no-reference blur detector based on the statistical features of IPC and image gradient. Blur detection is achieved by approximating the functional relationship between these features using a feed-forward neural network [120,121]. Similarly, Liu et al. combined IPC and image gradient, weighed by a saliency map, to estimate image blur [122].
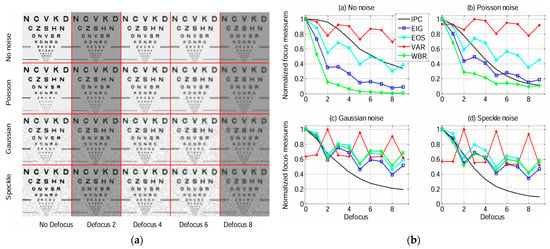
Figure 8.
Comparison of focus measures for autofocus. (a) Images with different types of noise and varying illumination/contrast. (b) Focus measure results for images in (a) (EIG: Energy of Image Gradient; EOS: Energy of Spectrum; VAR: Variance; WBR: Wavelet Band Ratio) (Reproduced with permission from Tian et al. [11]; Copyright 2011 Optical Society of America).
It should be noted that autofocus systems typically need to run in real time. The computational complexity of IPC-based blur detection is a significant burden for low-cost image systems, especially for consumer electronics.
4.4. Image Super-Resolution Using IPC
Image super-resolution aims to produce high-resolution images from low-resolution inputs. It utilizes algorithms and models to recover missing high-frequency details from low-resolution images, resulting in clearer and more detailed ones.
Wong et al. formulated image super-resolution as a constrained optimization problem using a third-order Markov prior model and adapted the priors using the phase variations of low-resolution mammograms [123]. Diskin et al. computed the phase congruency of each pixel’s neighborhood and produced nonlinearly interpolated high-resolution images for dense 3D reconstruction [124]. Zhou et al. proposed a complexity reduction method in multi-dictionary-based super-resolution using IPC. The IPC of a low image is extracted and binarized to distinct the importance of individual image patches. Important high-resolution patches are reconstructed by multi-dictionary-based super-resolution and the unimportant ones by single-dictionary method [125,126]. Nayak et al. put forward a regularization-based super-resolution method by imposing two regularization constraints of structural regularization and high frequency energy. Both terms are computed from IPC. Gradient descent method optimizes the regularized cost function [127].
IPC has also been combined with an encoder–decoder neural network to obtain high resolution ultrasound images from low-resolution ones [18].
4.5. Image Watermarking and Slicing Detection Using IPC
IPC has been used to detect the local feature regions of an image, and then a watermark is infused into it using different ways, such as adaptive alpha–beta blending [128,129,130]. Nayak et al. developed an adaptive digital watermarking algorithm in multi-parametric solution space for hiding the copyright information by means of IPC and singular value decomposition-supported information hiding technique [131].
Chen et al. proposed a scheme extracting image features from moments of wavelet characteristic functions and IPC for image splicing detection [132]. Uliyan et al. constructed an image forgery detection algorithm relying on blur metric evaluation and IPC [133]. Hansda et al. presented a hybrid copy–move image forgery detection method using phase adaptive spatio-structured SIFT [134] and the histogram of oriented IPC to localize forgery regions in the presence of intermediate and post-processing attacks [135]. In a more sophisticated vision-based document security system where the content and location of alterations can be detected, IPC was adopted at various stages of the pipeline [136].
5. Applications of Phase Congruency in Mid-Level Computer Vision
5.1. Feature Detection Using IPC
The definition of a feature can vary depending on the specific problem or application. In general, a feature is a distinctive or interesting part of an image. A crucial aspect of feature detection is its reproducibility; that is, the extracted features should be consistent across different images of the same scene. However, this is not without challenges due to noise, geometric and photometric variations arising from image sensors, and perspective and illumination variations. The origination of IPC was closely related to feature detection, especially due to its space-scale and contrast-invariant nature. It has a significant advantage over gradient-based methods as it is a dimensionless quantity invariant to changes in image brightness or contrast [2,3,7].
5.1.1. Edge Detection
A simple threshold value can be applied to the IPC map to obtain edges over a wide class of images, as shown in Kovesi’s seminal work [3,7,8]. Figure 9 shows an example of using such simple threshold-based IPC edge detection in comparison with several widely used traditional edge detectors, i.e., Sobel, Laplacian of Gaussian, Zero-crossing, and Canny [4,5,6,137].

Figure 9.
Comparison of various edge detectors. (a) Gray image. (b–f) Edge detection from Sobel, Laplacian of Gaussian, Zero-crossing, Canny, and IPC, respectively (Sobel, Laplacian of Gaussian, Zero-crossing, and Canny all used built-in functions in Matlab 2023 with default parameters, and IPC also used default parameters in Kovesi’s implementation, and a fixed threshold of 0.2 was applied to the IPC to obtain the edge map).
More sophisticated IPC-based edge detectors have been proposed. Xiang et al. combined ratio-based edge detector and IPC-based edge features as a SAR phase congruency (SAR-PC) edge detector [16]. Shi et al. proposed a conformal monogenic phase congruency-based edge detector that has a good analytical capability in the spatial domain for local structural features [138]. Yang et al. studied edge detection using modified differential IPC [139]. Huang et al. presented an edge detector using the point flow method based on the fusion of multi-scale phase congruency [140].
It should be noted that line detection has both similarities and differences with edge detection. In digital images, a line has two edges. Obviously, we can detect lines by two-stage methods, that is, detecting edges first and then employing post-processing to obtain lines. However, with the proper scales, IPC can directly extract lines in images in one step [141]. This can be seen in Figure 10, particularly obvious for the window structure on the left and the door on the right, where IPC edge detection produces lines while the other detectors mostly generate more complex edges.

Figure 10.
Comparison of various corner detectors. From top to bottom, image with no noise, image with Gaussian noise, and noisy image after median filtering. From left to right, gray image, results from Harris detector (purple dots), SURF detector (red dots), and IPC-based corner detector (blue dots) (Harris and SURF detectors used built-in functions in Matlab 2023 with default parameters, and IPC also used default parameters in Kovesi’s implementation, and a fixed threshold of 0.1 was applied to the minimum moment of IPC to obtain the corners).
5.1.2. Corner Detection
Similar to edge detection, Kovesi also used simple thresholding of the minimum moment of phase congruency for corner detection. Phase congruency was calculated independently in multiple orientations; its moments and their variations with orientations were obtained [8].
Figure 10 shows examples of such simple IPC corner detectors outperforming Harris and SURF detectors [142,143]. It should be noted that for this type of image with significant noise, geometric distortion, and/or non-uniform illumination, a few other widely utilized feature detectors, such as SIFT, ORB [144], and BRISK [145], behave similar to SURF. The robustness of such an IPC-based corner detector was utilized for visual servoing in robotic grasping applications [146].
5.1.3. Ridge Detection
Similar to line, ridge is also a compound feature that is not simply an edge. Micheal et al. proposed a method for automatic ridge detection in lunar images using phase symmetry and phase congruency [147]. Schnek et al. detected ridges, among other sophisticated features, by adjusting the scales of IPC to the proper value [141]. Rensenhofer et al. further developed a ridge detector that exploits the symmetry properties of directionally sensitive analyzing functions in multiscale systems in the framework of alpha-molecules, which is based on IPC [148].
5.2. Image Segmentation Using IPC
5.2.1. Image Binarization
Image binarization is a special case of segmenting an image as foreground and background, which is widely utilized in certain image processing applications, such as Optical Character Recognition (OCR).
Tian et al. calculated IPC for a camera-captured document image, from which connected component analysis was carried out to segment out a local window for each symbol; afterwards, a local threshold was calculated for each window to binarize the corresponding grayscale image patch (results illustrated in Figure 11a) [149]. Nafchi et al. initially also employed IPC to select Regions of Interest (ROI) of a document’s foreground [150], but later utilized IPC in more sophisticated fashion by combining the maximum moment of phase congruency covariance, a locally weighted mean phase angle, and a phase-preserved denoised image for ancient document binarization [151,152]. More recently, Bhat et al. proposed a model consisting of phase congruency and a Gaussian model for background elimination using the expectation maximization algorithm in inscription image preprocessing [153].
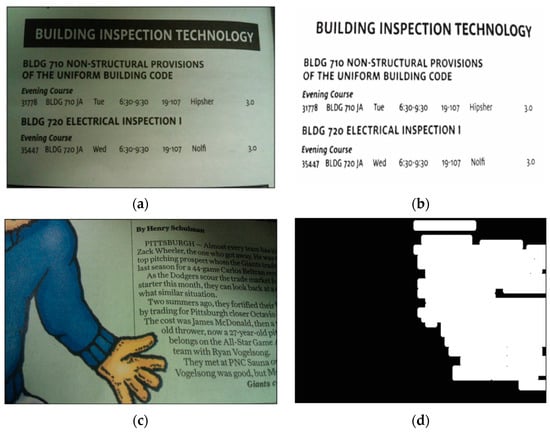
Figure 11.
Document image binarization and segmentation examples. (a,c) Camera-captured document images. (b) Binarization results of (a). (d) Text segmentation results of (c).
5.2.2. Image Segmentation
Tian et al. utilized IPC maps to help segment text and non-text areas of the grayscale document images [154]. Li et al. applied a contour-based method to IPC for object segmentation, in particular to reduce the impact of uneven illumination [155]. Figure 11b shows an example of such segmentation.
For medical image processing, Amin et al. employed IPC to segment blood vessels from fundus images [156]. Mapayi et al. combined IPC with fuzzy C-means and gray level co-occurrence matrix sum entropy for the segmentation of retinal vessels [12]. Azzopardi et al. fed IPC of ultrasound images into a Deep Neural Network (DNN) for carotid artery segmentation [157]. Sethi et al. used an edge-based and phase-congruent region enhancement method to segment cancerous regions in liver [158]. Szilagyi et al. utilized an IPC-based feature map to drive level-set segmentation for brain tumors in MRI images [159].
For remote sensing, Wang et al. proposed a high-resolution image segmentation method combining phase congruency with local homogeneity [160]. Zhang et al. used IPC for glacial lake segmentation in the Himalayas in SAR images [161].
5.3. Image Matching and Registration Using IPC
5.3.1. Same-Mode Image Registration
Zhang et al. proposed a registration method for images with affine transform relationships. They first used the Maximally Stable Extreme Region (MSER) pairs to carry out a course registration, then IPC-based feature points were obtained from the coarsely aligned image pairs to conduct another step of fine registration [162]. Fan et al. utilized the combination of SIFT, nonlinear diffusion, and IPC for SAR image registration, where IPC was mainly used for removal of erroneous key points [162]. Ma et al. used IPC and spatial constraints for SAR image registration [163]. Dalvi et al. utilized IPC feature points and Iterative Closest Point (ICP) matching for slice-to-volume MRI image registration [164].
5.3.2. Multi-Modal Image Registration
Yu et al. computed an oriented magnitude histogram and the orientation of the minimum moment of an IPC-based histogram and normalized and concatenated the two histograms as feature descriptors for general purpose multi-modal image registration [165].
For remote sensing, Ye et al. used IPC for registering optical and SAR images as well as LiDAR data [166]. Fan et al. combined nonlinear diffusion and phase congruency structural descriptors for optical and SAR image registration [167]. For the same purpose, Wang et al. proposed a uniform Harris feature detection method based on multi-moment of the IPC map and a local feature descriptor based on the histogram of IPC orientation on multi-scale amplitude index maps [168]. Xiang et al. proposed an improved IPC model specifically for SAR images while using the traditional IPC for optical image feature extractions [169]. Hu et al. presented a multispectral line segment matching algorithm based on IPC and multiple local homographies for image pairs captured by cross-spectrum sensors [170]. Further improvement has been explored by more sophisticated feature extractions from IPC or the intermediate output of IPC calculations for optical and SAR image registrations [23,171,172].
For biomedical imaging, Xia et al. applied a SIFT detector on IPC and coherent point drift for multi-modal image registration [173]. For the same purpose, Zhang et al. combined regional mutual information and IPC to utilize both structural and neighborhood information to obtain more robust and higher accuracy [174]. Later, a more sophisticated approach was developed. A Local Phase mean and Phase Congruency values of different Orientations (LPPCO) using filter banks at different orientations and frequencies are first computed. Then, a similarity measure using the normalized cross correlation (NCC) of the LPPCO descriptors is obtained, followed by a fast template matching for detecting correspondences between different images [174].
5.4. Image Fusion Using IPC
5.4.1. Same-Mode Image Fusion
Zhan et al. used IPC for multi-focus image fusion, where IPC was essentially used to replace focus measures to be more robust to noise [175]. Mei et al. decomposed images into a base layer and a detail layer and used total variation and IPC for the two layers, respectively, for multi-focus image fusion [176]. For the same purpose, Yazdi et al. proposed to combine IPC and Non-Subsampled Contourlet Transform (NSCT) [177,178]. Asadi et al. carried out multi-exposure image fusion via a pyramidal integration of IPC with the intensity-based maps [179].
5.4.2. Multi-Modal Image Fusion
Zhao et al. made use of IPC and its moments comparing the local cross-correlation of corresponding feature maps of input images and fused output to access its quality without a reference [180]. Zhang et al. proposed a multi-modal image fusion algorithm with the shiftable complex directional pyramid transform, where phase and magnitudes of complex coefficients are jointly considered [181].
For remote sensing, Huang et al. combined IPC and NSCT with entropy for fusing infrared and visible images [14]. For the same purpose, Liu et al. used IPC and a guided filter in Non-Subsampled Shearlet Transform (NSST) to fuse the images. And Wang et al. introduced quadtree decomposition and Bezier interpolation to extract crucial infrared features and proposed a saliency advertising IPC-based rule and local Laplacian energy-based rule for low- and high-pass sub-band fusion [182]. Chen et al. employed saliency detection and Gaussian filters to decompose source images into salient, detail, and base layers. Furthermore, they adopted a nonlinear function to calculate the weight coefficients to fuse salient layers and used an IPC-based fusion rule to fuse the detail layers so that the details could be retained better [183]. Fu et al. utilized IPC and a simplified Pulse-Coupled Neural Network (PCNN) as a basic fusion framework using the generalized intensity–hue–saturation transform and NSCT for SAR and optical image fusion [184]. Ye et al. presented an illumination-robust subpixel Fourier-based image correlation method using IPC. Both the magnitude and orientation information of IPC features were adopted to construct a structural image representation, which is embedded into the correlation scheme of the subpixel methods, either by linear phase estimation in the frequency domain or by kernel fitting in the spatial domain, achieving improved subpixel methods [185]. More recently, Fan et al. constructed pyramid features of orientated self-similarity for multi-modal remote sensing image matching, which integrates IPC into the self-similarity model for better encoding structural information [22]. They also proposed a modified uniform nonlinear diffusion-based Harris detector to extract local features, which employs IPC instead of image intensity for feature extraction and thus obtains well-distributed and highly repeatable feature points. A local structural descriptor, namely IPC order-based local structure, was designed for the extracted points [172].
For biomedical imaging, Dhengre et al. decomposed CT and MRI images into low and high frequency sub-bands by NSCT. The low frequency sub-bands were processed to extract IPC image features; the details were extracted from the high frequency sub-bands by using a guided filter to preserve the edge details [186]. Bhatnagar et al. also transformed the source images by NSCT and used two different fusion rules based on IPC and directive contrast to fuse low- and high-frequency coefficients [187]. Similarly, Zhu et al. presented a multi-modality medical image fusion method using IPC and local Laplacian energy. NSCT was first performed on image pairs to decompose them into high- and low-pass sub-bands. The high-pass sub-bands were integrated by an IPC-based fusion rule to enhance the detailed features; a local Laplacian energy-based fusion rule was used for low-pass sub-bands [188]. Arathi et al. used slantlet transform and IPC for CT and MIR image fusion [189]. Tang et al. proposed an IPC-based green fluorescent protein and phase contrast image fusion method in NSST. The source images were decomposed by NSST to multiscale and multidirection representations. The high-frequency coefficients are fused with IPC and parameter-adaptive PCNN, while the low-frequency coefficients are integrated through a local energy-based rule [190].
6. Applications of Phase Congruency in High-Level Computer Vision
6.1. Object Detection, Tracking, and Recognition Using IPC
Object detection, tracking, and recognition are often intertwined, and as such, we discuss them together.
Tian et al. proposed a simplified IPC computation scheme and applied it to detect endotracheal tubes in X-ray images [191]. Sattar et al. also used IPC for tooth detection in dental radiographs [192]. Rahmatullah et al. employed local features from an intensity image and global feature symmetry from its IPC for the detection of the stomach and the umbilical vein in fetal ultrasound abdominal images [193]. Verikas et al. combined IPC-based circular object detection, stochastic optimization-based object contour determination, and SVM as well as random forest classifications for Prorocentrum minimum cell recognition in phytoplankton images [15]. Teutsch et al. used IPC for automated recognition of bacteria colonies, as well as coded markers for both 3D object tracking and automated camera calibration [194].
Santhaseelan et al. developed a robust method to track objects of low resolution in wide-area aerial surveillance imagery using IPC and derived rotation invariant features [195]. Zhang et al. introduced IPC-based on sub-aperture coherent method and the differences of texture feature in sub-aperture to realize target detection in SAR images [196]. Zhang et al. computed three local features under the IPC framework using a set of quadrature pair filters and integrated them by score-level fusion to improve finger–knuckle–print recognition accuracy [197].
Not surprisingly, a number of face recognition algorithms have utilized IPC for its characteristics of being insensitive to illumination and image contrast variations. Bezalel et al. combined IPC and Gabor wavelet for efficient face recognition [198]. Basavaraj et al. achieved improved face recognition using neighborhood-defined modular IPC-based kernel principle component analysis [199]. Hamd et al. combined IPC, gradient edges, and their associate angles for face classification [200]. Essa et al. used local directional patterns of IPC for illumination-invariant face recognition [201,202]. While Koley et al. achieved illumination-invariant face recognition using a more sophisticated fused cross-lattice pattern of IPC [203].
6.2. Other High-Level Applications Using IPC
Cinar et al. utilized IPC to detect and quantify cracks and openings in quasi-brittle (granitic rock) and ductile (aluminium alloy) materials [93,204]. Deng et al. came up with iterative IPC for 3D volume CT images for crack detection, which is particularly effective to detect radially distributed cracks in cylindrical objects [205].
Bucie et al. introduced an IPC-based method to extract the facial features for facial expression recognition. It computes the IPC between the images, and analysis is performed in the frequency space where the similarity between image phases is measured to form discriminant features [206]. Others have extracted different features, such as binary patterns, from IPC for facial expression recognition [207,208].
7. Challenges for Practical Applications of IPC
As discussed above, there are many advantages of IPC, especially its insensitivity to image scale and orientation, image contrast, and illumination conditions. However, for wider adoption for practical applications, there are still a number of challenges.
7.1. Noise Sensitivity
In noisy images, IPC can lead to inaccurate or spurious feature detection. Though the impact of noise can be mitigated to a certain degree by subtracting a noise threshold in IPC computation as is typically done, doing so inevitably reduces the IPC sensitivity to high-frequency details in images. When noise reaches a significant level, as happens in active thermography images [209], this approach may fail to distinguish noise from high-frequency image features, especially when the number of scales is small. As demonstrated below, in the presence of heavy noise in thermograms, IPC performed much better in Figure 12 compared to Figure 13, where the noise is more severe, though the images were from the same application scenario.
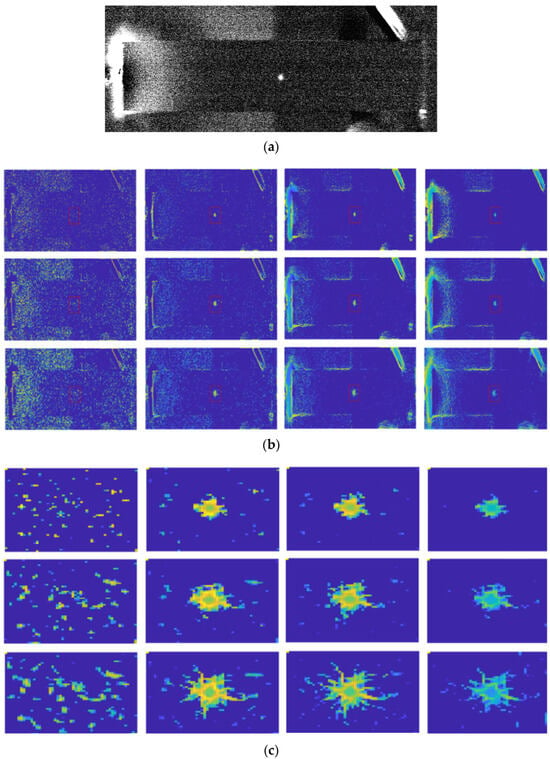
Figure 12.
IPC computed with different scales and orientations. (a) An active thermography image with significant noise. (b) Pseudo-color representations of IPCs computed from (a), from left to right: scales of 2, 4, 6, and 8, respectively; from top to bottom: orientation of 2, 4, and 6, respectively. (c) Magnified regions as indicated by red rectangles in (a), not in proportion.

Figure 13.
IPC computed with different scales and orientations. (a) An active thermography image with heavy noise. (b) Pseudo-color representations of IPCs computed from (a), from left to right: scales of 2, 4, 6, and 8, respectively; from top to bottom: orientation of 2, 4, and 6, respectively. (c) Magnified regions as indicated by red rectangles in (a), not in proportion.
7.2. Computational Complexity
Due to the multi-scale and multi-orientation nature of IPC computation, its computational cost via log-Gabor filter banks is very high, especially when large numbers of scales and orientations are used. Though the adoption of monogenic filters for computing IPC can alleviate the computational complexity to a certain degree [86,87], it is still not as simple as some other image transformations. This is a significant issue when dealing with large-size images or real-time applications. Furthermore, reduced IPC computations from monogenic filters come at the cost of reduced scale feature maps, which have been utilized in various IPC-based applications. Reducing the number of scales and orientations can improve the computational efficiency significantly, but at the cost of low IPC accuracy, as happens in any approximation problems (see examples in Figure 12 and Figure 13). Computational time is compared for different scales and orientations using image Figure 11a and its up-sampled version using Kovesi’s IPC implementation in Matlab 2023a. Computations were carried out in single thread on a personal computer using a single core of a 12th Gen Intel i7-12700K 3.6 GHz CPU with 16G memory, and the results are shown in Figure 14. Generally speaking, computational time increases linearly with the number of either scales or orientations, as well as the number of pixels in the image. As the number of pixels is the power function of resolution and dimension in images, IPC computational time can increase dramatically for high-resolution and high-dimension ones.
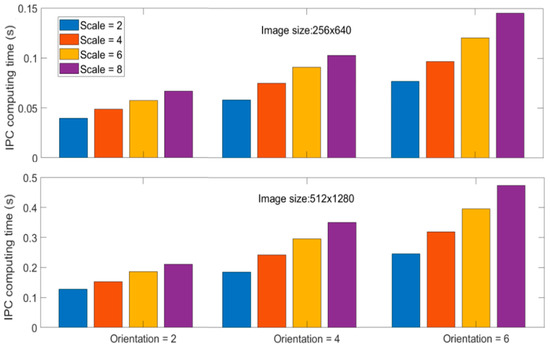
Figure 14.
IPC computing time for different scales, orientations, and image sizes. The image of size 256 × 640 is from Figure 11a, and the other image is its up-sampled version. Computations were carried out in single thread in Matlab 2023a on a personal computer using a single core of a 12th Gen Intel i7-12700K 3.6 GHz CPU with 16G memory. Each number is the median of 10 repeated identical runs to reduce the randomness of runtime due to various factors.
7.3. Parameter Tuning
IPC computation algorithms have multiple parameters that need to be adjusted for optimal performance. Determining the best parameter settings can be challenging and often requires extensive experimentation and fine-tuning. Though improvement has been made, it is still not fully resolved [71,210]. For example, in Figure 12, if we only consider the red rectangular ROI, a scale of 8 and orientation of 2 produce the cleanest IPC (i.e., the impact of noise is alleviated); when taking into other regions in the image, a scale of 6 and orientation of 4 probably produce the overall best IPC. In Figure 13, none of the combinations of scales and orientations produces very clean IPC; the overall best IPC is likely to be at scale 6 and orientation 2. Increasing the orientation number actually leads to some undesirable artifacts in IPC.
7.4. Integration with Other Image Features
In many cases, it may be desirable to combine IPC with other image features, such as color, texture, etc., to improve the performance of vision algorithms. However, effectively and efficiently fusing these features is challenging and requires considering their complementarity and redundancy [211]. By and large, such integration is still carried out case by case, i.e., feature engineering, based on the user’s domain expertise, as described in numerous examples in Section 4, Section 5 and Section 6.
8. Potential Improvement of IPC Using Deep Learning
As mentioned in previous sections, DNNs have been combined with IPC in various application studies. IPC has been combined with an encoder–decoder neural network to reduce noise in low-resolution ultrasound images and achieve super resolution [18]. IPC and its derived quantities have been employed as inputs to a regression neural network to perform no-reference IQA that does not require training with subjective evaluations [110,111]. Blur detection has been achieved by approximating the functional relationship between the statistical features of IPC using a feed-forward neural network [119,120]. IPC of ultrasound images has been fed into a deep neural network for carotid artery segmentation [157]. It has also been utilized together with a simplified PCNN as a basic fusion framework using the generalized intensity–hue–saturation transform and NSCT for SAR and optical image fusion [184]. A fused cross-lattice pattern of IPC has been used as input to a lightweight CNN for illumination-invariant face recognition [203]. These studies used IPC and/or its derivatives as inputs to some DNNs, and such integrations are not very tight; that is, IPC computation and DNN training are essentially separate and can be easily decoupled.
In recent years, DNNs have also been utilized to implement some traditional image transforms; this is very relevant to IPC as it is essentially a nonlinear image transform. For example, Guan et al. proposed an interpretable wavelet DNN integrating multi-resolution analysis at the core of its design. By using a lifting scheme, it can generate a wavelet representation and a neural network capable of learning wavelet coefficients in an end-to-end form [212]. And a number of other studies have come up with different ways to implement wavelet DNNs [213,214,215].
As the most widely employed IPC implementation is based on log-Gabor wavelets, we believe it is feasible to extend some of the aforementioned wavelet DNNs to compute IPC. And such IPC-DNNs can be concatenated or combined in parallel with other network modules for various computer vision applications. This approach is illustrated in Figure 15 using the widely used encoder–decoder UNet architecture [216,217]. In this paradigm, it is not difficult to build in noise removal schemes in the network adaptable to different noise levels and characteristics. In this framework, IPC computations are built into the DNN structure and may lead to more efficient and effective computer vision application pipelines than those simply concatenating them, as discussed above.
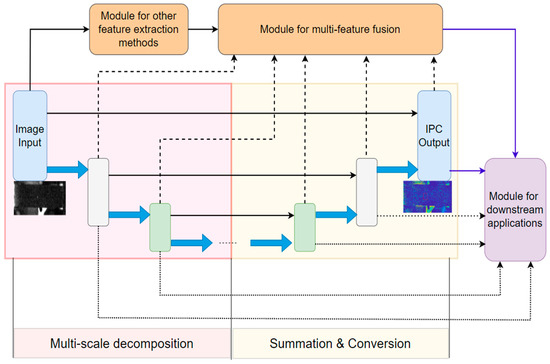
Figure 15.
Illustration of the concept of DNN-based IPC implementation and its tight integration with other network modules for various computer vision applications.
In a simpler approach, we can also utilize machine learning to learn the appropriate parameters for IPC computation for higher efficiency and better performance at runtime. For example, for specific applications, the optimal numbers of scales and orientations, as well as other parameters, can be learned in advance using the cost functions defined with desired application outputs. The structured forests for edge detection method can be viewed as a good example of this approach [218].
9. Conclusions
Image Phase Congruency (IPC) is closely connected to how the human visual system interprets and processes spatial frequency information. In this survey, evidence from biological vision research that supports the use of IPC by the human perceptual system is introduced. Next, the fundamental mathematical model and different computational implementations of IPC are described and compared. Various applications of IPC in computer vision, from low-, mid-, to high-level vision, have been comprehensively summarized and categorized. Multiple graphical examples are presented for some of these applications to highlight the benefits of using IPC. The current challenges in implementing IPC in practice and potential ways to improve its effectiveness using deep learning are also briefly discussed. This review is expected to introduce IPC to a wider audience and foster future work to overcome its limitations and expand its applications.
Author Contributions
Conceptualization, Y.T. and Y.T.; methodology, Y.T.; software, M.W. and Y.T.; validation, D.L. and Y.T.; formal analysis, Y.T.; investigation, Y.T.; resources, Y.T., X.Z. and Z.W.; data curation, Y.T.; writing—original draft preparation, Y.T. and M.W.; writing—review and editing, D.L. and Y.T.; visualization, Y.T.; supervision, X.Z. and Z.W.; project administration, Y.T.; funding acquisition, Y.T., X.Z. and Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the National Natural Science Foundation of China (Grant No. 62327808), the Shenzhen Fundamental Research Fund (Grant No. JCYJ20230808105212023), the Shenzhen University 2035 Program for Excellent Research (Grant No. 00000224), and the Equipment Development Project of Shenzhen University (Grant No. 868/03010315).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Data will be available upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Morrone, M.C.; Ross, J.; Burr, D.C.; Owens, R. Mach bands are phase dependent. Nature 1986, 324, 250–253. [Google Scholar] [CrossRef]
- Morrone, M.C.; Owens, R.A. Feature detection from local energy. Pattern Recognit. Lett. 1987, 6, 303–313. [Google Scholar] [CrossRef]
- Kovesi, P. Image features from phase congruency. Videre J. Comput. Vis. Res. 1999, 1, 1–26. [Google Scholar]
- Kittler, J. On the accuracy of the Sobel edge detector. Image Vis. Comput. 1983, 1, 37–42. [Google Scholar] [CrossRef]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Marr, D.; Hildreth, E. Theory of edge detection. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1980, 207, 187–217. [Google Scholar]
- Kovesi, P. Phase congruency: A low-level image invariant. Psychol. Res. 2000, 64, 136–148. [Google Scholar] [CrossRef] [PubMed]
- Kovesi, P. Phase congruency detects corners and edges. In Proceedings of the Australian Pattern Recognition Society Conference: DICTA, Sydney, Australia, 10–12 December 2003. [Google Scholar]
- Liu, D.; Xu, Y.; Quan, Y.; Le Callet, P. Reduced reference image quality assessment using regularity of phase congruency. Signal Process. Image Commun. 2014, 29, 844–855. [Google Scholar] [CrossRef]
- Wang, Z.; Simoncelli, E. Local phase coherence and the perception of blur. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2003; Volume 16. [Google Scholar]
- Tian, Y. Autofocus using image phase congruency. Opt. Express 2011, 19, 261–270. [Google Scholar] [CrossRef]
- Mapayi, T.; Tapamo, J.-R.; Viriri, S. Retinal vessel segmentation: A comparative study of fuzzy C-means and sum entropy information on phase congruency. Int. J. Adv. Robot. Syst. 2015, 12, 133. [Google Scholar] [CrossRef]
- Fan, J.; Wu, Y.; Wang, F.; Zhang, Q.; Liao, G.; Li, M. SAR image registration using phase congruency and nonlinear diffusion-based SIFT. IEEE Geosci. Remote Sens. Lett. 2014, 12, 562–566. [Google Scholar]
- Huang, X.; Qi, G.; Wei, H.; Chai, Y.; Sim, J. A novel infrared and visible image information fusion method based on phase congruency and image entropy. Entropy 2019, 21, 1135. [Google Scholar] [CrossRef]
- Verikas, A.; Gelzinis, A.; Bacauskiene, M.; Olenina, I.; Olenin, S.; Vaiciukynas, E. Phase congruency-based detection of circular objects applied to analysis of phytoplankton images. Pattern Recognit. 2012, 45, 1659–1670. [Google Scholar] [CrossRef]
- Xiang, Y.; Wang, F.; Wan, L.; You, H. SAR-PC: Edge detection in SAR images via an advanced phase congruency model. Remote Sens. 2017, 9, 209. [Google Scholar] [CrossRef]
- Liu, H.; Fu, Z.; Han, J.; Shao, L.; Hou, S.; Chu, Y. Single image super-resolution using multi-scale deep encoder–decoder with phase congruency edge map guidance. Inf. Sci. 2019, 473, 44–58. [Google Scholar] [CrossRef]
- Kim, R.; Kim, K.; Lee, Y. A multiscale deep encoder–decoder with phase congruency algorithm based on deep learning for improving diagnostic ultrasound image quality. Appl. Sci. 2023, 13, 12928. [Google Scholar] [CrossRef]
- da Fonseca, A.U.; Parreira, P.L.; da Silva Vieira, G.; Felix, J.P.; Conte, M.B.; Rabahi, M.F.; Soares, F. A novel tuberculosis diagnosis approach using feed-forward neural networks and binary pattern of phase congruency. Intell. Syst. Appl. 2024, 21, 200317. [Google Scholar] [CrossRef]
- Nunes, C.F.; Pádua, F.L. An orientation-robust local feature descriptor based on texture and phase congruency for visible-infrared image matching. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Wang, Z.; Feng, X.; Xu, G.; Wu, Y. A robust visible and infrared image matching algorithm for power equipment based on phase congruency and scale-invariant feature. Opt. Lasers Eng. 2023, 164, 107517. [Google Scholar] [CrossRef]
- Fan, J.; Xiong, Q.; Ye, Y.; Li, J. Combining phase congruency and self-similarity features for multimodal remote sensing image matching. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Jia, L.; Dong, J.; Huang, S.; Liu, L.; Zhang, J. Optical and SAR image registration based on multi-scale orientated map of phase congruency. Electronics 2023, 12, 1635. [Google Scholar] [CrossRef]
- Lv, W.; Ma, H.; Li, Y. A finger vein authentication system based on pyramid histograms and binary pattern of phase congruency. Infrared Phys. Technol. 2023, 132, 104728. [Google Scholar] [CrossRef]
- Moore, B.C.; Glasberg, B.R. Frequency discrimination of complex tones with overlapping and non-overlapping harmonics. J. Acoust. Soc. Am. 1990, 87, 2163–2177. [Google Scholar] [CrossRef] [PubMed]
- Moore, B.C.; Glasberg, B.R. Suggested formulae for calculating auditory-filter bandwidths and excitation patterns. J. Acoust. Soc. Am. 1983, 74, 750–753. [Google Scholar] [CrossRef] [PubMed]
- Bregman, A.S. Auditory Scene Analysis: The Perceptual Organization of Sound; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Sachs, M.B.; Nachmias, J.; Robson, J.G. Spatial-frequency channels in human vision. J. Opt. Soc. Am. 1971, 61, 1176–1186. [Google Scholar] [CrossRef] [PubMed]
- Stromeyer III, C.; Klein, S. Spatial frequency channels in human vision as asymmetric (edge) mechanisms. Vis. Res. 1974, 14, 1409–1420. [Google Scholar] [CrossRef] [PubMed]
- Campbell, F.W.; Robson, J.G. Application of Fourier analysis to the visibility of gratings. J. Physiol. 1968, 197, 551. [Google Scholar] [CrossRef] [PubMed]
- De Valois, R.L.; Albrecht, D.G.; Thorell, L.G. Spatial frequency selectivity of cells in macaque visual cortex. Vis. Res. 1982, 22, 545–559. [Google Scholar] [CrossRef] [PubMed]
- Graham, N.V.S. Visual Pattern Analyzers; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Duhamel, P.; Vetterli, M. Fast Fourier transforms: A tutorial review and a state of the art. Signal Process. 1990, 19, 259–299. [Google Scholar] [CrossRef]
- Davis, M.H.; Johnsrude, I.S. Hierarchical processing in spoken language comprehension. J. Neurosci. 2003, 23, 3423–3431. [Google Scholar] [CrossRef] [PubMed]
- Kruger, N.; Janssen, P.; Kalkan, S.; Lappe, M.; Leonardis, A.; Piater, J.; Rodriguez-Sanchez, A.J.; Wiskott, L. Deep hierarchies in the primate visual cortex: What can we learn for computer vision? IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 1847–1871. [Google Scholar] [CrossRef] [PubMed]
- Herrmann, B.; Johnsrude, I.S. Neural signatures of the processing of temporal patterns in sound. J. Neurosci. 2018, 38, 5466–5477. [Google Scholar] [CrossRef] [PubMed]
- Alais, D.; Newell, F.; Mamassian, P. Multisensory processing in review: From physiology to behaviour. Seeing Perceiving 2010, 23, 3–38. [Google Scholar] [CrossRef] [PubMed]
- Kim, R.S.; Seitz, A.R.; Shams, L. Benefits of stimulus congruency for multisensory facilitation of visual learning. PLoS ONE 2008, 3, e1532. [Google Scholar] [CrossRef] [PubMed]
- Ratliff, F. Mach Bands: Quantitative Studies on Neural Networks in the Retina; Holden-Day: San Francisco, CA, USA, 1965. [Google Scholar]
- von Békésy, G. Mach-and Hering-type lateral inhibition in vision. Vis. Res. 1968, 8, 1483–1499. [Google Scholar] [CrossRef] [PubMed]
- Ratliff, F. Why Mach bands are not seen at the edges of a step. Vis. Res. 1984, 24, 163–165. [Google Scholar] [CrossRef] [PubMed]
- Burr, D.C.; Morrone, M.C.; Spinelli, D. Evidence for edge and bar detectors in human vision. Vis. Res. 1989, 29, 419–431. [Google Scholar] [CrossRef] [PubMed]
- Concetta Morrone, M.; Burr, D.C. Feature detection in human vision: A phase-dependent energy model. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1988, 235, 221–245. [Google Scholar]
- Burr, D.C.; Morrone, M.C. Edge detection in biological and artificial visual systems. In Vision: Coding and Efficiency; Cambridge University Press: New York, NY, USA, 1990; p. 1. [Google Scholar]
- Ross, J.; Morrone, M.C.; Burr, D.C. The conditions under which Mach bands are visible. Vis. Res. 1989, 29, 699–715. [Google Scholar] [CrossRef] [PubMed]
- Ronse, C. On idempotence and related requirements in edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 484–491. [Google Scholar] [CrossRef]
- Pudney, C.; Kovesi, P.; Stretch, D. Surface detection using local energy for 3D confocal microscope images. Image Anal. 1994, 94, 68–73. [Google Scholar]
- Ringach, D.L. Spatial structure and symmetry of simple-cell receptive fields in macaque primary visual cortex. J. Neurophysiol. 2002, 88, 455–463. [Google Scholar] [CrossRef] [PubMed]
- Perna, A.; Tosetti, M.; Montanaro, D.; Morrone, M.C. BOLD response to spatial phase congruency in human brain. J. Vis. 2008, 8, 15. [Google Scholar] [CrossRef] [PubMed]
- Henriksson, L.; Hyvärinen, A.; Vanni, S. Representation of cross-frequency spatial phase relationships in human visual cortex. J. Neurosci. 2009, 29, 14342–14351. [Google Scholar] [CrossRef] [PubMed]
- Hyvärinen, A.; Gutmann, M.; Hoyer, P.O. Statistical model of natural stimuli predicts edge-like pooling of spatial frequency channels in V2. BMC Neurosci. 2005, 6, 12. [Google Scholar] [CrossRef] [PubMed]
- Thomson, M.G. Visual coding and the phase structure of natural scenes. Netw. Comput. Neural Syst. 1999, 10, 123. [Google Scholar] [CrossRef]
- Engbert, R.; Kliegl, R. Microsaccades keep the eyes’ balance during fixation. Psychol. Sci. 2004, 15, 431. [Google Scholar] [CrossRef] [PubMed]
- Cavanagh, P.; Mather, G. Motion: The long and short of it. Spat. Vis. 1989, 4, 103–129. [Google Scholar] [PubMed]
- Derrington, A.; Ukkonen, O. Second-order motion discrimination by feature-tracking. Vis. Res. 1999, 39, 1465–1475. [Google Scholar] [CrossRef] [PubMed]
- Adelson, E.H.; Bergen, J.R. Spatiotemporal energy models for the perception of motion. J. Opt. Soc. Am. A 1985, 2, 284–299. [Google Scholar] [CrossRef] [PubMed]
- Watson, A.B.; Ahumada, A.J. Model of human visual-motion sensing. J. Opt. Soc. Am. A 1985, 2, 322–342. [Google Scholar] [CrossRef] [PubMed]
- Van Santen, J.P.; Sperling, G. Elaborated reichardt detectors. J. Opt. Soc. Am. A 1985, 2, 300–321. [Google Scholar] [CrossRef] [PubMed]
- Burr, D.; Ross, J. Visual processing of motion. Trends Neurosci. 1986, 9, 304–307. [Google Scholar] [CrossRef]
- Friederich, U.; Billings, S.A.; Hardie, R.C.; Juusola, M.; Coca, D. Fly photoreceptors encode phase congruency. PLoS ONE 2016, 11, e0157993. [Google Scholar] [CrossRef] [PubMed]
- Brinkworth, R.S.; Mah, E.-L.; Gray, J.P.; O’Carroll, D.C. Photoreceptor processing improves salience facilitating small target detection in cluttered scenes. J. Vis. 2008, 8, 8. [Google Scholar] [CrossRef] [PubMed]
- Olshausen, B.A.; Field, D.J. Natural image statistics and efficient coding. Netw. Comput. Neural Syst. 1996, 7, 333. [Google Scholar] [CrossRef] [PubMed]
- Simoncelli, E.P.; Olshausen, B.A. Natural image statistics and neural representation. Annu. Rev. Neurosci. 2001, 24, 1193–1216. [Google Scholar] [CrossRef] [PubMed]
- Del Viva, M.M.; Morrone, M.C. A feature-tracking model simulates the motion direction bias induced by phase congruency. J. Vis. 2006, 6, 1. [Google Scholar] [CrossRef] [PubMed]
- Fleet, D.J.; Jepson, A.D. Computation of component image velocity from local phase information. Int. J. Comput. Vis. 1990, 5, 77–104. [Google Scholar] [CrossRef]
- Singer, W.; Gray, C. Visual feature integration and the temporal correlation hypothesis. Annu. Rev. Neurosci. 1995, 18, 555–586. [Google Scholar] [CrossRef] [PubMed]
- Foroosh, H.; Zerubia, J.B.; Berthod, M. Extension of phase correlation to subpixel registration. IEEE Trans. Image Process. 2002, 11, 188–200. [Google Scholar] [CrossRef] [PubMed]
- Geng, J.; Gan, W.; Xu, J.; Yang, R.; Wang, S. Support vector machine regression (SVR)-based nonlinear modeling of radiometric transforming relation for the coarse-resolution data-referenced relative radiometric normalization (RRN). Geo-Spat. Inf. Sci. 2020, 23, 237–247. [Google Scholar] [CrossRef]
- Eckstein, A.; Vlachos, P.P. Digital particle image velocimetry (DPIV) robust phase correlation. Meas. Sci. Technol. 2009, 20, 055401. [Google Scholar] [CrossRef]
- Venkatesh, S.; Owens, R. An energy feature detection scheme. In Proceedings of the IEEE International Conference on Image Processing, Singapore, 5–8 September 1989. [Google Scholar]
- Forero, M.G.; Jacanamejoy, C.A. Unified Mathematical Formulation of Monogenic Phase Congruency. Mathematics 2021, 9, 3080. [Google Scholar] [CrossRef]
- Felsberg, M.; Sommer, G. A new extension of linear signal processing for estimating local properties and detecting features. In Proceedings of the Mustererkennung DAGM-Symposium, Zurich, Switzerland, 16–18 September 2000; pp. 195–202. [Google Scholar]
- Lindeberg, T. Feature detection with automatic scale selection. Int. J. Comput. Vis. 1998, 30, 79–116. [Google Scholar] [CrossRef]
- Donoho, D.L.; Huo, X. Beamlets and Multiscale Image Analysis; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Zhang, D. Wavelet transform. In Fundamentals of Image Data Mining: Analysis, Features, Classification and Retrieval; Springer: Cham, Switzerland, 2019; pp. 35–44. [Google Scholar]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Lee, T.-W. Independent Component Analysis; Springer: Boston, MA, USA, 1998. [Google Scholar]
- Starck, J.-L.; Candès, E.J.; Donoho, D.L. The curvelet transform for image denoising. IEEE Trans. Image Process. 2002, 11, 670–684. [Google Scholar] [CrossRef] [PubMed]
- Lang, M.; Guo, H.; Odegard, J.E.; Burrus, C.S.; Wells, R.O. Noise reduction using an undecimated discrete wavelet transform. IEEE Signal Process. Lett. 1996, 3, 10–12. [Google Scholar] [CrossRef]
- Wang, K.; Xiao, P.; Feng, X.; Wu, G. Image feature detection from phase congruency based on two-dimensional Hilbert transform. Pattern Recognit. Lett. 2011, 32, 2015–2024. [Google Scholar] [CrossRef]
- Lyu, S.; Simoncelli, E.P. Nonlinear image representation using divisive normalization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008. [Google Scholar]
- Pizer, S.M.; Amburn, E.P.; Austin, J.D.; Cromartie, R.; Geselowitz, A.; Greer, T.; ter Haar Romeny, B.; Zimmerman, J.B.; Zuiderveld, K. Adaptive histogram equalization and its variations. Comput. Vis. Graph. Image Process. 1987, 39, 355–368. [Google Scholar] [CrossRef]
- Liu, Y.-W. Hilbert transform and applications. In Fourier Transform Applications; InTech: Rijeka, Croatia, 2012; pp. 291–300. [Google Scholar]
- Kovesi, P. Invariant Measures of Image Features from Phase Information; University of Western Australia: Crawley, WA, Australia, 1996. [Google Scholar]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Felsberg, M. Low-Level Image Processing with the Structure Multivector. PhD Thesis, Kiel University, Kiel, Germany, 2002. [Google Scholar]
- Wang, L.; Zhang, C.; Liu, Z.; Sun, B.; Tian, H. Image feature detection based on phase congruency by Monogenic filters. In Proceedings of the 26th Chinese Control and Decision Conference (CCDC2014), Changsha, China, 31 May–2 June 2014. [Google Scholar]
- Kovesi, P. Image Processing Based on Image Phase Information (Computer Code in Julia). Github. 2018. Available online: https://github.com/peterkovesi/ImagePhaseCongruency.jl (accessed on 1 April 2024).
- Weisstein, E.W. Heaviside Step Function. 2002. Available online: https://mathworld.wolfram.com/ (accessed on 1 April 2024).
- Kovesi, P.; Richardson, B.; Holden, E.-J.; Shragge, J. Phase-based image analysis of 3D seismic data. ASEG Ext. Abstr. 2012, 2012, 1–4. [Google Scholar] [CrossRef]
- Pudney, C.; Kovesi, P.; Robbins, B. A 3D local energy surface detector for confocal microscope images. In Proceedings of the Third Australian and New Zealand Conference on Intelligent Information Systems (ANZIIS-95), Perth, Australia, 27 November 1995. [Google Scholar]
- Shafiq, M.A.; Alaudah, Y.; AlRegib, G.; Deriche, M. Phase Congruency for image understanding with applications in computational seismic interpretation. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA 5–9 March 2017. [Google Scholar]
- Cinar, A.; Hollis, D.; Tomlinson, R.; Marrow, T.; Mostafavi, M. Application of 3D phase congruency in crack identification within materials. In Proceedings of the 11th International Conference on Advances in Experimental Mechanics, Exeter, UK, 5–7 September 2016. [Google Scholar]
- Huang, J.; Wang, Y.; Cui, J.; Tan, T. Noise removal and impainting model for iris image. In Proceedings of the International Conference on Image Processing (ICIP04), Singapore, 24–27 October 2004. [Google Scholar]
- Zhu, L.; Wang, W.; Qin, J.; Wong, K.-H.; Choi, K.-S.; Heng, P.-A. Fast feature-preserving speckle reduction for ultrasound images via phase congruency. Signal Process. 2017, 134, 275–284. [Google Scholar] [CrossRef]
- Luo, X.; Lv, J.; Wang, J. Nonconvex low rank approximation with phase congruency regularization for mixed noise removal. IEEE Access 2019, 7, 179538–179551. [Google Scholar]
- Huang, J.; Yang, F.; Chai, L. An image denoising method based on PM model with phase congruency. In Proceedings of the 1st International Conference on Industrial Artificial Intelligence (IAI), Shenyang, China, 23–27 July 2019. [Google Scholar]
- Ben Gharsallah, M.; Seddik, H. Phase congruency-based filtering approach combined with a convolutional network for lung CT image analysis. Imaging Sci. J. 2021, 69, 275–287. [Google Scholar] [CrossRef]
- Avcibas, I.; Sankur, B.; Sayood, K. Statistical evaluation of image quality measures. J. Electron. Imaging 2002, 11, 206–223. [Google Scholar]
- Liu, Z.; Laganiere, R. On the use of phase congruency to evaluate image similarity. In Proceedings of the IEEE International Conference on Acoustics Speech and Signal Processing, Toulouse, France, 14–19 May 2006. [Google Scholar]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A feature similarity index for image quality assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef]
- Kumar, R.; Moyal, V. Visual image quality assessment technique using FSIM. Int. J. Comput. Appl. Technol. Res. 2013, 2, 250–254. [Google Scholar] [CrossRef]
- Okarma, K. Weighted Feature Similarity–a nonlinear combination of gradient and phase congruency for full-reference image quality assessment. In Image Processing and Communications Challenges; Springer: Berlin/Heidelberg, Germany, 2013; pp. 187–194. [Google Scholar]
- Sara, U.; Akter, M.; Uddin, M.S. Image quality assessment through FSIM, SSIM, MSE and PSNR—A comparative study. J. Comput. Commun. 2019, 7, 8–18. [Google Scholar] [CrossRef]
- Chen, Q.; Xu, Y.; Li, C.; Liu, N.; Yang, X. An image quality assessment metric based on quaternion wavelet transform. In Proceedings of the IEEE International Conference on Multimedia and Expo Workshops (ICMEW), San Jose, CA, USA, 15–19 July 2013. [Google Scholar]
- Saha, A.; Wu, Q.J. Perceptual image quality assessment using phase deviation sensitive energy features. Signal Process. 2013, 93, 3182–3191. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, B.; Zhang, R.; Zhang, X. SPCM: Image quality assessment based on symmetry phase congruency. Appl. Soft Comput. 2020, 87, 105987. [Google Scholar] [CrossRef]
- Chen, C.; Mou, X. Phase congruency based on derivatives of circular symmetric Gaussian function: An efficient feature map for image quality assessment. EURASIP J. Image Video Process. 2023, 2023, 11. [Google Scholar] [CrossRef]
- Hassen, R.; Wang, Z.; Salama, M. No-reference image sharpness assessment based on local phase coherence measurement. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, TX, USA, 14–19 March 2010. [Google Scholar]
- Li, C.; Bovik, A.C.; Wu, X. Blind image quality assessment using a general regression neural network. IEEE Trans. Neural Netw. 2011, 22, 793–799. [Google Scholar] [PubMed]
- Li, C.; Ju, Y.; Bovik, A.C.; Wu, X.; Sang, Q. No-training, no-reference image quality index using perceptual features. Opt. Eng. 2013, 52, 057003. [Google Scholar] [CrossRef]
- Zhao, M.; Tu, Q.; Lu, Y.; Chang, Y.; Yang, B. No-reference image quality assessment based on phase congruency and spectral entropies. In Proceedings of the Picture Coding Symposium (PCS), Cairns, Australia, 31 May–3 June 2015. [Google Scholar]
- Miao, X.; Chu, H.; Liu, H.; Yang, Y.; Li, X. Quality assessment of images with multiple distortions based on phase congruency and gradient magnitude. Signal Process. Image Commun. 2019, 79, 54–62. [Google Scholar] [CrossRef]
- Shao, X.; Zhong, C. Phase congruency assesses hyperspectral image quality. In Proceedings of the Satellite Data Compression, Communications, and Processing VIII, San Diego, CA, USA, 12–13 August 2012. [Google Scholar]
- Mait, J.N.; Euliss, G.W.; Athale, R.A. Computational imaging. Adv. Opt. Photonics 2018, 10, 409–483. [Google Scholar] [CrossRef]
- Tian, Y.; Lu, D.; Deng, H.; Zhang, Z.; Zhong, X.; Wu, Z. Image reconstruction for lensless imaging using a phase congruency perception model. In Proceedings of the China Automation Congress (CAC), Chongqing, China, 17–19 November 2023. [Google Scholar]
- Kirillov, A.; Mintun, E.; Ravi, N.; Mao, H.; Rolland, C.; Gustafson, L.; Xiao, T.; Whitehead, S.; Berg, A.C.; Lo, W.-Y. Segment anything. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–3 October 2023. [Google Scholar]
- Zhang, Y.; Liu, L.; Gong, W.; Yu, H.; Wang, W.; Zhao, C.; Wang, P.; Ueda, T. Autofocus system and evaluation methodologies: A literature review. Sens. Mater. 2018, 30, 1165–1174. [Google Scholar]
- Tian, Y.; Shieh, K.; Wildsoet, C.F. Performance of focus measures in the presence of nondefocus aberrations. J. Opt. Soc. Am. A 2007, 24, B165–B173. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, S.; Shukla, V.; Biradar, S.; Singh, A. A blind blur detection scheme using statistical features of phase congruency and gradient magnitude. Adv. Electr. Eng. 2014, 2014, 521027. [Google Scholar] [CrossRef]
- Li, C.F.; Ju, Y.W.; Hou, Q.L. A novel no-reference perceptual blur metric. Appl. Mech. Mater. 2014, 568, 716–720. [Google Scholar] [CrossRef]
- Liu, Y.; Gu, K.; Zhai, G.; Liu, X.; Zhao, D.; Gao, W. Quality assessment for real out-of-focus blurred images. J. Vis. Commun. Image Represent. 2017, 46, 70–80. [Google Scholar] [CrossRef]
- Wong, A.; Scharcanski, J. Phase-adaptive superresolution of mammographic images using complex wavelets. IEEE Trans. Image Process. 2009, 18, 1140–1146. [Google Scholar] [CrossRef] [PubMed]
- Diskin, Y.; Asari, V.K. Dense point-cloud creation using superresolution for a monocular 3d reconstruction system. In Proceedings of the Visual Information Processing XXI, Baltimore, MD, USA, 24–25 April 2012. [Google Scholar]
- Zhou, Y.; Kwong, S.; Gao, W.; Zhang, X.; Wang, X. Complexity reduction in multi-dictionary based single-image superresolution reconstruction via pahse congtuency. In Proceedings of the International Conference on Wavelet Analysis and Pattern Recognition (ICWAPR), Guangzhou, China, 12–15 July 2015. [Google Scholar]
- Zhou, Y.; Kwong, S.; Gao, W.; Wang, X. A phase congruency based patch evaluator for complexity reduction in multi-dictionary based single-image super-resolution. Inf. Sci. 2016, 367, 337–353. [Google Scholar] [CrossRef]
- Nayak, R.; Patra, D. Super resolution image reconstruction using penalized-spline and phase congruency. Comput. Electr. Eng. 2017, 62, 232–248. [Google Scholar] [CrossRef]
- Koley, S. A feature adaptive image watermarking framework based on phase congruency and symmetric key cryptography. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 636–645. [Google Scholar] [CrossRef]
- Sinha Roy, S.; Basu, A.; Chattopadhyay, A. Intelligent Color Image Watermarking Using Phase Congruency. In Intelligence Enabled Research: DoSIER; Springer: Singapore, 2020; pp. 113–121. [Google Scholar]
- Basu, A.; Saha, A.; Das, J.; Roy, S.; Mitra, S.; Mal, I.; Sarkar, S.K. On the implementation of a digital watermarking based on phase congruency. In Proceedings of the 3rd International Conference on Frontiers of Intelligent Computing: Theory and Applications (FICTA), Bhubaneswar, Odisha, India, 14–15 November 2014. [Google Scholar]
- Nayak, M.R.; Bag, J.; Sarkar, S.; Sarkar, S.K. Hardware implementation of a novel water marking algorithm based on phase congruency and singular value decomposition technique. AEU-Int. J. Electron. Commun. 2017, 71, 1–8. [Google Scholar] [CrossRef]
- Chen, W.; Shi, Y.Q.; Su, W. Image splicing detection using 2D phase congruency and statistical moments of characteristic function. In Proceedings of the Security, Steganography, and Watermarking of Multimedia Contents IX, San Jose, CA, USA, 28 January 2007. [Google Scholar]
- Uliyan, D.M.; Jalab, H.A.; Wahab, A.W.A.; Shivakumara, P.; Sadeghi, S. A novel forged blurred region detection system for image forensic applications. Expert Syst. Appl. 2016, 64, 1–10. [Google Scholar] [CrossRef]
- Wu, J.; Cui, Z.; Sheng, V.S.; Zhao, P.; Su, D.; Gong, S. A comparative study of SIFT and its variants. Meas. Sci. Rev. 2013, 13, 122–131. [Google Scholar] [CrossRef]
- Hansda, R.; Nayak, R.; Balabantaray, B.K.; Samal, S. Copy-move image forgery detection using phase adaptive Spatio-structured SIFT algorithm. SN Comput. Sci. 2022, 3, 1–16. [Google Scholar] [CrossRef]
- Tian, Y.; Zhan, X.; Wu, C.; Ming, W. Self-verifiable paper documents and automatic content verification. In Proceedings of the Media Watermarking, Security, and Forensics, San Francisco, CA, USA, 2 February 2014. [Google Scholar]
- Berzins, V. Accuracy of Laplacian edge detectors. Comput. Vis. Graph. Image Process. 1984, 27, 195–210. [Google Scholar] [CrossRef]
- Shi, M.; Zhao, X.; Qiao, D.; Xu, B.; Li, C. Conformal monogenic phase congruency model-based edge detection in color images. Multimed. Tools Appl. 2019, 78, 10701–10716. [Google Scholar] [CrossRef]
- Yang, Y.; Kou, K.I.; Zou, C. Edge detection methods based on modified differential phase congruency of monogenic signal. Multidimens. Syst. Signal Process. 2018, 29, 339–359. [Google Scholar] [CrossRef]
- Huang, J.; Bai, B.; Yang, F. An effective salient edge detection method based on point flow with phase congruency. Signal Image Video Process. 2022, 16, 1019–1026. [Google Scholar] [CrossRef]
- Schenk, V.U.; Brady, M. Improving phase-congruency based feature detection through automatic scale-selection. In Proceedings of the Progress in Pattern Recognition, Speech and Image Analysis: 8th Iberoamerican Congress on Pattern Recognition (CIARP2003), Havana, Cuba, 26–29 November 2003. [Google Scholar]
- Harris, C.; Stephens, M. A combined corner and edge detector. In Proceedings of the Alvey Vision Conference, Manchester, UK, 1–2 September 1988. [Google Scholar]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Leutenegger, S.; Chli, M.; Siegwart, R.Y. BRISK: Binary robust invariant scalable keypoints. In Proceedings of the International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Burlacu, A.; Lazar, C. Image features detection using phase congruency and its application in visual servoing. In Proceedings of the 4th International Conference on Intelligent Computer Communication and Processing, Cluj-Napoca, Romania, 28–30 August 2008. [Google Scholar]
- Micheal, A.A.; Vani, K.; Sanjeevi, S. Automatic detection of ridges in lunar images using phase symmetry and phase congruency. Comput. Geosci. 2014, 73, 122–131. [Google Scholar] [CrossRef]
- Reisenhofer, R.; King, E.J. Edge, ridge, and blob detection with symmetric molecules. SIAM J. Imaging Sci. 2019, 12, 1585–1626. [Google Scholar] [CrossRef]
- Tian, Y.; Ming, W. Adaptive Binarization of Document Images Using Phase Congruency; Konica Minolta Technology Report; Konica Minolta: Tokyo, Japan, 2013; Volume 10. [Google Scholar]
- Nafchi, H.Z.; Kanan, H.R. A phase congruency based document binarization. In Proceedings of the Image and Signal Processing: 5th International Conference (ICISP), Agadir, Morocco, 28–30 June 2012. [Google Scholar]
- Nafchi, H.Z.; Moghaddam, R.F.; Cheriet, M. Phase-based binarization of ancient document images: Model and applications. IEEE Trans. Image Process. 2014, 23, 2916–2930. [Google Scholar] [CrossRef] [PubMed]
- Ziaei Nafchi, H.; Farrahi Moghaddam, R.; Cheriet, M. Historical document binarization based on phase information of images. In Proceedings of the Computer Vision-ACCV 2012 Workshops, Daejeon, Korea, 5–6 November 2013. [Google Scholar]
- Bhat, S.; Seshikala, G. Preprocessing and binarization of Inscription images using phase based features. In Proceedings of the Second International Conference on Advances in Electronics, Computers and Communications (ICAECC), Bangalore, India, 9–10 February 2018. [Google Scholar]
- Tian, Y. Document Image Binarization and Segmentation Using Image Phase Congruency. U.S. Patent 8,818,099, 26 August 2014. [Google Scholar]
- Li, Y.; Belkasim, S.; Chen, X.; Fu, X. Contour-based object segmentation using phase congruency. In Proceedings of the International Congress of Imaging Science ICIS, Rochester, NY, USA, 7–12 May 2006. [Google Scholar]
- Amin, M.A.; Yan, H. High speed detection of retinal blood vessels in fundus image using phase congruency. Soft Comput. 2011, 15, 1217–1230. [Google Scholar] [CrossRef]
- Azzopardi, C.; Hicks, Y.A.; Camilleri, K.P. Automatic carotid ultrasound segmentation using deep convolutional neural networks and phase congruency maps. In Proceedings of the IEEE 14th International Symposium on Biomedical Imaging (ISBI 2017), Melbourne, Australia, 18–21 April 2017. [Google Scholar]
- Sethi, G.; Saini, B.S.; Singh, D. Segmentation of cancerous regions in liver using an edge-based and phase congruent region enhancement method. Comput. Electr. Eng. 2016, 53, 244–262. [Google Scholar] [CrossRef]
- Szilágyi, T.; Brady, M.; Berényi, E. Phase congruency map driven brain tumour segmentation. In Proceedings of the Medical Imaging: Image Processing, Orlando, FL, USA, 24–26 February 2015. [Google Scholar]
- Wang, C.; Shi, A.; Zhang, X.; Liu, Q. Segmentation of high-resolution remote sensing image combining phase congruency with local homogeneity. Arab. J. Geosci. 2019, 12, 195. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, F.; Tian, B.; Liang, D. Using a phase-congruency-based detector for glacial lake segmentation in high-temporal resolution sentinel-1a/1b data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2771–2780. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Y.; Wang, L. Registration of images with affine geometric distortion based on maximally stable extremal regions and phase congruency. Image Vis. Comput. 2015, 36, 23–39. [Google Scholar] [CrossRef]
- Ma, W.; Wu, Y.; Liu, S.; Su, Q.; Zhong, Y. Remote sensing image registration based on phase congruency feature detection and spatial constraint matching. IEEE Access 2018, 6, 77554–77567. [Google Scholar] [CrossRef]
- Dalvi, R.; Abugharbieh, R. Fast feature based multi slice to volume registration using phase congruency. In Proceedings of the 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 21–24 August 2008. [Google Scholar]
- Yu, G.; Zhao, S. A new feature descriptor for multimodal image registration using phase congruency. Sensors 2020, 20, 5105. [Google Scholar] [CrossRef] [PubMed]
- Ye, Y.; Xiong, L.; Shan, J. Automated multi-source remote sensing image registration based on phase congruency. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 189–194. [Google Scholar] [CrossRef]
- Fan, J.; Wu, Y.; Li, M.; Liang, W.; Cao, Y. SAR and optical image registration using nonlinear diffusion and phase congruency structural descriptor. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5368–5379. [Google Scholar] [CrossRef]
- Wang, L.; Sun, M.; Liu, J.; Cao, L.; Ma, G. A robust algorithm based on phase congruency for optical and SAR image registration in suburban areas. Remote Sens. 2020, 12, 3339. [Google Scholar] [CrossRef]
- Xiang, Y.; Tao, R.; Wang, F.; You, H.; Han, B. Automatic registration of optical and SAR images via improved phase congruency model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5847–5861. [Google Scholar] [CrossRef]
- Hu, H.; Li, B.; Yang, W.; Wen, C.-Y. A novel multispectral line segment matching method based on phase congruency and multiple local homographies. Remote Sens. 2022, 14, 3857. [Google Scholar] [CrossRef]
- Xie, Z.; Zhang, W.; Wang, L.; Zhou, J.; Li, Z. Optical and SAR Image Registration Based on the Phase Congruency Framework. Appl. Sci. 2023, 13, 5887. [Google Scholar] [CrossRef]
- Fan, J.; Ye, Y.; Li, J.; Liu, G.; Li, Y. A novel multiscale adaptive binning phase congruency feature for SAR and optical image registration. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Xia, R.; Zhao, J.; Liu, Y. A robust feature-based registration method of multimodal image using phase congruency and coherent point drift. In Proceedings of the MIPPR 2013: Pattern Recognition and Computer Vision, Wuhan, China, 26–27 October 2013. [Google Scholar]
- Zhang, L.; Li, B.; Tian, L.; Zhu, W. LPPCO: A novel multimodal medical image registration using new feature descriptor based on the local phase and phase congruency of different orientations. IEEE Access 2018, 6, 71976–71987. [Google Scholar] [CrossRef]
- Zhan, K.; Li, Q.; Teng, J.; Wang, M.; Shi, J. Multifocus image fusion using phase congruency. J. Electron. Imaging 2015, 24, 033014. [Google Scholar] [CrossRef]
- Mei, J.; Nie, R.; Zhou, D.; Liu, D. Multi-focus Image Fusion Framework Using Total Variation and Phase Congruency. In Proceedings of the IEEE 4th International Conference on Computer and Communications (ICCC), Chengdu, China, 7–10 December 2018. [Google Scholar]
- Liu, D.; Zhou, D.; Nie, R.; Hou, R. Multi-focus image fusion based on phase congruency motivate pulse coupled neural network-based in NSCT domain. J. Comput. Appl. 2018, 38, 3006. [Google Scholar]
- Yazdi, M.; Ghasrodashti, E.K. Image fusion based on non-subsampled contourlet transform and phase congruency. In Proceedings of the 19th International Conference on Systems, Signals and Image Processing (IWSSIP), Vienna, Austria, 11–13 April 2012. [Google Scholar]
- Asadi, A.; Ezoji, M. Multi-exposure image fusion via a pyramidal integration of the phase congruency of input images with the intensity-based maps. IET Image Process. 2020, 14, 3127–3133. [Google Scholar] [CrossRef]
- Zhao, J.; Laganiere, R.; Liu, Z. Performance assessment of combinative pixel-level image fusion based on an absolute feature measurement. Int. J. Innov. Comput. Inf. Control 2007, 3, 1433–1447. [Google Scholar]
- Zhang, Q.; Ma, Z.; Wang, L. Multimodality image fusion by using both phase and magnitude information. Pattern Recognit. Lett. 2013, 34, 185–193. [Google Scholar] [CrossRef]
- Wang, S.; Shen, Y. Multi-modal image fusion based on saliency guided in NSCT domain. IET Image Process. 2020, 14, 3188–3201. [Google Scholar] [CrossRef]
- Chen, J.; Wu, K.; Cheng, Z.; Luo, L. A saliency-based multiscale approach for infrared and visible image fusion. Signal Process. 2021, 182, 107936. [Google Scholar] [CrossRef]
- Fu, Y.; Yang, S.; Li, Y.; Yan, H.; Zheng, Y. A novel SAR and optical image fusion algorithm based on an improved SPCNN and phase congruency information. Int. J. Remote Sens. 2023, 44, 1328–1347. [Google Scholar] [CrossRef]
- Ye, Z.; Tong, X.; Zheng, S.; Guo, C.; Gao, S.; Liu, S.; Xu, X.; Jin, Y.; Xie, H.; Liu, S. Illumination-robust subpixel Fourier-based image correlation methods based on phase congruency. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1995–2008. [Google Scholar] [CrossRef]
- Dhengre, N.; Upla, K.P.; Patel, H.; Chudasama, V.M. Bio-medical image fusion based on phase-congruency and guided filter. In Proceedings of the Fourth International Conference on Image Information Processing (ICIIP), Shimla, India, 21–23 December 2017. [Google Scholar]
- Bhatnagar, G.; Wu, Q.J.; Liu, Z. Directive contrast based multimodal medical image fusion in NSCT domain. IEEE Trans. Multimed. 2013, 15, 1014–1024. [Google Scholar] [CrossRef]
- Zhu, Z.; Zheng, M.; Qi, G.; Wang, D.; Xiang, Y. A phase congruency and local Laplacian energy based multi-modality medical image fusion method in NSCT domain. IEEE Access 2019, 7, 20811–20824. [Google Scholar] [CrossRef]
- Arathi, T.; Parameswaran, L. An image fusion technique using Slantlet transform and phase congruency for MRI/CT. Int. J. Biomed. Eng. Technol. 2013, 13, 87–103. [Google Scholar] [CrossRef]
- Tang, W.; Liu, Y.; Cheng, J.; Li, C.; Peng, H.; Chen, X. A phase congruency-based green fluorescent protein and phase contrast image fusion method in nonsubsampled shearlet transform domain. Microsc. Res. Tech. 2020, 83, 1225–1234. [Google Scholar] [CrossRef] [PubMed]
- Tian, X.; Yang, X. A new localized phase congruency based object detector for X-ray images. In Proceedings of the International Conference on Machine Learning and Cybernetics, Baoding, China, 12–15 July 2009. [Google Scholar]
- Sattar, F.; Karray, F. Dental X-ray image segmentation and object detection based on phase congruency. In Proceedings of the 9th International Conference on Image Analysis and Recognition (ICIAR2012), Aveiro, Portugal, 25–27 June 2012. [Google Scholar]
- Rahmatullah, B.; Papageorghiou, A.T.; Noble, J.A. Integration of local and global features for anatomical object detection in ultrasound. In Proceedings of the 15th International Conference on Medical Image Computing and Computer-Assisted Intervention–(MICCAI2012), Nice, France, 1–5 October 2012. [Google Scholar]
- Teutsch, C.; Berndt, D.; Trostmann, E.; Weber, M. Real-time detection of elliptic shapes for automated object recognition and object tracking. In Proceedings of the Machine Vision Applications in Industrial Inspection XIV, San Jose, CA, USA, 16–17 January 2006. [Google Scholar]
- Santhaseelan, V.; Asari, V. Tracking in wide area motion imagery using phase vector fields. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Portland, OR, USA, 23–28 June 2013. [Google Scholar]
- Zhang, Z.; Wang, X.; Xu, L. Target detection in sar images based on sub-aperture coherence and phase congruency. Intell. Autom. Soft Comput. 2012, 18, 831–843. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Zhang, D.; Guo, Z. Phase congruency induced local features for finger-knuckle-print recognition. Pattern Recognit. 2012, 45, 2522–2531. [Google Scholar] [CrossRef]
- Bezalel, E.; Efron, U. Efficient face recognition method using a combined phase congruency/Gabor wavelet technique. In Proceedings of the Optical Information Systems III, San Diego, CA, USA, 31 July–4 August 2005. [Google Scholar]
- Basavaraj, G.; Reddy, G. An Improved Face Recognition Using Neighborhood Defined Modular Phase Congruency Based Kernel PCA. Int. J. Eng. Res. Appl. 2012, 2, 528–535. [Google Scholar]
- Hamd, M.H.; Rasool, R.A. Towards better performance: Phase congruency based face recognition. TELKOMNIKA (Telecommun. Comput. Electron. Control) 2020, 18, 3041–3049. [Google Scholar] [CrossRef]
- Essa, A.E.; Asari, V.K. Local directional pattern of phase congruency features for illumination invariant face recognition. In Proceedings of the Optical Pattern Recognition XXV, Baltimore, MD, USA, 5–9 May 2014. [Google Scholar]
- Kusuma, H.; Soeprijanto, A. Face recognition against varying lighting conditions using oriented phase congruency image features. J. Theor. Appl. Inf. Technol. 2016, 88, 115–122. [Google Scholar]
- Koley, S.; Roy, H.; Dhar, S.; Bhattacharjee, D. Illumination invariant face recognition using fused cross lattice pattern of phase congruency (FCLPPC). Inf. Sci. 2022, 584, 633–648. [Google Scholar] [CrossRef]
- Cinar, A.; Barhli, S.; Hollis, D.; Flansbjer, M.; Tomlinson, R.; Marrow, T.; Mostafavi, M. An autonomous surface discontinuity detection and quantification method by digital image correlation and phase congruency. Opt. Lasers Eng. 2017, 96, 94–106. [Google Scholar] [CrossRef]
- Deng, X.; Zuo, F.; Li, H. Cracks detection using iterative phase congruency. J. Math. Imaging Vis. 2018, 60, 1065–1080. [Google Scholar] [CrossRef]
- Buciu, I.; Nafornita, I. Feature extraction through cross-phase congruency for facial expression analysis. Int. J. Pattern Recognit. Artif. Intell. 2009, 23, 617–635. [Google Scholar] [CrossRef]
- Shojaeilangari, S.; Yau, W.-Y.; Li, J.; Teoh, E.-K. Feature extraction through binary pattern of phase congruency for facial expression recognition. In Proceedings of the 12th International Conference on Control Automation Robotics & Vision (ICARCV), Guangzhou, China, 5–7 December 2012. [Google Scholar]
- Shojaeilangari, S.; Yau, W.-Y.; Teoh, E.-K. A novel phase congruency based descriptor for dynamic facial expression analysis. Pattern Recognit. Lett. 2014, 49, 55–61. [Google Scholar] [CrossRef]
- Xie, J.; Zeng, Z.; Ma, Y.; Pan, Y.; Wu, X.; Han, X.; Tian, Y. Defect recognition in sonic infrared imaging by deep learning of spatiotemporal signals. Eng. Appl. Artif. Intell. 2024, 133, 108174. [Google Scholar] [CrossRef]
- Forero, M.G.; Jacanamejoy, C.A.; Machado, M.; Penagos, K.L. Generalized Quantification Function of Monogenic Phase Congruency. Mathematics 2023, 11, 3795. [Google Scholar] [CrossRef]
- Dai, Y.; Gieseke, F.; Oehmcke, S.; Wu, Y.; Barnard, K. Attentional feature fusion. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Virtual conference, 5–9 January 2021; pp. 3560–3569. [Google Scholar]
- Rodriguez, M.X.B.; Gruson, A.; Polania, L.; Fujieda, S.; Prieto, F.; Takayama, K.; Hachisuka, T. Deep adaptive wavelet network. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Snowmass Village, CO, USA, 2–5 March 2020. [Google Scholar]
- Liu, P.; Zhang, H.; Lian, W.; Zuo, W. Multi-level wavelet convolutional neural networks. IEEE Access 2019, 7, 74973–74985. [Google Scholar] [CrossRef]
- Guan, J.; Lai, R.; Xiong, A. Wavelet deep neural network for stripe noise removal. IEEE Access 2019, 7, 44544–44554. [Google Scholar] [CrossRef]
- Chen, T.; Lin, L.; Zuo, W.; Luo, X.; Zhang, L. Learning a wavelet-like auto-encoder to accelerate deep neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI2015), Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Cao, Z.; Zeng, Z.; Xie, J.; Zhai, H.; Yin, Y.; Ma, Y.; Tian, Y. Diabetic plantar foot segmentation in active thermography using a two-stage adaptive gamma transform and a deep neural network. Sensors 2023, 23, 8511. [Google Scholar] [CrossRef] [PubMed]
- Dollár, P.; Zitnick, C.L. Structured forests for fast edge detection. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).