Research on Predicting the Safety Factor of Plain Shotcrete Support in Laneways Based on BO-CatBoost Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Definition of Safety Factor
2.2. CRITIC Method
2.3. CatBoost
2.4. Bayesian Optimization Algorithm
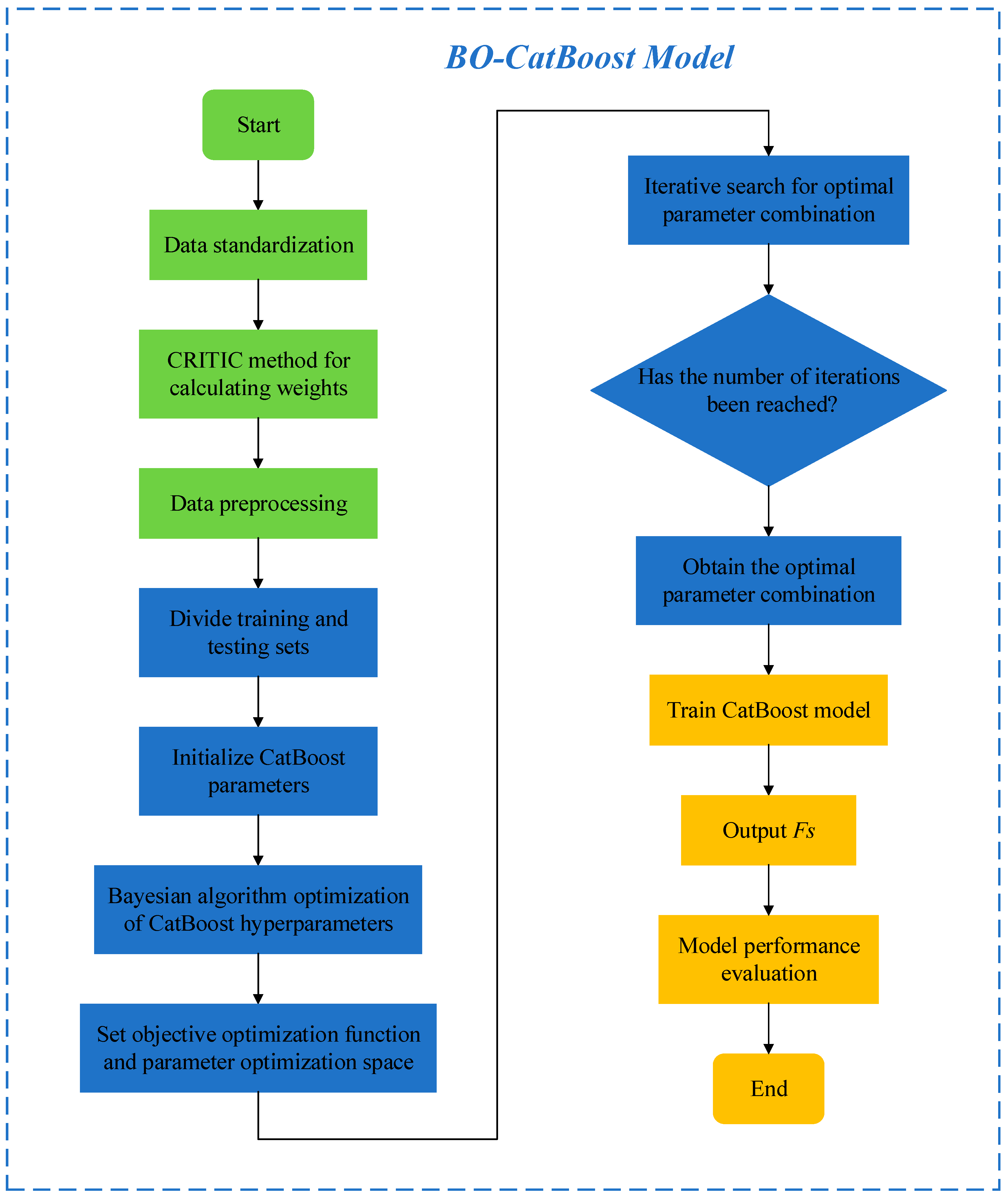
3. Establishment of BO-CatBoost Model
3.1. CRITIC Method for Data Preprocessing
- (1)
- The evaluation indicators of safety factor samples form the initial indicator data matrix .
- (2)
- The data are standardized according to Formulas (3) and (4) .
- (3)
- The comprehensive information contained in each indicator is calculated using Formulas (5)–(7).
- (4)
- According to the comprehensive information, the comprehensive weight of each evaluation indicator is calculated using Formula (8).
- (5)
- The processed data are obtained according to Formula (9).
3.2. BO-CatBoost Model
4. Application: Case Studies
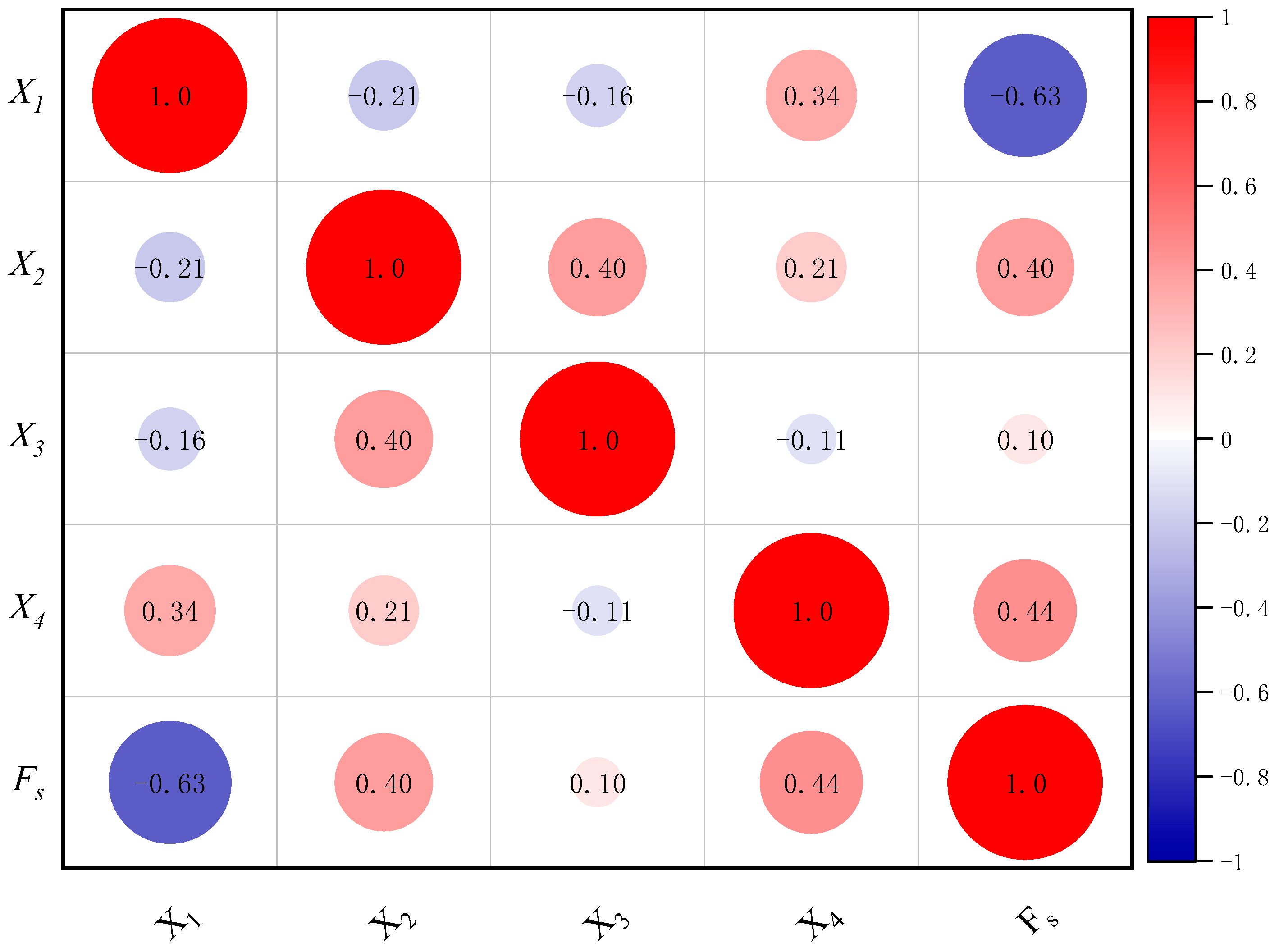
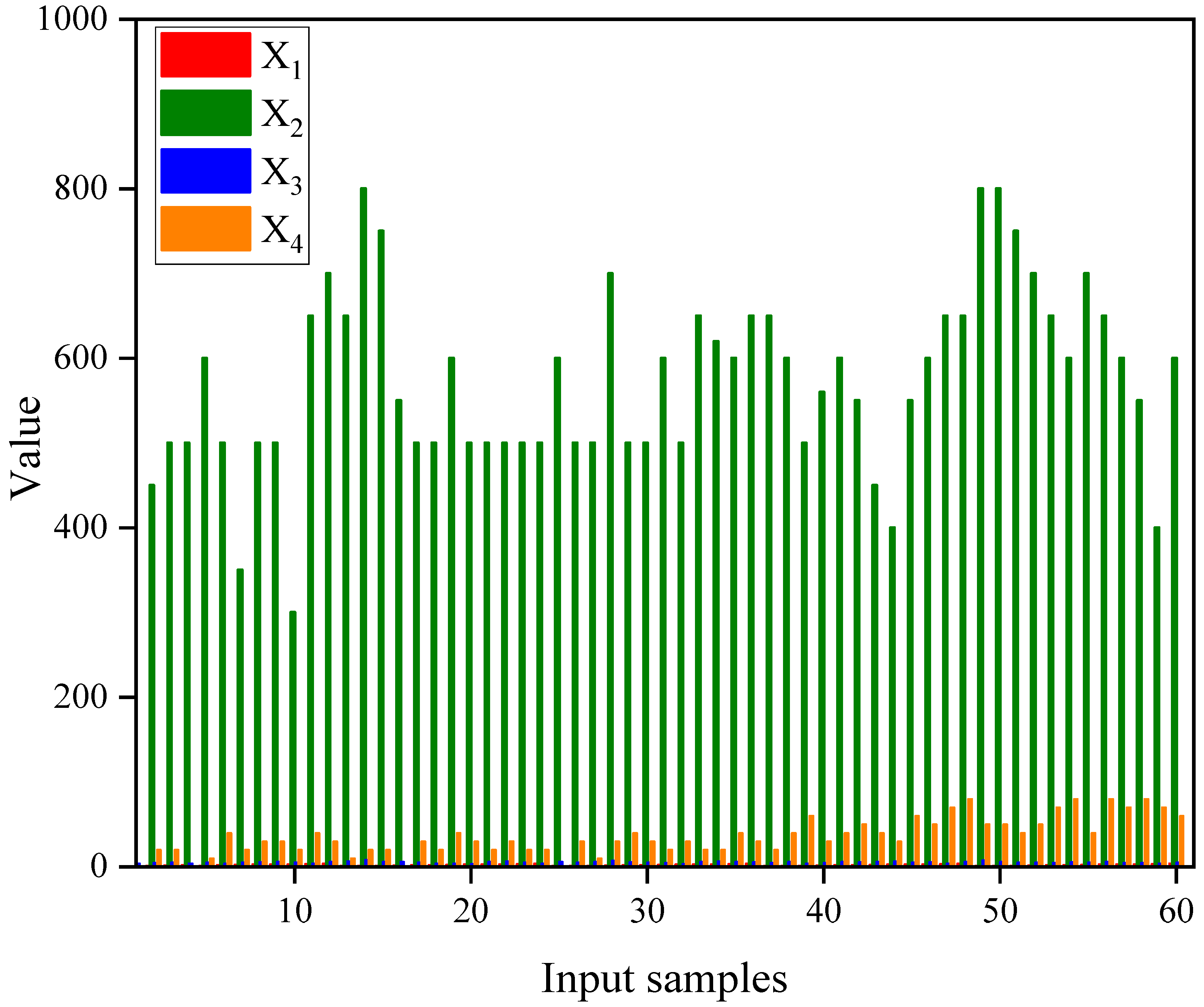
4.1. Establishment of Safety Factor Evaluation Indicators
4.2. Optimization Results of Bayesian Algorithm
4.3. Comparison Algorithm Selection
4.3.1. SVR
4.3.2. RF
4.4. Selection of Model Performance Evaluation Indicators
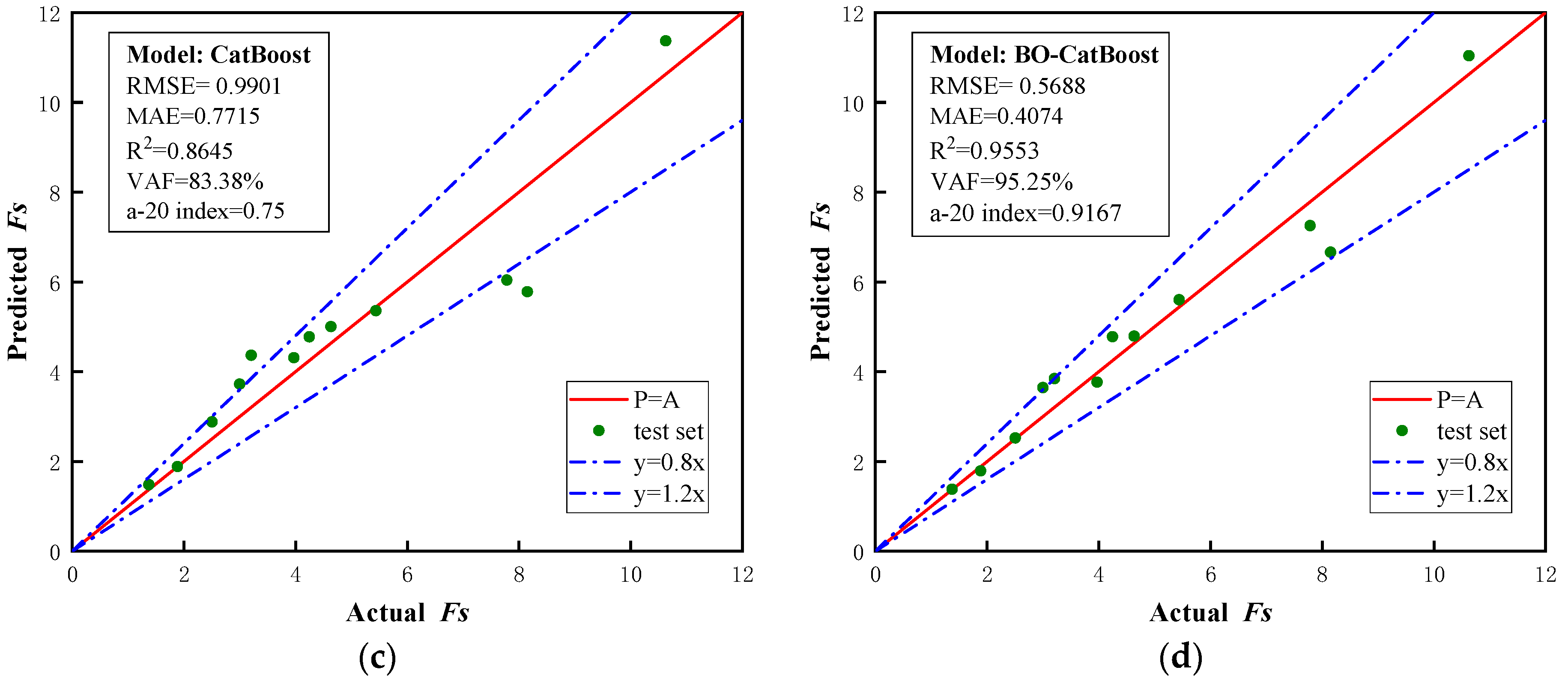
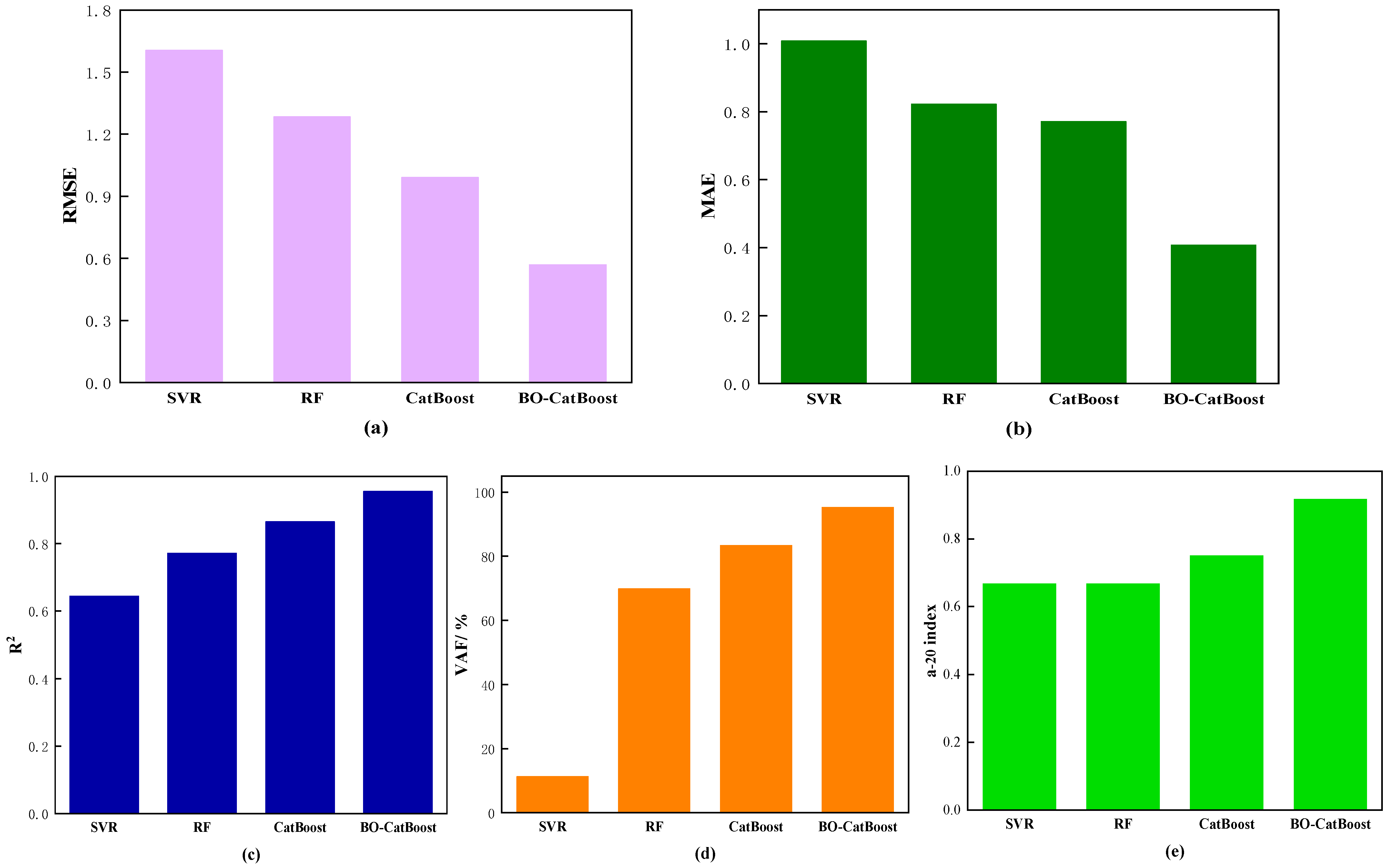
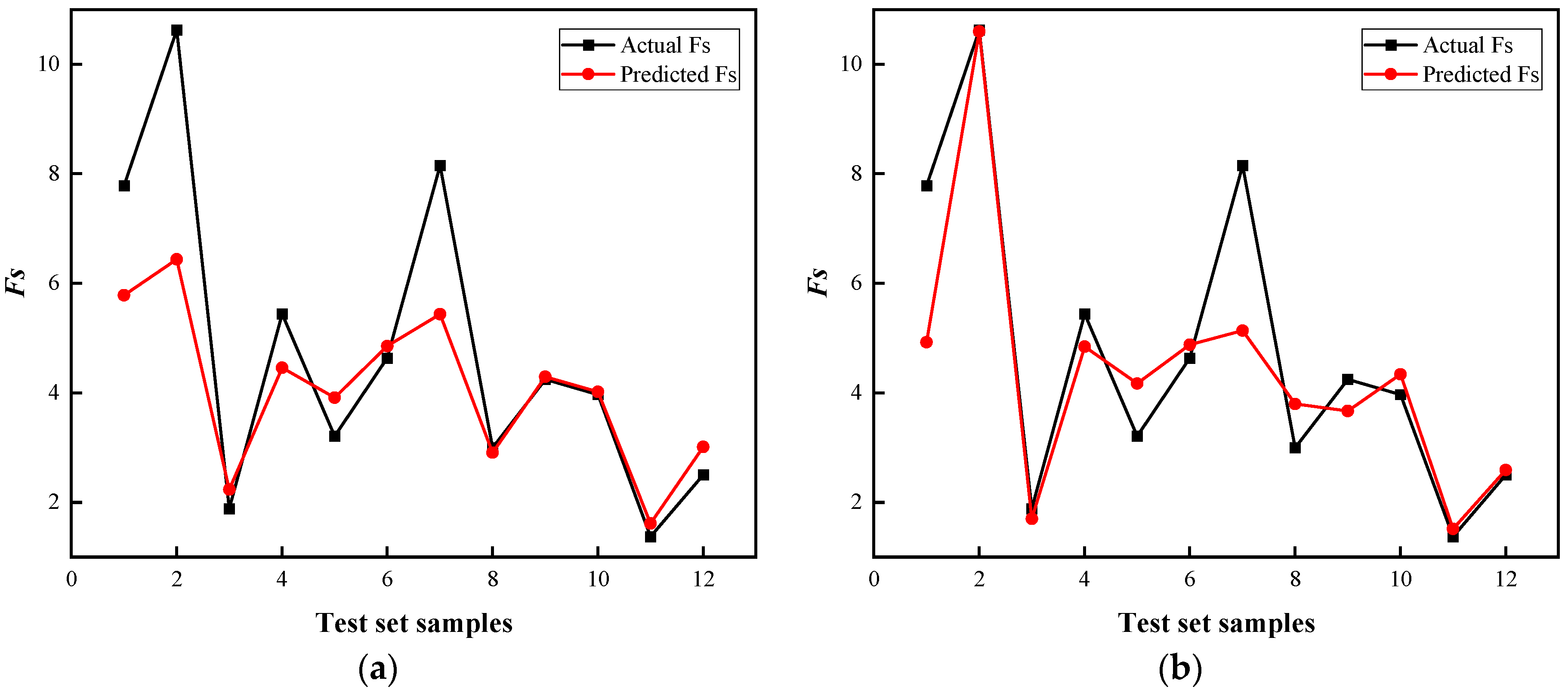
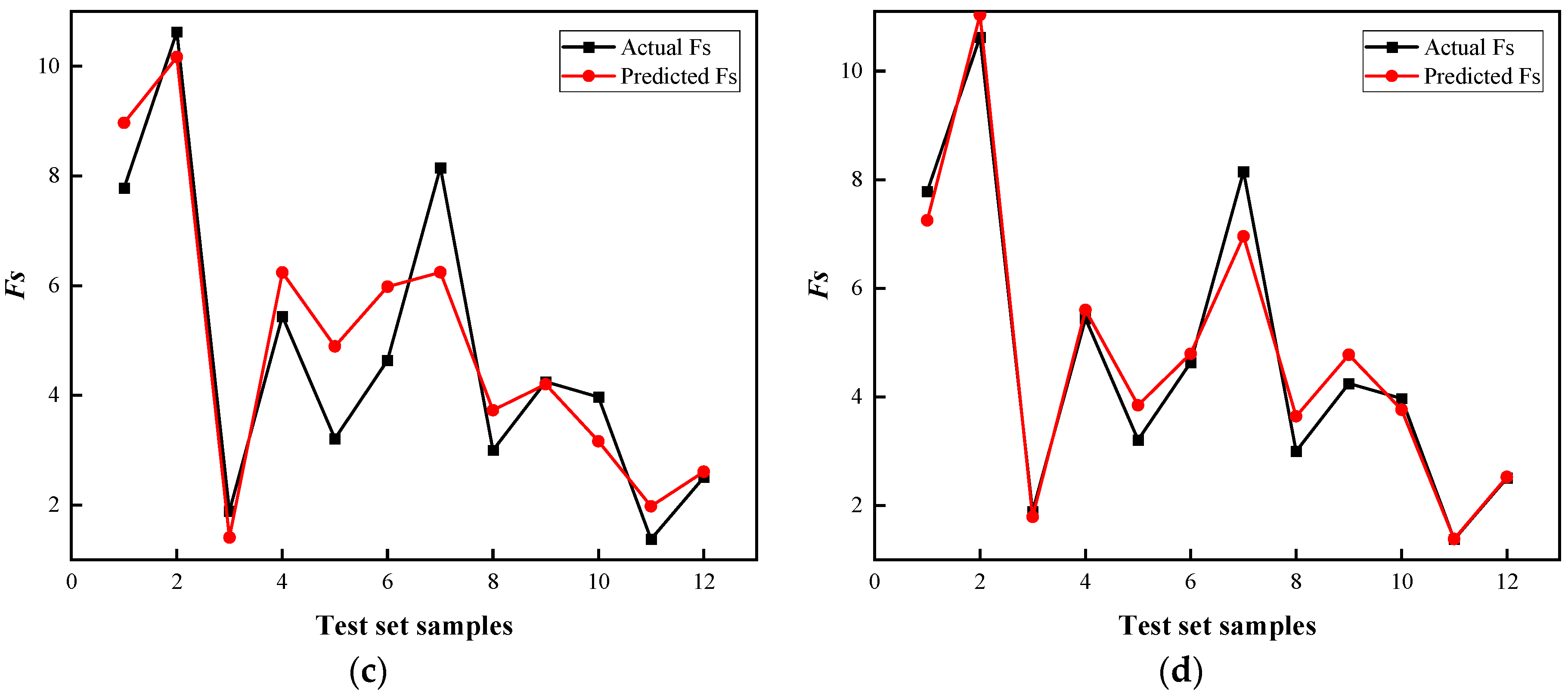
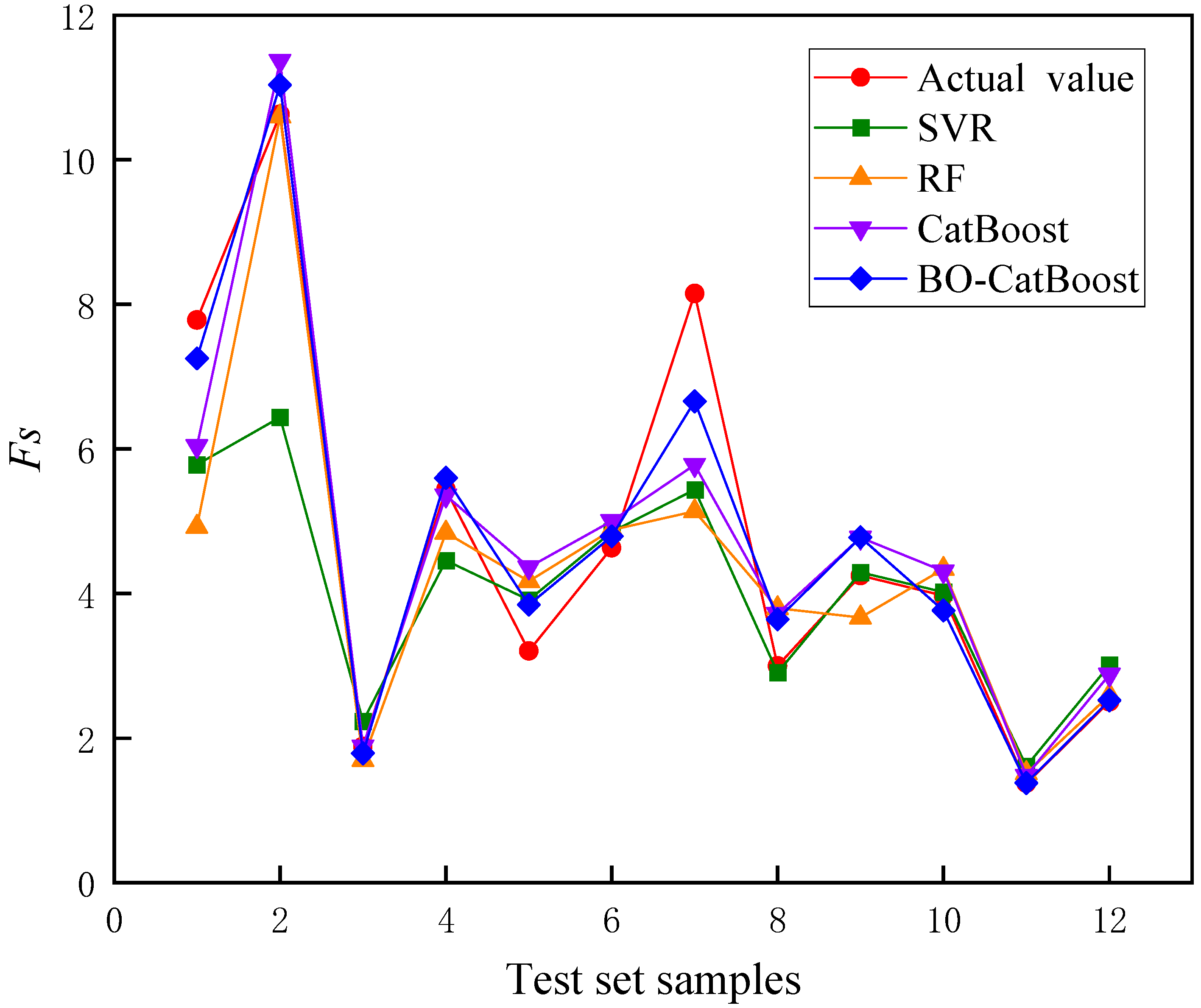
4.5. Performance Analysis of Safety Factor Prediction Model
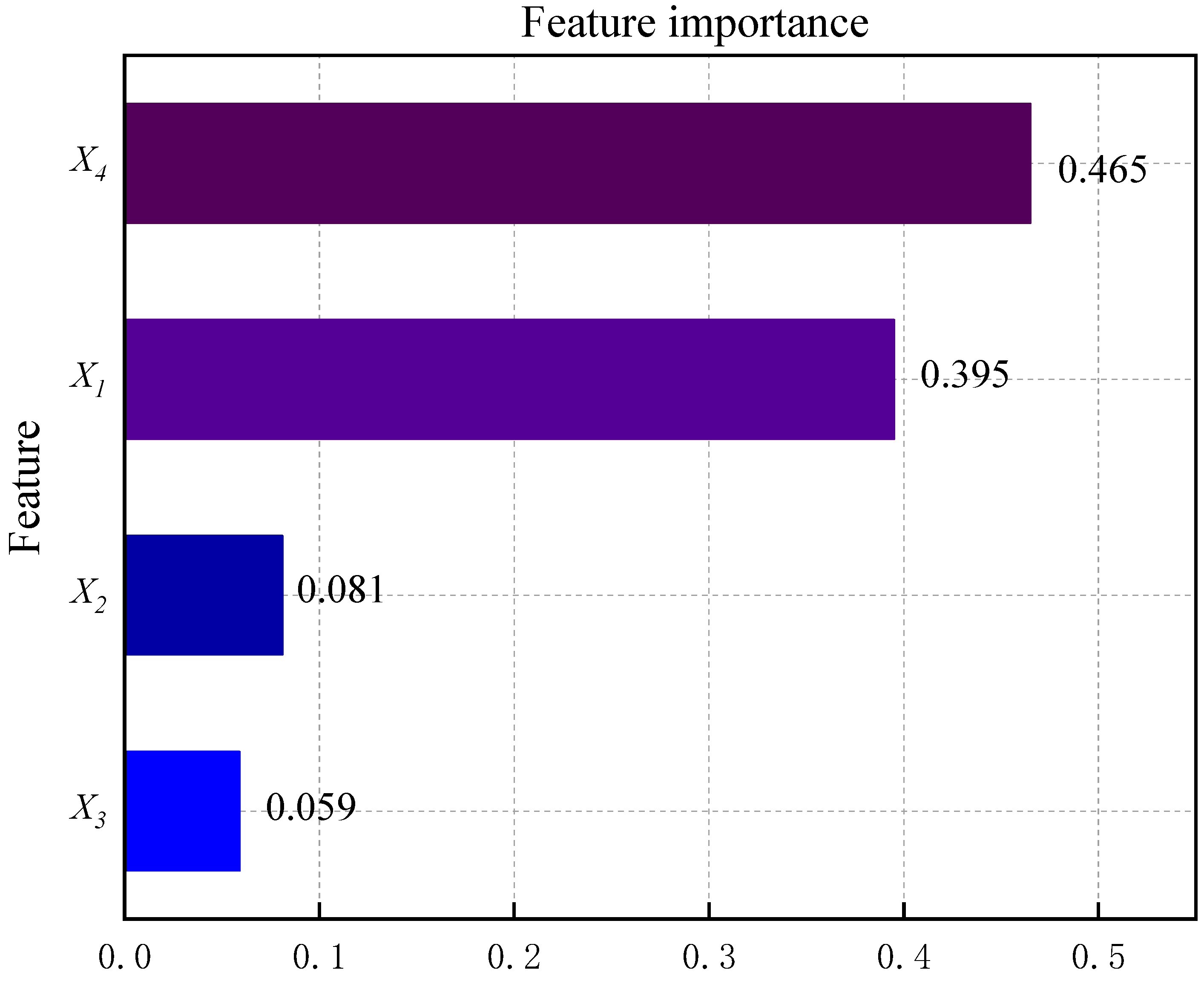
4.6. Feature Importance Analysis
5. Conclusions
- (1)
- In this paper, the safety factor was introduced into the quantitative research and analysis of roadway support, which has provided an updated research method for rationally determining the laneway support parameters, optimizing support design, and quantitatively evaluating the safety of laneways.
- (2)
- In contrast to the rest of the models, such as the SVR, the RF, and the CatBoost models, the BO-CatBoost model demonstrated the optimal predictive output item for safety factors with the lowest RMSE and MAE, the largest R2 and VAF, and an appropriate a-20 index, with values of 0.5688, 0.4074, 0.9553, 95.25%, and 0.9167 in the test set, respectively. Thus, the BO-CatBoost model is found to be the best machine learning method that can most precisely predict the Fs.
- (3)
- Compared with the unoptimized CatBoost model, the values of RMSE and MAE in the BO-CatBoost model decreased from 0.9901 and 0.7715 to 0.5688 and 0.4074, respectively. Moreover, the values of R2, VAF, and the a-20 index of the BO-CatBoost model improved from 0.8645, 83.38%, and 0.75 to 0.9553, 95.25%, and 0.9167, respectively. This indicates that the optimization of the Bayesian algorithm plays a crucial role in enhancing the predictive performance of the CatBoost model.
- (4)
- According to the analysis of feature importance, the thickness of support and the refinement rank of rock mass quality in the mining area emerged as the two most critical elements for predicting the safety factors of mining laneways. Consequently, in terms of the design and support work of mine laneway stability, the essential task is to focus on the evaluation of the quality rank of mining rock mass and to set different support thicknesses with respect to various laneway burial depths and spans, so as to achieve economic and effective mine laneway support design.
- (5)
- It is worth mentioning that expanding the dataset is beneficial for reducing the impact of extreme information, thereby improving the prediction accuracy of the model. Currently, there are insufficient practical cases of optimizing mine laneway support in existing mines, and the expansion of the dataset needs to be followed up with further research and discussion.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, A.Q.; Wu, A.X.; Wang, Y.M.; Li, J.Y.; Wang, S.Y. Research on support technology and zoning and grading support system for complex fractured soft rock tunnels. Min. Res. Dev. 2021, 41, 15–20. [Google Scholar]
- Zhu, H.H.; Yan, J.X.; Liang, W.H. Challenges and Development Prospects of Ultra-Long and Ultra-Deep Mountain Tunnels. Engineering 2019, 5, 384–392. [Google Scholar] [CrossRef]
- Ma, Z.Q.; Jiang, Y.D.; Wu, G.Y.; Zuo, Y.J.; Gao, L. Research and application of difficulty classification for thick mud roof roadway support. Chin. J. Saf. Sci. 2017, 27, 121–125. [Google Scholar]
- Zhan, Q.J.; Zheng, X.G.; Du, J.P.; Xiao, T. Coupling Instability Mechanism and Joint Control Technology of Soft-Rock Roadway with a Buried Depth of 1336 m. Rock Mech. Rock Eng. 2020, 53, 2233–2248. [Google Scholar] [CrossRef]
- Tang, S.H.; Wang, P.W.; Guo, X.Q.; Zou, N.R. Optimization of rock drilling chambers and mining access support in deep mining areas. Min. Res. Dev. 2020, 40, 36–40. [Google Scholar]
- Palmstrom, A.; Broch, E. Use and misuse of rock mass classification systems with particular reference to the Q-system. Tunn. Undergr. Space Technol. 2006, 21, 575–593. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, H.Y.; Fang, Q.C. Design of underground mine roadway support based on rock mass quality grading. Min. Res. Dev. 2021, 41, 84–88. [Google Scholar]
- Chen, N.Q. Research on the evaluation of the effectiveness of tunnel anchor net support based on the grade of surrounding rock. Min. Res. Dev. 2023, 43, 67–73. [Google Scholar]
- Zhang, S.K.; Yin, S.D. Analytical Approach Based on Full-Space Synergy Technology to Optimization Support Design of Deep Mining Roadway. Minerals 2022, 12, 746. [Google Scholar] [CrossRef]
- Zhu, W.X.; Jing, H.W.; Yang, L.J.; Pan, B.; Su, H.J. Strength and deformation behaviors of bedded rock mass under bolt reinforcement. Int. J. Min. Sci. Technol. 2018, 28, 593–599. [Google Scholar] [CrossRef]
- Yuan, L.; Jiang, Y.D.; He, X.Q.; Dou, L.M.; Zhao, Y.X.; Zhao, X.S.; Wang, K.; Yu, Q.; Lu, X.M.; Li, H.C. Research progress on key technologies for accurate identification, monitoring, and early warning of typical power disaster risks in coal mines. J. Coal Sci. 2018, 43, 306–318. [Google Scholar]
- Dou, J.; Xiang, Z.L.; Xu, Q.; Zheng, P.L.; Wang, X.K.; Su, A.J.; Liu, J.Q.; Luo, W.Q. The application and development trend of machine learning in intelligent disaster prevention and reduction of landslides. Earth Sci. 2023, 48, 1657–1674. [Google Scholar]
- Gong, L.; Wei, X.Y.; Qi, Y.D.; Jin, C.L.; Tian, J. Prediction and evaluation of surrounding rock safety in railway tunnels based on PCA-IRBF model. J. Railw. Eng. 2021, 38, 86–91. [Google Scholar]
- Li, S.G.; Shen, Y.J.; Lin, P.; Xie, J.S.; Tian, S.S.; Lv, Y.; Ma, W. Classification method of surrounding rock of plateau tunnel based on BP neural network. Front. Earth Sci. 2023, 11, 1283520. [Google Scholar]
- Zhou, J.; Zhu, S.L.; Qiu, Y.G.; Armaghani, D.; Zhou, A.N.; Yong, W.X. Predicting tunnel squeezing using support vector machine optimized by whale optimization algorithm. Acta Geotech. 2022, 17, 1343–1366. [Google Scholar] [CrossRef]
- Lessmann, S.; Baesens, B.; Seow, H.V.; Thomas, L.C. Benchmarking state-of-the-art classification algorithms for credit scoring: An update of research. Eur. J. Oper. Res. 2015, 247, 124–136. [Google Scholar] [CrossRef]
- Zhao, H.L.; Wang, Y.X.; Li, X.; Guo, P.P.; Lin, H. Prediction of Maximum Tunnel Uplift Caused by Overlying Excavation Using XGBoost Algorithm with Bayesian Optimization. Appl. Sci. 2023, 13, 9726. [Google Scholar] [CrossRef]
- Zhou, J.; Li, X.B.; Mitri, H.S. Classification of Rockburst in Underground Projects: Comparison of Ten Supervised Learning Methods. J. Comput. Civ. Eng. 2016, 30, 04016003. [Google Scholar] [CrossRef]
- Shahani, N.M.; Kamran, M.; Zheng, X.; Liu, C.; Guo, X. Application of gradient boosting machine learning algorithms to predict uniaxial compressive strength of soft sedimentary rocks at thar coalfield. Adv. Civ. Eng. 2021, 2021, 2565488. [Google Scholar] [CrossRef]
- Huang, G.M.; Wu, L.F.; Ma, X.; Zhang, W.Q.; Fan, J.L.; Yu, X.; Zeng, W.Z.; Zhou, H.M. Evaluation of CatBoost method for prediction of reference evapotranspiration in humid regions. J. Hydrol. 2019, 574, 1029–1041. [Google Scholar] [CrossRef]
- Yuan, H.P.; Ye, C.X.; Wang, W.H. Mechanical parameter assignment of different levels of rock tunnels and evaluation of the effectiveness of plain spray support. Metal Mines 2022, 51–56. [Google Scholar]
- Li, X.B.; Peng, D.X.; Feng, F.; Li, X.S. Stability analysis of deep collapse to backfill isolation pillars based on the theory of medium thick plates. J. China Univ. Min. Technol. 2019, 48, 484–494. [Google Scholar]
- Krishnan, A.R.; Kasim, M.M.; Hamid, R.; Ghazali, M.F. A Modified CRITIC Method to Estimate the Objective Weights of Decision Criteria. Symmetry 2021, 13, 973. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, P.Y.; Mu, P.; Wang, M.L.; Han, L.F.; Sun, J.L. A Comprehensive Evaluation Method for the Service Status of Groins in Waterways Based on an AHP-Improved CRITIC Combination Weighting Optimization Model. Sustainability 2022, 14, 10709. [Google Scholar] [CrossRef]
- Ren, J.J.; Liu, Y.M.; Yuan, Y.L.; Yan, H.Y.; Liu, H.Q. Predicting education building occupants’ thermal sensation through CatBoost-DF algorithm. Appl. Artif. Intell. 2023, 37, 2175115. [Google Scholar] [CrossRef]
- Chen, Q.; Li, J.L.; Feng, J.Y.; Qian, J.P. Dynamic comprehensive quality assessment of post-harvest grape in different transportation chains using SAHP-CatBoost machine learning. Food Qual. Saf. 2024, 8, 007. [Google Scholar] [CrossRef]
- Shahriari, B.; Swersky, K.; Wang, Z.Y.; Adams, R.P.; de Freitas, N. Taking the Human Out of the Loop: A Review of Bayesian Optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef]
- Ahmed, M.O.; Vaswani, S.; Schmidt, M. Combining Bayesian optimization and Lipschitz optimization. Mach. Learn. 2020, 109, 79–102. [Google Scholar] [CrossRef]
- Xie, X.B.; Li, D.X.; Kong, L.Y.; Ye, Y.F.; Gao, S. A prediction model for rock burst tendency level based on CRITIC-XGB algorithm. J. Rock Mech. Eng. 2020, 39, 1975–1982. [Google Scholar]
- Zheng, S.; Jiang, A.N.; Yang, X.R.; Luo, G.C. A New Reliability Rock Mass Classification Method Based on Least Squares Support Vector Machine Optimized by Bacterial Foraging Optimization Algorithm. Adv. Civ. Eng. 2020, 2020, 1–13. [Google Scholar] [CrossRef]
- Wu, X.G.; Feng, Z.B.; Liu, Y.; Qin, Y.W.; Yang, T.Y.; Duan, J.C. Enhanced safety prediction of vault settlement in urban tunnels using the pair-copula and Bayesian network. Appl. Soft Comput. 2023, 132, 109711. [Google Scholar] [CrossRef]
- Balogun, A.L.; Rezaie, F.; Pham, Q.B.; Gigovic, L.; Drobnjak, S.; Aina, Y.A.; Panahi, M.; Yekeen, S.T.; Lee, S. Spatial prediction of landslide susceptibility in western Serbia using hybrid support vector regression (SVR) with GWO, BAT and COA algorithms. Geosci. Front. 2021, 12, 101104. [Google Scholar] [CrossRef]
- Schonlau, M.; Zou, R.Y. The random forest algorithm for statistical learning. Stata J. 2020, 20, 3–29. [Google Scholar] [CrossRef]
- Adoko, A.C.; Gokceoglu, C.; Yagiz, S. Bayesian prediction of TBM penetration rate in rock mass. Eng. Geol. 2017, 226, 245–256. [Google Scholar] [CrossRef]
- Shahani, N.M.; Kamran, M.; Zheng, X.G.; Liu, C.C. Predictive modeling of drilling rate index using machine learning approaches: LSTM, simple RNN, and RFA. Pet. Sci. Technol. 2022, 40, 534–555. [Google Scholar] [CrossRef]


| Number | /m | /m | /mm | ||
|---|---|---|---|---|---|
| 1 | 1 | 500 | 4 | 0 | 4.91 |
| 2 | 1.5 | 450 | 4.5 | 20 | 4.868 |
| 3 | 1.8 | 500 | 5 | 20 | 3.631 |
| 4 | 2 | 500 | 4 | 0 | 0.825 |
| ⋯⋯ | |||||
| 59 | 3.5 | 400 | 4 | 70 | 3.988 |
| 60 | 4 | 600 | 5 | 60 | 2.997 |
| Number | /m | /m | /mm | ||
|---|---|---|---|---|---|
| 1 | 0.282 | 112.5 | 0.74 | 0 | 4.91 |
| 2 | 0.423 | 101.25 | 0.8325 | 6.16 | 4.86 |
| 3 | 0.5076 | 112.5 | 0.925 | 6.16 | 3.631 |
| 4 | 0.564 | 112.5 | 0.74 | 0 | 0.825 |
| ⋯⋯ | |||||
| 59 | 0.987 | 90 | 0.74 | 21.56 | 3.988 |
| 60 | 1.128 | 135 | 0.925 | 18.48 | 2.997 |
| Parameters | Implication | Search Range | Optimal Value |
|---|---|---|---|
| iterations | Maximum number of iterations | [100, 1000] | 681 |
| learning_rate | Learning rate | [0.01, 0.1] | 0.1 |
| depth | The maximum depth of the tree | [4, 10] | 4 |
| l2_leaf_reg | L2 regularization to reduce overfitting | [1, 10] | 1 |
| random_strength | Disturbance term of feature splitting information gain to avoid overfitting | [1, 10] | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, H.; Ji, S.; Zhu, C.; Wang, L. Research on Predicting the Safety Factor of Plain Shotcrete Support in Laneways Based on BO-CatBoost Model. Biomimetics 2024, 9, 394. https://doi.org/10.3390/biomimetics9070394
Yuan H, Ji S, Zhu C, Wang L. Research on Predicting the Safety Factor of Plain Shotcrete Support in Laneways Based on BO-CatBoost Model. Biomimetics. 2024; 9(7):394. https://doi.org/10.3390/biomimetics9070394
Chicago/Turabian StyleYuan, Haiping, Shuaijie Ji, Chuanqi Zhu, and Lei Wang. 2024. "Research on Predicting the Safety Factor of Plain Shotcrete Support in Laneways Based on BO-CatBoost Model" Biomimetics 9, no. 7: 394. https://doi.org/10.3390/biomimetics9070394
APA StyleYuan, H., Ji, S., Zhu, C., & Wang, L. (2024). Research on Predicting the Safety Factor of Plain Shotcrete Support in Laneways Based on BO-CatBoost Model. Biomimetics, 9(7), 394. https://doi.org/10.3390/biomimetics9070394







