Coordinated Transport by Dual Humanoid Robots Using Distributed Model Predictive Control
Abstract
1. Introduction
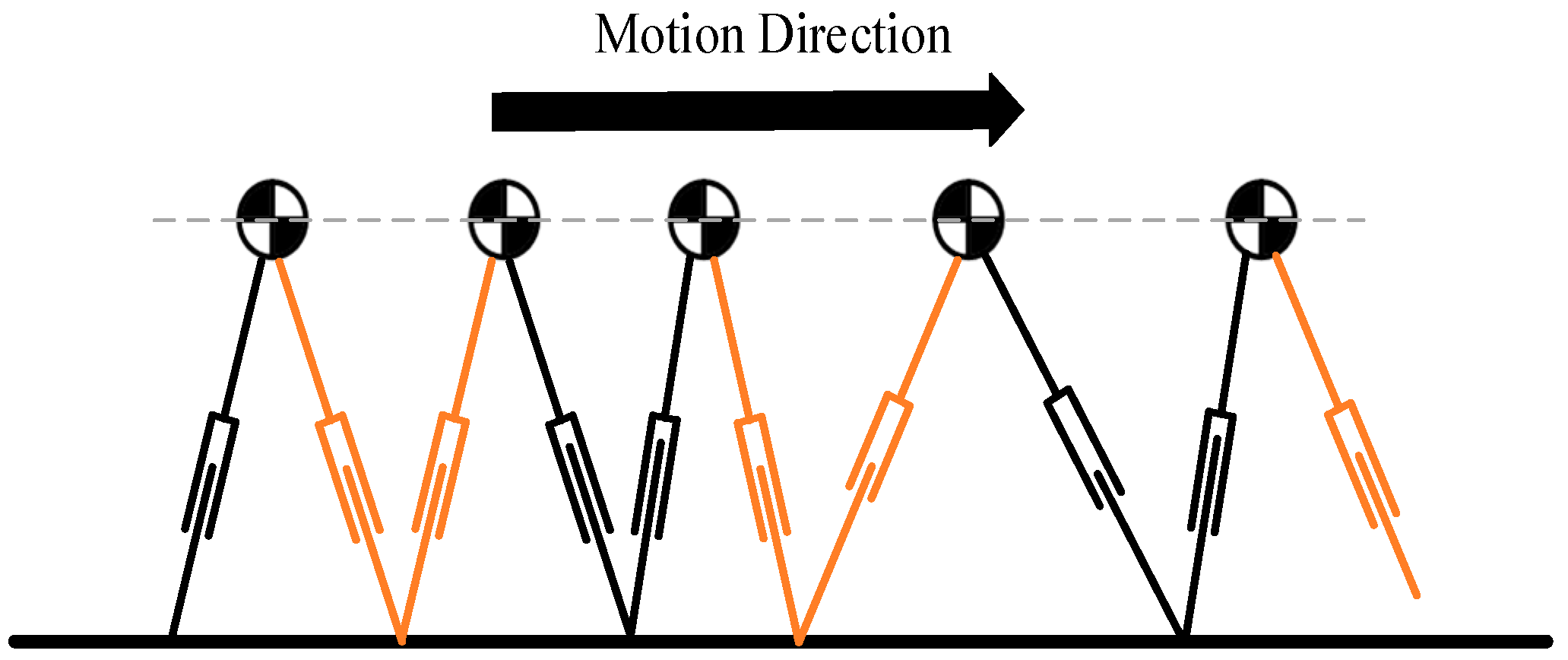
2. Robot Motion Model
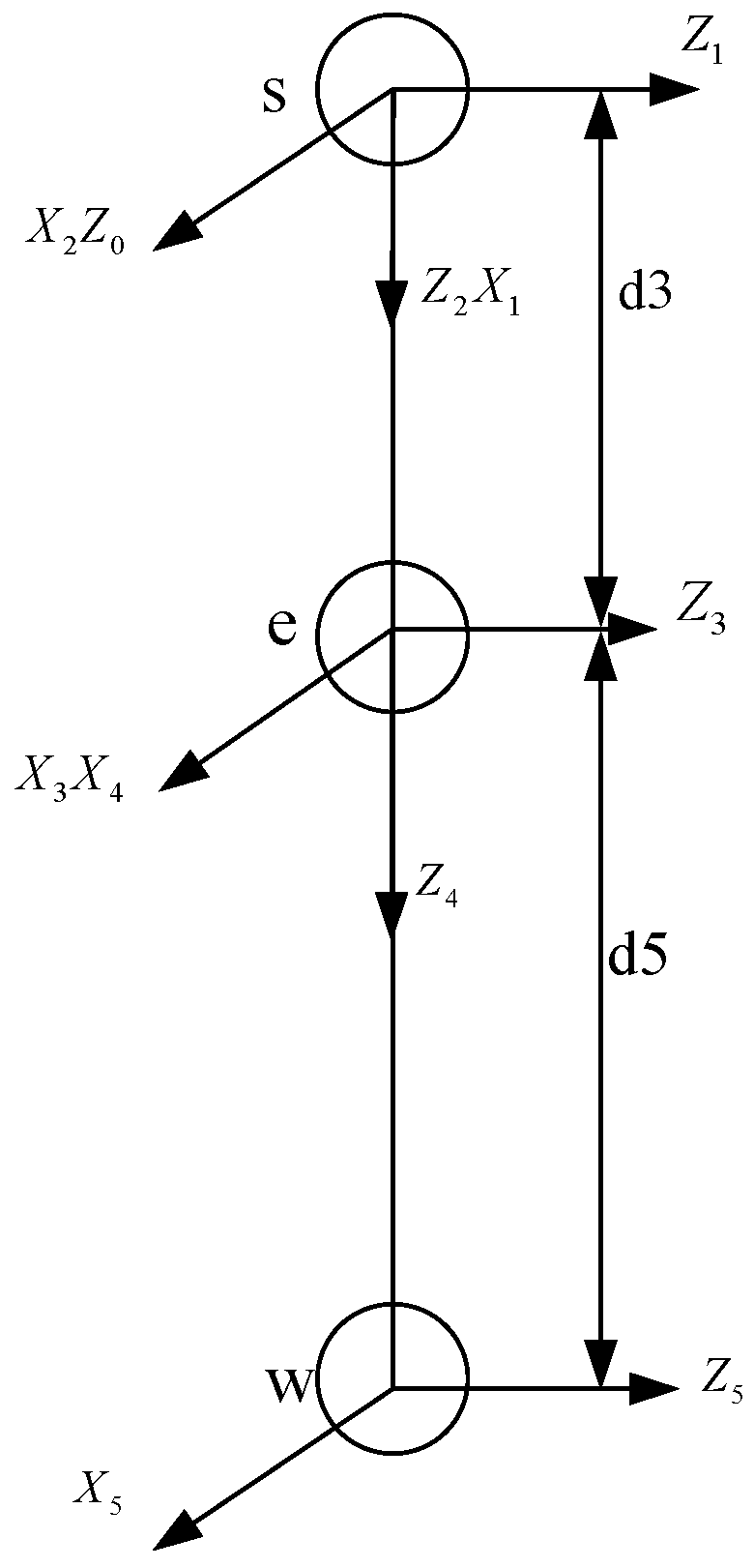
2.1. Humanoid Robot Kinematics Analysis
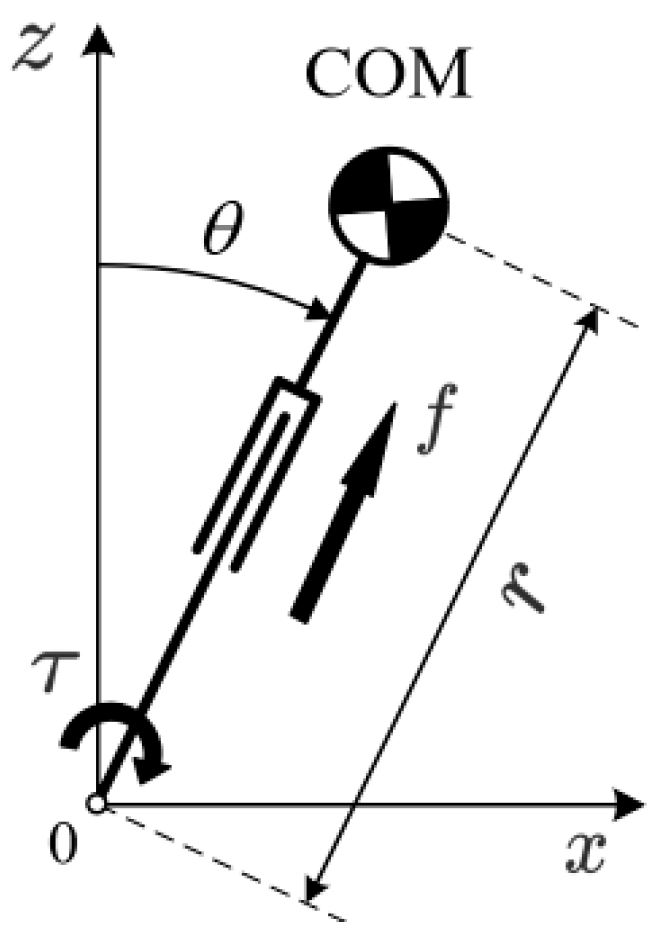
2.2. NAO Robot Kinematics and Dynamics Modeling
2.3. State Space Equation Based on ZMP
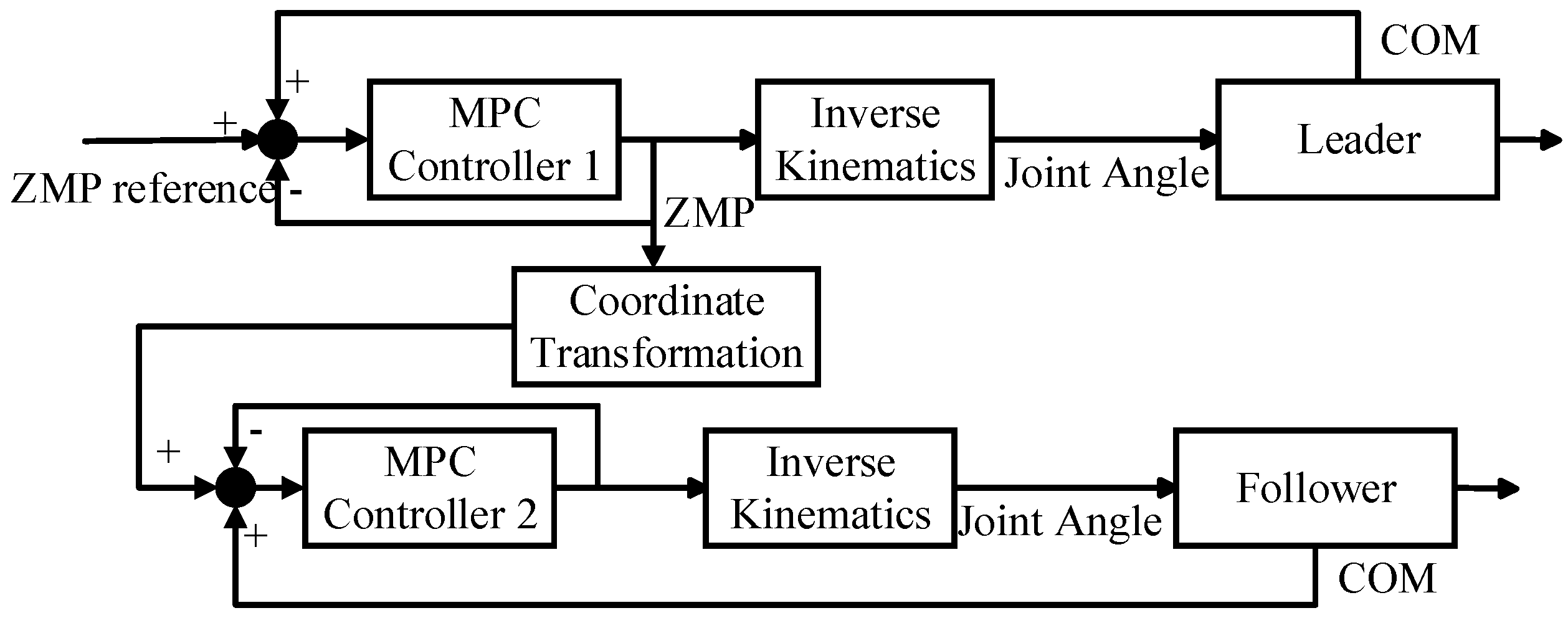
3. Dual Robot Cooperative Control
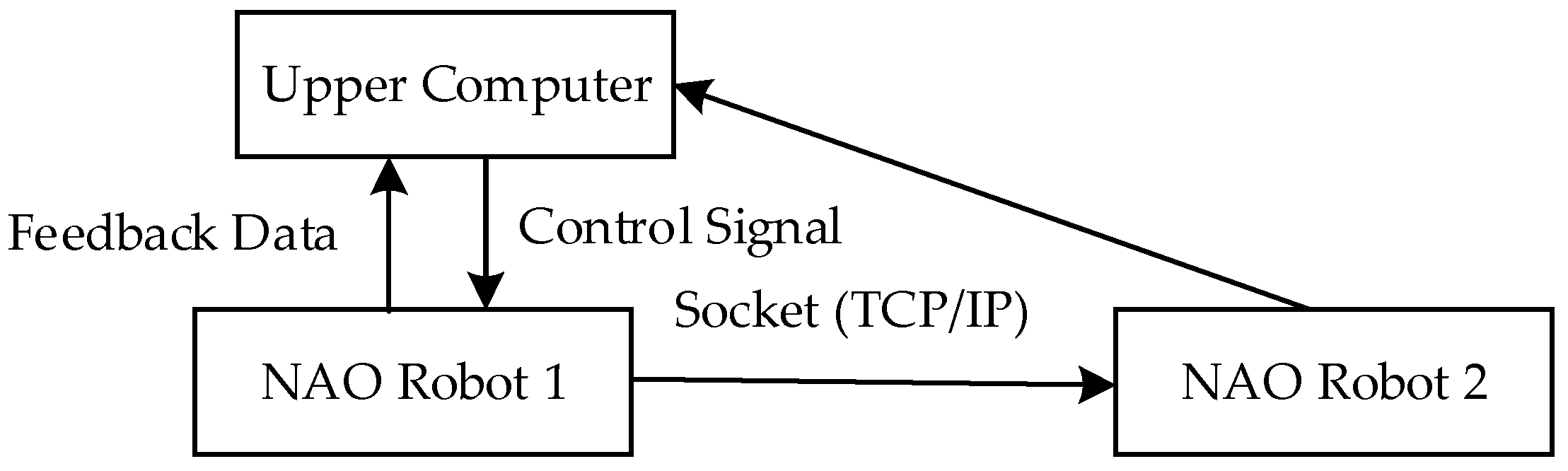
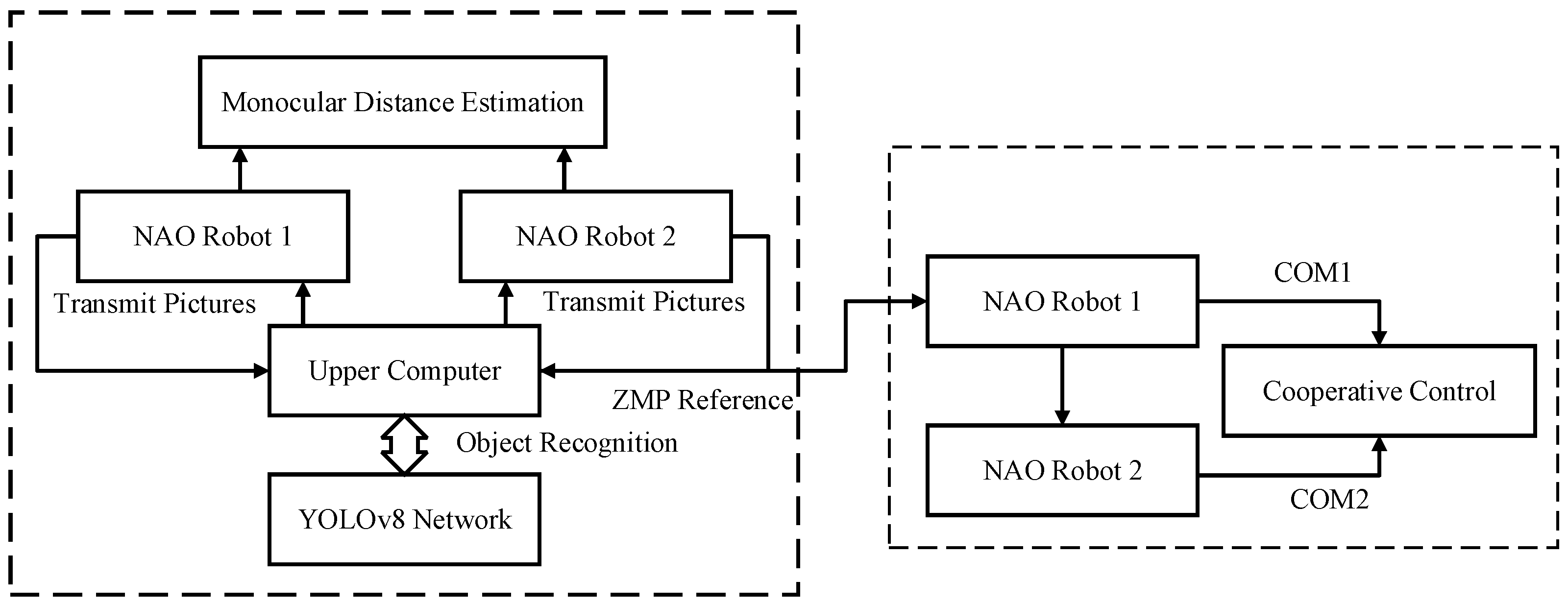
3.1. Dual-Robot Communication System
3.2. Leader DMPC Controller Design
3.3. Follower DMPC Controller Design
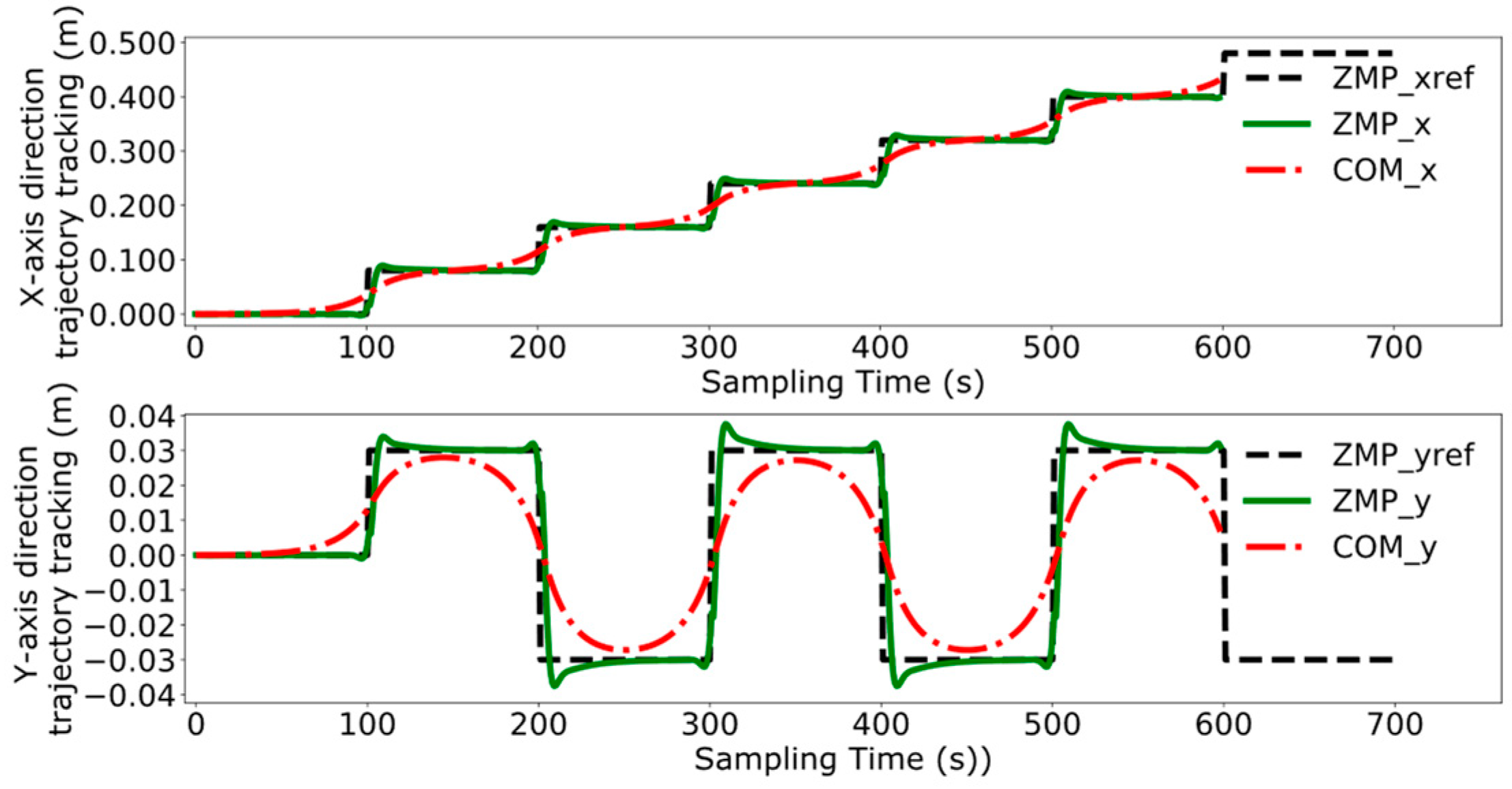
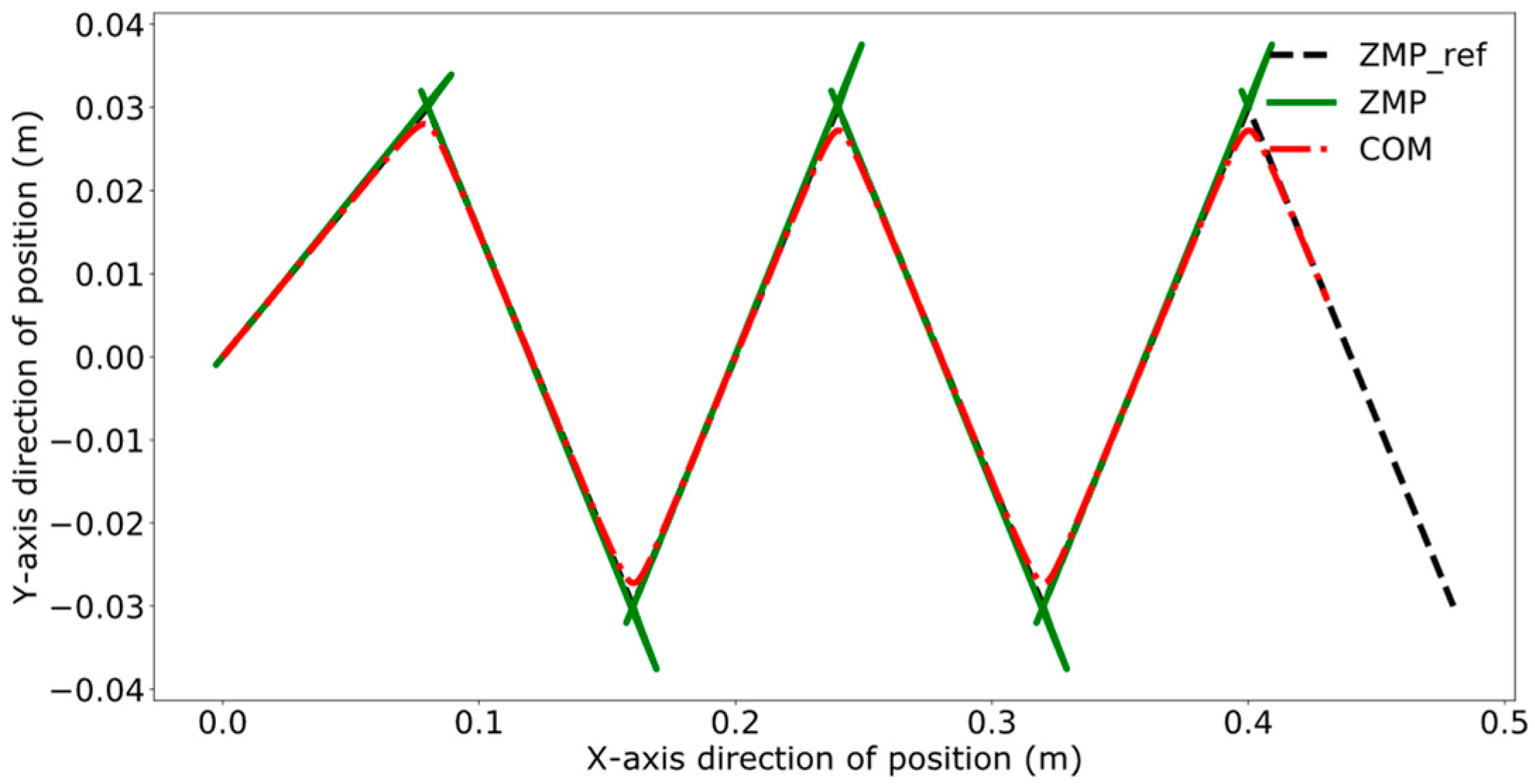
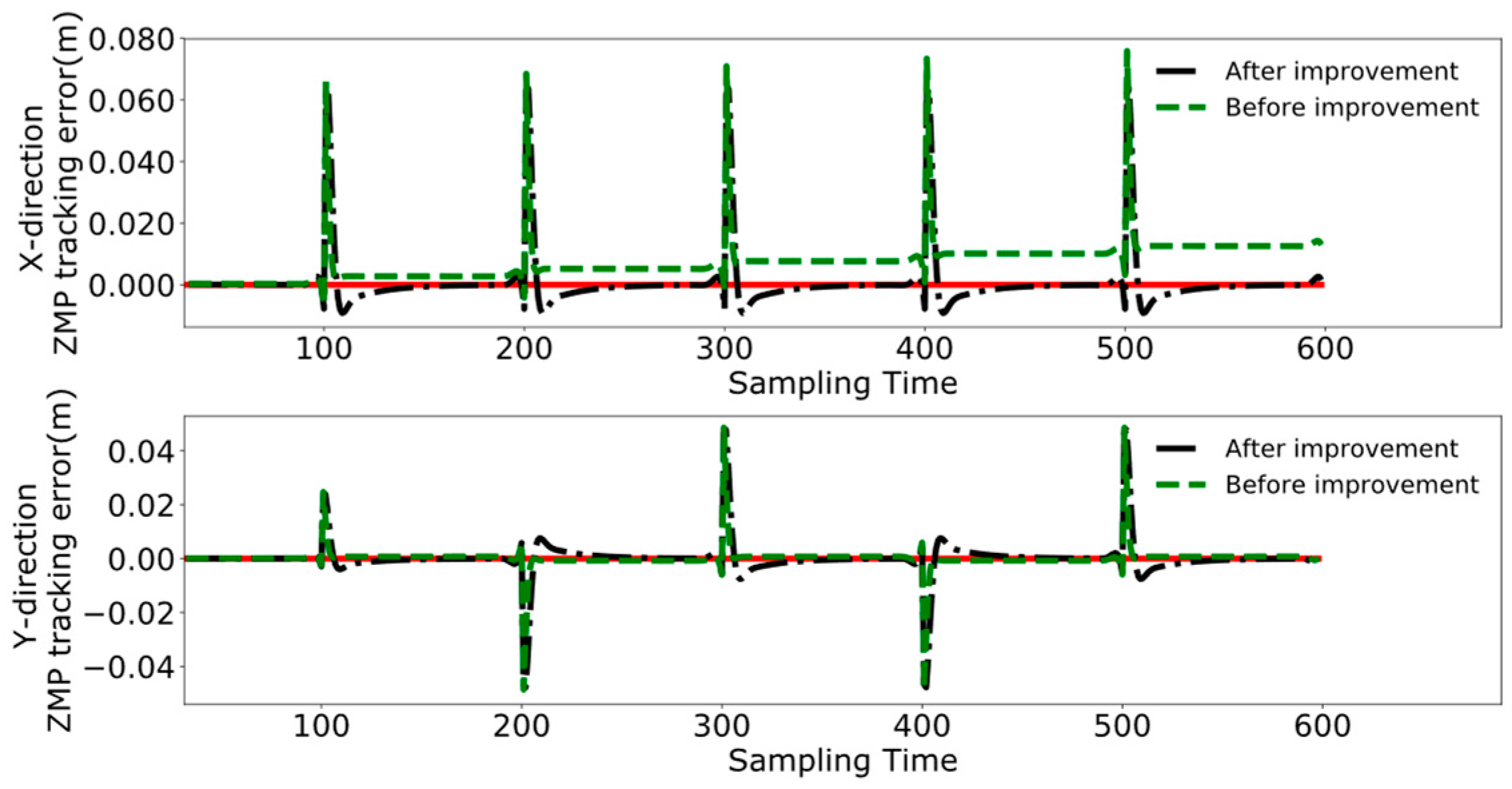
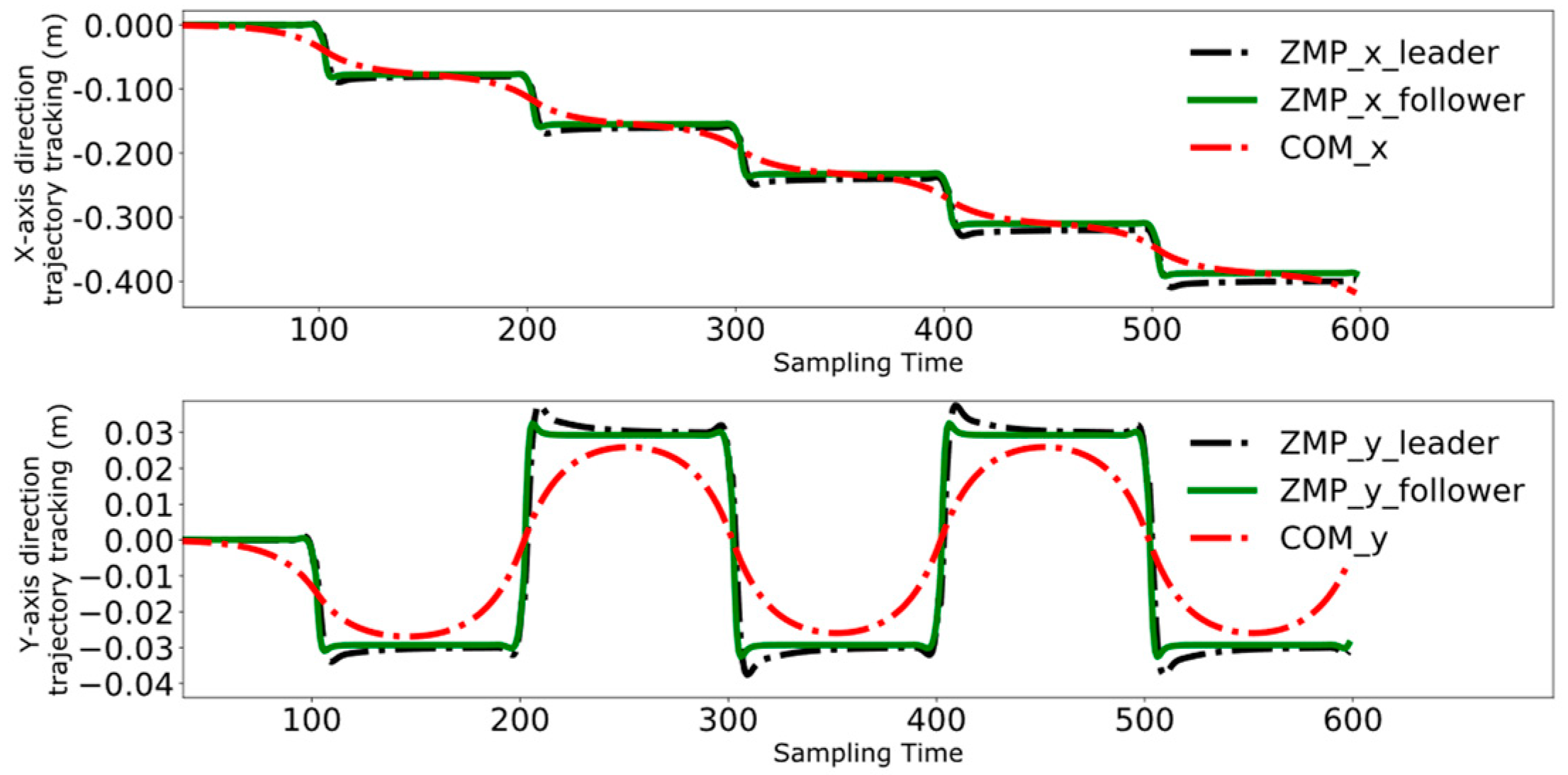
4. Experimental Results and Analysis
4.1. Collaborative Control Experimental Design
4.2. Object Positioning and Grasping
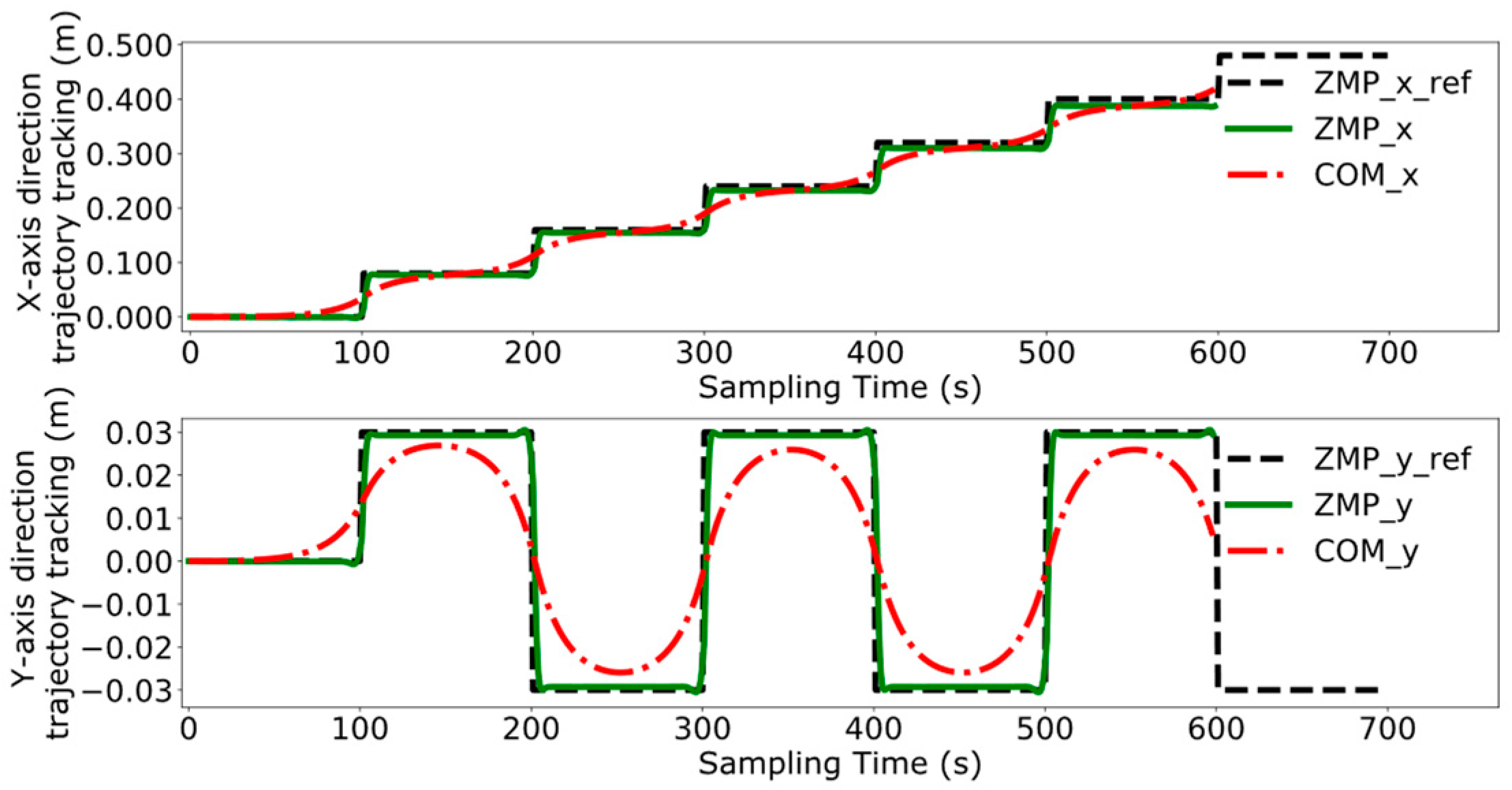
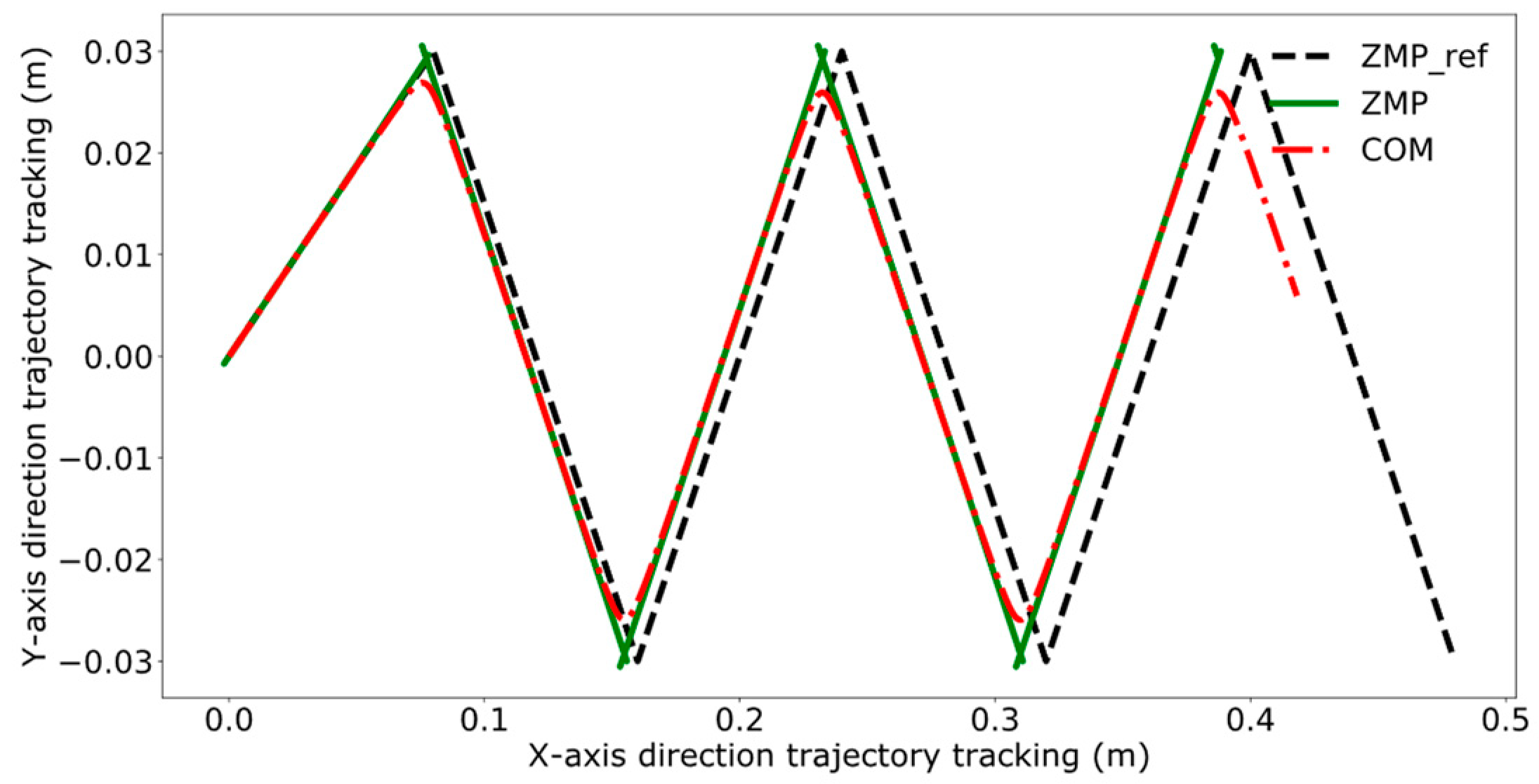
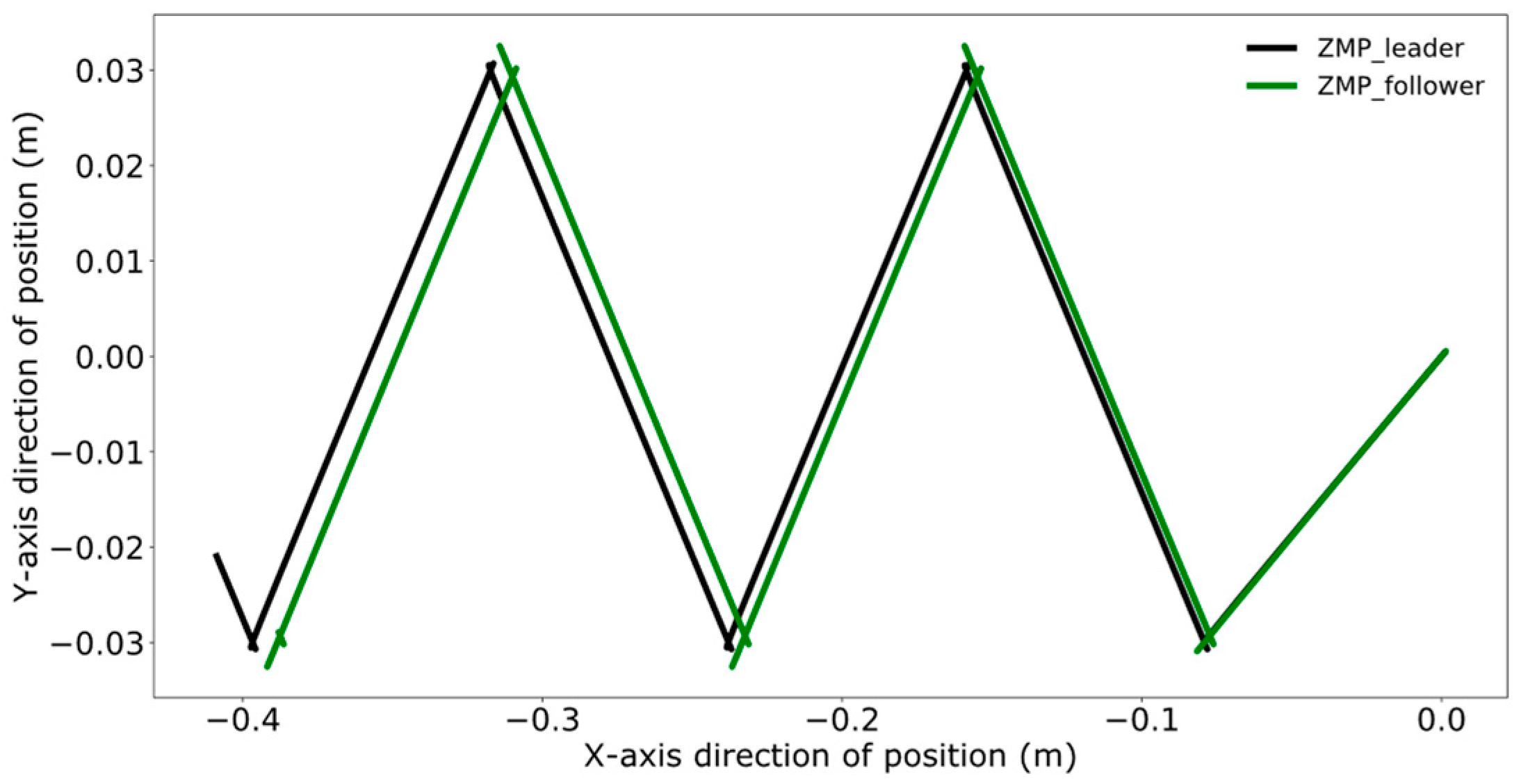
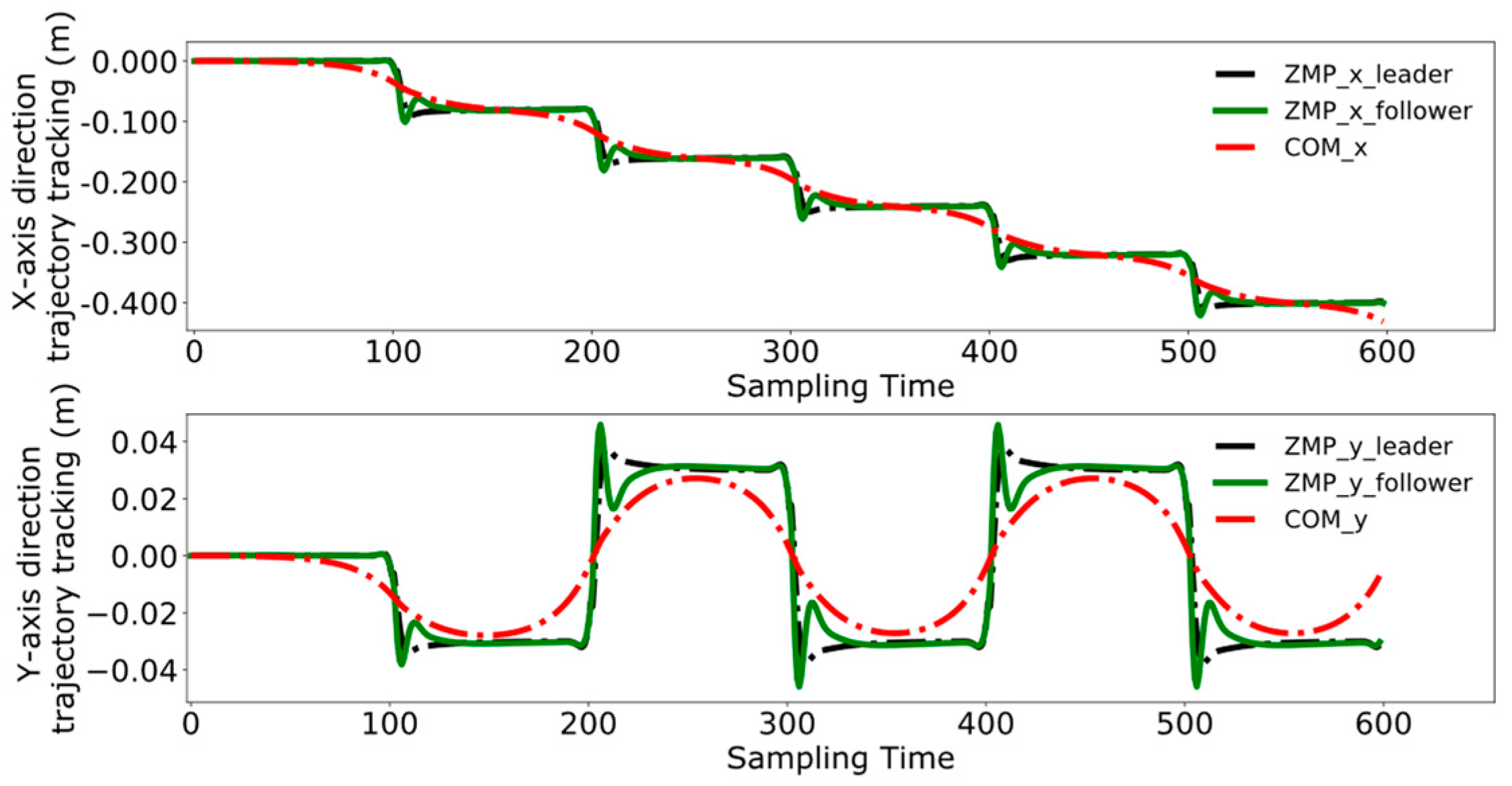
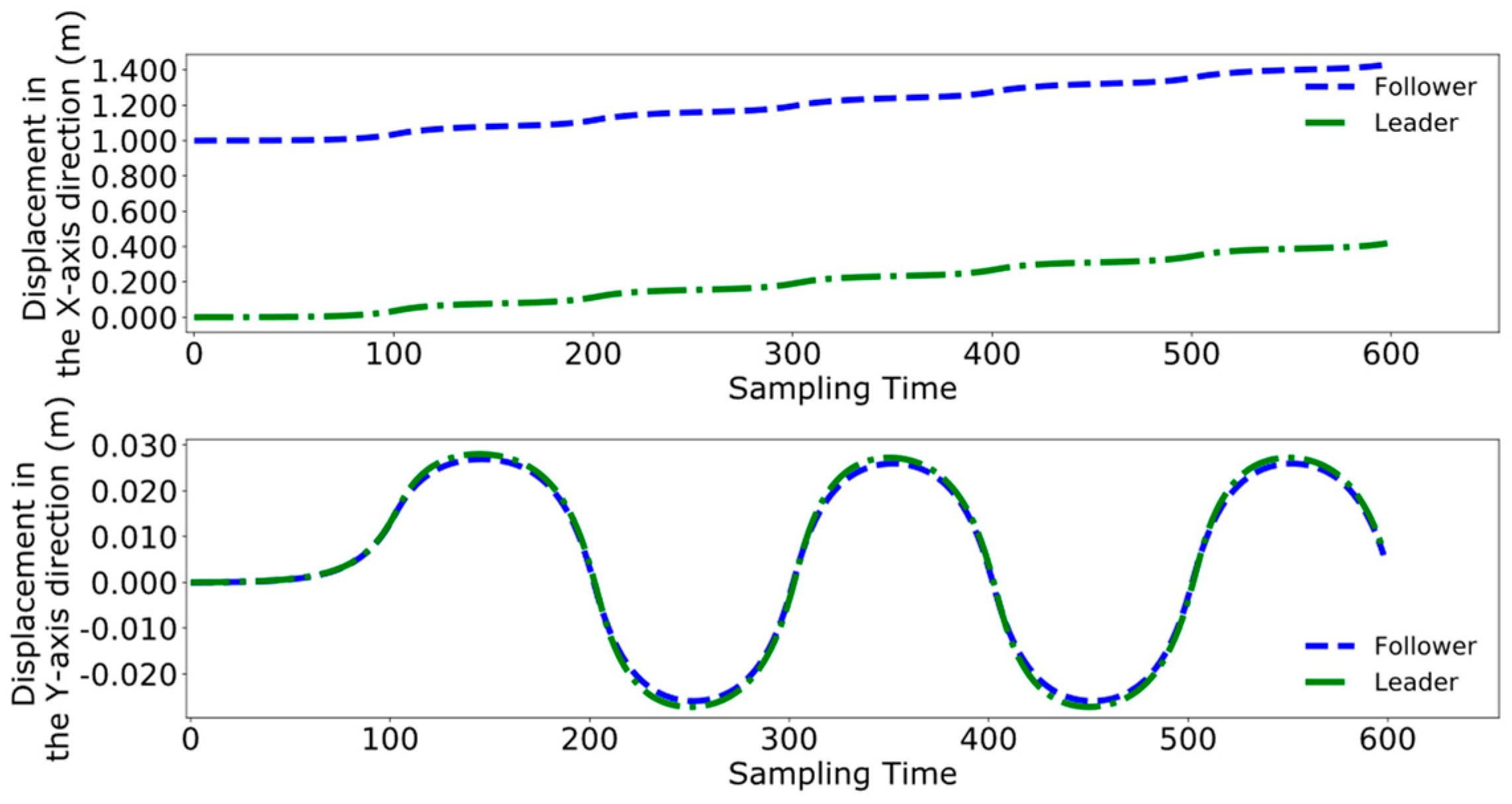
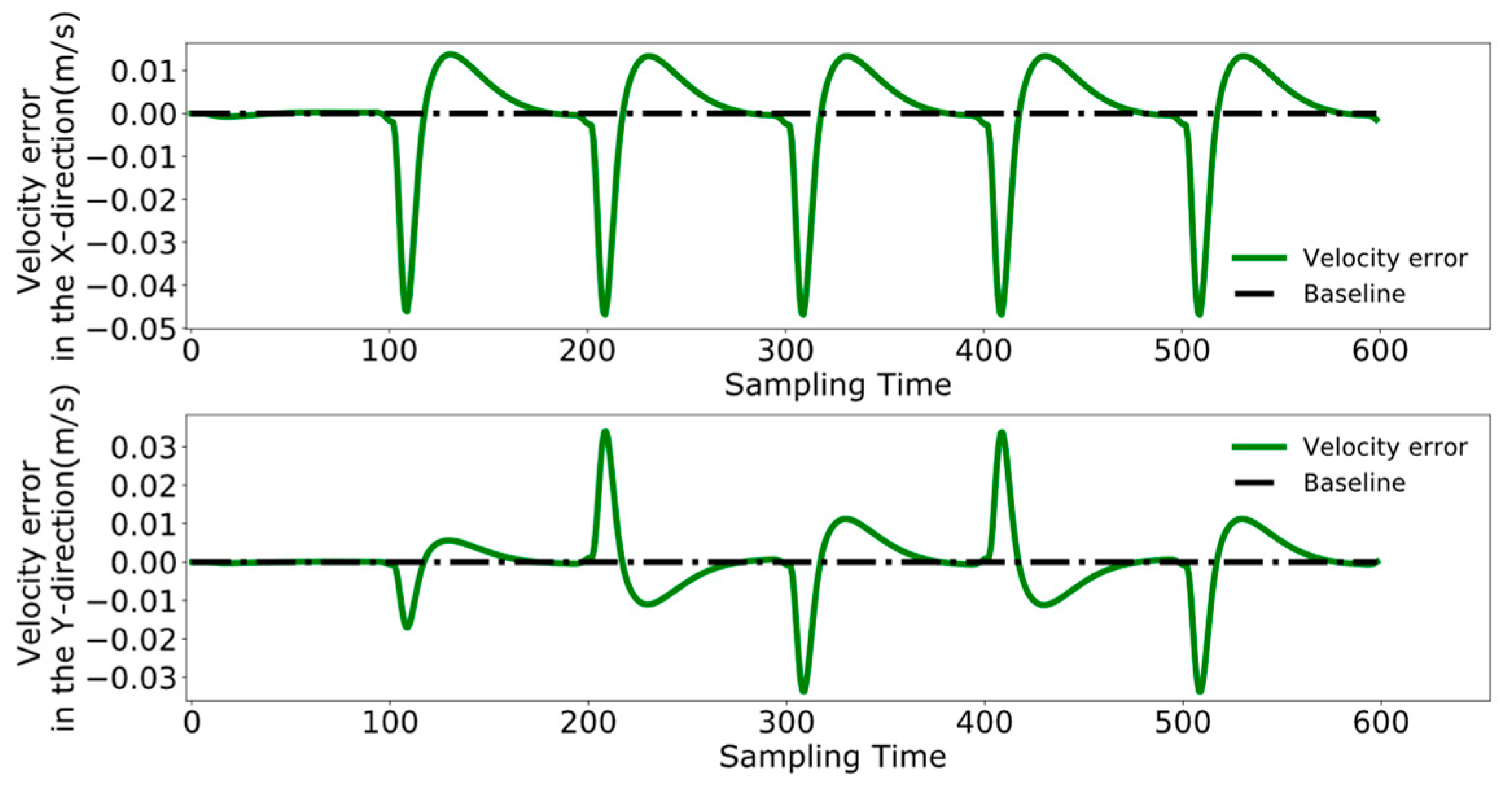
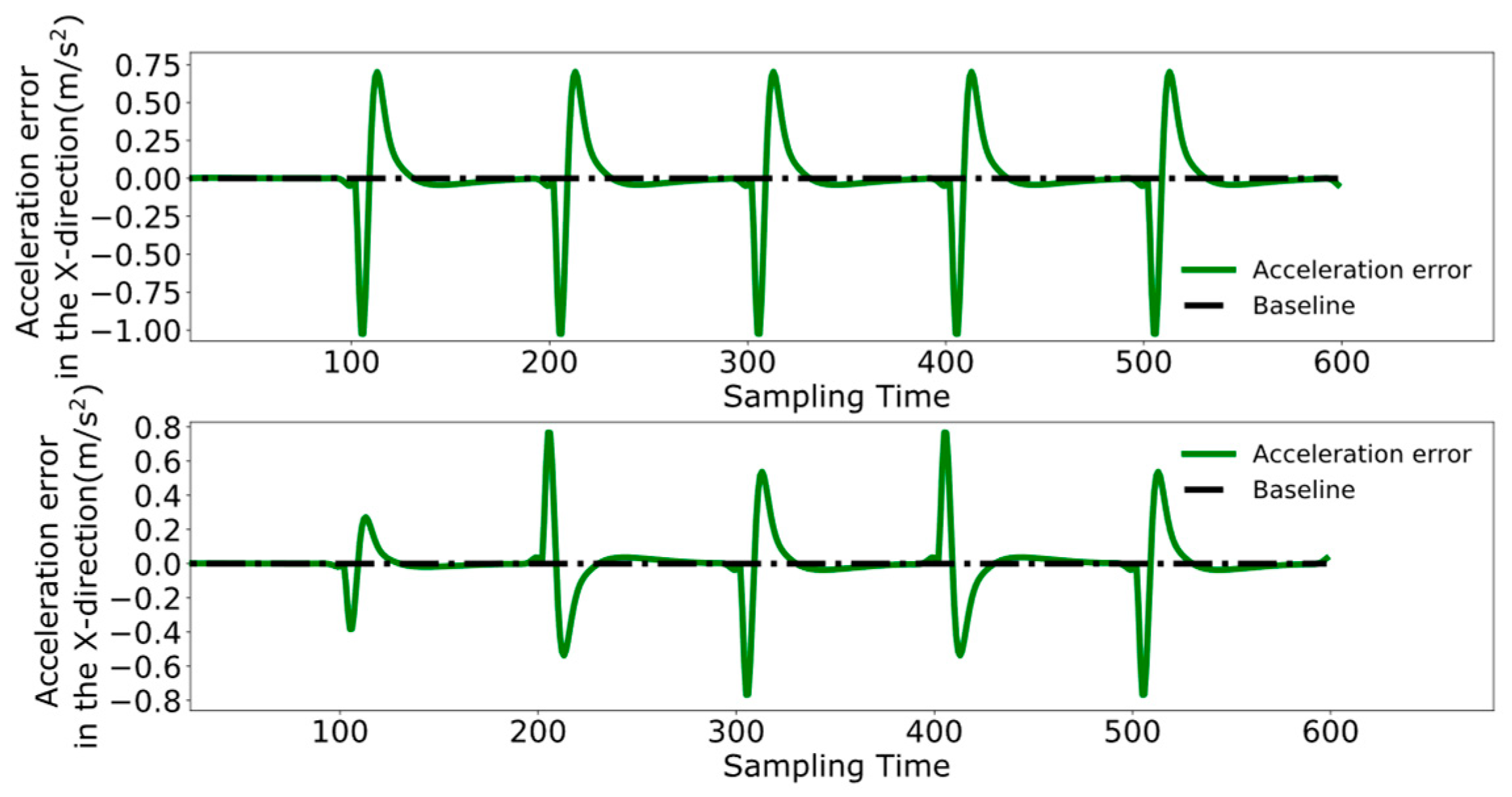
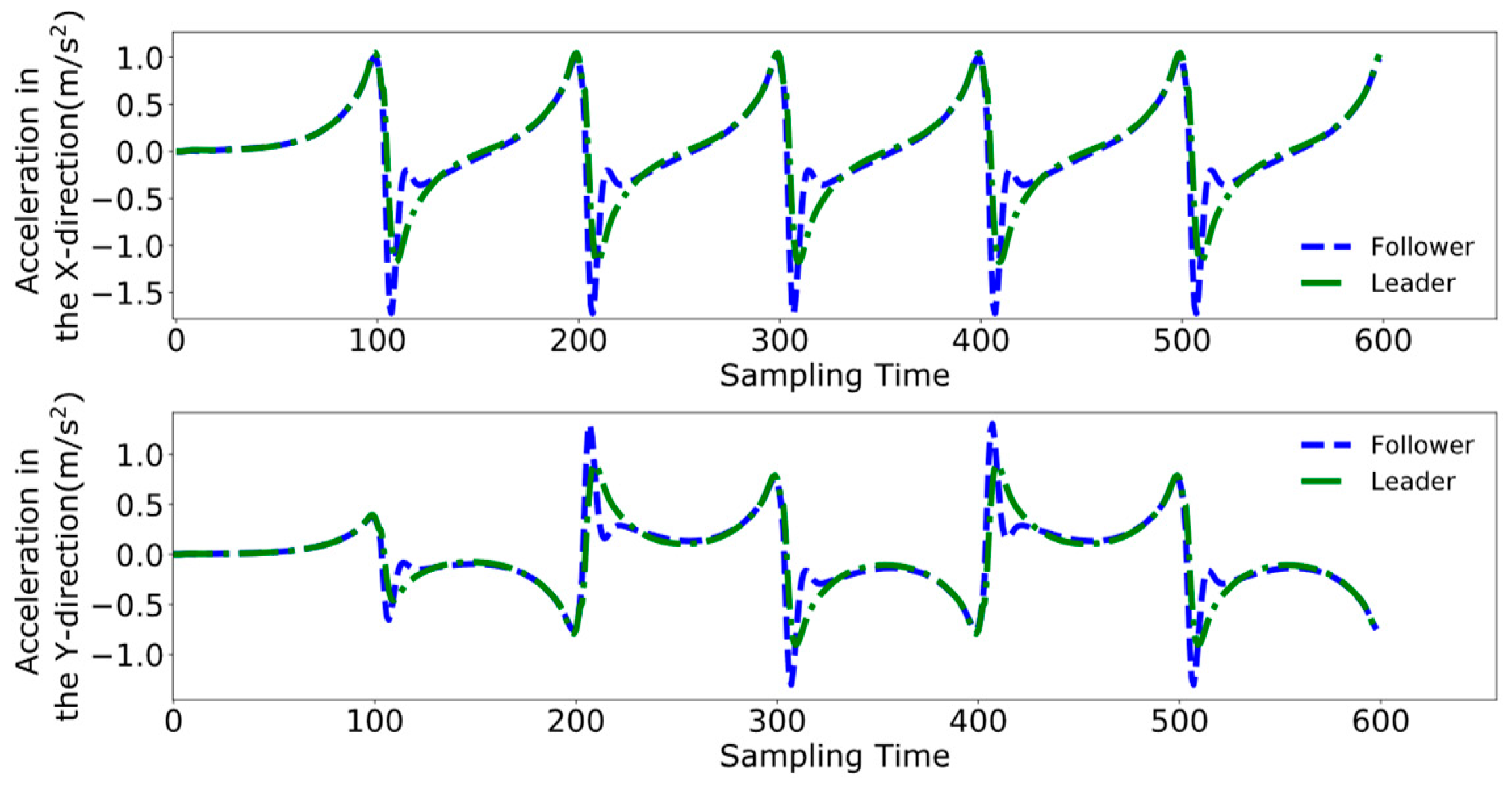
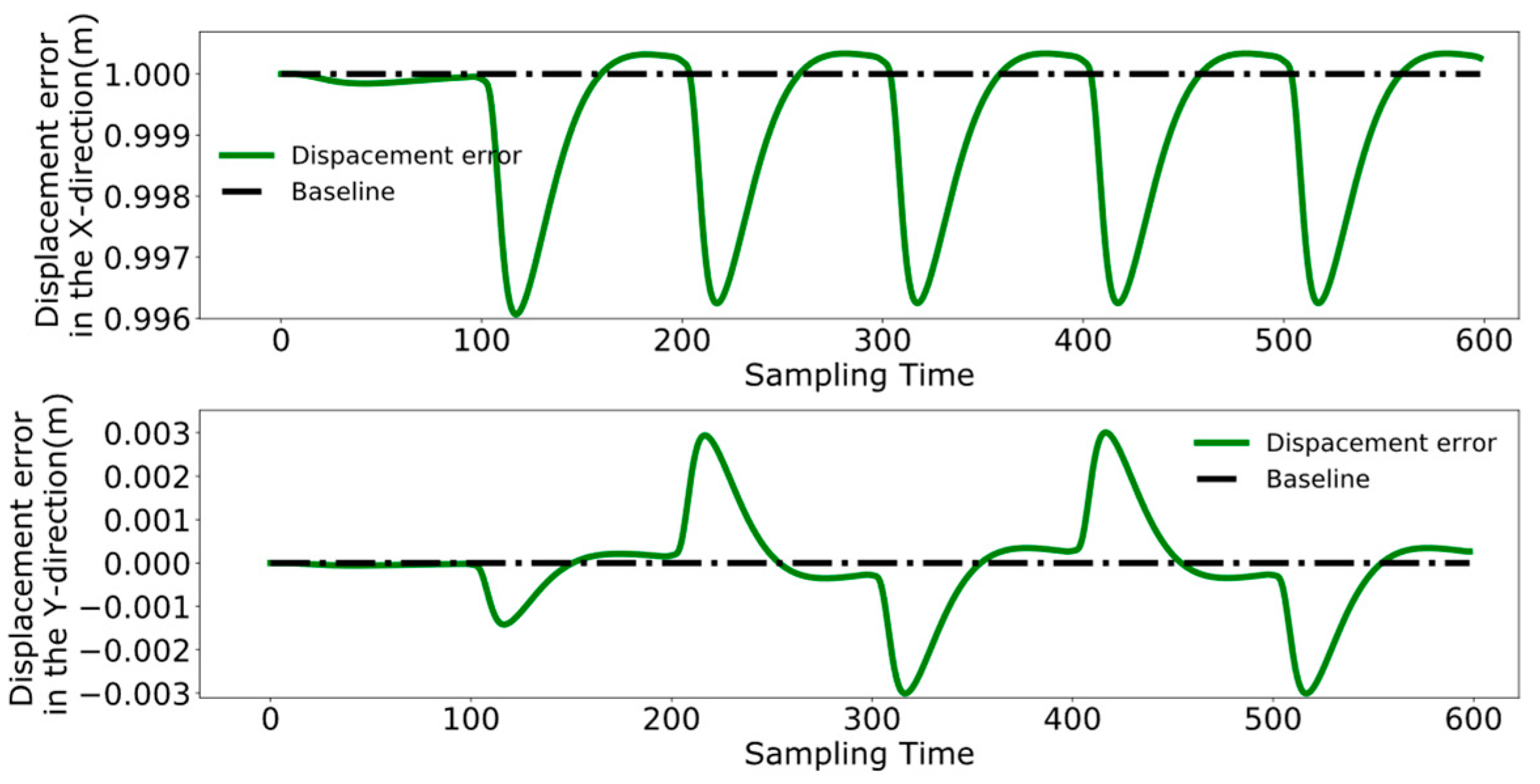
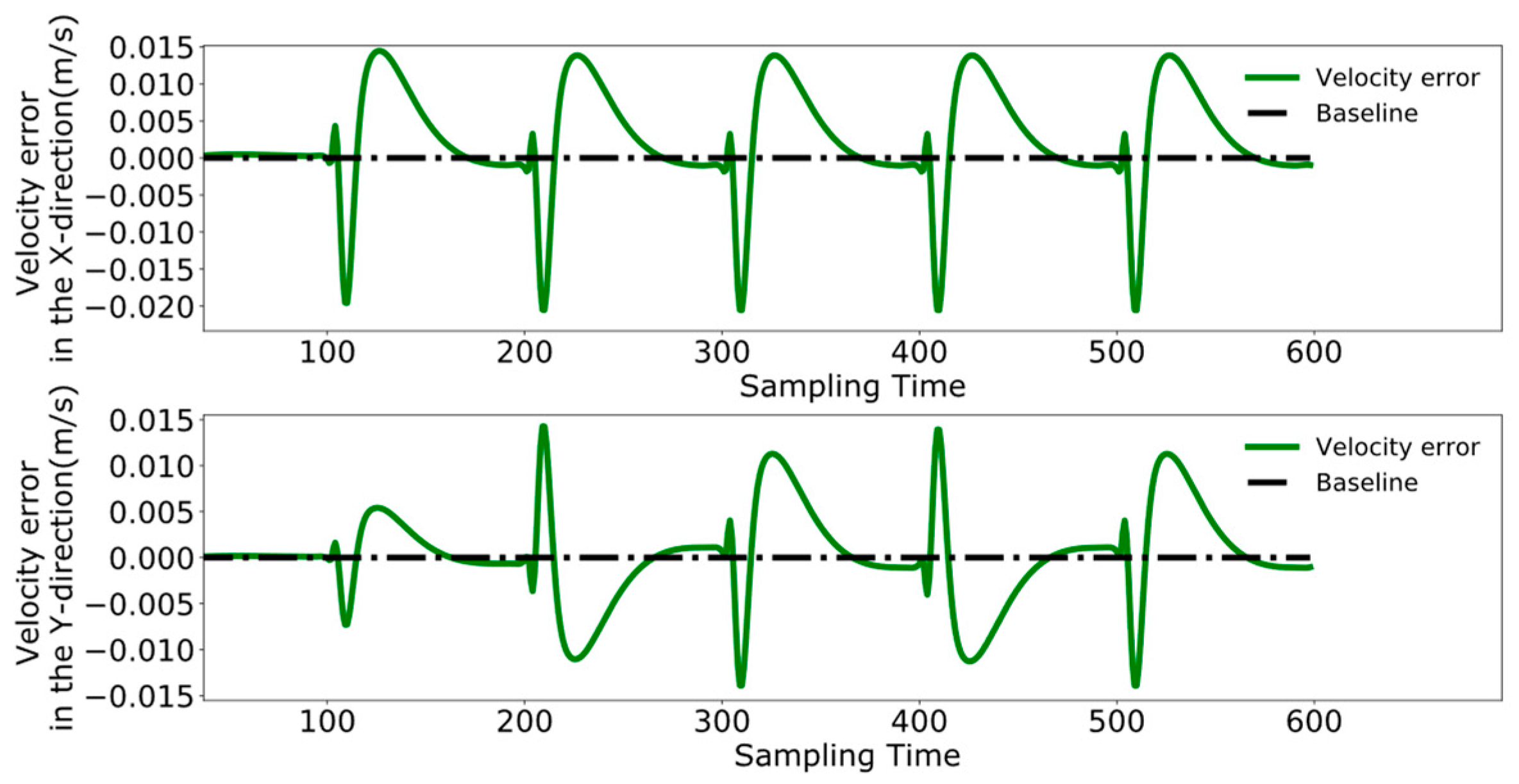
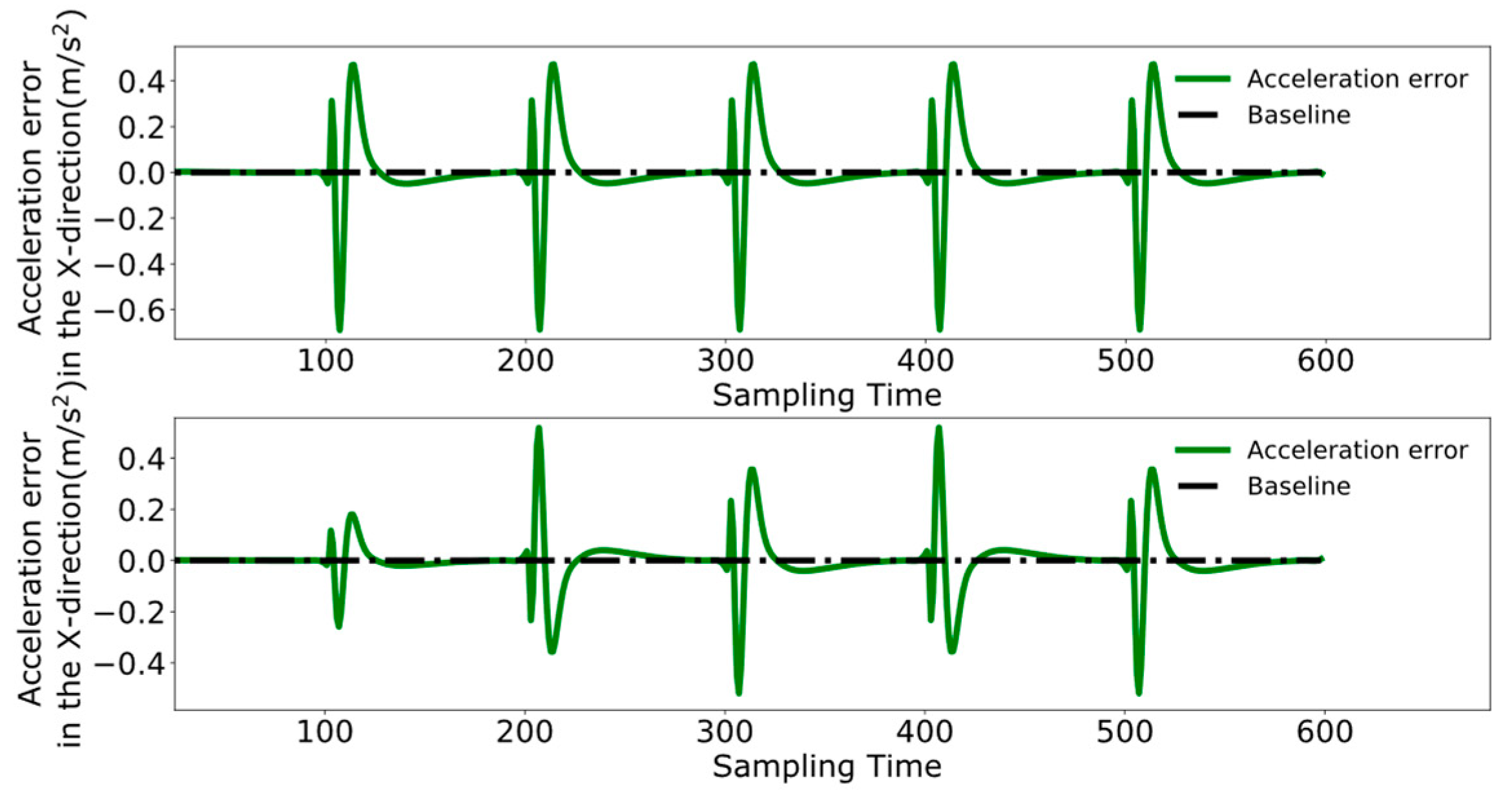
4.3. Dual-Robot Collaborative Transportation Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, X.; Tao, B.; Ding, H. Multimobile Robot Cluster System for Robot Machining of Large-Scale Workpieces. IEEE/ASME Trans. Mechatron. 2022, 27, 561–571. [Google Scholar] [CrossRef]
- Li, B.; Liu, H.; Xiao, D.; Yu, G.; Zhang, Y. Centralized and optimal motion planning for large-scale AGV systems: A generic approach. Adv. Eng. Softw. 2017, 106, 33–46. [Google Scholar] [CrossRef]
- Yu, X.; Ma, J.; Ding, N.; Zhang, A. Cooperative target enclosing control of multiple mobile robots subject to input disturbances. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 3440–3449. [Google Scholar] [CrossRef]
- Hu, Z.; Shi, P.; Wu, L. Polytopic event-triggered robust model predictive control for constrained linear systems. IEEE Trans. Circuits Syst. Regul. Pap. 2021, 68, 2594–2603. [Google Scholar] [CrossRef]
- Ning, B.; Han, Q.L.; Zuo, Z.; Ding, L.; Lu, Q.; Ge, X. Fixed-time and prescribed-time consensus control of multiagent systems and its applications: A survey of recent trends and methodologies. IEEE Trans. Ind. Inform. 2023, 19, 1121–1135. [Google Scholar] [CrossRef]
- Zhang, H.; Feng, T.; Liang, H.; Luo, Y. LQR-based optimal distributed cooperative design for linear discrete-time multiagent systems. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 599–611. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.Z.; Gong, I.W.; Chen, H.Y.; Li, Z.; Gong, C. Tracking and aiming adaptive control for unmanned combat ground vehicle on the move based on reinforcement learning compensation. Acta Armamentarii 2022, 3, 1947–1955. [Google Scholar]
- Li, C.Y.; Guo, Z.C.; Zheng, D.D.; Wei, Y.L. Multi-robot Cooperative Formation Based on Distributed Model Predictive Control. Acta Armamentarii 2023, 44, 178–189. [Google Scholar]
- Shen, C.; Shi, Y. Distributed Implementation of Nonlinear Model Predictive Control for AUV Trajectory Tracking. Automatica 2020, 115, 1626–1640. [Google Scholar] [CrossRef]
- Mohseni, F.; Frisk, E.; Nielsen, L. Distributed Cooperative MPC for Autonomous Driving in Different Traffic Scenarios. IEEE Trans. Intell. Veh. 2020, 6, 299–309. [Google Scholar] [CrossRef]
- Cao, Y.; Wen, J.; Ma, L. Tracking and Collision Avoidance of Virtual Coupling Train Control System. Future Gener. Comput. Syst. 2021, 120, 76–90. [Google Scholar] [CrossRef]
- Wei, H.; Sun, Q.; Chen, J.; Shi, Y. Robust Distributed Model Predictive Platooning Control for Heterogeneous Autonomous Surface Vehicles. Control Eng. Pract. 2021, 107, 533–542. [Google Scholar] [CrossRef]
- Dai, L.; Hao, Y.; Xie, H.; Sun, Z.; Xia, Y. Distributed Robust MPC for Nonholonomic Robots with Obstacle and Collision Avoidance. Control Theory Technol. 2022, 20, 32–45. [Google Scholar] [CrossRef]
- Pan, Z.; Sun, Z.; Deng, H.; Li, D. A Multilayer Graph for Multiagent Formation and Trajectory Tracking Control Based on MPC Algorithm. J. IEEE Trans. Cybern. 2021, 52, 13586–13597. [Google Scholar] [CrossRef]
- Zhou, J.J.; Shi, Z.F. Research on multi-UAY formation flying control method based on improved leader-follower algorithm. In Proceedings of the 4th China Aeronautical Science and Technology Conference, Beijing, China, 14–19 September 2018; China Aviation Publishing & Media Co.: Shenyang, China, 2019; Volume 11. [Google Scholar]
- Munir, M.; Khan, Q.; Ullah, S.; Syeda, T.M.; Algethami, A.A. Control Design for Uncertain Higher-Order Networked Nonlinear Systems via an Arbitrary Order Finite-Time Sliding Mode Control Law. Sensors 2022, 22, 2748. [Google Scholar] [CrossRef] [PubMed]
- Ullah, S.; Khan, Q.; Zaidi, M.M.; Hua, L.G. Neuro-adaptive Non-singular Terminal Sliding Mode Control for Distributed Fixer-time Synchronization of Higher-order Uncertain Multi-agent Nonlinear Systems. Inf. Sci. 2024, 659, 120087. [Google Scholar] [CrossRef]
- Zhang, H.S.; Zhang, H.; Wang, C.S. Collaborative transportation for bulky items based on multi-robot formation control. J. Shandong Univ. 2023, 53, 157–162. [Google Scholar]
- Liu, Q.; Gong, Z.; Nie, Z.; Liu, X.-J. Enhancing the terrain adaptability of a multirobot cooperative transportation system via novel connectors and optimized cooperative strategies. Front. Mech. Eng. 2023, 18, 38. [Google Scholar] [CrossRef]
- Wu, X.; Yu, W.; Lou, P.H. Coordinated Guidance Control for Multi-robot Cooperative Transportations of Large-sized objects. China Mech. Eng. 2022, 33, 1586–1595. [Google Scholar]
- Ding, Y.P.; Zhu, X.J.; Sun, X.Q. Kinematics simulation and control system design of robot. Control. Eng. China 2021, 28, 546–552. [Google Scholar]
- Liu, X.; Li, S.; Liang, T.; Li, J.; Lou, C.; Wang, H. Follow control of upper limb rehabilitation training based on Kinect and NAO robot. J. Biomed. Eng. 2022, 39, 1189–1198. [Google Scholar]
- Mohamed, S.A.; Maged, S.A.; Awad, M.I. A performance comparison between closed form and numerical optimization solutions for humanoid robot walking pattern generation. Int. J. Adv. Robot. Syst. 2021, 18, 17298814211029774. [Google Scholar] [CrossRef]
- Meng, Y.; Zhou, F.N.; Lu, Z.Q.; Wang, P.P. Implementation Method of Predictive control of Five-Centroid Model for Biped Robot. Mach. Des. Manuf. 2022, 3, 254–257. [Google Scholar]
- Neri, F.; Forlini, M.; Scoccia, C.; Palmieri, G.; Callegari, M. Experimental Evaluation of Collision Avoidance Techniques for Collaborative Robots. Appl. Sci. 2023, 13, 2944. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, J.R. Distributed collision avoidance control of UAV formation based on navigation function and model predictive control. Electron. Opt. Control 2023, 30, 100–104. [Google Scholar]
- Wang, Y.; Cang, S.; Yu, H. A Survey on Wearable Sensor Modality Centred Human Activity Recognition in Health Care. Expert Syst. Appl. 2019, 137, 167–190. [Google Scholar] [CrossRef]











| Hardware Components | Parameters |
|---|---|
| CPU | 2 × Intel Atom Z530 Processors |
| Memory | 1 GB RAM, 2 GB Flash Memory |
| Network Connection | Ethernet, Wi-Fi |
| Battery | Lithium Battery |
| Link | /° | /mm | /mm | /° |
|---|---|---|---|---|
| 1 | 0 | 0 | 90 | |
| 2 | (−90°) | 0 | 0 | −90 |
| 3 | d3 | 0 | 90 | |
| 4 | 0 | 0 | −90 | |
| 5 | (−90°) | d5 | 0 | 90 |
| Protocol Field | Data Type |
|---|---|
| Command Content | string |
| Execution Time | datetime |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, S.; Shi, Z.; Li, H. Coordinated Transport by Dual Humanoid Robots Using Distributed Model Predictive Control. Biomimetics 2024, 9, 332. https://doi.org/10.3390/biomimetics9060332
Wen S, Shi Z, Li H. Coordinated Transport by Dual Humanoid Robots Using Distributed Model Predictive Control. Biomimetics. 2024; 9(6):332. https://doi.org/10.3390/biomimetics9060332
Chicago/Turabian StyleWen, Shengjun, Zhaoyuan Shi, and Hongjun Li. 2024. "Coordinated Transport by Dual Humanoid Robots Using Distributed Model Predictive Control" Biomimetics 9, no. 6: 332. https://doi.org/10.3390/biomimetics9060332
APA StyleWen, S., Shi, Z., & Li, H. (2024). Coordinated Transport by Dual Humanoid Robots Using Distributed Model Predictive Control. Biomimetics, 9(6), 332. https://doi.org/10.3390/biomimetics9060332










