Control of Corner Separation in Compressor Cascade Using Biomimetic Fish Scales Structure
Abstract
1. Introduction
2. Numerical Investigation
2.1. The Design Concept
2.2. The Computational Domains
2.2.1. Computational Domain for the Flat Plate
2.2.2. Computational Domain for Compressor Cascade
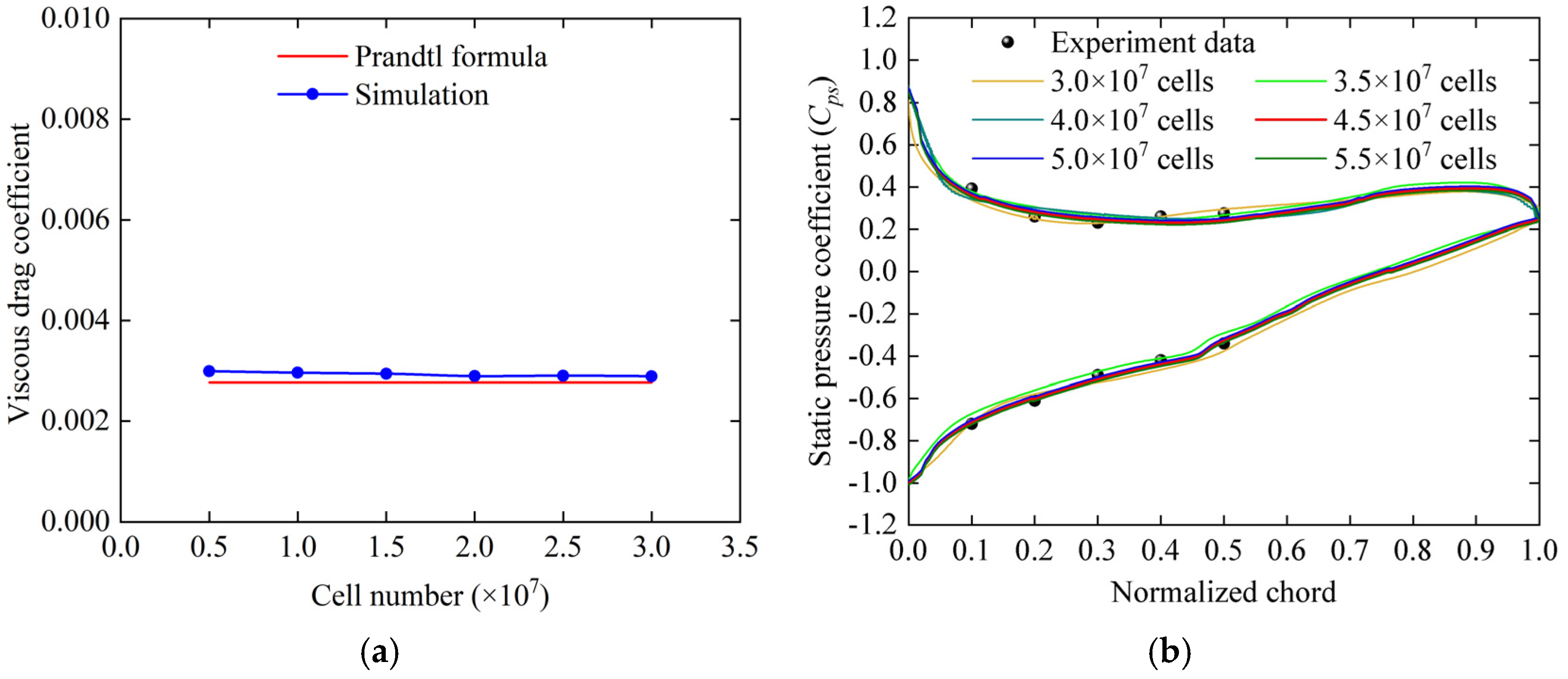
2.3. Grid Independence Analysis
2.4. Numerical Method and Analysis
2.4.1. Viscous Drag Coefficient for the Plate
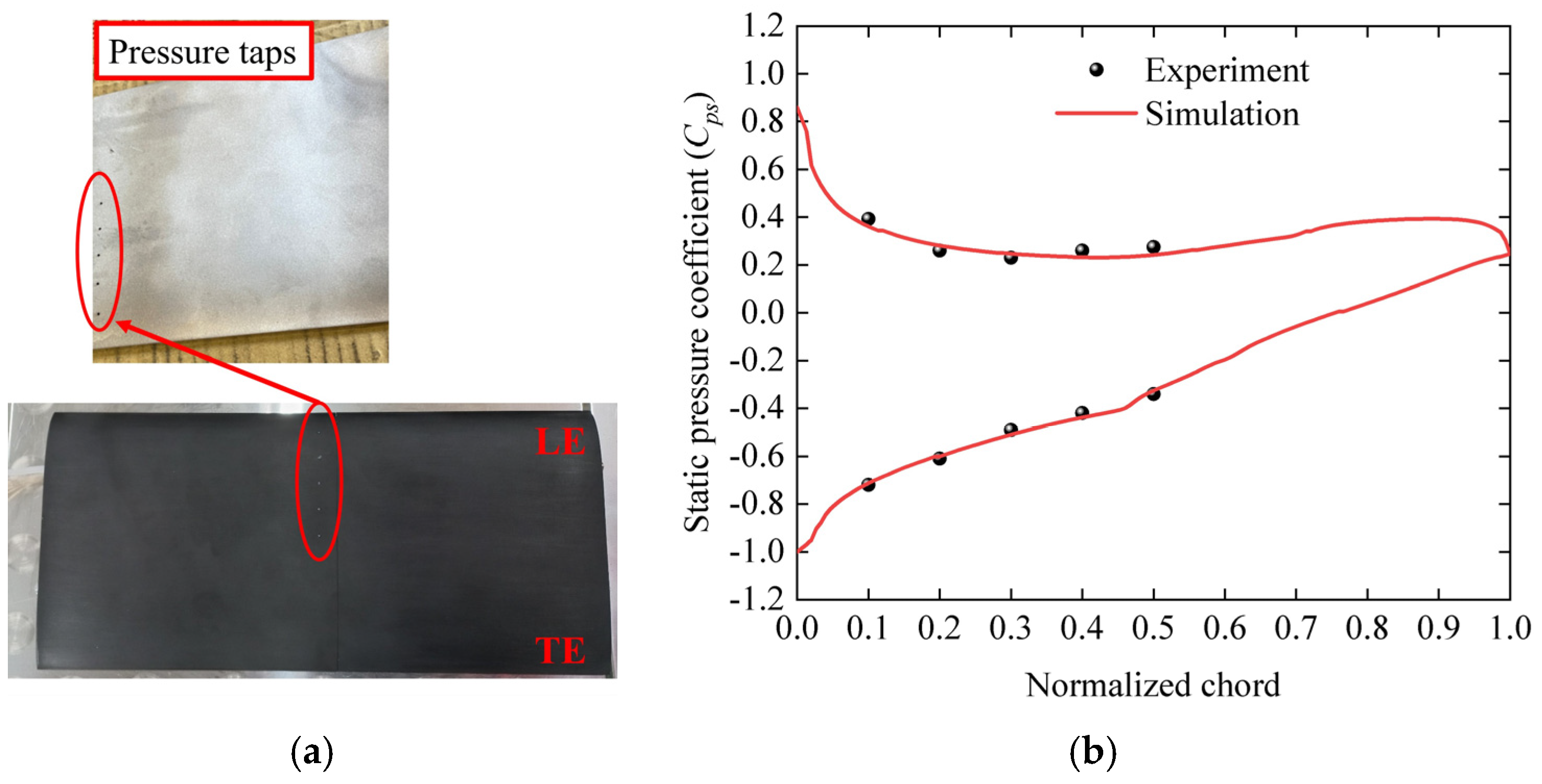
2.4.2. Static Pressure Coefficient for Cascade
2.4.3. Total Pressure Coefficient
2.4.4. Vortex Visualization
3. Results and Discussion
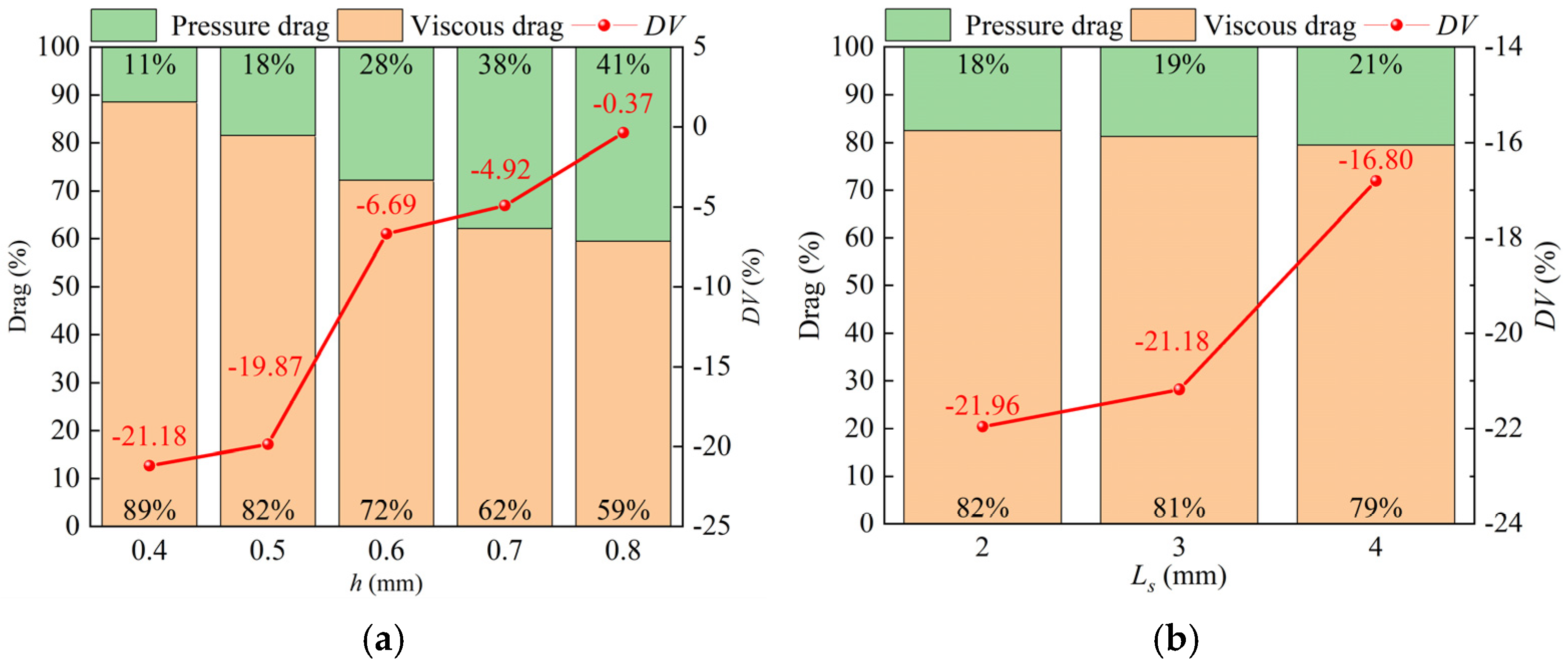
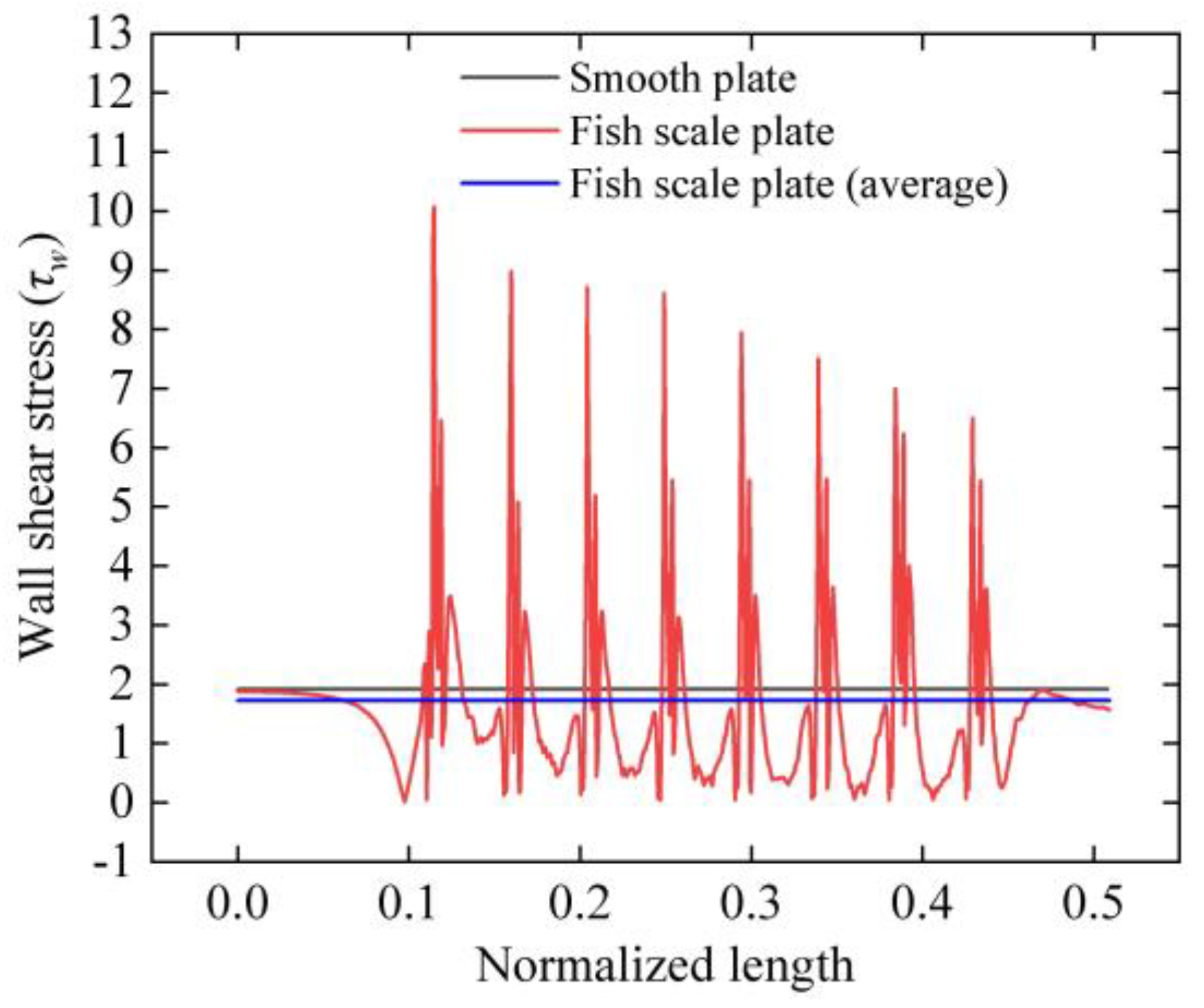
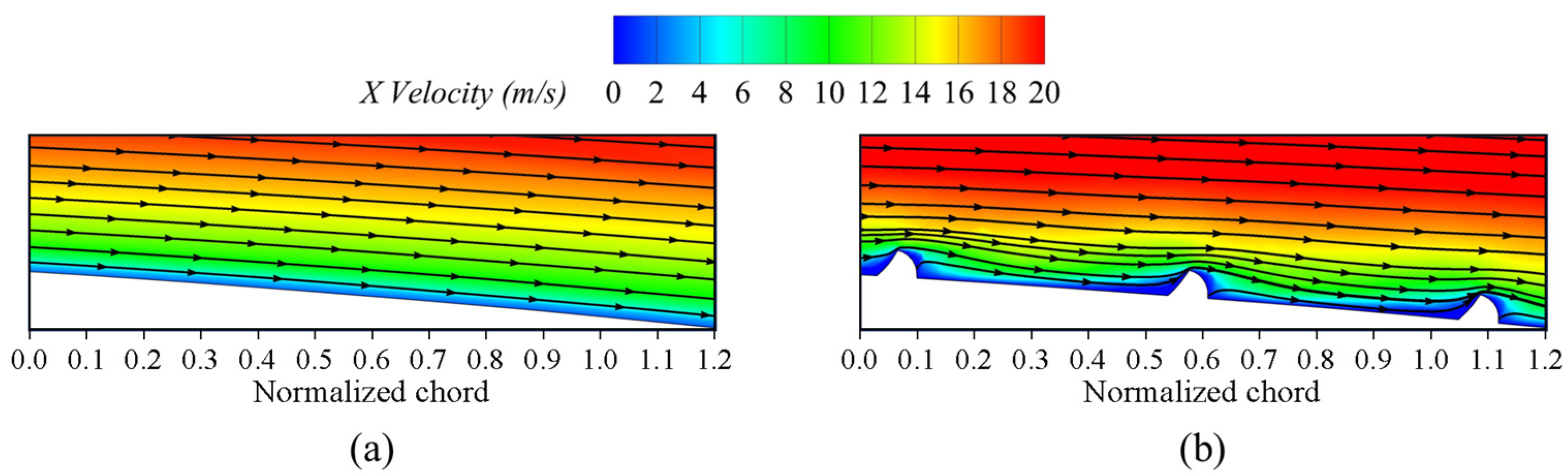
3.1. Drag Reduction Evaluation of Plate
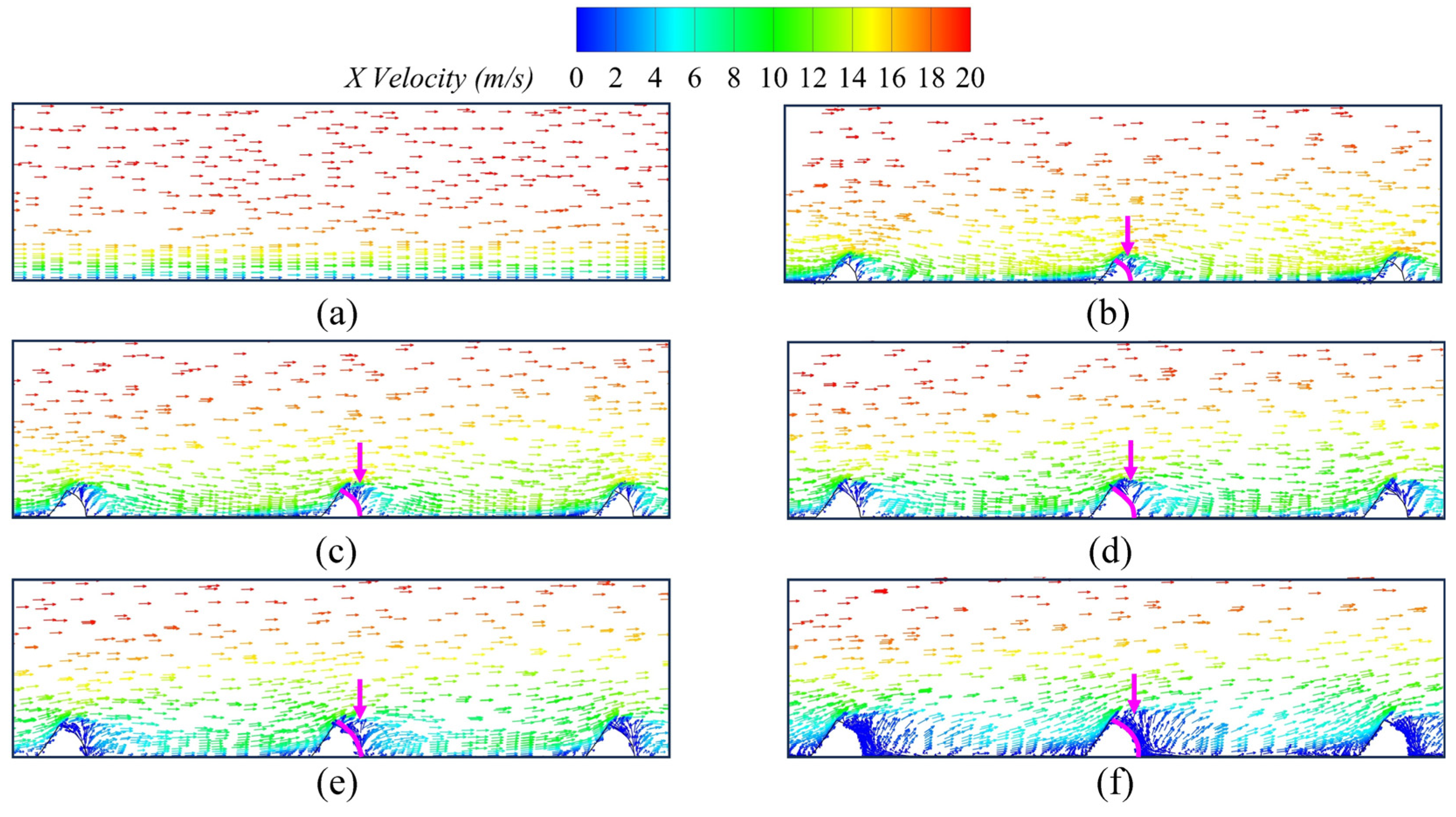
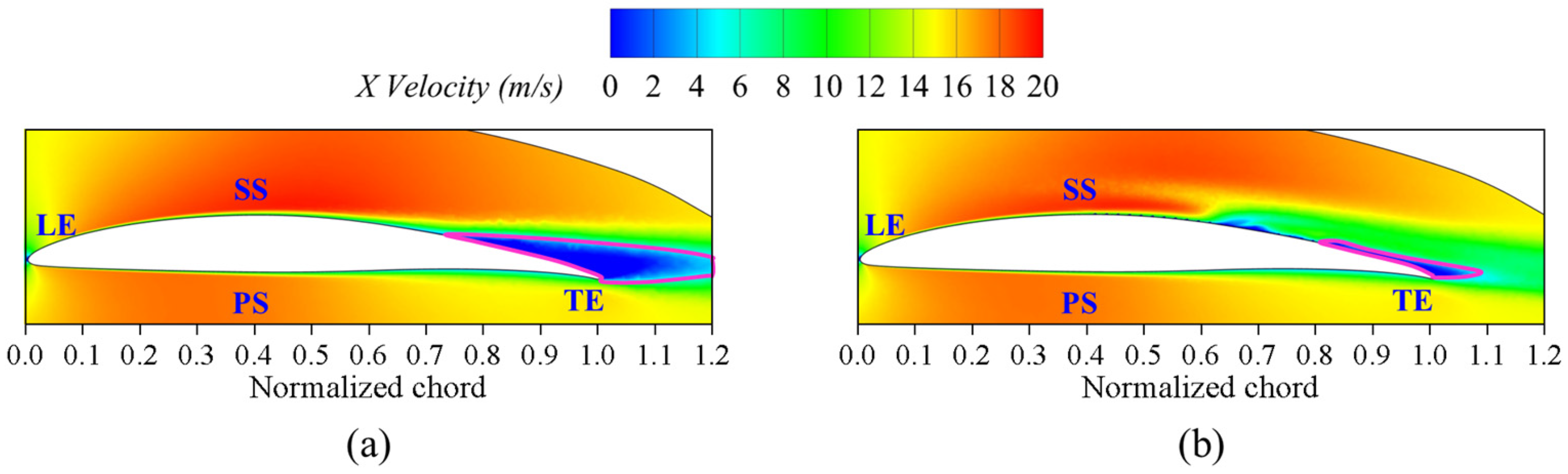
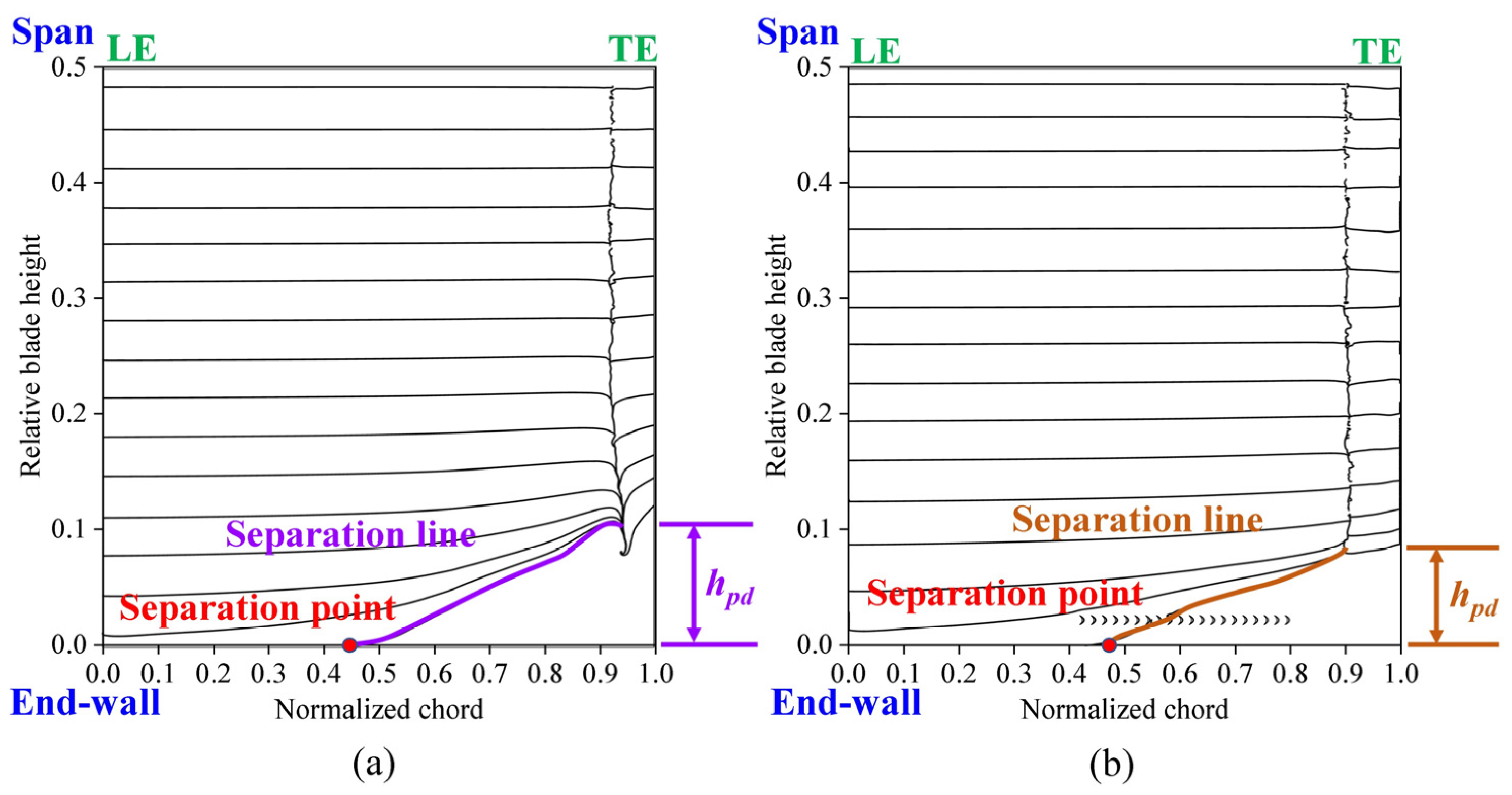
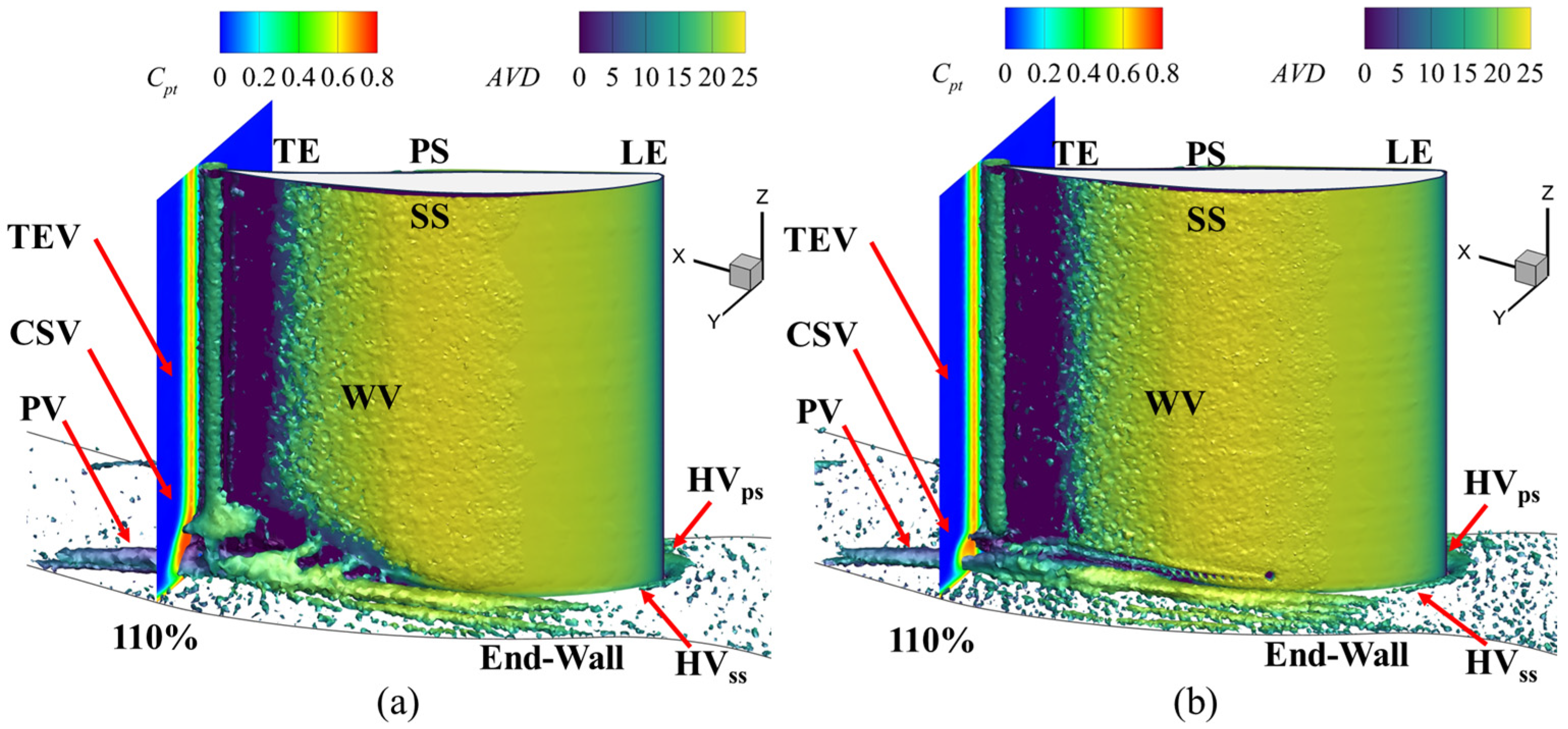
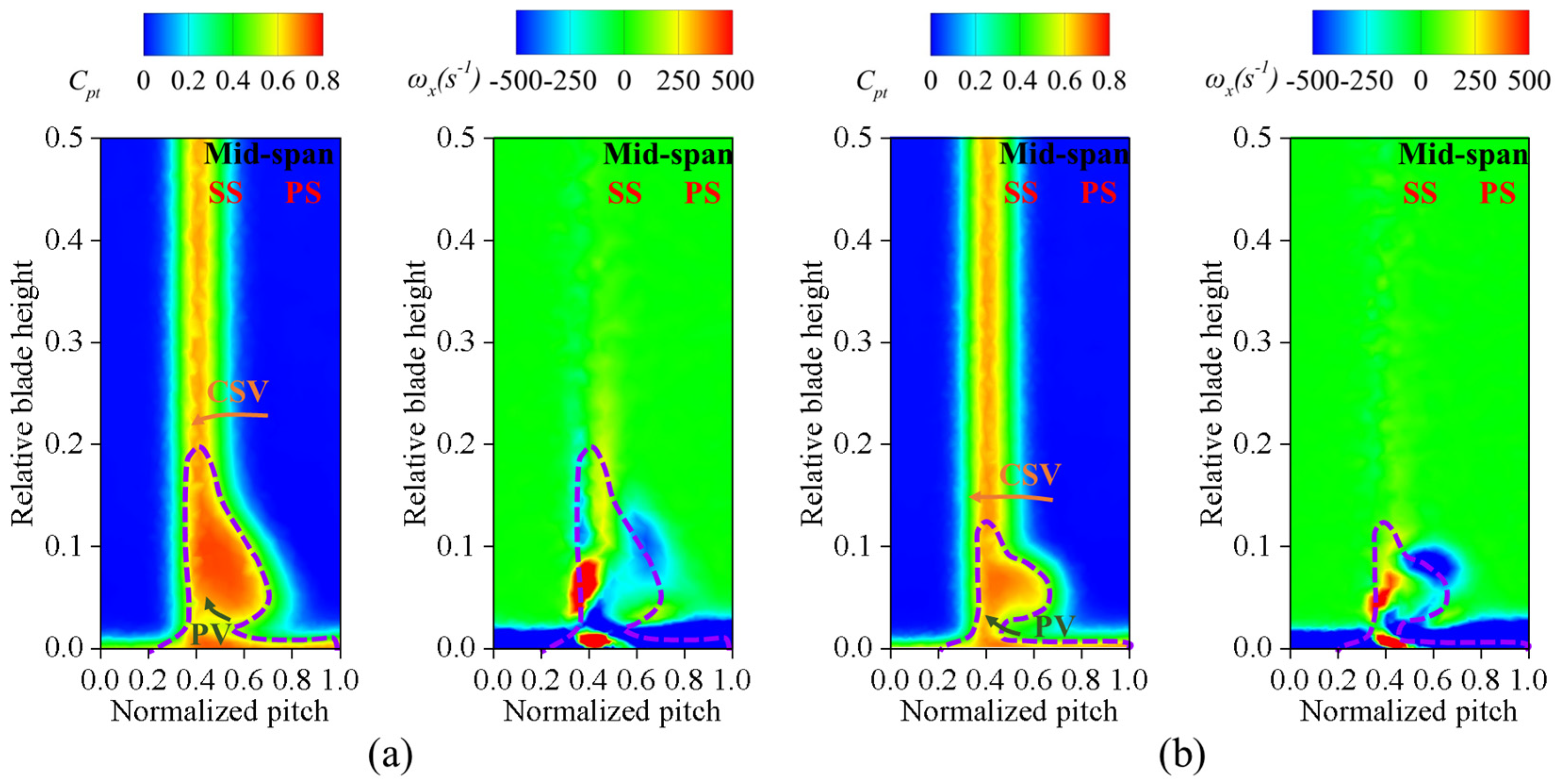
3.2. Flow Field Analysis of Cascade
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yoon, Y.S.; Song, S.J.; Shin, H.-W. Influence of flow coefficient, stagger angle, and tip clearance on tip vortex in axial compressors. J. Fluids Eng. 2006, 128, 1274–1280. [Google Scholar] [CrossRef]
- Wang, B.; Wu, Y. Vortical characteristics of the corner separation flow in a high-speed compressor cascade. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 8300–8320. [Google Scholar] [CrossRef]
- Chen, S.; Gong, Y.; Zeng, C. Pulsed suction towards unsteady active flow control in an axial compressor cascade including clearance leakage effects. Appl. Therm. Eng. 2023, 219, 119654. [Google Scholar] [CrossRef]
- Zhang, H.; Yu, X.; Liu, B.; Wu, Y.; Li, Y. Control of corner separation with plasma actuation in a high-speed compressor cascade. Appl. Sci. 2017, 7, 465. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, S.; Meng, Q.; Wang, S. Flow separation control using unsteady pulsed suction through endwall bleeding holes in a highly loaded compressor cascade. Aerosp. Sci. Technol. 2018, 72, 455–464. [Google Scholar] [CrossRef]
- Li, L.; Song, Y.; Chen, F.; Liu, H. Flow control investigations of steady and pulsed jets in bowed compressor cascades. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Seoul, Republic of Korea, 13–17 June 2016; p. V02AT37A025. [Google Scholar]
- Matejka, M.; Popelka, L.; Safarik, P.; Nozicka, J. Influence of active methods of flow control on compressor blade cascade flow. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Berlin, Republic of Germany, 9–13 June 2008; pp. 591–599. [Google Scholar]
- Liu, H.; Li, D.; Chen, H.; Zhang, D. Effects of vortex generator jet on corner separation/stall in high-turning compressor cascade. Trans. Tianjin Univ. 2016, 22, 555–562. [Google Scholar] [CrossRef]
- Ma, Y.; Teng, J.; Zhu, M.; Qiang, X. Effective strategy of non-axisymmetric endwall contouring in a linear compressor cascade. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2022, 236, 1473–1487. [Google Scholar] [CrossRef]
- Zhong, J.; Wu, W.; Han, S. Research progress of tip winglet technology in compressor. J. Therm. Sci. 2021, 30, 18–31. [Google Scholar] [CrossRef]
- Zhang, P.; Cheng, R.; Li, Y. Numerical Study on the Corner Separation Control for a Compressor Cascade via Bionic Herringbone Riblets. Aerospace 2024, 11, 90. [Google Scholar] [CrossRef]
- Herzog, D.; Seyda, V.; Wycisk, E.; Emmelmann, C. Additive manufacturing of metals. Acta Mater. 2016, 117, 371–392. [Google Scholar] [CrossRef]
- Zhang, D.; Qiu, D.; Gibson, M.A.; Zheng, Y.; Fraser, H.L.; StJohn, D.H.; Easton, M.A. Additive manufacturing of ultrafine-grained high-strength titanium alloys. Nature 2019, 576, 91–95. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Mandal, S.; Barui, S.; Vasireddi, R.; Gbureck, U.; Gelinsky, M.; Basu, B. Low temperature additive manufacturing of three dimensional scaffolds for bone-tissue engineering applications: Processing related challenges and property assessment. Mater. Sci. Eng. R Rep. 2016, 103, 1–39. [Google Scholar] [CrossRef]
- Nune, K.; Kumar, A.; Murr, L.; Misra, R. Interplay between self-assembled structure of bone morphogenetic protein-2 (BMP-2) and osteoblast functions in three-dimensional titanium alloy scaffolds: S timulation of osteogenic activity. J. Biomed. Mater. Res. Part A 2016, 104, 517–532. [Google Scholar] [CrossRef] [PubMed]
- Haque, F.; Luscher, A.F.; Mitchell, K.-A.S.; Sutradhar, A. Optimization of Fixations for Additively Manufactured Cranial Implants: Insights from Finite Element Analysis. Biomimetics 2023, 8, 498. [Google Scholar] [CrossRef] [PubMed]
- Oehlert, K.; Seume, J.R.; Siegel, F.; Ostendorf, A.; Wang, B.; Denkena, B.; Vynnyk, T.; Reithmeier, E.; Hage, W.; Knobloch, K. Exploratory experiments on machined riblets for 2-D compressor blades. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Seattle, WA, USA, 11–15 November 2007; pp. 25–39. [Google Scholar]
- Zhou, H.; Liu, C.; Tian, G.; Feng, X.; Jia, C. Research on the drag reduction property of puffer (Takifugu flavidus) spinal nonsmooth structure surface. Microsc. Res. Tech. 2020, 83, 795–803. [Google Scholar] [CrossRef]
- Liu, P.; Zhu, D.; Wang, J.; Bui, T.Q. Structure, mechanical behavior and puncture resistance of grass carp scales. J. Bionic Eng. 2017, 14, 356–368. [Google Scholar] [CrossRef]
- Wu, L.; Jiao, Z.; Song, Y.; Ren, W.; Niu, S.; Han, Z. Water-trapping and drag-reduction effects of fish Ctenopharyngodon idellus scales and their simulations. Sci. China Technol. Sci. 2017, 60, 1111–1117. [Google Scholar] [CrossRef]
- Wu, L.; Jiao, Z.; Song, Y.; Liu, C.; Wang, H.; Yan, Y. Experimental investigations on drag-reduction characteristics of bionic surface with water-trapping microstructures of fish scales. Sci. Rep. 2018, 8, 12186. [Google Scholar] [CrossRef]
- Qu, A.; Li, F. Influence of 3D printing on compressor impeller fatigue crack propagation life. Int. J. Mech. Sci. 2023, 245, 108107. [Google Scholar] [CrossRef]
- Su, L.; Qiang, X.; Zheng, T.; Teng, J. Effect of undulating blades on highly loaded compressor cascade performance. Proc. Inst. Mech. Eng. Part A J. Power Energy 2021, 235, 17–28. [Google Scholar] [CrossRef]
- Meyer, R.; Bechert, D.; Hage, W. Secondary flow control on compressor blades to improve the performance of axial turbomachines. In Proceedings of the Proceedings 5th European Conference on Turbomachinery, Prag, Tschechische Republik, Prague, Czech Republic, 17–22 March 2003. [Google Scholar]
- Hergt, A.; Meyer, R.; Engel, K. Effects of vortex generator application on the performance of a compressor cascade. J. Turbomach. 2013, 135, 021026. [Google Scholar] [CrossRef]
- Diaa, A.M.; El-Dosoky, M.F.; Ahmed, M.A.; Abdel-Hafez, O.E. Boundary layer control of an axial compressor cascade using nonconventional vortex generators. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 13–19 November 2015; p. V001T001A044. [Google Scholar]
- Hu, J.; Wang, R.; Huang, D. Improvements of performance and stability of a single-stage transonic axial compressor using a combined flow control approach. Aerosp. Sci. Technol. 2019, 86, 283–295. [Google Scholar] [CrossRef]
- Benner, M.W.; Sjolander, S.; Moustapha, S. An empirical prediction method for secondary losses in turbines—Part I: A new loss breakdown scheme and penetration depth correlation. J. Turbomach. 2006, 128, 273–280. [Google Scholar] [CrossRef]
- Benner, M.W.; Sjolander, S.; Moustapha, S. An empirical prediction method for secondary losses in turbines—Part II: A new secondary loss correlation. J. Turbomach. 2006, 128, 281–291. [Google Scholar] [CrossRef]
- Wang, B.; Wu, Y.; Spence, S. Loss reduction in a high-speed compressor cascade using an L-shaped endwall groove to generate a streamwise vortex. Aerosp. Sci. Technol. 2022, 123, 107486. [Google Scholar] [CrossRef]
- Hergt, A.; Meyer, R.; Engel, K. Experimental investigation of flow control in compressor cascades. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; pp. 231–240. [Google Scholar]
- Wang, L.; Wang, C.; Lan, X.; Sun, G.; You, B.; Zhong, Y.; Hu, Y. High-fidelity surface flow data-driven aerodynamic solution strategy for non-smooth configurations: Study of compressor cascade with micro riblet surface. Phys. Fluids 2022, 34, 127114. [Google Scholar] [CrossRef]
- Herrig, L.J.; Emery, J.C.; Erwin, J.R. Effect of Section Thickness and Trailing-Edge Radius on the Performance of NACA 65-Series Compressor Blades in Cascade at Low Speeds; NASA Technical Reports Server Report NACA-RM-L51J16; NASA: Washington, DC, USA, 1951. [Google Scholar]
- Herrig, L.J.; Emery, J.C.; Erwin, J.R. Systematic Two-Dimensional Cascade Tests of NACA 65-Series Compressor Blades at Low Speeds; NASA: Washington, DC, USA, 1957. [Google Scholar]
- Fluent, A. Ansys Fluent Theory Guide; NASA Technical Reports Server Report NACA-RM-L51G31; NASA: Washington, DC, USA, 2018. [Google Scholar]
- Lazauskas, L.V. Hydrodynamics of Advanced High-Speed Sealift Vessels. Master’s Thesis, The University of Adelaide, Adelaide, Australia, 2005. [Google Scholar]
- Hunt, J.C.; Wray, A.A.; Moin, P. Eddies, streams, and convergence zones in turbulent flows. In Studying Turbulence Using Numerical Simulation Databases, 2. Proceedings of the 1988 Summer Program; NASA Technical Reports Server Report Accession Number 89N24555; NASA: Washington, DC, USA, 1988. [Google Scholar]
- Langston, L. Secondary flows in axial turbines—A review. Ann. N. Y. Acad. Sci. 2001, 934, 11–26. [Google Scholar] [CrossRef]
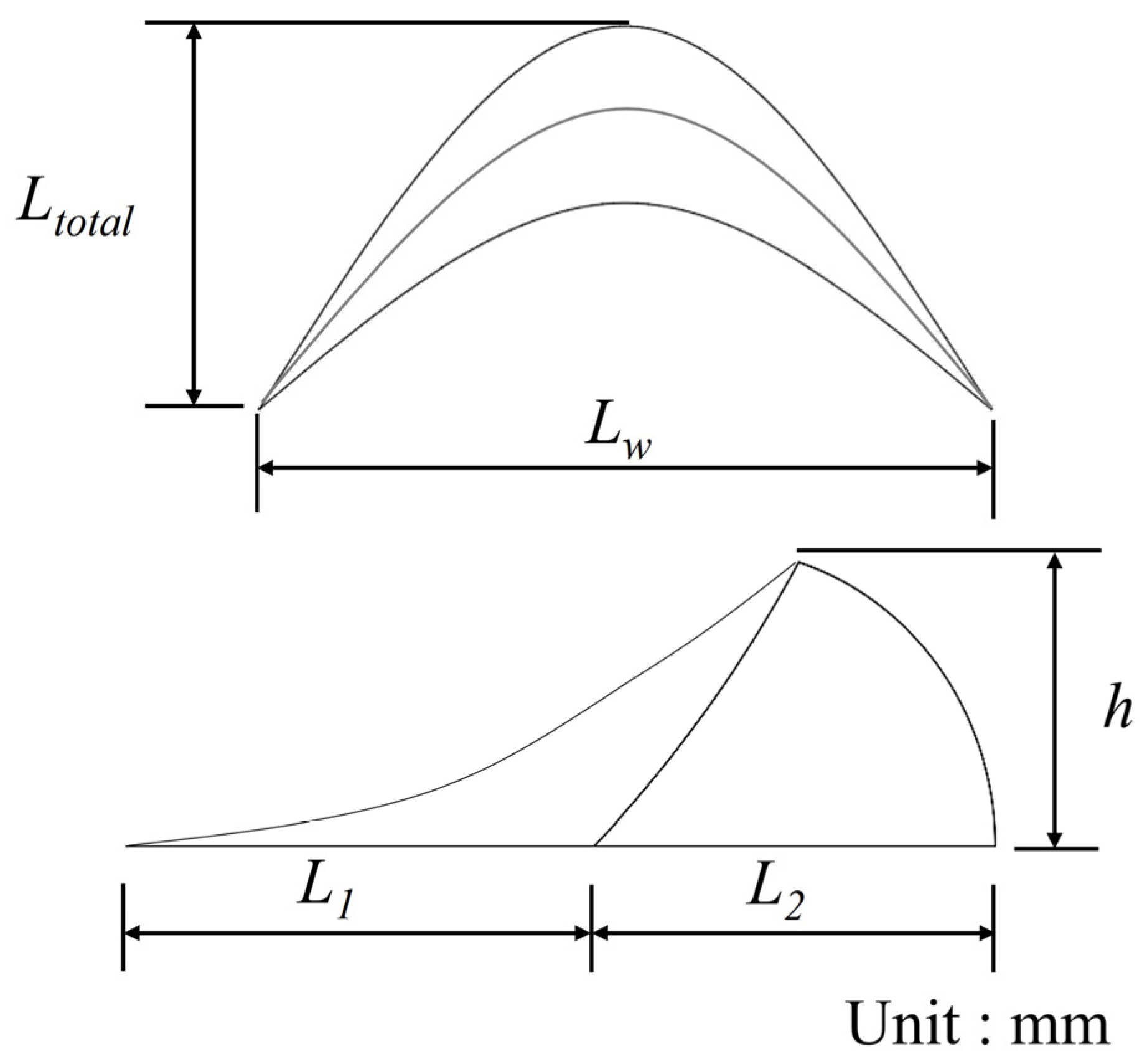
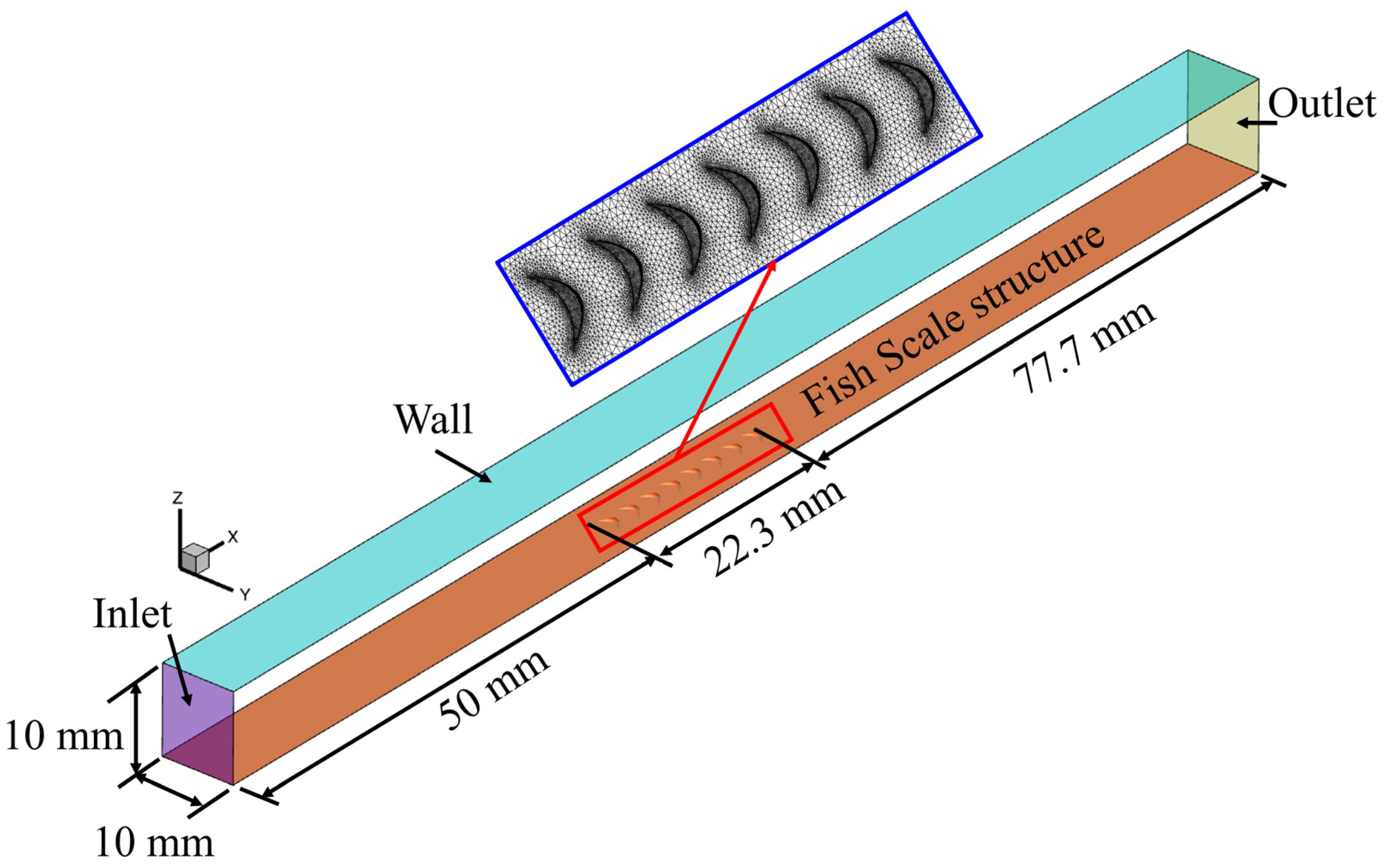
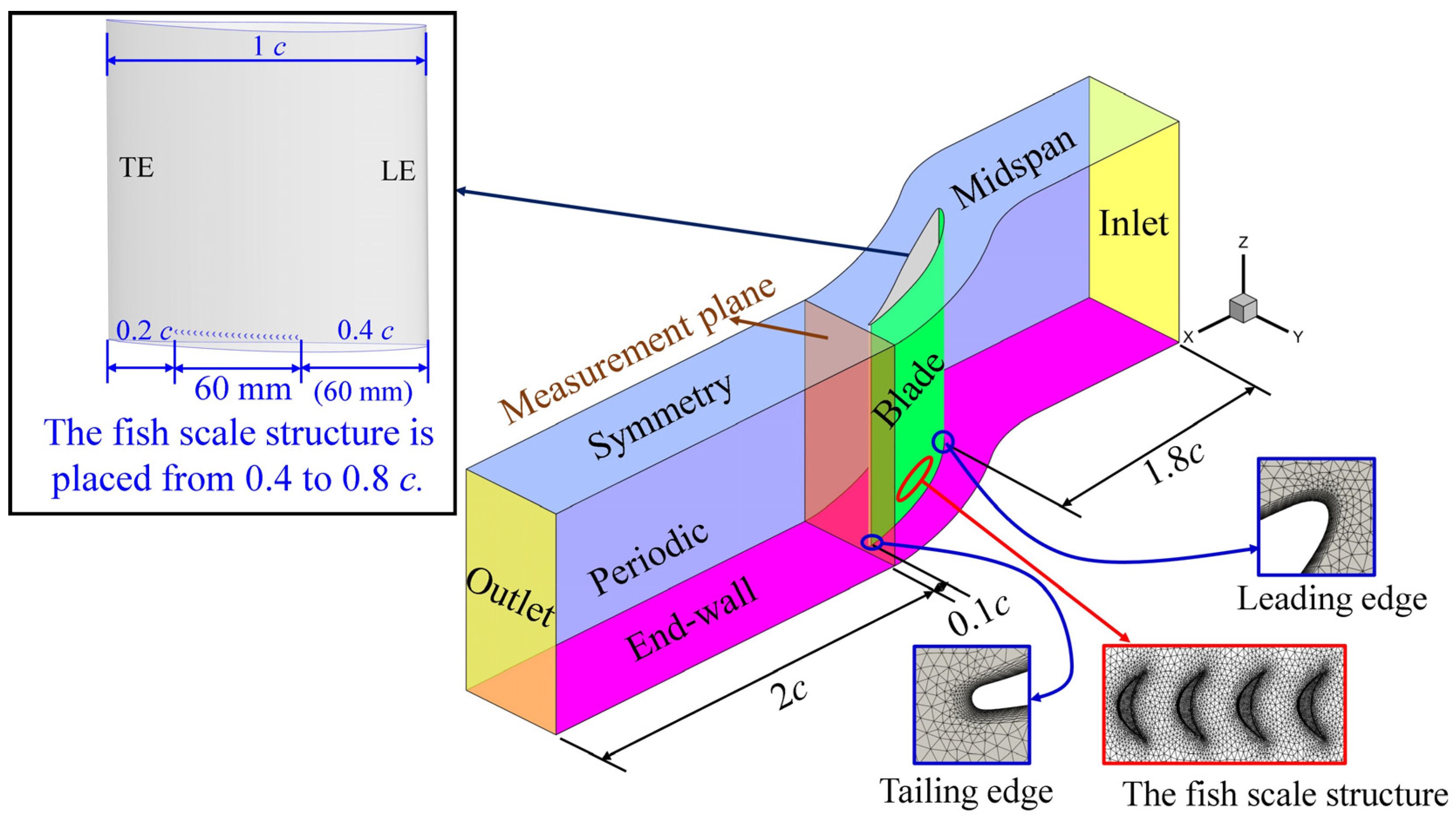


| Case | Scale Height () [mm] | Scale Width () [mm] | Scale Length () [mm] | Scale Front Length () [mm] | Scale Back Length () [mm] |
|---|---|---|---|---|---|
| 1 | 0.4 | 2.5 | 1.3 | 0.7 | 0.6 |
| 2 | 0.5 | 3.125 | 1.625 | 0.875 | 0.75 |
| 3 | 0.6 | 3.75 | 1.95 | 1.05 | 0.9 |
| 4 | 0.7 | 4.375 | 2.275 | 1.225 | 1.05 |
| 5 | 0.8 | 5 | 2.6 | 1.4 | 1.2 |
| Parameter | Value |
|---|---|
| Blade span, [mm] | 315 |
| Chord length, [mm] | 150 |
| Pitch, [mm] | 78 |
| Solidity, | 1.92 |
| Inlet flow angle, [°] | 45 |
| Outlet flow angle, [°] | 22.5 |
| Angle of attack, [°] | 15 |
| Inlet velocity [m/s] | 20 |
| Viscous Drag Coefficient (CF) | Viscous Drag Coefficient (Cf) | Error (Cf − CF)/CF × 100% |
|---|---|---|
| 0.002766 | 0.002891 | 4.54% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, J.-L.; Yeh, S.-I. Control of Corner Separation in Compressor Cascade Using Biomimetic Fish Scales Structure. Biomimetics 2024, 9, 746. https://doi.org/10.3390/biomimetics9120746
Shen J-L, Yeh S-I. Control of Corner Separation in Compressor Cascade Using Biomimetic Fish Scales Structure. Biomimetics. 2024; 9(12):746. https://doi.org/10.3390/biomimetics9120746
Chicago/Turabian StyleShen, Jin-Long, and Szu-I Yeh. 2024. "Control of Corner Separation in Compressor Cascade Using Biomimetic Fish Scales Structure" Biomimetics 9, no. 12: 746. https://doi.org/10.3390/biomimetics9120746
APA StyleShen, J.-L., & Yeh, S.-I. (2024). Control of Corner Separation in Compressor Cascade Using Biomimetic Fish Scales Structure. Biomimetics, 9(12), 746. https://doi.org/10.3390/biomimetics9120746






