Mimicking Marker Spread After Disruption of the Blood–Brain Barrier with a Collagen-Based Hydrogel Phantom
Abstract
1. Introduction
2. Materials and Methods
3. Results
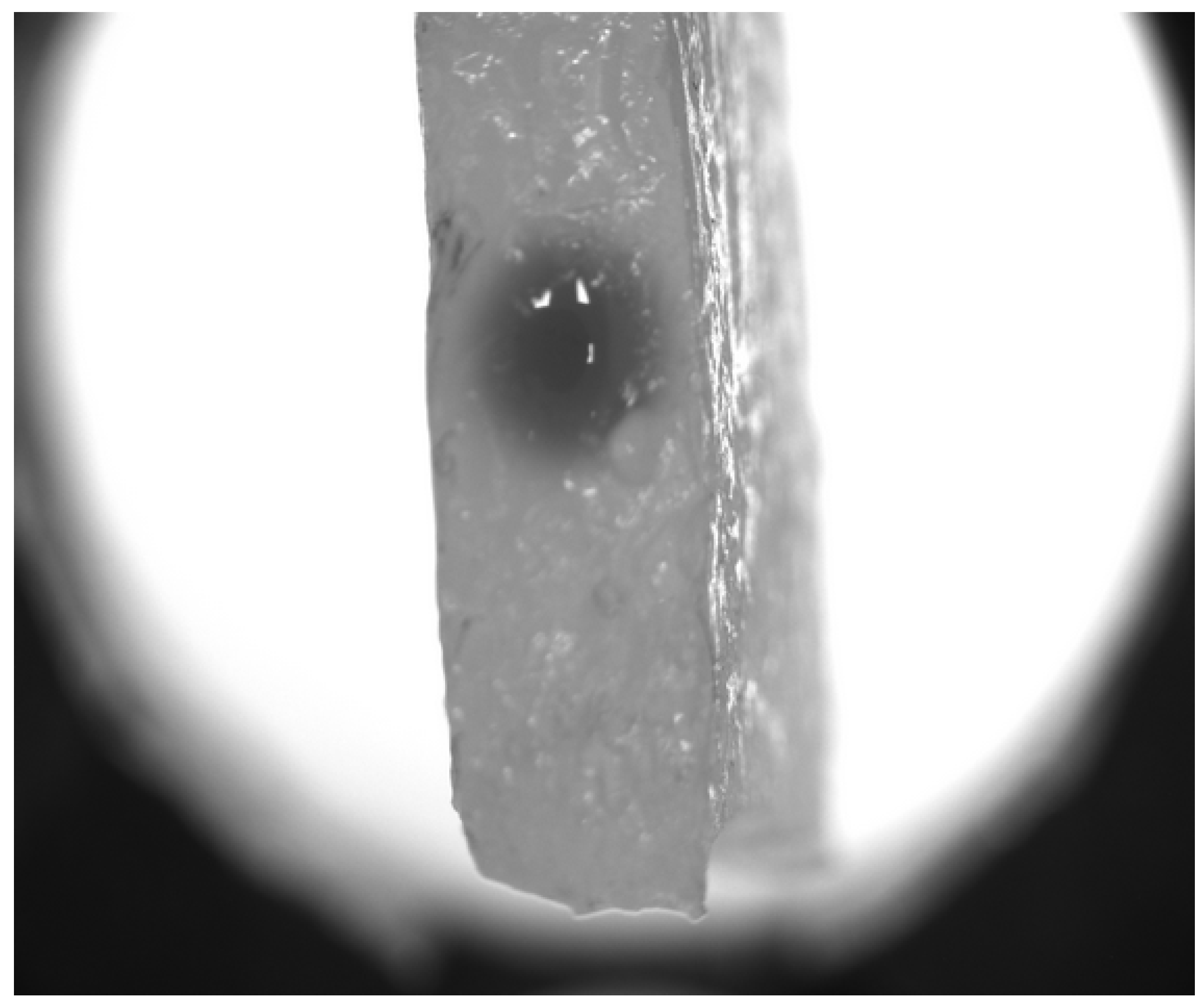
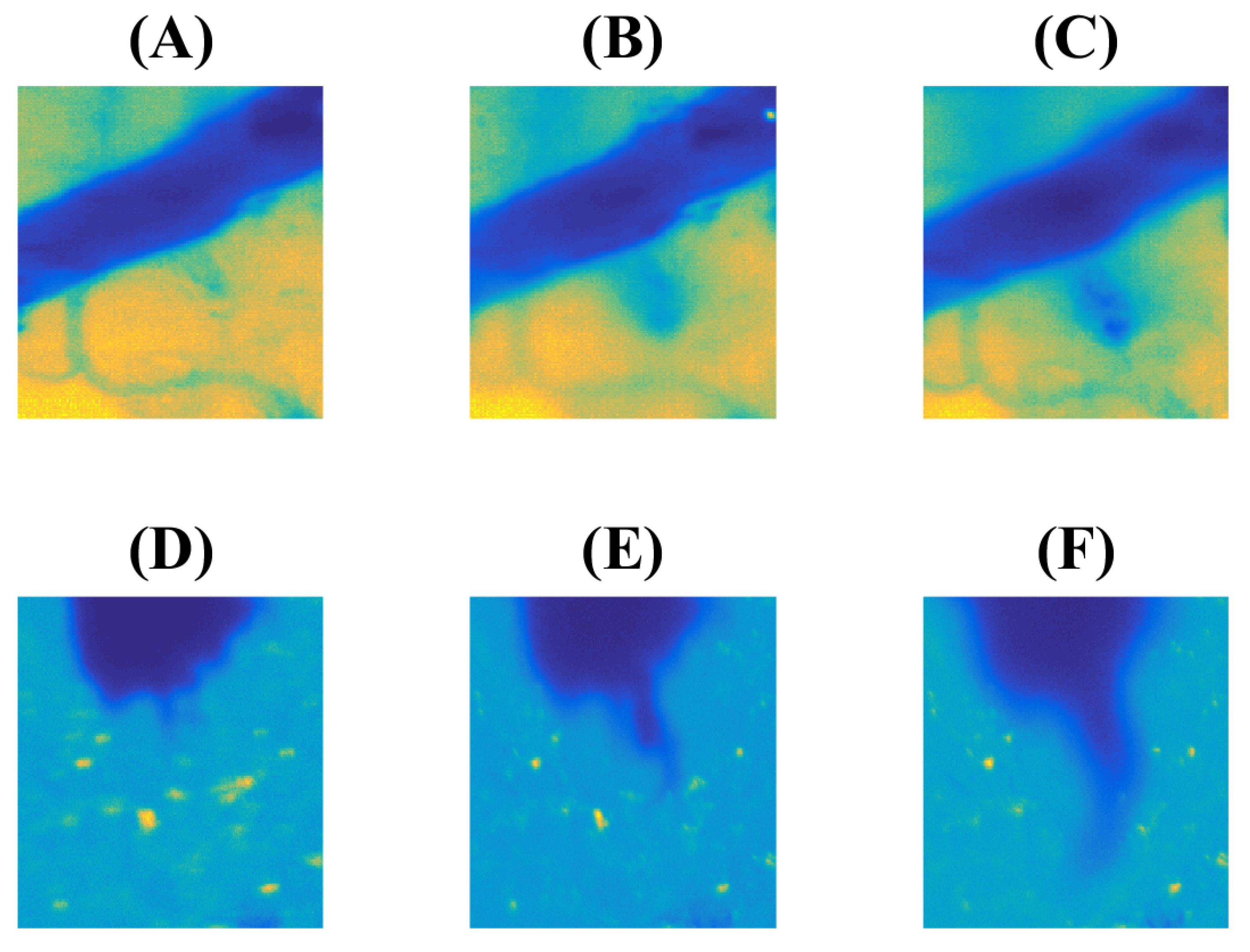
3.1. Experiment
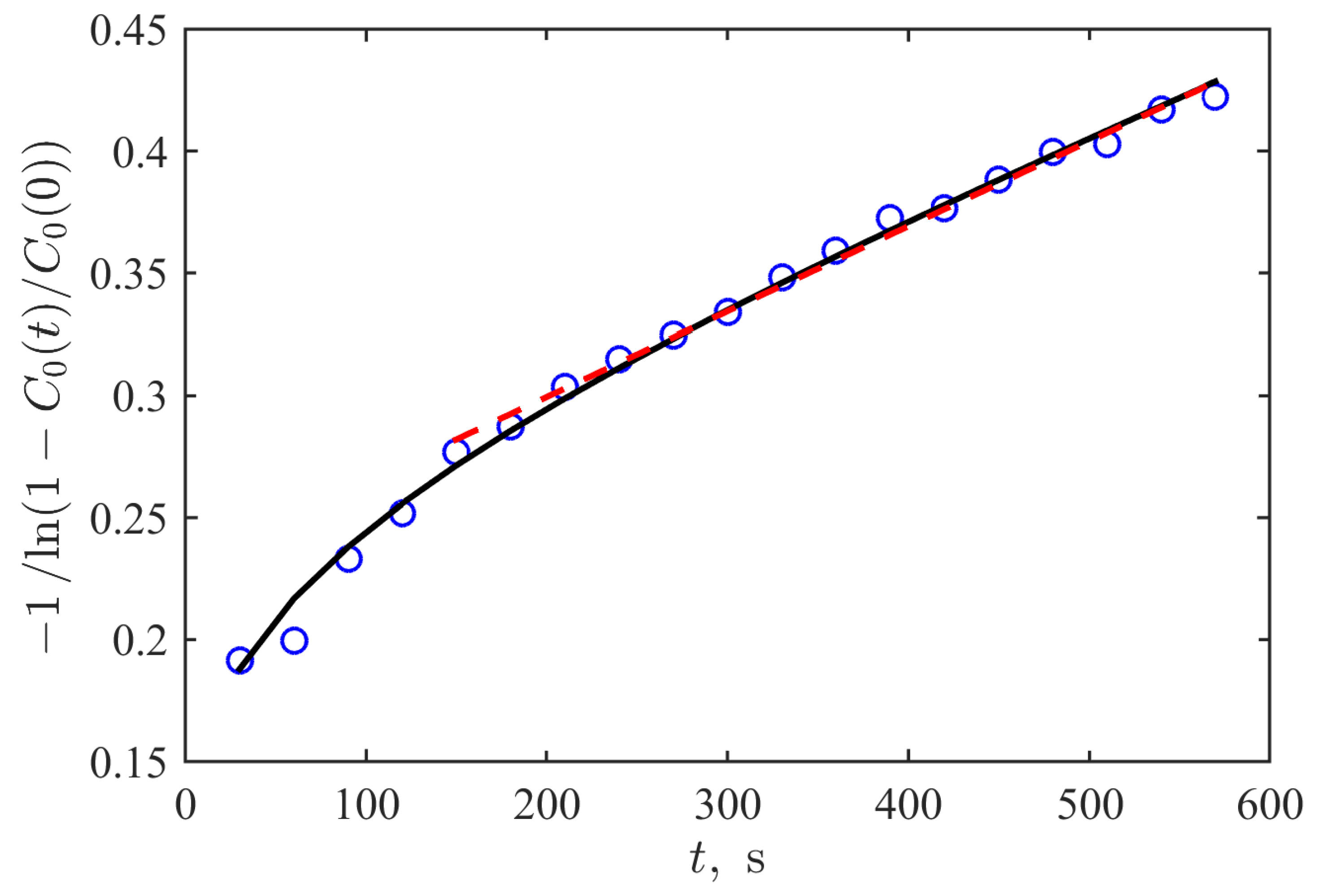
3.2. Mathematical Modeling
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Pandit, R.; Chen, L.; Götz, J. The blood-brain barrier: Physiology and strategies for drug delivery. Adv. Drug Deliv. Rev. 2020, 165, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Chen, Q.; Chen, X.; Han, F.; Chen, Z.; Wang, Y. The blood–brain barrier: Structure, regulation, and drug delivery. Signal Transduct. Target. Ther. 2023, 8, 217. [Google Scholar] [CrossRef]
- Thrippleton, M.J.; Backes, W.H.; Sourbron, S.; Ingrisch, M.; van Osch, M.J.P.; Dichgans, M.; Fazekas, F.; Ropele, S.; Frayne, R.; van Oostenbrugge, R.J.; et al. Quantifying blood-brain barrier leakage in small vessel disease: Review and consensus recommendations. Alzheimer’s Dement. 2019, 15, 840–858. [Google Scholar] [CrossRef] [PubMed]
- Semyachkina-Glushkovskaya, O.; Postnov, D.; Kurths, J. Blood–brain barrier, lymphatic clearance, and recovery: Ariadne’s thread in labyrinths of hypotheses. Int. J. Mol. Sci. 2018, 19, 3818. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Guo, Y.; Zhang, C.; Zeng, Y.; Luo, Y.; Wang, G. Clearance systems in the brain, from structure to function. Front. Cell. Neurosci. 2022, 15, 729706. [Google Scholar] [CrossRef] [PubMed]
- Postnikov, E.B.; Namykin, A.A.; Semyachkina-Glushkovskaya, O.V.; Postnov, D.E. Diffusion assessment through image processing: Beyond the point-source paradigm. Eur. Phys. J. Plus 2021, 136, 480. [Google Scholar] [CrossRef]
- Conti, A.; Magnin, R.; Gerstenmayer, M.; Tsapis, N.; Dumont, E.; Tillement, O.; Lux, F.; Le Bihan, D.; Mériaux, S.; Della Penna, S.; et al. Empirical and Theoretical Characterization of the Diffusion Process of Different Gadolinium-Based Nanoparticles within the Brain Tissue after Ultrasound-Induced Permeabilization of the Blood-Brain Barrier. Contrast Media Mol. Imaging 2019, 2019, 6341545. [Google Scholar] [CrossRef]
- Postnikov, E.B.; Lavrova, A.I.; Postnov, D.E. Transport in the brain extracellular space: Diffusion, but which kind? Int. J. Mol. Sci. 2022, 23, 12401. [Google Scholar] [CrossRef]
- Lang, G.E.; Vella, D.; Waters, S.L.; Goriely, A. Mathematical modelling of blood–brain barrier failure and oedema. Math. Med. Biol. 2017, 34, 391–414. [Google Scholar] [CrossRef]
- Hassanzadeganroudsari, M.; Soltani, M.; Heydarinasab, A.; Nakhjiri, A.T.; Hossain, M.D.K.; Khiyavi, A.A. Mathematical modeling and simulation of molecular mass transfer across blood brain barrier in brain capillary. J. Mol. Liq. 2020, 310, 113254. [Google Scholar] [CrossRef]
- Neumaier, F.; Zlatopolskiy, B.D.; Neumaier, B. Drug penetration into the central nervous system: Pharmacokinetic concepts and in vitro model systems. Pharmaceutics 2021, 13, 1542. [Google Scholar] [CrossRef] [PubMed]
- Ferro, M.P.; Heilshorn, S.C.; Owens, R.M. Materials for blood brain barrier modeling in vitro. Mater. Sci. Eng. R Rep. 2020, 140, 100522. [Google Scholar] [CrossRef] [PubMed]
- Tan, S.Y.; Feng, X.; Cheng, L.K.W.; Wu, A.R. Vascularized human brain organoid on-chip. Lab Chip 2023, 23, 2693–2709. [Google Scholar] [CrossRef] [PubMed]
- Aazmi, A.; Zhou, H.; Lv, W.; Yu, M.; Xu, X.; Yang, H.; Zhang, Y.S.; Ma, L. Vascularizing the brain in vitro. Iscience 2022, 25, 104110. [Google Scholar] [CrossRef]
- Potjewyd, G.; Kellett, K.A.B.; Hooper, N.M. 3D hydrogel models of the neurovascular unit to investigate blood–brain barrier dysfunction. Neuronal Signal. 2021, 5, NS20210027. [Google Scholar] [CrossRef]
- Royse, M.K.; Fowler, M.; Mai, A.K.; He, Y.; Durante, M.R.; Buist, N.; Procopio, A.; Xu, J.; Veiseh, O. Development of a 3D printed perfusable in vitro blood–brain barrier model for use as a scalable screening tool. Biomater. Sci. 2024, 12, 4363–4375. [Google Scholar] [CrossRef]
- Pérez-López, A.; Torres-Suárez, A.I.; Martín-Sabroso, C.; Aparicio-Blanco, J. An overview of in vitro 3D models of the blood-brain barrier as a tool to predict the in vivo permeability of nanomedicines. Adv. Drug Deliv. Rev. 2023, 196, 114816. [Google Scholar] [CrossRef] [PubMed]
- Alekou, T.; Giannakou, M.; Damianou, C. Focused ultrasound phantom model for blood brain barrier disruption. Ultrasonics 2021, 110, 106244. [Google Scholar] [CrossRef] [PubMed]
- Agathe, F.; Yasuhiro, N.; Yukari, S.M.; Tomomi, F.; Kaoru, S.; Matsusaki, M. An in vitro self-organized three-dimensional model of the blood-brain barrier microvasculature. Biomed. Mater. 2020, 16, 015006. [Google Scholar] [CrossRef]
- Oh, H.; Kang, M.; Bae, E.; Jung, Y.; Cho, J.; Poirier, J.; Kim, J.S.; Frampton, J.P.; Choi, N.; Chung, S. Fabrication of hydrogel microchannels using aqueous two-phase printing for 3D blood brain barrier. BioChip J. 2023, 17, 369–383. [Google Scholar] [CrossRef]
- Rauti, R.; Renous, N.; Maoz, B.M. Mimicking the brain extracellular matrix in vitro: A review of current methodologies and challenges. Isr. J. Chem. 2020, 60, 1141–1151. [Google Scholar] [CrossRef]
- Ozgun, A.; Lomboni, D.; Arnott, H.; Staines, W.A.; Woulfe, J.; Variola, F. Biomaterials-based strategies for in vitro neural models. Biomater. Sci. 2022, 10, 1134–1165. [Google Scholar] [CrossRef] [PubMed]
- Taneja, H.; Salodkar, S.M.; Parmar, A.S.; Chaudhary, S. Hydrogel based 3D printing: Bio ink for tissue engineering. J. Mol. Liq. 2022, 367, 120390. [Google Scholar] [CrossRef]
- Vanina, A.S.; Sychev, A.V.; Lavrova, A.I.; Gavrilov, P.V.; Andropova, P.L.; Grekhnyova, E.V.; Kudryavtseva, T.N.; Postnikov, E.B. A hydrogel-based phantom of the brain tissue aimed at modelling complex metabolic transport processes. Eur. Phys. J. Spec. Top. 2023, 232, 475–483. [Google Scholar] [CrossRef]
- Vanina, A.S.; Sychev, A.V.; Lavrova, A.I.; Gavrilov, P.V.; Andropova, P.L.; Grekhnyova, E.V.; Kudryavtseva, T.N.; Postnikov, E.B. Computed Tomography-Assisted Study of the Liquid Contrast Agent’s Spread in a Hydrogel Phantom of the Brain Tissue. Fluids 2023, 8, 167. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Cattaneo, C. Sulla conduzione del calore. Atti Del Semin. Mat. E Fis. Dell’Univ. Di Modena E Reggio Emilia 1948, 3, 83–101. [Google Scholar]
- Özişik, M.N.; Tzou, D.Y. On the Wave Theory in Heat Conduction. ASME J. Heat Transfer. 1994, 116, 526–535. [Google Scholar] [CrossRef]
- Tzou, D.Y. Macro-to Microscale Heat Transfer: The Lagging Behavior; John Wiley & Sons: Chichester, UK, 2015. [Google Scholar]
- Mitra, K.; Kumar, S.; Vedevarz, A.; Moallemi, M.K. Experimental Evidence of Hyperbolic Heat Conduction in Processed Meat. ASME J. Heat Mass Transf. 1995, 117, 568–573. [Google Scholar] [CrossRef]
- Metzler, R.; Compte, A. Stochastic foundation of normal and anomalous Cattaneo-type transport. Phys. A Stat. Mech. Its Appl. 1999, 268, 454–468. [Google Scholar] [CrossRef]
- Awad, E.; Metzler, R. Crossover dynamics from superdiffusion to subdiffusion: Models and solutions. Fract. Calc. Appl. Anal. 2020, 23, 55–102. [Google Scholar] [CrossRef]
- Keller, J.B. Diffusion at finite speed and random walks. Proc. Natl. Acad. Sci. USA 2004, 101, 1120–1122. [Google Scholar] [CrossRef] [PubMed]
- Górska, K.; Horzela, A.; Lenzi, E.K.; Pagnini, G.; Sandev, T. Generalized Cattaneo (telegrapher’s) equations in modeling anomalous diffusion phenomena. Phys. Rev. E 2020, 102, 022128. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vanina, A.S.; Lavrova, A.I.; Safonov, D.A.; Sychev, A.V.; Proskurkin, I.S.; Postnikov, E.B. Mimicking Marker Spread After Disruption of the Blood–Brain Barrier with a Collagen-Based Hydrogel Phantom. Biomimetics 2024, 9, 667. https://doi.org/10.3390/biomimetics9110667
Vanina AS, Lavrova AI, Safonov DA, Sychev AV, Proskurkin IS, Postnikov EB. Mimicking Marker Spread After Disruption of the Blood–Brain Barrier with a Collagen-Based Hydrogel Phantom. Biomimetics. 2024; 9(11):667. https://doi.org/10.3390/biomimetics9110667
Chicago/Turabian StyleVanina, Anastasia S., Anastasia I. Lavrova, Dmitry A. Safonov, Alexander V. Sychev, Ivan S. Proskurkin, and Eugene B. Postnikov. 2024. "Mimicking Marker Spread After Disruption of the Blood–Brain Barrier with a Collagen-Based Hydrogel Phantom" Biomimetics 9, no. 11: 667. https://doi.org/10.3390/biomimetics9110667
APA StyleVanina, A. S., Lavrova, A. I., Safonov, D. A., Sychev, A. V., Proskurkin, I. S., & Postnikov, E. B. (2024). Mimicking Marker Spread After Disruption of the Blood–Brain Barrier with a Collagen-Based Hydrogel Phantom. Biomimetics, 9(11), 667. https://doi.org/10.3390/biomimetics9110667






