A Hybrid Nonlinear Whale Optimization Algorithm with Sine Cosine for Global Optimization
Abstract
1. Introduction
2. WOA
2.1. Encompassing Prey
2.2. Bubble-Net Devouring Prey
2.3. Stochastic Capturing for Prey
| Algorithm 1 WOA |
| Step 1. Initialize population Step 2. Investigate each attainable alternative’s fitness Step 3.) do for each attainable alternative Customize , , , and if1 Customize the attainable alternative’s location via Equation (2) Customize the attainable alternative’s location via Equation (10) end if2 else if1 Customize the attainable alternative’s location via Equation (7) end if1 end for Validate if any attainable alternative exists outside the search zone and readjust location Investigate each attainable alternative’s fitness if a superior location vector exists end while |
3. SCWOA
3.1. Nonlinear WOA
3.2. SCA
3.3. SCWOA
| Algorithm 2 SCWOA |
| Step 1. Initialize population Step 2. Investigate each attainable alternative’s fitness Step 3. while) do for each attainable alternative Customize , , , and if1 The nonlinear strategy is introduced into the encompassing prey Combine SCA with the encompassing prey Customize the attainable alternative’s location via Equations (12) and (17) The nonlinear strategy is introduced into the stochastic capturing for prey Combine SCA with the stochastic capturing for prey (exploration phase) Customize the attainable alternative’s location via Equations (14) and (17) end if2 else if1 The nonlinear strategy is introduced into the bubble-net devouring prey Combine SCA with the bubble-net devouring prey (exploitation phase) Customize the attainable alternative’s location via Equations (13) and (17) end if1 end for Validate if any attainable alternative exists outside the search zone and readjust the location Investigate each attainable alternative’s fitness if a superior location vector exists end while |
3.4. Complexity Analysis
4. Simulation Assessment and Results Interpretation
4.1. Experimental Configuration
4.2. Benchmark Functions
4.3. SCWOA for Addressing Engineering Design
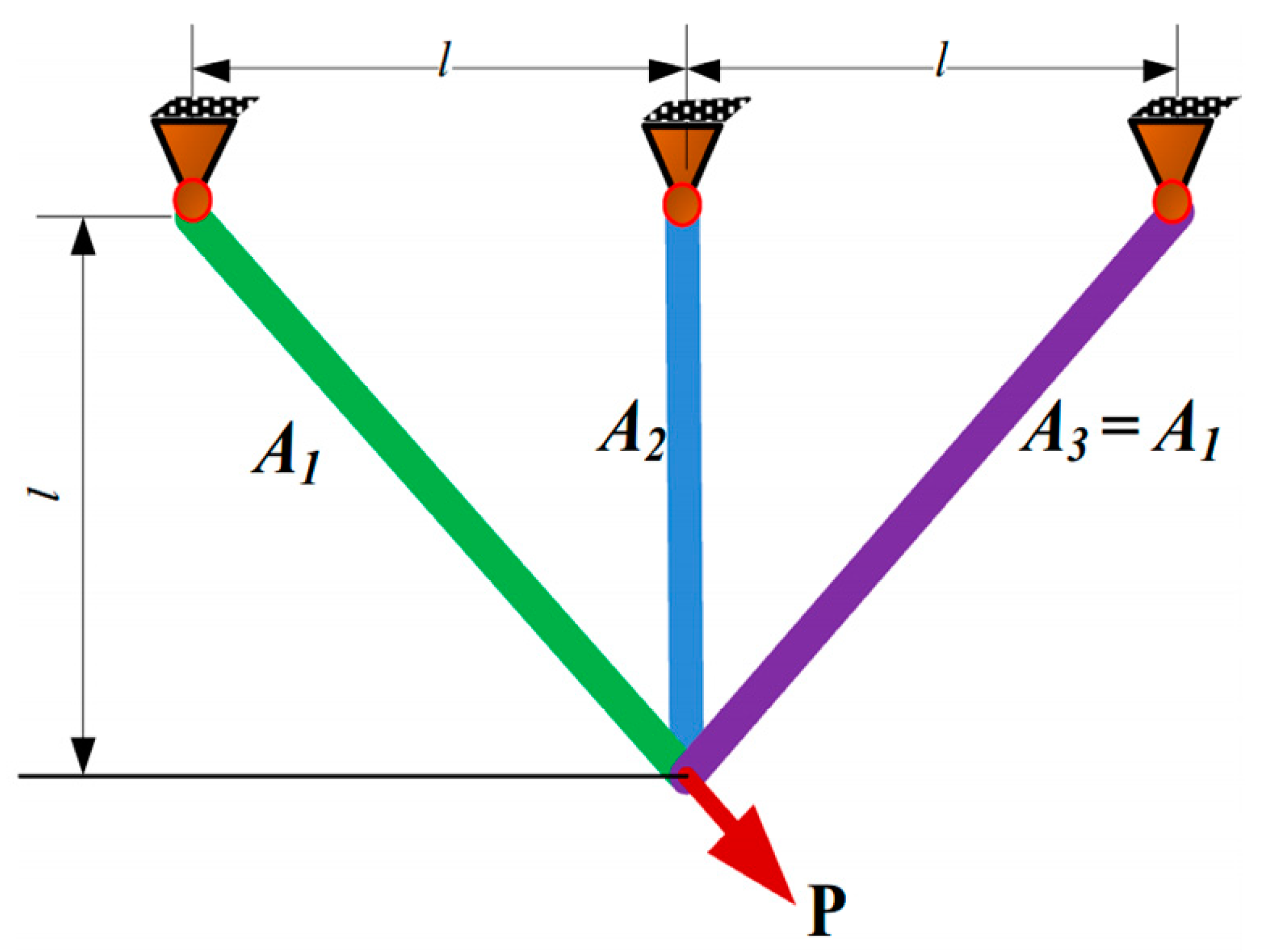
4.3.1. Three-Bar Truss Design
4.3.2. Tubular Column Design
4.3.3. Speed Reducer Design
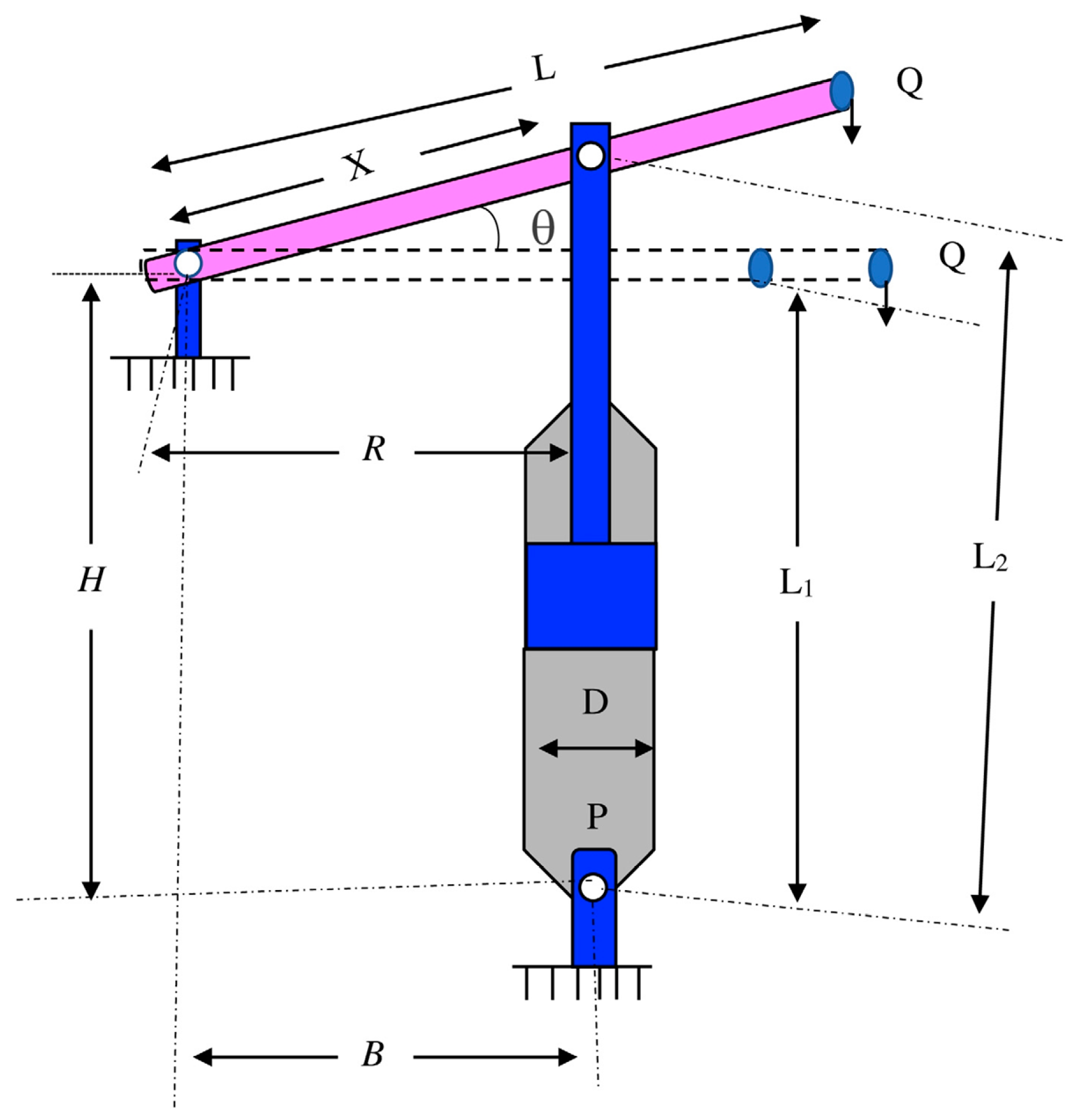
4.3.4. Piston Lever Design
4.3.5. Tension/Compression Spring Design
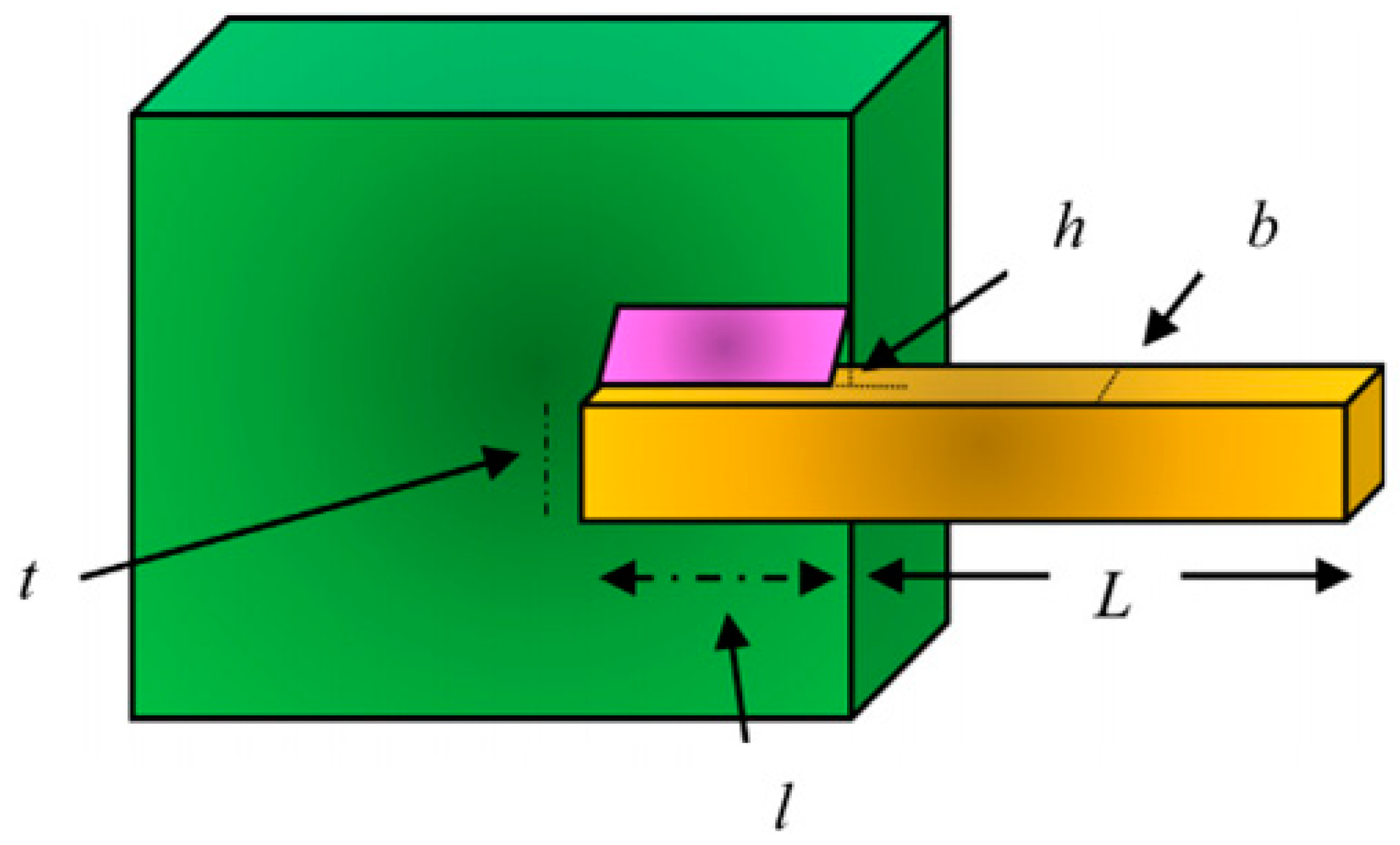
4.3.6. Welded Beam Design
4.3.7. Gear Train Design
4.3.8. Car Side Impact Design
5. Conclusions and Future Investigation
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, X.S.; Hossein Gandomi, A. Bat Algorithm: A Novel Approach for Global Engineering Optimization. Eng. Comput. 2012, 29, 464–483. [Google Scholar] [CrossRef]
- Braik, M.; Sheta, A.; Al-Hiary, H. A Novel Meta-Heuristic Search Algorithm for Solving Optimization Problems: Capuchin Search Algorithm. Neural Comput. Appl. 2021, 33, 2515–2547. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-Flame Optimization Algorithm: A Novel Nature-Inspired Heuristic Paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-Verse Optimizer: A Nature-Inspired Algorithm for Global Optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Salawudeen, A.T.; Mu’azu, M.B.; Yusuf, A.; Adedokun, A.E. A Novel Smell Agent Optimization (SAO): An Extensive CEC Study and Engineering Application. Knowl.-Based Syst. 2021, 232, 107486. [Google Scholar] [CrossRef]
- Rizk-Allah, R.M.; Hassanien, A.E. A Movable Damped Wave Algorithm for Solving Global Optimization Problems. Evol. Intell. 2019, 12, 49–72. [Google Scholar] [CrossRef]
- Uzer, M.S.; Inan, O. Application of Improved Hybrid Whale Optimization Algorithm to Optimization Problems. Neural Comput. Appl. 2023, 35, 12433–12451. [Google Scholar] [CrossRef]
- Elmogy, A.; Miqrish, H.; Elawady, W.; El-Ghaish, H. ANWOA: An Adaptive Nonlinear Whale Optimization Algorithm for High-Dimensional Optimization Problems. Neural Comput. Appl. 2023, 35, 22671–22686. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, J.; Wu, Z.; He, S. A Fusion Algorithm Based on Whale and Grey Wolf Optimization Algorithm for Solving Real-World Optimization Problems. Appl. Soft Comput. 2023, 146, 110701. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, T.; Zhang, G.; Kong, M. Parameter Optimization of PID Controller Based on an Enhanced Whale Optimization Algorithm for AVR System. Oper. Res. 2023, 23, 44. [Google Scholar] [CrossRef]
- Quan, R.; Guo, H.; Liu, D.; Chang, Y.; Wan, H. Performance Optimization of a Thermoelectric Generator for Automotive Application Using an Improved Whale Optimization Algorithm. Sustain. Energy Fuels 2023, 7, 5528–5545. [Google Scholar] [CrossRef]
- Wei, F.; Li, J.; Zhang, Y. Improved Neighborhood Search Whale Optimization Algorithm and Its Engineering Application. Soft Comput. 2023, 27, 17687–17709. [Google Scholar] [CrossRef]
- Wu, Z.; Lu, X. Microgrid Fault Diagnosis Based on Whale Algorithm Optimizing Extreme Learning Machine. J. Electr. Eng. Technol. 2024, 19, 1827–1836. [Google Scholar] [CrossRef]
- Fan, Z.; Gou, J. Predicting Body Fat Using a Novel Fuzzy-Weighted Approach Optimized by the Whale Optimization Algorithm. Expert Syst. Appl. 2023, 217, 119558. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Zamani, H.; Asghari Varzaneh, Z.; Mirjalili, S. A Systematic Review of the Whale Optimization Algorithm: Theoretical Foundation, Improvements, and Hybridizations. Arch. Comput. Methods Eng. 2023, 30, 4113–4159. [Google Scholar] [CrossRef]
- Mohite, S.S.; Kolekar, U.D. Resource Allocation in Macrocell–Femtocells via Combined Rain and Whale Optimization Algorithm. Cybern. Syst. 2023, 1–23. [Google Scholar] [CrossRef]
- Routa, A.K.; Mohanty, P.R. Seismic Response Prediction and Velocity Model Building Inversion by the Whale Optimization Algorithm. Pure Appl. Geophys. 2023, 180, 2087–2109. [Google Scholar] [CrossRef]
- Chakraborty, S.; Saha, A.K.; Ezugwu, A.E.; Chakraborty, R.; Saha, A. Horizontal Crossover and Co-Operative Hunting-Based Whale Optimization Algorithm for Feature Selection. Knowl. Based Syst. 2023, 282, 111108. [Google Scholar] [CrossRef]
- Kumar, M.; Samriya, J.K.; Dubey, K.; Gill, S.S. QoS-Aware Resource Scheduling Using Whale Optimization Algorithm for Microservice Applications. Softw. Pract. Exp. 2024, 54, 546–565. [Google Scholar] [CrossRef]
- Zhang, H.; Gao, Z.; Pan, Y.; Yang, G.; Zhang, W.C.; Wang, J. A Synergy of the Adaptive Whale Optimization Algorithm and Differential Evolution for Abrupt Motion Tracking. Appl. Soft Comput. 2023, 144, 110554. [Google Scholar] [CrossRef]
- Deng, H.; Liu, L.; Fang, J.; Qu, B.; Huang, Q. A Novel Improved Whale Optimization Algorithm for Optimization Problems with Multi-Strategy and Hybrid Algorithm. Math. Comput. Simul. 2023, 205, 794–817. [Google Scholar] [CrossRef]
- Li, M.; Xu, G.; Zeng, L.; Lai, Q. Hybrid Whale Optimization Algorithm Based on Symbiosis Strategy for Global Optimization. Appl. Intell. 2023, 53, 16663–16705. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, G.; Kong, M.; Zhang, T.; Wang, D.; Chen, R. CWOA: A Novel Complex-Valued Encoding Whale Optimization Algorithm. Math. Comput. Simul. 2023, 207, 151–188. [Google Scholar] [CrossRef]
- Zhang, J.; Kong, M.; Zhang, G.; Huang, Y. Weapon–Target Assignment Using a Whale Optimization Algorithm. Int. J. Comput. Intell. Syst. 2023, 16, 62. [Google Scholar] [CrossRef]
- Liu, J.; Shi, J.; Hao, F.; Dai, M. A Reinforced Exploration Mechanism Whale Optimization Algorithm for Continuous Optimization Problems. Math. Comput. Simul. 2022, 201, 23–48. [Google Scholar] [CrossRef]
- Lin, X.; Yu, X.; Li, W. A Heuristic Whale Optimization Algorithm with Niching Strategy for Global Multi-Dimensional Engineering Optimization. Comput. Ind. Eng. 2022, 171, 108361. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Dehkordi, A.A.; Sadiq, A.S.; Mirjalili, S.; Ghafoor, K.Z. Nonlinear-Based Chaotic Harris Hawks Optimizer: Algorithm and Internet of Vehicles Application. Appl. Soft Comput. 2021, 109, 107574. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for Solving Optimization Problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Malela-Majika, J.-C. New Distribution-Free Memory-Type Control Charts Based on the Wilcoxon Rank-Sum Statistic. Qual. Technol. Quant. Manag. 2021, 18, 135–155. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Azeem, S.A.A.; Jameel, M.; Abouhawwash, M. Kepler Optimization Algorithm: A New Metaheuristic Algorithm Inspired by Kepler’s Laws of Planetary Motion. Knowl.-Based Syst. 2023, 268, 110454. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, D.; Yang, J. Hybrid-Flash Butterfly Optimization Algorithm with Logistic Mapping for Solving the Engineering Constrained Optimization Problems. Entropy 2022, 24, 525. [Google Scholar] [CrossRef]
- Meng, K.; Chen, C.; Xin, B. MSSSA: A Multi-Strategy Enhanced Sparrow Search Algorithm for Global Optimization. Front. Inf. Technol. Electron. Eng. 2022, 23, 1828–1847. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F. Sand Cat Swarm Optimization: A Nature-Inspired Algorithm to Solve Global Optimization Problems. Eng. Comput. 2023, 39, 2627–2651. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. Starling Murmuration Optimizer: A Novel Bio-Inspired Algorithm for Global and Engineering Optimization. Comput. Methods Appl. Mech. Eng. 2022, 392, 114616. [Google Scholar] [CrossRef]
- Zhang, Y.; Mo, Y. Chaotic Adaptive Sailfish Optimizer with Genetic Characteristics for Global Optimization. J. Supercomput. 2022, 78, 10950–10996. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, C.; Gharehchopogh, F.S.; Mirjalili, S. An Improved Whale Optimization Algorithm Based on Multi-Population Evolution for Global Optimization and Engineering Design Problems. Expert Syst. Appl. 2023, 215, 119269. [Google Scholar] [CrossRef]
- Ong, K.M.; Ong, P.; Sia, C.K. A Carnivorous Plant Algorithm for Solving Global Optimization Problems. Appl. Soft Comput. 2021, 98, 106833. [Google Scholar] [CrossRef]
- Kaveh, A.; Eslamlou, A.D. Water Strider Algorithm: A New Metaheuristic and Applications. Structures 2020, 25, 520–541. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.S.; Alavi, A.H. Cuckoo Search Algorithm: A Metaheuristic Approach to Solve Structural Optimization Problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Ray, T.; Saini, P. Engineering Design Optimization Using a Swarm with an Intelligent Information Sharing among Individuals. Eng. Optim. 2001, 33, 735–748. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The Arithmetic Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Raj, K.H.; Sharma, R.S.; Mishra, G.; Dua, A.; Patvardhan, C. An Evolutionary Computational Technique for Constrained Optimisation in Engineering Design. J. Inst. Eng. Part MC Mech. Eng. Div. 2005, 86, 121–128. [Google Scholar]
- Das, S.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for CEC 2011 Competition on Testing Evolutionary Algorithms on Real World Optimization Problems; Jadavpur University: Kolkata, India; Nanyang Technological University: Singapore, 2010; pp. 341–359. [Google Scholar]
- Mohammadi-Balani, A.; Nayeri, M.D.; Azar, A.; Taghizadeh-Yazdi, M. Golden Eagle Optimizer: A Nature-Inspired Metaheuristic Algorithm. Comput. Ind. Eng. 2021, 152, 107050. [Google Scholar] [CrossRef]
- Po\lap, D.; Woźniak, M. Red Fox Optimization Algorithm. Expert Syst. Appl. 2021, 166, 114107. [Google Scholar] [CrossRef]
- Chen, Z.; Francis, A.; Li, S.; Liao, B.; Xiao, D.; Ha, T.T.; Li, J.; Ding, L.; Cao, X. Egret Swarm Optimization Algorithm: An Evolutionary Computation Approach for Model Free Optimization. Biomimetics 2022, 7, 144. [Google Scholar] [CrossRef]
- Hashim, F.A.; Mostafa, R.R.; Hussien, A.G.; Mirjalili, S.; Sallam, K.M. Fick’s Law Algorithm: A Physical Law-Based Algorithm for Numerical Optimization. Knowl.-Based Syst. 2023, 260, 110146. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F.; Sabbagh Molahosseini, A. Hunter–Prey Optimization: Algorithm and Applications. Soft Comput. 2022, 26, 1279–1314. [Google Scholar] [CrossRef]
- Desuky, A.S.; Cifci, M.A.; Kausar, S.; Hussain, S.; El Bakrawy, L.M. Mud Ring Algorithm: A New Meta-Heuristic Optimization Algorithm for Solving Mathematical and Engineering Challenges. IEEE Access 2022, 10, 50448–50466. [Google Scholar] [CrossRef]
- Akyol, S. A New Hybrid Method Based on Aquila Optimizer and Tangent Search Algorithm for Global Optimization. J. Ambient Intell. Humaniz. Comput. 2023, 14, 8045–8065. [Google Scholar] [CrossRef]
- Emami, H. Stock Exchange Trading Optimization Algorithm: A Human-Inspired Method for Global Optimization. J. Supercomput. 2022, 78, 2125–2174. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, X.; Song, L.; Zhang, Y.; Gu, L.; Zhao, X. Wild Geese Migration Optimization Algorithm: A New Meta-Heuristic Algorithm for Solving Inverse Kinematics of Robot. Comput. Intell. Neurosci. 2022, 2022, 5191758. [Google Scholar] [CrossRef]
- Rechenberg, I. Evolutionsstrategien. In Simulationsmethoden in der Medizin und Biologie: Workshop, Hannover; Springer: Berlin/Heidelberg, Germany, 1978; Volume 29, pp. 83–114. [Google Scholar]
- Gandomi, A.H.; Roke, D.A. Engineering Optimization Using Interior Search Algorithm. In Proceedings of the 2014 IEEE symposium on swarm intelligence, Orlando, FL, USA, 9–12 December 2014; pp. 1–7. [Google Scholar] [CrossRef]
- Bayzidi, H.; Talatahari, S.; Saraee, M.; Lamarche, C.P. Social Network Search for Solving Engineering Optimization Problems. Comput. Intell. Neurosci. 2021, 2021, 8548639. [Google Scholar] [CrossRef]
- Rao, S.S. Engineering Optimization: Theory and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Feng, Z.; Niu, W.; Liu, S. Cooperation Search Algorithm: A Novel Metaheuristic Evolutionary Intelligence Algorithm for Numerical Optimization and Engineering Optimization Problems. Appl. Soft Comput. 2021, 98, 106734. [Google Scholar] [CrossRef]
- Meng, O.K.; Pauline, O.; Kiong, S.C.; Wahab, H.A.; Jafferi, N. Application of Modified Flower Pollination Algorithm on Mechanical Engineering Design Problem. IOP Conf. Ser. Mater. Sci. Eng. 2017, 165, 012032. [Google Scholar] [CrossRef]
- Garg, H. A Hybrid GSA-GA Algorithm for Constrained Optimization Problems. Inf. Sci. 2019, 478, 499–523. [Google Scholar] [CrossRef]
- Kumar, N.; Mahato, S.K.; Bhunia, A.K. A New QPSO Based Hybrid Algorithm for Constrained Optimization Problems via Tournamenting Process. Soft Comput. 2020, 24, 11365–11379. [Google Scholar] [CrossRef]
- Nigdeli, S.M.; Bekdaş, G.; Yang, X.S. Application of the Flower Pollination Algorithm in Structural Engineering. In Metaheuristics and Optimization in Civil Engineering; Springer: Berlin/Heidelberg, Germany, 2016; pp. 25–42. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. An Introduction of Krill Herd Algorithm for Engineering Optimization. J. Civ. Eng. Manag. 2016, 22, 302–310. [Google Scholar] [CrossRef][Green Version]
- Rocha, A.M.A.; Fernandes, E.M. Hybridizing the Electromagnetism-like Algorithm with Descent Search for Solving Engineering Design Problems. Int. J. Comput. Math. 2009, 86, 1932–1946. [Google Scholar] [CrossRef]
- Ezugwu, A.E.; Agushaka, J.O.; Abualigah, L.; Mirjalili, S.; Gandomi, A.H. Prairie Dog Optimization Algorithm. Neural Comput. Appl. 2022, 34, 20017–20065. [Google Scholar] [CrossRef]
- Guedria, N.B. Improved Accelerated PSO Algorithm for Mechanical Engineering Optimization Problems. Appl. Soft Comput. 2016, 40, 455–467. [Google Scholar] [CrossRef]
- Saruhan, H.; Uygur, İ. Design Optimization of Mechanical Systems Using Genetic Algorithms. Sak. Univ. J. Sci. 2003, 7, 77–84. [Google Scholar]
- Mezura-Montes, E.; Coello, C.C.; Landa-Becerra, R. Engineering Optimization Using Simple Evolutionary Algorithm. In Proceedings of the 15th IEEE international conference on tools with artificial intelligence, Sacramento, CA, USA, 5 November 2003; pp. 149–156. [Google Scholar] [CrossRef]
- Stephen, S.; Christu, D.; Dalvi, A. Design Optimization of Weight of Speed Reducer Problem through Matlab and Simulation Using Ansys. Int. J. Mech. Eng. Technol. 2018, 9, 339–349. [Google Scholar]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Kamboj, V.K.; Nandi, A.; Bhadoria, A.; Sehgal, S. An Intensify Harris Hawks Optimizer for Numerical and Engineering Optimization Problems. Appl. Soft Comput. 2020, 89, 106018. [Google Scholar] [CrossRef]
- Lu, S.; Kim, H.M. A Regularized Inexact Penalty Decomposition Algorithm for Multidisciplinary Design Optimization Problems with Complementarity Constraints. J. Mech. Des. 2010, 132, 041005. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A New Heuristic Optimization Algorithm: Harmony Search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Mahdavi, M.; Fesanghary, M.; Damangir, E. An Improved Harmony Search Algorithm for Solving Optimization Problems. Appl. Math. Comput. 2007, 188, 1567–1579. [Google Scholar] [CrossRef]
- Braik, M.S. Chameleon Swarm Algorithm: A Bio-Inspired Optimizer for Solving Engineering Design Problems. Expert Syst. Appl. 2021, 174, 114685. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New Metaheuristic Algorithm for Solving Optimization Problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Dehghani, M.; Hubálovskỳ, Š.; Trojovskỳ, P. Northern Goshawk Optimization: A New Swarm-Based Algorithm for Solving Optimization Problems. IEEE Access 2021, 9, 162059–162080. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Seagull Optimization Algorithm: Theory and Its Applications for Large-Scale Industrial Engineering Problems. Knowl.-Based Syst. 2019, 165, 169–196. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Trojovská, E.; Trojovskỳ, P. Coati Optimization Algorithm: A New Bio-Inspired Metaheuristic Algorithm for Solving Optimization Problems. Knowl.-Based Syst. 2023, 259, 110011. [Google Scholar] [CrossRef]
- Chakraborty, S.; Saha, A.K.; Sharma, S.; Chakraborty, R.; Debnath, S. A Hybrid Whale Optimization Algorithm for Global Optimization. J. Ambient Intell. Humaniz. Comput. 2023, 14, 431–467. [Google Scholar] [CrossRef]
- Rao, Y.; He, D.; Qu, L. A Probabilistic Simplified Sine Cosine Crow Search Algorithm for Global Optimization Problems. Eng. Comput. 2023, 39, 1823–1841. [Google Scholar] [CrossRef]
- Wang, S.; Jia, H.; Liu, Q.; Zheng, R. An Improved Hybrid Aquila Optimizer and Harris Hawks Optimization for Global Optimization. Math. Biosci. Eng. 2021, 18, 7076–7109. [Google Scholar] [CrossRef]
- Azizi, M.; Aickelin, U.; Khorshidi, H.A.; Baghalzadeh Shishehgarkhaneh, M. Energy Valley Optimizer: A Novel Metaheuristic Algorithm for Global and Engineering Optimization. Sci. Rep. 2023, 13, 226. [Google Scholar] [CrossRef]
- Kim, P.; Lee, J. An Integrated Method of Particle Swarm Optimization and Differential Evolution. J. Mech. Sci. Technol. 2009, 23, 426–434. [Google Scholar] [CrossRef]
- Azizi, M.; Talatahari, S.; Giaralis, A. Optimization of Engineering Design Problems Using Atomic Orbital Search Algorithm. IEEE Access 2021, 9, 102497–102519. [Google Scholar] [CrossRef]
- Sadeeq, H.T.; Abdulazeez, A.M. Giant Trevally Optimizer (GTO): A Novel Metaheuristic Algorithm for Global Optimization and Challenging Engineering Problems. IEEE Access 2022, 10, 121615–121640. [Google Scholar] [CrossRef]
- Sattar, D.; Salim, R. A Smart Metaheuristic Algorithm for Solving Engineering Problems. Eng. Comput. 2021, 37, 2389–2417. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and Application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-Qaness, M.A.; Gandomi, A.H. Aquila Optimizer: A Novel Meta-Heuristic Optimization Algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Coello, C.A.C. Use of a Self-Adaptive Penalty Approach for Engineering Optimization Problems. Comput. Ind. 2000, 41, 113–127. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. African Vultures Optimization Algorithm: A New Nature-Inspired Metaheuristic Algorithm for Global Optimization Problems. Comput. Ind. Eng. 2021, 158, 107408. [Google Scholar] [CrossRef]
- Kaur, S.; Awasthi, L.K.; Sangal, A.; Dhiman, G. Tunicate Swarm Algorithm: A New Bio-Inspired Based Metaheuristic Paradigm for Global Optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Xie, L.; Han, T.; Zhou, H.; Zhang, Z.-R.; Han, B.; Tang, A. Tuna Swarm Optimization: A Novel Swarm-Based Metaheuristic Algorithm for Global Optimization. Comput. Intell. Neurosci. 2021, 2021, 9210050. [Google Scholar] [CrossRef]
- Abualigah, L.; Elaziz, M.A.; Hussien, A.G.; Alsalibi, B.; Jalali, S.M.J.; Gandomi, A.H. Lightning Search Algorithm: A Comprehensive Survey. Appl. Intell. 2021, 51, 2353–2376. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z. Artificial Ecosystem-Based Optimization: A Novel Nature-Inspired Meta-Heuristic Algorithm. Neural Comput. Appl. 2020, 32, 9383–9425. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium Optimizer: A Novel Optimization Algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Zitouni, F.; Harous, S.; Maamri, R. A Novel Quantum Firefly Algorithm for Global Optimization. Arab. J. Sci. Eng. 2021, 46, 8741–8759. [Google Scholar] [CrossRef]
- Shami, T.M.; Mirjalili, S.; Al-Eryani, Y.; Daoudi, K.; Izadi, S.; Abualigah, L. Velocity Pausing Particle Swarm Optimization: A Novel Variant for Global Optimization. Neural Comput. Appl. 2023, 35, 9193–9223. [Google Scholar] [CrossRef]
- Kaveh, A.; Khayatazad, M. A New Meta-Heuristic Method: Ray Optimization. Comput. Struct. 2012, 112, 283–294. [Google Scholar] [CrossRef]
- Huang, F.; Wang, L.; He, Q. An Effective Co-Evolutionary Differential Evolution for Constrained Optimization. Appl. Math. Comput. 2007, 186, 340–356. [Google Scholar] [CrossRef]
- Deb, K. Optimal Design of a Welded Beam via Genetic Algorithms. AIAA J. 1991, 29, 2013–2015. [Google Scholar] [CrossRef]
- Ragsdell, K.; Phillips, D. Optimal Design of a Class of Welded Structures Using Geometric Programming. J. Eng. Ind. 1976, 98, 1021–1025. [Google Scholar] [CrossRef]
- Lee, K.S.; Geem, Z.W. A New Meta-Heuristic Algorithm for Continuous Engineering Optimization: Harmony Search Theory and Practice. Comput. Methods Appl. Mech. Eng. 2005, 194, 3902–3933. [Google Scholar] [CrossRef]
- Mezura-Montes, E.; Coello, C.A.C. An Empirical Study about the Usefulness of Evolution Strategies to Solve Constrained Optimization Problems. Int. J. Gen. Syst. 2008, 37, 443–473. [Google Scholar] [CrossRef]
- Coello, C.A.C. Theoretical and Numerical Constraint-Handling Techniques Used with Evolutionary Algorithms: A Survey of the State of the Art. Comput. Methods Appl. Mech. Eng. 2002, 191, 1245–1287. [Google Scholar] [CrossRef]
- Siddall, J.N. Analytical Decision-Making in Engineering Design; Prentice-Hall: Hoboken, NJ, USA, 1972. [Google Scholar]
- Li, Y.; Zhao, Y.; Liu, J. Dimension by Dimension Dynamic Sine Cosine Algorithm for Global Optimization Problems. Appl. Soft Comput. 2021, 98, 106933. [Google Scholar] [CrossRef]
- Zheng, Y.-J. Water Wave Optimization: A New Nature-Inspired Metaheuristic. Comput. Oper. Res. 2015, 55, 1–11. [Google Scholar] [CrossRef]
- Zou, D.; Liu, H.; Gao, L.; Li, S. A Novel Modified Differential Evolution Algorithm for Constrained Optimization Problems. Comput. Math. Appl. 2011, 61, 1608–1623. [Google Scholar] [CrossRef]
- Emami, H. Anti-Coronavirus Optimization Algorithm. Soft Comput. 2022, 26, 4991–5023. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Chen, H.; Heidari, A.A.; Gandomi, A.H. Hunger Games Search: Visions, Conception, Implementation, Deep Analysis, Perspectives, and towards Performance Shifts. Expert Syst. Appl. 2021, 177, 114864. [Google Scholar] [CrossRef]
- Pereira, J.L.J.; Francisco, M.B.; Diniz, C.A.; Oliver, G.A.; Cunha, S.S., Jr.; Gomes, G.F. Lichtenberg Algorithm: A Novel Hybrid Physics-Based Meta-Heuristic for Global Optimization. Expert Syst. Appl. 2021, 170, 114522. [Google Scholar] [CrossRef]
- Li, C.; Liang, K.; Chen, Y.; Pan, M. An Exploitation-Boosted Sine Cosine Algorithm for Global Optimization. Eng. Appl. Artif. Intell. 2023, 117, 105620. [Google Scholar] [CrossRef]
- Mohammadi, D.; Abd Elaziz, M.; Moghdani, R.; Demir, E.; Mirjalili, S. Quantum Henry Gas Solubility Optimization Algorithm for Global Optimization. Eng. Comput. 2022, 38, 2329–2348. [Google Scholar] [CrossRef]
- Yu, C.; Chen, M.; Cheng, K.; Zhao, X.; Ma, C.; Kuang, F.; Chen, H. SGOA: Annealing-Behaved Grasshopper Optimizer for Global Tasks. Eng. Comput. 2022, 38, 3761–3788. [Google Scholar] [CrossRef]
- Akay, B.; Karaboga, D. Artificial Bee Colony Algorithm for Large-Scale Problems and Engineering Design Optimization. J. Intell. Manuf. 2012, 23, 1001–1014. [Google Scholar] [CrossRef]
- Han, X.; Yue, L.; Dong, Y.; Xu, Q.; Xie, G.; Xu, X. Efficient Hybrid Algorithm Based on Moth Search and Fireworks Algorithm for Solving Numerical and Constrained Engineering Optimization Problems. J. Supercomput. 2020, 76, 9404–9429. [Google Scholar] [CrossRef]
- Sadollah, A.; Bahreininejad, A.; Eskandar, H.; Hamdi, M. Mine Blast Algorithm: A New Population Based Algorithm for Solving Constrained Engineering Optimization Problems. Appl. Soft Comput. 2013, 13, 2592–2612. [Google Scholar] [CrossRef]
- Mirjalili, S. The Ant Lion Optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Chegini, S.N.; Bagheri, A.; Najafi, F. PSOSCALF: A New Hybrid PSO Based on Sine Cosine Algorithm and Levy Flight for Solving Optimization Problems. Appl. Soft Comput. 2018, 73, 697–726. [Google Scholar] [CrossRef]
- Sandgren, E. Nonlinear Integer and Discrete Programming in Mechanical Design. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Kissimmee, FL, USA, 25–28 September 1998; American Society of Mechanical Engineers: New York, NY, USA, 1988; Volume 26584, pp. 95–105. [Google Scholar]
- Kannan, B.; Kramer, S.N. An Augmented Lagrange Multiplier Based Method for Mixed Integer Discrete Continuous Optimization and Its Applications to Mechanical Design. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Albuquerque, NM, USA, 19–22 September 1993; Volume 97690, pp. 103–112. [Google Scholar]
- Deb, K.; Goyal, M. A Combined Genetic Adaptive Search (GeneAS) for Engineering Design. Comput. Sci. Inform. 1996, 26, 30–45. [Google Scholar]
- Karami, H.; Anaraki, M.V.; Farzin, S.; Mirjalili, S. Flow Direction Algorithm (FDA): A Novel Optimization Approach for Solving Optimization Problems. Comput. Ind. Eng. 2021, 156, 107224. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly Optimization Algorithm: A Novel Approach for Global Optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Das, A.K.; Pratihar, D.K. Bonobo Optimizer (BO): An Intelligent Heuristic with Self-Adjusting Parameters over Continuous Spaces and Its Applications to Engineering Problems. Appl. Intell. 2022, 52, 2942–2974. [Google Scholar] [CrossRef]
- Singh, H.; Singh, B.; Kaur, M. An Improved Elephant Herding Optimization for Global Optimization Problems. Eng. Comput. 2022, 38, 3489–3521. [Google Scholar] [CrossRef]
- Wang, L.; Cao, Q.; Zhang, Z.; Mirjalili, S.; Zhao, W. Artificial Rabbits Optimization: A New Bio-Inspired Meta-Heuristic Algorithm for Solving Engineering Optimization Problems. Eng. Appl. Artif. Intell. 2022, 114, 105082. [Google Scholar] [CrossRef]
- Yadav, D. Blood Coagulation Algorithm: A Novel Bio-Inspired Meta-Heuristic Algorithm for Global Optimization. Mathematics 2021, 9, 3011. [Google Scholar] [CrossRef]
- Tarkhaneh, O.; Alipour, N.; Chapnevis, A.; Shen, H. Golden Tortoise Beetle Optimizer: A Novel Nature-Inspired Meta-Heuristic Algorithm for Engineering Problems. arXiv 2021, arXiv:210401521. [Google Scholar]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Mixed Variable Structural Optimization Using Firefly Algorithm. Comput. Struct. 2011, 89, 2325–2336. [Google Scholar] [CrossRef]
- Yildiz, A.R.; Abderazek, H.; Mirjalili, S. A Comparative Study of Recent Non-Traditional Methods for Mechanical Design Optimization. Arch. Comput. Methods Eng. 2020, 27, 1031–1048. [Google Scholar] [CrossRef]
- Talatahari, S.; Azizi, M.; Toloo, M. Fuzzy Adaptive Charged System Search for Global Optimization. Appl. Soft Comput. 2021, 109, 107518. [Google Scholar] [CrossRef]
- Yildiz, B.S.; Pholdee, N.; Bureerat, S.; Yildiz, A.R.; Sait, S.M. Robust Design of a Robot Gripper Mechanism Using New Hybrid Grasshopper Optimization Algorithm. Expert Syst. 2021, 38, e12666. [Google Scholar] [CrossRef]
- Yildiz, B.S.; Pholdee, N.; Bureerat, S.; Yildiz, A.R.; Sait, S.M. Enhanced Grasshopper Optimization Algorithm Using Elite Opposition-Based Learning for Solving Real-World Engineering Problems. Eng. Comput. 2022, 38, 4207–4219. [Google Scholar] [CrossRef]







| Benchmark Test Functions | Dim | Range | |
|---|---|---|---|
| 30 | [−100, 100] | 0 | |
| 30 | [−10, 10] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−30, 30] | 0 | |
| 30 | [−1.28, 1.28] | 0 | |
| 30 | [−5.12, 5.12] | 0 | |
| 30 | [−32, 32] | 0 | |
| 30 | [−600, 600] | 0 | |
| 30 | [−50, 50] | 0 | |
| 2 | [−65, 65] | 0.998 | |
| 4 | [−5, 5] | 0.000308 | |
| 2 | [−5.12, 5.12] | −1 | |
| 4 | [0, 10] | −10.5364 | |
| 2 | [−100, 100] | −1 | |
| 10 | [−10, 10] | 0 |
| Methodology | Parameter | Value |
|---|---|---|
| BA | Pulse frequency | [0, 2] |
| Echo loudness | 0.25 | |
| Decreasing coefficient | 0.5 | |
| CapSA | Disordered solution | [0, 1] |
| Balance probability | 0.7 | |
| Gravitational force | 9.81 | |
| Disordered solution | [0, 1] | |
| Solution | 2 | |
| Solution | 21 | |
| Solution | 2 | |
| Inertia coefficient | 0.7 | |
| MFO | Constant | 1 |
| Disordered solution | [−1, 1] | |
| Disordered solution | [−2, −1] | |
| MVO | Disordered solution | [0, 1] |
| Disordered solution | [0, 1] | |
| Disordered solution | [0, 1] | |
| Disordered solution | [0, 1] | |
| Exploitation accuracy | 6 | |
| Minimum probability | 0.2 | |
| Maximum probability | 1 | |
| SAO | Disordered solution | (0, 1] |
| Smell constant | 0.6 | |
| Temperature of smell molecules | 0.95 | |
| Mass of smell molecules | 0.9 | |
| Disordered solution | (0, 1] | |
| Disordered solution | (0, 1] | |
| Disordered solution | (0, 1] | |
| Disordered solution | (0, 1] | |
| MDWA | Constant | 1 |
| Constant | 0 | |
| WOA | Disordered solution | [0, 1] |
| Disordered solution | [0, 1] | |
| Convergence factor | [0, 2] | |
| Constant coefficient | 1 | |
| Disordered solution | [−1, 1] | |
| SCWOA | Disordered solution | [0, 1] |
| Disordered solution | [0, 1] | |
| Convergence factor | [0, 2] | |
| Constant coefficient | 1 | |
| Disordered solution | [−1, 1] | |
| Constant | 2 | |
| Disordered solution | [0, 2] | |
| Disordered solution | [−2, 2] | |
| Disordered solution | [0, 1] |
| Function | Result | BA | CapSA | MFO | MVO | SAO | MDWA | WOA | SCWOA | Rank |
|---|---|---|---|---|---|---|---|---|---|---|
| Best | 0.001159 | 5.36 | 4.42 | 0.092868 | 5.56 | 9.20 | 1.5 | 0 | 1 | |
| Worst | 0.001622 | 8.63 | 20000.00 | 0.359012 | 0.007819 | 2.41 | 8.8 | 0 | ||
| Mean | 0.001375 | 1.15 | 2000.000 | 0.192690 | 0.001067 | 4.70 | 3.3 | 0 | ||
| Std | 0.000136 | 2.14 | 4842.342 | 0.065528 | 0.001461 | 6.10 | 0 | 0 | ||
| Best | 0.143627 | 7.53 | 5.34 | 0.164170 | 0.040695 | 4.05 | 4.9 | 0 | 1 | |
| Worst | 1.486102 | 1.65 | 60.00000 | 0.561635 | 0.322152 | 6.99 | 6.8 | 0 | ||
| Mean | 0.362503 | 3.36 | 32.00004 | 0.297294 | 0.126300 | 1.80 | 4.6 | 0 | ||
| Std | 0.310119 | 4.01 | 19.19046 | 0.080973 | 0.071809 | 1.46 | 1.5 | 0 | ||
| Best | 0.002828 | 1.73 | 361.1944 | 7.282789 | 0.019636 | 1.24 | 1157.308 | 0 | 1 | |
| Worst | 0.007281 | 3.46 | 43673.20 | 35.59056 | 68711.49 | 6.88 | 26934.37 | 0 | ||
| Mean | 0.005109 | 3.75 | 16485.94 | 16.95300 | 8723.780 | 1.03 | 12424.99 | 0 | ||
| Std | 0.001217 | 7.74 | 12964.40 | 7.354255 | 15170.22 | 1.94 | 6176.585 | 0 | ||
| Best | 0.014087 | 4.13 | 26.51955 | 0.281197 | 0.002479 | 1.29 | 0.001146 | 0 | 1 | |
| Worst | 0.027422 | 7.12 | 74.51734 | 1.083297 | 0.021852 | 6.39 | 83.74666 | 0 | ||
| Mean | 0.018084 | 1.65 | 52.37642 | 0.613720 | 0.008145 | 1.31 | 26.99115 | 0 | ||
| Std | 0.002698 | 1.73 | 12.46703 | 0.222156 | 0.004628 | 1.34 | 25.65131 | 0 | ||
| Best | 22.68025 | 1.60 | 24.41747 | 27.27617 | 0.001503 | 22.18621 | 25.89678 | 25.58608 | 4 | |
| Worst | 29.52813 | 9.42 | 90079.05 | 2449.732 | 0.298228 | 88.62291 | 27.02118 | 28.57163 | ||
| Mean | 27.39530 | 9.80 | 15426.22 | 408.6292 | 0.091653 | 33.16911 | 26.49432 | 27.21915 | ||
| Std | 1.590533 | 1.86 | 33959.41 | 672.6372 | 0.079147 | 18.13722 | 0.308641 | 0.525503 | ||
| Best | 0.013535 | 0.047475 | 0.018017 | 0.003399 | 0.001207 | 0.000658 | 8.93 | 1.33 | 1 | |
| Worst | 0.070121 | 0.955523 | 26.86892 | 0.032807 | 0.118872 | 0.011541 | 0.005396 | 5.06 | ||
| Mean | 0.039194 | 0.529563 | 1.848647 | 0.014375 | 0.016951 | 0.004033 | 0.000751 | 1.50 | ||
| Std | 0.013420 | 0.293325 | 5.042738 | 0.007323 | 0.021682 | 0.002478 | 0.001026 | 1.16 |
| Function | Result | BA | CapSA | MFO | MVO | SAO | MDWA | WOA | SCWOA | Rank |
|---|---|---|---|---|---|---|---|---|---|---|
| Best | 18.13550 | 0 | 57.70755 | 59.76117 | 0.005055 | 0 | 0 | 0 | 1 | |
| Worst | 42.08115 | 0 | 219.1031 | 143.3769 | 208.2966 | 1.51 | 0 | 0 | ||
| Mean | 29.38550 | 0 | 139.8432 | 104.8220 | 13.16234 | 1.77 | 0 | 0 | ||
| Std | 6.161807 | 0 | 40.22221 | 24.85516 | 38.81178 | 3.03 | 0 | 0 | ||
| Best | 2.122723 | 1.41 | 7.20 | 0.103777 | 0.004603 | 6.24 | 8.88 | 8.88 | 1 | |
| Worst | 3.225303 | 7.86 | 19.96283 | 1.817965 | 0.593776 | 1.60 | 7.99 | 8.88 | ||
| Mean | 2.683390 | 1.70 | 10.62669 | 0.643666 | 0.037979 | 4.64 | 4.32 | 8.88 | ||
| Std | 0.295728 | 1.82 | 9.346467 | 0.585947 | 0.105724 | 3.68 | 2.55 | 0 | ||
| Best | 5.18 | 0 | 9.94 | 0.205425 | 9.44 | 0 | 0 | 0 | 1 | |
| Worst | 9.63 | 0 | 90.51281 | 0.652374 | 12.51340 | 0.007407 | 0.073058 | 0 | ||
| Mean | 7.37 | 0 | 18.05093 | 0.428925 | 1.112332 | 0.000247 | 0.005121 | 0 | ||
| Std | 1.14 | 0 | 36.69684 | 0.112703 | 2.882955 | 0.001352 | 0.016458 | 0 | ||
| Best | 8.75 | 1.10 | 1.87 | 1.09 | 1.06 | 0.005529 | 0.000197 | 0.027374 | 5 | |
| Worst | 1.56 | 4.60 | 1.438733 | 4.361125 | 14.41869 | 0.015736 | 0.002311 | 0.145999 | ||
| Mean | 1.28 | 8.43 | 0.311838 | 1.166543 | 1.245729 | 0.010707 | 0.000483 | 0.073446 | ||
| Std | 1.98 | 1.05 | 0.422497 | 1.122964 | 2.863611 | 0.002669 | 0.000441 | 0.025835 |
| Function | Result | BA | CapSA | MFO | MVO | SAO | MDWA | WOA | SCWOA | Rank |
|---|---|---|---|---|---|---|---|---|---|---|
| Best | 0.998004 | 0.998004 | 0.998004 | 0.998004 | 0.998004 | 0.998004 | 0.998004 | 0.998004 | 3 | |
| Worst | 12.67051 | 0.998004 | 5.928845 | 0.998004 | 11.72054 | 6.903342 | 10.76318 | 2.982105 | ||
| Mean | 10.19202 | 0.998004 | 1.394041 | 0.998004 | 3.579868 | 4.592604 | 1.588057 | 1.064298 | ||
| Std | 3.783086 | 1.49 | 1.024618 | 5.84 | 2.187821 | 2.453027 | 1.863075 | 0.362216 | ||
| Best | 0.000308 | 0.000307 | 0.000457 | 0.000407 | 0.000410 | 0.000316 | 0.000309 | 0.000308 | 1 | |
| Worst | 0.001660 | 0.001223 | 0.002237 | 0.020363 | 0.014274 | 0.020364 | 0.002176 | 0.000330 | ||
| Mean | 0.000649 | 0.000430 | 0.000979 | 0.007278 | 0.002660 | 0.001933 | 0.000597 | 0.000315 | ||
| Std | 0.000499 | 0.000317 | 0.000416 | 0.009413 | 0.003165 | 0.005024 | 0.000409 | 5.24 × 10−6 | ||
| Best | −1 | −1 | −1 | −1 | −0.99988 | −1 | −1 | −1 | 1 | |
| Worst | −0.78575 | −1 | −0.93625 | −1 | −0.93625 | −1 | −0.93625 | −1 | ||
| Mean | −0.93046 | −1 | −0.97662 | −1 | −0.97136 | −1 | −0.98512 | −1 | ||
| Std | 0.042517 | 0 | 0.031248 | 4.58 × 10−7 | 0.029805 | 0 | 0.027426 | 0 | ||
| Best | −10.5364 | −10.5364 | −10.5364 | −10.5364 | −10.5358 | −10.5364 | −10.5364 | −10.5364 | 4 | |
| Worst | −2.87114 | −10.5364 | −2.42173 | −2.42733 | −5.12804 | −1.85948 | −2.80656 | −5.11863 | ||
| Mean | −5.37063 | −10.5364 | −9.28154 | −9.13569 | −9.80391 | −6.55031 | −8.82645 | −8.13141 | ||
| Std | 1.479732 | 2.56 | 2.593989 | 2.898399 | 1.852026 | 3.203155 | 2.665397 | 2.521657 | ||
| Best | −1 | −1 | −1 | −1 | −0.99028 | −1 | −1 | −1 | 1 | |
| Worst | −0.99028 | −1 | −0.99028 | −0.99028 | −0.87301 | −1 | −0.99028 | −1 | ||
| Mean | −0.99644 | −1 | −0.99126 | −0.99967 | −0.97129 | −1 | −0.99644 | −1 | ||
| Std | 0.004762 | 0 | 0.002965 | 0.001773 | 0.031843 | 0 | 0.004762 | 0 | ||
| Best | 0.001669 | 2.03 | 1.11 | 0.005771 | 0.000755 | 6.83 | 3.3 | 0 | 1 | |
| Worst | 0.003717 | 1.01 | 4.440211 | 0.345920 | 3.664003 | 6.88 | 3.892485 | 0 | ||
| Mean | 0.002333 | 8.64 | 0.148007 | 0.112455 | 0.126119 | 1.45 | 0.489671 | 0 | ||
| Std | 0.000388 | 1.95 | 0.810668 | 0.096192 | 0.668206 | 2.04 | 1.117403 | 0 |
| Function | BA | CapSA | MFO | MVO | SAO | MDWA | WOA |
|---|---|---|---|---|---|---|---|
| 1.21 | 1.21 | 1.21 | 1.21 | 1.21 | 1.21 | 1.21 | |
| 1.21 | 1.21 | 1.21 | 1.21 | 1.21 | 1.21 | 1.21 | |
| 1.21 | 1.21 | 1.21 | 1.21 | 1.21 | 1.21 | 1.21 | |
| 1.21 | 1.21 | 1.21 | 1.21 | 1.21 | 1.21 | 1.21 | |
| N/A | 3.02 | 8.48 | 1.61 | 3.02 | 1.84 | 6.52 | |
| 3.02 | 3.02 | 3.02 | 3.02 | 3.02 | 3.02 | 3.02 | |
| 1.21 | N/A | 1.21 | 1.21 | 1.21 | 4.52 | N/A | |
| 1.21 | 1.21 | 1.21 | 1.21 | 1.21 | 1.21 | 1.16 | |
| 1.21 | N/A | 1.21 | 1.21 | 1.21 | 1.10 | 8.15 | |
| 3.02 | 3.02 | N/A | 1.31 | 1.95 | 3.02 | 3.02 | |
| 6.12 | 1.41 | 2.73 | 3.02 | 1.87 | 7.69 | 8.29 | |
| 8.53 | 1.09 | 3.02 | 3.02 | 3.02 | 2.15 | 5.09 | |
| 1.21 | N/A | 3.06 | 1.21 | 1.21 | N/A | 5.54 | |
| 2.52 | 1.36 | 4.98 | 1.43 | 6.01 | 8.77 | 6.77 | |
| 1.21 | N/A | 3.94 | 1.21 | 1.21 | N/A | 3.08 | |
| 1.21 | 1.21 | 1.21 | 1.21 | 1.21 | 1.21 | 1.21 |
| Algorithm | Optimal Value for Elements | Optimal Cost | |
|---|---|---|---|
| A1 | A2 | ||
| GWO [39] | 0.788648 | 0.408325 | 263.8960063 |
| CS [40] | 0.78867 | 0.40902 | 263.9716 |
| MFO [3] | 0.78824477 | 0.4094669 | 263.8959796 |
| Ray and Sain [41] | 0.795 | 0.395 | 264.3 |
| AOA [42] | 0.79369 | 0.39426 | 263.9154 |
| Raj et al. [43] | 0.789764410 | 0.405176050 | 263.89671 |
| Das et al. [44] | 0.78867 | 0.40902 | 263.9716 |
| GEO [45] | 0.79369 | 0.39426 | 263.9154 |
| RFO [46] | 0.75356 | 0.55373 | 268.51195 |
| GSA [34] | 0.747070495056356 | 0.530675746732991 | 264.769804538555 |
| ESOA [47] | 0.788192 | 0.409618 | 263.896 |
| DE [47] | 0.788675 | 0.408248 | 263.896 |
| L-Shade [47] | 0.78867514 | 0.40824829 | 263.896 |
| MPEDE [47] | 0.78924889 | 0.40662803 | 263.896 |
| HGSO [48] | 0.778254 | 0.440528 | 264.1762 |
| HGS [48] | 0.7884562 | 0.40886831 | 263.8959 |
| SC-GWO [49] | 0.78941 | 0.40617 | 263.8963 |
| COA [31] | 0.788057 | 0.410073 | 263.903379 |
| MRA [50] | 0.788574 | 0.408536 | 263.8959 |
| AO-TSA [51] | 0.790512 | 0.403105 | 263.9010 |
| TSA [51] | 0.797520 | 0.387339 | 264.3067 |
| I-GWO [51] | 0.784408 | 0.420579 | 263.9220 |
| BO [51] | 0.792187 | 0.398517 | 263.9159 |
| KH [35] | 0.785125499417041 | 0.420705357829172 | 264.137561671 |
| BOA [35] | 0.823331535298134 | 0.313381441824923 | 266.734135381 |
| SELO [52] | 0.7878 | 0.4108 | 263.8964 |
| HBO [52] | 0.7887 | 0.4082 | 263.8959 |
| LFD [52] | 0.7879 | 0.4106 | 263.8963 |
| KABC [53] | 0.7886 | 0.4084 | 263.8959 |
| SCWOA | 0.788674 | 0.408234 | 263.895843 |
| Algorithm | Optimal Value for Elements | Optimal Cost | |
|---|---|---|---|
| d | t | ||
| CS [54] | 5.45139 | 0.29196 | 26.53217 |
| ISA [55] | 5.45115623 | 0.29196547 | 26.5313 |
| SNS [56] | 5.45115632 | 0.29196547 | 26.4994969 |
| Rao [57] | 5.44 | 0.293 | 26.5323 |
| Gandomi [40] | 5.45139 | 0.29196 | 26.5321 |
| CSA [58] | 5.451163397 | 0.291965509 | 26.531364472 |
| MFPA [59] | 5.4512 | 0.29197 | 26.49995 |
| GSA-GA [60] | 5.45115623 | 0.29196548 | 26.531328 |
| AGQPSO [61] | 5.451156 | 0.29196 | 26.531328 |
| FPA [62] | 5.45116 | 0.291965 | 26.49948 |
| KH [32] | 5.451278 | 0.291957 | 26.5314 |
| BOA [32] | 5.448426 | 0.292463 | 26.512782 |
| HFBOA [32] | 5.451157 | 0.291966 | 26.499503 |
| Rocha and Fernandes [63] | 5.45139 | 0.29199 | 26.53227 |
| EM [64] | 5.452383 | 0.29190 | 26.53380 |
| HEM [64] | 5.451083 | 0.29199 | 26.53227 |
| KOA [31] | 5.4512 | 0.2920 | 26.499497 |
| FLA [31] | 5.4801 | 0.2905 | 26.563266 |
| COA [31] | 5.4511 | 0.2920 | 26.501823 |
| GTO [31] | 5.4512 | 0.2920 | 26.499497 |
| RUN [31] | 5.4512 | 0.2920 | 26.499497 |
| GWO [31] | 5.4511 | 0.2920 | 26.499770 |
| SMA [31] | 5.4512 | 0.2920 | 26.499538 |
| DO [31] | 5.4512 | 0.2920 | 26.499497 |
| POA [31] | 5.4512 | 0.2920 | 26.499497 |
| FA [65] | N/A | N/A | 26.5200 |
| AOS [65] | N/A | N/A | 26.5313783 |
| SCWOA | 5.5537 | 0.2502 | 25.5346 |
| Algorithm | Optimal Values for Elements | Optimal Cost | ||||||
|---|---|---|---|---|---|---|---|---|
| APSO [66] | 3.50131 | 0.7 | 18 | 8.12781 | 8.04212 | 3.35245 | 5.28708 | 3187.63049 |
| GA [67] | 3.510253 | 0.7 | 17 | 8.35 | 7.8 | 3.362201 | 5.287723 | 3067.561 |
| SES [68] | 3.506163 | 0.700831 | 17 | 7.460181 | 7.962143 | 3.3629 | 5.308949 | 3025.005127 |
| PSO [69] | 3.5001 | 0.7 | 17 | 7.5177 | 7.7832 | 3.3508 | 5.2867 | 3145.922 |
| GSA [70] | 3.6 | 0.7 | 17 | 8.3 | 7.8 | 3.369658 | 5.289224 | 3051.12 |
| hHHO-SCA [71] | 3.506119 | 0.7 | 17 | 7.3 | 7.99141 | 3.452569 | 5.286749 | 3029.873076 |
| MDA [72] | 3.5 | 0.7 | 17 | 7.3 | 7.670396 | 3.542421 | 5.245814 | 3019.583365 |
| SCA [29] | 3.508755 | 0.7 | 17 | 7.3 | 7.8 | 3.46102 | 5.289213 | 3030.563 |
| HS [73] | 3.520124 | 0.7 | 17 | 8.37 | 7.8 | 3.36697 | 5.288719 | 3029.002 |
| HIS [74] | 3.520124 | 0.7 | 17 | 8.37 | 7.8 | 3.36697 | 5.288719 | 3029.002 |
| GSA [75] | 3.6 | 0.7 | 17 | 8.3 | 7.802442 | 3.369658 | 5.289224 | 3051.1209 |
| EA [68] | 3.506163 | 0.700831 | 17 | 7.46018 | 7.962143 | 3.3629 | 5.3090 | 3025.005 |
| CMA-ES [76] | 2.6 | 0.8 | 17 | 7.3 | 7.8 | 2.9 | 5 | 8962.48 |
| L-SHADE [76] | 3.4367 | 0.7179 | 17.2544 | 8.1541 | 7.9808 | 3.2999 | 5.3498 | 7361.25 |
| EHO [76] | 3.4889 | 0.7782 | 23.2193 | 7.849 | 8.1021 | 3.5603 | 5.2459 | 73504.7 |
| GOA [76] | 3.5126 | 0.7033 | 17.2246 | 7.9131 | 7.9627 | 3.6567 | 5.2784 | 3169.32 |
| TEO [76] | 3.4261 | 0.7 | 17.6222 | 7.7408 | 7.9775 | 3.4145 | 5.2758 | 3595.59 |
| TLBO [77] | 3.508755 | 0.7 | 17 | 7.3 | 7.8 | 3.46102 | 5.2892113 | 3030.563 |
| BWO [34] | 3.58 | 0.72 | 18.28 | 7.73 | 7.73 | 3.43 | 5.28 | 3417.1535 |
| DE [78] | 3.520124 | 0.7 | 17 | 8.37 | 7.8 | 3.36697 | 5.288719 | 3029.002 |
| INFO [79] | 3.514301 | 0.7 | 17 | 7.307301 | 7.8078 | 3.466456 | 5.29752 | 3036.931 |
| CPA [79] | 3.525688 | 0.7 | 17 | 8.378957 | 7.8078 | 3.372258 | 5.29702 | 3035.367 |
| BOA [80] | 3.5239 | 0.7003 | 17.0088 | 8.0962 | 8.004 | 3.4048 | 5.3286 | 3061.6 |
| HIWOA [80] | 3.5605 | 0.7 | 17 | 7.3 | 8.1169 | 3.4631 | 5.2913 | 3059.6 |
| PSCA [81] | 3.54562 | 0.7 | 17.0023 | 8.3 | 8.3 | 3.37846 | 5.27946 | 3038.885 |
| HOA [82] | 3.56008 | 0.7 | 17 | 7.34912 | 7.8 | 3.49325 | 5.28415 | 3058.577 |
| ES [83] | 3.506163 | 0.700831 | 17 | 7.460181 | 7.962143 | 3.3629 | 5.309 | 3025.005 |
| CKGSA [33] | 3.5926 | 0.7134 | 17.1221 | 7.7464 | 8.1030 | 3.4464 | 5.3013 | 3163.2207 |
| SCWOA | 3.50228 | 0.7 | 17 | 7.88793 | 7.82363 | 3.36347 | 5.29537 | 3017.596 |
| Algorithm | Optimal Value for Elements | Optimal Cost | ||
|---|---|---|---|---|
| SFOA [87] | 0.051800 | 0.359000 | 11.279000 | 0.012700 |
| APSO [66] | 0.052588 | 0.378343 | 10.138862 | 0.012700 |
| GSA [88] | 0.050276 | 0.323680 | 13.525410 | 0.0127022 |
| CC [89] | 0.050000 | 0.315900 | 14.250000 | 0.0128334 |
| GA [90] | 0.051480 | 0.351661 | 11.632201 | 0.01270478 |
| MVO [4] | 0.05251 | 0.37602 | 10.33513 | 0.012790 |
| Arora [91] | 0.053396 | 0.399180 | 9.185400 | 0.012730 |
| SA [76] | 0.0570 | 0.4953 | 6.2225 | 0.01321 |
| CMA-ES [76] | 0.0973 | 1.1488 | 13.54530 | 0.85621 |
| GOA [76] | 0.0516 | 0.3360 | 13.500 | 0.01389 |
| HHO [76] | 0.0570 | 0.4991 | 6.2180 | 0.01281 |
| TLBO [77] | 0.050780 | 0.334779 | 12.72269 | 0.012709667 |
| CSO [34] | 0.0671 | 0.8482 | 2.4074 | 0.01682958 |
| SCSO [34] | 0.0500 | 0.3175 | 14.0200 | 0.012717020 |
| SCA [92] | 0.050780 | 0.334779 | 12.72269 | 0.012709667 |
| hHHO-SCA [93] | 0.054693 | 0.433378 | 7.891402 | 0.0128229 |
| RFO [46] | 0.05189 | 0.36142 | 11.58436 | 0.01321 |
| LSA [94] | 0.05027598 | 0.3236795 | 13.52541 | 0.01272045 |
| CA [95] | 0.05 | 0.317395 | 14.031795 | 0.012721 |
| SI [96] | 0.050417 | 0.321532 | 13.97991 | 0.01306 |
| ESOA [47] | 0.05 | 0.317168 | 14.0715 | 0.01274345 |
| MPEDE [47] | 0.05956062 | 0.5767404 | 4.71717282 | 0.01374 |
| HGS [48] | 0.05 | 0.3174 | 14.0306 | 0.0127 |
| FLA [48] | 0.0499 | 0.315 | 14.3045 | 0.0127 |
| COA [31] | 0.05 | 0.31137 | 14.862261 | 0.0131260069 |
| RUN [31] | 0.053107 | 0.391807 | 9.493688 | 0.0127011107 |
| I-GWO [51] | 0.050773 | 0.334713 | 12.77824 | 0.012803 |
| FA [97] | 0.052459 | 0.356839 | 11.130281 | 0.012894 |
| CRCC [97] | 0.05 | 0.3159 | 14.25 | 0.012833 |
| PF [97] | 0.053396 | 0.39918 | 9.1854 | 0.01273 |
| PSCA [81] | 0.05 | 0.317407 | 14.1166 | 0.012789 |
| CASFO [36] | 0.1413 | 1.3627 | 10.9889 | 3.6387 |
| SFO [36] | 0.1406 | 1.3608 | 10.92481 | 3.6477 |
| CLPSO [35] | 0.0528162 | 0.38365734 | 9.9234572 | 0.01276085 |
| VPPSO [98] | 0.0525 | 0.3756 | 10.2659 | 0.0127 |
| KABC [53] | 0.0556 | 0.4575 | 7.148 | 0.013017 |
| SCWOA | 0.054627 | 0.325243 | 11.654662 | 0.0126653 |
| Algorithm | Optimal Value for Elements | Optimal Cost | |||
|---|---|---|---|---|---|
| PSO [84] | 133.3 | 2.44 | 117.14 | 4.75 | 122 |
| DE [84] | 129.4 | 2.43 | 119.8 | 4.75 | 159 |
| GA [84] | 250 | 3.96 | 60.03 | 5.91 | 161 |
| HPSO [84] | 135.5 | 2.48 | 116.62 | 4.75 | 162 |
| CS [54] | 0.050 | 2.043 | 120 | 4.085 | 8.427 |
| SNS [56] | 0.050 | 2.042 | 120 | 4.083 | 8.412698349 |
| SCSO [34] | 0.050 | 2.040 | 119.99 | 4.083 | 8.40901438899551 |
| CSO [34] | 0.050 | 2.399 | 85.68 | 4.0804 | 13.7094866557362 |
| GWO [34] | 0.060 | 2.0390 | 120 | 4.083 | 8.40908765909047 |
| WAO [34] | 0.099 | 2.057 | 118.4 | 4.112 | 9.05943208079399 |
| SSA [34] | 0.050 | 2.073 | 116.32 | 4.145 | 8.80243253777633 |
| GSA [34] | 497.49 | 500 | 60.041 | 2.215 | 168.094363238712 |
| BWO [34] | 12.364 | 12.801 | 172.02 | 3.074 | 95.9980864948937 |
| AOS [85] | 0.05 | 2.042112482 | 119.951727 | 4.084004492 | 8.419142742 |
| GTO [86] | 0.05 | 2.052859 | 119.6392 | 4.089713 | 8.41270 |
| MFO [86] | 0.05 | 2.041514 | 120 | 4.083365 | 8.412698 |
| WOA [86] | 0.051874 | 2.045915 | 119.9579 | 4.085849 | 8.449975 |
| DMOA [65] | 0.05 | 0.125073578 | 120 | 4.116042166 | 4.695 |
| AOA [65] | 0.05 | 0.125073578 | 120 | 4.116042166 | 7.738 |
| CPSOGSA [65] | 500 | 500 | 120 | 2.578147082 | 4.6949 |
| BBO [65] | 129.4 | 2.43 | 119.8 | 4.75 | 4.6956 |
| ISA [65] | N/A | N/A | N/A | N/A | 8.4 |
| CGO [65] | N/A | N/A | N/A | N/A | 8.41281381 |
| MGA [65] | N/A | N/A | N/A | N/A | 8.41340665 |
| SCWOA | 0.05 | 0.138542 | 120 | 4.116025 | 4.6827 |
| Algorithm | Optimal Value for Elements | Optimal Cost | |||
|---|---|---|---|---|---|
| h | l | t | b | ||
| BBO [39] | 0.1854860 | 4.3129000 | 8.4399030 | 0.2359020 | 1.9180550 |
| PSO [39] | 0.219292 | 3.430416 | 8.433559 | 0.236204 | 1.852720 |
| GSA [88] | 0.182129 | 3.856979 | 10.000 | 0.202376 | 1.87995 |
| RO [99] | 0.203687 | 3.528467 | 9.004233 | 0.207241 | 1.735344 |
| CSCA [100] | 0.203137 | 3.542998 | 9.033498 | 0.206179 | 1.733461 |
| GA [101] | 0.2489 | 6.1730 | 8.1789 | 0.2533 | 2.4300 |
| DAVID [102] | 0.2434 | 6.2552 | 8.2915 | 0.2444 | 2.3841 |
| SIMPLEX [102] | 0.2792 | 5.6256 | 7.7512 | 0.2796 | 2.5307 |
| APPROX [102] | 0.2444 | 6.2189 | 8.2915 | 0.2444 | 2.3815 |
| HS [103] | 0.2442 | 6.2231 | 8.2915 | 0.2400 | 2.3807 |
| SCA [29] | 0.204695 | 3.536291 | 9.004290 | 0.210025 | 1.759173 |
| ES [104] | 0.199742 | 3.612060 | 9.037500 | 0.20682 | 1.73730 |
| CS [40] | 0.2015 | 3.562 | 9.0414 | 0.2057 | 1.73121 |
| Coello [105] | 0.208800 | 3.420500 | 8.997500 | 0.2100 | 1.74831 |
| CMA-ES [76] | 0.5617 | 4.3786 | 4.6772 | 0.9286 | 2.28384 |
| L-SHADE [76] | 0.4819 | 3.2140 | 5.4763 | 0.5753 | 3.43372 |
| EHO [76] | 1.0149 | 4.7616 | 4.8130 | 0.8722 | 3.36770 |
| GOA [76] | 0.4069 | 2.1411 | 6.3834 | 0.4123 | 2.43534 |
| HHO [76] | 0.1961 | 3.7449 | 9.0061 | 0.2071 | 1.75163 |
| TLBO [77] | 0.204695 | 3.536291 | 9.004290 | 0.210025 | 1.759173 |
| CSO [34] | 0.2044 | 3.3125 | 8.9941 | 0.2108 | 1.7321 |
| Random [102] | 0.4575 | 4.7313 | 5.0853 | 0.6600 | 4.11856 |
| Ragsdell [102] | 0.2455 | 6.1960 | 8.2730 | 0.2455 | 2.38594 |
| Siddall [106] | 0.2444 | 6.2189 | 8.2915 | 0.2444 | 2.38154 |
| DDSCA [107] | 0.20516 | 3.4759 | 9.0797 | 0.20552 | 1.7305 |
| hHHO-SCA [71] | 0.190086 | 3.696496 | 9.386343 | 0.204157 | 1.779032 |
| WWO [108] | 0.22214 | 3.67812 | 8.84965 | 0.23489 | 1.96842 |
| NMDE [109] | 0.2450054 | 6.284511 | 8.19911 | 2.450054 | 2.377135 |
| SaDE [110] | 0.306 | 3.02 | 6.33 | 0.419 | 2.48 |
| PSOGSA [110] | 0.24 | 3.09 | 8.36 | 0.24 | 1.99 |
| HGSA [110] | 0.211 | 3.40 | 8.90 | 0.212 | 1.75 |
| ACVO [110] | 0.205 | 3.48 | 9.04 | 0.206 | 1.73 |
| HPSO [95] | 0.20573 | 3.470489 | 9.036624 | 0.20573 | 1.728024 |
| CDE [95] | 0.203137 | 3.542998 | 9.033498 | 0.206179 | 1.733462 |
| SBM [96] | 0.2407 | 6.4851 | 8.2399 | 0.2497 | 2.4426 |
| BFOA [96] | 0.2057 | 3.4711 | 9.0367 | 0.2057 | 2.3868 |
| EA [96] | 0.2443 | 6.2201 | 8.2940 | 0.2444 | 2.3816 |
| T-Cell [96] | 0.2444 | 6.1286 | 8.2915 | 0.2444 | 2.3811 |
| FSA [96] | 0.2444 | 6.1258 | 8.2939 | 0.2444 | 2.3811 |
| IPSO [96] | 0.2444 | 6.2175 | 8.2915 | 0.2444 | 2.3810 |
| DSS-DE [96] | 0.2444 | 6.1275 | 8.2915 | 0.2444 | 2.3810 |
| HSA-GA [96] | 0.2231 | 1.5815 | 12.8468 | 0.2445 | 2.2500 |
| FLA [48] | 0.1983 | 3.6664 | 9.0705 | 0.2057 | 1.75 |
| HGS [111] | 0.26 | 5.1025 | 8.03961 | 0.26 | 2.302076 |
| LFD [49] | 0.1857 | 3.9070 | 9.1552 | 0.2051 | 1.7700 |
| COA [31] | 0.174041 | 7.087014 | 8.997138 | 0.207648 | 2.1324620263 |
| LA [112] | 0.2213 | 3.2818 | 8.7579 | 0.2216 | 1.8446 |
| FA [6] | 0.201762 | 6.804895 | 9.627042 | 0.205249 | 2.2837 |
| MDWA [6] | 0.203494 | 7.244195 | 9.058998 | 0.206944 | 2.2474 |
| EBSCA [113] | 0.17758 | 4.7517 | 9.0406 | 0.20573 | 1.8435 |
| SFO [36] | 0.2038 | 3.6630 | 9.0506 | 0.2064 | 1.73231 |
| EEGWO [22] | 0.2444 | 0.2444 | 8.2928 | 0.2444 | 2.3813 |
| RCGA [22] | N/A | N/A | N/A | N/A | 2.381133 |
| QHGSO [114] | 0.2152 | 6.8889 | 8.815 | 0.216 | 2.2864 |
| MCSS [114] | 0.2434 | 6.2552 | 8.2915 | 0.2444 | 2.3841 |
| BA [115] | 2 | 0.1 | 3.174303 | 2 | 1.818138 |
| CLPSO [35] | 0.20043684951 | 3.61781217135 | 9.12632634245 | 0.205392564 | 1.74936011824 |
| SCWOA | 0.205657 | 3.251177 | 9.039105 | 0.205468 | 1.69682 |
| Algorithm | Optimal Value for Elements | Optimal Cost | |||
|---|---|---|---|---|---|
| GA [39] | 49 | 19 | 16 | 43 | 2.70 |
| PSO [39] | 34 | 13 | 20 | 53 | 2.31 |
| ICA [39] | 43 | 16 | 19 | 49 | 2.70 |
| BBO [39] | 53 | 26 | 15 | 51 | 2.31 |
| NNA [39] | 49 | 16 | 19 | 43 | 2.70 |
| GWO [39] | 49 | 19 | 16 | 43 | 2.70 |
| WSA [39] | 43 | 16 | 19 | 49 | 2.70 |
| CS [54] | 43 | 16 | 19 | 49 | 2.70 |
| ABC [116] | 49 | 16 | 19 | 43 | 2.70 |
| MSFWA [117] | 49 | 19 | 16 | 43 | 2.70 |
| MBA [118] | 43 | 16 | 19 | 49 | 2.70 |
| ISA [55] | 43 | 19 | 16 | 49 | 2.70 |
| APSO [66] | 43 | 16 | 19 | 49 | 2.70 |
| IAPSO [66] | 43 | 16 | 19 | 49 | 2.70 |
| MVO [4] | 43 | 16 | 19 | 49 | 2.70 |
| MFO [3] | 43 | 19 | 16 | 49 | 2.70 |
| ALO [119] | 49 | 19 | 16 | 43 | 2.70 |
| PSOSCALF [120] | 49 | 19 | 16 | 43 | 2.70 |
| SNS [56] | 43 | 19 | 16 | 49 | 2.70085714 |
| Sandgren [121] | 45 | 22 | 18 | 60 | 5.712 |
| Kannan and Kramer [122] | 33 | 15 | 13 | 41 | 2.146 |
| Deb and Goya [123] | 49 | 16 | 19 | 43 | 2.701 |
| Gandomi er al. [40] | 43 | 16 | 19 | 49 | 2.701 |
| CSA [58] | 43 | 16 | 19 | 49 | 2.701 |
| ALM [122] | 33 | 15 | 13 | 41 | 2.1469 |
| MFPA [59] | 60 | 28 | 17 | 55 | 3.69 |
| FDA [124] | 49 | 19 | 16 | 43 | 2.7008571 |
| CAPSO [125] | 49 | 19 | 16 | 43 | 2.701 |
| GeneAS [125] | 33 | 14 | 17 | 50 | 1.362 |
| BOA [125] | 43 | 16 | 19 | 49 | 2.701 |
| Simulated annealing [125] | 52 | 15 | 30 | 60 | 2.36 |
| Sequential linearization approach [125] | 42 | 16 | 19 | 50 | 2.3 |
| Mixed-variable evolutionary programming [125] | 52 | 15 | 30 | 60 | 2.36 |
| Mixed integer discrete continuous programming [125] | 47 | 29 | 14 | 59 | 4.5 |
| Mixed integer discrete continuous optimization [125] | 33 | 15 | 13 | 41 | 2.146 |
| Nonlinear integer and discrete programming [125] | 45 | 22 | 18 | 60 | 5.712 |
| BO [126] | 43 | 19 | 16 | 49 | 2.700857 |
| KOA [31] | 44 | 20 | 16 | 50 | 2.700857 |
| FLA [31] | 44 | 16 | 20 | 49 | 2.700857 |
| COA [31] | 23 | 14 | 12 | 48 | 9.92158 |
| RUN [31] | 44 | 17 | 19 | 49 | 2.700857 |
| SMA [31] | 52 | 30 | 13 | 53 | 2.307816 |
| DO [31] | 49 | 16 | 19 | 44 | 2.700857 |
| POA [31] | 44 | 17 | 19 | 49 | 2.70085 |
| PDO [65] | 48 | 17 | 22 | 54 | 2.70 |
| DMOA [65] | 49 | 19 | 16 | 43 | 2.70 |
| AOA [65] | 49 | 19 | 19 | 54 | 2.70 |
| CPSOGSA [65] | 55 | 16 | 16 | 43 | 2.31 |
| SSA [65] | 49 | 19 | 19 | 49 | 2.70 |
| SCA [65] | 49 | 19 | 34 | 49 | 2.700857 |
| IEHO [127] | 19 | 16 | 43 | 49 | 2.70085 |
| MEWOA [37] | 49 | 16 | 19 | 43 | 2.7099 |
| ARO [128] | 49 | 19 | 16 | 43 | 2.7009 |
| BCA [129] | 43 | 16 | 19 | 49 | 2.7009 |
| BWO [130] | 50 | 18 | 17 | 46 | 7.5421 |
| GMO [53] | 43 | 19 | 16 | 49 | 2.700857 |
| SCWOA | 51 | 33 | 17 | 53 | 2.6574 |
| Algorithm | Optimal Value for Elements | Optimal Cost | |||||
|---|---|---|---|---|---|---|---|
| PSO [131] | 0.5 | 1.1167 | 0.5 | 1.30208 | 0.5 | 1.5 | |
| 0.5 | 0.345 | 0.192 | −19.54935 | −0.00431 | 22.84474 | ||
| GA [131] | 0.5 | 1.28017 | 0.50001 | 1.03302 | 0.50001 | 0.5 | |
| 0.5 | 0.34994 | 0.192 | 10.3119 | 0.00167 | 22.85653 | ||
| CS [54] | 0.5 | 1.11643 | 0.5 | 1.30208 | 0.5 | 1.5 | |
| 0.5 | 0.345 | 0.192 | −19.54935 | −0.00431 | 22.84294 | ||
| BA [55] | 0.5 | 1.1167 | 0.5 | 1.30208 | 0.5 | 1.5 | |
| 0.5 | 0.345 | 0.192 | −19.54935 | −0.00431 | 22.84474 | ||
| SNS [56] | 0.5 | 1.115933208 | 0.5 | 1.302918991 | 0.5 | 1.5 | |
| 0.5 | 0.345 | 0.192 | −19.6388662 | 1.49192 × 10−6 | 22.84297965 | ||
| DE [38] | 0.5 | 1.1167 | 0.5 | 1.30208 | 0.5 | 1.5 | |
| 0.5 | 0.345 | 0.192 | −19.54935 | −0.00431 | 22.84474 | ||
| FA [38] | 0.5 | 1.36 | 0.5 | 1.202 | 0.5 | 1.12 | |
| 0.5 | 0.345 | 0.192 | 8.87307 | −18.99808 | 22.84298 | ||
| TLBO [38] | 0.5 | 1.1135 | 0.5 | 1.307 | 0.5 | 1.5 | |
| 0.5 | 0.345 | 0.192 | −20.0655 | 0.1139 | 22.8436 | ||
| TLCS [38] | 0.5 | 1.1163 | 0.5 | 1.3023 | 0.5 | 1.5 | |
| 0.5 | 0.345 | 0.192 | −19.5721 | 0.0157 | 22.8430 | ||
| CPA [38] | 0.5 | 1.1157586 | 0.5 | 1.30321196 | 0.5 | 1.5 | |
| 0.5 | 0.345 | 0.27247957 | −19.67009727 | 0.00000206 | 22.84298982 | ||
| ABC [132] | 0.5 | 1.0624205 | 0.5148211 | 1.4491503 | 0.5 | 1.5 | |
| 0.5 | 0.345 | 0.192 | −29.34755 | 0.7410998 | 23.17588963 | ||
| MFO [132] | 0.5 | 1.116539 | 0.5 | 1.301908 | 0.5 | 1.5 | |
| 0.5 | 0.345 | 0.345 | −19.5304 | −0.000006 | 22.84297087 | ||
| ALO [132] | 0.5 | 1.11596 | 0.5 | 1.30286 | 0.5 | 1.5 | |
| 0.5 | 0.345 | 0.192 | −19.6330 | 0.023649 | 22.84298071 | ||
| ER-WCA [132] | 0.5 | 1.118688 | 0.5 | 1.298407 | 0.5 | 1.5 | |
| 0.5 | 0.345 | 0.192 | −19.1461 | −0.01527 | 22.84326462 | ||
| GWO [132] | 0.5 | 1.111484 | 0.5 | 1.312203 | 0.501214 | 1.5 | |
| 0.5 | 0.345 | 0.192 | −20.6057 | −25531 | 22.85279276 | ||
| WCA [132] | 0.5 | 1.1155932 | 0.5 | 1.3034919 | 0.5000146 | 1.5 | |
| 0.5 | 0.345 | 0.192 | −19.69967 | −0.023854 | 22.84303648 | ||
| MBA [132] | 0.5 | 1.1172701 | 0.5 | 1.30008438 | 0.5 | 1.499987 | |
| 0.5 | 0.345 | 0.345 | −19.40045 | −0.379205 | 22.84359640 | ||
| SSA [132] | 0.5 | 1.1093195 | 0.5 | 1.3148 | 0.5 | 1.499999 | |
| 0.5 | 0.345 | 0.192 | −20.821793 | 0.4412962 | 22.84651410 | ||
| WOA [132] | 0.5 | 1.108001 | 0.534477 | 1.30577 | 0.5 | 1.473844 | |
| 0.5 | 0.345 | 0.192 | −19.69924 | 3.4816923 | 23.04216220 | ||
| CSS [132] | 0.5 | 1.184389 | 0.5 | 1.230036 | 0.5 | 1.5 | |
| 0.5 | 0.280792 | 0.342425 | −7.394733 | 0.042206 | 23.00733588 | ||
| FACSS [133] | 0.5 | 1.127288 | 0.5 | 1.285546 | 0.5 | 1.499999 | |
| 0.5 | 0.344991 | 0.202079 | −17.607749 | 8.297 × 10−5 | 22.84907401 | ||
| GOA [134] | 0.5 | 1.1167 | 0.5 | 1.30208 | 0.5 | 1.5 | |
| 0.5 | 0.345 | 0.192 | −19.54935 | −0.00431 | 22.84474 | ||
| HGOANM [134] | 0.5 | 1.11643 | 0.5 | 1.30208 | 0.5 | 1.5 | |
| 0.5 | 0.345 | 0.192 | −19.54935 | −0.00431 | 22.84294 | ||
| EOBL-GOA [135] | 0.5 | 1.11643 | 0.5 | 1.30208 | 0.5 | 1.5 | |
| 0.5 | 0.345 | 0.192 | −19.54935 | −0.00431 | 22.84294 | ||
| CLPSO [35] | 0.5061 | 1.17379 | 0.5013 | 1.24706 | 0.5037 | 1.4956 | |
| 0.5 | 0.345 | 0.345 | −9.5985 | 3.3627 | 23.06244 | ||
| ACO [35] | 0.5 | 1.12004 | 0.5 | 1.29627 | 0.5 | 1.5 | |
| 0.5 | 0.345 | 0.192 | −18.905 | −0.0008 | 22.84371 | ||
| KH [35] | 0.5 | 1.14747 | 0.5 | 1.26118 | 0.5 | 1.5 | |
| 0.5 | 0.345 | 0.345 | −13.998 | −0.8984 | 22.88596 | ||
| HHO [35] | 0.5 | 1.15627 | 0.5 | 1.27133 | 0.5 | 1.4777 | |
| 0.5 | 0.345 | 0.192 | −14.592 | −2.4898 | 22.98537 | ||
| BOA [35] | 0.8246 | 1.03224 | 0.54007 | 1.35639 | 0.6377 | 1.26889 | |
| 0.5854 | 0.192 | 0.345 | −5.7333 | 0.4352 | 25.06573 | ||
| HGSO [35] | 0.5 | 1.22375 | 0.5 | 1.27111 | 0.5 | 1.31085 | |
| 0.5 | 0.345 | 0.345 | −4.3235 | 2.93676 | 23.43457 | ||
| LIACO [35] | 0.5 | 1.11593 | 0.5 | 1.30293 | 0.5 | 1.5 | |
| 0.5 | 0.192 | 0.345 | −19.64 | −0.000003 | 22.84299 | ||
| SMO [35] | 0.5 | 1.11634 | 0.5 | 1.30224 | 0.5 | 1.5 | |
| 0.5 | 0.345 | 0.345 | −19.566 | 0.000001 | 22.84298 | ||
| SCWOA | 0.5 | 1.11643 | 0.5 | 1.30178 | 0.5 | 1.5 | |
| 0.5 | 0.345 | 0.192 | −19.48754 | −0.00453 | 22.84278 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Zhang, J. A Hybrid Nonlinear Whale Optimization Algorithm with Sine Cosine for Global Optimization. Biomimetics 2024, 9, 602. https://doi.org/10.3390/biomimetics9100602
Xu Y, Zhang J. A Hybrid Nonlinear Whale Optimization Algorithm with Sine Cosine for Global Optimization. Biomimetics. 2024; 9(10):602. https://doi.org/10.3390/biomimetics9100602
Chicago/Turabian StyleXu, Yubao, and Jinzhong Zhang. 2024. "A Hybrid Nonlinear Whale Optimization Algorithm with Sine Cosine for Global Optimization" Biomimetics 9, no. 10: 602. https://doi.org/10.3390/biomimetics9100602
APA StyleXu, Y., & Zhang, J. (2024). A Hybrid Nonlinear Whale Optimization Algorithm with Sine Cosine for Global Optimization. Biomimetics, 9(10), 602. https://doi.org/10.3390/biomimetics9100602






