Abstract
The nutcracker optimizer algorithm (NOA) is a metaheuristic method proposed in recent years. This algorithm simulates the behavior of nutcrackers searching and storing food in nature to solve the optimization problem. However, the traditional NOA struggles to balance global exploration and local exploitation effectively, making it prone to getting trapped in local optima when solving complex problems. To address these shortcomings, this study proposes a reinforcement learning-based bi-population nutcracker optimizer algorithm called RLNOA. In the RLNOA, a bi-population mechanism is introduced to better balance global and local optimization capabilities. At the beginning of each iteration, the raw population is divided into an exploration sub-population and an exploitation sub-population based on the fitness value of each individual. The exploration sub-population is composed of individuals with poor fitness values. An improved foraging strategy based on random opposition-based learning is designed as the update method for the exploration sub-population to enhance diversity. Meanwhile, Q-learning serves as an adaptive selector for exploitation strategies, enabling optimal adjustment of the exploitation sub-population’s behavior across various problems. The performance of the RLNOA is evaluated using the CEC-2014, CEC-2017, and CEC-2020 benchmark function sets, and it is compared against nine state-of-the-art metaheuristic algorithms. Experimental results demonstrate the superior performance of the proposed algorithm.
1. Introduction
Metaheuristic algorithms, as a class of optimization techniques, are specifically engineered to address complex optimization problems that are challenging or infeasible to solve using traditional methods [1,2]. These algorithms are inspired by natural phenomena, biological processes, physical systems, or social behaviors, offering flexible frameworks for identifying solutions within a reasonable time frame [3,4]. Their advantages, such as simple structure, ease of implementation, and robustness to initial values, have led to their widespread application across various fields, such as power system optimization [5,6], industrial design [7,8], path planning [9,10], and parameter optimization [11,12].
Metaheuristic algorithms rely on two fundamental concepts: exploration and exploitation [13]. These concepts are essential for effectively navigating the search space to identify optimal or near-optimal solutions for complex optimization problems [14]. Exploration involves the algorithm’s capability to explore the broader search space and uncover new regions that may harbor promising solutions [15]. Exploration aims to avoid local optima and ensure a broad investigation of various areas within the search space. In contrast, exploitation involves focusing the search on specific regions that have previously shown promise, with the goal of refining solutions and converging toward the optimal solution by thoroughly searching near high-quality solutions [16]. A significant challenge in the design of metaheuristic algorithms is achieving an appropriate balance between exploration and exploitation [17].
In recent years, numerous metaheuristic algorithms have been proposed, including the grey wolf optimizer (GWO) [18], snake optimizer (SO) [19], white shark optimizer (WSO) [20,21], reptile search algorithm (RSA) [22], crested porcupine optimizer (CPO) [23], and nutcracker optimizer algorithm (NOA) [24]. Among these, the NOA mimics the search, caching, and recovery behaviors of nutcrackers, incorporating two exploration strategies and two exploitation strategies that enhance its fast convergence and robust search capabilities. However, in NOA, the transition between search strategies is governed by random numbers. When applied to complex problems, the NOA encounters limitations, such as an inadequate balance between exploration and exploitation and a propensity to become trapped in local optima.
Several techniques have been adopted to improve the performance of metaheuristic algorithms. The local search method focuses on exploring the neighborhood of a solution to find improvements, enabling the metaheuristic algorithms to escape local optima and continue the search for a global optimum. The authors of ref. [25] proposed a novel local search strategy to improve the particle swarm optimization (PSO) algorithm. After optimizing the population in each iteration, a local search strategy is introduced to enhance the present individuals in the population to accelerate the searching process and prevent becoming trapped in local optima. To improve the population diversity and convergence ability, ref. [26] proposed a variant of GWO with the fusion of a stochastic local search technique, evolutionary operators, and a memory mechanism. The stochastic local search can check the neighborhood of each individual to promote GWO’s exploitation performance. The authors of ref. [27] presented a local search and chaos mapping-based binary group teaching optimization algorithm called BGTOALC. Local search was introduced to increase exploitation. The authors of ref. [28] proposed an oppositional chaotic local search strategy to improve the aquila optimizer. Local search techniques play a critical role in refining solutions within metaheuristic algorithms. However, their embedding may cause the optimizer to perform more exploitation operations during the iterative process. This could exacerbate the imbalance between exploitation and exploration in metaheuristic algorithms.
An elite mechanism is a technique used to preserve the best-performing individuals across iterations for metaheuristic algorithms. The authors of ref. [29] proposed an elite symbiotic organism search algorithm called Elite-SOS. The global convergence ability was enhanced by using the evolutionary information of elite individuals. The authors of ref. [30] built an elite gene pool to guide the reproduction operator and acquire superior offspring. To improve the optimization performance of PSO, ref. [31] built three types of elite archives to save elite individuals with different ranks. Elite individuals could be retained directly during the iteration process, which can make full use of the whole population’s information. The authors of ref. [32] introduced an elite-guided hierarchical mutation strategy to improve the performance of the differential evolution (DE) algorithm. Elite individuals were scheduled for a local search, and the remaining individuals performed a global search guided by the former. The elite mechanism speeds up convergence by ensuring the information of the best solutions persist across generations. However, by focusing on the best solutions, the algorithm might overly emphasize exploitation at the cost of exploration. This imbalance can result in the algorithm getting trapped in local optima.
Incorporating supervised learning into metaheuristic algorithms is an emerging area of research that uses training knowledge to assist in the acquisition of optimal solutions in the iterative process. The authors of ref. [33] proposed a kernelized autoencoder that can learn from past search experiences to speed up the optimization process. The authors of ref. [34] presented autoencoding to predict the moving of the optimal solutions. To solve the problems of parameter setting and strategy selection, ref. [35] proposed an adaptive distributed DE algorithm. The individual and population parameters were updated adaptively based on the best solutions and historically successful experience. The authors of ref. [36] introduced a learning-aided evolutionary optimization framework that learns knowledge from the historical optimization process by using artificial neural networks. The learned knowledge can help metaheuristic algorithms to better approach the global optimum. While supervised learning can guide the search process more effectively, the training phase requires additional computational resources and is not suitable for time-constrained problems. In addition, the generalization of supervised learning also limits the application scenarios of this kind of strategy.
Reinforcement learning (RL) is a subfield of machine learning in which an agent learns to make decisions by taking actions within an environment to maximize cumulative rewards [37,38]. Due to its strong environmental interaction capabilities, RL has been increasingly employed by researchers to guide the selection of search strategies in metaheuristic algorithms. The authors of ref. [39] introduced an inverse reinforcement learning-based moth-flame optimization algorithm, IRLMFO, to solve large-scale optimization problems. RL was utilized to select effective search strategies based on historical data from the strategy pool established by IRLMFO. To overcome the drawbacks of getting trapped in local optima easily, ref. [40] presented a reinforcement learning-based RSA known as RLNSA, where RL managed the switching between exploration and exploitation strategies. Additionally, refs. [41,42] applied RL to address mutation strategy selection within the evolutionary process of differential evolution algorithms. The authors of ref. [43] embedded RL in the teaching–learning-based optimization algorithm (RLTLBO) to solve optimization problems. The authors of ref. [44] proposed a reinforcement learning-based memetic particle swarm optimization algorithm called RLMPSO. The selection of five search operations is controlled by the RL algorithm. The authors of ref. [45] designed a reinforcement learning-based comprehensive learning grey wolf optimizer (RLCGWO) to adaptively adjust strategies. Although the introduction of RL can enable metaheuristic algorithms to adaptively select exploration and exploitation strategies, it does not always effectively enhance algorithm performance. Typically, exploration is enhanced through methods such as large step sizes, random perturbations, or probabilistic jumps, which enable the algorithm to search beyond the current solutions [46]. Consequently, in RL-based metaheuristic algorithms, exploration strategies often receive rewards mainly during the early optimization stages, leading RL to favor exploitation strategies as optimization progresses. This tendency can cause existing RL-based metaheuristic algorithms to struggle in escaping local optima, as exploration strategies are less frequently selected.
To overcome the aforementioned problems, this paper introduces an RL-based bi-population NOA called RLNOA. The RLNOA introduces a bi-population mechanism to better balance exploration and exploitation in the optimization process. At the beginning of each iteration, the population is divided into the exploration sub-populations and the exploitation sub-populations. Individuals with poor fitness in the raw population form the exploration sub-population. A random opposition-based learning (ROBL)-based foraging method is proposed as the update strategy for the exploration sub-population to avoid local optima. The remaining outstanding individuals of the raw population formed the exploitation sub-populations, which use Q-learning within RL to adaptively select between the NOA’s two exploitation strategies (storage and recovery) to accelerate convergence and improve generalization. The division of these sub-populations is based on fitness ranking and optimization progress. Experimental results show that the RLNOA achieves superior optimization performance compared to current state-of-the-art algorithms. The primary contributions of this paper are as follows:
- An RL-based bi-population nutcracker optimizer algorithm (RLNOA) is developed to solve complex optimization problems;
- The foraging strategy of the NOA is enhanced using ROBL, improving its ability to search for feasible solutions;
- Q-learning is utilized to control the selection of the most appropriate exploitation strategy for each iteration, dynamically improving the refinement of the optimal solution.
2. Preliminaries
2.1. Nutcracker Optimization Algorithm
The NOA is a metaheuristic algorithm inspired by the natural behavior of nutcrackers [24]. It solves optimization problems by simulating the nutcracker’s behavior in collecting, storing, and searching for food. The optimization process in the NOA is carried out through four strategies: foraging, storage, cache search, and recovery. Table A1 summarizes the nomenclature of this study.
2.1.1. Foraging and Storage Strategies
During the foraging phase, individuals start searching for potential food sources within the search space. This behavior is mathematically modeled as follows:
where is the new position of the ith individual generated in the foraging phase; is the jth dimension of the ith individual in the iteration ; is the mean position of the jth dimensions for the current population in the iteration ; indicates the maximum generations; and are the lower and upper bounds of the optimization problem in the jth dimension; A, B, and C are three different integers randomly selected in the range of [0, NP]; NP is the population size; is a parameter generated by the levy flight; the values of , , , , and are random numbers selected within the range [0, 1]; is a control parameter; and is a parameter chosen among (chosen randomly between zero and one), (the normal distribution), and (levy flight), as follows:
where , , and are random numbers selected within the range [0, 1].
At the storage phase, individuals store foods as follows:
where is the new position of the ith individual generated in the storage phase; is a parameter generated by the levy flight; and , , , and are random numbers selected within the range [0, 1]. is a parameter that linearly decreased from 1 to 0 during the optimization process.
The exchange between the foraging and storage strategies is used to balance exploration and exploitation phases as follows:
where is random numbers selected within the range [0, 1] and is a parameter that linearly decreased from 1 to 0 during the optimization process.
2.1.2. Cache Search and Recovery Strategies
At the cache search phase, individuals locate their caches through two reference points:
and
where is a parameter chosen in the range of [0, ]; is an integer chosen randomly between zero and one; , are random numbers selected within the range [0, 1]; is a global exploration threshold; and is a convergence parameter and can be acquired as follows:
where and are random numbers selected within the range [0, 1]. The new position of the individual during the cache search phase can be acquired as follows:
where and are the jth position of and , respectively; , , , and are random numbers selected within the range [0, 1]; and C is the index of a solution selected randomly from the population.
During the recovery phase, nutcrackers find the hidden caches and retrieve the buried pine seeds. The new position of a nutcracker is obtained using the following equation:
Finally, the exchange between the cache search and recovery strategies is applied according to the following formula:
where is random numbers selected within the range [0, 1] and represents a probability value.
2.2. Reinforcement Learning
RL has been applied across various domains due to its effectiveness in problem-solving [47,48]. In RL, the agent interacts with the environment to learn how to perform optimal actions. As the representative method of RL, Q-learning defines the Q-table to control an agent’s actions. The Q-table is an m × n matrix, where m represents the number of states and n represents the number of actions available to the agent. By making a decision in the current state based on the Q-table values, the agent ultimately maximizes its reward. The Q-table is dynamically updated as follows:
where and represent the current and next states, respectively; and represent the current and next actions, respectively; is the reward acquired after performing action ; is the learning rate; is the discount factor; and represents the corresponding value in the Q-table.
3. The Development of the Proposed Algorithm
3.1. Overview
The traditional NOA is limited to specific problems and is prone to getting trapped in local optima. To overcome these limitations, this paper introduces a hybrid strategy called the RLNOA. In each iteration of the RLNOA, the population is segmented into two groups based on fitness ranking: the exploration sub-population and the exploitation sub-population. The exploration sub-population consists of individuals with poor fitness in the current population. A ROBL-based foraging strategy is employed as the update strategy for individuals in the exploration sub-population, with a sine-based perturbation introduced to adjust the size of the exploration sub-population to ensure convergence. The remaining individuals form the exploitation sub-population, which implements two types of exploitation strategies: storage and recovery. The selection of the exploitation strategy is governed by Q-learning.
Furthermore, the RLNOA utilizes a single Q-table to map individual states to actions. States in the RLNOA are encoded by relative changes in fitness value and local diversity, while actions correspond to exploitation strategies. The exploitation sub-population updates based on the strategy selected by each individual, generating offspring. Rewards are assigned based on the selection process outcomes, and the Q-table is subsequently updated for the next generation. Figure 1 illustrates the flowchart of the RLNOA, with the main steps detailed in Algorithm 1.
| Algorithm 1: The pseudocode of the RLNOA |
| Learning rate Discount factor , , . Set the initial Q-table: Q(s, a) = 0 Set t = 1 While t < Tmax do Acquire sub-population by Equation (19) belong to exploration sub-population by Equation (16) Else Determine the state of the exploitation sub-population by Equations (20) and (21) Choose the best a for the current s from Q-table Switch action Case 1: Storage by Equation (4) Case 2: Recovery by Equation (13) End Switch Set the reward by Equation (25) End if if its fitness is improved End for Calculate the relative changes of fitness and local diversity for the population Update Q-table by the exploitation sub-population t = t + 1 End While Return results Terminate |
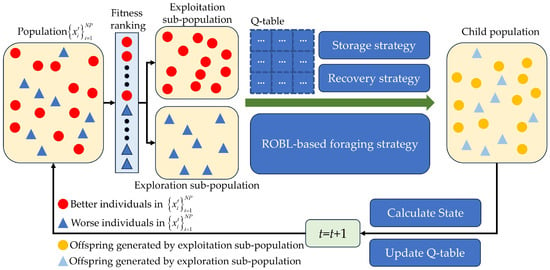
Figure 1.
Illustration of the RLNOA.
3.2. ROBL-Based Foraging Strategy
In the RLNOA, based on the ROBL method, an improved foraging strategy is introduced to construct the exploration behavior for the exploration sub-population [18]. The offspring in the exploration sub-population can be generated as follows:
where is the new position of the ith individual generated in the foraging phase; is the jth dimension of the ith individual in the iteration ; is the mean position of the jth dimensions for the current population in the iteration ; indicates the maximum generations; and are the lower and upper bounds of the optimization problem in the jth dimension; A, B, and C are three different integers randomly selected in the range of [0, NP]; NP is the population size; is a parameter generated by the levy flight; , , , , and are random numbers selected within the range [0, 1]; is a control parameter; and is a parameter generated based on Equation (3). The size of the exploration sub-population can be calculated as follows:
where is the control parameter. At the beginning of each iteration, individuals with poor fitness values are chosen from the total population to form the exploration sub-population. For example, assuming that , and . The variation of is illustrated in Figure 2. To ensure population diversity and prevent premature convergence, the value of decreases slowly in the early stages of the optimization process. In the later stages, decays rapidly, allowing most individuals to focus on local exploitation.
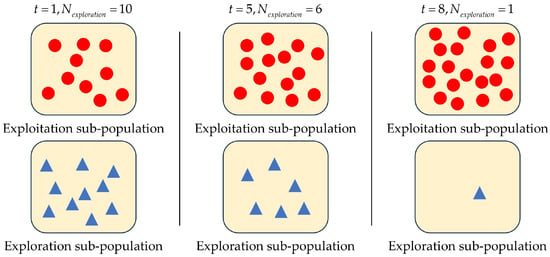
Figure 2.
The variation of when , , and .
3.3. Q-Learning-Based Exploitation Behavior
To ensure dynamic optimization of benefits at different stages for solving the optimization problem, Q-learning is employed as the selector for the exploitation sub-population to control the switch between storage (Equation (4)) and recovery (Equation (13)) strategies. The settings for Q-learning are specified as follows:
3.3.1. State Encoding
The state of each individual is encoded as the relative changes of local diversity and fitness values, which are defined as follows:
where is the relative changes in local diversity; is the relative changes in fitness value; and represents the local diversity of individual and can be calculated as follows:
where is the neighborhood set of ; is the dimension of the search space; and is the number of near neighbors. As shown in Figure 3, the exploitation population consists of 32 states in total. Among these, the dimension of is divided into eight states: [0, 0.25), [0.25, 0.5), [0.5, 0.75), [0.75, 1.0), [1, 1.5), [1.5, 2), [2, 3), and [3, ). Moreover, the dimension of is divided into four states: [0, 0.25), [0.25, 0.5), [0.5, 0.75), and [0.75, 1.0].
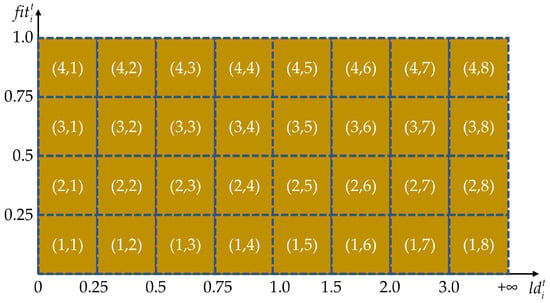
Figure 3.
The illustration of states in the exploitation population.
3.3.2. Action Options
The action of each individual is encoded as the selection of exploitation strategies. The probability of selecting each action is computed using the SoftMax function:
where is the value in the Q-table in the iteration ; is the jth action; and is the total number of actions. Each individual sample has an optimization strategy based on the probability of each action.
3.3.3. Reward Options
The reward is determined based on the selection results of each generation, reflecting the performance of the current optimization strategy. If the fitness value of the new position is better than the old position , the individual is rewarded with 1. Otherwise, the individual is punished with −1. The reward settings are defined as follows:
Based on the above settings, the Q-table can be updated by Equation (15). The pseudocode of the RLNOA is shown in Algorithm 1.
3.4. Time Complexity
As can be seen from the pseudocode of the RLNOA in Algorithm 1, the proposed algorithm mainly consists of the following parts.
(1) Initializing the population and updating the fitness values and local diversity for each individual, with a time complexity of .
(2) Acquiring the sub-populations, with a time complexity of .
(3) Updating the position for the exploration sub-population and exploitation sub-population, with a time complexity of .
(4) Calculating the relative changes in fitness and local diversity for the populations, with a time complexity of .
(5) Updating the Q-table using the exploitation sub-population, with a time complexity of .
Therefore, the maximum computing complexity of the RLNOA is , which is the same as that of the NOA.
4. Experimental Results
In this section, we perform a series of experiments on publicly available benchmark problems to assess the effectiveness of the RLNOA. The results are compared and analyzed against other state-of-the-art methods that have shown promising performances in the literature.
4.1. Test Conditions
The performance of the proposed RLNOA was tested on three global optimization test suites, including CEC-2014, CEC-2017, and CEC-2020 [49]. These test suites consist of unimodal, multimodal, hybrid, and composition functions, each with only one global optimum. The proposed RLNOA was compared with the NOA [24], SO [19], RSA [22], crested porcupine optimizer (CPO) [23], GWO [10], PSO [3], RLTLBO [43], RLMPSO [44], and RLCGWO [45]. The PSO and GWO are classical algorithms, while the NOA, SO, RSA, and CPO are well-known and recently proposed algorithms. The RLTLBO, RLMPSO, and RLCGWO are RL-based and recently proposed algorithms.
The common parameters for the experimental algorithms are presented in Table 1. The maximum number of iterations is set to 1000. To assess the experimental results, several performance metrics are used, including the average (Ave) and standard deviation (Std) of fitness values from 30 independent runs, and a ranking metric to assess the order of each method according to its average fitness value. Additionally, to highlight the significant differences between the RLNOA’s results and those of competing algorithms, convergence curves and box plots are utilized. The experiments were implemented in MATLAB R2024a on a device with Intel(R) Core(TM) i7-14700KF CPU @ 3.40 GHz and 64 GB RAM.

Table 1.
The common parameters of the experimental algorithms.
4.2. Comparison over CEC-2014
We performed optimization experiments on the CEC-2014 test suite to verify the effectiveness of the proposed RLNOA. The CEC-2014 test suite is a diverse collection of 30 test functions, including three unimodal functions, 13 multimodal functions, six hybrid functions, and eight composite functions. Each category is designed to test different aspects of an optimization algorithm’s capability, such as its ability to handle multiple local optima, locate the global optimum, and efficiently explore and exploit the search space. These functions are characterized by various levels of difficulty, dimensionality, and complexity, making them comprehensive tools for assessing the robustness, efficiency, and accuracy of optimization algorithms.
Table 2 shows the experimental results of various algorithms applied to the CEC-2014 test suite. As shown in the table, except for F3 and F30, the proposed RLNOA ranks first among all comparative algorithms in the remaining functions. Additionally, the second-to-last row in Table 2 confirms that the RLNOA achieves the highest average ranking, with a value of 1.0345. The second highest is the NOA, with a value of 2.1724, while the SO algorithm performs the worst.

Table 2.
Results of the CEC-2014 test suite.
Figure 4 illustrates the convergence curves of different algorithms applied to the CEC-2014 test suite. It can be seen from the figure that the convergence speed of the RLNOA is generally not the fastest. This is primarily because RL allows the population to learn the best exploitation strategy in the current state during the early stages of the search. As a result, the convergence speed of the RLNOA in the early stages is not the best, but its overall convergence performance remains competitive compared to the other algorithms. Moreover, due to RL combined with a dynamic exploration mechanism, the RLNOA can avoid local optima. Particularly for functions F5, F6, F8, F9, F10, F11, and F16, the RLNOA achieves better convergence results. Figure 5 shows the box plots of different algorithms applied to the CEC-2014 test suite, where the RLNOA achieves superior results.
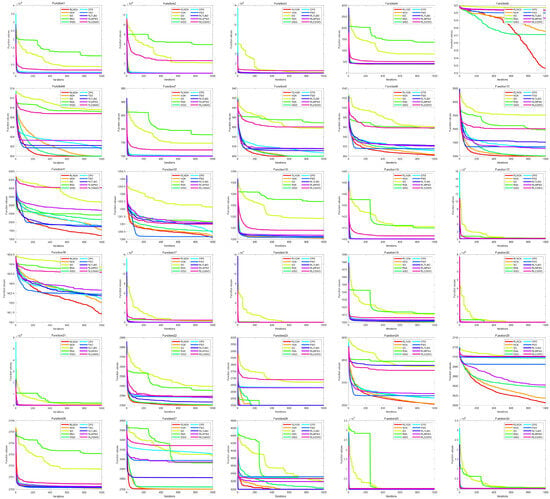
Figure 4.
The convergence curves of different algorithms applied to the CEC-2014 test suite.

Figure 5.
The box plots of different algorithms applied to the CEC-2014 test suite.
4.3. Comparison over CEC-2017
In this experiment, the ability of the RLNOA to solve the optimization problems within the CEC-2017 test suite is evaluated, with the results presented in Table 3. The CEC-2017 benchmark suite consists of 30 test functions, categorized into unimodal functions, basic multimodal functions, expanded multimodal functions, hybrid functions, and composition functions. These categories encompass a wide range of optimization challenges, assessing the ability of algorithms to locate global optima, avoid local optima, and effectively explore the search space. It is also noted that the CEC-2017-F2 function was excluded from the test suite due to its unstable behavior.

Table 3.
Results of the CEC-2017 test suite.
As shown in Table 3, the proposed RLNOA obtained the most optimal values, ranking first overall. For the five functions where the RLNOA did not achieve the optimal value, it ranked second. The RSA performed the worst when applied to the CEC-2017 test suite, ranking last. Figure 6 illustrates the convergence curves of the different algorithms applied to the CEC-2017 test suite. It can be seen that the RLNOA converges faster than other methods for functions such as F16, F20, and F24. In most cases, its convergence speed surpasses that of algorithms such as the SO and RSA. Figure 7 presents the box plots of different algorithms on the CEC-2017 test suite, indicating that the RLNOA consistently achieved superior results.
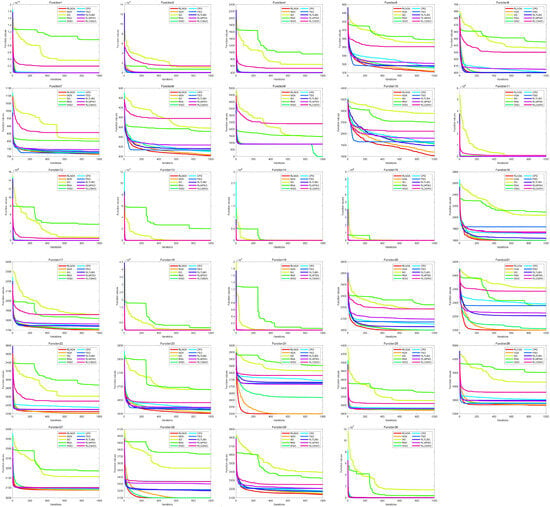
Figure 6.
The convergence curves of different algorithms applied to the CEC-2017 test suite.

Figure 7.
The box plots of different algorithms applied to the CEC-2017 test suite.
4.4. Comparison over CEC-2020
To verify the effectiveness of the proposed algorithm for problems with enhanced complexity and realism, we performed optimization experiments on the CEC-2020 test suite. This suite comprises 10 benchmark functions and places a greater emphasis on dynamic and noisy functions, reflecting the evolving nature of real-world problems. Such a focus allows for a comprehensive evaluation of an algorithm’s performance under more variable and unpredictable conditions.
Table 4 presents the results of different algorithms applied to the CEC-2020 test suite. It can be seen that the RLNOA ranks first in eight out of the 10 functions. For functions F4 and F9, the RLNOA ranks second, but the gap between its results and the first-ranked results is minimal. The average ranking and final ranking of each algorithm across all test functions are shown in the last two rows of Table 4. The RLNOA performs the best, with an average ranking of 1.2222 and a final ranking of 1. Figure 8 and Figure 9, respectively, show the convergence curves and box plots of different algorithms applied to the CEC-2020 test suite. These figures confirm that the RLNOA consistently demonstrates superior performance across all benchmark functions.

Table 4.
Results of the CEC-2020 test suite.
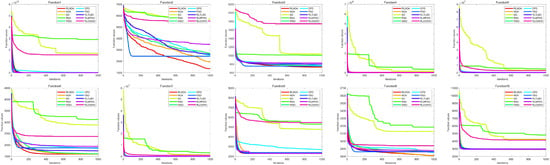
Figure 8.
The convergence curves of different algorithms applied to the CEC-2020 test suite.

Figure 9.
The box plots of different algorithms applied to the CEC-2020 test suite.
4.5. Analysis of the Q-Table
We take test function F1 in CEC2014 as an example to illustrate the Q-table update process. As shown in Figure 10, the state represents different stages of the relative changes in local diversity and fitness values. Actions and represent the storage strategy and recovery strategy, respectively. The Q-table is initialized as a zero matrix. After five iterations, the Q-values for different states in the Q-table change. The individual will execute the action corresponding to the highest Q-value in the current state. For example, the Q-value of the storage strategy (action ) in state is −0.93, which is much lower than the Q-value of the recovery strategy (action ), which is 1.32. When the individual is in state during the next iteration, it will execute the recovery strategy. In the later stages of the optimization process, when the population has converged close to the global optimum, selecting any exploitation strategy is unlikely to yield better results. As a result, almost all Q-values in the Q-table become negative.
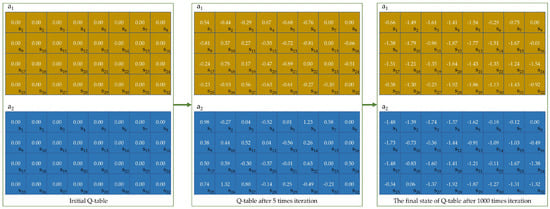
Figure 10.
Q-table update process for the F1 function.
4.6. Analysis of the RLNOA’s Parameters
The RLNOA contains some parameters that affect its performance, similar to other metaheuristic algorithms. Here are some suggestions for selecting and tuning these parameters.
(1) Population size NP
A larger population size generally allows for better exploration of the solution space, as more diverse solutions are maintained. However, increasing the population size typically leads to higher computational costs, as more solutions need to be evaluated during each iteration. This can slow down the algorithm, especially for complex or large-scale problems. Therefore, population sizes often range from a few dozen to several hundred individuals, depending on the problem’s complexity and the specific metaheuristic used. Reasonable values are within [20, 200].
(2) Maximum iterations
More iterations allow the algorithm to refine and improve solutions gradually. However, there may be diminishing returns after a certain number of iterations, where further improvements become minimal. Reasonable values are within [100, 2000].
(3) Learning rate
This parameter determines how much new information overrides old information. A high learning rate means the agent learns quickly, but it may also make the learning process unstable. A low learning rate ensures stability but can slow down the learning process. Reasonable values are within [0.1, 0.9].
(4) Discount factor
This factor determines the importance of future rewards. A value close to 0 makes the agent prioritize immediate rewards, while a value close to 1 encourages the agent to consider long-term rewards. The discount factor helps balance immediate versus future gains, influencing the agent’s overall strategy. Reasonable values are within [0.1, 0.9].
We also studied the sensitivity of the RLNOA’s partial parameters. This analysis helps determine the impact of small changes in these parameters on the performance of the proposed algorithm. The functions used in these experiments are F1, F4, F17, and F23 from CEC-2014, which represent unimodal, multimodal, hybrid, and composite functions, respectively. The maximum number of iterations is set to 1000. The population size is set to 100. The average (Ave) of fitness values from 30 independent runs is used to acquire the sensitivity analysis results. Experimental results are as follows:
- Global exploration threshold : to verify the effect of on the efficiency of the RLNOA, experiments are performed for several values of , taken as 0.2, 0.4, 0.6, and 0.8, while other parameters are unchanged. As shown in Table 5, the RLNOA is insensitive to this parameter. The results of F17 indicate that the RLNOA performs best when is set to a specific value.
 Table 5. Results of the RLNOA with different values for the parameter .
Table 5. Results of the RLNOA with different values for the parameter . - Control parameter : experiments are performed for several values of , taken as 0.05, 0.1, 0.2, and 0.5, while other parameters are unchanged. As shown in Table 6, the RLNOA is not sensitive to small changes in the parameter .
 Table 6. Results of the RLNOA with different values for the parameter .
Table 6. Results of the RLNOA with different values for the parameter . - Number of near neighbors : Table 7 shows the results of the RLNOA with different values for the parameter . It is evident from Table 7 that the RLNOA is not sensitive to small changes in the parameter .
 Table 7. Results of the RLNOA with different values for the parameter .
Table 7. Results of the RLNOA with different values for the parameter . - Control parameter : to explore the sensitivity of the RLNOA to the parameter , experiments are caried out for different values of , as shown in Table 8. It is apparent that the RLNOA is sensitive to . This is primarily because controls the variation trend of the exploration sub-population during the optimization process. Table 8 also shows that the RLNOA acquires the best results when the value of is set to 1.
 Table 8. Results of the RLNOA with different values for the parameter .
Table 8. Results of the RLNOA with different values for the parameter .
5. Conclusions
In this paper, we propose an RL-based bi-population nutcracker optimizer algorithm. We developed a bi-population mechanism that uses fitness ranking to separate the raw population into exploration and exploitation sub-populations at the start of each iteration. The exploration sub-population, comprising individuals with lower fitness, employs a foraging strategy based on ROBL to maintain diversity. The exploitation sub-population includes two strategies, storage and recovery, with the selection of strategy controlled by Q-learning in RL. Experiments were conducted on the CEC-2014, CEC-2017, and CEC-2020 benchmark suites. The results, including optimization performance, convergence curves, and box plots, demonstrate that the proposed algorithm outperforms nine other comparative algorithms.
However, the proposed algorithm still has limitations. First, the exploration strategy needs to be further enhanced to improve the algorithm’s ability to escape local optima. Second, there is some redundancy in boundary states within the Q-learning process. In the future, based on the existing RLNOA framework, the development of search strategies and the encoding of states will be further studied to improve optimization performance. Additionally, complex engineering applications will be introduced to test future work.
Author Contributions
Conceptualization, Y.L. and Y.Z.; methodology, Y.L.; software, Y.L.; validation, Y.L. and Y.Z.; formal analysis, Y.L.; investigation, Y.L.; resources, Y.L.; data curation, Y.L.; writing—original draft preparation, Y.L.; writing—review and editing, Y.L. and Y.Z.; visualization, Y.L.; supervision, Y.Z.; project administration, Y.Z.; funding acquisition, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
The nomenclature of this study.
Table A1.
The nomenclature of this study.
| Indices | A, B, and C | Integers randomly selected in the range of [0, NP] | |
| Index of individuals in the population | The lower bound of the optimization problem in the jth dimension | ||
| Index of dimensions | NP | The population size | |
| Index of individuals in the neighborhood set | A probability value | ||
| Index of iteration | A global exploration threshold | ||
| Sets | The maximum iterations | ||
| The population in the iteration | The upper bound of the optimization problem in the jth dimension | ||
| The neighborhood set of | Variables | ||
| Parameters | and | The current and next actions respectively | |
| The learning rate | The relative changes of fitness value | ||
| The discount factor | The relative changes of local diversity | ||
| and | Control parameter | and | The current and next states respectively |
| , , and | A parameter generated by the levy flight | The new position of the ith individual generated in the foraging phase | |
| A parameter chosen in the range of [0, ] | The jth dimension of the ith individual in the iteration | ||
| and | A parameter that linearly decreased from 1 to 0 | The new position of the ith individual generated in the storage phase | |
| A random number selected within the range [0, 1] | The mean position of the jth dimensions for current population in the iteration | ||
| A random number generated based on a normal distribution | The local diversity of individual | ||
| The dimension of the search space | The size of the exploration sub-population | ||
| The number of near neighbors | The corresponding value in the Q-table | ||
| and | Random numbers selected within the range [0, 1] | The reward acquired after performing action | |
| An integer chosen randomly between zero and one |
References
- Hubálovsky, S.; Hubálovská, M.; Matousová, I. A New Hybrid Particle Swarm Optimization-Teaching-Learning-Based Optimization for Solving Optimization Problems. Biomimetics 2024, 9, 8. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.T.; Zhang, S.S.; Zou, G.Y. An Improved Multi-Strategy Crayfish Optimization Algorithm for Solving Numerical Optimization Problems. Biomimetics 2024, 9, 361. [Google Scholar] [CrossRef] [PubMed]
- Pardo, X.C.; González, P.; Banga, J.R.; Doallo, R. Population based metaheuristics in Spark: Towards a general framework using PSO as a case study. Swarm Evol. Comput. 2024, 85, 101483. [Google Scholar] [CrossRef]
- Tatsis, V.A.; Parsopoulos, K.E. Reinforcement learning for enhanced online gradient-based parameter adaptation in metaheuristics. Swarm Evol. Comput. 2023, 83, 101371. [Google Scholar] [CrossRef]
- Wang, Y.; Xiong, G.J.; Xu, S.P.; Suganthan, P.N. Large-scale power system multi-area economic dispatch considering valve point effects with comprehensive learning differential evolution. Swarm Evol. Comput. 2024, 89, 101620. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, H.F.; Tian, Y.Z.; Li, C.W.; Yue, D. Cooperative constrained multi-objective dual-population evolutionary algorithm for optimal dispatching of wind-power integrated power system. Swarm Evol. Comput. 2024, 87, 101525. [Google Scholar] [CrossRef]
- Feng, X.; Pan, A.Q.; Ren, Z.Y.; Hong, J.C.; Fan, Z.P.; Tong, Y.H. An adaptive dual-population based evolutionary algorithm for industrial cut tobacco drying system. Appl. Soft Comput. 2023, 144, 110446. [Google Scholar] [CrossRef]
- Luo, T.; Xie, J.P.; Zhang, B.T.; Zhang, Y.; Li, C.Q.; Zhou, J. An improved levy chaotic particle swarm optimization algorithm for energy-efficient cluster routing scheme in industrial wireless sensor networks. Expert Syst. Appl. 2024, 241, 122780. [Google Scholar] [CrossRef]
- Qu, C.Z.; Gai, W.D.; Zhang, J.; Zhong, M.Y. A novel hybrid grey wolf optimizer algorithm for unmanned aerial vehicle (UAV) path planning. Knowl.-Based Syst. 2020, 194, 105530. [Google Scholar] [CrossRef]
- Qu, C.Z.; Gai, W.D.; Zhong, M.Y.; Zhang, J. A novel reinforcement learning based grey wolf optimizer algorithm for unmanned aerial vehicles (UAVs) path planning. Appl. Soft Comput. 2020, 89, 106099. [Google Scholar] [CrossRef]
- Qu, C.; Zhang, Y.; Ma, F.; Huang, K. Parameter optimization for point clouds denoising based on no-reference quality assessment. Measurement 2023, 211, 112592. [Google Scholar] [CrossRef]
- Chauhan, D.; Yadav, A. An archive-based self-adaptive artificial electric field algorithm with orthogonal initialization for real-parameter optimization problems. Appl. Soft Comput. 2024, 150, 111109. [Google Scholar] [CrossRef]
- Li, G.Q.; Zhang, W.W.; Yue, C.T.; Wang, Y.R. Balancing exploration and exploitation in dynamic constrained multimodal multi-objective co-evolutionary algorithm. Swarm Evol. Comput. 2024, 89, 101652. [Google Scholar] [CrossRef]
- Ahadzadeh, B.; Abdar, M.; Safara, F.; Khosravi, A.; Menhaj, M.B.; Suganthan, P.N. SFE: A Simple, Fast, and Efficient Feature Selection Algorithm for High-Dimensional Data. IEEE Trans. Evol. Comput. 2023, 27, 1896–1911. [Google Scholar] [CrossRef]
- Fu, S.; Huang, H.; Ma, C.; Wei, J.; Li, Y.; Fu, Y. Improved dwarf mongoose optimization algorithm using novel nonlinear control and exploration strategies. Expert Syst. Appl. 2023, 233, 120904. [Google Scholar] [CrossRef]
- Li, J.; Li, G.; Wang, Z.; Cui, L. Differential evolution with an adaptive penalty coefficient mechanism and a search history exploitation mechanism. Expert Syst. Appl. 2023, 230, 120530. [Google Scholar] [CrossRef]
- Hu, C.; Zeng, S.; Li, C. A framework of global exploration and local exploitation using surrogates for expensive optimization. Knowl.-Based Syst. 2023, 280, 111018. [Google Scholar] [CrossRef]
- Chang, D.; Rao, C.; Xiao, X.; Hu, F.; Goh, M. Multiple strategies based Grey Wolf Optimizer for feature selection in performance evaluation of open-ended funds. Swarm Evol. Comput. 2024, 86, 101518. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A novel meta-heuristic optimization algorithm. Knowl.-Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Braik, M.; Hammouri, A.; Atwan, J.; Al-Betar, M.A.A.; Awadallah, M.A. White Shark Optimizer: A novel bio-inspired meta-heuristic algorithm for global optimization problems. Knowl.-Based Syst. 2022, 243, 108457. [Google Scholar] [CrossRef]
- Kumar, S.; Sharma, N.K.; Kumar, N. WSOmark: An adaptive dual-purpose color image watermarking using white shark optimizer and Levenberg-Marquardt BPNN. Expert Syst. Appl. 2023, 226, 120137. [Google Scholar] [CrossRef]
- Abualigah, L.; Abd Elaziz, M.; Sumari, P.; Geem, Z.W.; Gandomi, A.H. Reptile Search Algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 2022, 191, 116158. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Abouhawwash, M. Crested Porcupine Optimizer: A new nature-inspired metaheuristic. Knowl.-Based Syst. 2024, 284, 111257. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Jameel, M.; Abouhawwash, M. Nutcracker optimizer: A novel nature-inspired metaheuristic algorithm for global optimization and engineering design problems. Knowl.-Based Syst. 2023, 262, 110248. [Google Scholar] [CrossRef]
- Qaraad, M.; Amjad, S.; Hussein, N.K.; Farag, M.A.; Mirjalili, S.; Elhosseini, M.A. Quadratic interpolation and a new local search approach to improve particle swarm optimization: Solar photovoltaic parameter estimation. Expert Syst. Appl. 2024, 236, 121417. [Google Scholar] [CrossRef]
- Ahmed, R.; Rangaiah, G.P.; Mahadzir, S.; Mirjalili, S.; Hassan, M.H.; Kamel, S. Memory, evolutionary operator, and local search based improved Grey Wolf Optimizer with linear population size reduction technique. Knowl.-Based Syst. 2023, 264, 110297. [Google Scholar] [CrossRef]
- Khosravi, H.; Amiri, B.; Yazdanjue, N.; Babaiyan, V. An improved group teaching optimization algorithm based on local search and chaotic map for feature selection in high-dimensional data. Expert Syst. Appl. 2022, 204, 117493. [Google Scholar] [CrossRef]
- Ekinci, S.; Izci, D.; Abualigah, L.; Abu Zitar, R. A Modified Oppositional Chaotic Local Search Strategy Based Aquila Optimizer to Design an Effective Controller for Vehicle Cruise Control System. J. Bionic Eng. 2023, 20, 1828–1851. [Google Scholar] [CrossRef]
- Xiao, J.; Wang, Y.J.; Xu, X.K. Fuzzy Community Detection Based on Elite Symbiotic Organisms Search and Node Neighborhood Information. IEEE Trans. Fuzzy Syst. 2022, 30, 2500–2514. [Google Scholar] [CrossRef]
- Zhu, Q.L.; Lin, Q.Z.; Li, J.Q.; Coello, C.A.C.; Ming, Z.; Chen, J.Y.; Zhang, J. An Elite Gene Guided Reproduction Operator for Many-Objective Optimization. IEEE Trans. Cybern. 2021, 51, 765–778. [Google Scholar] [CrossRef]
- Zhang, Y.Y. Elite archives-driven particle swarm optimization for large scale numerical optimization and its engineering applications. Swarm Evol. Comput. 2023, 76, 101212. [Google Scholar] [CrossRef]
- Zhong, X.X.; Cheng, P. An elite-guided hierarchical differential evolution algorithm. Appl. Intell. 2021, 51, 4962–4983. [Google Scholar] [CrossRef]
- Zhou, L.; Feng, L.; Gupta, A.; Ong, Y.S. Learnable Evolutionary Search Across Heterogeneous Problems via Kernelized Autoencoding. IEEE Trans. Evol. Comput. 2021, 25, 567–581. [Google Scholar] [CrossRef]
- Feng, L.; Zhou, W.; Liu, W.C.; Ong, Y.S.; Tan, K.C. Solving Dynamic Multiobjective Problem via Autoencoding Evolutionary Search. IEEE Trans. Cybern. 2022, 52, 2649–2662. [Google Scholar] [CrossRef]
- Zhan, Z.H.; Wang, Z.J.; Jin, H.; Zhang, J. Adaptive Distributed Differential Evolution. IEEE Trans. Cybern. 2020, 50, 4633–4647. [Google Scholar] [CrossRef]
- Zhan, Z.H.; Li, J.Y.; Kwong, S.; Zhang, J. Learning-Aided Evolution for Optimization. IEEE Trans. Evol. Comput. 2023, 27, 1794–1808. [Google Scholar] [CrossRef]
- Zabihi, Z.; Moghadam, A.M.E.; Rezvani, M.H. Reinforcement Learning Methods for Computation Offloading: A Systematic Review. Acm Comput. Surv. 2024, 56, 1–41. [Google Scholar] [CrossRef]
- Wang, D.; Gao, N.; Liu, D.; Li, J.; Lewis, F.L. Recent Progress in Reinforcement Learning and Adaptive Dynamic Programming for Advanced Control Applications. IEEE-CAA J. Autom. Sin. 2024, 11, 18–36. [Google Scholar] [CrossRef]
- Zhao, F.; Wang, Q.; Wang, L. An inverse reinforcement learning framework with the Q-learning mechanism for the metaheuristic algorithm. Knowl.-Based Syst. 2023, 265, 110368. [Google Scholar] [CrossRef]
- Ghetas, M.; Issa, M. A novel reinforcement learning-based reptile search algorithm for solving optimization problems. Neural Comput. Appl. 2023, 36, 533–568. [Google Scholar] [CrossRef]
- Li, Z.; Shi, L.; Yue, C.; Shang, Z.; Qu, B. Differential evolution based on reinforcement learning with fitness ranking for solving multimodal multiobjective problems. Swarm Evol. Comput. 2019, 49, 234–244. [Google Scholar] [CrossRef]
- Tan, Z.; Li, K. Differential evolution with mixed mutation strategy based on deep reinforcement learning. Appl. Soft Comput. 2021, 111, 107678. [Google Scholar] [CrossRef]
- Wu, D.; Wang, S.; Liu, Q.; Abualigah, L.; Jia, H. An Improved Teaching-Learning-Based Optimization Algorithm with Reinforcement Learning Strategy for Solving Optimization Problems. Comput. Intell. Neurosci. 2022, 2022, 1535957. [Google Scholar] [CrossRef] [PubMed]
- Samma, H.; Lim, C.P.; Saleh, J.M. A new Reinforcement Learning-Based Memetic Particle Swarm Optimizer. Appl. Soft Comput. 2016, 43, 276–297. [Google Scholar] [CrossRef]
- Hu, Z.P.; Yu, X.B. Reinforcement learning-based comprehensive learning grey wolf optimizer for feature selection. Appl. Soft Comput. 2023, 149, 110959. [Google Scholar] [CrossRef]
- Li, J.; Dong, H.; Wang, P.; Shen, J.; Qin, D. Multi-objective constrained black-box optimization algorithm based on feasible region localization and performance-improvement exploration. Appl. Soft Comput. 2023, 148, 110874. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, S.; Li, G.; Zhang, Q. Multiobjective Combinatorial Optimization Using a Single Deep Reinforcement Learning Model. IEEE Trans. Cybern. 2024, 54, 1984–1996. [Google Scholar] [CrossRef]
- Huang, L.; Dong, B.; Xie, W.; Zhang, W. Offline Reinforcement Learning with Behavior Value Regularization. IEEE Trans. Cybern. 2024, 54, 3692–3704. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; El-Shahat, D.; Jameel, M.; Abouhawwash, M. Exponential distribution optimizer (EDO): A novel math-inspired algorithm for global optimization and engineering problems. Artif. Intell. Rev. 2023, 56, 9329–9400. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).