Intelligent Fish-Inspired Foraging of Swarm Robots with Sub-Group Behaviors Based on Neurodynamic Models
Abstract
1. Introduction
- (1)
- (2)
- (3)
- (1)
- A novel collective foraging approach is proposed for swarm robots in changing environments. The proposed approach takes inspiration from the locally interactive group behavior of fish.
- (2)
- A novel approach to collision-free virtual forces is proposed to guide swarm robots based on a neurodynamics model. During the foraging process, the swarm robots have self-adaptive ability to accommodate changes in complex environments.
- (3)
- An SOM algorithm is proposed to enable the sub-group behavior of the swarm robots, which enables the swarm robots to dynamically adjust their shape in complex environments.
2. Problem Description
- (1)
- The foraging behavior is based on local interactions between individual robots.
- (2)
- The swarm robots should be self-adaptive during the foraging process.
- (3)
- The robots should maintain the desired distance from their neighbors.
3. Proposed Approaches
3.1. Fish-Inspired Foraging Behavior
- (1)
- Based on the number of targets, swarm robots are divided into different subdivision groups using the SOM algorithm. Within each subdivision group, one robot is selected for pilot mode, while the other robots switch to foraging mode;
- (2)
- The pilot robot requests the coordinates and status of all the foraging robots in the subdivision group;
- (3)
- After the group of swarm robots is constructed, all the robots in the same subdivision group begin to move cooperatively to the target.
3.2. Sub-Group Mechanism Based on SOM
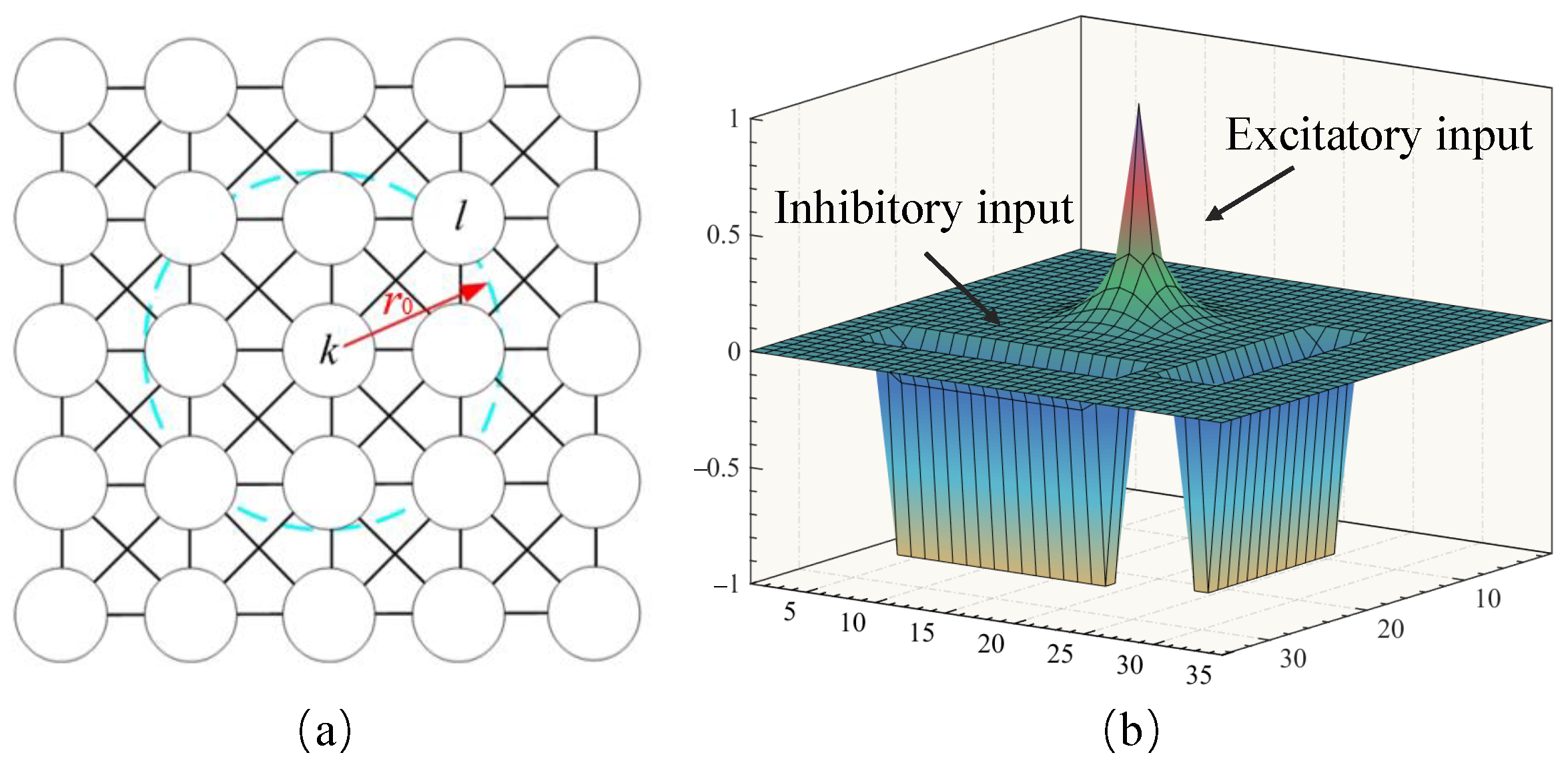
3.3. Virtual Force Generation Based on BINN
| Algorithm 1: Computing Dynamic Landscape of Neural Activity |
 |
| Algorithm 2: Neurodynamics-based self-adaptive mechanism |
 |
4. Results
4.1. Single Target without Sub-Group Behavior
4.2. Multiple Targets with Sub-Group Behavior
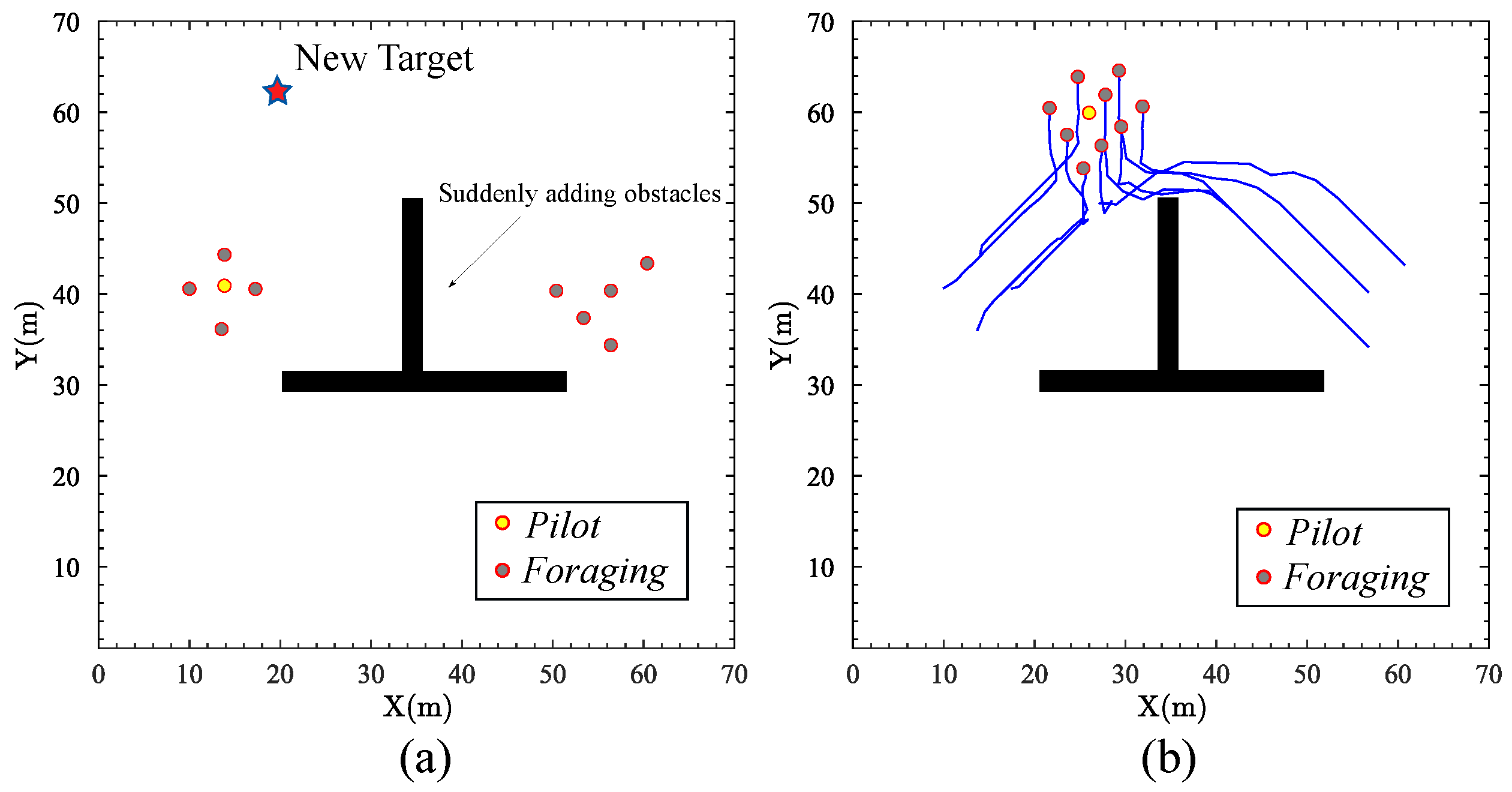
4.3. New Target in Sudden-Change Environments
4.4. Comparison Studies
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ioannou, C.C. Swarm intelligence in fish? The difficulty in demonstrating distributed and self-organised collective intelligence in (some) animal groups. Behav. Process. 2017, 141, 141–151. [Google Scholar] [CrossRef] [PubMed]
- Doran, C.; Bierbach, D.; Lukas, J.; Klamser, P.; Landgraf, T.; Klenz, H.; Habedank, M.; Arias-Rodriguez, L.; Krause, S.; Romanczuk, P.; et al. Fish waves as emergent collective antipredator behavior. Curr. Biol. 2022, 32, 708–714. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Yang, S.X. Intelligent escape of robotic systems: A survey of methodologies, applications, and challenges. J. Intell. Robot. Syst. 2023, 109, 55. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Y.; Wu, Z.; Ma, L.; Guo, M.; Li, Z.; Li, Y. A comprehensive review on fish-inspired robots. Int. J. Adv. Robot. Syst. 2022, 19, 17298806221103707. [Google Scholar] [CrossRef]
- Wang, T.; Yu, J.; Chen, D.; Meng, Y. A torque control strategy for a robotic dolphin platform based on angle of attack feedback. Biomimetics 2023, 8, 291. [Google Scholar] [CrossRef]
- Chen, D.; Wu, Z.; Meng, Y.; Tan, M.; Yu, J. Development of a high-speed swimming robot with the capability of fish-like leaping. IEEE/ASME Trans. Mechatronics 2022, 27, 3579–3589. [Google Scholar] [CrossRef]
- Weber, P.; Arampatzis, G.; Novati, G.; Verma, S.; Papadimitriou, C.; Koumoutsakos, P. Optimal flow sensing for schooling swimmers. Biomimetics 2020, 5, 10. [Google Scholar] [CrossRef]
- Hannard, F.; Mirkhalaf, M.; Ameri, A.; Barthelat, F. Segmentations in fins enable large morphing amplitudes combined with high flexural stiffness for fish-inspired robotic materials. Sci. Robot. 2021, 6, eabf9710. [Google Scholar] [CrossRef]
- Zhang, F.; Pang, J.; Wu, Z.; Liu, J.; Zhong, Y. Effects of different motion parameters on the interaction of fish school subsystems. Biomimetics 2023, 8, 510. [Google Scholar] [CrossRef]
- Cioarga, R.D.; Micea, M.V.; Cretu, V.; Groza, V. Evaluation of fish shoal inspired movement in collaborative robotic environments. In Proceedings of the 2010 IEEE Instrumentation & Measurement Technology Conference Proceedings, Austin, TX, USA, 3–6 May 2010; pp. 1539–1544. [Google Scholar]
- Berlinger, F.; Wulkop, P.; Nagpal, R. Self-organized evasive fountain maneuvers with a bioinspired underwater robot collective. In Proceedings of the IEEE International Conference on Robotics and Automation, Xi’an, China, 30 May–5 June 2021; pp. 9204–9211. [Google Scholar]
- Novák, F.; Walter, V.; Petráček, P.; Báča, T.; Saska, M. Fast collective evasion in self-localized swarms of unmanned aerial vehicles. Bioinspiration Biomim. 2021, 16, 066025. [Google Scholar] [CrossRef]
- Min, H.; Wang, Z. Design and analysis of group escape behavior for distributed autonomous mobile robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 6128–6135. [Google Scholar]
- Li, J. Biologically inspired approaches to escape and rescue of multiple robots based on neurodynamic models. Ph.D. Thesis, University of Guelph, Guelph, ON, Canada, 2023. [Google Scholar]
- Sun, B.; Li, W.; Wang, Z.; Zhu, Y.; He, Q.; Guan, X.; Dai, G.; Yuan, D.; Li, A.; Cui, W.; et al. Recent progress in modeling and control of bio-inspired fish robots. J. Mar. Sci. Eng. 2022, 10, 773. [Google Scholar] [CrossRef]
- Li, G.; Wong, T.W.; Shih, B.; Guo, C.; Wang, L.; Liu, J.; Wang, T.; Liu, X.; Yan, J.; Wu, B.; et al. Bioinspired soft robots for deep-sea exploration. Nat. Commun. 2023, 14, 7097. [Google Scholar] [CrossRef] [PubMed]
- Luo, J.; Qian, Z.; Gui, L.; Geng, X. Design and implementation of hybrid autonomous robotic fish platform for underwater emergency search and rescue. In Proceedings of the ISCTT 2022: 7th International Conference on Information Science, Computer Technology and Transportation, Xishuangbanna, China, 27–29 May 2022; VDE: Berlin, Germany, 2022; pp. 1–4. [Google Scholar]
- Shao, J.; Wang, L.; Yu, J. Development of an artificial fish-like robot and its application in cooperative transportation. Control Eng. Pract. 2008, 16, 569–584. [Google Scholar] [CrossRef]
- Song, Y.; Fang, X.; Liu, B.; Li, C.; Li, Y.; Yang, S.X. A novel foraging algorithm for swarm robotics based on virtual pheromones and neural network. Appl. Soft Comput. 2020, 90, 106156. [Google Scholar] [CrossRef]
- Pang, B.; Zhang, C.; Song, Y.; Wang, H. Self-organized task allocation in swarm robotics foraging based on dynamical response threshold approach. In Proceedings of the 2017 18th International Conference on Advanced Robotics (ICAR), Hong Kong, China, 10–12 July 2017; pp. 256–261. [Google Scholar]
- Lee, W.; Vaughan, N.; Kim, D. Task allocation into a foraging task with a series of subtasks in swarm robotic system. IEEE Access 2020, 8, 107549–107561. [Google Scholar] [CrossRef]
- Neshat, M.; Sepidnam, G.; Sargolzaei, M.; Toosi, A.N. Artificial fish swarm algorithm: A survey of the state-of-the-art, hybridization, combinatorial and indicative applications. Artif. Intell. Rev. 2014, 42, 965–997. [Google Scholar] [CrossRef]
- Li, X. A new intelligent optimization-artificial fish swarm algorithm. Doctor Thesis, Zhejiang University of Zhejiang, Hangzhou, China, 2003. [Google Scholar]
- Pourpanah, F.; Wang, R.; Lim, C.P.; Wang, X.Z.; Yazdani, D. A review of artificial fish swarm algorithms: Recent advances and applications. Artif. Intell. Rev. 2023, 56, 1867–1903. [Google Scholar] [CrossRef]
- Connor, J.; Joordens, M.; Champion, B. Fish-inspired robotic algorithm: Mimicking behaviour and communication of schooling fish. Bioinspiration Biomim. 2023, 18, 066007. [Google Scholar] [CrossRef]
- Berlinger, F.; Gauci, M.; Nagpal, R. Implicit coordination for 3D underwater collective behaviors in a fish-inspired robot swarm. Sci. Robot. 2021, 6, eabd8668. [Google Scholar] [CrossRef]
- Zhu, D.; Cao, X.; Sun, B.; Luo, C. Biologically inspired self-organizing map applied to task assignment and path planning of an AUV system. IEEE Trans. Cogn. Dev. Syst. 2017, 10, 304–313. [Google Scholar] [CrossRef]
- Grossberg, S. Nonlinear neural networks: Principles, mechanisms, and architectures. Neural Netw. 1988, 1, 17–61. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Yang, S.X.; Xu, Z. A survey on robot path planning using bio-inspired algorithms. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Dali, China, 6–8 December 2019; pp. 2111–2116. [Google Scholar]
- Li, J.; Xu, Z.; Zhu, D.; Dong, K.; Yan, T.; Zeng, Z.; Yang, S.X. Bio-inspired intelligence with applications to robotics: A survey. Intell. Robot. 2021, 1, 58–83. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, H.; Leung, Y.W.; Chu, X. Self-adaptive collective motion of swarm robots. IEEE Trans. Autom. Sci. Eng. 2018, 15, 1533–1545. [Google Scholar] [CrossRef]





| Method | Average Travel Distance | Foraging Time |
|---|---|---|
| FIRA [25] | 58.7 m | 41.3 s |
| Proposed method | 27.4 m | 23.5 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Yang, S.X. Intelligent Fish-Inspired Foraging of Swarm Robots with Sub-Group Behaviors Based on Neurodynamic Models. Biomimetics 2024, 9, 16. https://doi.org/10.3390/biomimetics9010016
Li J, Yang SX. Intelligent Fish-Inspired Foraging of Swarm Robots with Sub-Group Behaviors Based on Neurodynamic Models. Biomimetics. 2024; 9(1):16. https://doi.org/10.3390/biomimetics9010016
Chicago/Turabian StyleLi, Junfei, and Simon X. Yang. 2024. "Intelligent Fish-Inspired Foraging of Swarm Robots with Sub-Group Behaviors Based on Neurodynamic Models" Biomimetics 9, no. 1: 16. https://doi.org/10.3390/biomimetics9010016
APA StyleLi, J., & Yang, S. X. (2024). Intelligent Fish-Inspired Foraging of Swarm Robots with Sub-Group Behaviors Based on Neurodynamic Models. Biomimetics, 9(1), 16. https://doi.org/10.3390/biomimetics9010016







