Parameter Optimization and DEM Simulation of Bionic Sweep with Lower Abrasive Wear Characteristics
Abstract
1. Introduction
2. Materials and Methods
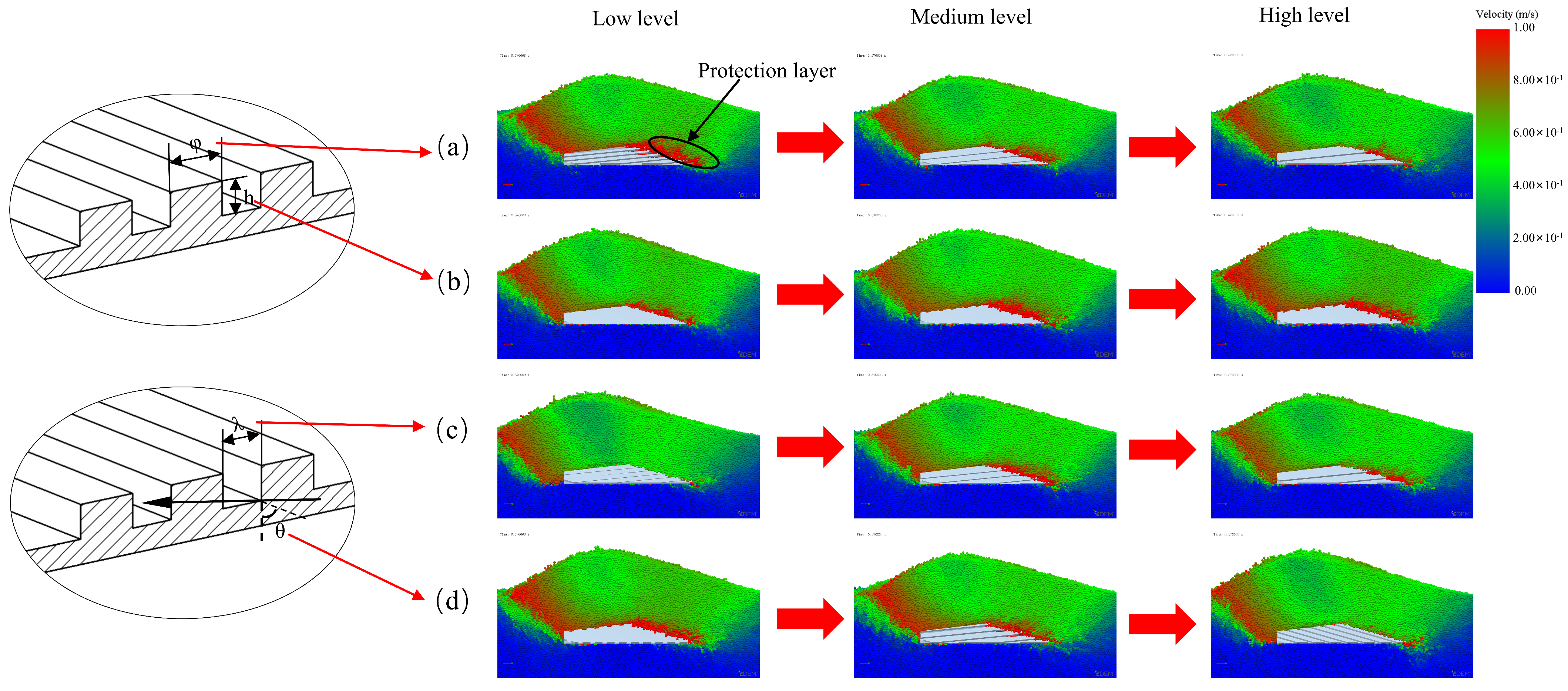
2.1. Design of BRS
2.2. DEM Simulation
2.2.1. Static Angle Tests and Simulation
2.2.2. DEM Soil Bin
2.3. RSM Experimental Design and Optimization
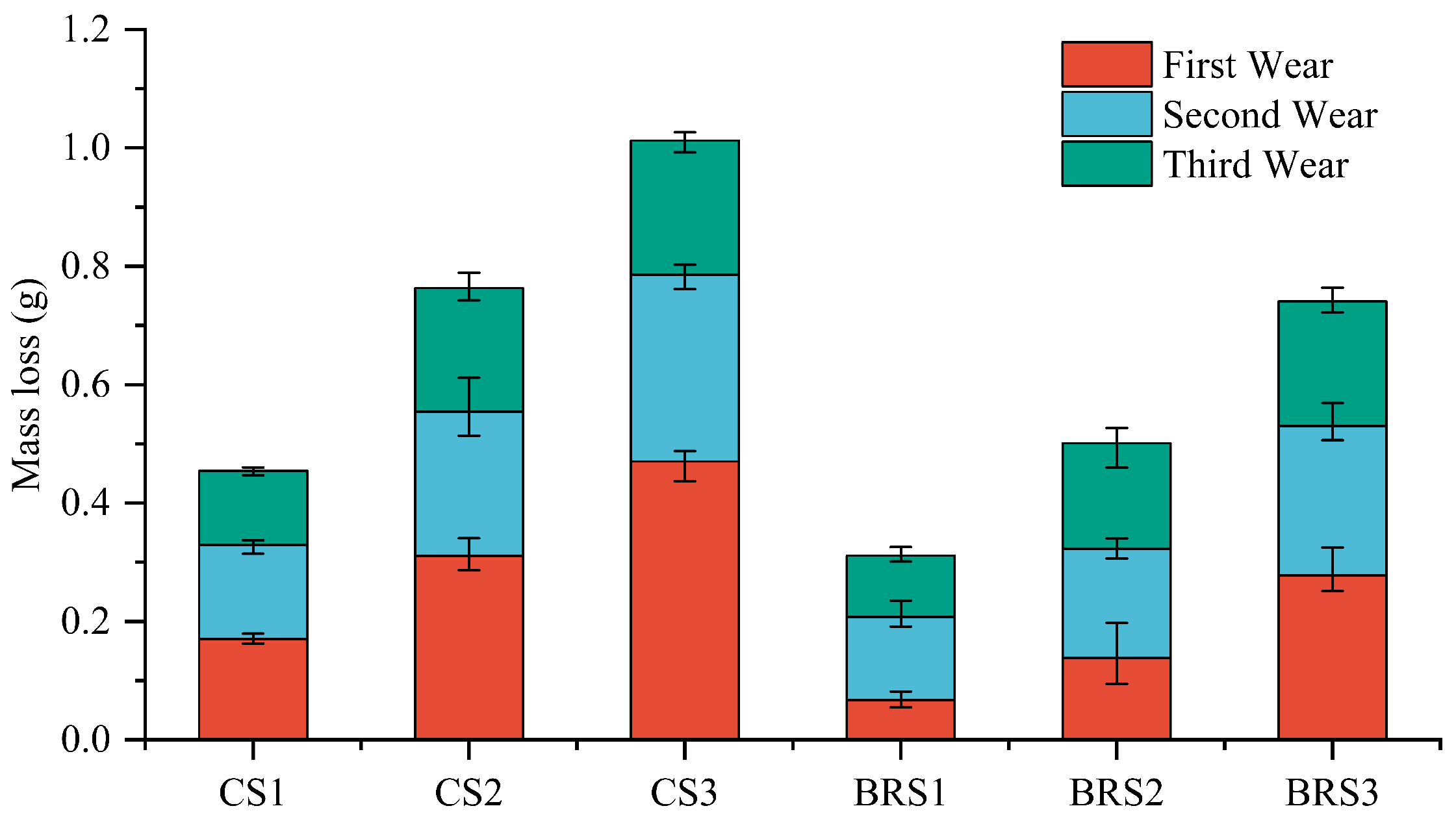
2.4. Abrasion Wear Test
3. Results
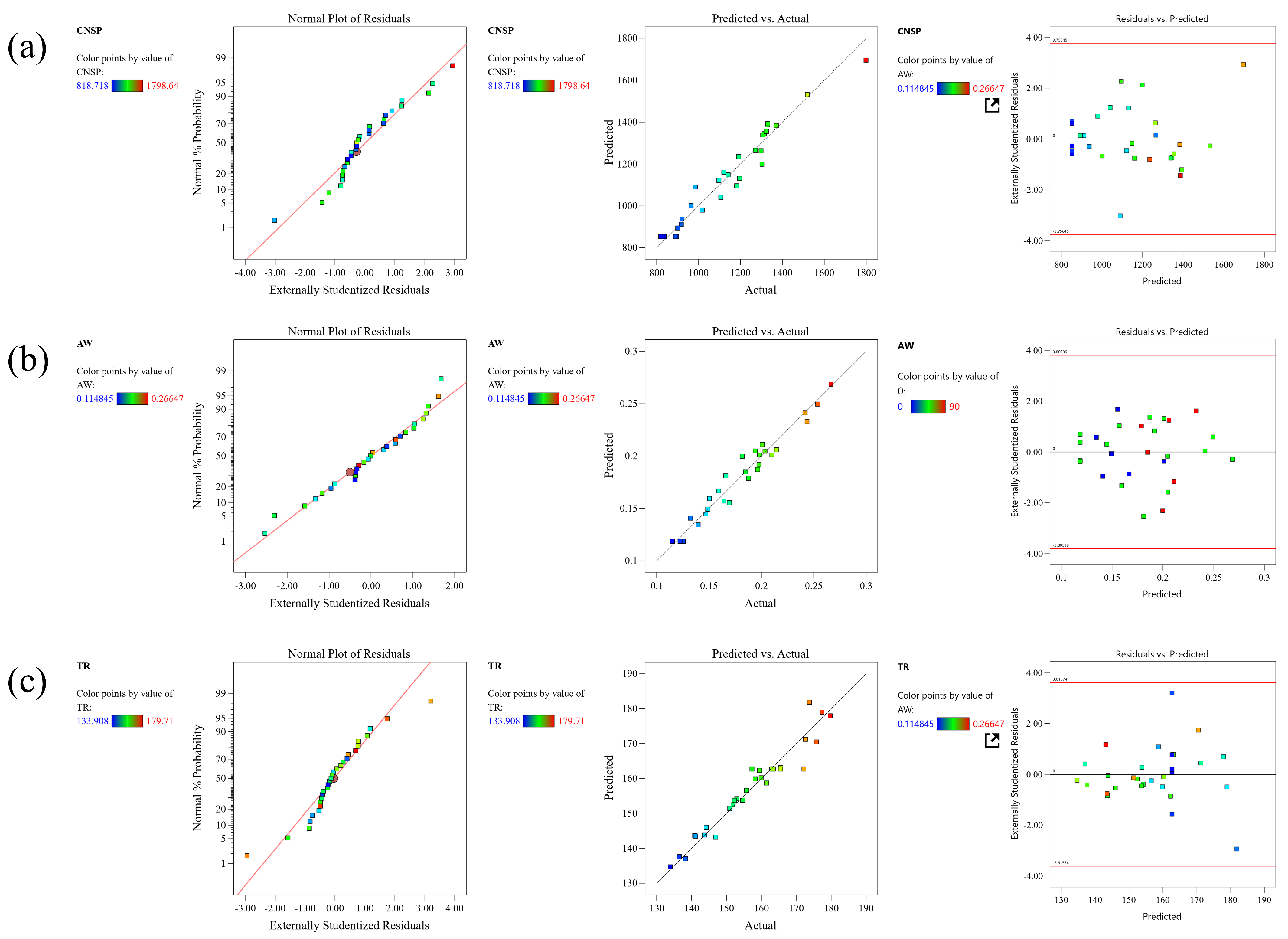
3.1. Model Fitting and Checking
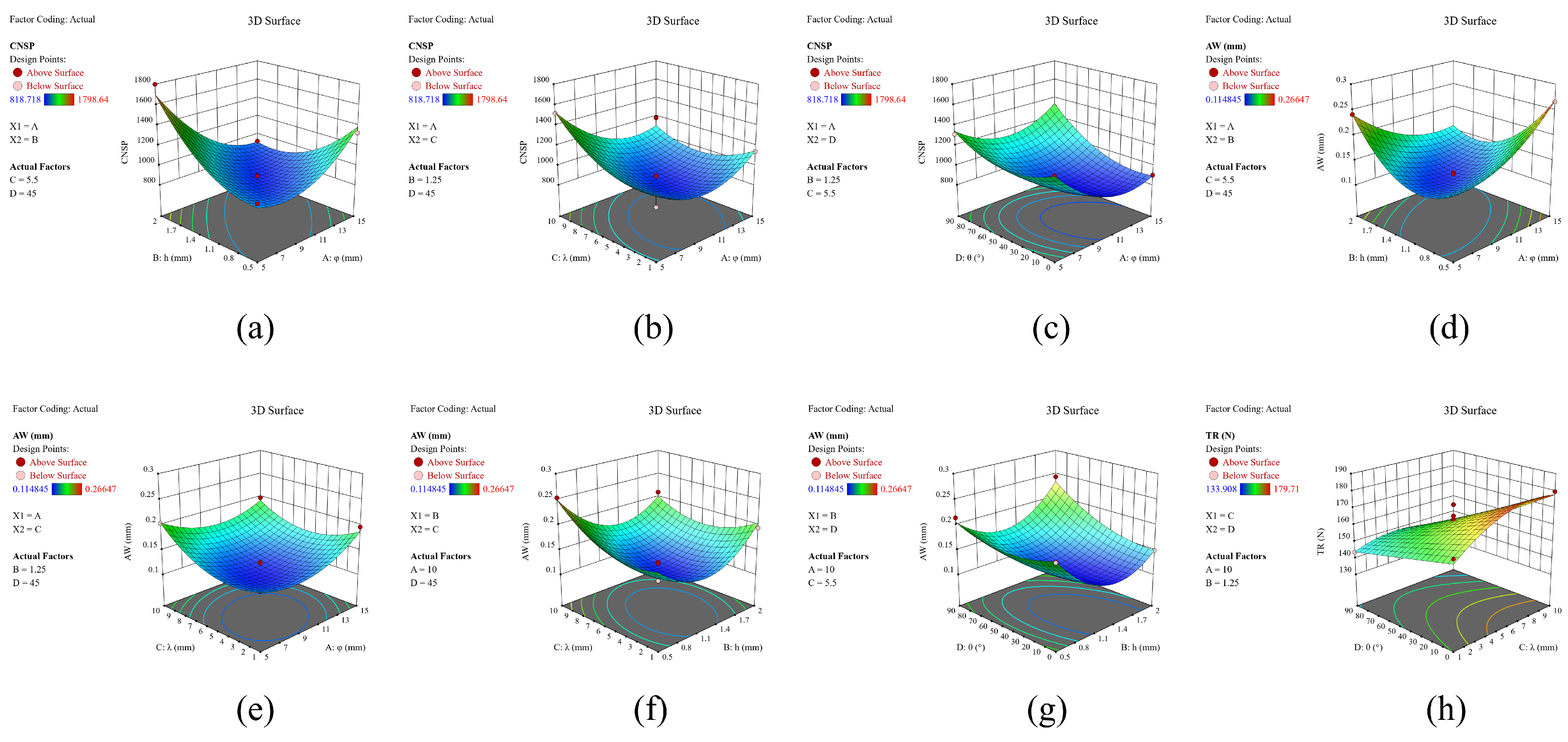
3.2. CNSP Prediction
3.3. AW Prediction
3.4. TR Prediction
3.5. Optimization Results
3.6. Results of Abrasive Wear Test
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Response | Name | Units | Observations | Minimum | Maximum | Mean | Std. Dev | Ratio |
|---|---|---|---|---|---|---|---|---|
| R1 | AW | mm | 29 | 0.114845 | 0.26647 | 0.1774 | 0.0429 | 2.32 |
| R2 | CNSP | 29 | 818.718 | 1798.64 | 1143.66 | 232.59 | 2.20 | |
| R3 | TR | N | 29 | 133.908 | 179.71 | 156.87 | 12.90 | 1.34 |
| Source | Sequential p-Value | Lack of Fit p-Value | Adjusted R2 | Predicted R2 | Remark |
|---|---|---|---|---|---|
| AW model fit summary statistics | |||||
| Linear | 0.2435 | 0.0003 | 0.0625 | −0.0927 | |
| 2FI | 0.2582 | 0.0003 | 0.1530 | −0.0506 | |
| Quadratic | <0.0001 | 0.0587 | 0.9444 | 0.8479 | Suggested |
| Cubic | 0.1217 | 0.0994 | 0.9718 | 0.4004 | |
| CNSP model fit summary statistics | |||||
| Linear | 0.0550 | 0.0014 | 0.1949 | 0.0580 | |
| 2FI | 0.0667 | 0.0023 | 0.4077 | 0.3697 | |
| Quadratic | <0.0001 | 0.1135 | 0.9298 | 0.8125 | Suggested |
| Cubic | 0.1133 | 0.2221 | 0.9654 | 0.4298 | |
| TR model fit summary statistics | |||||
| Linear | <0.0001 | 0.3292 | 0.7305 | 0.6791 | |
| 2FI | 0.5965 | 0.2916 | 0.7148 | 0.5783 | |
| Quadratic | 0.0003 | 0.9423 | 0.9136 | 0.8542 | Suggested |
| Cubic | 0.9737 | 0.5388 | 0.8440 | −0.3190 |
| AW (Quadratic) | CNSP (Quadratic) | TR (Quadratic) | ||||||
|---|---|---|---|---|---|---|---|---|
| Source | F-Value | p-Value | Source | F-Value | p-Value | Source | F-Value | p-Value |
| Model | 35.89 | <0.0001 1 | Model | 30.62 | <0.0001 1 | Model | 45.21 | <0.0001 1 |
| A | 5.67 | 0.0300 1 | A | 24.91 | 0.0001 1 | A | 24.43 | <0.0001 1 |
| B | 4.00 | 0.0629 2 | B | 10.16 | 0.0054 1 | B | 60.56 | <0.0001 1 |
| C | 27.07 | <0.0001 1 | C | 26.47 | <0.0001 1 | C | 9.16 | 0.0064 1 |
| D | 50.98 | <0.0001 1 | D | 48.11 | <0.0001 1 | D | 165.36 | <0.0001 1 |
| AB | 80.96 | <0.0001 1 | AB | 82.82 | <0.0001 1 | CD | 11.71 | 0.0026 1 |
| AC | 6.58 | 0.0208 1 | AC | 14.25 | 0.0015 1 | B2 | 17.40 | 0.0004 2 |
| AD | 4.19 | 0.0585 2 | AD | 7.78 | 0.0126 1 | C2 | 33.64 | <0.0001 1 |
| BC | 11.24 | 0.0040 1 | A2 | 63.28 | <0.0001 1 | |||
| BD | 13.37 | 0.0021 1 | B2 | 52.32 | <0.0001 1 | |||
| A2 | 52.02 | <0.0001 1 | C2 | 38.22 | <0.0001 1 | |||
| B2 | 185.72 | <0.0001 1 | D2 | 35.46 | <0.0001 1 | |||
| C2 | 61.04 | <0.0001 1 | ||||||
| D2 | 25.15 | 0.0001 1 | ||||||
| Lack of fit | 4.97 | 0.0675 2 | Lack of fit | 3.92 | 0.09862 | Lack of fit | 0.3613 | 0.93872 |
| Solution 1 | Predicted Mean | Predicted Median | Std Dev | SE Mean | 95% CI Low for Mean | 95% CI High for Mean | 95% TI Low for 99% Pop | 95% TI High for 99% Pop |
|---|---|---|---|---|---|---|---|---|
| AW | 0.114916 | 0.114916 | 0.009817 | 0.004112 | 0.10615 | 0.12368 | 0.07136 | 0.15847 |
| CNSP | 825.877 | 825.877 | 65.4314 | 26.8849 | 769.155 | 882.599 | 543.128 | 1108.63 |
| TR | 159.271 | 159.271 | 3.71592 | 1.16935 | 156.839 | 161.703 | 144.376 | 174.166 |
References
- Tong, J.; Mohammad, M.A.; Zhang, J.; Ma, Y.; Rong, B.; Chen, D.; Menon, C. DEM Numerical Simulation of Abrasive Wear Characteristics of a Bioinspired Ridged Surface. J. Bionic Eng. 2010, 7, 175–181. [Google Scholar] [CrossRef]
- Holmberg, K.; Kivikyto-Reponen, P.; Harkisaari, P.; Valtonen, K.; Erdemir, A. Global energy consumption due to friction and wear in the mining industry. Tribol. Int. 2017, 115, 116–139. [Google Scholar] [CrossRef]
- Blau, P.J.; Dehoff, R.R. Development of a two-body wet abrasion test method with attention to the effects of reused abradant. Wear 2013, 302, 1035–1039. [Google Scholar] [CrossRef]
- Tong, J.; Zhang, Z.; Ma, Y.; Chen, D.; Jia, B.; Menon, C. Abrasive wear of embossed surfaces with convex domes. Wear 2012, 274, 196–202. [Google Scholar] [CrossRef]
- Wang, J.; He, Q.; Hu, Y.; Wang, M. Study on the Microstructure and Performance of New Type Martensite Wear Resistant Steel. In Proceedings of the 2nd International Conference on Manufacturing Science and Engineering, Guilin, China, 9–11 April 2011; pp. 167–172. [Google Scholar]
- Chang, S.-H.; Tang, T.-P.; Huang, K.-T. Improvement of Aluminum Erosion Behavior and Corrosion Resistance of AISI H13 Tool Steel by Oxidation Treatment. ISIJ Int. 2010, 50, 569–573. [Google Scholar] [CrossRef]
- Er, U.; Par, B. Wear of plowshare components in SAE 950C steel surface hardened by powder boriding. Wear 2006, 261, 251–255. [Google Scholar] [CrossRef]
- Wang, X.H.; Han, F.; Liu, X.M.; Qu, S.Y.; Zou, Z.D. Effect of molybdenum on the microstructure and wear resistance of Fe-based hardfacing coatings. Mater. Sci. Eng. A 2008, 489, 193–200. [Google Scholar] [CrossRef]
- Wang, X.; Han, F.; Liu, X.; Qu, S.; Zou, Z. Microstructure and wear properties of the Fe-Ti-V-Mo-C hardfacing alloy. Wear 2008, 265, 583–589. [Google Scholar] [CrossRef]
- Shan, H.; Zhou, H.; Sun, N.; Ren, L.; Chen, L.; Li, X. Study on adhesion resistance behavior of sample with striated non-smooth surface by laser processing technique. J. Mater. Process. Technol. 2008, 199, 221–229. [Google Scholar] [CrossRef]
- Zhao, G.; Yuan, Y.; Zhang, P.; Zhou, T.; Zhou, H. Influence of orientations biomimetic units processed by laser on wear resistance of 6082 aluminium alloy. Opt. Laser Technol. 2020, 127, 106196. [Google Scholar] [CrossRef]
- Tian, L.; Tian, X.; Wang, Y.; Hu, G.; Ren, L. Anti-wear properties of the molluscan shell Scapharca subcrenata: Influence of surface morphology, structure and organic material on the elementary wear process. Mater. Sci. Eng. C 2014, 42, 7–14. [Google Scholar] [CrossRef] [PubMed]
- Su, W.; Zhou, T.; Zhang, P.; Zhou, H.; Li, H. Effect of distribution of striated laser hardening tracks on dry sliding wear resistance of biomimetic surface. Opt. Laser Technol. 2018, 98, 281–290. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, Y.; Ren, L. Particle Erosion Resistance of Bionic Samples Inspired from Skin Structure of Desert Lizard, Laudakin stoliczkana. J. Bionic Eng. 2012, 9, 465–469. [Google Scholar] [CrossRef]
- Yin, W.; Han, Z.; Feng, H.; Zhang, J.; Cao, H.; Tian, Y. Gas-Solid Erosive Wear of Biomimetic Pattern Surface Inspired from Plant. Tribol. Trans. 2017, 60, 159–165. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Q.; Ge, Y.; Jiang, Y. Analysis of the wear-resistance characteristics of bionic ridge structures. Appl. Eng. Agric. 2020, 36, 697–702. [Google Scholar] [CrossRef]
- Su, W.; Zhou, T.; Sui, Q.; Zhang, P.; Zhou, H.; Li, H.; Zhang, Z.H. Study on the relationship between intervals among laser stripes and the abrasion resistance of biomimetic laser textured surfaces. Opt. Laser Technol. 2018, 104, 216–224. [Google Scholar] [CrossRef]
- Su, W.; Zhou, T.; Zhang, P.; Zhou, H.; Li, H.; Sui, Q. Effect of the orientation of laser stripes on the abrasion resistance of biomimetic laser textured surfaces. Opt. Laser Technol. 2018, 107, 380–388. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Wang, Y.; Xue, W.; Ma, Y.; Tong, J.; Liu, X.; Sun, J. DEM and soil bin study on a biomimetic disc furrow opener. Comput. Electron. Agric. 2019, 156, 209–216. [Google Scholar] [CrossRef]
- Mak, J.; Chen, Y.; Sadek, M.A. Determining parameters of a discrete element model for soil-tool interaction. Soil Tillage Res. 2012, 118, 117–122. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, S.; Pan, H.; Zheng, Z.; Huang, Y.; Zhu, R. Effect of soil particle size on soil-subsoiler interactions using the discrete element method simulations. Biosyst. Eng. 2019, 182, 138–150. [Google Scholar] [CrossRef]
- Barr, J.B.; Ucgul, M.; Desbiolles, J.M.A.; Fielke, J.M. Simulating the effect of rake angle on narrow opener performance with the discrete element method. Biosyst. Eng. 2018, 171, 1–15. [Google Scholar] [CrossRef]
- Yuan, J.; Wu, C.; Li, H.; Qi, X.; Xiao, X.; Shi, X. Movement rules and screening characteristics of rice-threshed mixture separation through a cylinder sieve. Comput. Electron. Agric. 2018, 154, 320–329. [Google Scholar] [CrossRef]
- Wang, L.; Chai, J.; Wang, H.; Wang, Y. Design and performance of a countersunk screen in a maize cleaning device. Biosyst. Eng. 2021, 209, 300–314. [Google Scholar] [CrossRef]
- Kalacska, A.; De Baets, P.; Fauconnier, D.; Schramm, F.; Frerichs, L.; Sukumaran, J. Abrasive wear behaviour of 27MnB5 steel used in agricultural tines. Wear 2020, 442, 203107. [Google Scholar] [CrossRef]
- Zhang, Q.; Zuo, G.; Lai, Q.; Tong, J.; Zhang, Z. EDEM Investigation and Experimental Evaluation of Abrasive Wear Resistance Performance of Bionic Micro-Thorn and Convex Hull Geometrically Coupled Structured Surface. Appl. Sci. 2021, 11, 6655. [Google Scholar] [CrossRef]
- Awuah, E.; Zhou, J.; Liang, Z.; Aikins, K.A.; Gbenontin, B.V.; Mecha, P.; Makange, N.R. Parametric analysis and numerical optimisation of Jerusalem artichoke vibrating digging shovel using discrete element method. Soil Tillage Res. 2022, 219, 105344. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, W.; Li, B.; Niu, S.; Yu, H.; Liu, Y.; Yang, X.; Zhang, J.; Han, Z.; Ren, L. Optimum Anti-erosion Structures and Anti-erosion Mechanism for Rotatory Samples Inspired by Scorpion Armor of Parabuthus transvaalicus. J. Bionic Eng. 2021, 18, 92–102. [Google Scholar] [CrossRef]
- Yan, D.; Li, J.Q.; Pei, J.M.; Cui, J.; Nie, M.; Fang, C.M. The temperature sensitivity of soil organic carbon decomposition is greater in subsoil than in topsoil during laboratory incubation. Sci. Rep. 2017, 7, 5181. [Google Scholar] [CrossRef]
- Barr, J.; Desbiolles, J.; Ucgul, M.; Fielke, J.M. Bentleg furrow opener performance analysis using the discrete element method. Biosyst. Eng. 2020, 189, 99–115. [Google Scholar] [CrossRef]
- Ucgul, M.; Saunders, C.; Fielke, J.M. Discrete element modelling of tillage forces and soil movement of a one-third scale mouldboard plough. Biosyst. Eng. 2017, 155, 44–54. [Google Scholar] [CrossRef]
- Lei, Z.; Yang, S.; Xie, S. Soil Water Dynamics; Tsinghua University Press: Beijing, China, 1988. [Google Scholar]
- Zeng, Z.; Chen, Y. Simulation of straw movement by discrete element modelling of straw-sweep-soil interaction. Biosyst. Eng. 2019, 180, 25–35. [Google Scholar] [CrossRef]
- Forsstrom, D.; Jonsen, P. Calibration and validation of a large scale abrasive wear model by coupling DEM-FEM Local failure prediction from abrasive wear of tipper bodies during unloading of granular material. Eng. Fail. Anal. 2016, 66, 274–283. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Derringer, G.; Suich, R. Simultaneous optimization of several response variables. J. Qual. Technol. 1980, 12, 214–219. [Google Scholar] [CrossRef]
- Masoumi, H.R.F.; Basri, M.; Samiun, W.S.; Izadiyan, Z.; Lim, C.H.J. Enhancement of encapsulation efficiency of nanoemulsion-containing aripiprazole for the treatment of schizophrenia using mixture experimental design. Int. J. Nanomed. 2015, 10, 6469–6476. [Google Scholar] [CrossRef]
- Jafari, R.; Raoufat, M.H.; Hashjin, T.T. Soil-bin performance of a modified bent leg plow. Appl. Eng. Agric. 2008, 24, 301–307. [Google Scholar] [CrossRef]
- Mouazen, A.M.; Nemenyi, M.; Schwanghart, H.; Rempfer, M. Tillage tool design by the finite element method: Part 2. Experimental validation of the finite element results with soil bin test. J. Agric. Eng. Res. 1999, 72, 53–58. [Google Scholar] [CrossRef]
- Shi, Y.; Sun, X.; Wang, X.; Hu, Z.; Newman, D.; Ding, W. Numerical simulation and field tests of minimum-tillage planter with straw smashing and strip laying based on EDEM software. Comput. Electron. Agric. 2019, 166, 105021. [Google Scholar] [CrossRef]
- Goeke, S.; Biermann, D.; Stickel, D.; Stemmer, P.; Fischer, A.; Geenen, K.; Huth, S.; Theisen, W. Enhancing the Surface Integrity of Tribologically Stressed Contacting Surfaces by an Adjusted Surface Topography. In Proceedings of the 2nd CIRP Conference on Surface Integrity (CSI), Nottingham, UK, 28–30 May 2014; pp. 214–218. [Google Scholar]
- Han, Z.; Zhang, J.; Ge, C.; Wen, L.; Ren, L. Erosion Resistance of Bionic Functional Surfaces Inspired from Desert Scorpions. Langmuir 2012, 28, 2914–2921. [Google Scholar] [CrossRef]
- Tong, J.; Wang, H.; Ma, Y.; Ren, L. Two-body abrasive wear of the outside shell surfaces of mollusc Lamprotula fibrosa heude, Rapana venosa valenciennes and Dosinia anus philippi. Tribol. Lett. 2005, 19, 331–338. [Google Scholar] [CrossRef]
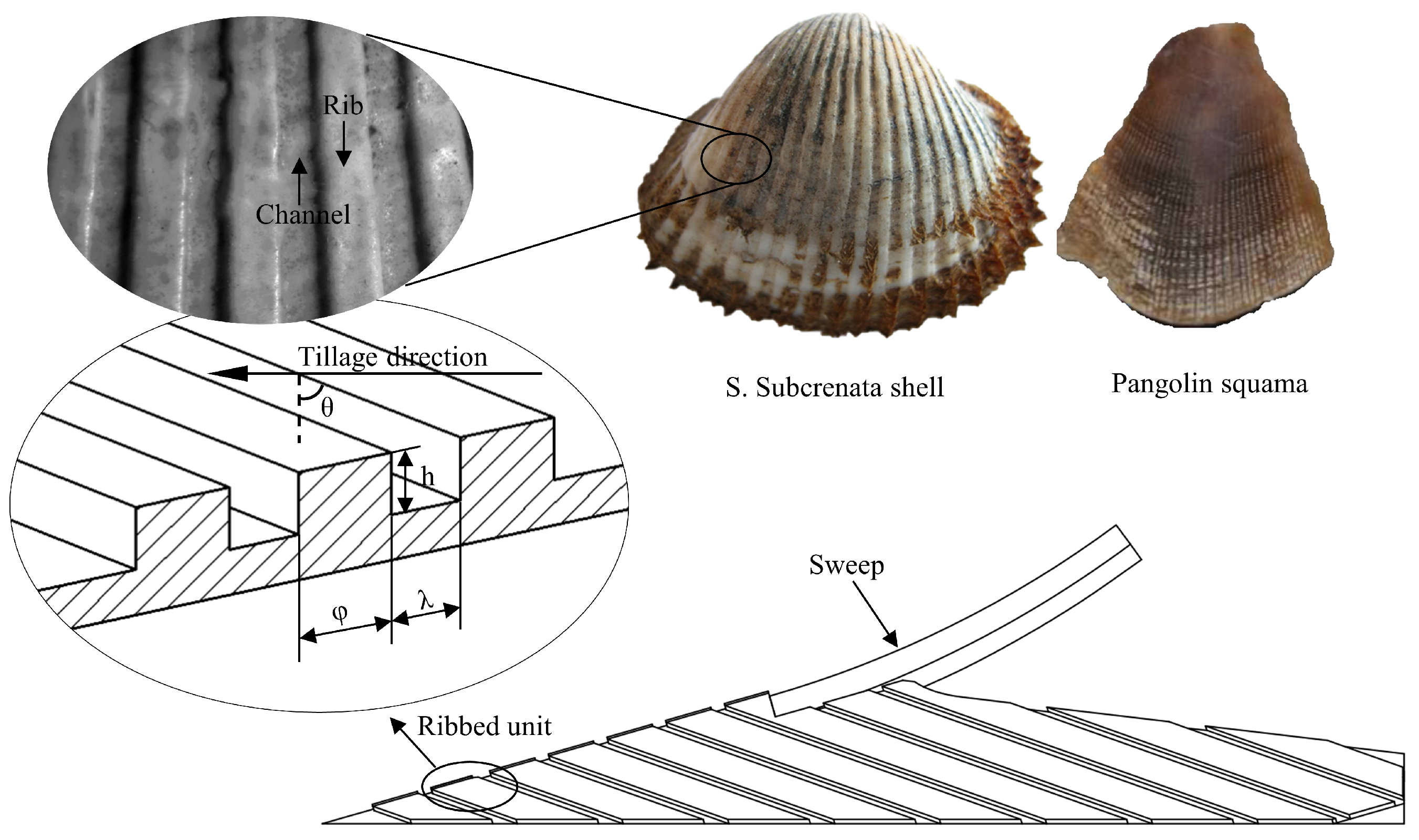
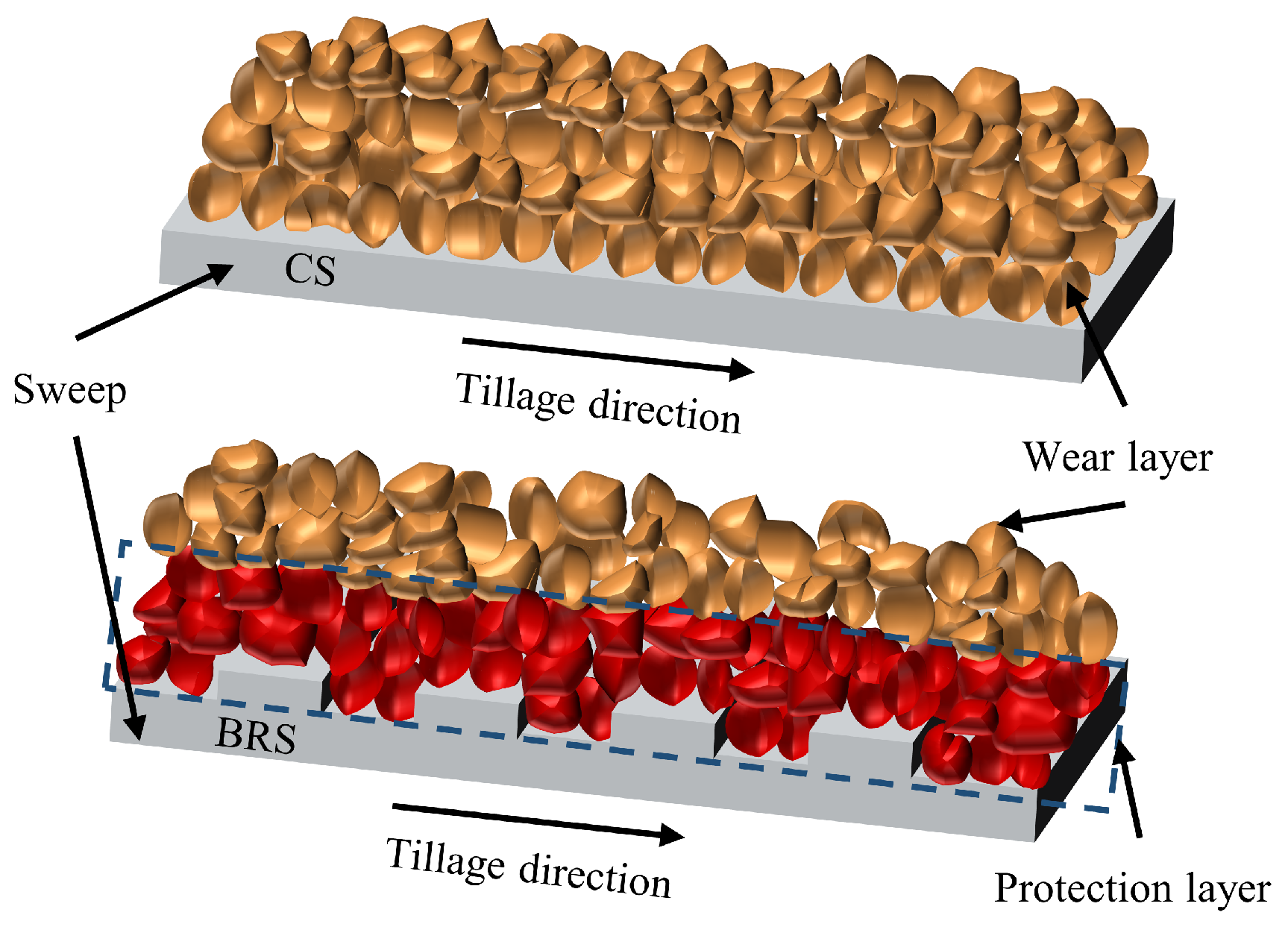




| Shoot Orientation (deg) | Static Angle of Experiment (deg) | Static Angle of Simulation (deg) |
|---|---|---|
| 0 | 36.9833 | 35.3445 |
| 30 | 34.5819 | 35.5740 |
| 60 | 34.3060 | 35.7740 |
| 90 | 34.8940 | 34.5803 |
| 120 | 37.2428 | 35.5314 |
| 150 | 36.1415 | 36.5112 |
| Parameter | Experiment Value | Simulation Value |
| Static angle (deg) | 35.6916 | 35.5526 |
| Std. Dev (deg) | 1.1594 | 1.0894 |
| C.V (%) | 3.2483 | 3.0643 |
| Parameters | Soil | Sweep (Steel) |
|---|---|---|
| Particle radius (mm) | 1.5 | |
| Density of soil particles (kg/m−3) | 2550 | 7850 |
| Poisson’s ratio of soil | 0.3 | 0.3 |
| Shear modulus of soil (MPa) | 1 × 108 | 7.9 × 1010 |
| Coefficient of restitution (with soil) | 0.6 | 0.5 |
| Coefficient of static friction (with soil) | 0.54 | 0.64 |
| Coefficient of rolling friction (with soil) | 0.3 | 0.2 |
| Φ (mm) | h (mm) | λ (mm) | θ (°) | AW (mm) | CNSP | TR (N) | Desirability (%) |
|---|---|---|---|---|---|---|---|
| 8.88 | 1.05 | 3.01 | 34.46 | 0.115 | 825.88 | 159.27 | 0.926 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Liu, X.; Tong, T.; Xu, Z.; Ma, Y. Parameter Optimization and DEM Simulation of Bionic Sweep with Lower Abrasive Wear Characteristics. Biomimetics 2023, 8, 201. https://doi.org/10.3390/biomimetics8020201
Wang S, Liu X, Tong T, Xu Z, Ma Y. Parameter Optimization and DEM Simulation of Bionic Sweep with Lower Abrasive Wear Characteristics. Biomimetics. 2023; 8(2):201. https://doi.org/10.3390/biomimetics8020201
Chicago/Turabian StyleWang, Shuo, Xuanting Liu, Tianjian Tong, Zihe Xu, and Yunhai Ma. 2023. "Parameter Optimization and DEM Simulation of Bionic Sweep with Lower Abrasive Wear Characteristics" Biomimetics 8, no. 2: 201. https://doi.org/10.3390/biomimetics8020201
APA StyleWang, S., Liu, X., Tong, T., Xu, Z., & Ma, Y. (2023). Parameter Optimization and DEM Simulation of Bionic Sweep with Lower Abrasive Wear Characteristics. Biomimetics, 8(2), 201. https://doi.org/10.3390/biomimetics8020201







