A Multi-Objective Carnivorous Plant Algorithm for Solving Constrained Multi-Objective Optimization Problems
Abstract
1. Introduction
- A new constrained multi-objective optimization algorithm, CMOCPA, is proposed. CMOCPA employs a two-population, two-stage method. The two populations, namely , , are employed for the original CMOP and the relaxed CMOP, respectively. concentrates on feasible solutions, while ignores all constraints in Stage 1 to quickly converge to the unconstrained Pareto front. In Stage 2, uses the -constrained handling method to guide the population back to CPF. The two populations are designed to help each other evolve, with providing guidance to in the search for feasible solutions, and providing diversity to by exploring the infeasible regions of the search space.
- Various novel mechanisms are introduced in CMOCPA, including a quasi-reflection learning mechanism in the growth process, quadratic interpolation in the reproduction process, and a cross-pollination method inspired by the trapping mechanism and pollination behavior of carnivorous plants. These mechanisms help the algorithm to improve the convergence speed, local exploitation ability, and ability to escape from local optima.
2. Related Work
2.1. Carnivorous Plant Algorithm
2.2. Constraints of CMOPs
2.3. Existing CMOEAs with Constraint-Handling Technologies
2.3.1. Feasibility-Driven CMOEAs
- Value is a feasible solution, and is an infeasible solution;
- Both and are feasible solutions, and ;
- Both and are infeasible solutions, and .
2.3.2. Infeasibility-Assisted CMOEAs
- Value is feasible, and is infeasible;
- Both and are infeasible, but violates fewer constraints than ;
- Both and violate the same number of constraints, but has a smaller sum of constraint violation values than .
3. The Proposed Algorithm
| Algorithm 1:Procedure of CMOCPA |
 |
- CPA parameters, such as , , and .
- The stage of the algorithm S. When , the algorithm is in Stage 1, and is evolving without constraints. On the other hand, when , the algorithm is in Stage 2, and is using the epsilon-constraints-handling method to ensure that its solutions are feasible with respect to the constraints.
- The initial value for , which is set to be sufficiently large to ensure that all solutions in are feasible during Stage 1 when using the epsilon constraint method to select individuals.
- The threshold to determine whether individuals in have reached a stable state and whether the algorithm should move from Stage 1 to Stage 2.
| Algorithm 2: Generate offspring of CMOCPA |
 |
- Classification and grouping: The algorithm divides the population into two categories: carnivorous plants and prey. The population is further divided into several groups, with the best prey assigned to the best carnivorous plant based on fitness value. Subsequent prey are then assigned to subsequent carnivorous plants in order of fitness value until all preys are assigned. Carnivorous plants only prey within their trapping range. Fitness calculation of the CMOPs version is carried out in the same way as in SPEA2 [33];
- The growth process: After classification and grouping, the carnivorous plant selects a prey randomly in its trapping range. When the random number is less than the attraction rate, the prey is trapped and digested by the carnivorous plant, and the plant’s position is updated according to Equation (6).where is the jth decision variable for the ith level of carnivorous plants, is the jth-dimension decision variable for a randomly selected prey, the growth rate is a predefined value, and rand is a randomly selected value from the range [0,1]. The magnitude of carnivorous plant growth is expressed as Growth and is calculated using Equation (7).If the random number is less than the attraction rate, the selected prey will not be trapped. This prey is considered a pollinator, helping the carnivorous plant to complete cross-pollination. Once an offspring is generated, the quasi-reflection learning mechanism is used to generate a quasi-reflection point between the offspring and the parent. These offspring and quasi-reflection points are added to the environmental selection to improve the population diversity and search efficiency of the algorithm. The quasi-reflection and cross-pollination are described in detail in Section 3.1 and Section 3.2, respectively.
- The reproduction process: The reproduction process begins once carnivorous plants complete the trapping process. Only carnivorous plants are eligible for reproduction to save computing resources. Since the original reproduction method is always guided by the optimal individual, the algorithm’s diversity gradually decreases as individuals become closer to the optimal solution. To address this issue, a cross-pollination method based on Lévy flight is proposed to increase the algorithm’s diversity and exploratory ability, thus avoiding getting trapped in local optima. The original reproduction method of CPA is treated as self-pollination. With a certain chance, carnivorous plants generate offspring by self-pollination as shown in Equation (8).where is the best solution, is a randomly selected carnivorous plant, and the reproduction rate is a predetermined utilization value. This process is repeated for each of the carnivorous plants. The value is selected based on the fitness values of the random carnivorous plant and the best carnivorous plant to ensure that the algorithm approaches the current best carnivorous plant; is calculated as shown in Equation (9).In addition, a quadratic interpolation method is introduced, where extreme points fitted by curve-fitting replace the current offspring with a certain probability. The cross-pollination behavior and the reproduction process based on quadratic interpolation will be described in detail in Section 3.2 and Section 3.3. The newly generated individuals are then merged into the original population for environmental selection.
3.1. Improved Growth Process Based on Quasi-Reflection Learning
3.2. Cross-Pollination Based on Lévy’s Flight
3.3. Improved Reproduction Process Based on Quadratic Interpolation Method
4. Simulation Experiments and Results Analysis
4.1. Experimental Settings
4.1.1. Benchmark Problems
- For all DC-DTLZ: , for DC1-DTLZ1, DC2-DTLZ1, and DC3-DTLZ1, D is set to 7; D is set to 12 for the remaining DC-DTLZ problems.
- For all FCP problems, ; for other parameters refer to ICMA [40];
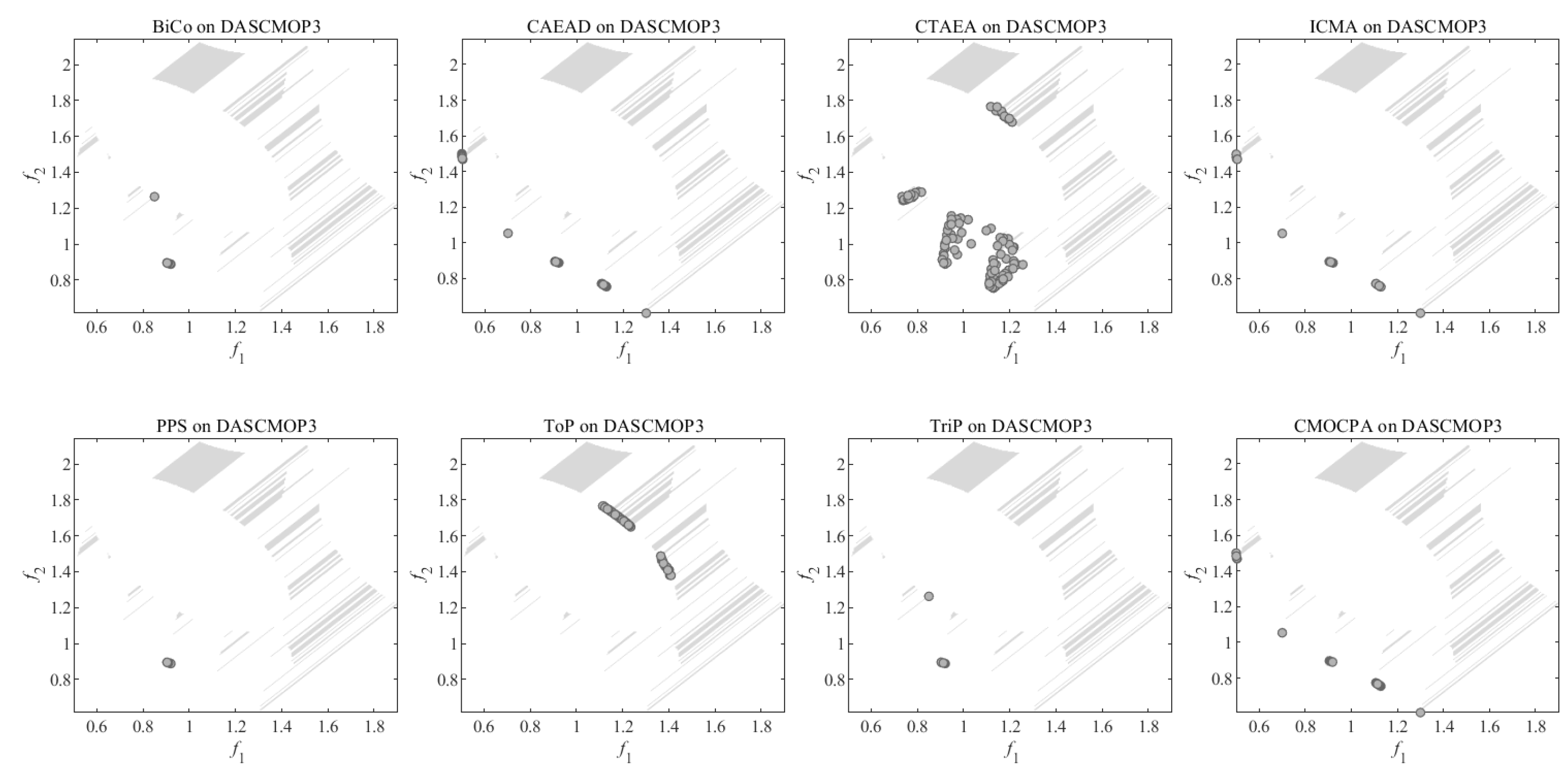
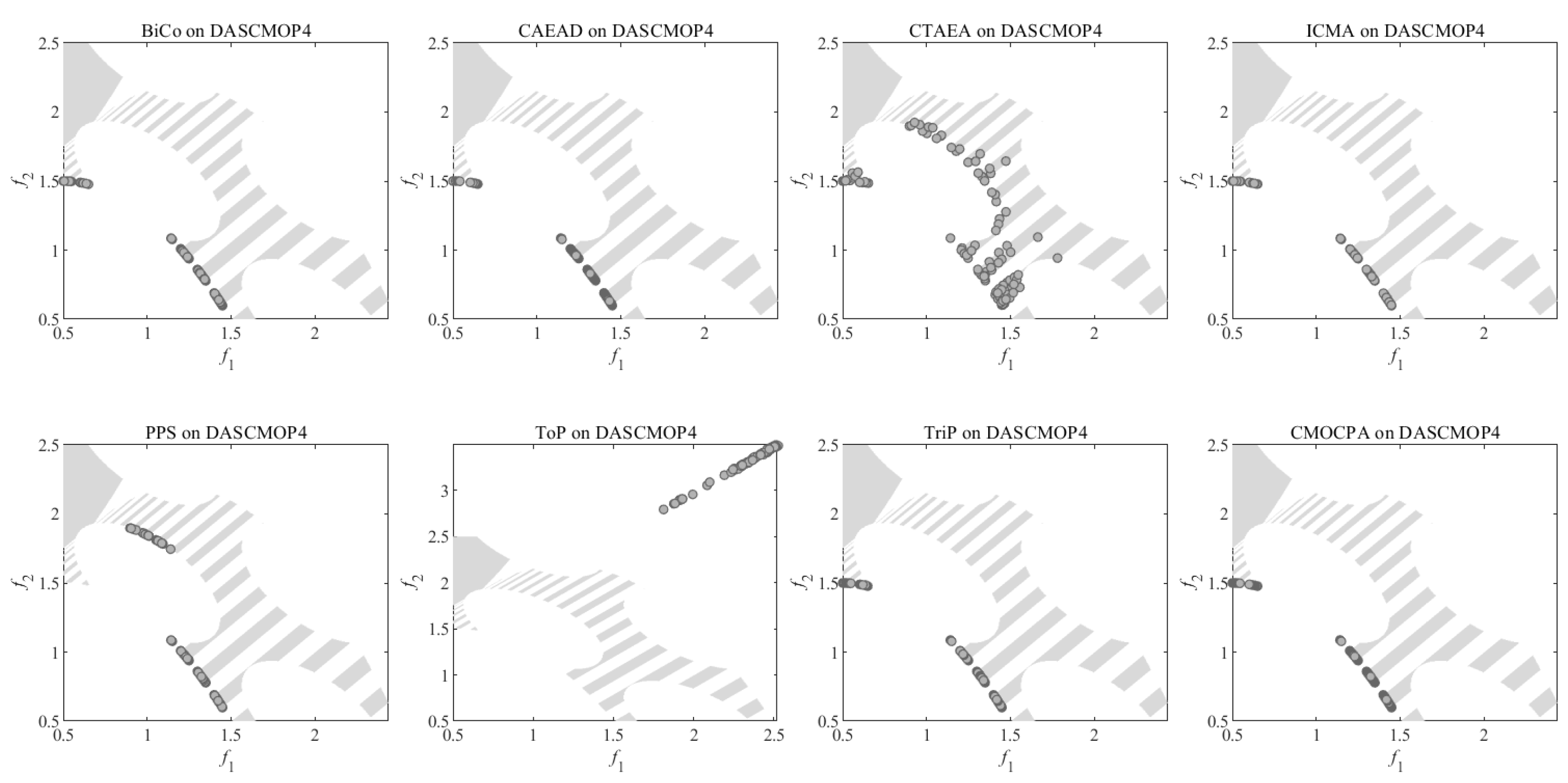
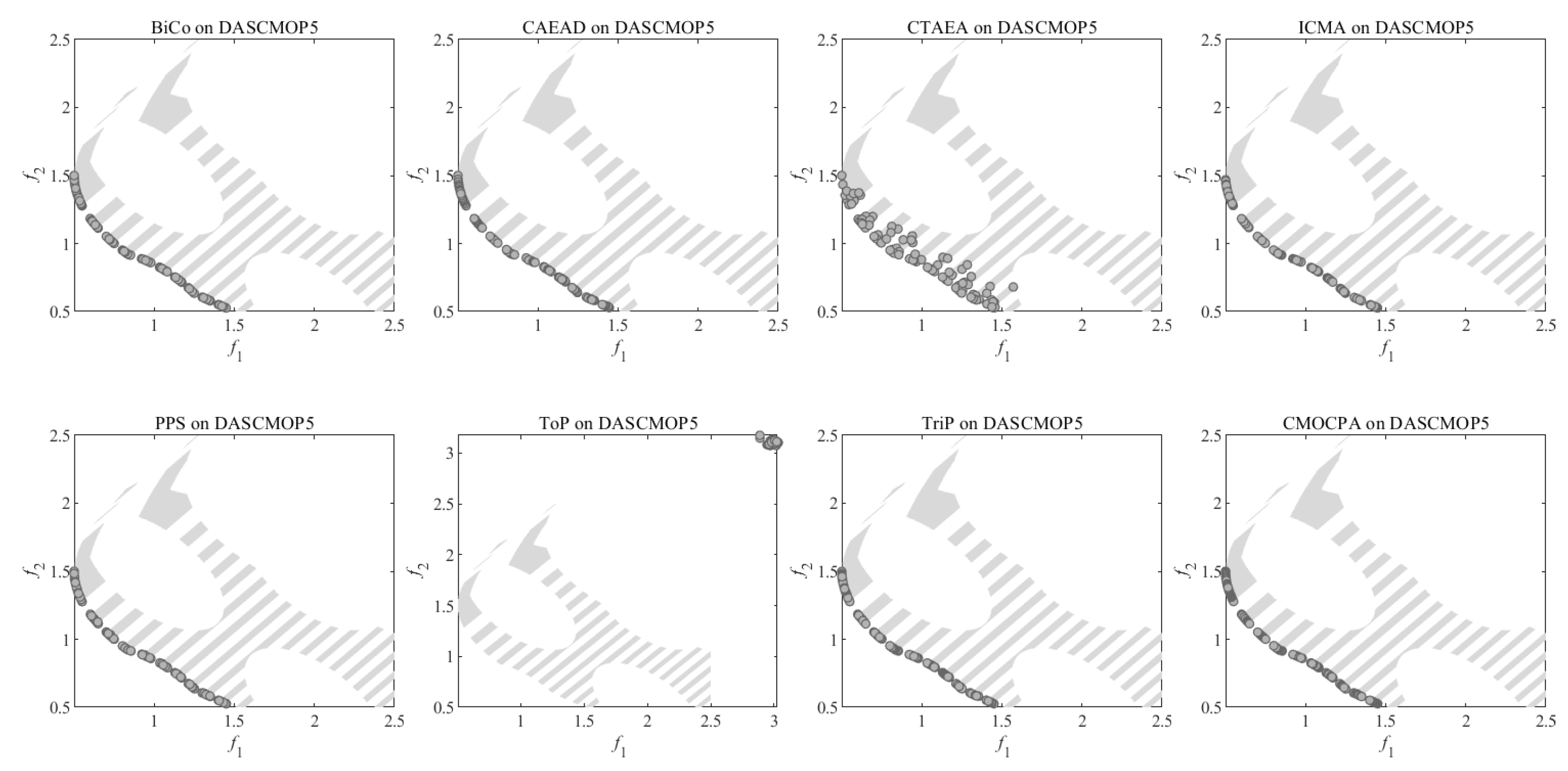
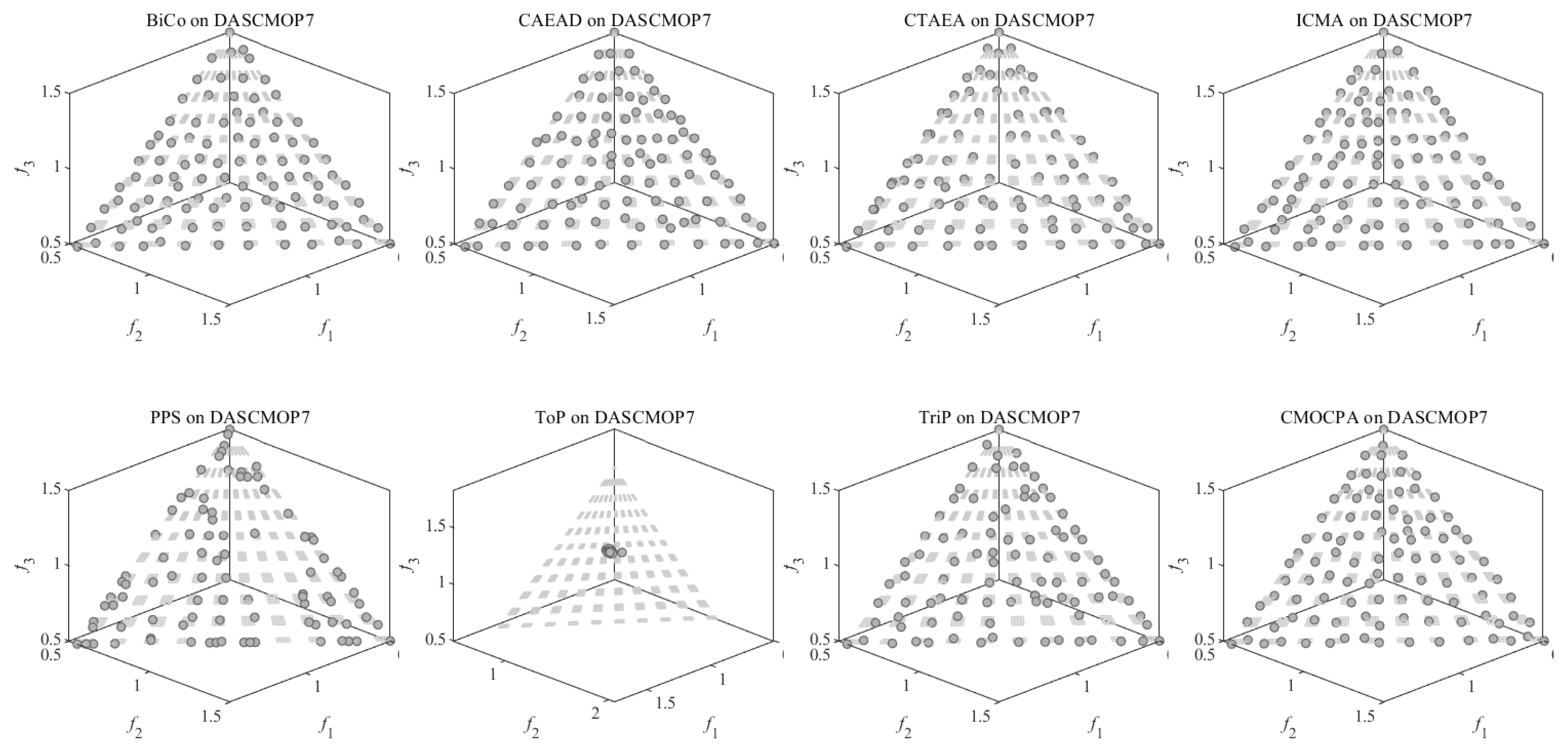
- For all DASCMOP problems, , ; for DASCMOP1-DASCMOP6, ; for DASCMOP7-DASCMOP9, .
- For ZDT and DTLZ, .
- For RWMOPs, all parameters are the same as in [45].
4.1.2. Genetic Operators and Parameter Settings
- Simulated binary crossover (SBX): , ;
- Polynomial mutation (PM): , ;
- DE operators: , ;
- ToP parameters: , ;
- PPS parameters: , , , , ;
- MOEAD parameters: ;
- eMOEAD parameters: ;
- MOPSO parameters: ;
- KnEA parameters: ;
- GrEA parameters: ;
- CMOCPA parameters: , , ;
4.1.3. Performance Metrics
4.2. Experimental Results
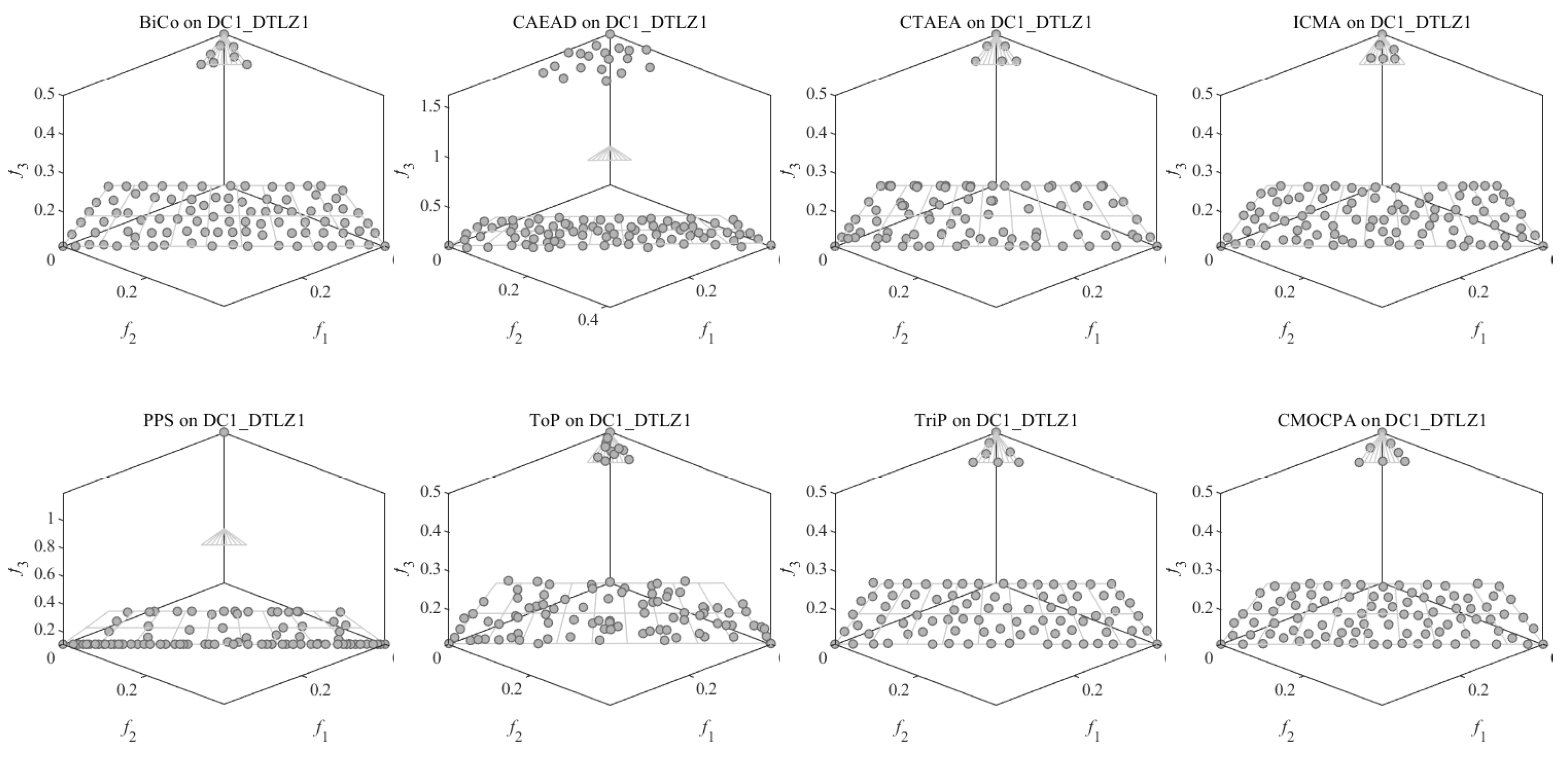
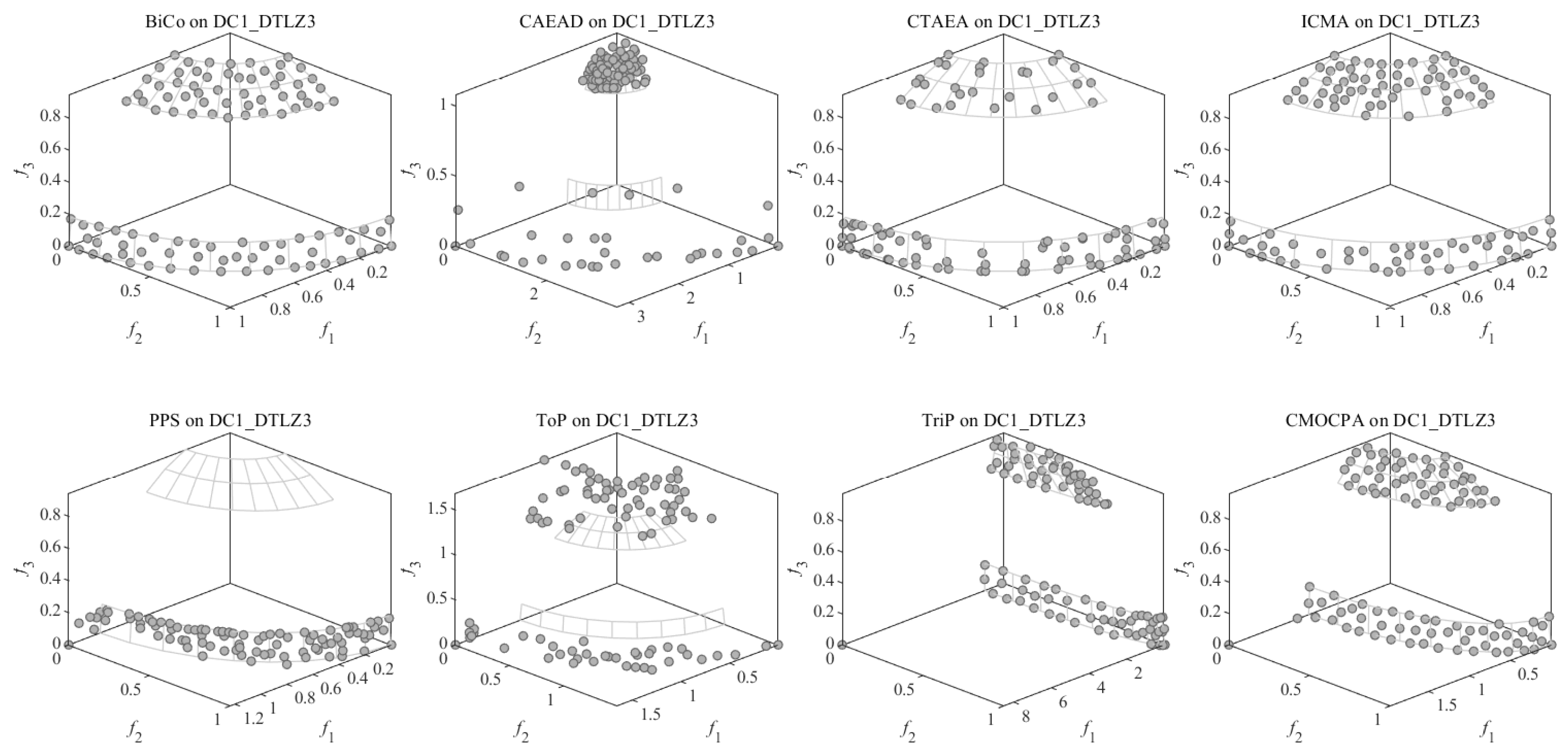
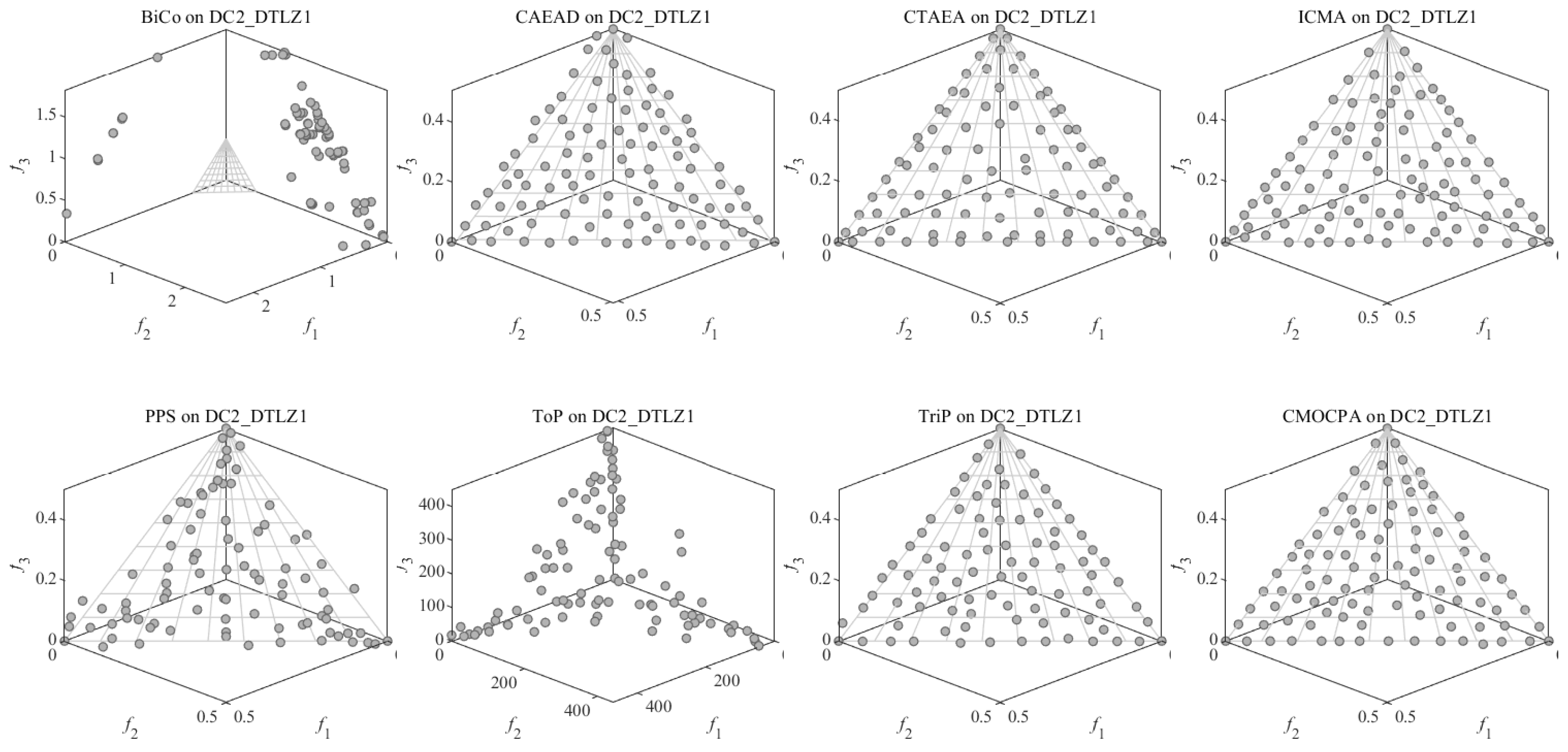
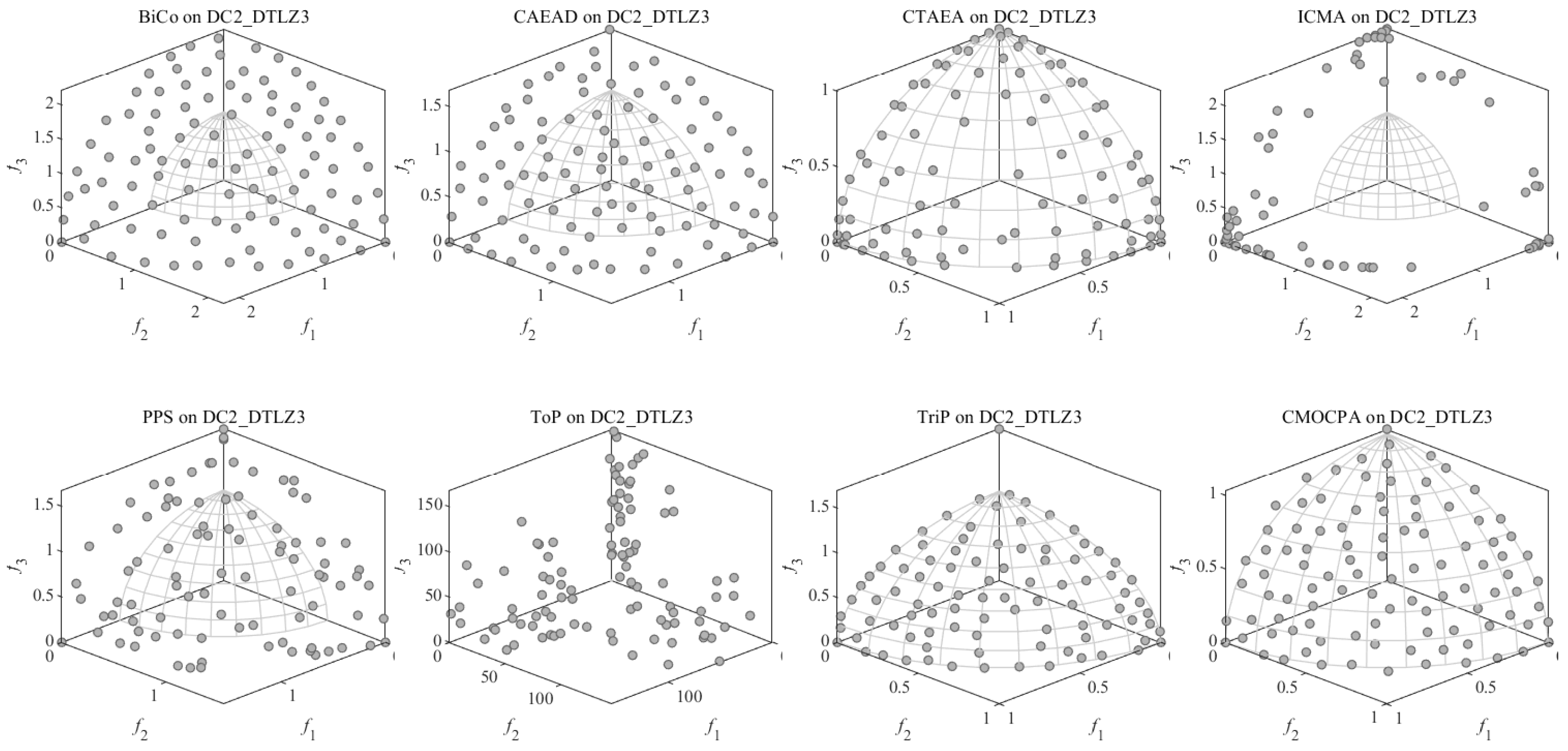
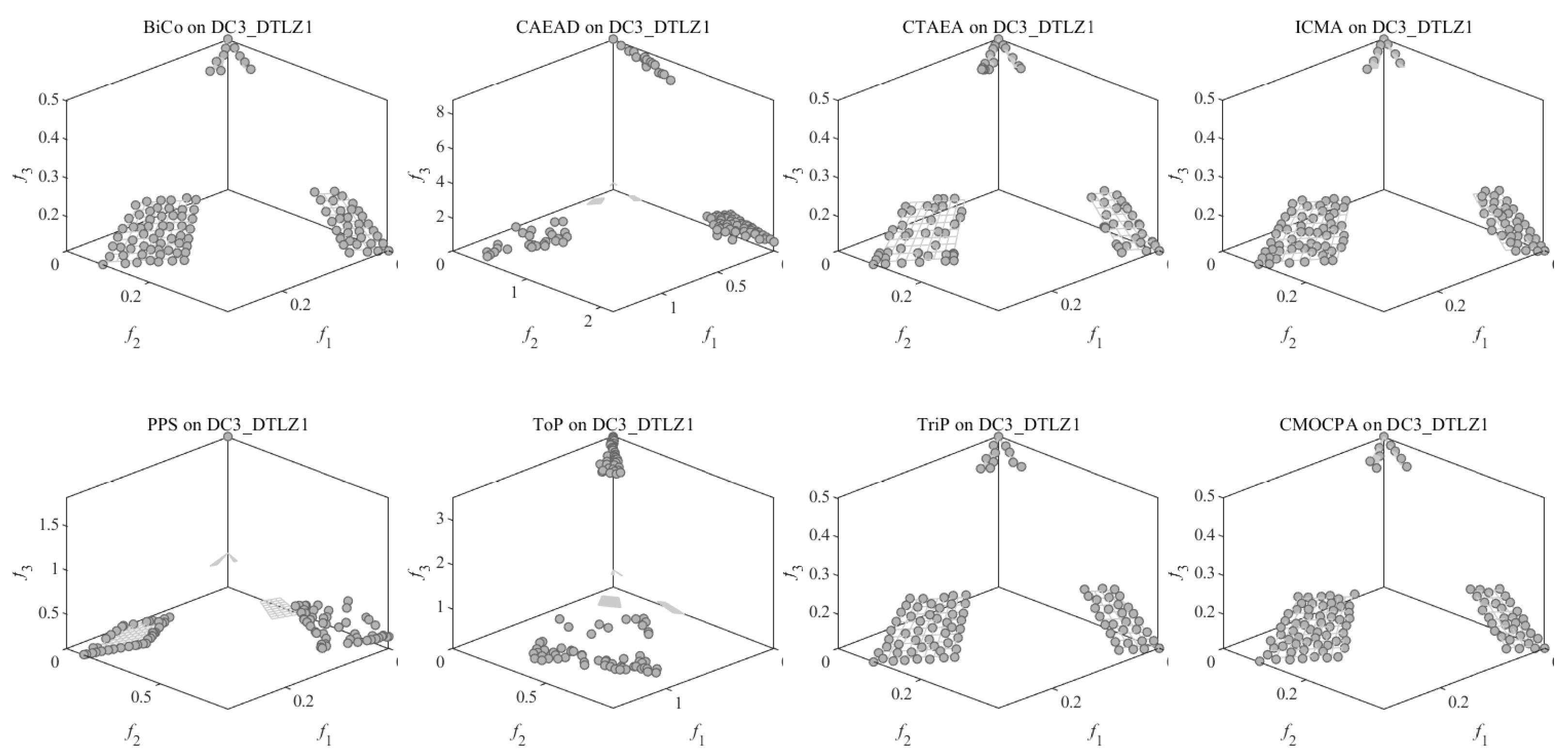
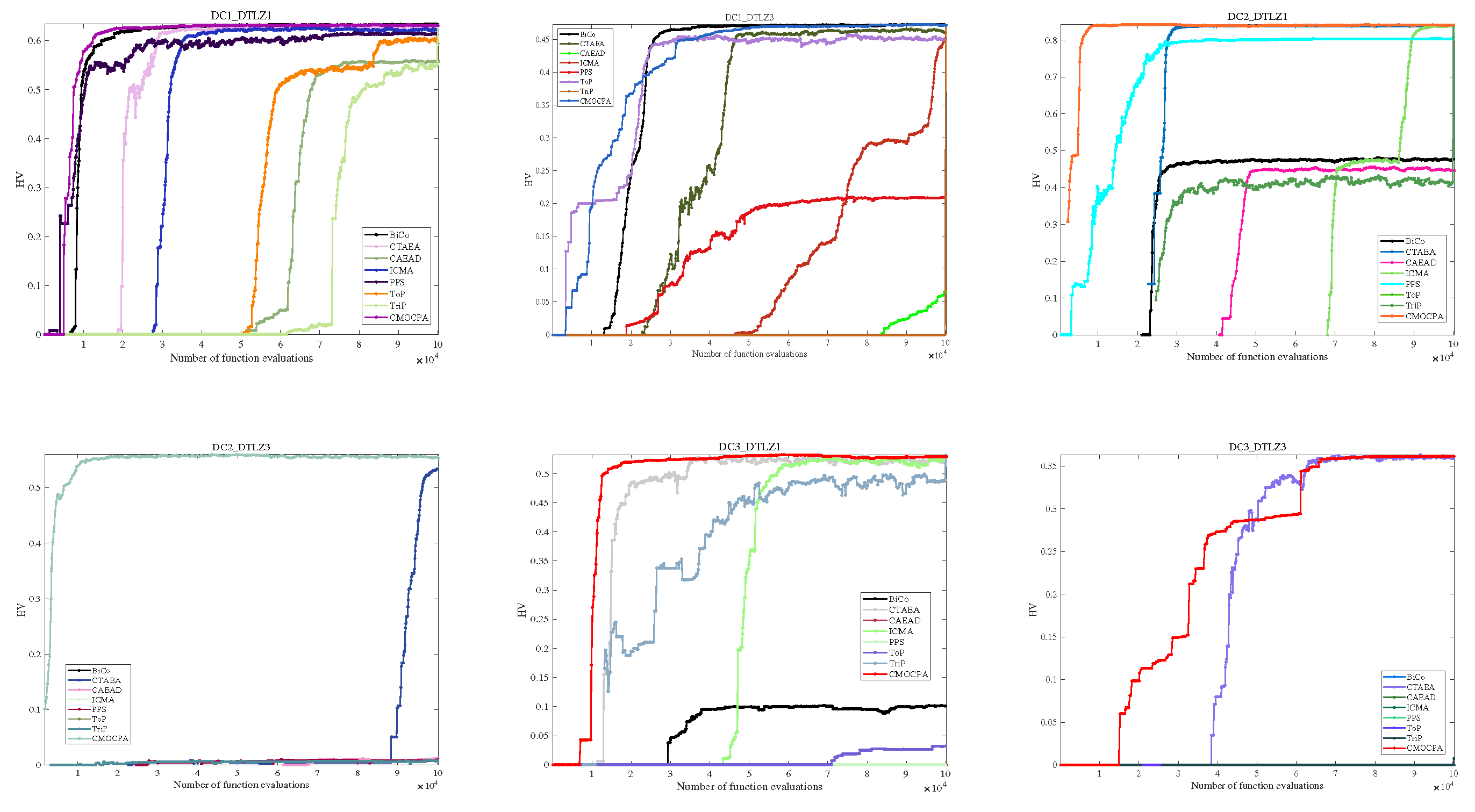
4.2.1. Result on DC-DTLZ Benchmark Problems
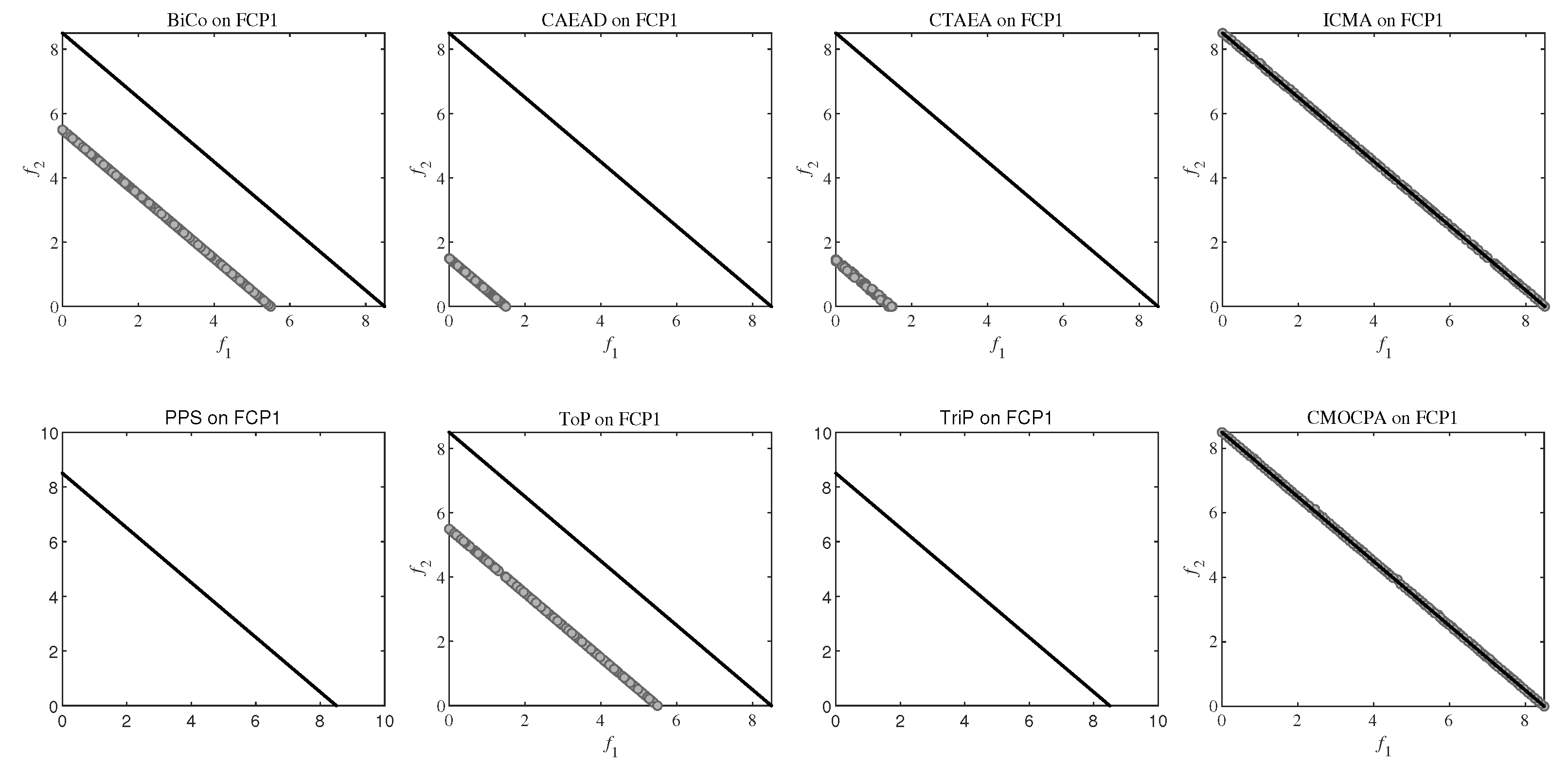
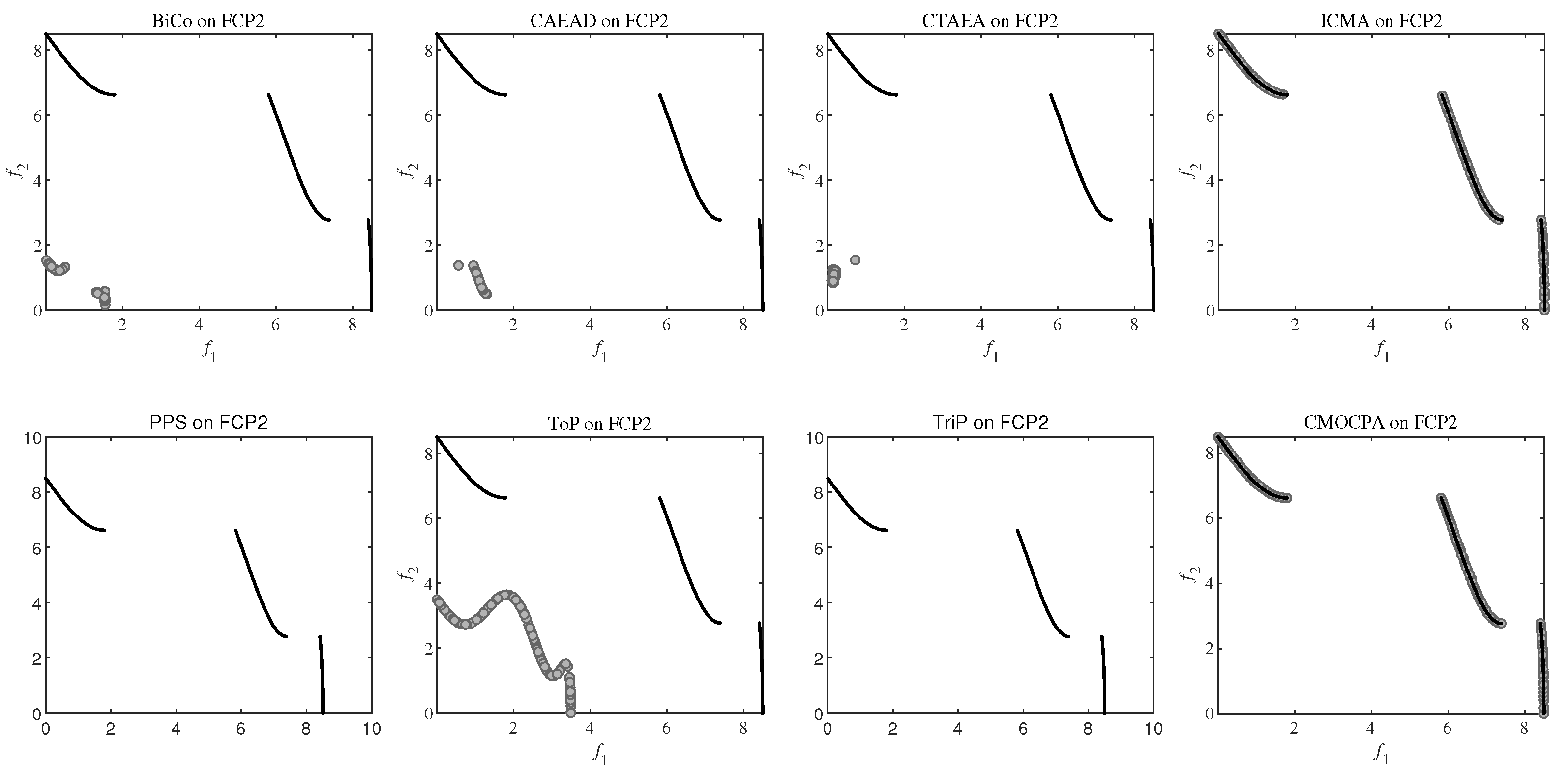
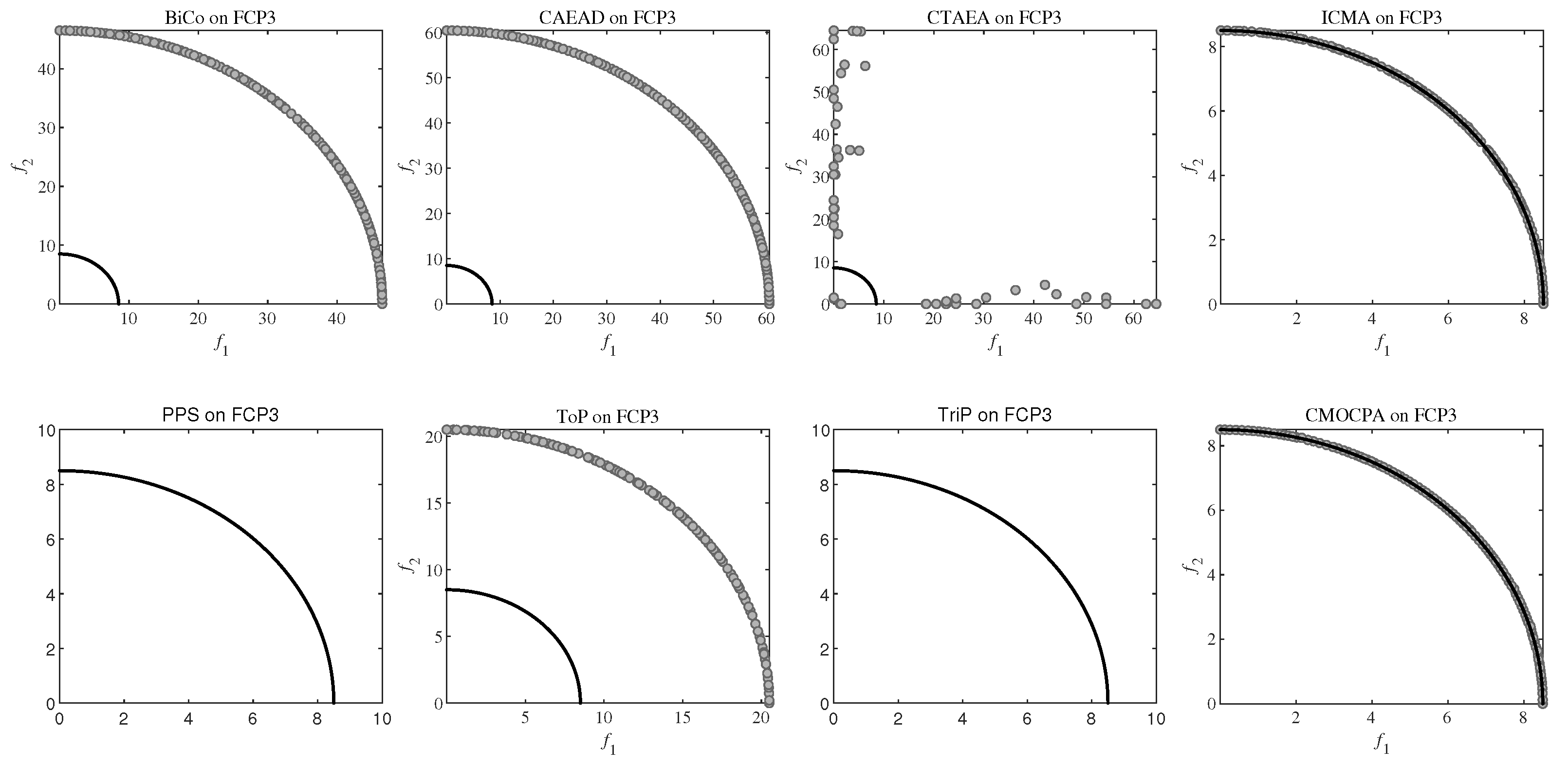
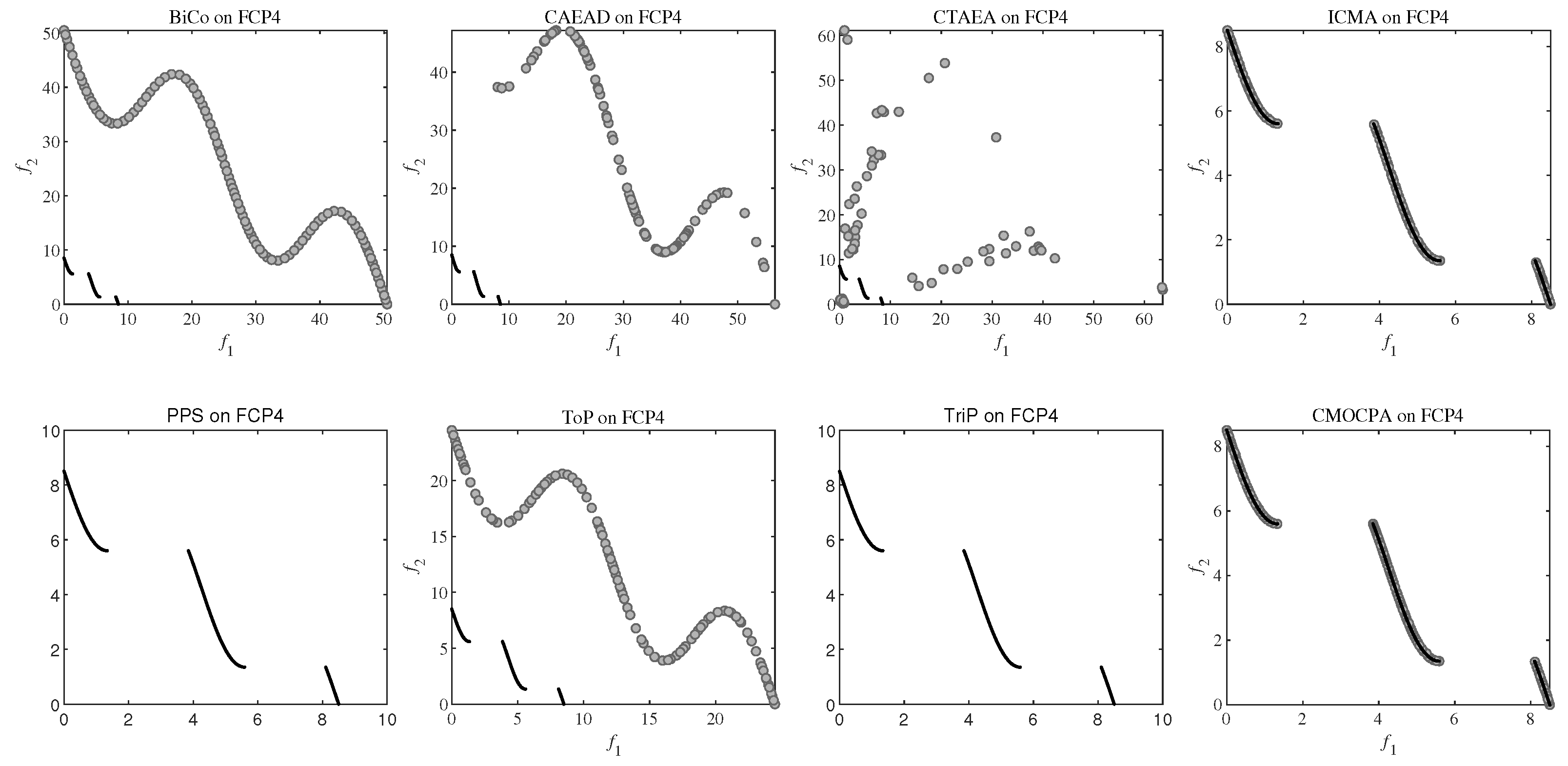
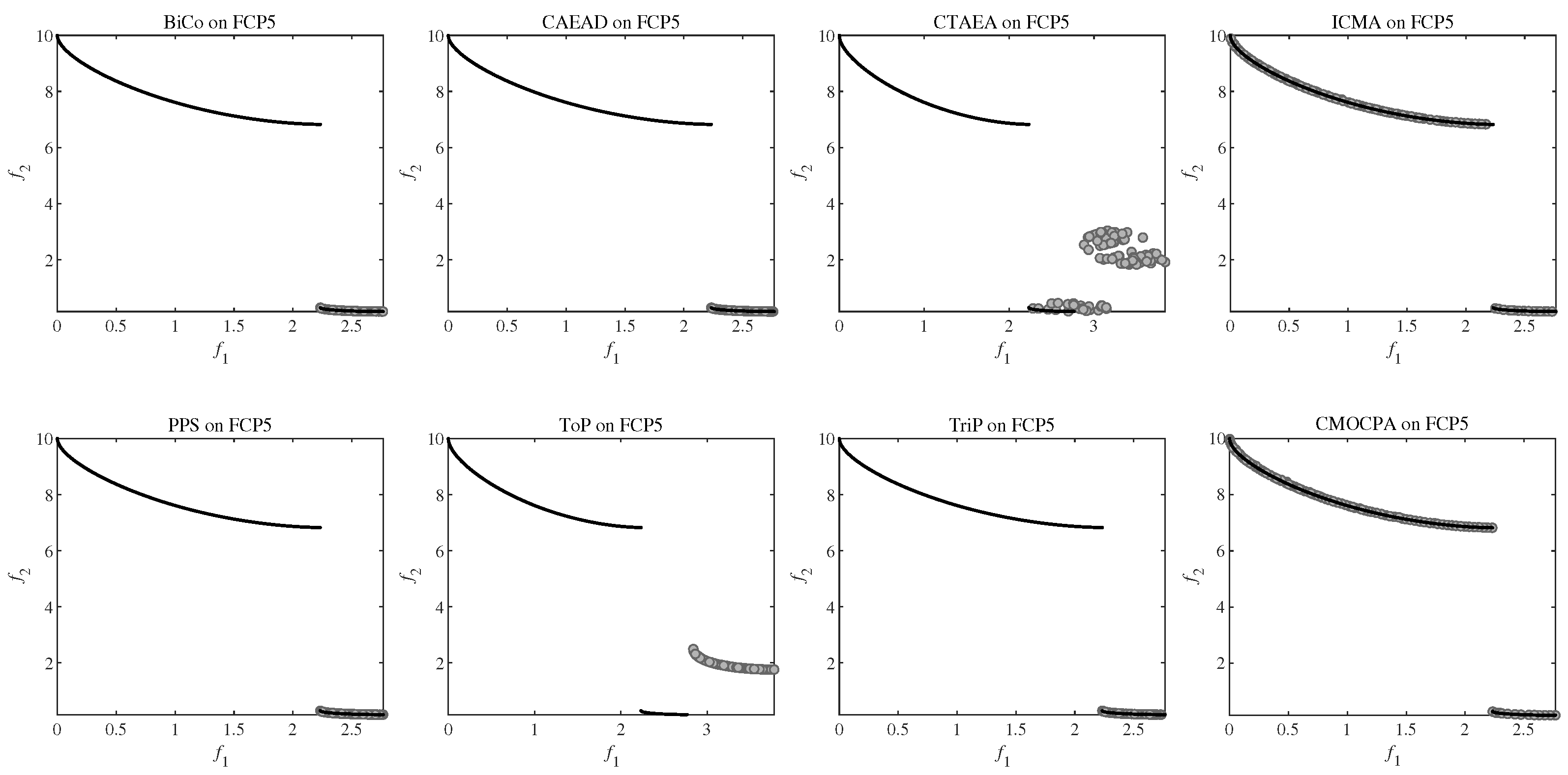
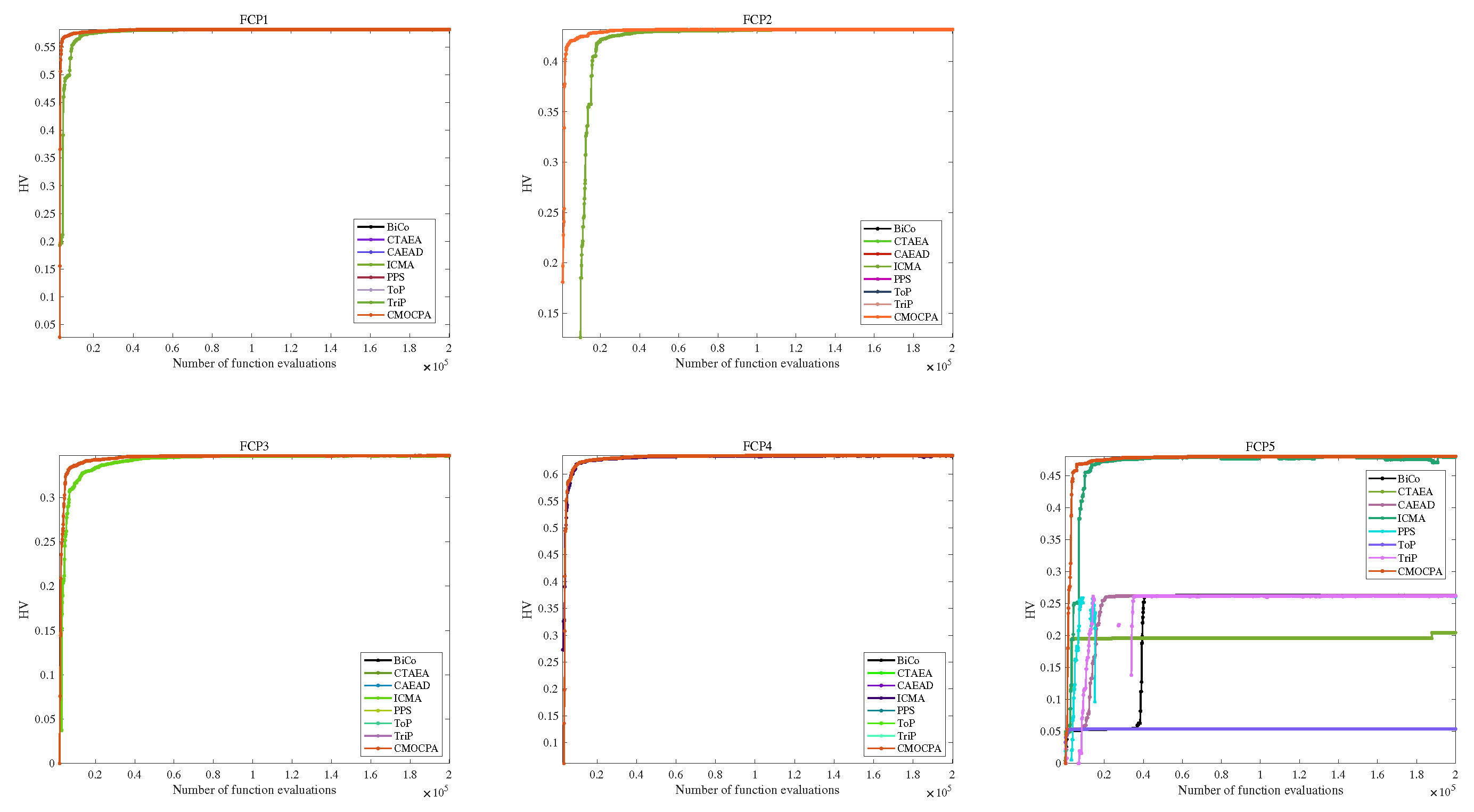
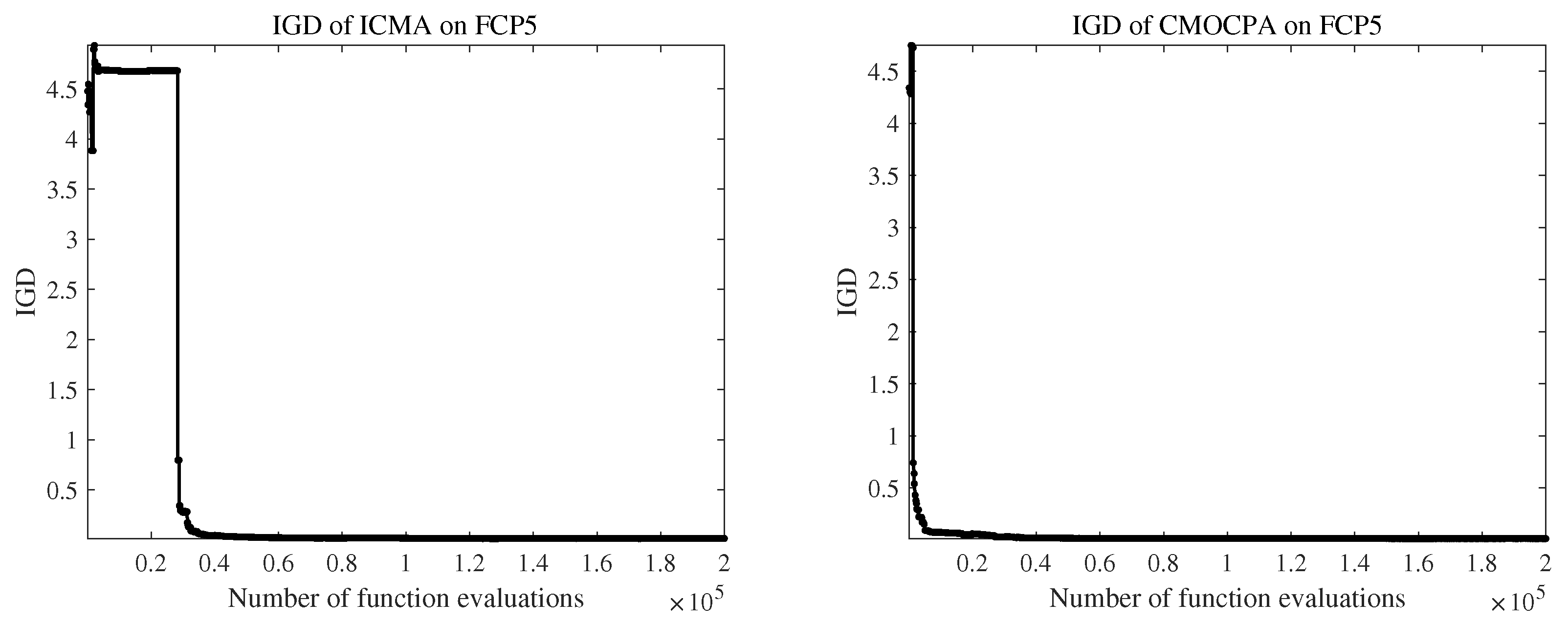
4.2.2. Result on FCP Benchmark Problems
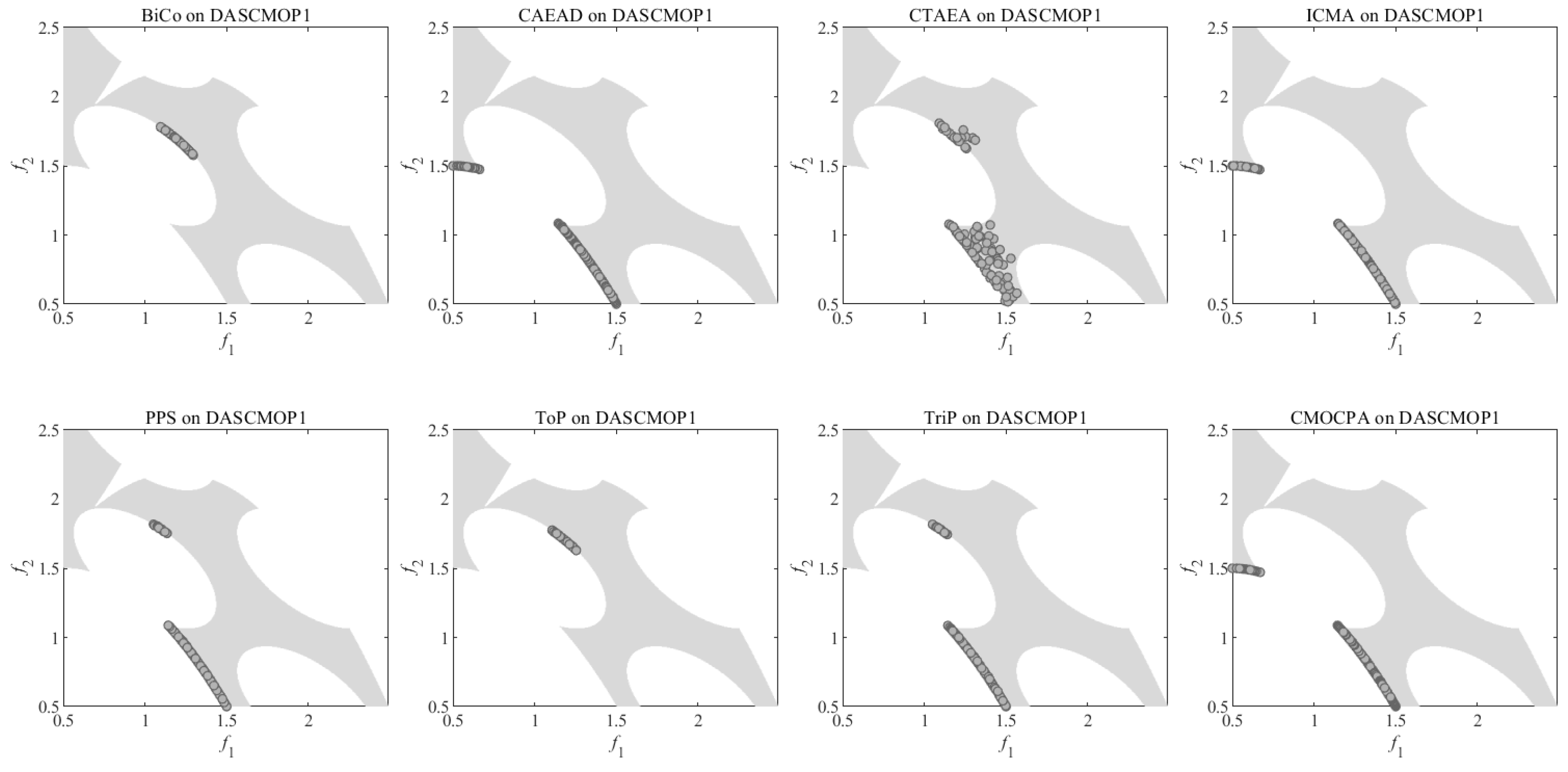
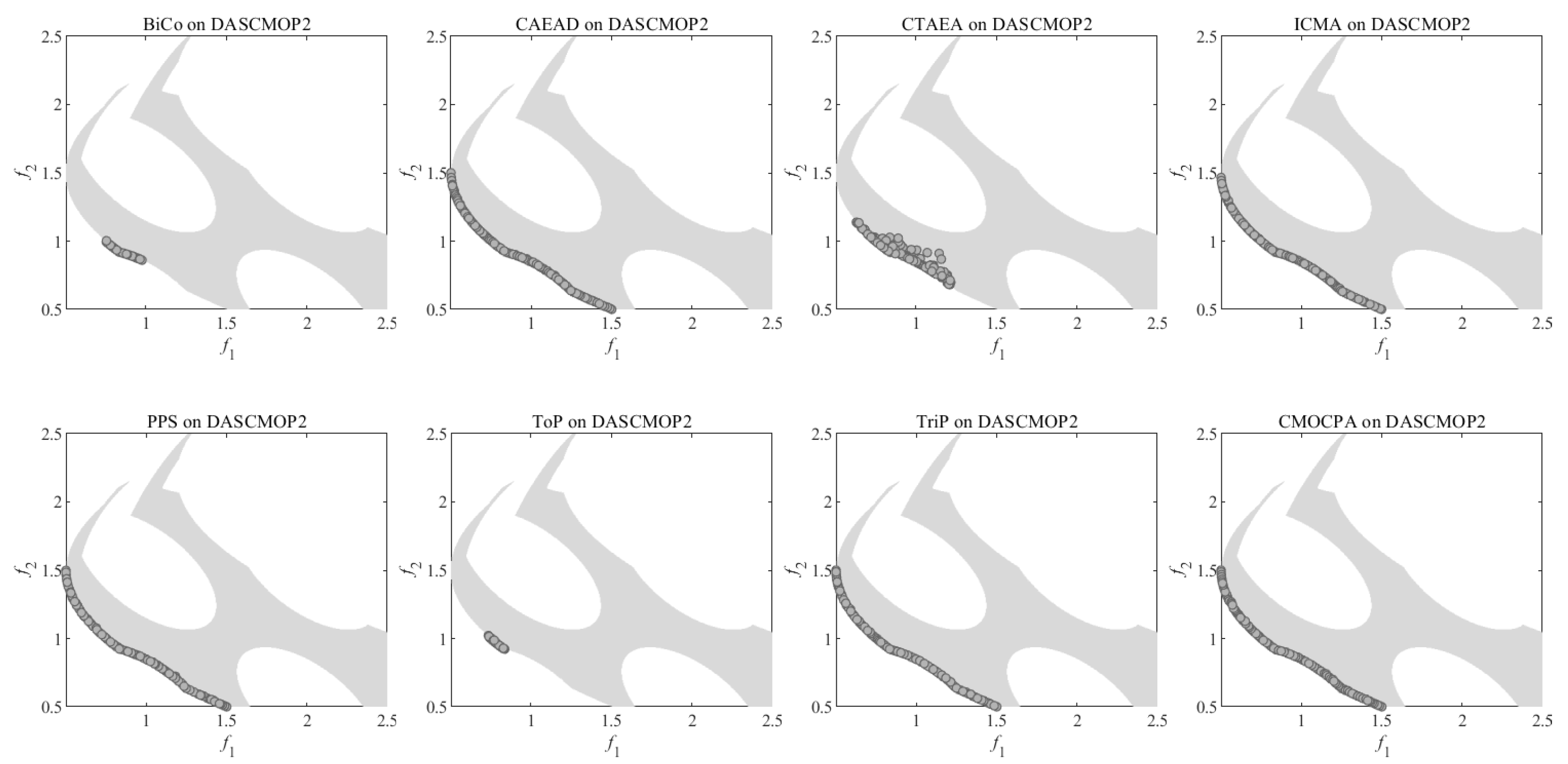
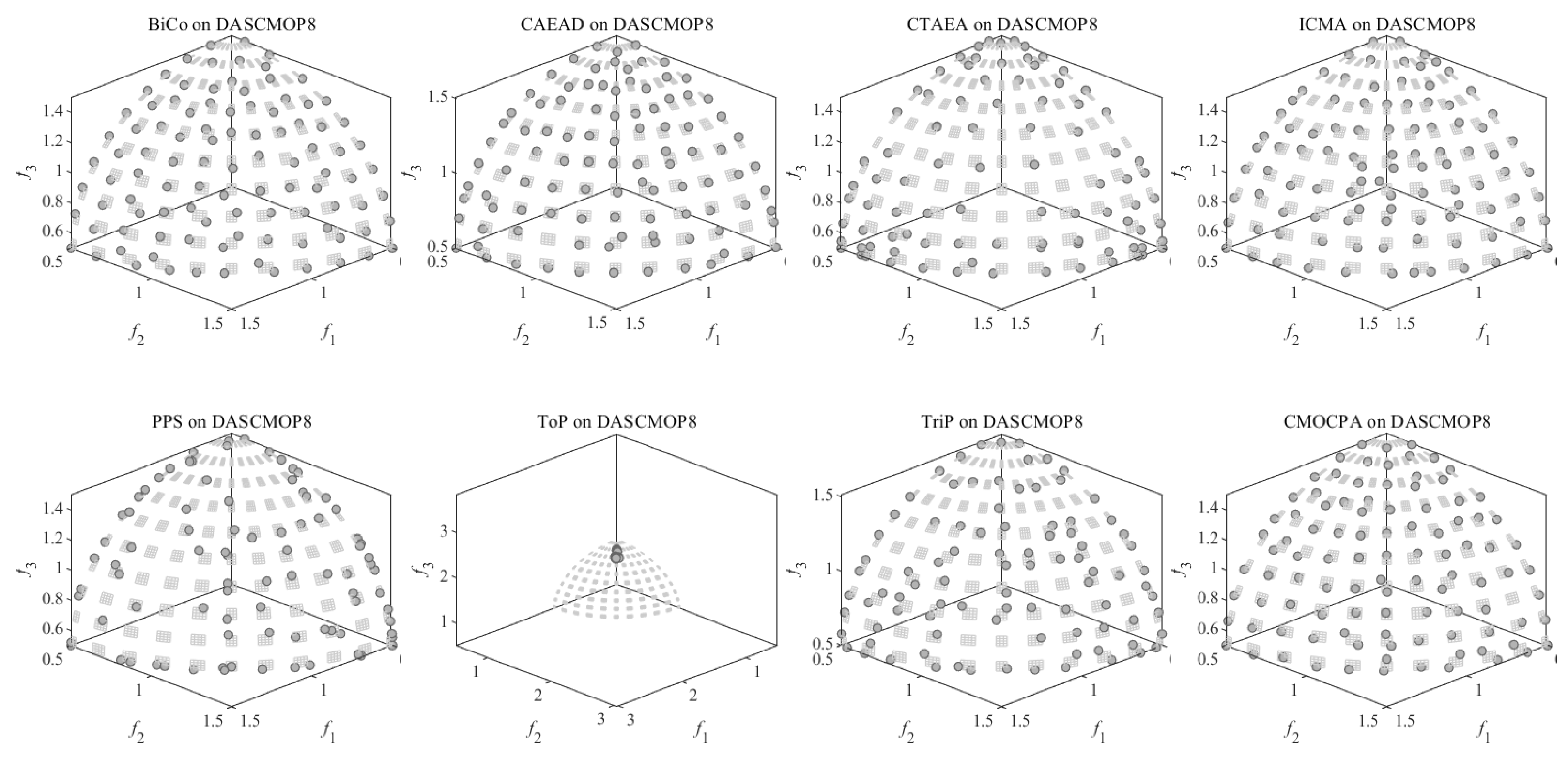
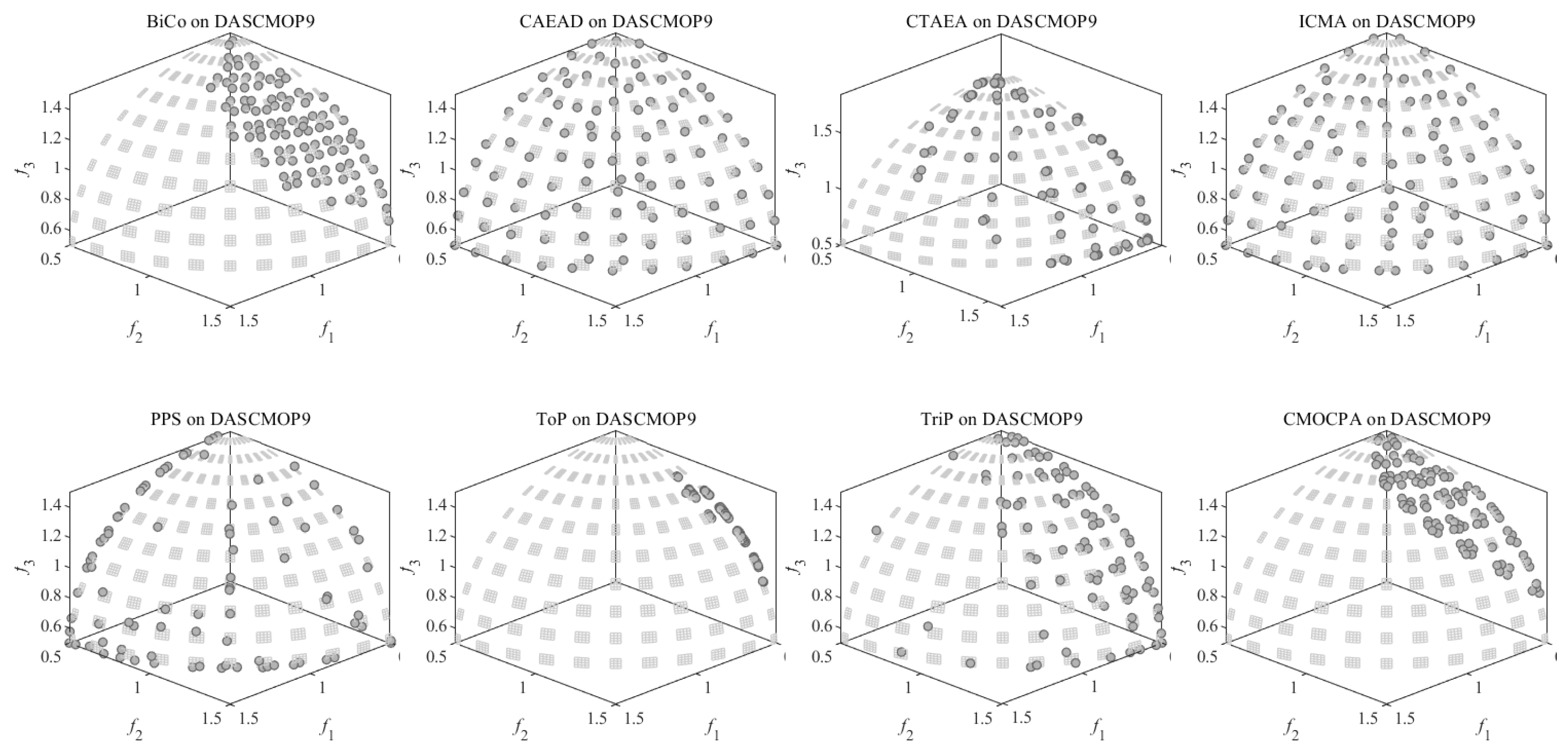
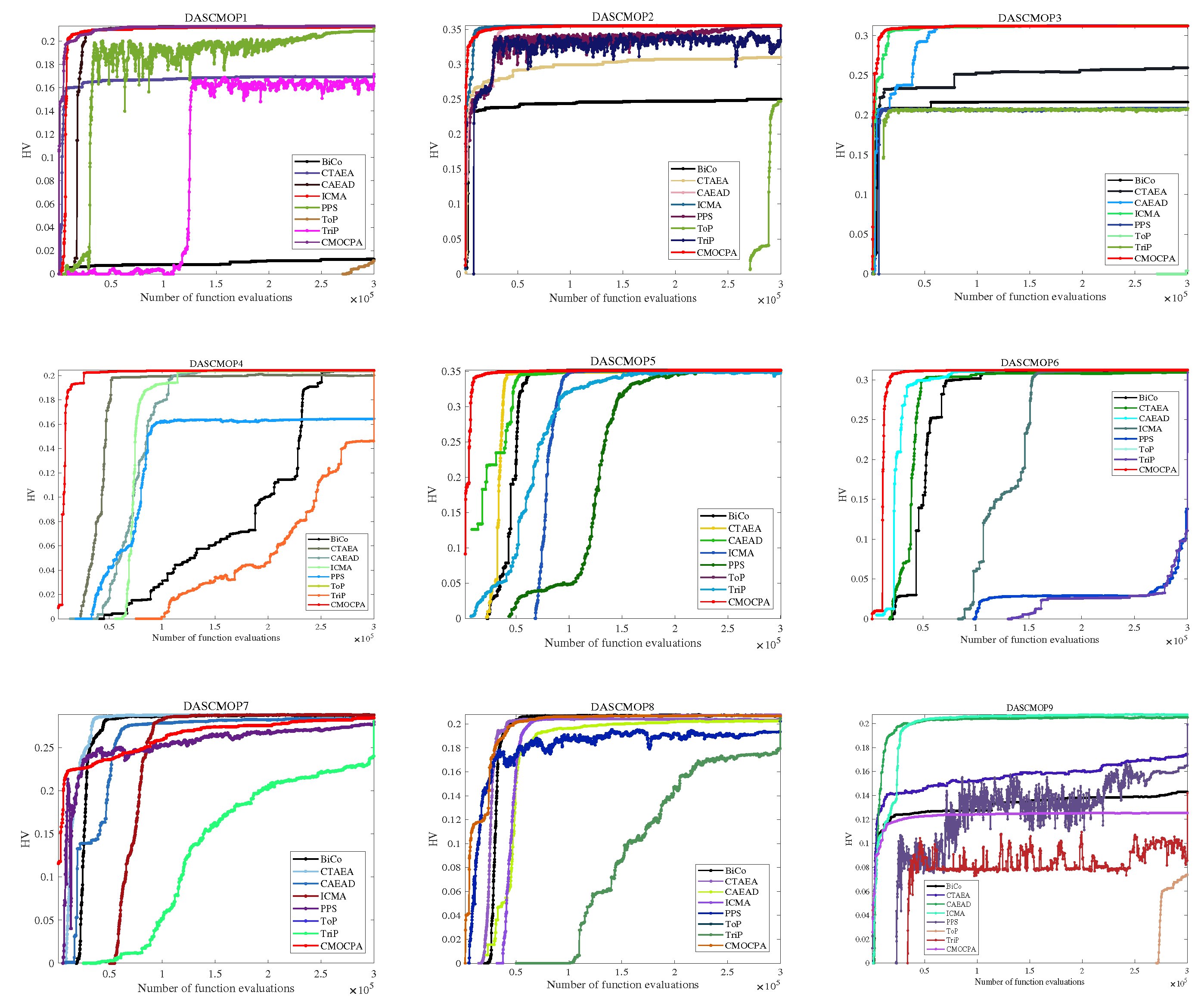
4.2.3. Result on DASCMOP Benchmark Problems
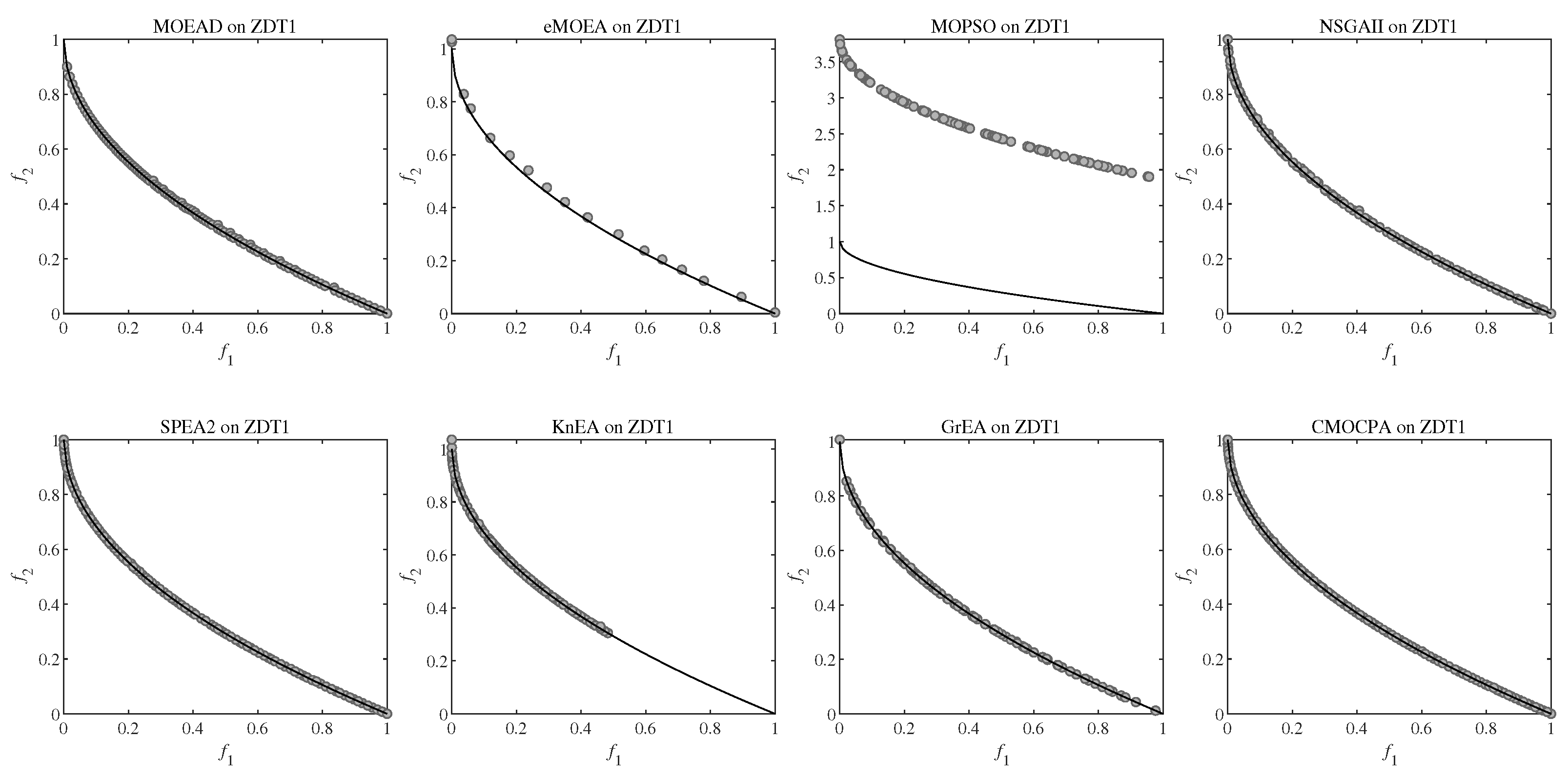
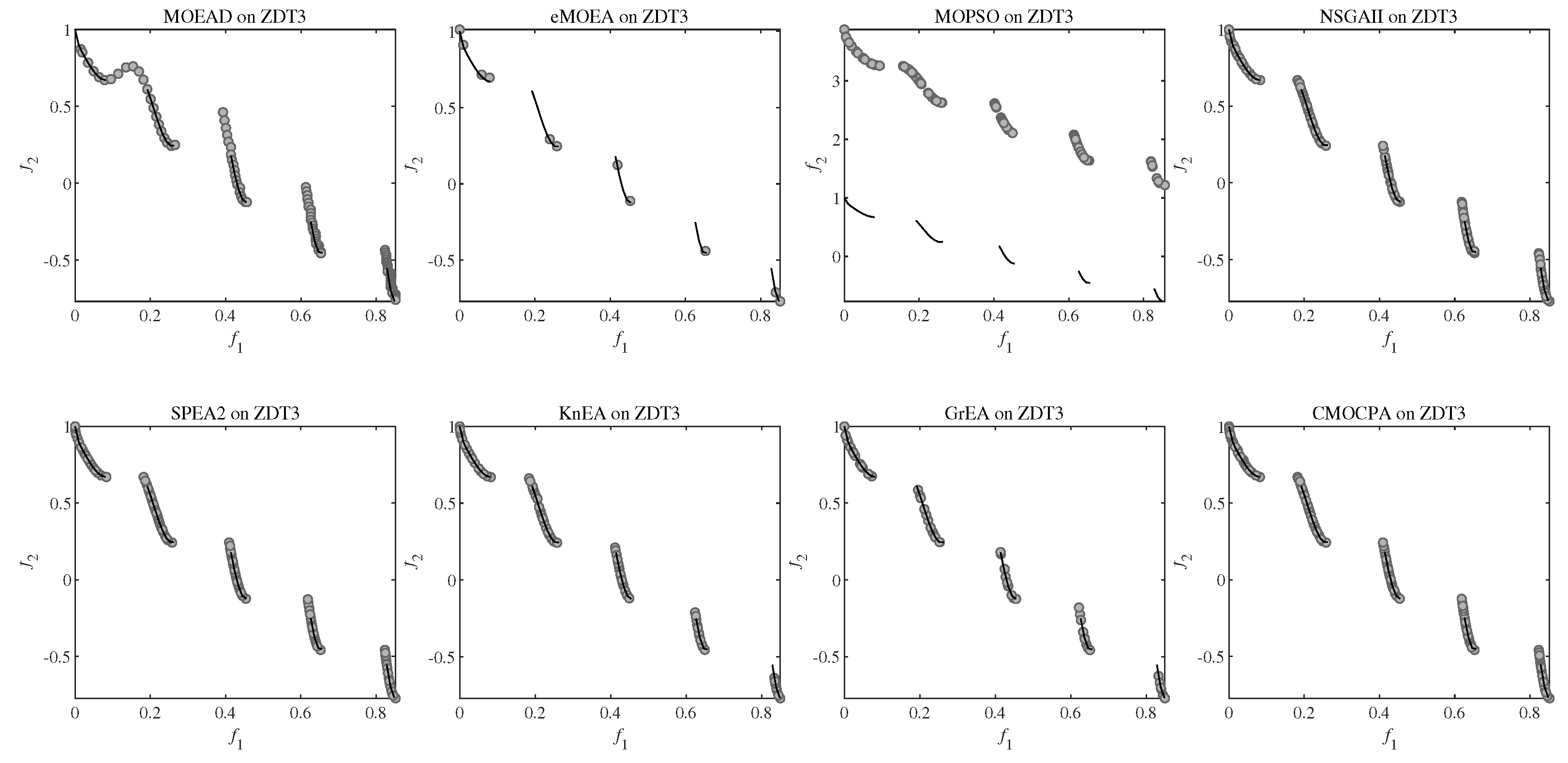
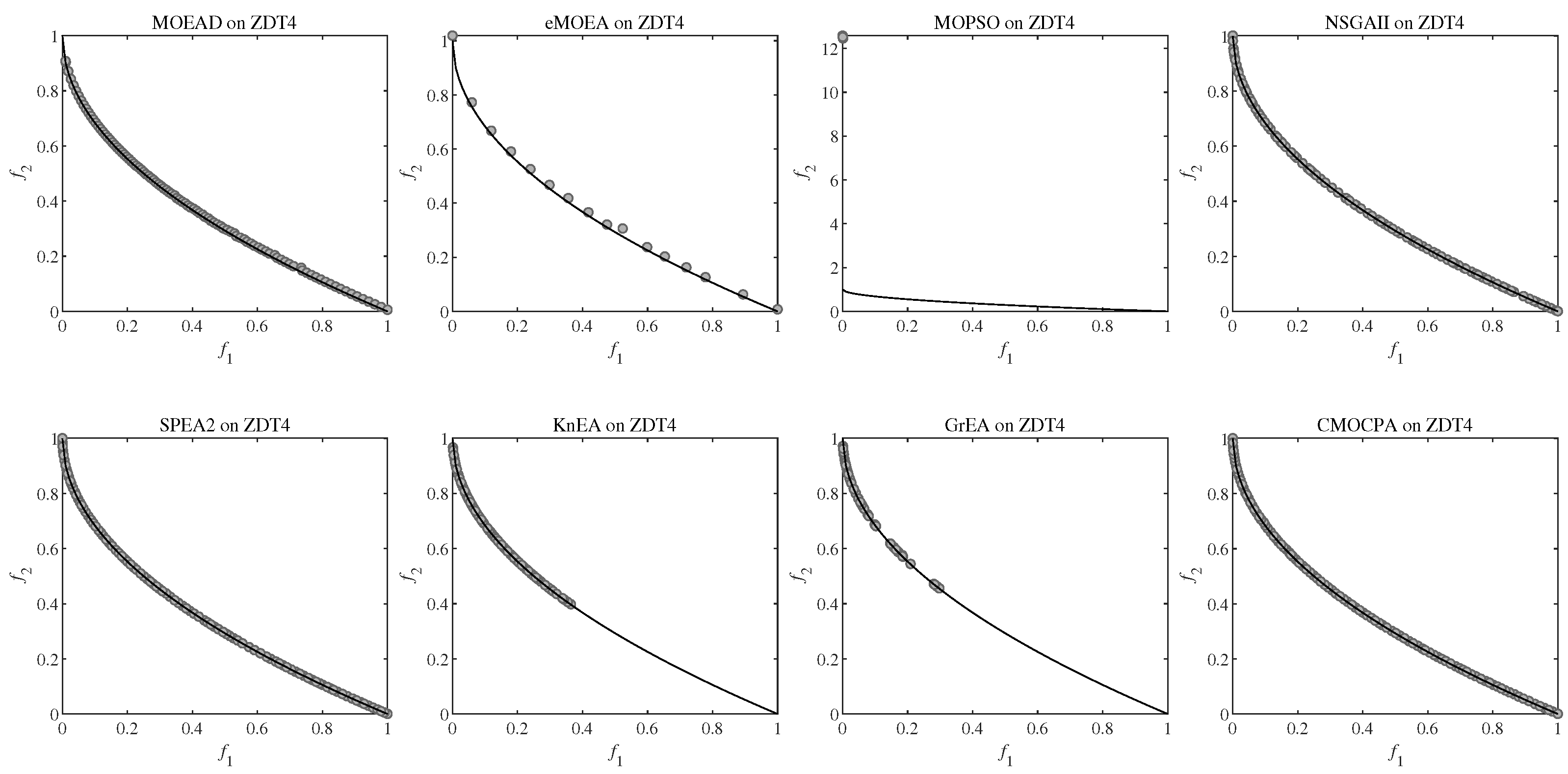
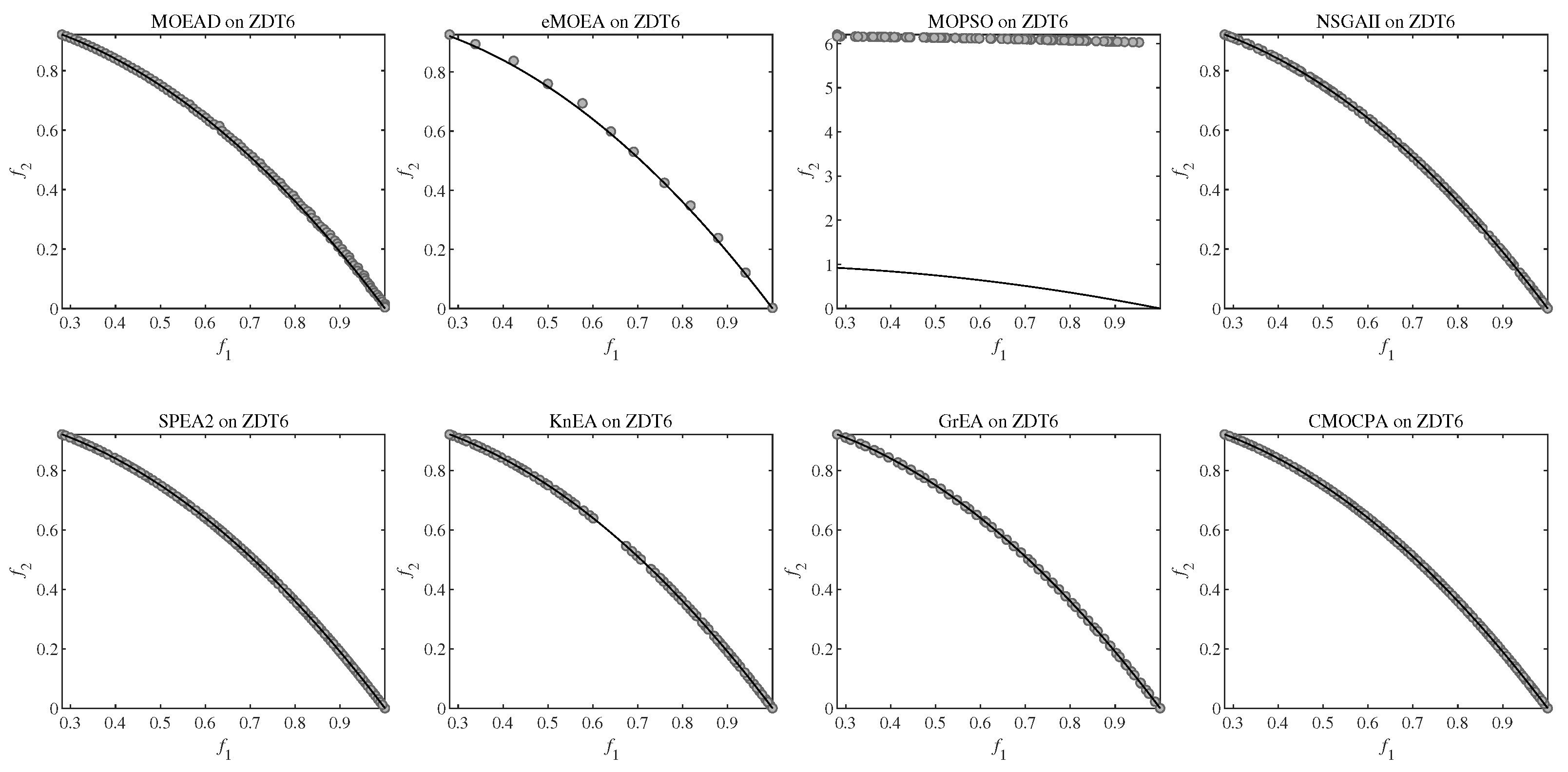
4.2.4. Result on ZDT and DTLZ Benchmark Problems
4.2.5. Result on RWMOPs Benchmark Problems
- (1)
- Results on mechanical design problems (RWMOP1-RWMOP21)
- (2)
- Results on chemical engineering problems (RWMOP22-RWMOP24)
- (3)
- Results on process, design, and synthesis problems (RWMOP25-RWMOP29)
- (4)
- Results on power electronics problems (RWMOP30-RWMOP35)
- (5)
- Results on power-system optimization problems (RWMOP36-RWMOP50)
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


References
- Koziel, S.; Pietrenko-Dabrowska, A. Constrained multi-objective optimization of compact microwave circuits by design triangulation and pareto front interpolation. Eur. J. Oper. Res. 2022, 299, 302–312. [Google Scholar] [CrossRef]
- Xiang, Y.; Yang, X.; Huang, H.; Wang, J. Balancing constraints and objectives by considering problem types in constrained multiobjective optimization. IEEE Trans. Cybern. 2021, 53, 88–101. [Google Scholar] [CrossRef] [PubMed]
- Saeed, K.; Ullah, M.O. Toward Reliable Controller Placements in Software-Defined Network Using Constrained Multi-Objective Optimization Technique. IEEE Access 2022, 10, 129865–129883. [Google Scholar] [CrossRef]
- Peng, C.; Huang, X.; Wu, Y.; Kang, J. Constrained Multi-Objective Optimization for UAV-Enabled Mobile Edge Computing: Offloading Optimization and Path Planning. IEEE Wirel. Commun. Lett. 2022, 11, 861–865. [Google Scholar] [CrossRef]
- Khalesian, M.; Delavar, M.R. Wireless sensors deployment optimization using a constrained Pareto-based multi-objective evolutionary approach. Eng. Appl. Artif. Intell. 2016, 53, 126–139. [Google Scholar] [CrossRef]
- Di Alesio, S. Optimal performance tuning in real-time systems using multi-objective constrained optimization. In Proceedings of the Principles and Practice of Constraint Programming: 22nd International Conference, CP 2016, Toulouse, France, 5–9 September 2016; pp. 556–574. [Google Scholar]
- Liang, J.; Qiao, K.; Yu, K.; Qu, B.; Yue, C.; Guo, W.; Wang, L. Utilizing the relationship between unconstrained and constrained Pareto fronts for constrained multiobjective optimization. IEEE Trans. Cybern. 2022, 2022, 3163759. [Google Scholar] [CrossRef]
- Cao, J.; Yan, Z.; Chen, Z.; Zhang, J. A Pareto front estimation-based constrained multi-objective evolutionary algorithm. Appl. Intell. 2022. [Google Scholar] [CrossRef]
- Ong, K.M.; Ong, P.; Sia, C.K. A carnivorous plant algorithm for solving global optimization problems. Appl. Soft Comput. 2021, 98, 106833. [Google Scholar] [CrossRef]
- Cheraghalipour, A.; Hajiaghaei-Keshteli, M.; Paydar, M.M. Tree Growth Algorithm (TGA): A novel approach for solving optimization problems. Eng. Appl. Artif. Intell. 2018, 72, 393–414. [Google Scholar] [CrossRef]
- Rahmani, A.M.; AliAbdi, I. Plant competition optimization: A novel metaheuristic algorithm. Expert Systems 2022, 39, e12956. [Google Scholar] [CrossRef]
- Kazimipour, B.; Li, X.; Qin, A.K. A review of population initialization techniques for evolutionary algorithms. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; p. 2585. [Google Scholar]
- Tharwat, A.; Schenck, W. Population initialization techniques for evolutionary algorithms for single-objective constrained optimization problems: Deterministic vs. stochastic techniques. Swarm Evol. Comput. 2021, 67, 100952. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, P.; Zhang, H.; Song, H.; Bei, J.; Sun, W.; Sun, X. A Carnivorous Plant Algorithm With Heuristic Decoding Method for Traveling Salesman Problem. IEEE Access 2022, 10, 97142–97164. [Google Scholar] [CrossRef]
- Zhang, P.L.; Sun, X.B.; Wang, J.Q.; Song, H.H.; Bei, J.L.; Zhang, H.Y. The Discrete Carnivorous Plant Algorithm with Similarity Elimination Applied to the Traveling Salesman Problem. Mathematics 2022, 10, 3249. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Chen, Y. Carnivorous Plant Algorithm and BP to Predict Optimum Bonding Strength of Heat-Treated Woods. Forests 2023, 14, 51. [Google Scholar] [CrossRef]
- Coello Coello, C.A.; Christiansen, A.D. MOSES: A multiobjective optimization tool for engineering design. Eng. Optim. 1999, 31, 337–368. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Jain, H.; Deb, K. An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part II: Handling constraints and extending to an adaptive approach. IEEE Trans. Evol. Comput. 2013, 18, 602–622. [Google Scholar] [CrossRef]
- Fan, Z.; Wang, Z.; Li, W.; Yuan, Y.; You, Y.; Yang, Z.; Sun, F.; Ruan, J. Push and pull search embedded in an M2M framework for solving constrained multi-objective optimization problems. Swarm Evol. Comput. 2020, 54, 100651. [Google Scholar] [CrossRef]
- Takahama, T.; Sakai, S. Constrained optimization by the ε constrained differential evolution with an archive and gradient-based mutation. In Proceedings of the IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010; pp. 1–9. [Google Scholar]
- Fan, Z.; Li, H.; Wei, C.; Li, W.; Huang, H.; Cai, X.; Cai, Z. An improved epsilon constraint handling method embedded in MOEA/D for constrained multi-objective optimization problems. In Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence (SSCI), Athens, Greece, 6–9 December 2016; pp. 1–8. [Google Scholar]
- Maldonado, H.M.; Zapotecas-Martínez, S. A dynamic penalty function within MOEA/D for constrained multi-objective optimization problems. In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Kraków, Poland, 28 June–1 July 2021; pp. 1470–1477. [Google Scholar]
- Panda, A.; Pani, S. A symbiotic organisms search algorithm with adaptive penalty function to solve multi-objective constrained optimization problems. Appl. Soft Comput. 2016, 46, 344–360. [Google Scholar] [CrossRef]
- Ming, M.; Trivedi, A.; Wang, R.; Srinivasan, D.; Zhang, T. A dual-population-based evolutionary algorithm for constrained multiobjective optimization. IEEE Trans. Evol. Comput. 2021, 25, 739–753. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, Y. Shift-based penalty for evolutionary constrained multiobjective optimization and its application. IEEE Trans. Cybern. 2021, 53, 18–30. [Google Scholar] [CrossRef]
- Singh, H.K.; Isaacs, A.; Nguyen, T.T.; Ray, T.; Yao, X. Performance of infeasibility driven evolutionary algorithm (IDEA) on constrained dynamic single objective optimization problems. In Proceedings of the 2009 IEEE Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009; pp. 3127–3134. [Google Scholar]
- Peng, C.; Liu, H.L.; Gu, F. An evolutionary algorithm with directed weights for constrained multi-objective optimization. Appl. Soft Comput. 2017, 60, 613–622. [Google Scholar] [CrossRef]
- Liu, Z.Z.; Wang, B.C.; Tang, K. Handling constrained multiobjective optimization problems via bidirectional coevolution. IEEE Trans. Cybern. 2021, 52, 10163–10176. [Google Scholar] [CrossRef]
- Fan, Z.; Li, W.; Cai, X.; Li, H.; Wei, C.; Zhang, Q.; Deb, K.; Goodman, E. Push and pull search for solving constrained multi-objective optimization problems. Swarm Evol. Comput. 2019, 44, 665–679. [Google Scholar] [CrossRef]
- Li, K.; Chen, R.; Fu, G.; Yao, X. Two-archive evolutionary algorithm for constrained multiobjective optimization. IEEE Trans. Evol. Comput. 2018, 23, 303–315. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, T.; Xiao, J.; Zhang, X.; Jin, Y. A coevolutionary framework for constrained multiobjective optimization problems. IEEE Trans. Evol. Comput. 2020, 25, 102–116. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength Pareto evolutionary algorithm. TIK Rep. 2001, 103, 1–22. [Google Scholar]
- Fan, Q.; Chen, Z.; Xia, Z. A novel quasi-reflected Harris hawks optimization algorithm for global optimization problems. Soft Comput. 2020, 24, 14825–14843. [Google Scholar] [CrossRef]
- Basha, J.; Bacanin, N.; Vukobrat, N.; Zivkovic, M.; Venkatachalam, K.; Hubálovskỳ, S.; Trojovskỳ, P. Chaotic harris hawks optimization with quasi-reflection-based learning: An application to enhance cnn design. Sensors 2021, 21, 6654. [Google Scholar] [CrossRef]
- Zhong, C.; Li, G.; Meng, Z.; He, W. Opposition-based learning equilibrium optimizer with Levy flight and evolutionary population dynamics for high-dimensional global optimization problems. Expert Syst. Appl. 2023, 215, 119303. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, T.; Liu, Z. A whale optimization algorithm based on quadratic interpolation for high-dimensional global optimization problems. Appl. Soft Comput. 2019, 85, 105744. [Google Scholar] [CrossRef]
- Chen, X.; Mei, C.; Xu, B.; Yu, K.; Huang, X. Quadratic interpolation based teaching-learning-based optimization for chemical dynamic system optimization. Knowl.-Based Syst. 2018, 145, 250–263. [Google Scholar] [CrossRef]
- Zou, J.; Sun, R.; Yang, S.; Zheng, J. A dual-population algorithm based on alternative evolution and degeneration for solving constrained multi-objective optimization problems. Inf. Sci. 2021, 579, 89–102. [Google Scholar] [CrossRef]
- Yuan, J.; Liu, H.L.; Ong, Y.S.; He, Z. Indicator-based evolutionary algorithm for solving constrained multiobjective optimization problems. IEEE Trans. Evol. Comput. 2021, 26, 379–391. [Google Scholar] [CrossRef]
- Liu, Z.Z.; Wang, Y. Handling constrained multiobjective optimization problems with constraints in both the decision and objective spaces. IEEE Trans. Evol. Comput. 2019, 23, 870–884. [Google Scholar] [CrossRef]
- Ming, F.; Gong, W.; Wang, L.; Lu, C. A tri-population based co-evolutionary framework for constrained multi-objective optimization problems. Swarm Evol. Comput. 2022, 70, 101055. [Google Scholar] [CrossRef]
- Zitzler, E.; Deb, K.; Thiele, L. Comparison of multiobjective evolutionary algorithms: Empirical results. Evol. Comput. 2000, 8, 173–195. [Google Scholar] [CrossRef]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable multi-objective optimization test problems. Proc. Congr. Evol. Comput. 2002, 1, 825–830. [Google Scholar]
- Kumar, A.; Wu, G.; Ali, M.Z.; Luo, Q.; Mallipeddi, R.; Suganthan, P.N.; Das, S. A benchmark-suite of real-world constrained multi-objective optimization problems and some baseline results. Swarm Evol. Comput. 2021, 67, 100961. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Deb, K.; Mohan, M.; Mishra, S. Evaluating the ϵ-domination based multi-objective evolutionary algorithm for a quick computation of Pareto-optimal solutions. Evol. Comput. 2005, 13, 501–525. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Zhang, X.; Tian, Y.; Jin, Y. A knee point-driven evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2014, 19, 761–776. [Google Scholar] [CrossRef]
- Yang, S.; Li, M.; Liu, X.; Zheng, J. A grid-based evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2013, 17, 721–736. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB platform for evolutionary multi-objective optimization [educational forum]. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef]
- Fan, Z.; Li, W.; Cai, X.; Li, H.; Wei, C.; Zhang, Q.; Deb, K.; Goodman, E. Difficulty adjustable and scalable constrained multiobjective test problem toolkit. Evol. Comput. 2020, 28, 339–378. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2013, 18, 577–601. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P.N. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2010, 15, 4–31. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Bosman, P.A.; Thierens, D. The balance between proximity and diversity in multiobjective evolutionary algorithms. IEEE Trans. Evol. Comput. 2003, 7, 174–188. [Google Scholar] [CrossRef]
- Van Veldhuizen, D.A.; Lamont, G.B. Evolutionary computation and convergence to a pareto front. In Late Breaking Papers at the Genetic Programming 1998 Conference; Stanford University Bookstore: Stanford, CA, USA, 1998; pp. 221–228. [Google Scholar]
- While, L.; Hingston, P.; Barone, L.; Huband, S. A faster algorithm for calculating hypervolume. IEEE Trans. Evol. Comput. 2006, 10, 29–38. [Google Scholar] [CrossRef]
- Hollander, M.; Wolfe, D.A.; Chicken, E. Nonparametric Statistical Methods; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
| Problem | BiCo | CTAEA | CAEAD | ICMA | PPS | ToP | TriP | CMOCPA |
|---|---|---|---|---|---|---|---|---|
| DC1_DTLZ1 | 1.1584e-2 (1.20e-4) − | 1.5158e-2 (2.56e-4) − | 1.0618e-1 (1.55e-1) − | 1.1893e-2 (1.60e-4) − | 2.8409e-2 (9.10e-3) − | 2.1664e-2 (6.14e-3) − | 1.2794e-2 (2.60e-4) − | 1.1488e-2 (2.06e-4) |
| DC1_DTLZ3 | 3.4686e-2 (7.70e-4) ≈ | 4.3288e-2 (1.50e-3) − | 1.0197e+0 (1.29e+0) − | 5.3560e-2 (3.73e-2) − | 3.7055e-1 (2.35e-1) − | 8.9654e-1 (1.11e+0) − | 3.6929e-2 (7.67e-4) − | 3.4627e-2 (1.39e-3) |
| DC2_DTLZ1 | 5.2700e-2 (6.42e-2) ≈ | 2.3224e-2 (1.87e-4) − | 7.7302e-2 (6.92e-2) − | 5.5734e-2 (6.54e-2) − | 5.1453e-2 (5.42e-2) − | NaN (NaN) | 2.2525e-2 (6.59e-4) − | 2.0804e-2 (4.65e-4) |
| DC2_DTLZ3 | 5.6324e-1 (1.81e-3) − | 1.4721e-1 (1.85e-1) − | 4.0076e-1 (2.61e-1) − | 2.6150e-1 (2.79e-1) − | 3.4354e-1 (2.54e-1) − | NaN (NaN) | 1.7668e-1 (1.93e-1) − | 5.4735e-2 (1.00e-3) |
| DC3_DTLZ1 | 2.9754e-2 (5.59e-2) − | 9.3533e-3 (2.12e-4) − | 9.8043e-1 (6.23e-1) − | 7.0463e-3 (1.35e-4) − | 3.1353e-1 (3.70e-1) − | 2.1104e+0 (2.31e+0) − | 7.6022e-3 (3.51e-4) − | 6.8449e-3 (8.80e-5) |
| DC3_DTLZ3 | 9.4436e-1 (4.65e-1) − | 2.8206e-2 (8.64e-3) + | 4.5099e+0 (3.57e+0) − | 9.4954e-1 (4.70e-1) − | 2.2421e+0 (2.11e+0) − | 8.3246e+0 (4.28e+0) − | 2.7967e-1 (2.49e-1) − | 3.0185e-2 (3.42e-2) |
| 0/4/2 | 1/5/0 | 0/6/0 | 0/6/0 | 0/6/0 | 0/4/0 | 0/6/0 |
| Problem | BiCo | CTAEA | CAEAD | ICMA | PPS | ToP | TriP | CMOCPA |
|---|---|---|---|---|---|---|---|---|
| DC1_DTLZ1 | 6.3234e-1 (6.43e-4) + | 6.2733e-1 (5.11e-4) − | 4.2919e-1 (2.23e-1) − | 6.2323e-1 (2.02e-3) − | 5.8118e-1 (2.36e-2) − | 5.8213e-1 (2.38e-2) − | 6.2773e-1 (1.69e-3) − | 6.3073e-1 (1.22e-3) |
| DC1_DTLZ3 | 4.7345e-1 (1.22e-3) + | 4.6238e-1 (1.95e-3) − | 1.1362e-1 (1.49e-1) − | 4.2699e-1 (7.22e-2) − | 2.6423e-1 (1.53e-1) − | 1.3585e-1 (1.80e-1) − | 4.6865e-1 (2.40e-3) − | 4.6982e-1 (3.62e-3) |
| DC2_DTLZ1 | 7.5947e-1 (1.62e-1) ≈ | 8.3810e-1 (4.37e-4) − | 6.8824e-1 (1.82e-1) − | 7.5158e-1 (1.66e-1) − | 7.4660e-1 (1.42e-1) − | NaN (NaN) | 8.3582e-1 (2.75e-3) − | 8.3958e-1 (1.71e-3) |
| DC2_DTLZ3 | 1.3824e-2 (1.30e-3) − | 4.5198e-1 (1.99e-1) − | 1.9546e-1 (2.54e-1) − | 3.3823e-1 (2.97e-1) ≈ | 2.4488e-1 (2.60e-1) − | NaN (NaN) | 4.0725e-1 (2.05e-1) − | 5.5451e-1 (3.68e-3) |
| DC3_DTLZ1 | 4.6968e-1 (1.49e-1) − | 5.2111e-1 (2.85e-3) − | 5.2955e-2 (1.42e-1) − | 5.2074e-1 (3.25e-3) − | 2.3702e-1 (2.06e-1) − | 1.5169e-2 (5.56e-2) − | 5.3229e-1 (3.00e-3) ≈ | 5.3349e-1 (1.36e-3) |
| DC3_DTLZ3 | 0.0000e+0 (0.00e+0) − | 3.5792e-1 (1.56e-2) ≈ | 4.2454e-2 (1.08e-1) − | 1.1401e-2 (6.24e-2) − | 4.0734e-2 (9.20e-2) − | 0.0000e+0 (0.00e+0) − | 1.7514e-1 (1.62e-1) − | 3.5426e-1 (2.08e-2) |
| 2/3/1 | 0/5/1 | 0/6/0 | 0/5/1 | 0/6/0 | 0/4/0 | 0/5/1 |
| Problem | BiCo | CTAEA | CAEAD | ICMA | PPS | ToP | TriP | CMOCPA |
|---|---|---|---|---|---|---|---|---|
| FCP1 | NaN (NaN) − | NaN (NaN) − | NaN (NaN) − | 3.5398e-2 (6.02e-4) − | NaN (NaN) − | NaN (NaN) − | NaN (NaN) − | 3.2784e-2 (4.59e-4) |
| FCP2 | NaN (NaN) − | NaN (NaN) − | NaN (NaN) − | 3.0284e-2 (3.96e-3) − | NaN (NaN) − | NaN (NaN) − | NaN (NaN) − | 2.6771e-2 (4.28e-4) |
| FCP3 | NaN (NaN) − | NaN (NaN) − | NaN (NaN) − | 3.8765e-2 (7.00e-4) − | NaN (NaN) − | NaN (NaN) − | NaN (NaN) − | 3.5363e-2 (4.54e-4) |
| FCP4 | NaN (NaN) − | NaN (NaN) − | NaN (NaN) − | 2.7470e-2 (5.64e-4) − | NaN (NaN) − | NaN (NaN) − | NaN (NaN) − | 2.5518e-2 (4.38e-4) |
| FCP5 | 4.6504e+0 (1.03e-1) − | 4.7204e+0 (2.60e-2) − | 4.6766e+0 (1.38e-3) − | 1.7074e-1 (8.53e-1) − | 4.6799e+0 (9.06e-3) − | 4.2654e+0 (4.62e-3) − | 4.6780e+0 (2.81e-3) − | 1.3151e-2 (4.78e-4) |
| 0/5/0 | 0/5/0 | 0/5/0 | 0/5/0 | 0/5/0 | 0/5/0 | 0/5/0 |
| Problem | BiCo | CTAEA | CAEAD | ICMA | PPS | ToP | TriP | CMOCPA |
|---|---|---|---|---|---|---|---|---|
| FCP1 | NaN (NaN) − | NaN (NaN) − | NaN (NaN) − | 5.8138e-1 (1.19e-4) − | NaN (NaN) − | NaN (NaN) − | NaN (NaN) − | 5.8168e-1 (1.12e-4) |
| FCP2 | NaN (NaN) − | NaN (NaN) − | NaN (NaN) − | 4.3132e-1 (2.76e-4) − | NaN (NaN) − | NaN (NaN −) | NaN (NaN) − | 4.3161e-1 (7.19e-5) |
| FCP3 | NaN (NaN) − | NaN (NaN) − | NaN (NaN) − | 3.4691e-1 (1.15e-4) − | NaN (NaN) − | NaN (NaN) − | NaN (NaN) − | 3.4706e-1 (1.14e-4) |
| FCP4 | NaN (NaN) − | NaN (NaN) − | NaN (NaN) − | 6.3405e-1 (2.62e-4) − | NaN (NaN) − | NaN (NaN) − | NaN (NaN) − | 6.3455e-1 (6.25e-5) |
| FCP5 | 2.4822e-1 (5.28e-2) − | 2.3073e-1 (2.28e-2) − | 2.6215e-1 (3.70e-5) − | 4.6845e-1 (3.95e-2) − | 2.6120e-1 (2.35e-3) − | 5.3823e-2 (2.44e-5) − | 2.6209e-1 (2.20e-4) − | 4.7986e-1 (1.03e-4) |
| 0/5/0 | 0/5/0 | 0/5/0 | 0/5/0 | 0/5/0 | 0/5/0 | 0/5/0 |
| Problem | BiCo | CTAEA | CAEAD | ICMA | PPS | ToP | TriP | CMOCPA |
|---|---|---|---|---|---|---|---|---|
| DASCMOP1 | 7.0996e-1 (3.86e-2) − | 1.8326e-1 (1.41e-2) − | 2.8895e-3 (2.16e-4) ≈ | 2.8510e-3 (2.42e-4) ≈ | 1.8950e-1 (2.31e-1) − | 7.3320e-1 (1.51e-1) − | 2.2514e-1 (2.21e-1) − | 2.8431e-3 (1.31e-4) |
| DASCMOP2 | 2.3555e-1 (1.97e-2) − | 9.1724e-2 (4.30e-2) − | 4.1915e-3 (1.13e-4) + | 4.1524e-3 (8.69e-5) + | 5.1338e-3 (1.76e-4) − | 4.8869e-1 (2.54e-1) − | 4.4553e-3 (1.19e-4) ≈ | 4.4568e-3 (1.23e-4) |
| DASCMOP3 | 2.7163e-1 (3.32e-2) − | 1.2803e-1 (1.04e-2) − | 1.9162e-2 (1.27e-3) − | 1.8978e-2 (2.15e-3) ≈ | 2.9289e-1 (1.07e-1) − | 7.0016e-1 (1.08e-1) − | 2.3729e-1 (1.23e-1) − | 1.9088e-2 (1.76e-3) |
| DASCMOP4 | 1.2904e-3 (2.01e-4) − | 1.0966e-2 (2.02e-3) − | 1.8708e-3 (7.96e-4) − | 1.7461e-3 (8.35e-4) − | 1.5584e-1 (1.16e-1) − | NaN (NaN) − | 1.6389e-3 (3.86e-4) − | 1.2186e-3 (1.76e-4) |
| DASCMOP5 | 2.8730e-3 (7.70e-4) − | 7.1383e-3 (4.82e-4) − | 8.8972e-2 (2.26e-1) − | 2.8957e-3 (8.51e-5) − | 4.1381e-3 (3.64e-4) − | NaN (NaN) − | 3.4980e-3 (8.80e-4) − | 2.7905e-3 (5.03e-5) |
| DASCMOP6 | 4.7748e-2 (9.48e-2) − | 2.3661e-2 (4.96e-3) − | 8.0642e-2 (1.75e-1) ≈ | 1.9401e-2 (1.27e-3) − | 1.6117e-1 (2.66e-1) − | NaN (NaN) − | 1.8982e-2 (2.18e-3) − | 1.8467e-2 (2.46e-3) |
| DASCMOP7 | 3.1651e-2 (8.35e-4) − | 3.8141e-2 (7.98e-4) − | 4.0516e-2 (1.78e-2) − | 3.3291e-2 (1.05e-3) − | 5.8472e-2 (1.20e-2) − | NaN (NaN) − | 4.3108e-2 (3.44e-3) − | 3.0844e-2 (7.42e-4) |
| DASCMOP8 | 4.1198e-2 (8.64e-4) − | 5.7532e-2 (9.49e-3) − | 7.1127e-2 (1.18e-1) − | 4.3247e-2 (9.58e-4) − | 6.9460e-2 (7.19e-3) − | NaN (NaN) − | 5.4660e-2 (5.18e-3) − | 3.9807e-2 (1.28e-3) |
| DASCMOP9 | 3.0573e-1 (5.44e-2) + | 2.2504e-1 (7.20e-2) + | 4.1371e-2 (1.06e-3) + | 4.2363e-2 (5.90e-4) + | 1.4368e-1 (1.10e-1) + | 5.9957e-1 (2.05e-1) − | 1.3114e-1 (7.30e-2) + | 3.9880e-1 (1.07e-2) |
| 1/8/0 | 1/8/0 | 2/5/2 | 2/5/2 | 1/8/0 | 0/9/0 | 1/7/1 |
| Problem | BiCo | CTAEA | CAEAD | ICMA | PPS | ToP | TriP | CMOCPA |
|---|---|---|---|---|---|---|---|---|
| DASCMOP1 | 1.0656e-2 (7.27e-3) − | 1.6840e-1 (3.89e-3) − | 2.1253e-1 (3.09e-4) − | 2.1249e-1 (2.51e-4) − | 1.7009e-1 (4.78e-2) − | 1.2917e-2 (3.86e-2) − | 1.6002e-1 (4.66e-2) − | 2.1278e-1 (3.34e-4) |
| DASCMOP2 | 2.5508e-1 (3.92e-3) − | 3.0983e-1 (1.26e-2) − | 3.5530e-1 (9.54e-5) + | 3.5554e-1 (4.64e-5) + | 3.5483e-1 (9.92e-5) − | 1.5024e-1 (1.11e-1) − | 3.5514e-1 (7.22e-5) − | 3.5519e-1 (8.41e-5) |
| DASCMOP3 | 2.1854e-1 (1.15e-2) − | 2.6212e-1 (4.00e-3) − | 3.1239e-1 (7.32e-5) + | 3.1228e-1 (1.98e-4) ≈ | 2.2503e-1 (3.39e-2) − | 3.5027e-2 (4.83e-2) − | 2.3708e-1 (4.05e-2) − | 3.1227e-1 (7.73e-5) |
| DASCMOP4 | 2.0413e-1 (3.72e-4) − | 1.9675e-1 (4.02e-3) − | 2.0349e-1 (3.80e-4) − | 2.0378e-1 (2.07e-4) − | 1.7059e-1 (2.52e-2) − | NaN (NaN) − | 2.0398e-1 (2.36e-4) − | 2.0424e-1 (1.15e-4) |
| DASCMOP5 | 3.5155e-1 (7.62e-4) + | 3.4841e-1 (3.47e-4) − | 3.1045e-1 (1.04e-1) − | 3.5117e-1 (9.21e-5) − | 3.5111e-1 (2.16e-4) − | NaN (NaN) − | 3.5092e-1 (5.00e-4) − | 3.5154e-1 (8.92e-5) |
| DASCMOP6 | 2.9357e-1 (5.30e-2) − | 3.0889e-1 (3.32e-3) − | 2.8328e-1 (8.17e-2) − | 3.1236e-1 (3.22e-4) ≈ | 2.5075e-1 (1.14e-1) − | NaN (NaN) − | 3.1222e-1 (3.18e-4) − | 3.1244e-1 (1.03e-4) |
| DASCMOP7 | 2.8785e-1 (4.88e-4) ≈ | 2.8779e-1 (1.74e-4) − | 2.8060e-1 (1.03e-2) − | 2.8782e-1 (3.85e-4) ≈ | 2.7840e-1 (6.51e-3) − | NaN (NaN) − | 2.8478e-1 (7.51e-4) − | 2.8796e-1 (2.79e-4) |
| DASCMOP8 | 2.0671e-1 (5.31e-4) ≈ | 2.0321e-1 (2.04e-3) − | 1.9222e-1 (3.95e-2) − | 2.0747e-1 (2.50e-4) + | 2.0051e-1 (1.65e-3) − | NaN (NaN) − | 2.0400e-1 (8.52e-4) − | 2.0654e-1 (3.66e-4) |
| DASCMOP9 | 1.3765e-1 (9.72e-3) + | 1.5234e-1 (1.55e-2) + | 2.0490e-1 (4.52e-4) + | 2.0750e-1 (1.82e-4) + | 1.7760e-1 (2.63e-2) + | 8.6488e-2 (3.73e-2) − | 1.7815e-1 (2.13e-2) + | 1.2667e-1 (3.47e-3) |
| 2/5/2 | 1/8/0 | 3/6/0 | 3/3/3 | 1/8/0 | 0/9/0 | 1/8/0 |
| Problem | MOEAD | eMOEA | MOPSO | NSGAII | SPEA2 | KnEA | GrEA | CMOCPA |
|---|---|---|---|---|---|---|---|---|
| ZDT1 | 5.0328e-3 (1.04e-3) − | 2.8606e-2 (1.82e-3) − | 1.6802e+0 (9.47e-2) − | 4.7933e-3 (2.19e-4) − | 3.9617e-3 (7.27e-5) − | 1.6000e-1 (8.99e-2) − | 7.7519e-3 (2.03e-3) − | 3.8891e-3 (7.68e-5) |
| ZDT2 | 5.8825e-3 (9.54e-4) − | 3.0931e-2 (3.38e-3) − | 3.1778e+0 (1.64e-1) − | 4.8971e-3 (2.04e-4) − | 3.9216e-3 (4.55e-5) − | 9.4728e-2 (2.16e-2) − | 7.9482e-3 (1.44e-4) − | 3.8472e-3 (4.65e-5) |
| ZDT3 | 1.4930e-2 (6.44e-3) − | 6.6691e-2 (1.16e-2) − | 1.1959e+0 (7.17e-2) − | 6.3819e-3 (5.33e-3) − | 4.9250e-3 (1.08e-4) − | 1.0725e-2 (5.43e-3) − | 1.3962e-2 (9.57e-4) − | 4.8095e-3 (8.46e-5) |
| ZDT4 | 7.4937e-3 (2.13e-3) − | 2.8669e-2 (1.79e-3) − | 1.3118e+1 (5.26e+0) − | 4.8101e-3 (4.12e-4) − | 4.0406e-3 (2.35e-4) + | 2.5345e-1 (9.47e-2) − | 3.3221e-1 (1.42e-1) − | 4.2835e-3 (3.62e-4) |
| ZDT6 | 4.6155e-3 (5.88e-4) − | 2.9127e-2 (1.43e-3) − | 5.5098e+0 (4.97e-1) − | 3.6581e-3 (9.10e-5) − | 3.0849e-3 (2.45e-5) − | 7.2564e-3 (1.77e-3) − | 6.0337e-3 (9.05e-5) − | 3.0663e-3 (3.14e-5) |
| DTLZ1 | 2.0639e-2 (7.92e-5) − | 3.6655e-2 (2.28e-3) − | 1.5378e+0 (1.01e+0) − | 2.6598e-2 (1.03e-3) − | 2.0254e-2 (2.38e-4) ≈ | 5.2936e-2 (2.87e-2) − | 9.0384e-2 (7.49e-2) − | 2.0306e-2 (2.48e-4) |
| DTLZ2 | 5.4464e-2 (4.51e-7) − | 6.4801e-2 (1.33e-3) − | 1.5407e-1 (3.38e-2) − | 6.9652e-2 (2.37e-3) − | 5.4266e-2 (5.08e-4) − | 6.6606e-2 (3.09e-3) − | 6.3790e-2 (5.49e-4) − | 5.3337e-2 (3.36e-4) |
| DTLZ3 | 5.9931e-2 (5.59e-3) + | 1.3317e-1 (1.99e-1) ≈ | 1.4438e+1 (6.98e+0) − | 7.1776e-2 (4.07e-3) ≈ | 5.6580e-2 (2.43e-3) + | 9.6273e-2 (2.15e-2) + | 1.7125e-1 (1.41e-1) ≈ | 2.9649e-1 (4.96e-1) |
| DTLZ4 | 2.7931e-1 (2.71e-1) − | 2.5799e-1 (2.65e-1) − | 2.6746e-1 (1.92e-1) − | 9.6517e-2 (1.60e-1) + | 2.7599e-1 (2.93e-1) − | 1.2482e-1 (2.23e-1) − | 1.3005e-1 (1.65e-1) − | 1.1868e-1 (1.68e-1) |
| DTLZ5 | 3.3860e-2 (2.79e-5) − | 6.8262e-2 (4.12e-3) − | 9.0944e-3 (1.13e-3) − | 5.8083e-3 (2.78e-4) − | 4.4163e-3 (1.16e-4) − | 9.2901e-3 (1.27e-3) − | 2.1806e-2 (1.11e-3) − | 4.2786e-3 (1.17e-4) |
| DTLZ6 | 3.3911e-2 (1.26e-5) − | 6.2350e-2 (2.03e-3) − | 9.2118e+0 (6.70e-2) − | 5.8309e-3 (3.81e-4) − | 4.0878e-3 (3.84e-5) − | 1.2456e-2 (6.70e-3) − | 2.2303e-2 (9.19e-5) − | 4.0298e-3 (2.55e-5) |
| DTLZ7 | 1.9844e-1 (1.64e-1) − | 2.2912e-1 (1.90e-1) − | 6.5150e+0 (8.39e-1) − | 7.6159e-2 (4.40e-3) − | 6.9672e-2 (5.21e-2) ≈ | 7.4722e-2 (5.24e-2) − | 9.2857e-2 (5.53e-2) − | 5.9811e-2 (1.27e-3) |
| 1/11/0 | 0/11/1 | 0/12/0 | 1/10/1 | 2/8/2 | 1/11/0 | 0/11/1 |
| Problem | MOEAD | eMOEA | MOPSO | NSGAII | SPEA2 | KnEA | GrEA | CMOCPA |
|---|---|---|---|---|---|---|---|---|
| ZDT1 | 7.1781e-1 (1.33e-3) − | 6.8614e-1 (3.32e-3) − | 0.0000e+0 (0.00e+0) − | 7.1920e-1 (2.73e-4) − | 7.2028e-1 (1.27e-4) − | 6.2622e-1 (5.17e-2) − | 7.1514e-1 (2.02e-3) − | 7.2035e-1 (1.18e-4) |
| ZDT2 | 4.4031e-1 (2.06e-3) − | 4.1083e-1 (3.17e-3) − | 0.0000e+0 (0.00e+0) − | 4.4398e-1 (2.26e-4) − | 4.4497e-1 (8.60e-5) ≈ | 3.5749e-1 (1.87e-2) − | 4.4153e-1 (5.66e-5) − | 4.4500e-1 (9.56e-5) |
| ZDT3 | 6.0068e-1 (1.76e-2) ≈ | 5.8614e-1 (2.92e-2) − | 4.4309e-4 (1.19e-3) − | 6.0236e-1 (1.62e-2) + | 5.9960e-1 (5.83e-5) − | 6.0128e-1 (1.62e-2) + | 5.9728e-1 (3.68e-4) − | 5.9964e-1 (6.12e-5) |
| ZDT4 | 7.1281e-1 (3.03e-3) − | 6.8414e-1 (4.70e-3) − | 0.0000e+0 (0.00e+0) − | 7.1866e-1 (1.03e-3) ≈ | 7.1956e-1 (7.55e-4) + | 5.6968e-1 (5.82e-2) − | 5.1348e-1 (9.92e-2) − | 7.1893e-1 (8.80e-4) |
| ZDT6 | 3.8551e-1 (1.00e-3) − | 3.5878e-1 (2.06e-3) − | 0.0000e+0 (0.00e+0) − | 3.8830e-1 (1.06e-4) − | 3.8888e-1 (4.50e-5) + | 3.8476e-1 (1.74e-3) − | 3.8599e-1 (9.16e-5) − | 3.8876e-1 (1.32e-4) |
| DTLZ1 | 8.4079e-1 (7.47e-4) ≈ | 7.2735e-1 (1.70e-2) − | 3.3631e-4 (1.84e-3) − | 8.2427e-1 (3.39e-3) − | 8.4138e-1 (1.40e-3) + | 7.4896e-1 (5.46e-2) − | 6.7294e-1 (1.42e-1) − | 8.4024e-1 (1.43e-3) |
| DTLZ2 | 5.5961e-1 (5.00e-6) + | 5.4650e-1 (2.54e-3) − | 4.1184e-1 (2.92e-2) − | 5.3141e-1 (4.33e-3) − | 5.5504e-1 (8.65e-4) − | 5.4381e-1 (3.60e-3) − | 5.5845e-1 (5.77e-4) + | 5.5764e-1 (1.22e-3) |
| DTLZ3 | 5.3562e-1 (1.76e-2) + | 4.7263e-1 (1.20e-1) ≈ | 0.0000e+0 (0.00e+0) − | 5.1877e-1 (1.37e-2) ≈ | 5.4425e-1 (7.96e-3) + | 4.9667e-1 (2.72e-2) ≈ | 4.5856e-1 (1.10e-1) ≈ | 4.0698e-1 (2.08e-1) |
| DTLZ4 | 4.5608e-1 (1.27e-1) ≈ | 4.5492e-1 (1.34e-1) − | 3.1868e-1 (7.29e-2) − | 5.2074e-1 (8.13e-2) − | 4.5444e-1 (1.39e-1) − | 5.1446e-1 (1.15e-1) − | 5.2844e-1 (7.88e-2) − | 5.2970e-1 (7.28e-2) |
| DTLZ5 | 1.8188e-1 (1.51e-5) − | 1.6809e-1 (1.83e-3) − | 1.9392e-1 (2.90e-3) − | 1.9912e-1 (1.91e-4) − | 1.9954e-1 (1.49e-4) − | 1.9408e-1 (1.39e-3) − | 1.8813e-1 (4.94e-4) − | 1.9977e-1 (1.13e-4) |
| DTLZ6 | 1.8185e-1 (6.54e-6) − | 1.7722e-1 (6.68e-4) − | 0.0000e+0 (0.00e+0) − | 1.9945e-1 (1.53e-4) − | 2.0006e-1 (4.95e-5) − | 1.9229e-1 (5.94e-3) − | 1.8765e-1 (2.83e-5) − | 2.0010e-1 (3.57e-5) |
| DTLZ7 | 2.5236e-1 (1.36e-2) − | 2.4692e-1 (2.12e-2) − | 0.0000e+0 (0.00e+0) − | 2.6839e-1 (1.90e-3) − | 2.7575e-1 (6.22e-3) − | 2.7673e-1 (7.07e-3) − | 2.7036e-1 (7.10e-3) − | 2.7737e-1 (7.87e-4) |
| 2/7/3 | 0/11/1 | 0/12/0 | 1/9/2 | 4/7/1 | 1/10/1 | 1/10/1 |
| Problem | MOEAD | eMOEA | MOPSO | NSGAII | SPEA2 | KnEA | GrEA | CMOCPA |
|---|---|---|---|---|---|---|---|---|
| RWMOP1 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 3.5961e+5 (8.69e+1) ≈ | NaN (NaN)− | 4.8572e+5 (2.15e+5) − | NaN (NaN)− | 3.5990e+5 (8.16e+2) |
| RWMOP2 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 5.4112e+1 (3.17e+1) ≈ | NaN (NaN)− | 5.6426e+1 (3.13e+1) ≈ | NaN (NaN)− | 6.1584e+1 (2.91e+1) |
| RWMOP3 | NaN (NaN)− | 3.7831e+4 (0.00e+0) ≈ | 9.9252e+14 (5.36e+15) − | 2.2125e+2 (3.47e+2) + | NaN (NaN)− | 1.4399e+4 (5.80e+3) − | NaN (NaN)− | 1.2378e+3 (1.15e+3) |
| RWMOP4 | NaN (NaN)− | NaN (NaN)− | 2.4187e+4 (6.09e+4) − | 1.2702e+0 (1.01e-1) + | NaN (NaN)− | 7.4940e+0 (2.95e+0) − | NaN (NaN)− | 1.3552e+0 (1.36e-2) |
| RWMOP5 | NaN (NaN)− | 1.8879e+0 (3.85e-3) + | NaN (NaN)− | 1.8882e+0 (4.11e-4) − | 1.8882e+0 (5.89e-5) − | 2.7303e+0 (3.24e-1) − | 1.8884e+0 (2.38e-4) − | 1.8881e+0 (1.31e-4) |
| RWMOP6 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 6.9699e+2 (3.01e+2) − | NaN (NaN) | 2.2970e+3 (8.40e+2) − | NaN (NaN)− | 6.0571e+2 (1.00e+0) |
| RWMOP7 | 1.5430e+1 (1.36e-1) − | 1.4185e+1 (1.37e+0) ≈ | 2.4624e+1 (1.15e+1) − | 1.3810e+1 (3.03e+0) ≈ | 1.4086e+1 (2.87e+0) ≈ | 1.5318e+1 (3.89e-1) − | 1.4800e+1 (6.98e-1) − | 1.2785e+1 (3.59e+0) |
| RWMOP8 | NaN (NaN)− | 2.6709e+1 (1.61e+1) − | 1.2085e+1 (1.26e+1) − | 2.1298e+0 (1.89e-4) − | 2.1235e+0 (3.50e-2) ≈ | 1.6635e+1 (1.45e+1) − | 6.0661e+0 (4.50e+0) − | 2.1098e+0 (3.05e-2) |
| RWMOP9 | 1.6484e+3 (3.49e-2) − | 3.8763e-2 (6.37e-3) − | 9.9729e+13 (3.62e+14) − | 3.7239e-2 (1.41e-17) ≈ | 3.7239e-2 (1.98e-12) ≈ | 5.8747e+2 (1.22e+2) − | 2.5868e+2 (8.81e+1) − | 3.7239e-2 (1.41e-17) |
| RWMOP10 | 1.5861e+2 (9.63e-5) − | 1.6677e-3 (2.04e-3) ≈ | 1.9116e+44 (1.03e+45) − | 7.5315e-3 (7.66e-3) ≈ | 5.9892e-3 (4.16e-3) ≈ | 8.2014e+0 (3.77e+0) − | 1.2891e+2 (1.55e+1) − | 5.5261e-3 (7.46e-3) |
| RWMOP11 | 3.7069e+6 (8.20e+2) − | 2.5043e+6 (9.02e+3) − | 1.1797e+7 (1.38e+7) − | 2.4589e+6 (4.09e+4) − | 2.4906e+6 (2.35e+5) − | 2.4559e+6 (5.11e+4) − | 2.5608e+6 (3.70e+4) − | 2.3088e+6 (7.19e+4) |
| RWMOP12 | NaN (NaN)− | 4.5903e+1 (0.00e+0) ≈ | 8.7901e+2 (9.82e+2) − | 3.7516e+0 (2.45e+0) − | 2.5646e+0 (1.64e+0) ≈ | 1.3507e+0 (7.96e-1) + | NaN (NaN)− | 2.0109e+0 (1.12e+0) |
| RWMOP13 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 4.5851e+2 (6.80e+1) − | NaN (NaN)− | 8.0857e+2 (9.97e+1) − | NaN (NaN)− | 3.8510e+2 (1.99e+1) |
| RWMOP14 | NaN (NaN)− | 1.2264e-2 (5.87e-4) − | 1.8289e+3 (0.00e+0) − | 1.2137e-2 (2.12e-14) ≈ | 1.2137e-2 (2.35e-12) ≈ | 6.5289e-1 (5.18e-2) − | NaN (NaN)− | 1.2137e-2 (3.53e-18) |
| RWMOP15 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 4.3236e+3 (4.14e+3) − | NaN (NaN)− | 2.9551e+4 (1.67e+4) − | NaN (NaN)− | 5.7265e+2 (8.93e+2) |
| RWMOP16 | NaN (NaN)− | 1.9989e-3 (1.32e-18) ≈ | 2.0269e+6 (7.98e+6) − | 1.9989e-3 (1.32e-18) ≈ | 1.9989e-3 (1.32e-18) ≈ | 5.9503e-2 (4.32e-2) − | 2.4842e+0 (1.13e-1) − | 1.9989e-3 (1.32e-18) |
| RWMOP17 | 4.4783e+9 (3.75e+9) − | NaN (NaN)− | 8.1597e+3 (5.52e+2) − | 5.1163e+3 (2.79e+2) − | NaN (NaN)− | 1.1209e+4 (1.84e+3) − | NaN (NaN)− | 4.6960e+3 (1.53e+2) |
| RWMOP18 | 9.4571e-2 (3.59e-6) − | 1.0726e-1 (1.89e-2) − | NaN (NaN)− | 9.4283e-2 (2.02e-4) + | 9.4458e-2 (1.25e-4) ≈ | 9.4784e-2 (8.18e-4) ≈ | 9.4414e-2 (2.61e-4) ≈ | 9.4514e-2 (8.82e-5) |
| RWMOP19 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 7.7965e+4 (2.50e+4) − | NaN (NaN)− | 1.3088e+5 (8.95e+3) − | NaN (NaN)− | 3.8623e+4 (1.01e+4) |
| RWMOP20 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 1.9764e+3 (2.05e+2) + | NaN (NaN)− | 1.9680e+3 (2.24e+2) + | NaN (NaN)− | 2.0864e+3 (1.73e+2) |
| RWMOP21 | 6.6237e+0 (3.95e-3) − | 1.4326e-1 (2.92e-1) − | 4.9022e+0 (6.43e+0) − | 1.3186e-1 (2.36e-1) − | 7.0673e-2 (1.25e-1) ≈ | 2.4790e+0 (3.75e-1) − | 4.4463e-1 (3.76e-1) − | 1.6050e-2 (7.06e-18) |
| 0/21/0 | 1/15/5 | 0/21/0 | 4/10/7 | 0/12/9 | 2/17/2 | 0/20/1 |
| Problem | MOEAD | eMOEA | MOPSO | NSGAII | SPEA2 | KnEA | GrEA | CMOCPA |
|---|---|---|---|---|---|---|---|---|
| RWMOP1 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 6.0523e-1 (4.27e-4) − | NaN (NaN)− | 5.9323e-1 (1.41e-2) − | NaN (NaN)− | 6.0766e-1 (3.43e-4) |
| RWMOP2 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 2.2625e-1 (1.49e-1) ≈ | NaN (NaN)− | 2.3799e-1 (1.43e-1) ≈ | NaN (NaN)− | 2.4536e-1 (1.52e-1) |
| RWMOP3 | NaN (NaN)− | 4.0552e-1 (0.00e+0) ≈ | 8.9848e-1 (2.44e-1) − | 9.0206e-1 (1.68e-4) + | NaN (NaN)− | 8.3815e-1 (4.08e-2) − | NaN (NaN)− | 9.0010e-1 (5.88e-4) |
| RWMOP4 | NaN (NaN)− | NaN (NaN)− | 8.8056e-1 (3.06e-1) + | 8.5888e-1 (3.41e-3) + | NaN (NaN)− | 7.6779e-1 (2.96e-2) − | NaN (NaN)− | 8.5619e-1 (1.49e-3) |
| RWMOP5 | NaN (NaN−) | 2.4936e-1 (1.38e-3) − | NaN (NaN)− | 4.3356e-1 (1.14e-3) ≈ | 2.7321e-1 (2.58e-3) − | 3.9767e-1 (1.27e-2) − | 2.7424e-1 (1.05e-3) − | 4.3417e-1 (1.80e-4) |
| RWMOP6 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 2.7715e-1 (5.39e-5) + | NaN (NaN)− | 2.4092e-1 (3.09e-2) − | NaN (NaN)− | 2.7482e-1 (1.07e-3) |
| RWMOP7 | 4.7784e-1 (3.64e-3) − | 4.8285e-1 (6.94e-4) − | 7.5277e-1 (1.72e-1) + | 4.8398e-1 (6.83e-5) − | 4.8285e-1 (1.92e-4) − | 4.8218e-1 (9.93e-4) − | 4.8178e-1 (4.08e-4) − | 4.8442e-1 (7.98e-5) |
| RWMOP8 | NaN (NaN)− | 2.1196e-2 (2.09e-3) − | 4.0212e-2 (1.46e-2) + | 2.5879e-2 (1.04e-4) ≈ | 2.3654e-2 (4.28e-4) − | 2.5050e-2 (5.47e-4) − | 2.2567e-2 (3.27e-4) − | 2.5794e-2 (1.85e-4) |
| RWMOP9 | 5.3068e-2 (5.05e-5) − | 2.5125e-1 (5.21e-2) − | 6.1315e-1 (1.80e-1) + | 4.0902e-1 (1.49e-4) − | 4.0947e-1 (1.13e-4) ≈ | 3.6925e-1 (8.76e-3) − | 4.0115e-1 (2.42e-3) − | 4.0950e-1 (1.19e-4) |
| RWMOP10 | 7.9369e-2 (6.24e-4) − | 5.7450e-1 (2.29e-1) − | 6.5537e-1 (2.93e-1) ≈ | 8.4728e-1 (2.23e-4) + | 8.4208e-1 (1.28e-3) ≈ | 8.2504e-1 (1.10e-2) − | 8.3621e-1 (5.73e-3) − | 8.4218e-1 (1.23e-3) |
| RWMOP11 | 5.7358e-2 (9.23e-4) − | 1.0791e-1 (1.96e-4) + | 6.7100e-3 (1.43e-2) − | 9.4453e-2 (1.33e-3) + | 6.1777e-2 (9.98e-3) − | 9.7678e-2 (1.22e-3) + | 8.4401e-2 (4.47e-3) − | 9.2711e-2 (2.09e-3) |
| RWMOP12 | NaN (NaN)− | 0.0000e+0 (0.00e+0) ≈ | 5.9992e-1 (2.70e-1) ≈ | 5.5982e-1 (3.88e-4) + | 5.3842e-1 (7.14e-3) − | 5.2949e-1 (6.15e-3) − | NaN (NaN) | 5.5653e-1 (1.25e-3) |
| RWMOP13 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 8.7936e-2 (1.04e-4) + | NaN (NaN)− | 8.7546e-2 (3.07e-4) ≈ | NaN (NaN)− | 8.7523e-2 (1.18e-4) |
| RWMOP14 | NaN (NaN)− | 1.4558e-1 (7.25e-2) − | 9.9956e-1 (0.00e+0) ≈ | 6.1748e-1 (1.31e-3) + | 3.4771e-1 (2.64e-3) − | 5.9485e-1 (9.49e-3) − | NaN (NaN)− | 6.1463e-1 (7.00e-4) |
| RWMOP15 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 5.4143e-1 (1.33e-3) − | NaN (NaN)− | 4.8584e-1 (2.84e-2) − | NaN (NaN)− | 5.4226e-1 (1.81e-4) |
| RWMOP16 | NaN (NaN)− | 3.4033e-1 (1.67e-1) − | 3.3888e-1 (3.36e-1) − | 7.6373e-1 (1.45e-4) + | 7.6167e-1 (3.80e-4) − | 7.6174e-1 (1.31e-3) − | 3.5934e-1 (1.44e-1) − | 7.6251e-1 (1.86e-4) |
| RWMOP17 | 2.0615e-1 (1.35e-1) ≈ | NaN (NaN)− | 6.1754e-1 (2.31e-2) + | 2.6369e-1 (9.01e-3) − | NaN (NaN)− | 4.3461e-1 (1.12e+0) + | NaN (NaN)− | 2.6714e-1 (9.74e-3) |
| RWMOP18 | 4.0246e-2 (3.71e-5) − | 2.9443e-2 (2.75e-3) − | NaN (NaN)− | 4.0493e-2 (4.44e-6) − | 4.0401e-2 (5.19e-5) − | 3.8136e-2 (7.82e-4) − | 4.0234e-2 (9.59e-5) − | 4.0509e-2 (4.24e-6) |
| RWMOP19 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 3.3547e-1 (9.62e-3) − | NaN (NaN)− | 2.8196e-1 (1.97e-2) − | NaN (NaN)− | 3.6157e-1 (2.88e-3) |
| RWMOP20 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 0.0000e+0 (0.00e+0) ≈ | NaN (NaN)− | 0.0000e+0 (0.00e+0) ≈ | NaN (NaN)− | 0.0000e+0 (0.00e+0) |
| RWMOP21 | 2.9319e-2 (3.47e-6) − | 3.0724e-2 (6.57e-4) − | 6.6135e-2 (1.59e-2) + | 3.1741e-2 (2.10e-5) − | 3.1721e-2 (1.59e-4) − | 2.5192e-2 (8.29e-4) − | 3.1485e-2 (3.69e-4) − | 3.1761e-2 (7.50e-7) |
| 0/20/1 | 1/18/2 | 6/12/3 | 9/8/4 | 0/19/2 | 2/16/3 | 0/21/0 |
| Problem | MOEAD | eMOEA | MOPSO | NSGAII | SPEA2 | KnEA | GrEA | CMOCPA |
|---|---|---|---|---|---|---|---|---|
| RWMOP22 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 1.7024e+3 (3.64e+2) |
| RWMOP23 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 1.2492e+0 (7.02e-1) ≈ | NaN (NaN)− | 1.0692e+0 (5.86e-1) ≈ | NaN (NaN)− | 8.8150e-1 (4.90e-1) |
| RWMOP24 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 1.7997e+4 (6.57e+4) |
| 0/3/0 | 0/3/0 | 0/3/0 | 0/2/1 | 0/3/0 | 0/2/1 | 0/3/0 |
| Problem | MOEAD | eMOEA | MOPSO | NSGAII | SPEA2 | KnEA | GrEA | CMOCPA |
|---|---|---|---|---|---|---|---|---|
| RWMOP22 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 8.2709e-1 (2.16e-1) |
| RWMOP23 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 3.6105e-1 (1.72e-1) ≈ | NaN (NaN)− | 3.1904e-1 (1.43e-1) ≈ | NaN (NaN)− | 2.6831e-1 (1.29e-1) |
| RWMOP24 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | NaN (NaN) | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 4.2171e-1 (4.37e-1) |
| 0/3/0 | 0/3/0 | 0/3/0 | 0/2/1 | 0/3/0 | 0/2/1 | 0/3/0 |
| Problem | MOEAD | eMOEA | MOPSO | NSGAII | SPEA2 | KnEA | GrEA | CMOCPA |
|---|---|---|---|---|---|---|---|---|
| RWMOP25 | 8.0323e-1 (1.17e-1) − | 7.4475e-1 (5.58e-4) − | 6.2586e+2 (1.19e+3) − | 7.4391e-1 (9.77e-5) ≈ | 7.4408e-1 (2.09e-4) − | 7.4388e-1 (3.03e-5) ≈ | 7.4389e-1 (7.73e-7) − | 7.4388e-1 (1.90e-5) |
| RWMOP26 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 2.6894e-1 (2.97e-2) − | NaN (NaN)− | 2.8814e-1 (4.48e-2) − | NaN (NaN)− | 2.4734e-1 (1.45e-4) |
| RWMOP27 | 1.0629e+0 (7.93e-2) − | 1.0306e+0 (7.22e-2) − | 1.7992e+0 (9.59e-2) − | 9.9000e-1 (1.90e-5) − | 1.0138e+0 (4.90e-2) − | 9.9000e-1 (5.11e-5) ≈ | 1.0452e+0 (3.53e-2) − | 9.8997e-1 (1.36e-4) |
| RWMOP28 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 8.8494e+0 (0.00e+0) |
| RWMOP29 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 9.4792e+0 (6.64e-1) ≈ | NaN (NaN)− | 9.7243e+0 (9.16e-1) ≈ | NaN (NaN)− | 9.2095e+0 (1.07e-1) |
| 0/5/0 | 0/5/0 | 0/5/0 | 0/3/2 | 0/5/0 | 0/2/3 | 0/5/0 |
| Problem | MOEAD | eMOEA | MOPSO | NSGAII | SPEA2 | KnEA | GrEA | CMOCPA |
|---|---|---|---|---|---|---|---|---|
| RWMOP25 | 2.6578e-1 (6.93e-2) + | 2.2908e-1 (2.17e-3) − | 9.9924e-1 (3.46e-3) + | 2.4107e-1 (6.17e-5) − | 2.3465e-1 (1.08e-3) − | 2.4096e-1 (2.58e-4) − | 2.3126e-1 (2.20e-5) − | 2.4150e-1 (1.09e-5) |
| RWMOP26 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 1.4281e-1 (2.31e-2) ≈ | NaN (NaN)− | 1.3589e-1 (2.77e-2) − | NaN (NaN)− | 1.4605e-1 (4.41e-3) |
| RWMOP27 | 4.3841e+1 (5.17e+1) − | 2.6239e+10 (1.03e+11) ≈ | 6.6799e+0 (4.14e-1) − | 1.8438e+10 (4.67e+10) + | 3.8284e+9 (1.73e+10) + | 2.1712e+11 (1.17e+12) + | 3.3008e+1 (3.04e+1) − | 1.2478e+9 (5.86e+9) |
| RWMOP28 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 1.6667e-2 (0.00e+0) |
| RWMOP29 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 7.5346e-1 (5.86e-2) ≈ | NaN (NaN)− | 7.4404e-1 (6.86e-2) − | NaN (NaN)− | 7.8077e-1 (2.47e-3) |
| 1/4/0 | 0/4/1 | 1/4/0 | 1/2/2 | 1/4/0 | 1/4/0 | 0/5/0 |
| Problem | MOEAD | eMOEA | MOPSO | NSGAII | SPEA2 | KnEA | GrEA | CMOCPA |
|---|---|---|---|---|---|---|---|---|
| RWMOP30 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 1.2752e-1 (2.88e-2) ≈ | NaN (NaN)− | 1.6247e-1 (3.73e-2) − | NaN (NaN)− | 1.1106e-1 (3.92e-2) |
| RWMOP31 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 1.7148e-1 (1.14e-1) ≈ | NaN (NaN)− | 1.9880e-1 (1.65e-1) ≈ | NaN (NaN)− | 1.5409e-1 (1.27e-1) |
| RWMOP32 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 2.6653e-1 (1.00e-1) ≈ | NaN (NaN)− | 3.6026e-1 (1.55e-1) − | NaN (NaN)− | 1.6997e-1 (1.15e-1) |
| RWMOP33 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 2.1002e+0 (7.05e-1) ≈ | NaN (NaN)− | 2.1525e+0 (8.35e-1) ≈ | NaN (NaN)− | 3.0123e+0 (3.65e-1) |
| RWMOP34 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 1.6020e+0 (8.63e-1) ≈ | NaN (NaN)− | 1.5357e+0 (8.71e-1) ≈ | NaN (NaN)− | 3.0357e+0 (1.14e+0) |
| RWMOP35 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 4.2593e+0 (1.57e+0) ≈ | NaN (NaN)− | 4.7182e+0 (1.74e+0) − | NaN (NaN)− | 2.7377e+0 (1.14e+0) |
| 0/6/0 | 0/6/0 | 0/6/0 | 0/0/6 | 0/6/0 | 0/3/3 | 0/6/0 |
| Problem | MOEAD | eMOEA | MOPSO | NSGAII | SPEA2 | KnEA | GrEA | CMOCPA |
|---|---|---|---|---|---|---|---|---|
| RWMOP30 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 5.7608e-1 (1.18e-1) ≈ | NaN (NaN)− | 5.6748e-1 (1.05e-1) ≈ | NaN (NaN)− | 4.8258e-1 (2.16e-1) |
| RWMOP31 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 4.9581e-1 (2.99e-1) ≈ | NaN (NaN)− | 4.3421e-1 (2.71e-1) ≈ | NaN (NaN)− | 3.1568e-1 (3.25e-1) |
| RWMOP32 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 7.2496e-1 (1.06e-1) + | NaN (NaN) | 6.6083e-1 (1.92e-1) + | NaN (NaN) | 4.0098e-1 (3.12e-1) |
| RWMOP33 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 0.0000e+0 (0.00e+0) ≈ | NaN (NaN)− | 0.0000e+0 (0.00e+0) ≈ | NaN (NaN)− | 0.0000e+0 (0.00e+0) |
| RWMOP34 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 0.0000e+0 (0.00e+0) ≈ | NaN (NaN)− | 0.0000e+0 (0.00e+0) ≈ | NaN (NaN)− | 0.0000e+0 (0.00e+0) |
| RWMOP35 | NaN (NaN)− | NaN (NaN)− | NaN (NaN)− | 4.6596e-1 (1.49e-1) + | NaN (NaN)− | 4.8053e-1 (1.21e-1) + | NaN (NaN)− | 3.2464e-1 (1.62e-1) |
| 0/6/0 | 0/6/0 | 0/6/0 | 2/0/4 | 0/6/0 | 2/0/4 | 0/6/0 |
| Problem | MOEAD | eMOEA | MOPSO | NSGAII | SPEA2 | KnEA | GrEA | CMOCPA |
|---|---|---|---|---|---|---|---|---|
| RWMOP36 | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ |
| RWMOP37 | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ |
| RWMOP38 | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ |
| RWMOP39 | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ |
| RWMOP40 | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ |
| RWMOP41 | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ |
| RWMOP42 | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ |
| RWMOP43 | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ |
| RWMOP44 | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ |
| RWMOP45 | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ |
| RWMOP46 | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ |
| RWMOP47 | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ |
| RWMOP48 | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ | NaN (NaN) ≈ |
| RWMOP49 | NaN (NaN) − | NaN (NaN) − | NaN (NaN) − | NaN (NaN) − | NaN (NaN) − | NaN (NaN) − | NaN (NaN) − | 2.8979e+0 (2.70e+0) |
| RWMOP50 | NaN (NaN) − | NaN (NaN) − | NaN (NaN) − | 1.1224e+3 (6.88e+2) ≈ | NaN (NaN) − | 1.4319e+3 (9.11e+2) ≈ | NaN (NaN) − | 9.9820e+2 (4.11e+2) |
| 0/2/13 | 0/2/13 | 0/2/13 | 0/1/14 | 0/2/13 | 0/1/14 | 0/2/13 |
| Problem | MOEAD | eMOEA | MOPSO | NSGAII | SPEA2 | KnEA | GrEA | CMOCPA |
|---|---|---|---|---|---|---|---|---|
| RWMOP37 | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ |
| RWMOP38 | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ |
| RWMOP39 | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ |
| RWMOP40 | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ |
| RWMOP41 | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ |
| RWMOP42 | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ |
| RWMOP43 | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ |
| RWMOP44 | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ |
| RWMOP45 | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ |
| RWMOP46 | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ |
| RWMOP47 | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ |
| RWMOP48 | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ | (NaN) ≈ |
| RWMOP49 | (NaN) − | (NaN) − | (NaN) − | (NaN) − | (NaN) − | (NaN) − | (NaN) − | 0.0000e+0 (0.00e+0) |
| RWMOP50 | (NaN) − | (NaN) − | (NaN) − | 1.1690e-2 (6.20e-4) ≈ | (NaN) − | 1.1492e-2 (5.81e-4) ≈ | (NaN) ≈ | 1.1622e-2 (9.08e-4) |
| 0/2/13 | 0/2/13 | 0/2/13 | 0/1/14 | 0/2/13 | 0/1/14 | 0/2/13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Zhang, C. A Multi-Objective Carnivorous Plant Algorithm for Solving Constrained Multi-Objective Optimization Problems. Biomimetics 2023, 8, 136. https://doi.org/10.3390/biomimetics8020136
Yang Y, Zhang C. A Multi-Objective Carnivorous Plant Algorithm for Solving Constrained Multi-Objective Optimization Problems. Biomimetics. 2023; 8(2):136. https://doi.org/10.3390/biomimetics8020136
Chicago/Turabian StyleYang, Yufei, and Changsheng Zhang. 2023. "A Multi-Objective Carnivorous Plant Algorithm for Solving Constrained Multi-Objective Optimization Problems" Biomimetics 8, no. 2: 136. https://doi.org/10.3390/biomimetics8020136
APA StyleYang, Y., & Zhang, C. (2023). A Multi-Objective Carnivorous Plant Algorithm for Solving Constrained Multi-Objective Optimization Problems. Biomimetics, 8(2), 136. https://doi.org/10.3390/biomimetics8020136





