A Hybrid Ensemble Equilibrium Optimizer Gene Selection Algorithm for Microarray Data
Abstract
1. Introduction
2. Methodology
2.1. Filtering Methods
2.1.1. Fisher Score
2.1.2. ReliefF
2.1.3. Chi-Square
2.1.4. Pearson Correlation Coefficient
2.1.5. Neighborhood Component Analysis
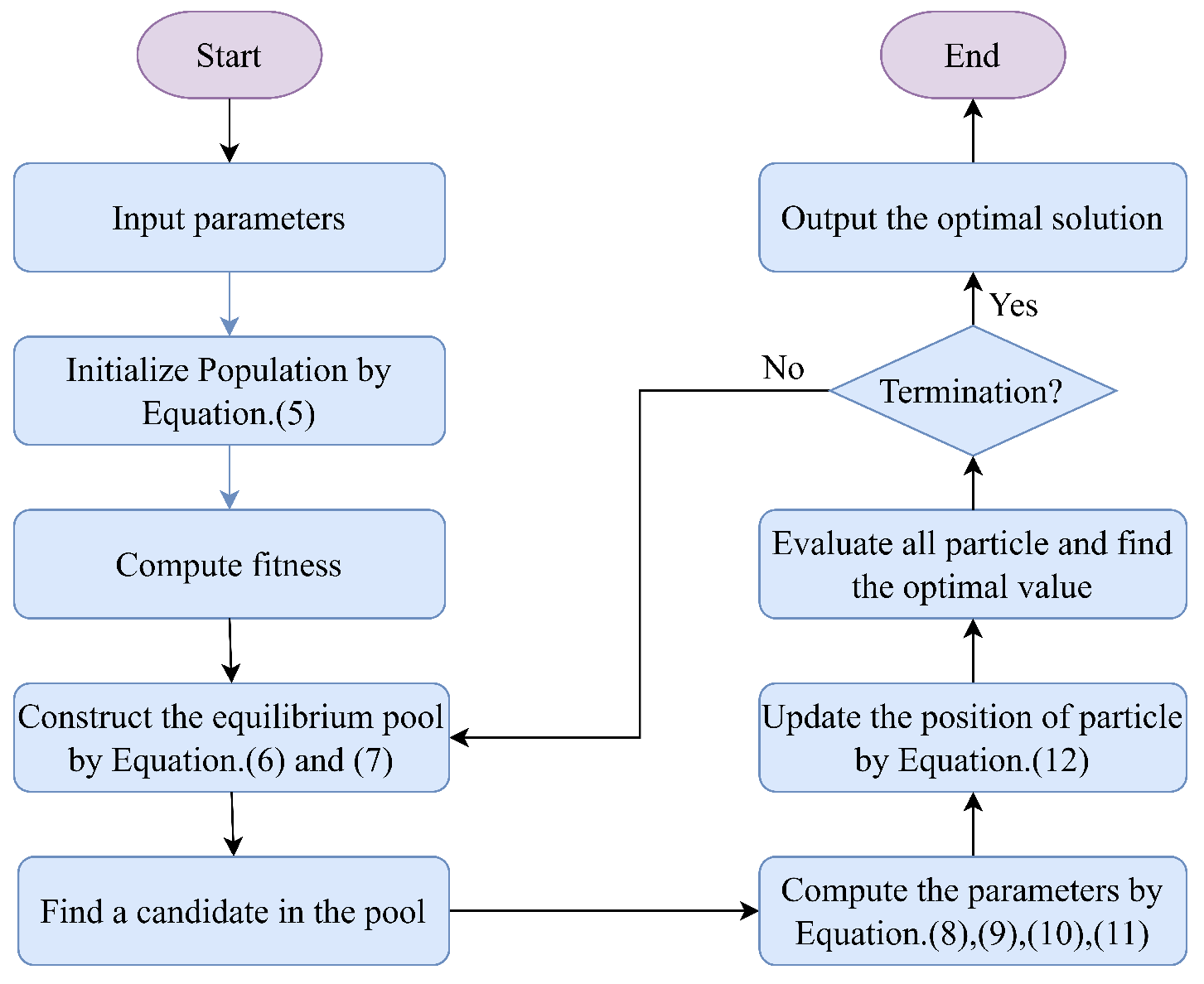
2.2. Equilibrium Optimizer
3. The Proposed Method
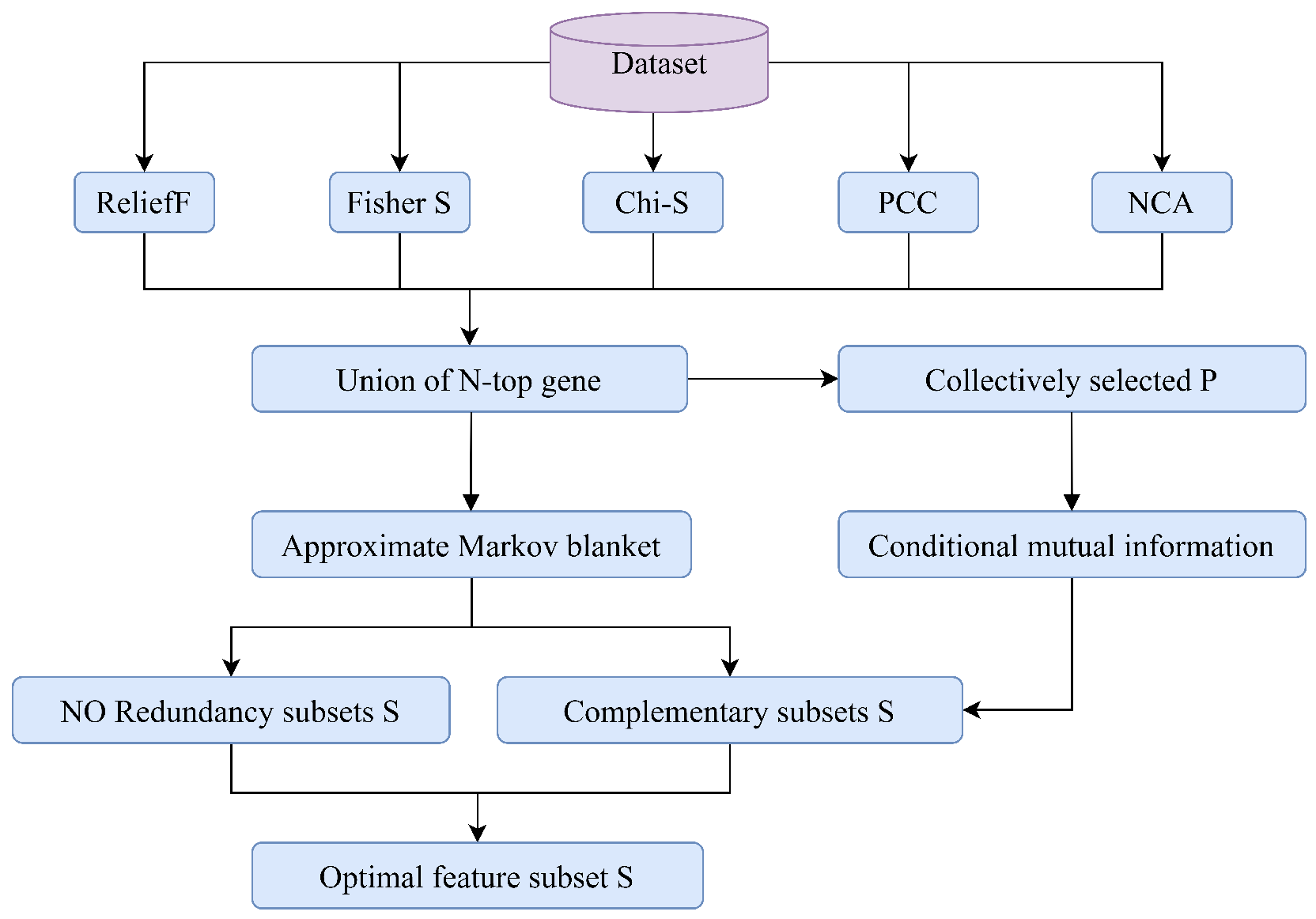
3.1. Stage 1: Multi-Filter Ensemble Strategy Based on Redundancy and Complementarity
3.1.1. Symmetric Uncertainty
3.1.2. Mutual Information and Conditional Mutual Information
3.1.3. The Proposed Strategy: RCMF
| Algorithm 1 The pseudo-code for RCMF |
| Input: Feature set representing the set of features consisting of the N-top features selected by the five filters, set representing the set of features collectively selected by the five filters, set , and class C. Output: The selected feature subset S for to n do for to n do calculate , , and if and then continue else add into set S← end if end for end for ← for to l do for to m do calculate if then continue else add into set S← end if end for end for return S |
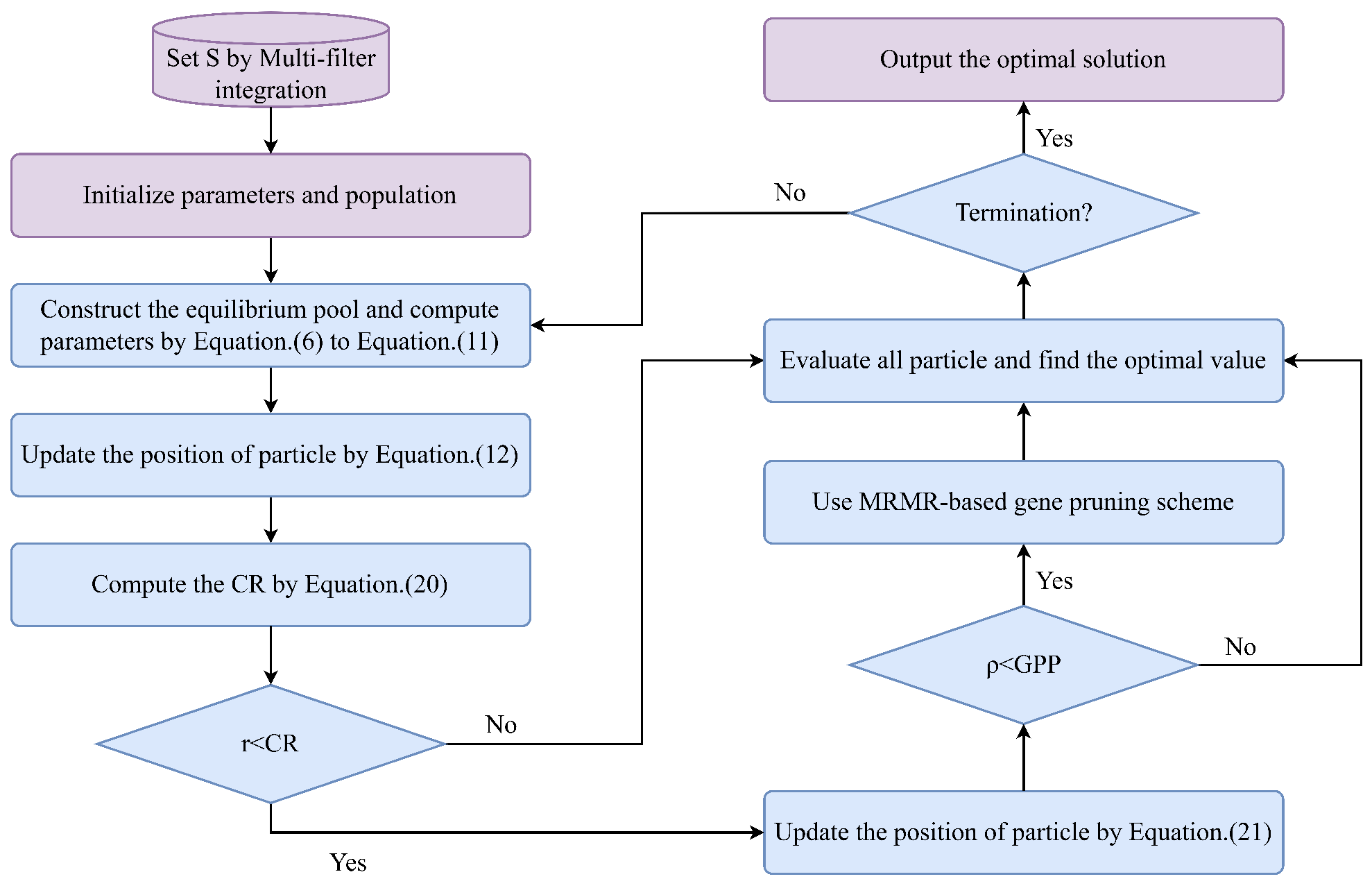
3.2. Stage 2: Equilibrium Optimizer Based on Gaussian Barebone Mechanism and Gene Pruning Strategy (GBGPSEO)
3.2.1. Improved Gaussian Barebone Mechanism
3.2.2. MRMR-Based Gene Pruning Strategy
| Algorithm 2 The pseudo-code of the MRMR-based gene pruning strategy |
| Input: A solution , , GPP Output: The solution if then Use MRMR with the selected genes in X to produce a ranking list . for to n do Prune the from the solution X and let . if then Let . end if end for end if return X |
3.3. Overall Overview of the Proposed Method (RCMF-GBGPSEO)
4. Experiment
4.1. Datasets
4.2. Performance Metrics
4.3. Comparison Algorithms and Parameter Settings
5. Results and Discussion
5.1. The Stability of RCMF
5.2. Comparison of RCMF Against Single Filters
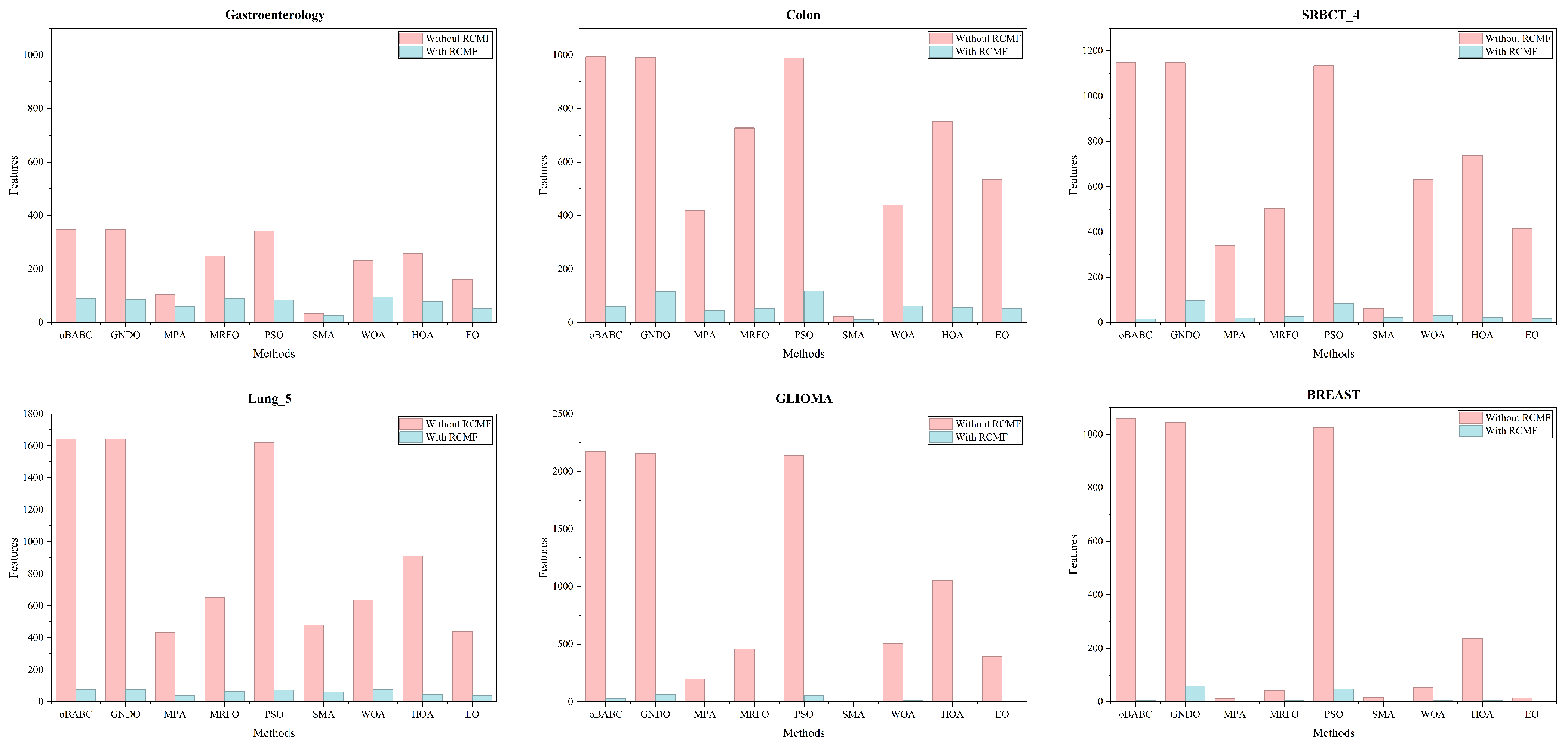
5.3. The Performance of the GBGPSEO Algorithm
5.4. Convergence Analysis
6. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Posner, A.; Prall, O.W.; Sivakumaran, T.; Etemadamoghadam, D.; Thio, N.; Pattison, A.; Balachander, S.; Fisher, K.; Webb, S.; Wood, C.; et al. A Comparison of DNA Sequencing and Gene Expression Profiling to Assist Tissue of Origin Diagnosis in Cancer of Unknown Primary. J. Pathol. 2023, 259, 81–92. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Li, X.; Ma, Z. Multi-Scale Three-Path Network (MSTP-Net): A New Architecture for Retinal Vessel Segmentation. Measurement 2025, 250, 117100. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, X.; Zhou, C.; Pen, H.; Zheng, Z.; Chen, J.; Ding, W. A Review of Cancer Data Fusion Methods Based on Deep Learning. Inf. Fusion 2024, 108, 102361. [Google Scholar] [CrossRef]
- Nssibi, M.; Manita, G.; Chhabra, A.; Mirjalili, S.; Korbaa, O. Gene Selection for High Dimensional Biological Datasets Using Hybrid Island Binary Artificial Bee Colony with Chaos Game Optimization. Artif. Intell. Rev. 2024, 57, 51. [Google Scholar] [CrossRef]
- Ouaderhman, T.; Chamlal, H.; Janane, F.Z. A New Filter-Based Gene Selection Approach in the DNA Microarray Domain. Expert Syst. Appl. 2024, 240, 122504. [Google Scholar] [CrossRef]
- Remeseiro, B.; Bolon-Canedo, V. A review of feature selection methods in medical applications. Comput. Biol. Med. 2019, 112, 103375. [Google Scholar] [CrossRef]
- Alhenawi, E.; Al-Sayyed, R.; Hudaib, A.; Mirjalili, S. Feature selection methods on gene expression microarray data for cancer classification: A systematic review. Comput. Biol. Med. 2022, 140, 105051. [Google Scholar] [CrossRef]
- Salesi, S.; Cosma, G.; Mavrovouniotis, M. TAGA: Tabu Asexual Genetic Algorithm embedded in a filter/filter feature selection approach for high-dimensional data. Inf. Sci. 2021, 565, 105–127. [Google Scholar] [CrossRef]
- Solorio-Fernandez, S.; Martínez-Trinidad, J.F.; Carrasco-Ochoa, J.A. A supervised filter feature selection method for mixed data based on spectral feature selection and information-theory redundancy analysis. Pattern Recognit. Lett. 2020, 138, 321–328. [Google Scholar] [CrossRef]
- Ansari, G.; Ahmad, T.; Doja, M.N. Hybrid filter–wrapper feature selection method for sentiment classification. Arab. J. Sci. Eng. 2019, 44, 9191–9208. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, Z. Feature selection with symmetrical complementary coefficient for quantifying feature interactions. Appl. Intell. 2020, 50, 101–118. [Google Scholar] [CrossRef]
- Bommert, A.; Welchowski, T.; Schmid, M.; Rahnenführer, J. Benchmark of filter methods for feature selection in high-dimensional gene expression survival data. Briefings Bioinform. 2022, 23, bbab354. [Google Scholar] [CrossRef] [PubMed]
- Deng, T.; Chen, S.; Zhang, Y.; Xu, Y.; Feng, D.; Wu, H.; Sun, X. A cofunctional grouping-based approach for non-redundant feature gene selection in unannotated single-cell RNA-seq analysis. Briefings Bioinform. 2023, 24, bbad042. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Li, X.; Li, Q. A discrete teaching–learning based optimization algorithm with local search for rescue task allocation and scheduling. Appl. Soft Comput. 2023, 134, 109980. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Zamani, H.; Mirjalili, S. Enhanced whale optimization algorithm for medical feature selection: A COVID-19 case study. Comput. Biol. Med. 2022, 148, 105858. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S. Genetic algorithm. In Evolutionary Algorithms and Neural Networks: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2019; pp. 43–55. [Google Scholar]
- Vivekanandan, T.; Iyengar, N.C.S.N. Optimal feature selection using a modified differential evolution algorithm and its effectiveness for prediction of heart disease. Comput. Biol. Med. 2017, 90, 125–136. [Google Scholar] [CrossRef]
- Almasoudy, F.H.; Al-Yaseen, W.L.; Idrees, A.K. Differential evolution wrapper feature selection for intrusion detection system. Procedia Comput. Sci. 2020, 167, 1230–1239. [Google Scholar] [CrossRef]
- Chen, H.; Li, S.; Li, X.; Zhao, Y.; Dong, J. A hybrid adaptive Differential Evolution based on Gaussian tail mutation. Eng. Appl. Artif. Intell. 2023, 119, 105739. [Google Scholar] [CrossRef]
- Sowan, B.; Eshtay, M.; Dahal, K.; Qattous, H.; Zhang, L. Hybrid PSO Feature Selection-Based Association Classification Approach for Breast Cancer Detection. Neural Comput. Appl. 2023, 35, 5291–5317. [Google Scholar] [CrossRef]
- Ghosh, M.; Guha, R.; Sarkar, R.; Abraham, A. A wrapper-filter feature selection technique based on ant colony optimization. Neural Comput. Appl. 2020, 32, 7839–7857. [Google Scholar] [CrossRef]
- Ma, W.; Zhou, X.; Zhu, H.; Li, L.; Jiao, L. A two-stage hybrid ant colony optimization for high-dimensional feature selection. Pattern Recognit. 2021, 116, 107933. [Google Scholar] [CrossRef]
- Fu, Q.; Li, Q.; Li, X. An improved multi-objective marine predator algorithm for gene selection in classification of cancer microarray data. Comput. Biol. Med. 2023, 160, 107020. [Google Scholar] [CrossRef] [PubMed]
- Meenachi, L.; Ramakrishnan, S. Differential evolution and ACO based global optimal feature selection with fuzzy rough set for cancer data classification. Soft Comput. 2020, 24, 18463–18475. [Google Scholar] [CrossRef]
- Hu, J.; Gui, W.; Heidari, A.A.; Cai, Z.; Liang, G.; Chen, H.; Pan, Z. Dispersed foraging slime mould algorithm: Continuous and binary variants for global optimization and wrapper-based feature selection. Knowl.-Based Syst. 2022, 237, 107761. [Google Scholar] [CrossRef]
- Qiu, F.; Guo, R.; Chen, H.; Liang, G. Boosting Slime Mould Algorithm for High-Dimensional Gene Data Mining: Diversity Analysis and Feature Selection. Comput. Math. Methods Med. 2022, 2022. [Google Scholar] [CrossRef]
- Hu, J.; Chen, H.; Heidari, A.A.; Wang, M.; Zhang, X.; Chen, Y.; Pan, Z. Orthogonal learning covariance matrix for defects of grey wolf optimizer: Insights, balance, diversity, and feature selection. Knowl.-Based Syst. 2021, 213, 106684. [Google Scholar] [CrossRef]
- Samieiyan, B.; MohammadiNasab, P.; Mollaei, M.A.; Hajizadeh, F.; Kangavari, M. Novel optimized crow search algorithm for feature selection. Expert Syst. Appl. 2022, 204, 117486. [Google Scholar] [CrossRef]
- Xu, Y.; Li, X.; Li, Q.; Zhang, W. An improved estimation of distribution algorithm for rescue task emergency scheduling considering stochastic deterioration of the injured. In Complex & Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2023; pp. 1–22. [Google Scholar]
- Tsai, C.F.; Sung, Y.T. Ensemble feature selection in high dimension, low sample size datasets: Parallel and serial combination approaches. Knowl.-Based Syst. 2020, 203, 106097. [Google Scholar] [CrossRef]
- Abeel, T.; Helleputte, T.; Van de Peer, Y.; Dupont, P.; Saeys, Y. Robust biomarker identification for cancer diagnosis with ensemble feature selection methods. Bioinformatics 2010, 26, 392–398. [Google Scholar] [CrossRef]
- Singh, N.; Singh, P. A hybrid ensemble-filter wrapper feature selection approach for medical data classification. Chemom. Intell. Lab. Syst. 2021, 217, 104396. [Google Scholar] [CrossRef]
- Lai, C.M.; Yeh, W.C.; Chang, C.Y. Gene selection using information gain and improved simplified swarm optimization. Neurocomputing 2016, 218, 331–338. [Google Scholar] [CrossRef]
- Mandal, M.; Singh, P.K.; Ijaz, M.F.; Shafi, J.; Sarkar, R. A tri-stage wrapper-filter feature selection framework for disease classification. Sensors 2021, 21, 5571. [Google Scholar] [CrossRef]
- Sun, Y.; Lu, C.; Li, X. The cross-entropy based multi-filter ensemble method for gene selection. Genes 2018, 9, 258. [Google Scholar] [CrossRef]
- Drotár, P.; Gazda, M.; Vokorokos, L. Ensemble feature selection using election methods and ranker clustering. Inf. Sci. 2019, 480, 365–380. [Google Scholar] [CrossRef]
- Yao, G.; Hu, X.; Wang, G. A novel ensemble feature selection method by integrating multiple ranking information combined with an SVM ensemble model for enterprise credit risk prediction in the supply chain. Expert Syst. Appl. 2022, 200, 117002. [Google Scholar] [CrossRef]
- Thejas, G.; Garg, R.; Iyengar, S.S.; Sunitha, N.; Badrinath, P.; Chennupati, S. Metric and accuracy ranked feature inclusion: Hybrids of filter and wrapper feature selection approaches. IEEE Access 2021, 9, 128687–128701. [Google Scholar] [CrossRef]
- Wang, A.; Liu, H.; Yang, J.; Chen, G. Ensemble feature selection for stable biomarker identification and cancer classification from microarray expression data. Comput. Biol. Med. 2022, 142, 105208. [Google Scholar] [CrossRef]
- Chiew, K.L.; Tan, C.L.; Wong, K.; Yong, K.S.; Tiong, W.K. A new hybrid ensemble feature selection framework for machine learning-based phishing detection system. Inf. Sci. 2019, 484, 153–166. [Google Scholar] [CrossRef]
- Ngo, G.; Beard, R.; Chandra, R. Evolutionary bagging for ensemble learning. Neurocomputing 2022, 510, 1–14. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Rizk-Allah, R.M.; Hassanien, A.E. A hybrid equilibrium algorithm and pattern search technique for wind farm layout optimization problem. ISA Trans. 2023, 132, 402–418. [Google Scholar] [CrossRef]
- Sun, Y.; Pan, J.S.; Hu, P.; Chu, S.C. Enhanced equilibrium optimizer algorithm applied in job shop scheduling problem. J. Intell. Manuf. 2023, 34, 1639–1665. [Google Scholar] [CrossRef]
- Seleem, S.I.; Hasanien, H.M.; El-Fergany, A.A. Equilibrium optimizer for parameter extraction of a fuel cell dynamic model. Renew. Energy 2021, 169, 117–128. [Google Scholar] [CrossRef]
- Soni, J.; Bhattacharjee, K. Multi-Objective Dynamic Economic Emission Dispatch Integration with Renewable Energy Sources and Plug-in Electrical Vehicle Using Equilibrium Optimizer. Environ. Dev. Sustain. 2024, 26, 8555–8586. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Chang, V.; Mohamed, R. A novel equilibrium optimization algorithm for multi-thresholding image segmentation problems. Neural Comput. Appl. 2021, 33, 10685–10718. [Google Scholar] [CrossRef]
- Houssein, E.H.; Dirar, M.; Abualigah, L.; Mohamed, W.M. An efficient equilibrium optimizer with support vector regression for stock market prediction. In Neural Computing and Applications; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1–36. [Google Scholar]
- Zhong, C.; Li, G.; Meng, Z.; Li, H.; He, W. A self-adaptive quantum equilibrium optimizer with artificial bee colony for feature selection. Comput. Biol. Med. 2023, 153, 106520. [Google Scholar] [CrossRef]
- Thapliyal, S.; Kumar, N. ASCAEO: Accelerated Sine Cosine Algorithm Hybridized with Equilibrium Optimizer with Application in Image Segmentation Using Multilevel Thresholding. Evol. Syst. 2024, 15, 1297–1358. [Google Scholar] [CrossRef]
- Agrawal, U.; Rohatgi, V.; Katarya, R. Normalized mutual information-based equilibrium optimizer with chaotic maps for wrapper-filter feature selection. Expert Syst. Appl. 2022, 207, 118107. [Google Scholar] [CrossRef]
- Guha, R.; Ghosh, K.K.; Bera, S.K.; Sarkar, R.; Mirjalili, S. Discrete equilibrium optimizer combined with simulated annealing for feature selection. J. Comput. Sci. 2023, 67, 101942. [Google Scholar] [CrossRef]
- Gu, Q.; Li, Z.; Han, J. Generalized fisher score for feature selection. arXiv 2012, arXiv:1202.3725. [Google Scholar] [CrossRef]
- Urbanowicz, R.J.; Meeker, M.; La Cava, W.; Olson, R.S.; Moore, J.H. Relief-based feature selection: Introduction and review. J. Biomed. Inform. 2018, 85, 189–203. [Google Scholar] [CrossRef]
- Su, C.T.; Hsu, J.H. An extended chi2 algorithm for discretization of real value attributes. IEEE Trans. Knowl. Data Eng. 2005, 17, 437–441. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y. On the importance of the Pearson correlation coefficient in noise reduction. IEEE Trans. Audio Speech Lang. Process. 2008, 16, 757–765. [Google Scholar] [CrossRef]
- Tuncer, T.; Ertam, F. Neighborhood component analysis and reliefF based survival recognition methods for Hepatocellular carcinoma. Phys. A Stat. Mech. Its Appl. 2020, 540, 123143. [Google Scholar] [CrossRef]
- Al-Betar, M.A.; Abu Doush, I.; Makhadmeh, S.N.; Al-Naymat, G.; Alomari, O.A.; Awadallah, M.A. Equilibrium Optimizer: A Comprehensive Survey. Multimed. Tools Appl. 2024, 83, 29617–29666. [Google Scholar] [CrossRef]
- Houssein, E.H.; Hassan, M.H.; Mahdy, M.A.; Kamel, S. Development and Application of Equilibrium Optimizer for Optimal Power Flow Calculation of Power System. Appl. Intell. 2023, 53, 7232–7253. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Trigg, L.; Hall, M.; Holmes, G.; Cunningham, S.J. Weka: Pracitcal Machine Learning Tools and Techniques with Java Implementations; Department of Computer Science, University of Waikato, New Zealand: Hamilton, New Zealand, 1999. [Google Scholar]
- Koller, D.; Sahami, M. Toward optimal feature selection. In Proceedings of the ICML, Bari, Italy, 3–6 July 1996; Volume 96, p. 292. [Google Scholar]
- Haque, M.N.; Sharmin, S.; Ali, A.A.; Sajib, A.A.; Shoyaib, M. Use of Relevancy and Complementary Information for Discriminatory Gene Selection from High-Dimensional Gene Expression Data. PLoS ONE 2021, 16, e0230164. [Google Scholar] [CrossRef]
- Wang, H.; Rahnamayan, S.; Sun, H.; Omran, M.G. Gaussian bare-bones differential evolution. IEEE Trans. Cybern. 2013, 43, 634–647. [Google Scholar] [CrossRef]
- Lai, C.M. Integrating simplified swarm optimization with AHP for solving capacitated military logistic depot location problem. Appl. Soft Comput. 2019, 78, 1–12. [Google Scholar] [CrossRef]
- Li, T.; Zhang, C.; Ogihara, M. A comparative study of feature selection and multiclass classification methods for tissue classification based on gene expression. Bioinformatics 2004, 20, 2429–2437. [Google Scholar] [CrossRef]
- Wang, Z.; Ning, X.; Blaschko, M. Jaccard Metric Losses: Optimizing the Jaccard Index with Soft Labels. Adv. Neural Inf. Process. Syst. 2023, 36, 75259–75285. [Google Scholar]
- Eelbode, T.; Bertels, J.; Berman, M.; Vandermeulen, D.; Maes, F.; Bisschops, R.; Blaschko, M.B. Optimization for Medical Image Segmentation: Theory and Practice When Evaluating With Dice Score or Jaccard Index. IEEE Trans. Med. Imaging 2020, 39, 3679–3690. [Google Scholar] [CrossRef]
- Ri, J.H.; Tian, G.; Liu, Y.; Xu, W.h.; Lou, J.g. Extreme Learning Machine with Hybrid Cost Function of G-mean and Probability for Imbalance Learning. Int. J. Mach. Learn. Cybern. 2020, 11, 2007–2020. [Google Scholar] [CrossRef]
- Góra, G.; Skowron, A. On kNN Class Weights for Optimising G-Mean and F1-Score. In Proceedings of the Rough International Joint Conference on Rough Sets, Krakow, Poland, 5–8 October 2023; Campagner, A., Urs Lenz, O., Xia, S., Ślęzak, D., Wąs, J., Yao, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2023; pp. 414–430. [Google Scholar]
- Zhu, F.; Shuai, Z.; Lu, Y.; Su, H.; Yu, R.; Li, X.; Zhao, Q.; Shuai, J. oBABC: A One-Dimensional Binary Artificial Bee Colony Algorithm for Binary Optimization. Swarm Evol. Comput. 2024, 87, 101567. [Google Scholar] [CrossRef]
- Qu, L.; He, W.; Li, J.; Zhang, H.; Yang, C.; Xie, B. Explicit and Size-Adaptive PSO-based Feature Selection for Classification. Swarm Evol. Comput. 2023, 77, 101249. [Google Scholar] [CrossRef]
- Liu, W.; Guo, Z.; Jiang, F.; Liu, G.; Wang, D.; Ni, Z. Improved WOA and Its Application in Feature Selection. PLoS ONE 2022, 17, e0267041. [Google Scholar] [CrossRef] [PubMed]
- Ewees, A.A.; Ismail, F.H.; Sahlol, A.T. Gradient-Based Optimizer Improved by Slime Mould Algorithm for Global Optimization and Feature Selection for Diverse Computation Problems. Expert Syst. Appl. 2023, 213, 118872. [Google Scholar] [CrossRef]
- Asghari Varzaneh, Z.; Hosseini, S.; Javidi, M.M. A Novel Binary Horse Herd Optimization Algorithm for Feature Selection Problem. Multimed. Tools Appl. 2023, 82, 40309–40343. [Google Scholar] [CrossRef]
- Alrasheedi, A.F.; Alnowibet, K.A.; Saxena, A.; Sallam, K.M.; Mohamed, A.W. Chaos Embed Marine Predator (CMPA) Algorithm for Feature Selection. Mathematics 2022, 10, 1411. [Google Scholar] [CrossRef]
- Amin, J.; Anjum, M.A.; Ahmad, A.; Sharif, M.I.; Kadry, S.; Kim, J. Microscopic Parasite Malaria Classification Using Best Feature Selection Based on Generalized Normal Distribution Optimization. PeerJ Comput. Sci. 2024, 10, e1744. [Google Scholar] [CrossRef]
- Got, A.; Zouache, D.; Moussaoui, A.; Abualigah, L.; Alsayat, A. Improved Manta Ray Foraging Optimizer-based SVM for Feature Selection Problems: A Medical Case Study. J. Bionic Eng. 2024, 21, 409–425. [Google Scholar] [CrossRef]
- Abdulrauf Sharifai, G.; Zainol, Z. Feature selection for high-dimensional and imbalanced biomedical data based on robust correlation based redundancy and binary grasshopper optimization algorithm. Genes 2020, 11, 717. [Google Scholar] [CrossRef] [PubMed]

| No. | Dataset Name | #Features | #Instances | #Classes |
|---|---|---|---|---|
| 1 | Gastroenterology | 698 | 72 | 2 |
| 2 | Colon | 2000 | 62 | 2 |
| 3 | DBWorld | 4702 | 64 | 2 |
| No. | Dataset Name | #Features | #Instances | #Classes |
|---|---|---|---|---|
| 1 | SRBCT_4 | 2308 | 83 | 4 |
| 2 | LUNG_5 | 3312 | 203 | 5 |
| 3 | DLBCL | 4026 | 47 | 2 |
| 4 | GLIOMA | 4434 | 50 | 2 |
| 5 | Brain_Tumor1 | 5920 | 90 | 5 |
| 6 | ALLAML | 7129 | 72 | 2 |
| 7 | CNS | 7130 | 60 | 2 |
| 8 | CAR | 9182 | 174 | 2 |
| 9 | Brain_Tumor2 | 10,367 | 50 | 4 |
| 10 | LUNG | 12,533 | 181 | 2 |
| 11 | MLL | 12,583 | 72 | 3 |
| 12 | BREAST | 24,482 | 97 | 2 |
| No. | Method | Parameter | Value |
|---|---|---|---|
| 1 | GBGPSEO | a1 | 2 |
| a2 | 1 | ||
| GP | 0.5 | ||
| CRmax | 1 | ||
| CRmin | 0 | ||
| GPP | 0.4 | ||
| 2 | oBABC | phiMax | 0.9 |
| phiMin | 0.5 | ||
| qStart | 0.3 | ||
| qEnd | 0.1 | ||
| 3 | PSO | c1 | 2 |
| c2 | 2 | ||
| w | 0.5 | ||
| 4 | WOA | Bound | 1 |
| 5 | SMA | Z | 0.03 |
| 6 | MPA | Beta | 1.5 |
| P | 0.5 | ||
| Fad | 0.2 | ||
| 7 | MRFO | S | 2 |
| 8 | BHOA | w | 0.99 |
| PN | 0.1 | ||
| QN | 0.2 |
| Dataset | Top = 50 | Top = 100 | Top = 150 | Top = 200 | Top = 250 | Top = 300 |
|---|---|---|---|---|---|---|
| Gastroenterology | 1 | 1 | 1 | 1 | 1 | 1 |
| DBWorld | 1 | 1 | 1 | 1 | 1 | 0.998 |
| Colon | 1 | 1 | 1 | 1 | 1 | 1 |
| SRBCT_4 | 1 | 1 | 1 | 1 | 1 | 1 |
| Lung_5 | 1 | 1 | 1 | 1 | 1 | 1 |
| DLBCL | 1 | 1 | 1 | 1 | 1 | 1 |
| GLIOMA | 1 | 1 | 1 | 1 | 1 | 1 |
| Brain_Tumor1 | 1 | 1 | 1 | 1 | 1 | 1 |
| ALLAML | 1 | 1 | 1 | 1 | 1 | 1 |
| CNS | 1 | 1 | 1 | 1 | 1 | 1 |
| CAR | 1 | 1 | 1 | 1 | 1 | 1 |
| Brain_Tumor2 | 1 | 1 | 1 | 1 | 1 | 1 |
| LUNG | 1 | 1 | 1 | 1 | 1 | 1 |
| MLL | 1 | 1 | 1 | 1 | 1 | 1 |
| BREAST | 1 | 1 | 1 | 1 | 1 | 1 |
| Dataset | Measure | ReliefF | Fisher Score | Chi-Square | PCC | NCA | RCMF |
|---|---|---|---|---|---|---|---|
| Gastroenterology | G-mean | 0.956 | 0.968 | 0.908 | 0.5 | 0.941 | 0.984 |
| AUC | 0.927 | 0.938 | 0.833 | 0.5 | 0.885 | 0.969 | |
| DBWorld | G-mean | 0.952 | 0.713 | 0.926 | 0.952 | 0.952 | 0.952 |
| AUC | 0.909 | 0.591 | 0.864 | 0.909 | 0.909 | 0.909 | |
| Colon | G-mean | 0.887 | 0.887 | 0.887 | 0.935 | 0.887 | 0.887 |
| AUC | 0.792 | 0.792 | 0.792 | 0.875 | 0.792 | 0.792 | |
| SRBCT_4 | G-mean | 1 | 1 | 1 | 1 | 1 | 1 |
| AUC | 1 | 1 | 1 | 1 | 1 | 1 | |
| Lung_5 | G-mean | 0.984 | 0.984 | 0.784 | 0.964 | 0.964 | 0.984 |
| AUC | 0.952 | 0.952 | 0.85 | 0.904 | 0.904 | 0.952 | |
| DLBCL | G-mean | 1 | 1 | 1 | 1 | 1 | 1 |
| AUC | 1 | 1 | 1 | 1 | 1 | 1 | |
| GLIOMA | G-mean | 0.5 | 0.908 | 0.5 | 0.908 | 0.5 | 0.908 |
| AUC | 0.5 | 0.833 | 0.5 | 0.833 | 0.5 | 0.833 | |
| Brain_Tumor 1 | G-mean | 0.6 | 0.582 | 0.558 | 0.584 | 0.582 | 0.774 |
| AUC | 0.774 | 0.713 | 0.675 | 0.729 | 0.726 | 0.828 | |
| ALLAML | G-mean | 0.982 | 0.963 | 0.982 | 0.963 | 1 | 1 |
| AUC | 0.964 | 0.929 | 0.964 | 0.929 | 1 | 1 | |
| CNS | G-mean | 0.878 | 0.977 | 0.875 | 0.977 | 0.963 | 0.977 |
| AUC | 0.786 | 0.955 | 0.766 | 0.955 | 0.929 | 0.955 | |
| CAR | G-mean | 0.789 | 0.979 | 0.898 | 0.979 | 0.898 | 0.99 |
| AUC | 0.667 | 0.959 | 0.813 | 0.959 | 0.813 | 0.98 | |
| Brain_Tumor 2 | G-mean | 0.96 | 0.874 | 0.96 | 0.96 | 0.96 | 1 |
| AUC | 0.925 | 0.736 | 0.925 | 0.925 | 0.925 | 1 | |
| LUNG | G-mean | 1 | 1 | 1 | 1 | 1 | 1 |
| AUC | 1 | 1 | 1 | 1 | 1 | 1 | |
| MLL | G-mean | 0.98 | 0.941 | 0.941 | 0.983 | 0.98 | 0.98 |
| AUC | 0.959 | 0.884 | 0.884 | 0.965 | 0.959 | 0.959 | |
| BREAST | G-mean | 0.91 | 0.869 | 0.871 | 0.5 | 0.929 | 0.947 |
| AUC | 0.831 | 0.764 | 0.762 | 0.5 | 0.864 | 0.898 |
| Dataset | Method | MeanA (Std) | MeanS (Std) | MeanF (Std) | Dataset | Method | MeanA (Std) | MeanS (Std) | MeanF (Std) |
|---|---|---|---|---|---|---|---|---|---|
| Gastroenterology | oBABC | 0.917 (0.019) | 90.5 (6.3) | 0.084 (0.019) | DBWorld | oBABC | 0.955 (0.013) | 21.4 (4.8) | 0.044 (0.007) |
| GNDO | 0.935 (0.016) | 85.7 (7.6) | 0.044 (0.011) | GNDO | 0.941 (0.015) | 73.0 (5.5) | 0.047 (0.009) | ||
| MPA | 0.934 (0.015) | 59.1 (18.2) | 0.042 (0.009) | MPA | 0.954 (0.013) | 30.3 (10.9) | 0.036 (0.009) | ||
| MRFO | 0.927 (0.020) | 89.5 (26.4) | 0.050 (0.010) | MRFO | 0.943 (0.015) | 51.1 (19.5) | 0.044 (0.009) | ||
| PSO | 0.929 (0.019) | 83.4 (7.5) | 0.051 (0.015) | PSO | 0.942 (0.021) | 68.6 (6.2) | 0.048 (0.011) | ||
| SMA | 0.913 (0.017) | 26.1 (33.6) | 0.074 (0.012) | SMA | 0.924 (0.018) | 17.0 (21.9) | 0.074 (0.014) | ||
| WOA | 0.917 (0.015) | 95.1 (41.2) | 0.061 (0.012) | WOA | 0.918 (0.021) | 53.3 (24.2) | 0.061 (0.019) | ||
| HOA | 0.811 (0.020) | 79.9 (8.3) | 0.082 (0.012) | HOA | 0.941 (0.010) | 36.7 (7.8) | 0.046 (0.008) | ||
| EO | 0.933 (0.018) | 52.9 (9.7) | 0.043 (0.011) | EO | 0.961 (0.010) | 29.0 (8.4) | 0.033 (0.037) | ||
| GBGPSED | 0.935 (0.010) | 21.7 (8.5) | 0.031 (0.011) | GBGPSED | 0.965 (0.015) | 9.6 (2.9) | 0.033 (0.012) | ||
| Colon | oBABC | 0.924 (0.015) | 60.8 (8.0) | 0.065 (0.006) | SRBCT_4 | oBABC | 0.991 (0.000) | 15.4 (3.6) | 0.0009 (0.000) |
| GNDO | 0.892 (0.010) | 115.7 (6.9) | 0.094 (0.008) | GNDO | 1.000 (0.000) | 97.0 (5.3) | 0.0036 (0.000) | ||
| MPA | 0.914 (0.017) | 43.3 (23.2) | 0.066 (0.010) | MPA | 0.994 (0.008) | 19.7 (3.3) | 0.0007 (0.000) | ||
| MRFO | 0.905 (0.019) | 52.7 (38.2) | 0.077 (0.014) | MRFO | 0.992 (0.009) | 24.9 (6.1) | 0.0009 (0.000) | ||
| PSO | 0.894 (0.012) | 117.8 (7.3) | 0.090 (0.009) | PSO | 0.996 (0.002) | 84.9 (7.6) | 0.0031 (0.000) | ||
| SMA | 0.908 (0.017) | 10.6 (5.0) | 0.077 (0.016) | SMA | 0.995 (0.006) | 23.6 (8.8) | 0.0008 (0.000) | ||
| WOA | 0.894 (0.019) | 62.0 (45.5) | 0.085 (0.015) | WOA | 0.991 (0.011) | 30.2 (8.7) | 0.0011 (0.000) | ||
| HOA | 0.938 (0.019) | 56.0 (15.3) | 0.067 (0.013) | HOA | 0.996 (0.003) | 23.0 (3.8) | 0.0004 (0.000) | ||
| EO | 0.920 (0.024) | 51.9 (16.1) | 0.068 (0.020) | EO | 0.995 (0.008) | 18.6 (3.2) | 0.0006 (0.000) | ||
| GBGPSED | 0.941 (0.019) | 9.8 (4.0) | 0.053 (0.016) | GBGPSED | 0.998 (0.005) | 8.1 (2.1) | 0.0003 (0.000) | ||
| Lung_5 | oBABC | 0.979 (0.002) | 77.4 (4.3) | 0.023 (0.000) | DLBCL | oBABC | 0.997 (0.004) | 80.1 (3.2) | 0.0036 (0.000) |
| GNDO | 0.978 (0.004) | 76.8 (6.5) | 0.022 (0.003) | GNDO | 0.996 (0.004) | 78.4 (4.2) | 0.0035 (0.000) | ||
| MPA | 0.978 (0.005) | 40.3 (14.4) | 0.018 (0.002) | MPA | 0.997 (0.007) | 6.6 (2.5) | 0.0003 (0.000) | ||
| MRFO | 0.978 (0.004) | 63.2 (15.4) | 0.022 (0.002) | MRFO | 0.984 (0.024) | 12.5 (4.5) | 0.0005 (0.000) | ||
| PSO | 0.977 (0.003) | 73.3 (8.9) | 0.023 (0.003) | PSO | 0.997 (0.004) | 66.6 (5.4) | 0.0030 (0.000) | ||
| SMA | 0.973 (0.005) | 61.2 (28.0) | 0.027 (0.002) | SMA | 0.982 (0.020) | 6.2 (3.2) | 0.0002 (0.000) | ||
| WOA | 0.974 (0.006) | 77.0 (26.8) | 0.023 (0.003) | WOA | 0.983 (0.015) | 16.0 (9.6) | 0.0007 (0.000) | ||
| HOA | 0.979 (0.004) | 46.7 (9.5) | 0.019 (0.002) | HOA | 0.998 (0.006) | 14.1 (3.0) | 0.0006 (0.000) | ||
| EO | 0.983 (0.004) | 41.1 (10.7) | 0.017 (0.003) | EO | 0.992 (0.013) | 7.1 (2.1) | 0.0003 (0.000) | ||
| GBGPSED | 0.991 (0.004) | 22.0 (11.1) | 0.015 (0.004) | GBGPSED | 0.998 (0.006) | 4.4 (1.9) | 0.0002 (0.000) | ||
| GLIOMA | oBABC | 0.996 (0.008) | 27.1 (3.4) | 0.0014 (0.000) | Brain_Tumor1 | oBABC | 0.929 (0.008) | 24.4 (5.3) | 0.080 (0.004) |
| GNDO | 0.995 (0.011) | 62.5 (3.9) | 0.0037 (0.000) | GNDO | 0.911 (0.007) | 82.9 (5.5) | 0.088 (0.006) | ||
| MPA | 0.995 (0.011) | 3.2 (1.5) | 0.0001 (0.000) | MPA | 0.921 (0.009) | 20.1 (6.9) | 0.080 (0.006) | ||
| MRFO | 0.997 (0.007) | 7.7 (6.3) | 0.0004 (0.000) | MRFO | 0.914 (0.011) | 39.2 (20.7) | 0.080 (0.008) | ||
| PSO | 0.993 (0.010) | 53.0 (6.2) | 0.0031 (0.000) | PSO | 0.911 (0.007) | 75.1 (7.9) | 0.088 (0.005) | ||
| SMA | 0.987 (0.015) | 2.5 (0.7) | 0.0001 (0.000) | SMA | 0.903 (0.012) | 21.1 (26.9) | 0.090 (0.008) | ||
| WOA | 0.989 (0.012) | 12.2 (15.7) | 0.0007 (0.001) | WOA | 0.906 (0.011) | 50.3 (31.5) | 0.087 (0.008) | ||
| HOA | 0.988 (0.010) | 5.8 (5.3) | 0.0005 (0.000) | HOA | 0.903 (0.010) | 39.1 (6.5) | 0.088 (0.008) | ||
| EO | 0.994 (0.009) | 4.7 (1.5) | 0.0002 (0.000) | EO | 0.923 (0.027) | 18.3 (6.3) | 0.071 (0.006) | ||
| GBGPSED | 0.997 (0.007) | 2.4 (0.6) | 0.0001 (0.000) | GBGPSED | 0.923 (0.015) | 9.4 (3.8) | 0.071 (0.014) | ||
| ALLAML | oBABC | 0.995 (0.000) | 11.8 (1.1) | 0.00086 (0.000) | CNS | oBABC | 0.920 (0.021) | 78.3 (8.9) | 0.050 (0.010) |
| GNDO | 1.000 (0.000) | 60.3 (4.7) | 0.00342 (0.000) | GNDO | 0.896 (0.019) | 161.3 (11.1) | 0.078 (0.010) | ||
| MPA | 0.996 (0.006) | 8.2 (2.0) | 0.00046 (0.000) | MPA | 0.908 (0.017) | 75.6 (38.2) | 0.059 (0.014) | ||
| MRFO | 0.995 (0.006) | 15.1 (7.6) | 0.00086 (0.000) | MRFO | 0.899 (0.019) | 142.8 (37.3) | 0.070 (0.011) | ||
| PSO | 0.999 (0.004) | 48.6 (5.8) | 0.00276 (0.000) | PSO | 0.893 (0.020) | 159.8 (8.9) | 0.073 (0.010) | ||
| SMA | 0.991 (0.010) | 8.0 (3.0) | 0.00045 (0.000) | SMA | 0.870 (0.028) | 32.3 (48.7) | 0.107 (0.013) | ||
| WOA | 0.990 (0.010) | 22.4 (9.4) | 0.00127 (0.001) | WOA | 0.875 (0.032) | 150.5 (81.0) | 0.091 (0.023) | ||
| HOA | 0.992 (0.008) | 9.7 (2.3) | 0.00172 (0.000) | HOA | 0.816 (0.022) | 50.2 (13.1) | 0.052 (0.019) | ||
| EO | 0.993 (0.011) | 7.9 (1.8) | 0.00045 (0.000) | EO | 0.938 (0.020) | 73.3 (18.9) | 0.056 (0.018) | ||
| GBGPSED | 0.998 (0.005) | 5.1 (1.7) | 0.00029 (0.000) | GBGPSED | 0.920 (0.024) | 25.0 (15.6) | 0.046 (0.027) | ||
| CAR | oBABC | 0.978 (0.011) | 30.3 (5.4) | 0.023 (0.005) | Brain_Tumor2 | oBABC | 0.950 (0.013) | 78.3 (4.8) | 0.043 (0.000) |
| GNDO | 0.964 (0.009) | 70.2 (6.7) | 0.028 (0.006) | GNDO | 0.950 (0.013) | 72.9 (6.6) | 0.043 (0.000) | ||
| MPA | 0.974 (0.007) | 20.7 (16.6) | 0.017 (0.005) | MPA | 0.952 (0.015) | 22.7 (8.5) | 0.045 (0.009) | ||
| MRFO | 0.967 (0.011) | 37.2 (21.3) | 0.022 (0.005) | MRFO | 0.937 (0.021) | 43.3 (17.9) | 0.041 (0.001) | ||
| PSO | 0.964 (0.010) | 69.1 (4.6) | 0.029 (0.006) | PSO | 0.948 (0.010) | 71.8 (5.6) | 0.043 (0.000) | ||
| SMA | 0.967 (0.007) | 9.7 (1.3) | 0.027 (0.008) | SMA | 0.933 (0.022) | 26.4 (26.2) | 0.051 (0.013) | ||
| WOA | 0.960 (0.012) | 27.8 (32.2) | 0.028 (0.007) | WOA | 0.926 (0.021) | 67.5 (31.3) | 0.050 (0.009) | ||
| HOA | 0.970 (0.008) | 9.4 (7.7) | 0.027 (0.004) | HOA | 0.933 (0.011) | 33.6 (7.4) | 0.051 (0.000) | ||
| EO | 0.977 (0.006) | 20.3 (4.5) | 0.017 (0.004) | EO | 0.951 (0.012) | 21.4 (5.8) | 0.038 (0.006) | ||
| GBGPSED | 0.988 (0.008) | 8.1 (10.2) | 0.016 (0.007) | GBGPSED | 0.956 (0.013) | 14.5 (10.6) | 0.038 (0.011) | ||
| LUNG | oBABC | 0.984 (0.001) | 14.2 (3.8) | 0.0007 (0.000) | MLL | oBABC | 0.999 (0.004) | 28.5 (4.0) | 0.0007 (0.000) |
| GNDO | 0.993 (0.003) | 55.1 (4.8) | 0.0100 (0.002) | GNDO | 0.999 (0.003) | 66.3 (5.2) | 0.0035 (0.000) | ||
| MPA | 0.998 (0.003) | 4.5 (1.8) | 0.0002 (0.000) | MPA | 0.996 (0.009) | 11.2 (2.9) | 0.0006 (0.000) | ||
| MRFO | 0.997 (0.004) | 8.8 (4.6) | 0.0011 (0.002) | MRFO | 0.990 (0.011) | 18.2 (7.4) | 0.0009 (0.000) | ||
| PSO | 0.994 (0.003) | 48.2 (5.6) | 0.0093 (0.003) | PSO | 0.999 (0.003) | 53.5 (6.5) | 0.0028 (0.000) | ||
| SMA | 0.995 (0.003) | 4.2 (1.3) | 0.0032 (0.003) | SMA | 0.992 (0.010) | 13.4 (7.1) | 0.0007 (0.000) | ||
| WOA | 0.993 (0.004) | 11.5 (10.1) | 0.0050 (0.004) | WOA | 0.988 (0.013) | 27.0 (14.6) | 0.0014 (0.001) | ||
| HOA | 0.998 (0.003) | 11.1 (4.3) | 0.0035 (0.002) | HOA | 0.995 (0.006) | 15.3 (3.7) | 0.0008 (0.000) | ||
| EO | 0.989 (0.003) | 5.4 (2.2) | 0.0003 (0.000) | EO | 0.999 (0.004) | 11.3 (2.4) | 0.0006 (0.000) | ||
| GBGPSED | 0.999 (0.002) | 4.0 (1.1) | 0.0001 (0.002) | GBGPSED | 1.000 (0.000) | 7.5 (2.1) | 0.0004 (0.000) | ||
| BREAST | oBABC | 1.000 (0.000) | 4.9 (3.8) | 0.00013 (0.000) | |||||
| GNDO | 1.000 (0.000) | 58.7 (5.7) | 0.00324 (0.000) | ||||||
| MPA | 0.998 (0.004) | 2.4 (0.6) | 0.00013 (0.000) | ||||||
| MRFO | 0.996 (0.007) | 4.8 (2.1) | 0.00026 (0.000) | ||||||
| PSO | 1.000 (0.000) | 48.5 (6.4) | 0.00268 (0.000) | ||||||
| SMA | 0.998 (0.004) | 2.6 (0.6) | 0.00014 (0.000) | ||||||
| WOA | 0.994 (0.009) | 5.6 (3.2) | 0.00031 (0.000) | ||||||
| HOA | 0.998 (0.003) | 4.7 (1.9) | 0.00017 (0.000) | ||||||
| EO | 0.998 (0.004) | 3.2 (1.2) | 0.00017 (0.000) | ||||||
| GBGPSED | 1.000 (0.000) | 2.1 (0.2) | 0.00011 (0.000) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, P.; Zhao, Y.; Li, X.; Ma, Z.; Wang, H. A Hybrid Ensemble Equilibrium Optimizer Gene Selection Algorithm for Microarray Data. Biomimetics 2025, 10, 523. https://doi.org/10.3390/biomimetics10080523
Su P, Zhao Y, Li X, Ma Z, Wang H. A Hybrid Ensemble Equilibrium Optimizer Gene Selection Algorithm for Microarray Data. Biomimetics. 2025; 10(8):523. https://doi.org/10.3390/biomimetics10080523
Chicago/Turabian StyleSu, Peng, Yuxin Zhao, Xiaobo Li, Zhendi Ma, and Hui Wang. 2025. "A Hybrid Ensemble Equilibrium Optimizer Gene Selection Algorithm for Microarray Data" Biomimetics 10, no. 8: 523. https://doi.org/10.3390/biomimetics10080523
APA StyleSu, P., Zhao, Y., Li, X., Ma, Z., & Wang, H. (2025). A Hybrid Ensemble Equilibrium Optimizer Gene Selection Algorithm for Microarray Data. Biomimetics, 10(8), 523. https://doi.org/10.3390/biomimetics10080523






