Aerodynamic Effects of a Blended Multi-Winglet on an Airliner in Subsonic and Transonic Regimes
Abstract
1. Introduction
2. Problem Setup
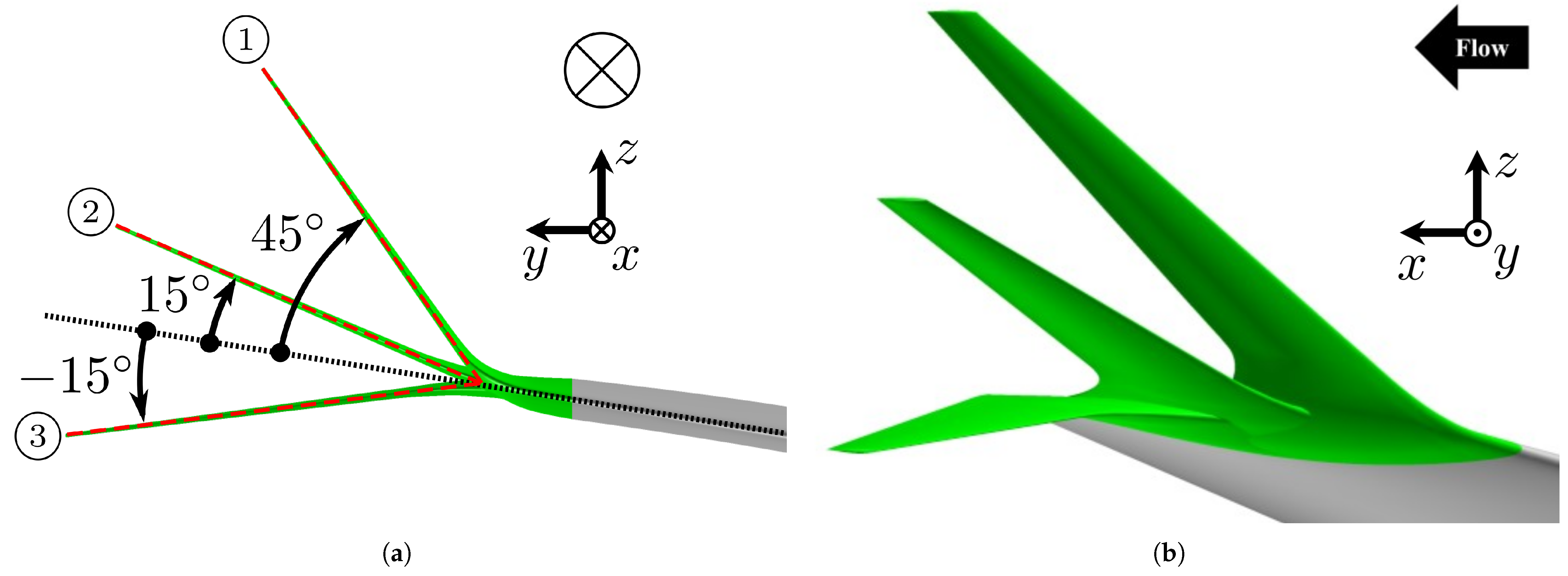
2.1. Configurations
2.1.1. Single-Winglet Configuration
2.1.2. Multi-Winglet Configuration
Airfoil
Cant Angle
2.2. Mesh Generation
2.3. Flow Solver
2.4. Computational Conditions
3. Numerical Results: Transonic Aerodynamics
3.1. Aerodynamic Discrepancies
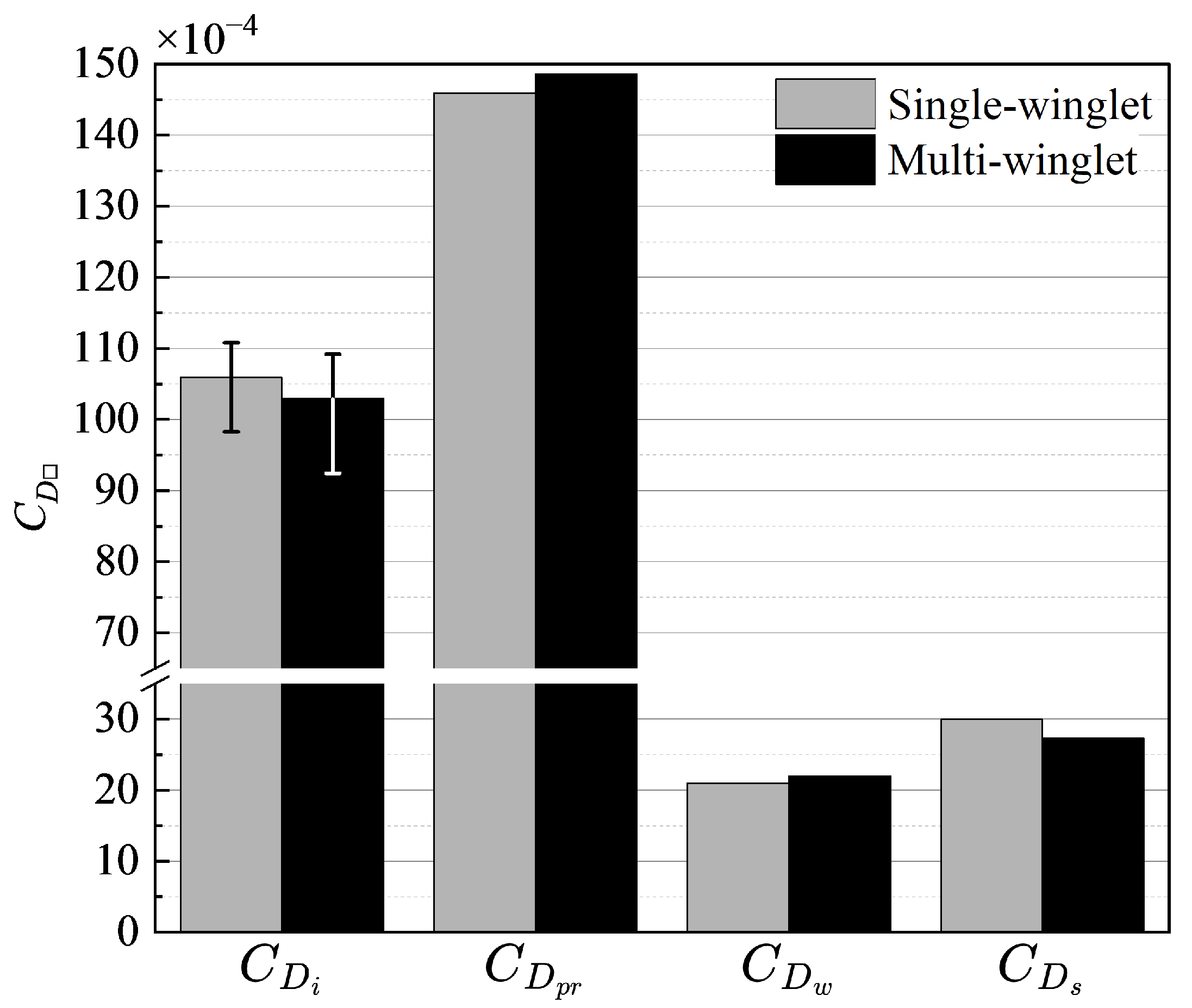
3.2. Drag Decomposition Results
- Profile Drag (): As shown in Figure 5, increases by 2.7 counts in the multi-winglet configuration, primarily due to its larger frontal projected area.
- Wave Drag (): also increases, by approximately 1.0 count. However, its contribution to the overall increase in is smaller than that of , owing to the relatively weak shock waves generated by the winglets.
- Induced Drag (): is reduced by 3.0 counts in the multi-winglet configuration, and this reduction is sufficient to offset the rise in .
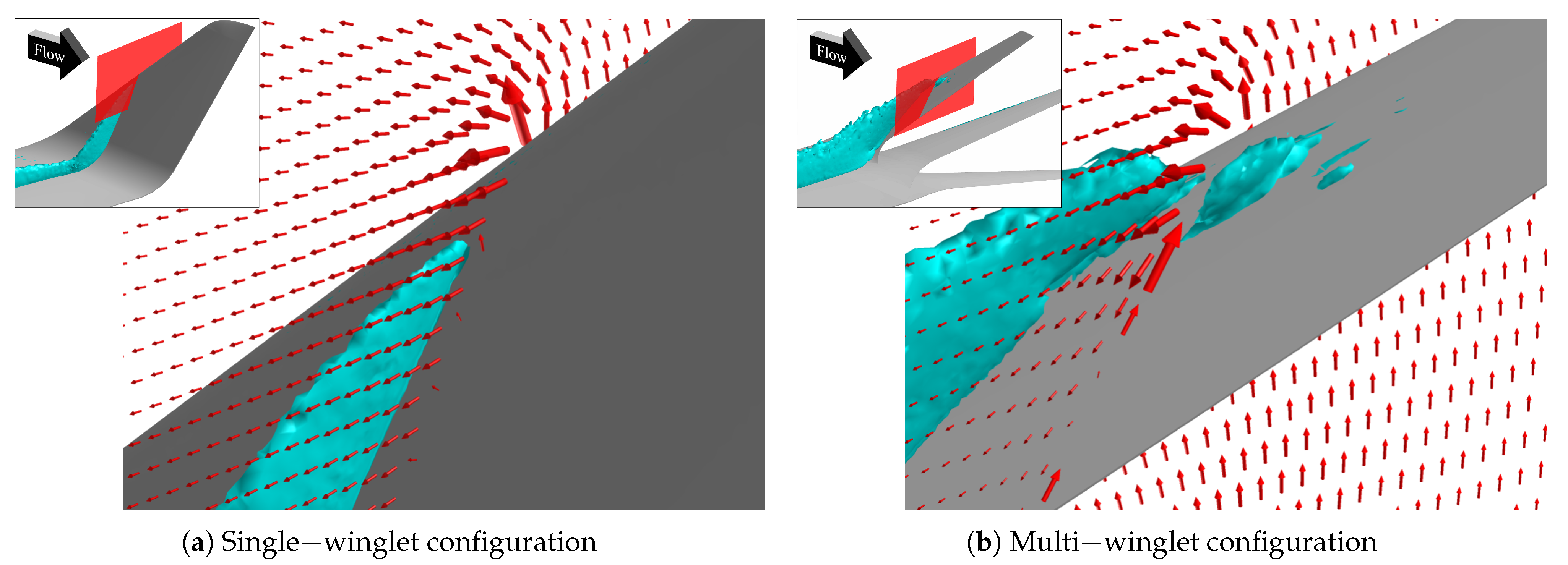
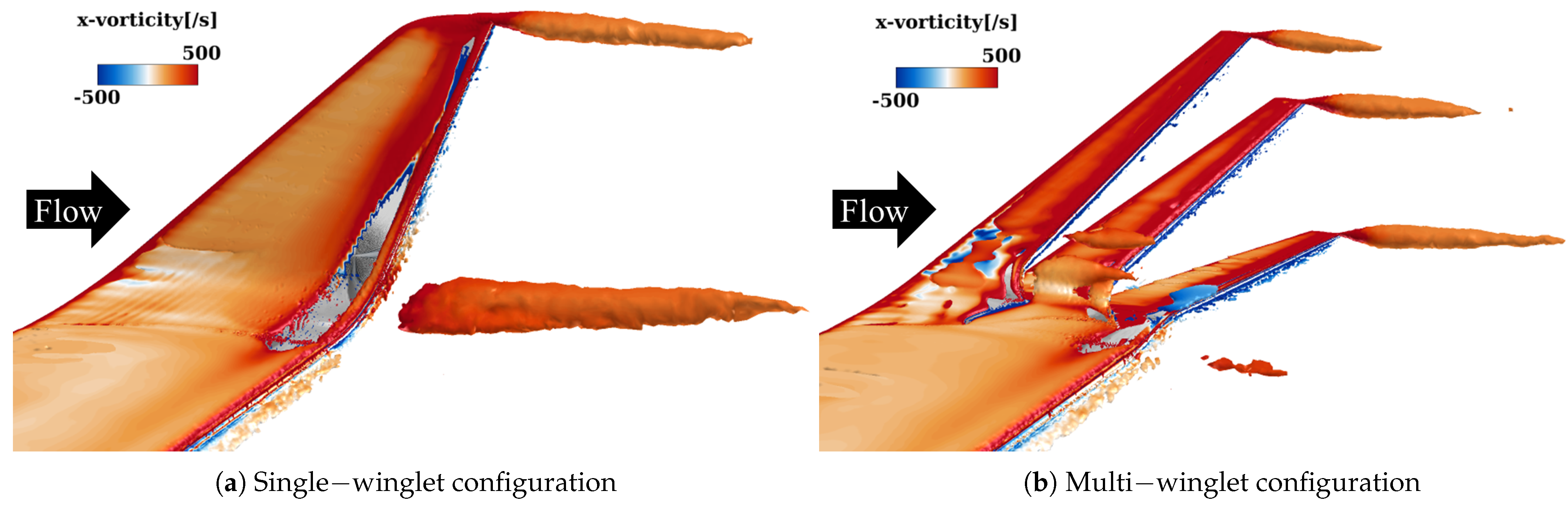
3.3. Comparison of Vortex Structures
- Vortex suppression effects of the multi-winglet:
- Vortex characteristics unique to the multi-winglet:
- A vortex originates near the 70% spanwise location of the first winglet (V3 in Figure 7b).
- Vortices are generated along the trailing edge of the first winglet between 30% and 60% of the span, and along the second winglet between 35% and 45% of the span (V4 in Figure 7b).
- The streamwise extent of wingtip vortices varies across the three winglets under uniform flow conditions.

3.3.1. Vortex Suppression Mechanism
Wingtip Vortex (V1)
Vortices at the Main Wing–Winglet Junction (V2)
3.3.2. Vortex Behavior Specific to the Multi-Winglet Configuration
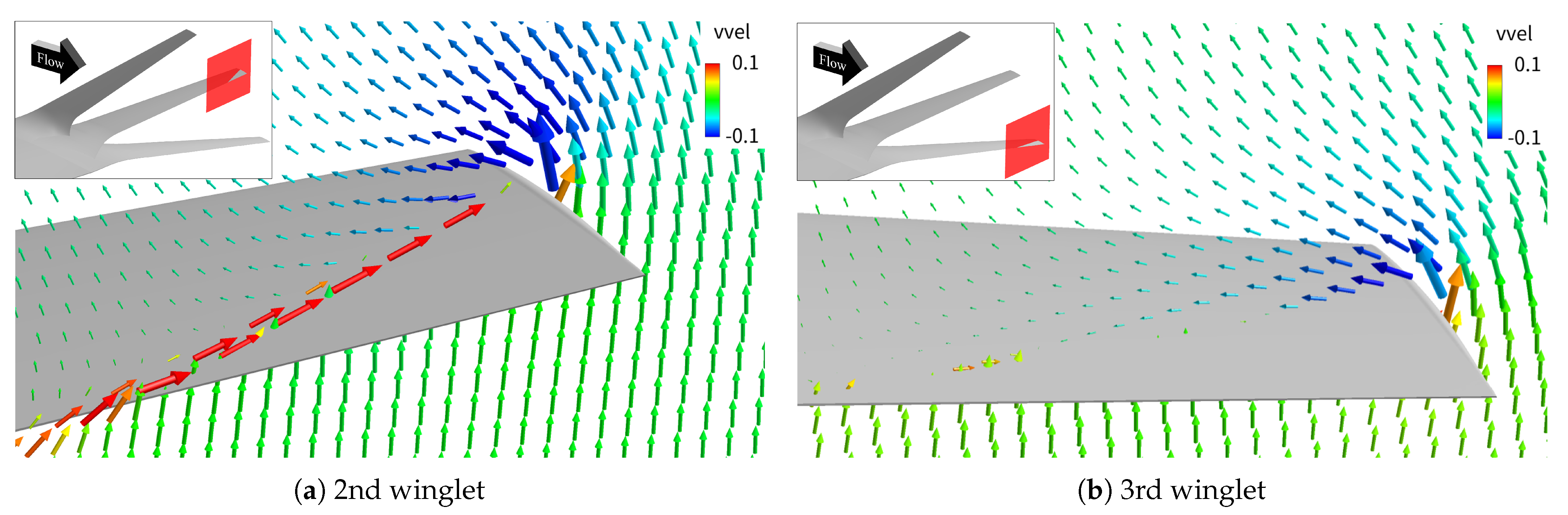
Vortex Formation near the 70% Spanwise Location of the First Winglet (V3)
Vortices at the Trailing Edge of the First and Second Winglets (V4)
Chordwise Variation in Wingtip Vortex Extent
4. Numerical Results: Subsonic Aerodynamics
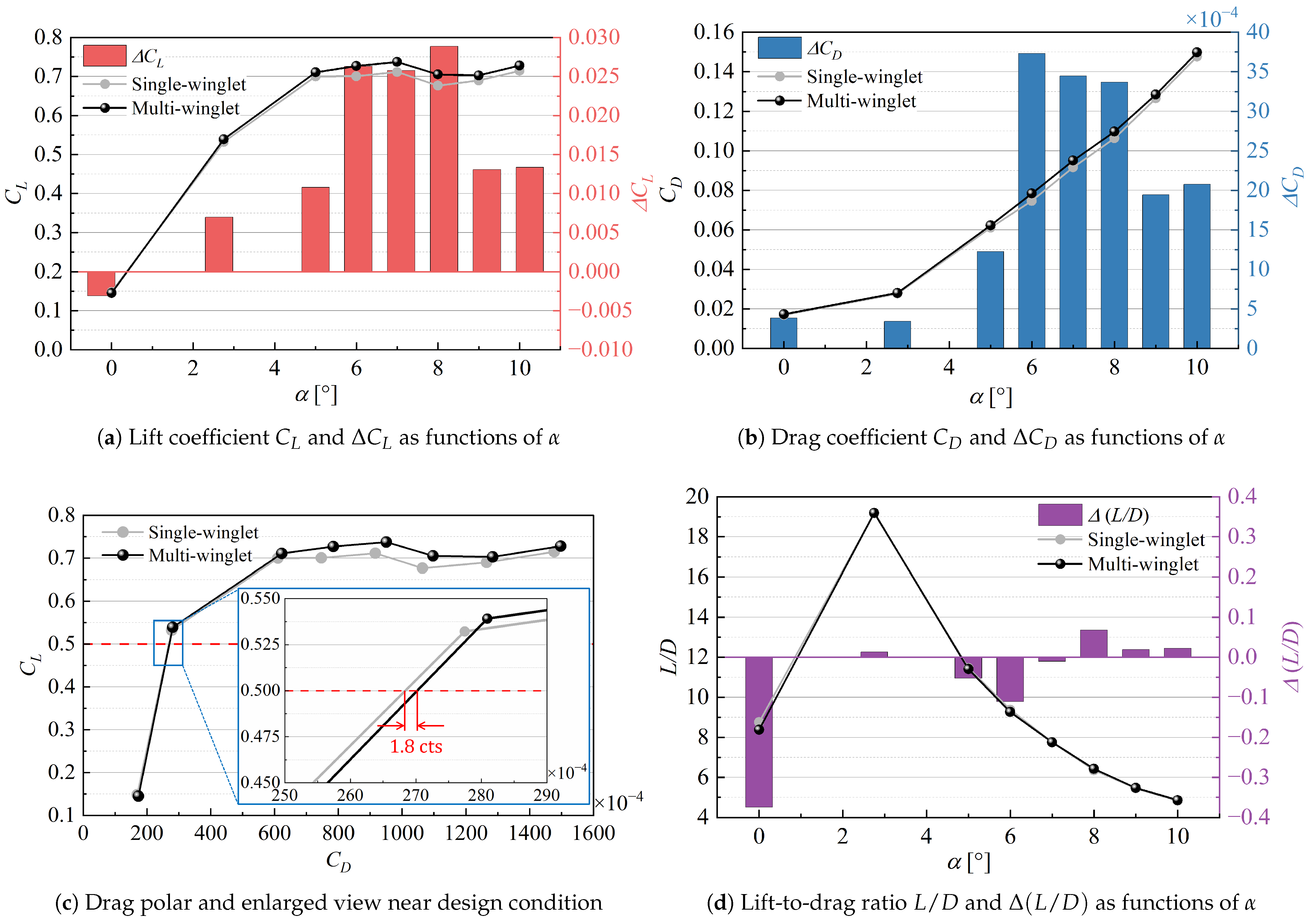
4.1. Aerodynamic Discrepancies
4.2. Mechanisms of Enhancement
4.2.1. Effect of the Multi-Winglet on Enhancement Prior to Stall
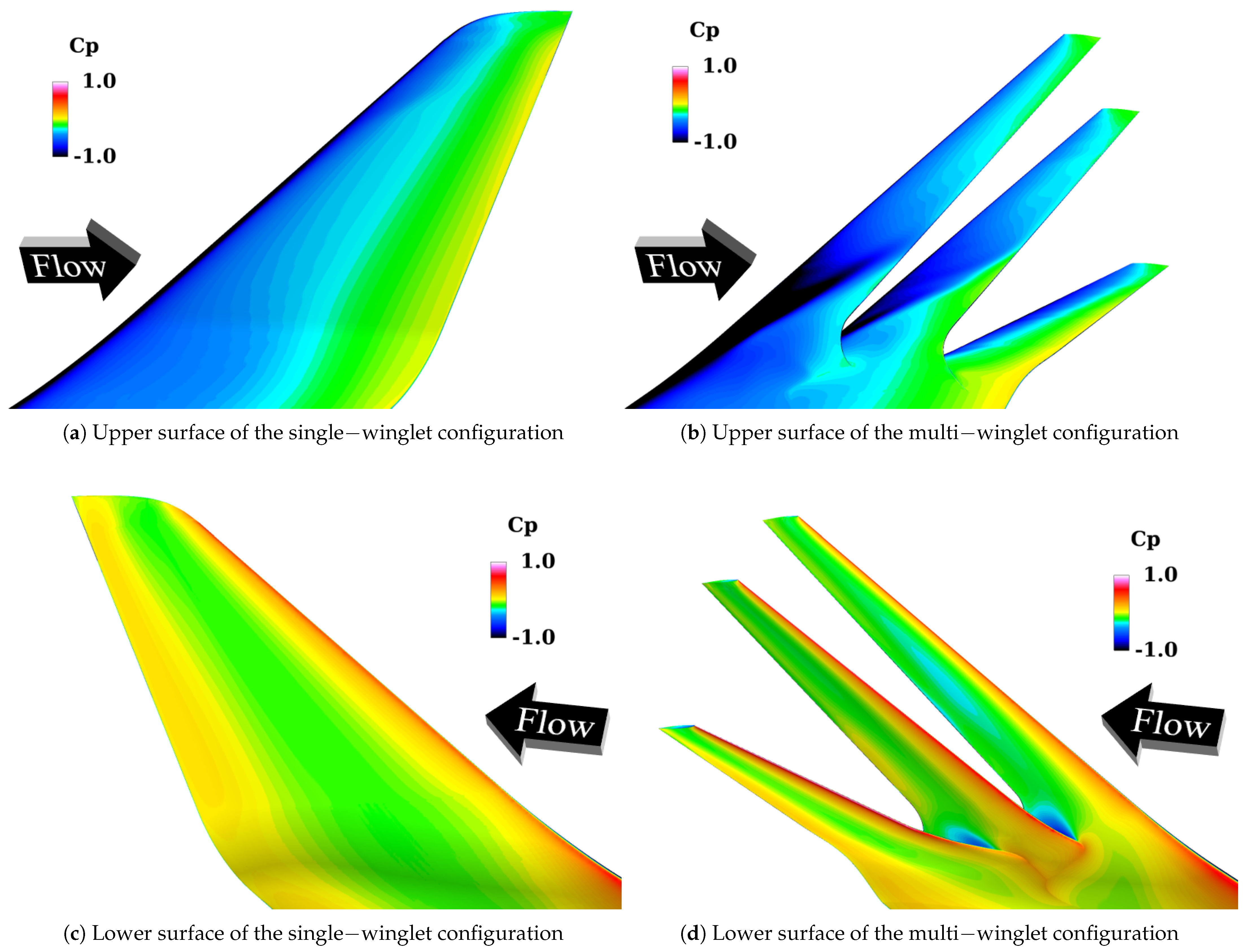
Upper Surface
Lower Surface
4.2.2. Effect of the Multi-Winglet on Enhancement in the Post-Stall Regime
Upper Surface
Lower Surface
4.3. Effects on Wake Turbulence
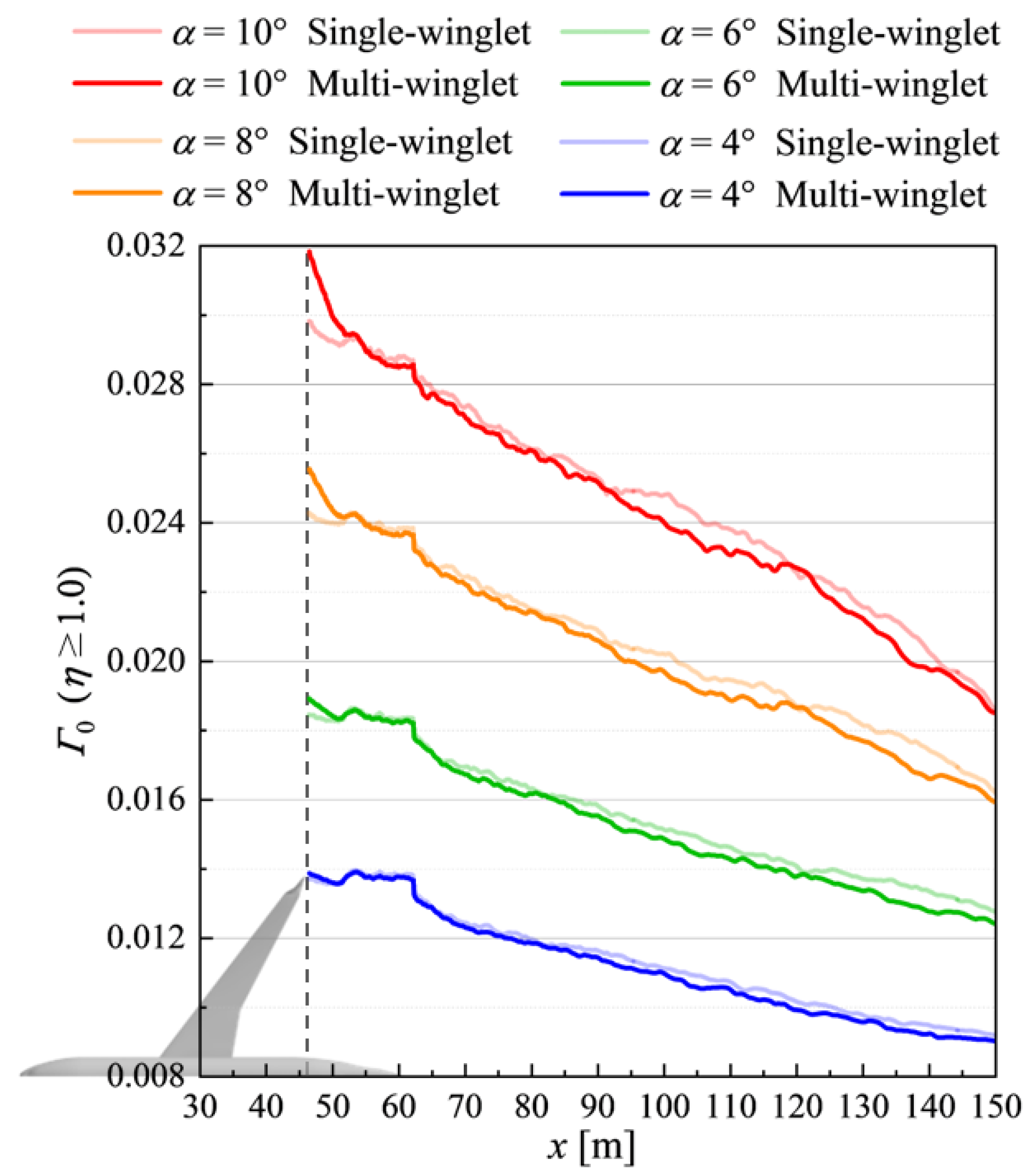
4.3.1. Disparity in Wingtip Wake Characteristics Based on Nondimensional Circulation
4.3.2. Analysis of Wake Turbulence Suppression by the Multi-Winglet Configuration
5. Conclusions
- Transonic conditions:Relative to the single-winglet configuration, the multi-winglet exhibited an increase in total drag of approximately three counts under cruise conditions. This increase was primarily attributed to greater profile drag, due to the enlarged frontal projected area, and additional wave drag induced by shock waves on the upper surfaces of the winglets. Conversely, the induced drag decreased by approximately 3.4 counts, primarily due to the shorter chord length of each winglet, which hinders the formation of wingtip vortices. Additionally, the negative cant angle of the rearmost winglet helps mitigate upward flow from the lower to the upper surface of the main wing, thereby reducing vortices at the wing–winglet junction. These results indicate that further geometric refinement of the multi-winglet may enable greater induced drag reduction, potentially offsetting the rise in other drag components. A future challenge under transonic conditions is to optimize the shape of the multi-winglet configuration to reduce profile drag or induced drag, thereby contributing to an overall reduction in total drag.
- Subsonic conditions:The multi-winglet consistently generated higher lift than the single winglet across most angles of attack. Prior to stall, this enhancement was primarily driven by the smaller leading-edge curvature of each winglet, which intensified flow acceleration over the upper surfaces. In the post-stall regime, the increased lift was attributed to leading-edge vortices that helped reattach separated flow to the upper surface, driven by accelerated airflow through the gaps between winglets. Reducing the spacing between the winglets enhances airflow across the entire upper surfaces, this effect is expected to be further amplified. In addition, the multi-winglet demonstrated improved wake vortex suppression compared to the single winglet, suggesting potential benefits for airport operations. However, the associated increase in bending moment at the wingtip—due to higher lift—may offset these benefits from a structural perspective, while the multi-winglet configuration offers notable aerodynamic advantages. Therefore, to compensate for its disadvantages and achieve improved lift performance, it is necessary to increase the area of the winglet relative to the main wing since lift is closely related to the projected area.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yamazaki, W.; Matsushima, K.; Nakahashi, K. Drag Prediction, Decomposition and Visualization in Unstructured Mesh CFD Solver of TAS-Code. Int. J. Numer. Methods Fluids 2008, 57, 417–436. [Google Scholar] [CrossRef]
- Kroo, I. Drag Due to Lift: Concepts for Prediction and Reduction. Annu. Rev. Fluid Mech. 2001, 33, 587–617. [Google Scholar] [CrossRef]
- Torenbeek, E. Advanced Aircraft Design: Conceptual Design, Analysis and Optimization of Subsonic Civil Airplanes; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Whitcomb, R.T. A Design Approach and Selected Wind Tunnel Results at High Subsonic Speeds for Wing-Tip Mounted Winglets. In NASA-TN-D-8260; NASA: Washington, DC, USA, 1976. [Google Scholar]
- Maughmer, M.D. Design of Winglets for High-Performance Sailplanes. J. Aircr. 2003, 40, 1099–1106. [Google Scholar] [CrossRef]
- Takenaka, K.; Hatanaka, K.; Yamazaki, W.; Nakahashi, K. Multidisciplinary Design Exploration for a Winglet. J. Aircr. 2008, 45, 1601–1611. [Google Scholar] [CrossRef]
- Elham, A.; van Tooren, M.J. Winglet Multi-Objective Shape Optimization. Aerosp. Sci. Technol. 2014, 37, 93–109. [Google Scholar] [CrossRef]
- Bourdin, P.; Gatto, A.; Friswell, M. Potential of Articulated Split Wingtips for Morphing-based Control of a Flying Wing. In Proceedings of the 25th AIAA Applied Aerodynamics Conference, Miami, FL, USA, 25–28 June 2007; p. 4443. [Google Scholar]
- Bourdin, P.; Gatto, A.; Friswell, M. Aircraft Control via Variable Cant-angle Winglets. J. Aircr. 2008, 45, 414–423. [Google Scholar] [CrossRef]
- Kaygan, E.; Gatto, A. Investigation of Adaptable Winglets for Improved UAV Control and Performance. Int. J. Mech. Aerospace, Ind. Mechatronics Eng. 2014, 8, 1281–1286. [Google Scholar]
- Kaygan, E. Aerodynamic Analysis of Morphing Winglets for Improved Commercial Aircraft Performance. J. Aviat. 2020, 4, 31–44. [Google Scholar] [CrossRef]
- Reddy, S.R.; Sobieczky, H.; Abdoli, A.; Dulikravic, G.S. Winglets-Multiobjective Optimization of Aerodynamic Shapes. In Proceedings of the 11th World Congress on Computational Mechanics, Barcelona, Spain, 20–25 July 2014. [Google Scholar]
- Afonso, F.; Vale, J.; Lau, F.; Suleman, A. Performance Based Multidisciplinary Design Optimization of Morphing Aircraft. Aerosp. Sci. Technol. 2017, 67, 1–12. [Google Scholar] [CrossRef]
- Tabata, S.; Yamazaki, W.; Yuhara, T. Drag/Weight Reduction Using Split-Tip Winglet for TRA2012A Model. Trans. Jpn. Soc. Aeronaut. Space Sci. 2020, 63, 69–79. [Google Scholar] [CrossRef]
- Smith, M.; Komerath, N.; Ames, R.; Wong, O.; Pearson, J. Performance Analysis of a Wing with Multiple Winglets. In Proceedings of the AIAA Paper-2001-2407 on 19th AIAA Applied Aerodynamics Conference, Anaheim, CA, USA, 11–14 June 2001; p. 2407. [Google Scholar] [CrossRef]
- Gerrero, J.E.; Maestro, D.; Bottaro, A. Biomimetic Spiroid Winglets for Lift and Drag Control. Comptes Rendus Mécanique 2012, 340, 67–80. [Google Scholar] [CrossRef]
- Tucker, V.A. Drag Reduction by Wing Tip Slots in a Gliding Harris’ Hawk, Parabuteo Unicinctus. J. Exp. Biol. 1995, 198, 775–781. [Google Scholar] [CrossRef] [PubMed]
- Shelton, A.; Tomar, A.; Prasad, J.V.R.; Smith, M.J.; Komerath, N. Active Multiple Winglets for Improved Unmanned-Aerial-Vehicle Performance. J. Aircr. 2006, 43, 110–116. [Google Scholar] [CrossRef]
- Miklosovic, D.S. Analytic and Experimental Investigation of Dihedral Configurations of Three-Winglet Planforms. J. Fluids Eng. 2008, 130, 071103. [Google Scholar] [CrossRef]
- Fluck, M.; Crawford, C. A Lifting Line Model to Investigate the Influence of Tip Feathers on Wing Performance. Bioinspiration Biomimetics 2014, 9, 046017. [Google Scholar] [CrossRef] [PubMed]
- Narayan, G.; John, B. Effect of Winglets Induced Tip Vortex Structure on the Performance of Subsonic Wings. Aerosp. Sci. Technol. 2016, 58, 328–340. [Google Scholar] [CrossRef]
- Hui, Z.; Cheng, G.; Chen, G. Experimental Investigation on Tip-Vortex Flow Characteristics of Novel Bionic Multi-Tip Winglet Configurations. Phys. Fluids 2021, 33, 011902. [Google Scholar] [CrossRef]
- Lynch, M.; Mandadzhiev, B.; Wissa, A. Bioinspired Wingtip Devices: A Pathway to Improve Aerodynamic Performance during Low Reynolds Number Flight. Bioinspiration Biomimetics 2018, 13, 036003. [Google Scholar] [CrossRef]
- Reddy, S.R.; Sobieczky, H.; Dulikravic, G.S.; Abdoli, A. Multi-Element Winglets: Multi-Objective Optimization of Aerodynamic Shapes. J. Aircr. 2016, 53, 992–1000. [Google Scholar] [CrossRef]
- Rivers, M.B. NASA Common Research Model: A History and Future Plans. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 3725. [Google Scholar] [CrossRef]
- Tinoco, E.N.; Brodersen, O.P.; Keye, S.; Laflin, K.R.; Feltrop, E.; Vassberg, J.C.; Mani, M.; Rider, B.; Wahls, R.A.; Morrison, J.H.; et al. Summary Data from the Sixth AIAA CFD Drag Prediction Workshop: CRM Cases. J. Aircr. 2018, 55, 1352–1379. [Google Scholar] [CrossRef]
- Catalano, F.; Ceron-Muñoz, H. Experimental Analysis of Aerodynamics Characteristics of Adaptive Multi-Winglets. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005; p. 1231. [Google Scholar]
- Ito, Y.; Nakahashi, K. Direct Surface Triangulation Using Stereolithography Data. AIAA J. 2002, 40, 490–496. [Google Scholar] [CrossRef]
- Ito, Y.; Nakahashi, K. Surface Triangulation for Polygonal Models Based on CAD Data. Int. J. Numer. Methods Fluids 2002, 39, 75–96. [Google Scholar] [CrossRef]
- Ito, Y.; Nakahashi, K. Improvements in the Reliability and Quality of Unstructured Hybrid Mesh Generation. Int. J. Numer. Methods Fluids 2004, 45, 79–108. [Google Scholar] [CrossRef]
- Ito, Y.; Shih, A.M.; Soni, B.K. Reliable Isotropic Tetrahedral Mesh Generation Based on an Advancing Front Method. In Proceedings of the 13th International Meshing Roundtable, Williamsburg, VA, USA, 19–22 September 2004; pp. 95–105. [Google Scholar]
- Ito, Y.; Shih, A.M.; Soni, B.K.; Nakahashi, K. Multiple Marching Direction Approach to Generate High Quality Hybrid Meshes. AIAA J. 2007, 45, 162–167. [Google Scholar] [CrossRef]
- Ito, Y.; Shih, A.M.; Soni, B.K. Octree-Based Reasonable-Quality Hexahedral Mesh Generation Using a New Set of Refinement Templates. Int. J. Numer. Methods Eng. 2009, 77, 1809–1833. [Google Scholar] [CrossRef]
- Ito, Y.; Murayama, M.; Yamamoto, K.; Shih, A.M.; Soni, B.K. Efficient Computational Fluid Dynamics Evaluation of Small Device Locations with Automatic Local Remeshing. AIAA J. 2009, 47, 1270–1276. [Google Scholar] [CrossRef]
- Ito, Y.; Shih, A.M.; Koomullil, R.P.; Kasmai, N.; Jankun-Kelly, M.; Thompson, D. Solution Adaptive Mesh Generation Using Feature-Aligned Embedded Surface Meshes. AIAA J. 2009, 47, 1879–1888. [Google Scholar] [CrossRef]
- Ito, Y.; Murayama, M.; Yamamoto, K.; Shih, A.M.; Soni, B.K. Efficient Hybrid Surface and Volume Mesh Generation for Viscous Flow Simulations. In Proceedings of the AIAA Paper-2011-3539 on the AIAA Aviation 2011 Forum, Virginia Beach, VA, USA, 21–22 September 2011; p. 3539. [Google Scholar] [CrossRef]
- Ito, Y.; Shih, A.M.; Soni, B.K. Three Dimensional Automatic Local Remeshing for Two or More Hybrid Meshes. Int. J. Numer. Methods Fluids 2011, 66, 1495–1505. [Google Scholar] [CrossRef]
- Ito, Y.; Shih, A.M.; Soni, B.K. Hybrid Mesh Generation with Embedded Surfaces Using a Multiple Marching Direction Approach. Int. J. Numer. Methods Fluids 2011, 67, 1–7. [Google Scholar] [CrossRef]
- Hashimoto, A.; Murakami, K.; Aoyama, T.; Ishiko, K.; Hishida, M.; Sakashita, M.; Lahur, P.R. Toward the Fastest Unstructured CFD Code “FaSTAR”. In Proceedings of the AIAA Paper-2012-1075 on the 50th AIAA Aerospace Sciences Meeting, Nashville, TN, USA, 9–12 January 2012; p. 1075. [Google Scholar] [CrossRef]
- van Leer, B. Towards the Ultimate Conservative Differences Scheme V. A Second Order Sequel to Godunov’s Method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Hishida, M.; Hashimoto, A.; Murakami, K.; Aoyama, T. A New Slope Limiter for Fast Unstructured CFD Solver FaSTAR. In Proceedings of the 42nd Fluid Dynamics Conference/Aerospace Numerical Simulation Symposium, Yonago, Tottori, Japan, 24–25 June 2010; pp. 85–90. (In Japanese). [Google Scholar]
- Obayashi, S.; Guruswamy, G.P. Convergence Acceleration of an Aeroelastic Navier-Stokes Solver. AIAA J. 1994, 33, 1134–1141. [Google Scholar] [CrossRef]
- Sharov, D.; Nakahashi, K. Reordering of Hybrid Unstructured Grids for Lower-Upper Symmetric Gauss-Seidel Computations. AIAA J. 1998, 36, 484–486. [Google Scholar] [CrossRef]
- Hellsten, A.K. New Advanced k-ω Turbulence Model for High-Lift Aerodynamics. AIAA J. 2005, 43, 1857–1869. [Google Scholar] [CrossRef]
- Wallin, S.; Johansson, A.V. An Explicit Algebraic Reynolds Stress Model for Incompressible and Compressible Turbulent Flows. J. Fluid Mech. 2000, 403, 89–132. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Rumsey, C.L.; Slotnick, J.P.; Woeber, C.D. Fourth High-Lift Prediction/third Geometry and Mesh Generation Workshops: Overview and Summary. J. Aircr. 2023, 60, 1160–1177. [Google Scholar] [CrossRef]
- Hunt, J.C.R.; Wray, A.A.; Moin, P. Eddies, Streams, and Convergence Zones in Turbulent Flows. In Proceedings of the Center for Turbulence Research Proceedings of the Summer Program, Stanford, CA, USA, 27 June–22 July 1988; pp. 193–208. [Google Scholar]
- Holzäpfel, F.; Gerz, T.; Köpp, F.; Stumpf, E.; Harris, M.; Young, R.I.; Dolfi-Bouteyre, A. Strategies for Circulation Evaluation of Aircraft Wake Vortices Measured by Lidar. J. Atmos. Ocean. Technol. 2003, 20, 1183–1195. [Google Scholar] [CrossRef]
- Misaka, T.; Yoshimura, R.; Obayashi, S.; Kikuchi, R. Large-Eddy Simulation of Wake Vortices at Tokyo/Haneda International Airport. J. Aircr. 2023, 60, 1819–1831. [Google Scholar] [CrossRef]
- Kantha, L.H. Empirical model of transport and decay of aircraft wake vortices. J. Aircr. 1998, 35, 649–653. [Google Scholar] [CrossRef]
- Gerz, T.; Holzäpfel, F.; Darracq, D. Commercial aircraft wake vortices. Prog. Aerosp. Sci. 2002, 38, 181–208. [Google Scholar] [CrossRef]
- Holzäpfel, F. Probabilistic two-phase wake vortex decay and transport model. J. Aircr. 2003, 40, 323–331. [Google Scholar] [CrossRef]








| Parameter | Symbol | Measurement |
|---|---|---|
| winglet sweep angle | 43° | |
| winglet cant angle | 63° | |
| winglet height | h | 2.56 m |
| chord length at winglet tip | 0.81 m | |
| chord length at winglet root | 2.73 m |
| Subsonic | Transonic | |
|---|---|---|
| Mach number M | 0.2 | 0.85 |
| Angle of attack [] | 0, 2, 4, 6, 8, 10, 12 | 0, 2.75, 5, 6, 7, 8, 9, 10 |
| Reynolds number |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kobayashi, E.; Chiba, K.; Yamazaki, W.; Kanazaki, M. Aerodynamic Effects of a Blended Multi-Winglet on an Airliner in Subsonic and Transonic Regimes. Biomimetics 2025, 10, 522. https://doi.org/10.3390/biomimetics10080522
Kobayashi E, Chiba K, Yamazaki W, Kanazaki M. Aerodynamic Effects of a Blended Multi-Winglet on an Airliner in Subsonic and Transonic Regimes. Biomimetics. 2025; 10(8):522. https://doi.org/10.3390/biomimetics10080522
Chicago/Turabian StyleKobayashi, Erina, Kazuhisa Chiba, Wataru Yamazaki, and Masahiro Kanazaki. 2025. "Aerodynamic Effects of a Blended Multi-Winglet on an Airliner in Subsonic and Transonic Regimes" Biomimetics 10, no. 8: 522. https://doi.org/10.3390/biomimetics10080522
APA StyleKobayashi, E., Chiba, K., Yamazaki, W., & Kanazaki, M. (2025). Aerodynamic Effects of a Blended Multi-Winglet on an Airliner in Subsonic and Transonic Regimes. Biomimetics, 10(8), 522. https://doi.org/10.3390/biomimetics10080522







