FROM: A Fish Recognition-Inspired Optimization Method for Multi-Agent Decision-Making Problems with a Fluid Environment
Abstract
1. Introduction
2. Background
2.1. Particle Swarm Optimization
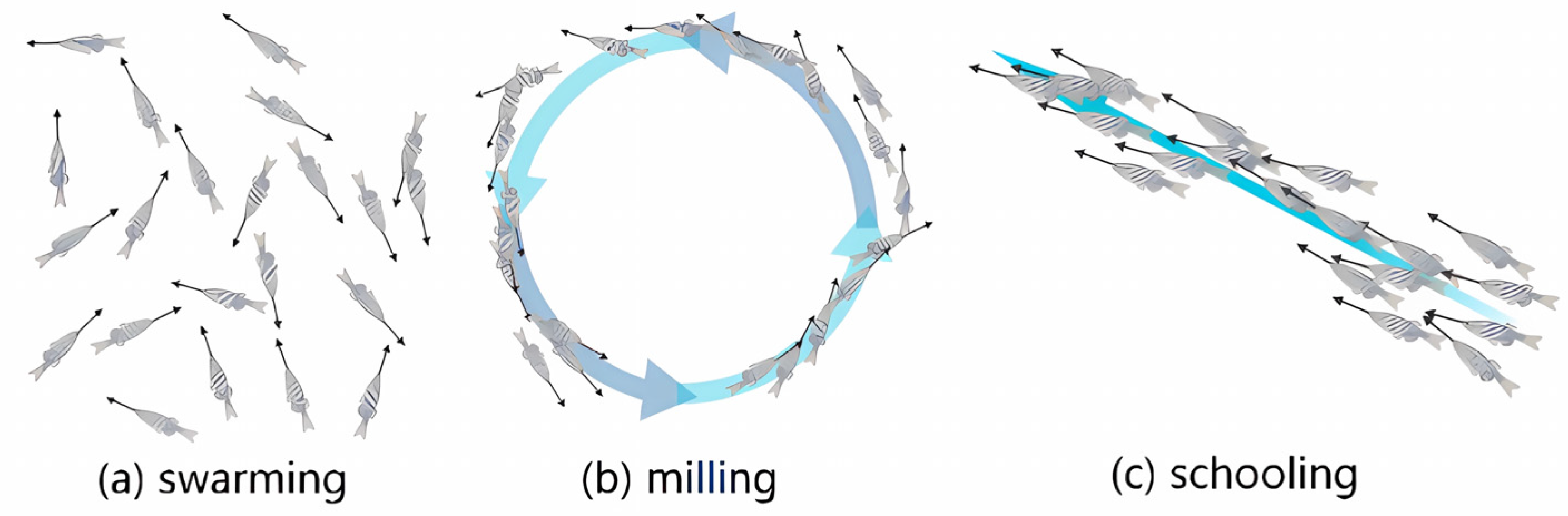
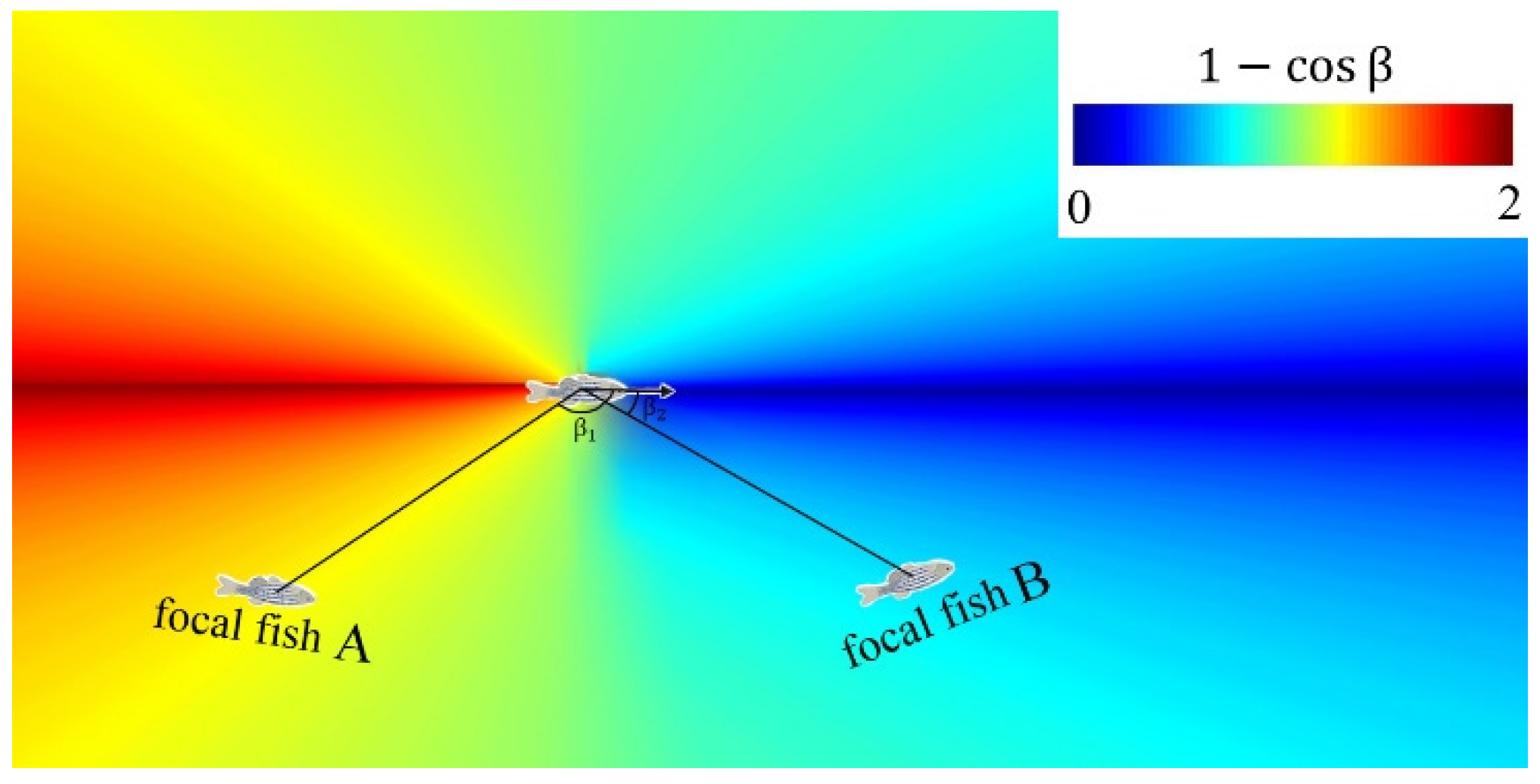
2.2. Fish Recognition
2.3. Voronoi Neighbor
2.4. Proposed Algorithm
3. Fish Recognition Optimization Method
3.1. Computational Complexity Analysis
3.2. Experiments
3.3. Benchmark Functions and Parameter Setting
4. Experimental Results
Convergence Curve of Algorithms
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rădulescu, R.; Mannion, P.; Roijers, D.M.; Nowé, A. Multi-objective multi-agent decision making: A utility-based analysis and survey. Auton. Agents Multi-Agent Syst. 2019, 34, 10. [Google Scholar]
- Pal, M.; Mittal, M.L.; Soni, G.; Chouhan, S.S.; Kumar, M. A multi-agent system for FJSP with setup and transportation times. Expert Syst. Appl. 2022, 216, 119474. [Google Scholar]
- Koops, W.; Jansen, N.; Junges, S.; Simão, T.D. Recursive small-step multi-agent A* for dec-POMDPs. In Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligenc, Macao, China, 19–25 August 2023. [Google Scholar]
- Liu, M.; Amato, C.; Anesta, E.; Griffith, J.; How, J. Learning for decentralized control of multiagent systems in large, partially-observable stochastic environments. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Dorigo, M.; Di Caro, G. Ant colony optimization: A new meta-heuristic. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99, Washington, DC, USA, 6–9 July 1999; IEEE: Piscataway, NJ, USA, 1999. Cat. No. 99TH8406. Volume 2, pp. 1470–1477. [Google Scholar]
- Lim, W.H.; Isa, N.A.M. An adaptive two-layer particle swarm optimization with elitist learning strategy. Inf. Sci. 2014, 273, 49–72. [Google Scholar] [CrossRef]
- Zhan, Z.H.; Zhang, J.; Liu, O. Orthogonal learning particle swarm optimization. IEEE Trans. Evol. Comput. 2011, 15, 832–847. [Google Scholar]
- Houssein, E.H.; Gad, A.G.; Hussain, K.; Suganthan, P.N. Major advances in particle swarm optimization: Theory, analysis, and application. Swarm Evol. Comput. 2021, 63, 100868. [Google Scholar]
- Dagal, I.; Akın, B.; Akboy, E. Improved salp swarm algorithm based on particle swarm optimization for maximum power point tracking of optimal photovoltaic systems. Int. J. Energy Res. 2022, 46, 8742–8759. [Google Scholar]
- Wang, Z.; Li, G.; Ren, J. Dynamic path planning for unmanned surface vehicle in complex offshore areas based on hybrid algorithm. Comput. Commun. 2021, 166, 49–56. [Google Scholar]
- Zeng, N.; Wang, Z.; Liu, W.; Zhang, H.; Hone, K.; Liu, X. A dynamic neighborhood-based switching particle swarm optimization algorithm. IEEE Trans. Cybern. 2020, 52, 9290–9301. [Google Scholar] [CrossRef]
- Whitley, D. A genetic algorithm tutorial. Stat. Comput. 1994, 4, 65–85. [Google Scholar]
- Boettcher, S.; Percus, A.G. Extremal optimization: Methods derived from co-evolution. In Proceedings of the 1st Annual Conference on Genetic and Evolutionary Computation, Orlando, FL, USA, 13–17 July 1999; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 1999; Volume 1, pp. 825–832. [Google Scholar]
- Eslami, M.; Shareef, H.; Khajehzadeh, M.; Mohamed, A. A survey of the state of the art in particle swarm optimization. Res. J. Appl. Sci. Eng. Technol. 2012, 4, 1181–1197. [Google Scholar]
- Parrott, D.; Li, X. Locating and tracking multiple dynamic optima by a particle swarm model using speciation. IEEE Trans. Evol. Comput. 2006, 10, 440–458. [Google Scholar] [CrossRef]
- Mendes, R.; Kennedy, J.; Neves, J. The fully informed particle swarm: Simpler, maybe better. IEEE Trans. Evol. Comput. 2004, 8, 204–210. [Google Scholar] [CrossRef]
- Liang, J.J.; Qin, A.K.; Suganthan, P.N.; Baskar, S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Brown, C.; Laland, K.; Krause, J. Fish Cognition and Behavior; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 21. [Google Scholar]
- Makowicz, A.M.; Tiedemann, R.; Steele, R.N.; Schlupp, I. Kin recognition in a clonal fish, Poecilia formosa. PLoS ONE 2016, 11, e0158442. [Google Scholar] [CrossRef]
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. In ACM SIGGRAPH Computer Graphics; ACM: New York, NY, USA, 1987; Volume 21, pp. 25–34. [Google Scholar]
- Shimoyama, N.; Sugawara, K.; Mizuguchi, T.; Hayakawa, Y.; Sano, M. Collective motion in a system of motile elements. Phys. Rev. Lett. 1996, 76, 3870–3873. [Google Scholar] [CrossRef]
- Cavagna, A.; Cimarelli, A.; Giardina, I.; Parisi, G.; Santagati, R.; Stefanini, F.; Viale, M. Scale-free correlations in starling flocks. Proc. Natl. Acad. Sci. USA 2010, 107, 11865–11870. [Google Scholar] [CrossRef]
- Ballerini, M.; Cabibbo, N.; Candelier, R.; Cavagna, A.; Cisbani, E.; Giardina, I.; Lecomte, V.; Orlandi, A.; Parisi, G.; Procaccini, A.; et al. Interaction ruling animal collective behavior depends on topological rather than metric distance: Evidence from a field study. Proc. Natl. Acad. Sci. USA 2008, 105, 1232–1237. [Google Scholar] [CrossRef]
- Calovi, D.S.; Lopez, U.; Ngo, S.; Sire, C.; Chaté, H.; Theraulaz, G. Swarming, schooling, milling: Phase diagram of a data-driven fish school model. New J. Phys. 2014, 16, 015026. [Google Scholar] [CrossRef]
- Solar, R.; Suppi, R.; Luque, E. High performance distributed cluster-based individual-oriented fish school simulation. Procedia Comput. Sci. 2011, 4, 76–85. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, B.; Zhang, Q.; Liang, J.; Suganthan, P.; Qu, B. Problem Definitions and Evaluation Criteria for CEC 2015 Special Session on Bound Constrained Single-Objective Computationally Expensive Numerical Optimization; Technical Report, Computational Intelligence Laboratory, Zhengzhou University, Zhengzhou, China and Technical Report; Nanyang Technological University: Singapore, 2014. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar]
- Yang, X.S. Firefly algorithms for multimodal optimization. In International Symposium on Stochastic Algorithms; Springer: Berlin/Heidelberg, Germany, 2009; pp. 169–178. [Google Scholar]
- Jordehi, A.R. Enhanced leader PSO (ELPSO): A new PSO variant for solving global optimisation problems. Appl. Soft Comput. 2015, 26, 401–417. [Google Scholar]
- Kiani, A.T.; Nadeem, M.F.; Ahmed, A.; Sajjad, I.A.; Raza, A.; Khan, I.A. Chaotic Inertia Weight Particle Swarm Optimization (CIWPSO): An Efficient Technique for Solar Cell Parameter Estimation. In Proceedings of the 2020 3rd International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 29–30 January 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]
- Ghasemi, M.; Aghaei, J.; Hadipour, M. New self-organising hierarchical PSO with jumping time-varying acceleration coefficients. Electron. Lett. 2017, 53, 1360–1362. [Google Scholar] [CrossRef]



| Functions | Name | Search Space |
|---|---|---|
| Sphere | ||
| Dixon&Price | ||
| Zakharov | ||
| Bent Cigar | ||
| Discus | ||
| Rastrigin | ||
| Levy | ||
| Griewank | ||
| Rosenbrock | ||
| Ackley | ||
| Katsuura | ||
| HGBat | ||
| Weierstrass | ||
| HappyCat |
| Algorithm | Parameter | Value |
|---|---|---|
| FROM | Inertia weight range | (0.4,0.9) |
| Learning factor | 2 | |
| Alignment intensity | 9 | |
| Dipole intensity | 0.01 | |
| DE | Crossover probability | 0.9 |
| Scaling factor | 0.5 | |
| ABC | Sole control | 50 |
| GA | Crossover rate | 0.8 |
| FSO | Attraction coefficient | 0.6 |
| Randomness factor | 0.5 | |
| Attraction exponent | 1 |
| FROM | DE | ABC | GA | FSO | ||
|---|---|---|---|---|---|---|
| Min | 1.30E−20 | 6.31E−09 * | 1.34E−09 * | 0.00398 * | 7.16E−06 * | |
| Max | 1.33E−13 | 1.85E−07 * | 3.69E−08 * | 0.06715 * | 0.00007 * | |
| Std | 1.60E−14 | 3.22E−08 * | 1.05E−08 * | 0.01580 * | 9.46E−06 * | |
| Mean | 4.59E−15 | 6.21E−08 * | 1.15E−08 * | 0.01253 * | 0.00002 * | |
| Mdn | 3.03E−16 | 4.48E−08 * | 9.65E−09 * | 0.00566 * | 0.00002 * | |
| Min | 5.63E−14 | 4.93E−04 * | 0.00378 * | 0.92415 * | 0.00029 * | |
| Max | 0.00969 | 0.01637 | 0.18252 * | 1.79E+01 * | 0.13001 * | |
| Std | 0.00028 | 0.00516 | 0.02304 * | 1.94616 * | 0.00035 | |
| Mean | 0.00038 | 0.00707 | 0.02247 * | 1.44535 * | 0.00106 | |
| Mdn | 4.35E−12 | 0.00709 * | 0.02457 * | 0.84357 * | 0.00093 * | |
| Min | 4.32E−15 | 9.83E−06 * | 0.00057 * | 0.00334 * | 0.00002 * | |
| Max | 2.12E−11 | 0.00014 * | 0.00948 * | 2.43237 * | 0.00021 * | |
| Std | 2.44E−12 | 0.00003 * | 0.00210 * | 0.35081 * | 0.00003 * | |
| Mean | 1.08E−12 | 0.00006 * | 0.00303 * | 0.07064 * | 0.00008 * | |
| Mdn | 4.47E−13 | 0.00005 * | 0.00206 * | 0.02581 * | 0.00009 * | |
| Min | 1.75E−12 | 1.32756 * | 2.43570 * | 1.10E+05 * | 3.20E+03 * | |
| Max | 7.37E−05 | 2.91E+01 * | 3.19E+01 * | 1.57E+04 * | 5.07E+04 * | |
| Std | 7.75E−06 | 6.01800 * | 5.84972 * | 1.68E+04 * | 7.95E+03 * | |
| Mean | 2.43E−06 | 7.89165 * | 1.08E+01 * | 1.66E+04 * | 2.18E+04 * | |
| Mdn | 1.18E−07 | 5.07370 * | 8.74219 * | 1.16E+04 * | 1.71E+04 * | |
| Min | 3.38E−16 | 0.00010 * | 0.00032 * | 9.10E+01 * | 2.47E+01 * | |
| Max | 1.58E−07 | 0.00802 * | 0.00704 * | 4.25E+04 * | 1.56E+03 * | |
| Std | 2.89E−08 | 0.00106 * | 0.00119 * | 6.77E+03 * | 3.78E+02 * | |
| Mean | 6.85E−09 | 0.00083 * | 0.00300 * | 1.81E+03 * | 5.32E+02 * | |
| Mdn | 3.89E−10 | 0.00050 * | 0.00259 * | 9.91E+01 * | 4.25E+02 * | |
| Min | 0 | 2.87513 * | 0.71500 * | 0.04474 * | 0.00447 * | |
| Max | 0.11801 | 8.89275 | 4.40550 | 8.65774 | 7.41608 | |
| Std | 0.11680 | 1.45278 | 0.92279 | 1.81062 | 1.38240 | |
| Mean | 0.04929 | 6.22205 * | 2.60928 * | 1.19091 * | 3.28183 * | |
| Mdn | 2.34E−09 | 6.24618 * | 2.63736 * | 0.40725 * | 3.47737 * | |
| Min | 2.38E−18 | 6.17E−07 * | 5.47E−07 * | 0.00490 * | 0.00004 * | |
| Max | 4.29E−14 | 0.00001 * | 0.00003 * | 0.04756 * | 0.00035 * | |
| Std | 6.02E−15 | 2.25E−06 * | 3.38E−06 * | 0.01162 * | 0.00009 * | |
| Mean | 3.02E−15 | 3.81E−06 * | 4.09E−06 * | 0.01583 * | 0.00017 * | |
| Mdn | 8.37E−16 | 3.59E−06 * | 3.39E−06 * | 0.00734 * | 0.00021 * | |
| Min | 0.01188 | 0.05090 | 0.04323 | 0.18396 | 0.01448 | |
| Max | 0.06633 | 0.28007 | 0.19701 | 0.83674 | 1.08647 * | |
| Std | 0.01046 | 0.04837 | 0.03117 | 0.08162 | 0.24884 | |
| Mean | 0.04200 | 0.16584 | 0.14280 | 0.35428 | 0.25656 | |
| Mdn | 0.04978 | 0.16560 | 0.12214 | 0.25374 | 0.19978 | |
| Min | 0.00464 | 0.23492 * | 0.18165 * | 0.50303 * | 0.00028 | |
| Max | 0.04824 | 0.83620 | 2.52288 * | 1.71746 * | 1.93466 * | |
| Std | 0.00917 | 0.14942 * | 0.35353 * | 0.31492 * | 0.25213 * | |
| Mean | 0.02054 | 0.48341 | 0.89425 | 0.54089 | 0.30615 | |
| Mdn | 0.01859 | 0.40361 | 0.89080 | 0.53205 | 0.31455 | |
| Min | 6.28E−09 | 0.00089 * | 0.00027 * | 3.71091 * | 0.01626 * | |
| Max | 3.06E−07 | 0.00554 * | 0.00162 * | 1.21E+01 * | 0.06134 * | |
| Std | 7.27E−08 | 0.00064 * | 0.00026 * | 1.38500 * | 0.01197 * | |
| Mean | 8.51E−08 | 0.00241 * | 0.00074 * | 7.85928 * | 0.03676 * | |
| Mdn | 3.91E−08 | 0.00232 * | 0.00067 * | 5.80086 * | 0.03803 * | |
| Min | 0 | 0 | 0 | 0 | 0 | |
| Max | 0 | 0 | 0 | 2.10E−07 * | 0 | |
| Std | 0 | 0 | 0 | 4.62E−08 * | 0 | |
| Mean | 0 | 0 | 0 | 6.58E−08 * | 0 | |
| Mdn | 0 | 0 | 0 | 4.29E−08 * | 0 | |
| Min | 0.49493 | 0.51290 | 0.52326 | 1.58312 | 0.58300 | |
| Max | 0.50285 | 0.55368 | 0.59951 | 6.95268 | 0.63250 | |
| Std | 0.00640 | 0.01712 | 0.00868 | 1.37484 * | 0.01470 | |
| Mean | 0.47134 | 0.64055 | 0.43431 | 2.41094 | 0.55364 | |
| Mdn | 0.55712 | 0.62216 | 0.60994 | 1.87850 | 0.64537 | |
| Min | 0 | 3.38E−15 * | 1.96924 * | 0.84638 * | 1.52E−14 * | |
| Max | 1.31E−14 | 1.51E−14 | 3.83714 * | 2.98080 * | 0.13062 * | |
| Std | 1.56E−15 | 1.46E−15 | 0.38622 * | 0.43279 * | 0.04251 * | |
| Mean | 2.14E−15 | 3.66E−15 | 2.85102 * | 2.70720 * | 0.01958 * | |
| Mdn | 1.49E−15 | 4.03E−15 | 3.26898 * | 2.74500 * | 0.00179 * | |
| Min | 0.04989 | 0.07565 | 0.08796 | 0.19671 | 0.06136 | |
| Max | 0.19393 | 0.41287 | 0.23612 | 1.74324 | 0.22415 | |
| Std | 0.01197 | 0.06424 | 0.04401 | 0.39480 | 0.03163 | |
| Mean | 0.02851 | 0.25064 | 0.15006 | 0.55733 | 0.11247 | |
| Mdn | 0.10068 | 0.20667 | 0.18804 | 0.47124 | 0.11113 | |
| FROM | ELPSO | CAIWPSO | CRIWPSO | TVAPSO | ||
|---|---|---|---|---|---|---|
| Min | 1.30E−20 | 4.95E−16 * | 6.25E−14 * | 1.28E−10 * | 4.66E−13 * | |
| Max | 1.33E−13 | 2.74E−12 | 3.55E−11 * | 1.68E−08 * | 1.74E−11 * | |
| Std | 1.60E−14 | 5.43E−12 * | 6.36E−12 * | 3.28E−09 * | 2.86E−12 * | |
| Mean | 4.59E−15 | 7.18E−15 | 1.58E−12 * | 2.15E−09 * | 4.09E−12 * | |
| Mdn | 3.03E−16 | 4.17E−15 | 6.33E−13 * | 1.11E−09 * | 3.10E−12 * | |
| Min | 5.63E−14 | 8.60E−13 | 1.09E−10 * | 3.28E−08 * | 2.02E−10 * | |
| Max | 0.00969 | 0.55669 * | 0.78004 * | 0.77471 * | 0.53669 * | |
| Std | 0.00028 | 0.18884 * | 0.16598 * | 0.17420 * | 0.17749 * | |
| Mean | 0.00038 | 0.03396 * | 0.03304 * | 0.05623 * | 0.04304 * | |
| Mdn | 4.35E−12 | 3.51E−10 * | 1.09E−08 * | 1.17E−06 * | 4.82E−09 * | |
| Min | 4.32E−15 | 4.51E−13 * | 1.39E−11 * | 6.07E−09 * | 1.52E−11 * | |
| Max | 2.12E−11 | 1.77E−10 | 3.51E−09 * | 1.58E−06 * | 2.38E−09 * | |
| Std | 2.44E−12 | 2.49E−11 | 8.77E−10 * | 2.29E−07 * | 3.10E−10 * | |
| Mean | 1.08E−12 | 1.63E−11 | 5.83E−10 * | 9.97E−08 * | 3.30E−10 * | |
| Mdn | 4.47E−13 | 5.44E−12 | 2.26E−10 * | 6.21E−08 * | 2.88E−10 * | |
| Min | 1.75E−12 | 7.86E−07 * | 0.00005 * | 0.01327 * | 0.00089 * | |
| Max | 7.37E−05 | 1.03E+04 * | 9.97E+03 * | 0.72730 * | 0.06350 * | |
| Std | 7.75E−06 | 2.40E+03 * | 1.15E+03 * | 0.12979 * | 0.01020 * | |
| Mean | 2.43E−06 | 6.39E+02 * | 1.97E+02 * | 0.17407 * | 0.01065 * | |
| Mdn | 1.18E−07 | 7.17E−06 | 0.00080 * | 0.12701 * | 0.00501 * | |
| Min | 3.38E−16 | 3.62E−10 * | 3.40E−08 * | 0.00002 * | 1.77E−06 * | |
| Max | 1.58E−07 | 1.42E−07 | 0.00003 * | 0.00200 * | 0.00017 * | |
| Std | 2.89E−08 | 2.95E−08 | 2.85E−06 * | 0.00048 * | 0.00005 * | |
| Mean | 6.85E−09 | 1.32E−08 | 2.10E−06 * | 0.00047 * | 0.00005 * | |
| Mdn | 3.89E−10 | 4.35E−09 | 7.46E−07 * | 0.00029 * | 0.00003 * | |
| Min | 0 | 2.49E−11 * | 6.78E−10 * | 2.98E−06 * | 6.66E−09 * | |
| Max | 0.11801 | 2.17271 | 0.90050 | 1.73373 | 1.06283 | |
| Std | 0.11680 | 0.45405 | 0.37369 | 0.48283 | 0.37693 | |
| Mean | 0.04929 | 0.16666 | 0.18609 | 0.33479 | 0.17190 | |
| Mdn | 2.34E−09 | 1.90E−06 * | 0.00004 * | 0.00897 * | 0.00013 * | |
| Min | 2.38E−18 | 5.71E−15 * | 1.24E−12 * | 2.96E−09 * | 1.02E−12 * | |
| Max | 4.29E−14 | 8.75E−13 | 3.21E−10 * | 1.60E−07 * | 3.67E−10 * | |
| Std | 6.02E−15 | 1.34E−13 * | 4.25E−11 * | 2.85E−08 * | 8.23E−11 * | |
| Mean | 3.02E−15 | 1.20E−13 * | 2.53E−11 * | 3.09E−08 * | 7.22E−11 * | |
| Mdn | 8.37E−16 | 7.99E−14 * | 1.12E−11 * | 1.51E−08 * | 6.69E−11 * | |
| Min | 0.01188 | 0.01036 | 0.00192 | 0.01254 | 0.00717 | |
| Max | 0.06633 | 0.21000 | 0.18537 | 0.19089 | 0.05865 | |
| Std | 0.01046 | 0.04513 | 0.03344 | 0.03242 | 0.00910 | |
| Mean | 0.04200 | 0.05674 | 0.06536 | 0.06012 | 0.03507 | |
| Mdn | 0.04978 | 0.04606 | 0.04698 | 0.03869 | 0.03546 | |
| Min | 0.00464 | 0.00076 | 0.05263 * | 0.01695 * | 0.00063 | |
| Max | 0.04824 | 2.03537 * | 1.32526 * | 5.98459 * | 0.03487 | |
| Std | 0.00917 | 0.33229 * | 0.15340 * | 0.79859 * | 0.00386 | |
| Mean | 0.02054 | 0.34094 * | 0.32745 * | 0.45111 * | 0.00553 | |
| Mdn | 0.01859 | 0.26697 * | 0.35009 * | 0.38428 * | 0.00211 | |
| Min | 6.28E−09 | 9.20E−08 | 1.95E−06 * | 0.00006 * | 4.25E−06 * | |
| Max | 3.06E−07 | 2.19E−06 | 0.00002 * | 0.00069 * | 0.00004 * | |
| Std | 7.27E−08 | 3.24E−07 | 4.74E−06 * | 0.00015 * | 7.52E−06 * | |
| Mean | 8.51E−08 | 7.10E−07 | 9.40E−06 * | 0.00039 * | 0.00002 * | |
| Mdn | 3.91E−08 | 6.21E−07 | 8.71E−06 * | 0.00029 * | 0.00001 * | |
| Min | 0 | 0 | 0 | 0 | 0 | |
| Max | 0 | 0 | 0 | 0 | 0 | |
| Std | 0 | 0 | 0 | 0 | 0 | |
| Mean | 0 | 0 | 0 | 0 | 0 | |
| Mdn | 0 | 0 | 0 | 0 | 0 | |
| Min | 0.49493 | 0.49998 | 0.51538 | 0.41493 | 0.56342 | |
| Max | 0.50285 | 0.51123 | 0.60289 | 0.45152 | 0.57651 | |
| Std | 0.00640 | 0.00993 | 0.00907 | 0.00369 | 0.00524 | |
| Mean | 0.47134 | 0.59616 | 0.42643 | 0.41689 | 0.51907 | |
| Mdn | 0.55712 | 0.57819 | 0.59783 | 0.46012 | 0.60424 | |
| Min | 0 | 0 | 1.73E−15 * | 1.49E−15 * | 2.46E−14 * | |
| Max | 1.31E−14 | 1.51E−14 | 3.35861 * | 2.22042 * | 2.61827 * | |
| Std | 1.56E−15 | 3.86E−15 | 0.79514 * | 0.50589 * | 1.03460 * | |
| Mean | 2.14E−15 | 2.97E−15 | 0.69415 * | 0.32486 * | 1.33731 * | |
| Mdn | 1.49E−15 | 2.02E−15 | 0.22951 * | 3.40E−14 | 1.35667 * | |
| Min | 0.04989 | 0.04242 | 0.06914 | 0.02379 | 0.04127 | |
| Max | 0.19393 | 0.31693 | 0.22975 | 0.13560 | 0.23886 | |
| Std | 0.01197 | 0.05514 | 0.05050 | 0.00497 | 0.04110 | |
| Mean | 0.02851 | 0.14643 | 0.13524 | 0.01523 | 0.10104 | |
| Mdn | 0.10068 | 0.10974 | 0.16777 | 0.09275 | 0.09319 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Sun, L. FROM: A Fish Recognition-Inspired Optimization Method for Multi-Agent Decision-Making Problems with a Fluid Environment. Biomimetics 2025, 10, 215. https://doi.org/10.3390/biomimetics10040215
Wang Y, Sun L. FROM: A Fish Recognition-Inspired Optimization Method for Multi-Agent Decision-Making Problems with a Fluid Environment. Biomimetics. 2025; 10(4):215. https://doi.org/10.3390/biomimetics10040215
Chicago/Turabian StyleWang, Yuchen, and Lei Sun. 2025. "FROM: A Fish Recognition-Inspired Optimization Method for Multi-Agent Decision-Making Problems with a Fluid Environment" Biomimetics 10, no. 4: 215. https://doi.org/10.3390/biomimetics10040215
APA StyleWang, Y., & Sun, L. (2025). FROM: A Fish Recognition-Inspired Optimization Method for Multi-Agent Decision-Making Problems with a Fluid Environment. Biomimetics, 10(4), 215. https://doi.org/10.3390/biomimetics10040215





