Battery Impedance Spectroscopy Embedded Measurement System
Abstract
:1. Introduction
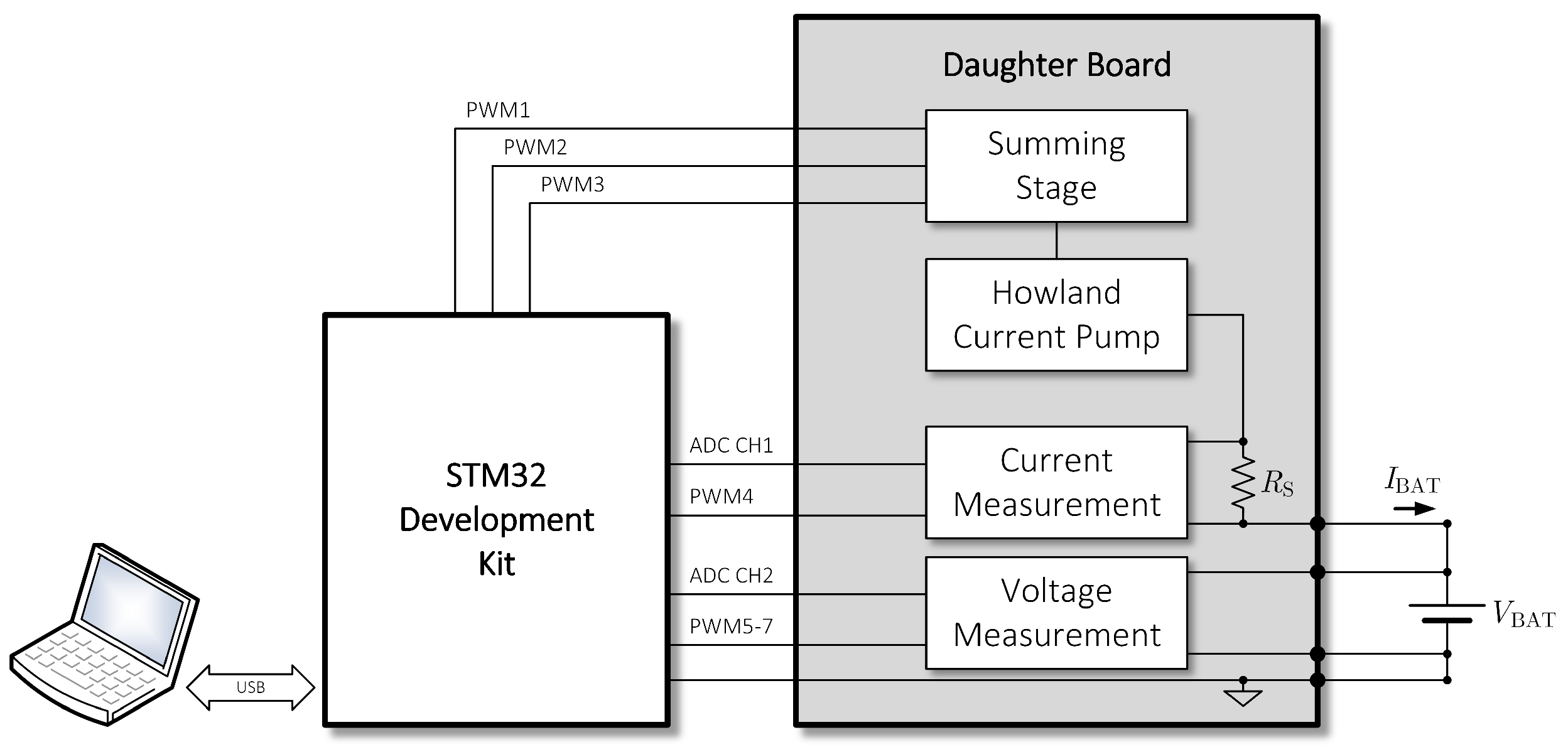
2. Embedded Measurement System
2.1. STM32 Development Kit
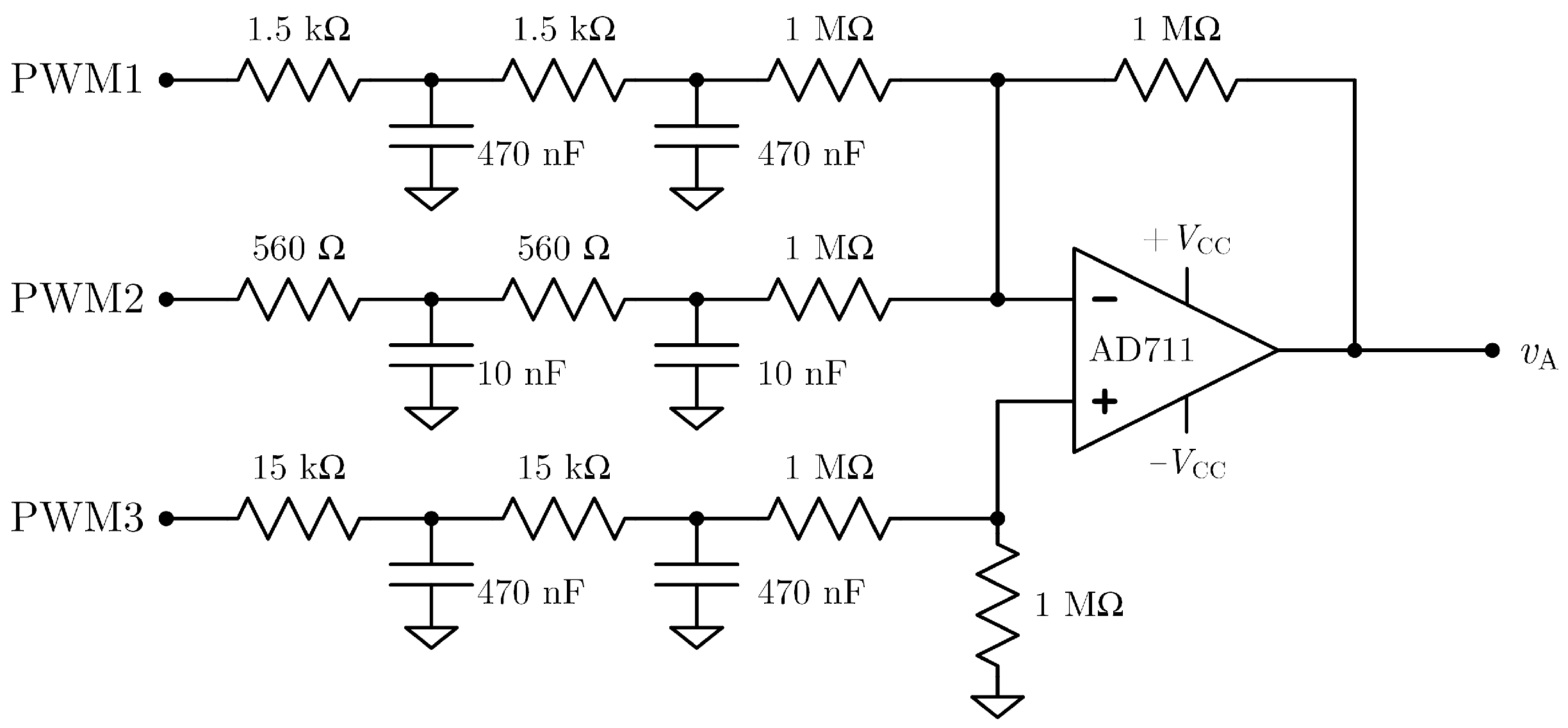
2.2. Summing Stage
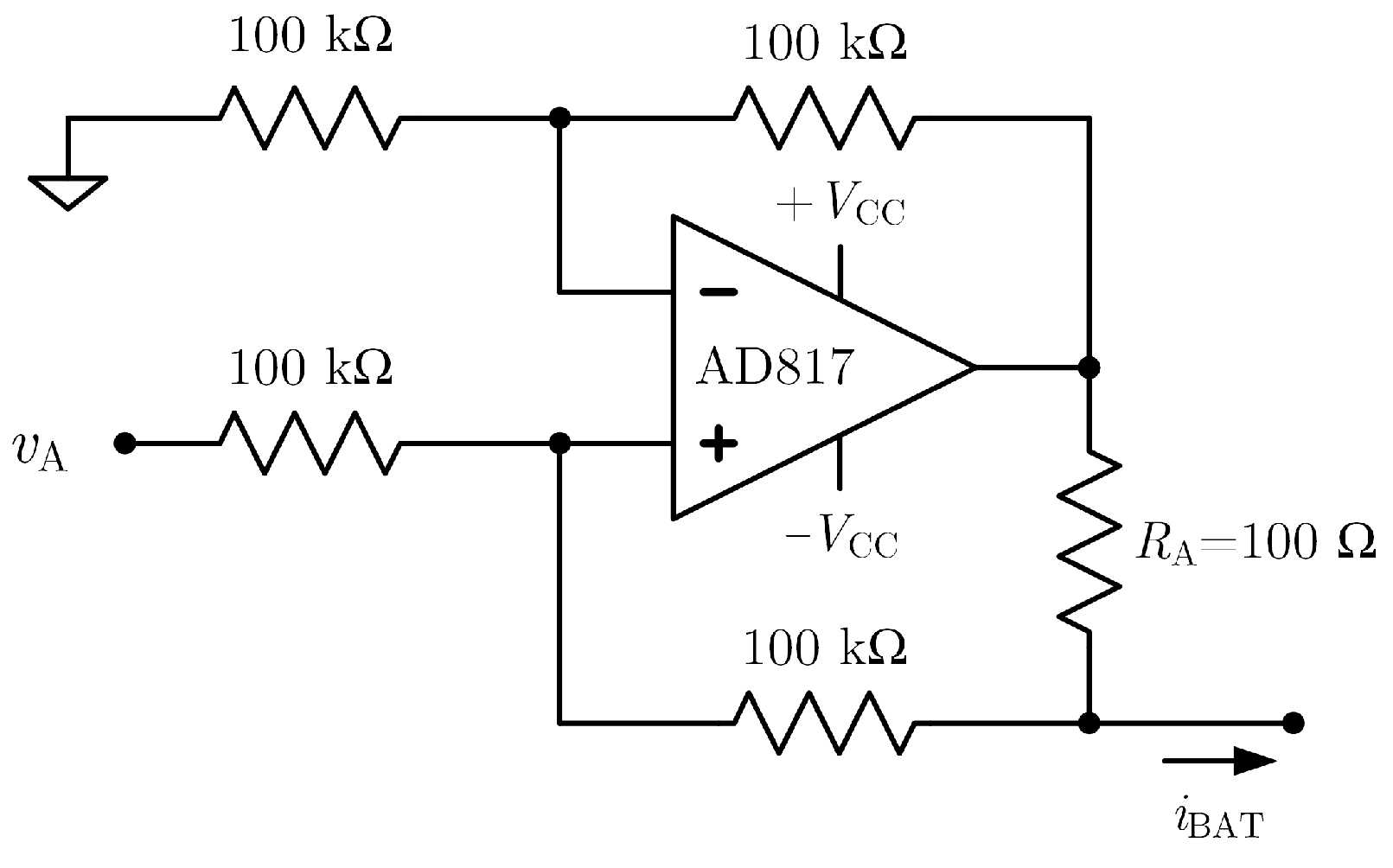
2.3. Improved Howland Current Pump
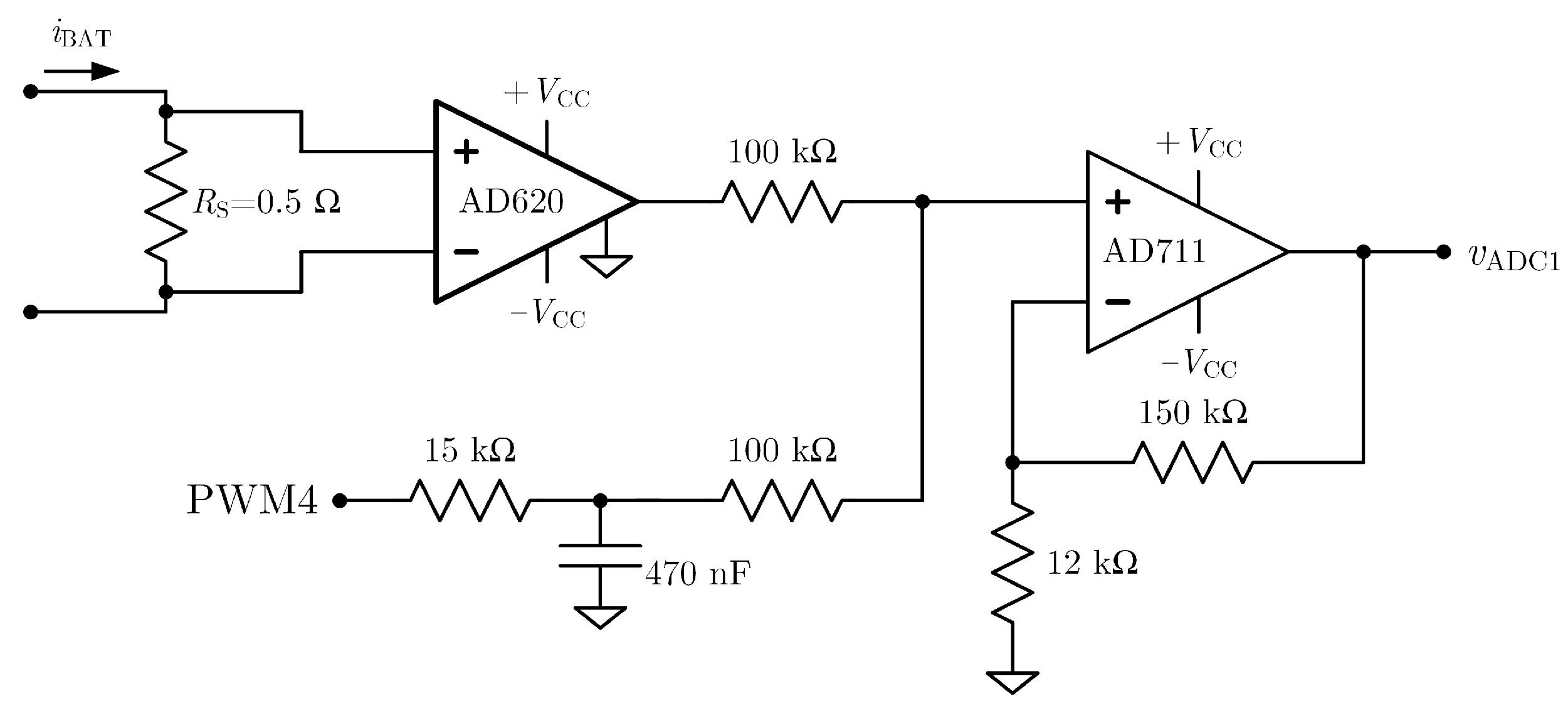
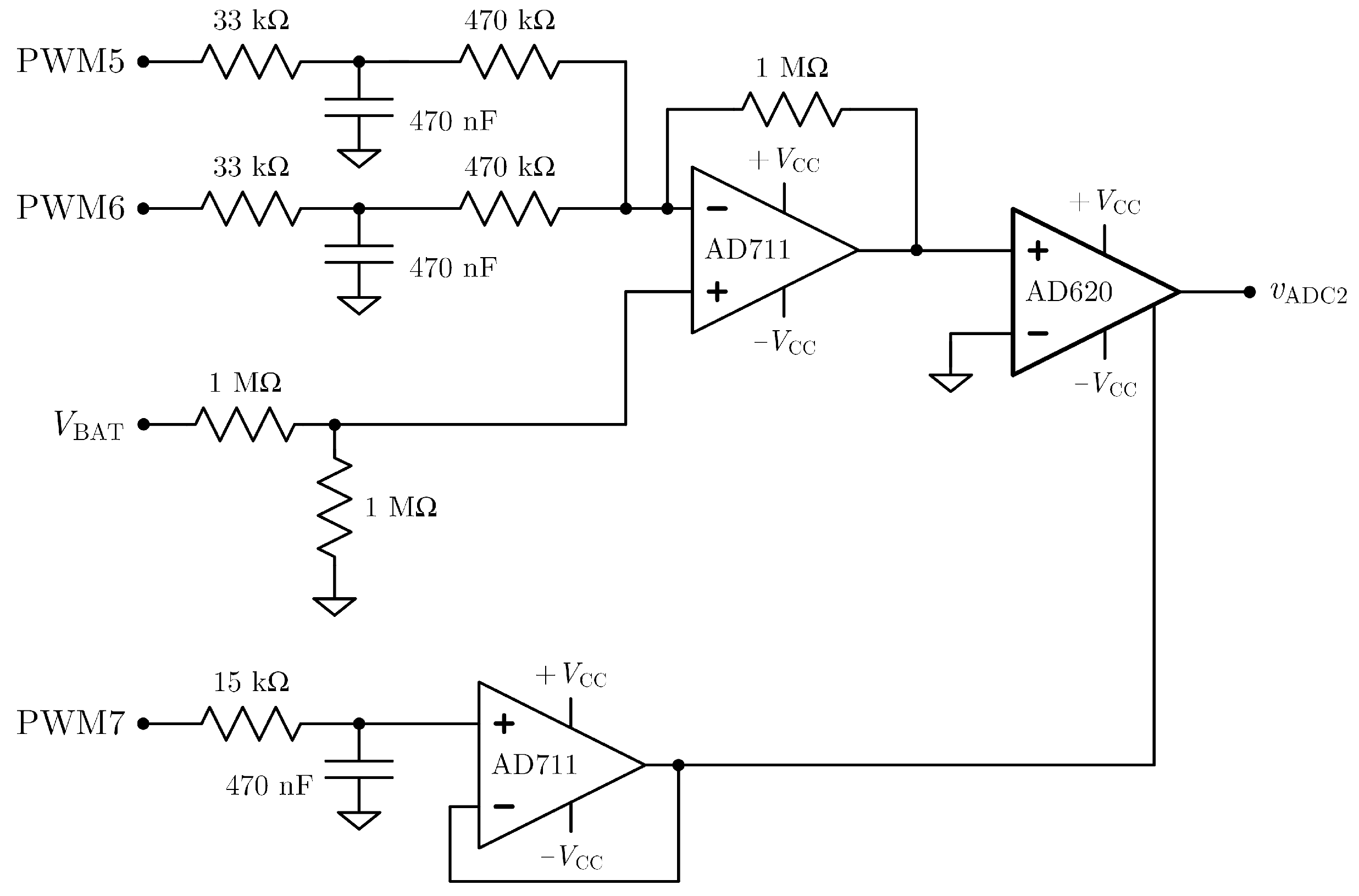
2.4. Battery Current Measurement Circuit
2.5. Battery Voltage Measurement Circuit
3. Stimulus Generation and System Calibration
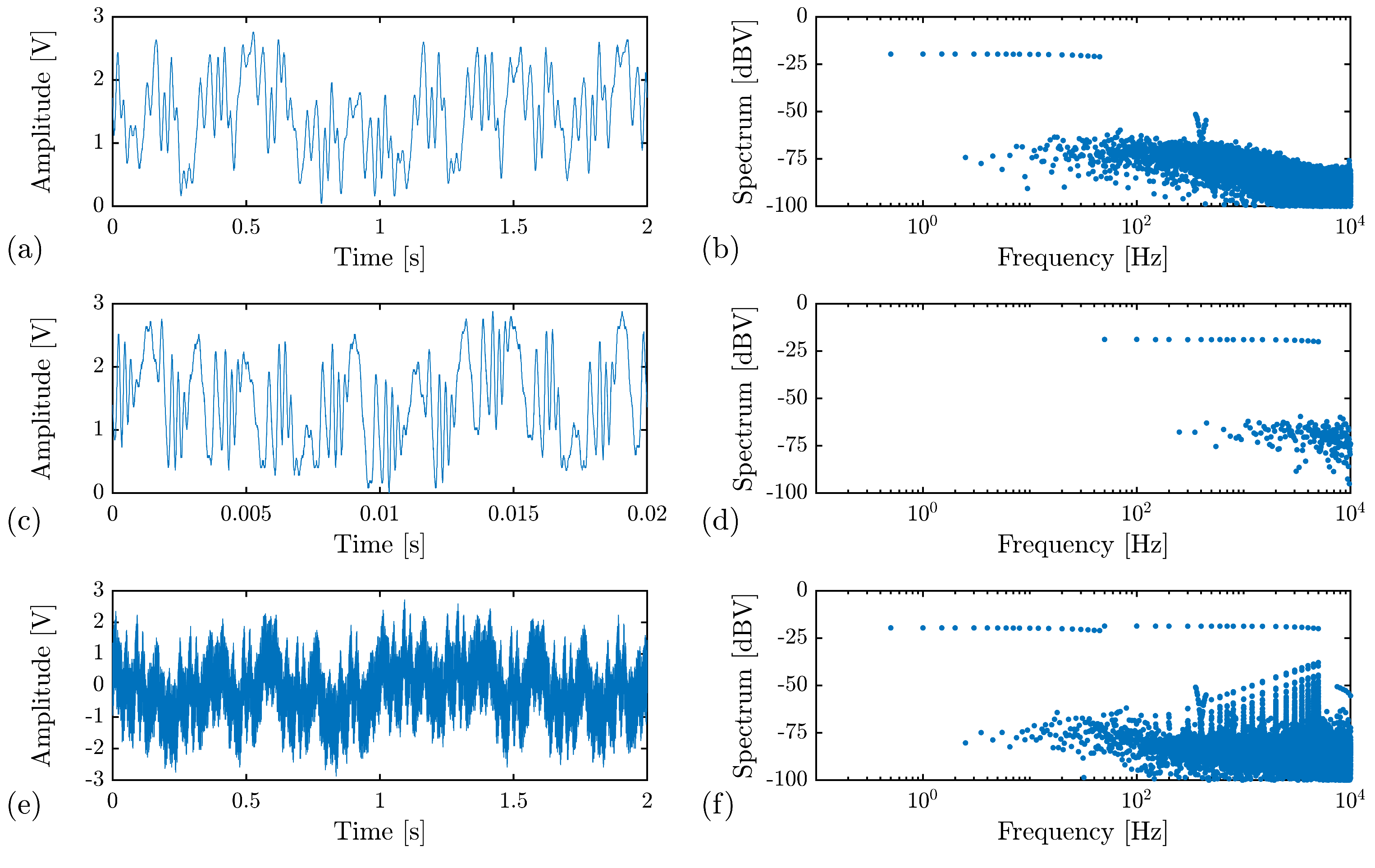
3.1. Stimulus Generation
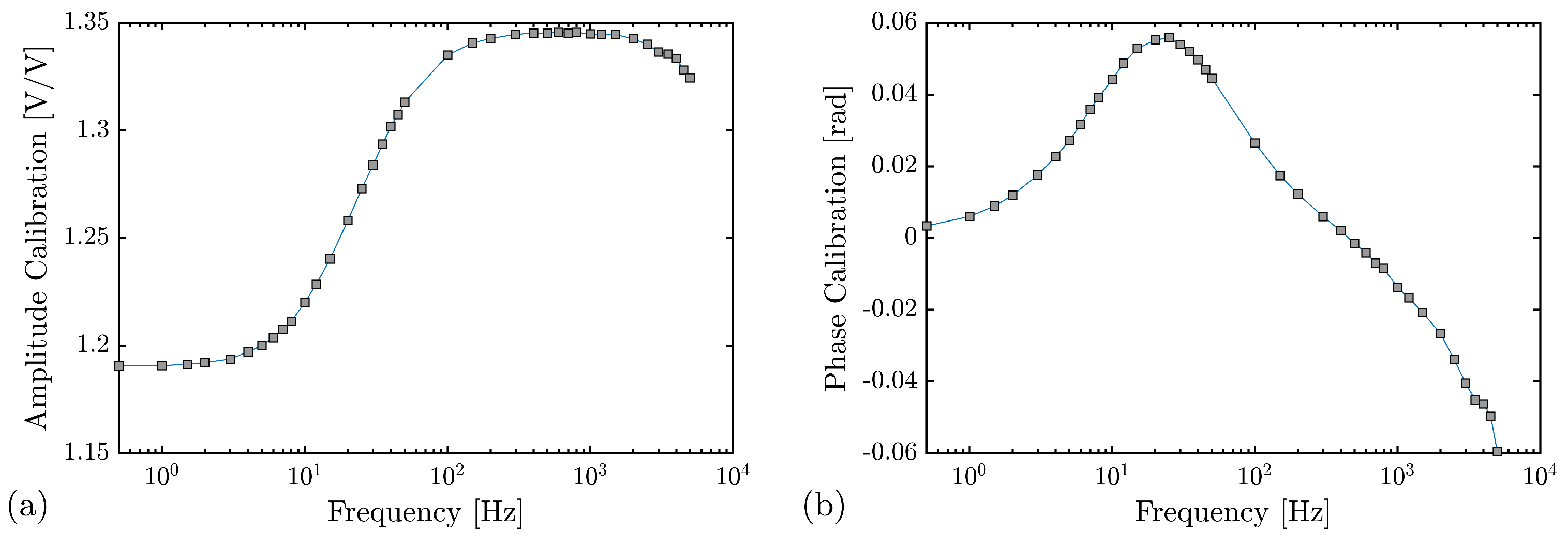
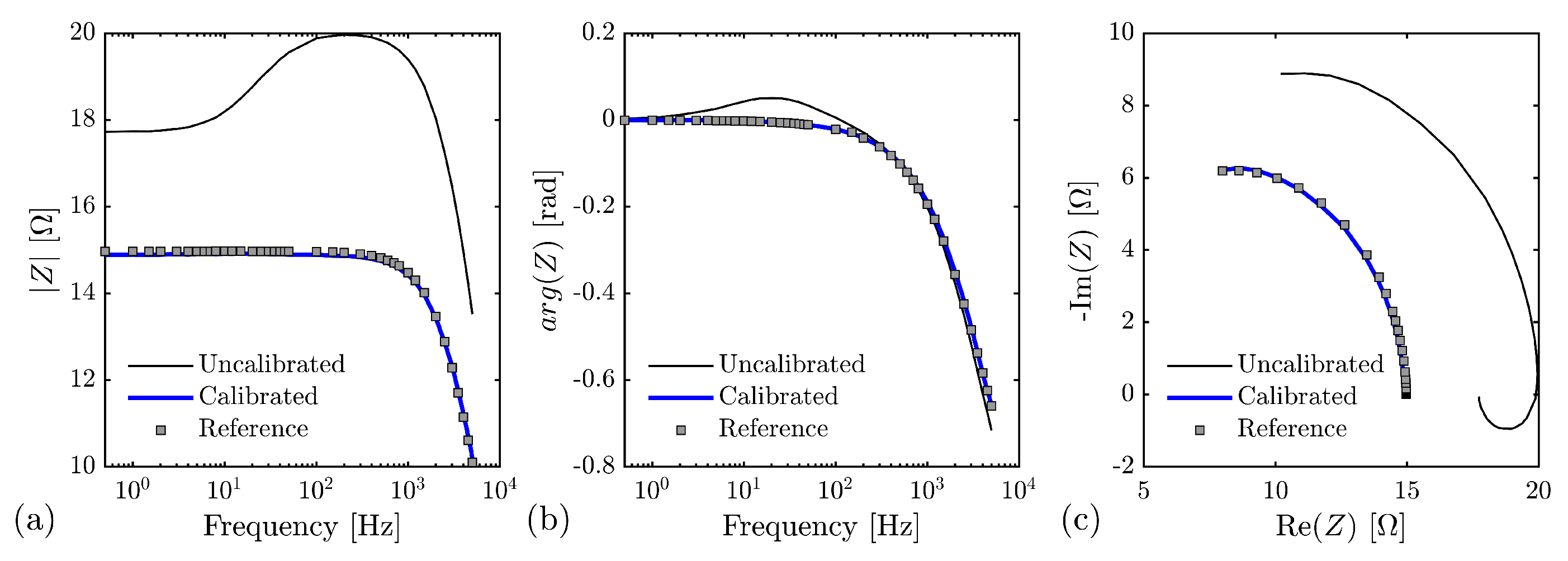
3.2. System Calibration
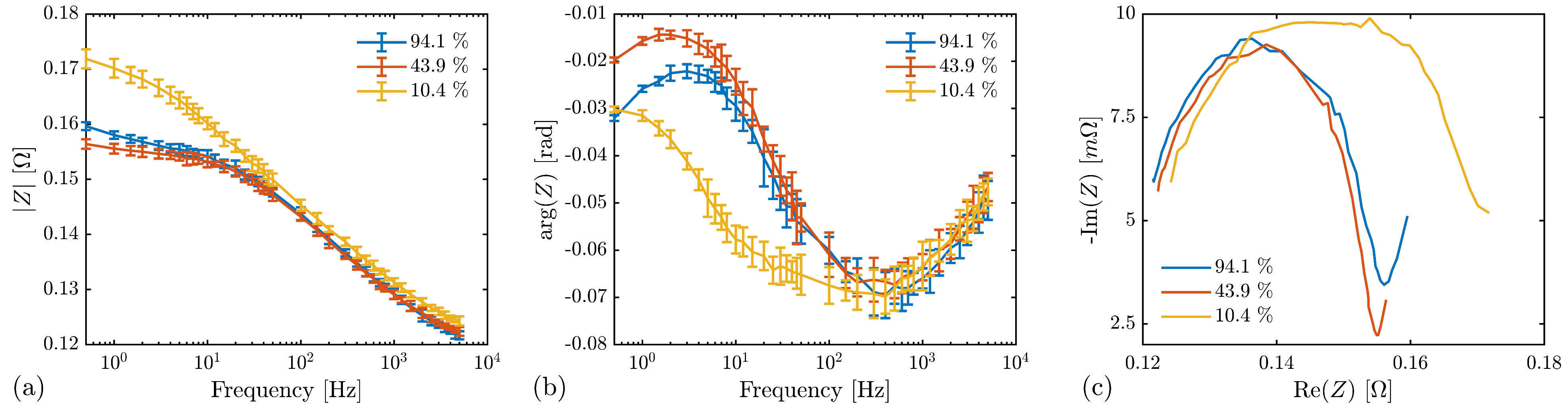
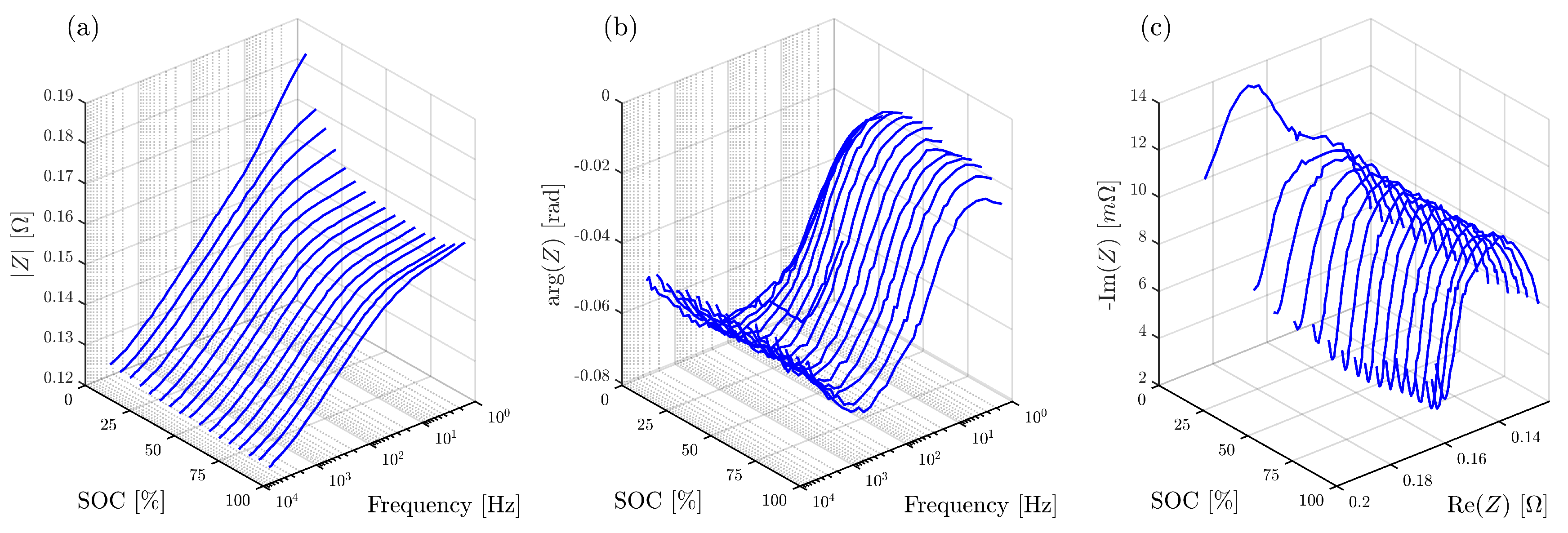
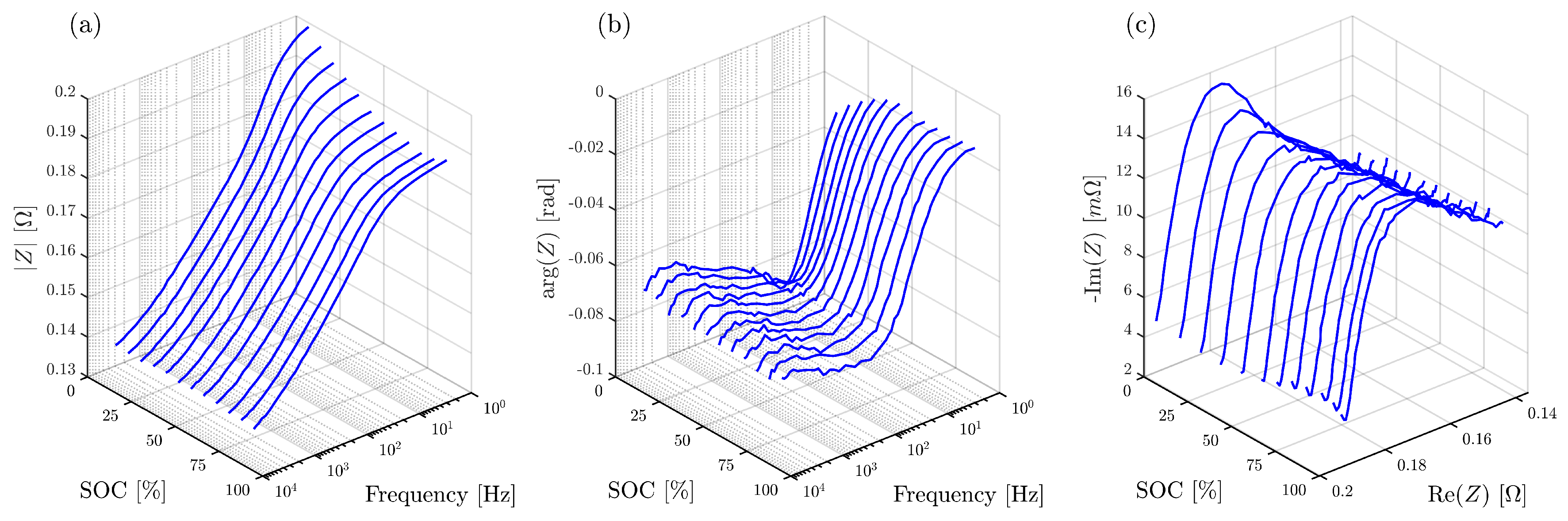
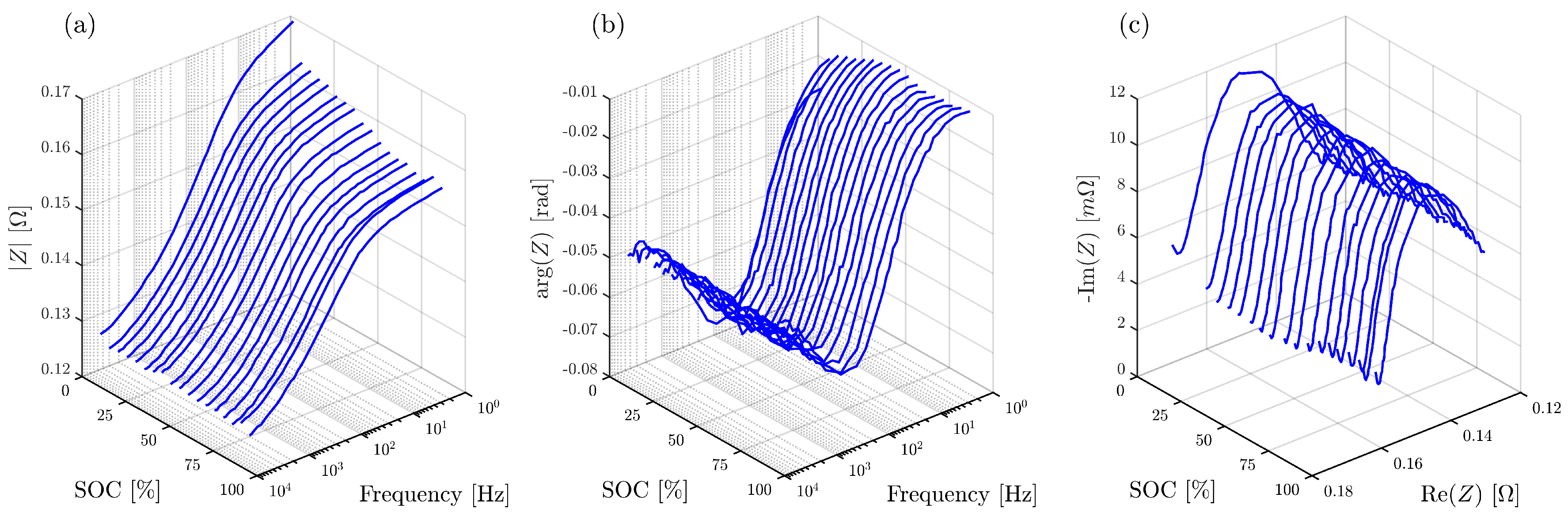
4. Battery Impedance Measurement Results
- (i)
- Fully charge the battery and stop the charge process when the battery charging current is below 10 mA.
- (ii)
- Wait for the battery open voltage to stabilize, setting a threshold of to terminate the stabilization period (this threshold was set to ).
- (iii)
- Perform the impedance measurement procedure, repeating the process 10 times.
- (iv)
- Discharge the battery using a small resistor and end the discharge process when the discharge reaches 25 mAh.
- (v)
- If the battery is fully discharged (detected by the battery internal protection circuit), the procedure ends; otherwise, go back to step (ii).
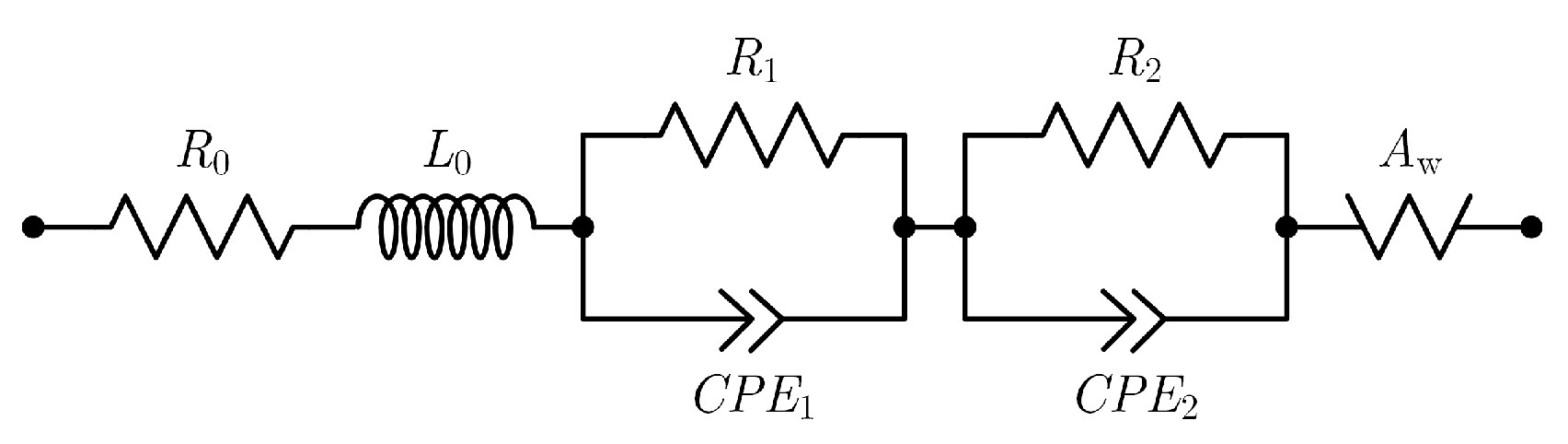
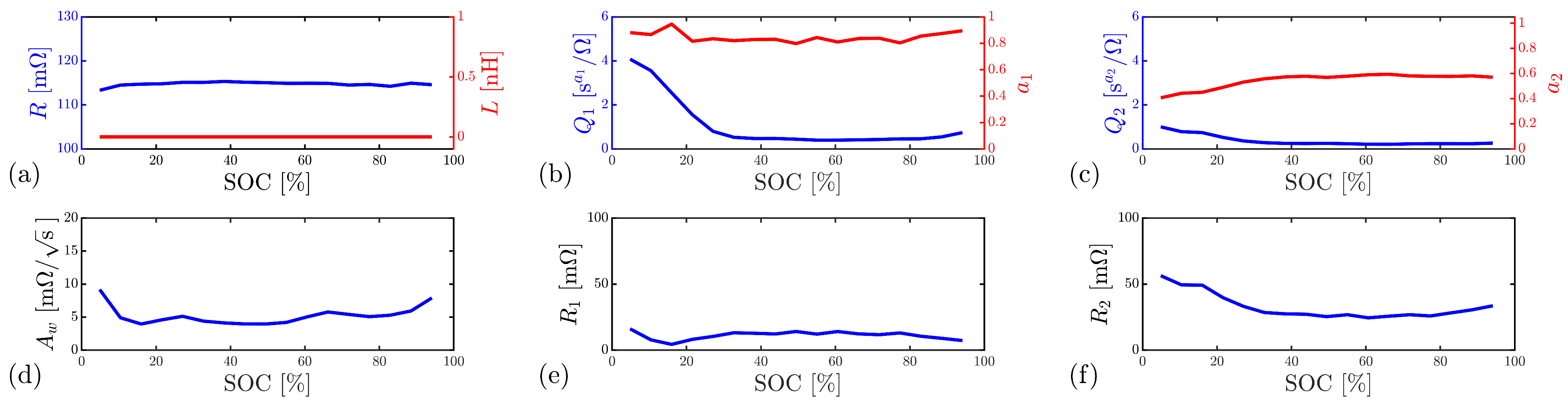
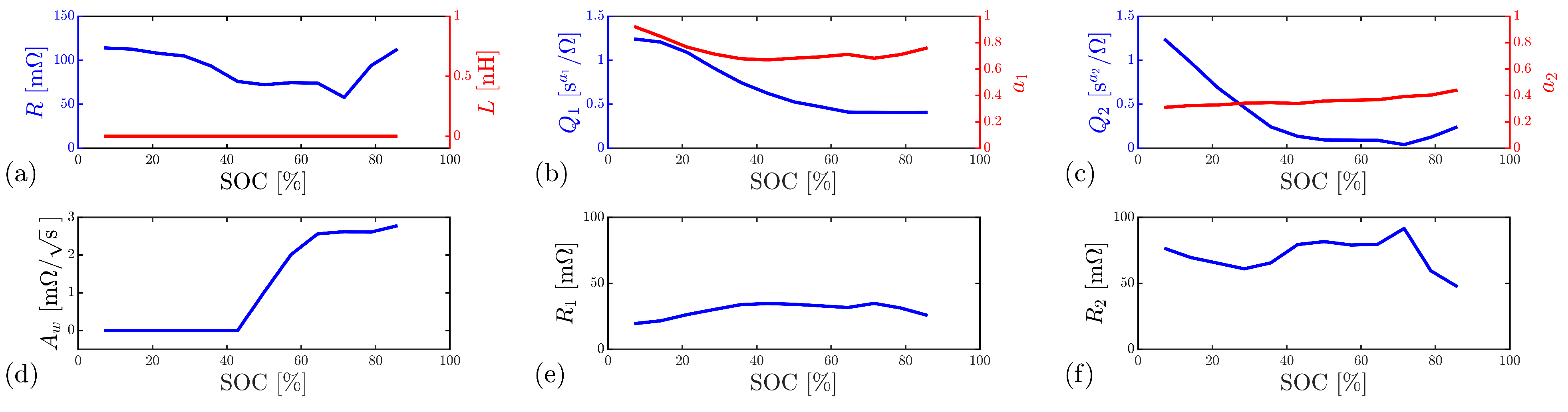
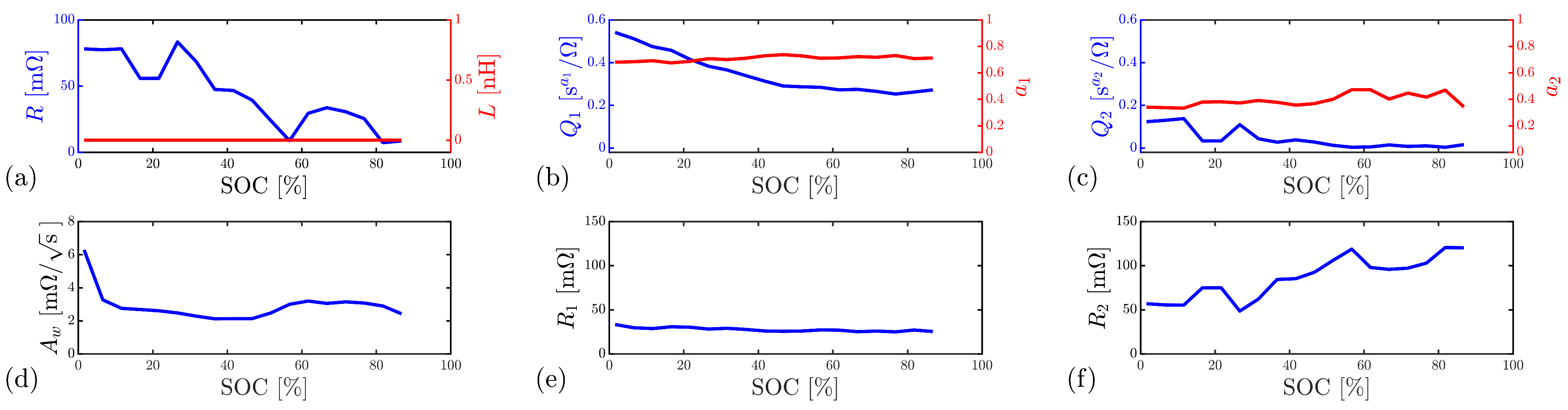
5. Battery Impedance Equivalent Circuit
6. Discussion, Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, X.; Zou, C.; Zhang, C.; Li, Y. Technological Developments in Batteries: A Survey of Principal Roles, Types, and Management Needs. IEEE Power Energy Mag. 2017, 15, 20–31. [Google Scholar] [CrossRef]
- Luo, X.; Wang, J.; Donner, M.; Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 2015, 137, 511–536. [Google Scholar] [CrossRef]
- Mohamad, F.; Teh, J.; Lai, C.-M.; Chen, L.-R. Development of Energy Storage Systems for Power Network Reliability: A Review. Energies 2018, 11, 2278. [Google Scholar] [CrossRef]
- Murnane, M.; Ghazel, A. A Closer Look at State of Charge (SOC) and State of Health (SOH) Estimation Techniques for Batteries. Analog Devices Technical Note. 2017. Available online: https://www.analog.com/media/en/technical-documentation/tech-articles/a-closer-look-at-state-of-charge-and-state-health-estimation-tech.pdf (accessed on 25 October 2023).
- International Energy Agency. Global EV Outlook. 2023. Available online: http://www.iea.org (accessed on 25 October 2023).
- Moncecchi, M.; Brivio, C.; Mandelli, S.; Merlo, M. Battery Energy Storage Systems in Microgrids: Modeling and Design Criteria. Energies 2006, 13, 2006. [Google Scholar] [CrossRef]
- González, I.; Calderón, A.J.; Folgado, F.J. IoT real time system for monitoring lithium-ion battery long-term operation in microgrid. J. Energy Storage 2022, 52, 104596. [Google Scholar] [CrossRef]
- Xing, Y.; He, W.; Pecht, M.; Tsui, K.L. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures. Appl. Energy 2014, 113, 106–115. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Idris, M.; Mekhilef, S. Overview of model-based online state-of-charge estimation using Kalman filter family for lithium-ion batteries. Renew. Sust. Energ. Rev. 2019, 113, 109233. [Google Scholar] [CrossRef]
- Hossain, M.; Haque, M.E.; Arif, M.T. Kalman filtering techniques for the online model parameters and state of charge estimation of the Li-ion batteries: A comparative analysis. J. Energy Storage 2022, 51, 104174. [Google Scholar] [CrossRef]
- Guo, Y.; Tian, J.; Li, X.; Song, B.; Tian, Y. State of Charge Estimation of Lithium-Ion Batteries Based on Vector Forgetting Factor Recursive Least Square and Improved Adaptive Cubature Kalman Filter. Batteries 2023, 9, 499. [Google Scholar] [CrossRef]
- Lee, S.; Lee, D. A Novel Battery State of Charge Estimation Based on Voltage Relaxation Curve. Batteries 2023, 9, 517. [Google Scholar] [CrossRef]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; Van Mierlo, J.; Van den Bossche, P. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sust. Energ. Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Mc Carthy, K.; Gullapalli, H.; Ryan, K.M.; Kennedy, T. Review—Use of Impedance Spectroscopy for the Estimation of Li-ion Battery State of Charge, State of Health and Internal Temperature. J. Electrochem. Soc. 2021, 168, 080517. [Google Scholar] [CrossRef]
- Galeotti, M.; Cinà, L.; Giammanco, C.; Cordiner, S.; Di Carlo, A. Performance analysis and SOH (state of health) evaluation of lithium polymer batteries through electrochemical impedance spectroscopy. Energies 2015, 89, 678–686. [Google Scholar] [CrossRef]
- Kallel, A.Y.; Hu, Z.; Kanoun, O. Comparative Study of AC Signal Analysis Methods for Impedance Spectroscopy Implementation in Embedded Systems. Appl. Sci. 2022, 12, 591. [Google Scholar] [CrossRef]
- STMicroelectronics NV. UM1842, User Manual, Discovery Kit with STM32F411VE MCU, Rev. 2. 2020. Available online: https://www.st.com/resource/en/user_manual/um1842-discovery-kit-with-stm32f411ve-mcu-stmicroelectronics.pdf (accessed on 25 October 2023).
- ADP5070, Data Sheet, Rev. E. Analog Devices. 2020. Available online: https://www.analog.com/media/en/technical-documentation/data-sheets/ADP5070.pdf (accessed on 25 October 2023).
- Lam, I.V. Analysis of Improved Howland Current Pump, Texas Instruments Application Note, SBOA437A. 2023. Available online: https://www.ti.com/lit/pdf/sboa437 (accessed on 25 October 2023).
- Pintelon, R.; Schoukens, J. System Identification—A Frequency Domain Approach; John Wiley & Sons: Hoboken, NJ, USA, 2001; pp. 137–138. [Google Scholar]
- Guillaume, P.; Schoukens, J.; Pintellon, R.; Kollár, I. Crest-factor minimization using nonlinear chebyshev approximation methods. IEEE Trans. Instrum. Meas. 1991, 40, 982–989. [Google Scholar] [CrossRef]
- Retzler, A.; Cseppentő, B.; Swevers, J.; Gillis, J.; Leitold, L.; Kollár, Z. Improved crest factor minimization of multisine excitation signals using nonlinear optimization. Automatica 2022, 140, 110654. [Google Scholar] [CrossRef]
- Janeiro, F.M.; Hu, Y.; Ramos, P.M. Peak factor optimization of multi-harmonic signals using artificial bee colony algorithm. Measurement 2020, 150, 107040. [Google Scholar] [CrossRef]
- Crescentini, M.; De Angelis, A.; Ramilli, R.; De Angelis, G.; Tartagni, M.; Moschitta, A.; Traverso, A.; Carbone, P. Online EIS and Diagnostics on Lithium-Ion Batteries by Means of Low-Power Integrated Sensing and Parametric Modeling. IEEE Trans. Instrumen. Meas. 2021, 70, 2001711. [Google Scholar] [CrossRef]
- Alavi, S.M.M.; Birkl, C.R.; Howey, D.A. Time-domain fitting of battery electrochemical impedance models. J. Power Sources 2015, 288, 345–351. [Google Scholar] [CrossRef]
- Orazem, M.E.; Tribollet, B. Electrochemical Impedance Spectroscopy, Chapter 14, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2017; ISBN 978-1-118-52739-9. [Google Scholar]
- Macdonald, R. LEVM/LEVMW, Version 8.13. 2015. Available online: http://jrossmacdonald.com/levmlevmw/ (accessed on 25 October 2023).
- Janeiro, F.M.; Ramos, P.M. Application of genetic algorithms for estimation of impedance parameters of two-terminal networks. In Proceedings of the 2009 IEEE Instrumentation and Measurement Technology Conference, Singapore, 5–7 May 2009; pp. 602–606. [Google Scholar] [CrossRef]
- Janeiro, F.M.; Ramos, P.M. Threshold estimation for least-squares fitting in impedance spectroscopy. Measurement 2018, 124, 479–485. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Buchicchio, E.; De Angelis, A.; Santoni, F.; Carbone, P.; Bianconi, F.; Smeraldi, F. Battery SOC estimation from EIS data based on machine learning and equivalent circuit model. Energy 2023, 283, 128461. [Google Scholar] [CrossRef]
- De Angelis, A.; Buchicchio, E.; Santoni, F.; Moschitta, A.; Carbone, P. Uncertainty Characterization of a Practical System for Broadband Measurement of Battery EIS. IEEE Trans. Instrumen. Meas. 2022, 71, 1002609. [Google Scholar] [CrossRef]
- Howey, D.A.; Mitcheson, P.D.; Yufit, V.; Offer, G.J.; Brandon, N.P. Online Measurement of Battery Impedance Using Motor Controller Excitation. IEEE Trans. Veh. Tech. 2014, 633, 2557–2566. [Google Scholar] [CrossRef]
- Koseoglou, M.; Tsioumas, E.; Papagiannis, D.; Jabbour, N.; Mademlis, C. A Novel On-Board Electrochemical Impedance Spectroscopy System for Real-Time Battery Impedance Estimation. IEEE Trans. Power Electron. 2021, 36, 10776–10787. [Google Scholar] [CrossRef]
- Zhang, F.; Teng, Z.; Rutkove, S.; Yang, Y.; Li, J. A simplified time-domain fitting method based on fractional operational matrix for Cole parameter estimation. IEEE Trans. Instrumen. Meas. 2019, 69, 1566–1575. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cicioni, G.; De Angelis, A.; Janeiro, F.M.; Ramos, P.M.; Carbone, P. Battery Impedance Spectroscopy Embedded Measurement System. Batteries 2023, 9, 577. https://doi.org/10.3390/batteries9120577
Cicioni G, De Angelis A, Janeiro FM, Ramos PM, Carbone P. Battery Impedance Spectroscopy Embedded Measurement System. Batteries. 2023; 9(12):577. https://doi.org/10.3390/batteries9120577
Chicago/Turabian StyleCicioni, Gabriele, Alessio De Angelis, Fernando M. Janeiro, Pedro M. Ramos, and Paolo Carbone. 2023. "Battery Impedance Spectroscopy Embedded Measurement System" Batteries 9, no. 12: 577. https://doi.org/10.3390/batteries9120577
APA StyleCicioni, G., De Angelis, A., Janeiro, F. M., Ramos, P. M., & Carbone, P. (2023). Battery Impedance Spectroscopy Embedded Measurement System. Batteries, 9(12), 577. https://doi.org/10.3390/batteries9120577








