Adaptation of Deep Network in Transfer Learning for Estimating State of Health in Electric Vehicles during Operation

Abstract

Battery state of health (SOH) is a significant metric for evaluating battery life and predicting battery safety. Currently, SOH research is largely based on laboratory data, with a dearth of research on electric vehicle (EV) operating data. Due to the difficulty in obtaining complete charge data under EV operating conditions, this study presents a SOH estimation method utilizing deep network adaptation. First, a data-driven approach is employed to extract voltage, current, state of charge (SOC), and incremental capacity (IC) data features. To compensate for the lack of aging information in the EV operation data domain, transfer learning is employed to construct the SOH estimation model. Additionally, to resolve inconsistent data distribution between the source laboratory battery data domain and the target EV operation data domain, an adaptive layer is added to the network, and adaptation of deep network (ADN) is utilized to enhance the model’s performance. Finally, the model is validated using electric bus operational data. Results indicate that this model’s average Mean Absolute Error (MAE) is less than 3.0%, and, compared to support vector machine (SVM) regression and Gaussian Process Regression (GPR) algorithms, the MAE is reduced by 27.7% and 38.4%, respectively.

1. Introduction

The effective management of an electric vehicle (EV) battery pack relies heavily on the incorporation of a sophisticated battery management system (BMS), with state of charge (SOC) and state of health (SOH) estimations serving as fundamental components. SOH, specifically, serves as a critical metric in evaluating battery performance degradation and thus plays a crucial role in ensuring battery safety, preempting potential failure and avoiding unnecessary resource waste. Accurate and real-time assessment of SOH is therefore imperative in minimizing the risk of vehicle accidents and injuries, as well as enhancing resource utilization [1].

Numerous studies have been conducted on SOH estimation for lithium-ion batteries using various approaches. Jungsoo Kim et al. introduced a practical approach for pinpointing and choosing pertinent parameters of a P2D model that undergo substantial changes with battery aging. The collected experimental data were employed to fine-tune the P2D model via the use of a genetic algorithm [2]. Longxing Wu et al. proposed an Electrochemical–Thermal Model (ETM) to assess heat generation in cylindrical lithium-ion batteries (LIBs) concerning discharge rates and the N/P ratio. The ETM, validated using experimental data at 25 °C and 35 °C, studies the heat generation distribution under different conditions [3]. Pengfei Wen et al. proposed a new framework for lithium-ion battery prediction and health management (PHM) using physical information neural networks (PINNs). It blends empirical and data-driven models to leverage a variety of information sources. The capacity degradation associated with operational cycle and health status was quantified [4]. Model-based methods often require a lot of prior knowledge about the system when developing complex systems. However, the mechanism of the aging reaction inside the battery is not clear, so the accuracy will be lost in the process of model construction. As a result, the focus of research has shifted towards data-driven SOH estimation methods. For instance, Ji Wu et al. proposed an SOH estimation model based on an improved radial basis neural network (IRBFNN), which was combined to obtain the final SOH estimation model [5]. Chang et al. proposed an online method for estimating the SOH of lithium-ion batteries under current discharge using incremental capacity and the fusion of a wavelet neural network and a genetic algorithm [6]. Li et al. developed an SOH estimation method based on Long Short-Term Memory (LSTM), achieving an average absolute percentage error of 0.76% in the best case and demonstrating strong robustness when dealing with input noise [7]. J. Qu et al. introduced the PA-LSTM method, which utilized a long-term and short-term memory network attention mechanism to build the model. Additionally, a particle swarm optimization algorithm was used to optimize key parameters and pre-train the model. The experimental results demonstrated that the proposed model achieved more accurate SOH estimation compared to Recurrent Neural Network (RNN), LSTM, and Relevance Vector Machine (RVM) models [8]. Shen et al. introduced a method for estimating the SOC of lithium-ion batteries using a Transformer [9]. The proposed method utilizes the Transformer algorithm to model the relationship between the battery’s SOC and the features extracted from the current pulse response. The experimental results demonstrate that the proposed method is effective and accurate for estimating the SOC of lithium-ion batteries. Vidal et al. proposed a novel method for estimating the SOC of lithium-ion batteries, which utilized the two kinds of neural networks to estimate the SOC [10]. D. Stroe et al. presented a SOH estimation model based on the capacity increment method, which was verified for its applicability under different conditions [11]. Duo Yang et al. developed a novel Gaussian Process Regression (GPR) model for estimating the SOH of lithium-ion batteries using charging curves and evaluated the model’s performance on experimental data from four batteries. The results indicate that the proposed model achieves good accuracy with a final error of about 1.67% [12]. J. Meng et al. proposed a method for automatically selecting multiple optimal voltage ranges using NSGA-II and grid search to estimate the SOH of lithium-ion batteries at different charging stages. The effectiveness of this method was verified using 360 days of aging test data for the battery [13]. Ang Yang et al. presented a novel approach for battery state-of-health (SOH) estimation based on the dynamic Peukert’s function [14]. This method offers an efficient way to estimate the SOH of the battery by considering the effect of discharge rate on the battery capacity. Meanwhile, Xiao D et al. proposed a new algorithm for decoupled state-of-charge (SOC) and SOH co-estimation using convex optimization. This approach allows for a robust estimation of SOC and SOH, as well as weak interaction between the two states [15]. Furthermore, Joelianto E et al. presented a method for joint estimation of SOH and SOC using the dual extended Kalman filter (DEKF) [16]. This method provides an effective and accurate way to estimate the two important battery states simultaneously.

Song et al. proposed an SOH estimation method for lithium-ion batteries based on the XGBoost algorithm. The XGBoost model was developed to estimate SOH using an integrated learning algorithm with high prediction accuracy and generalization ability. The SOH estimation value was corrected using the Markov chain. The proposed method showed improved accuracy over other algorithms such as machine forest, KNN, and SVM [17]. In a similar vein, Chen et al. proposed a degradation state model based on extreme learning machine (ELM) to represent the intricate battery degradation mechanism. The final model was tested on different batteries and achieved an estimated error of less than 1.93% [18]. Park et al. proposed a statistical model for SOH prediction using a combination of the double extended Kalman filter and autoregressive model. This model can predict SOH when the amount of measured data are insufficient, and it achieved an average absolute error of 0.5183% [19].

While the methods mentioned above have demonstrated effective results in the prediction of SOH of lithium-ion batteries, they are primarily based on laboratory experiments involving full impulse and discharge of batteries. Hence, the applicability of these models under actual working conditions of electric vehicles remains unverified. Currently, only limited research has been conducted based on real-world electric vehicle data. To address this gap, Zhou et al. proposed an EKF-GPR SOH estimation model based on Gaussian process regression and an extended Kalman filter that was tailored to vehicle data. Through comparison with the capacity increment model, the authors verified the superiority of their proposed model [20,21,22]. Vichard et al. proposed an SOH estimation model based on circuit model, optimization algorithm, and Kalman filter, utilizing three years of data from ten vehicles [23]. Xiao et al. developed an indirect feature extraction scheme based on incremental capacity analysis using vehicle operation data to realize online SOH estimation with Gaussian process regression [24]. Despite their potential, these algorithms still have limitations, such as requiring a large amount of data for modeling and potential issues with accuracy.

In conclusion, whereas various models and algorithms have been proposed for SOH estimation of lithium-ion batteries, their effectiveness has mainly been evaluated based on laboratory experiments involving full charge and full discharge cycles. There is a lack of research that verifies the performance of these models under real-world electric vehicle operating conditions. To address this limitation, more studies based on real electric vehicle data are needed. Obtaining labeled data from electric vehicle operations is challenging due to the time and cost required for full charge and discharge experiments and the fact that such data may not be generated during daily EV operation. Nonetheless, the development of accurate SOH estimation models based on real-world data is crucial for optimizing battery management strategies and improving the overall reliability and safety of electric vehicles.

The estimation of SOH for lithium-ion batteries in operating electric vehicles is challenging due to the difficulty in obtaining labeled data. However, a significant amount of aging information is available in the laboratory experimental data of lithium-ion batteries. If this information can be utilized in the operating vehicle data field, it can compensate for the scarcity of information in that field. Transfer learning is a subfield of machine learning that aims to apply the knowledge learned in one field or task to other relevant fields or tasks. In 2010, Professor Yang Q et al. published the most representative review of transfer learning, which divided transfer learning into four categories according to learning methods, namely, based on samples, models, features, and relationships [25]. The idea of the sample-based method is to find the samples in the source domain that can be used by the target domain and transfer them to make up for the lack of data information in the target domain. The idea of feature-based methods is to find appropriate features to reduce the difference between the source data domain and the target data domain to reduce the bias of the classification or regression model. The idea of model-based transfer learning is that, in different domain models, some parameters or hyperparameters can be borrowed from each other or even directly copied. The relationship-based transfer learning method is less studied than other methods, and it mainly focuses on the similarity between the relationship between the samples in the source domain and the target domain. Utilizing transfer learning can facilitate the transfer of aging information between the laboratory and operating vehicle data fields [25]. The common method of transfer learning is Fine-Tune, but, as the data distribution of experimental data and operating vehicle data are inconsistent, the direct use of Fine-Tune transfer may even lead to negative transfer. Therefore, we present a novel approach for estimating the SOH in Electric Vehicles (EVs) during operation, utilizing an adapted deep network in transfer learning. The proposed model leverages the knowledge learned from a pre-trained deep network on a source domain and adapts it to a target domain specific to EVs. Our approach addresses the challenge of limited training data availability in the target domain and improves the accuracy of SOH estimation in EVs. The experimental results demonstrate the efficacy of our proposed approach and its superiority over existing SOH estimation methods in terms of accuracy and computational efficiency. Our contribution holds potential to enhance the reliability and efficiency of EVs, which is critical for promoting sustainable transportation. In this study, we propose a novel approach for enhancing the performance of a network by introducing a domain adaptive layer that brings the source and target domains closer in terms of their distribution [26]. We demonstrate the effectiveness of our approach on lithium-ion electric vehicle data, where we extract relevant features and evaluate the performance of our adaptive SOH estimation model. To evaluate the effectiveness of our model, we compare it with two widely used regression algorithms, namely, support vector machine and Gaussian process regression. Our experimental results indicate that our proposed model achieves higher accuracy than the baseline models in predicting SOH based on operating vehicles data.

The remainder of this paper is organized as follows. Section 2 presents the details of our data preparation process, including the source of data, data preprocessing, and feature extraction. Section 3 outlines the procedure for establishing the SOH prediction model using the proposed approach. In Section 4, we present the experimental results and analysis, including the effectiveness analysis of feature extraction, the result analysis of the model, and the comparative analysis with support vector machine and Gaussian regression algorithms. Finally, in Section 5, we conclude our study by summarizing the main findings and discussing the implications of our work.

2. Data Preparation

This study employs data obtained from 18 Type K9B electric buses from a bus company in Shenzhen to estimate the SOH. As the temperature of Shenzhen City is 22 °C, we do not consider the influence of temperature in this paper with the buses data set. As traditional data-driven methods for SOH estimation rely on full charge and full discharge data, the lack of such data in this dataset presents a challenge. The dataset comprises daily charging data from 2013 to 2017, as well as 60 full charging test data from 2013, 2016, and 2017. The dataset contains information on time, voltage, current, and SOC.

The battery aging experimental data of 18650 lithium batteries carried out by NASA were selected as the source domain data of transfer learning. The data mainly included time, voltage, current, and temperature, and the sampling period was 1 s. A total of 11 batteries, B0005–B0007, B0018 and B0029–B0036, were selected as the data set, with a total of 1343 charging cycles.

The attenuation parameters of battery SOH are usually expressed from the perspective of its capacity and impedance or power. In this paper, the SOH definition method characterized by battery capacity attenuation is used. This definition method is recognized by most scholars, and its definition is as follows (1):

$$SOH=\frac{Ca{p}_k}{Ca{p}_o}\times 100\%$$

(1)

where $Ca{p}_0$ represents the initial capacity (Ah) of lithium ion, and $Ca{p}_k$ represents the maximum available capacity (Ah) of lithium-ion battery in this cycle.

As both NASA experimental data and electric bus full charge data have current and time terms, the ampere hour integration method (2) can be used to calculate the maximum available capacity of the cycle $Ca{p}_k$. Where $t_{start}$ is the start time of the full charge experiment, $\eta$ representing the coulomb efficiency, $t_{end}$ is the end time of the full charge, and the $I(t)$ is the current value at time $t$.

$$Ca{p}_k={\displaystyle \int \begin{array}{c}{t}_{end}\\ t_{start}\end{array}\eta \cdot I(t)dt}$$

(2)

After obtaining the maximum usable capacity $Ca{p}_k$ of this cycle, it is also necessary to know the initial capacity $Ca{p}_0$ of the lithium-ion battery. For electric bus data, after checking the battery specifications, we learned that its initial capacity, $Ca{p}_0$, is 600 Ah. For NASA experimental data, the initial capacity cannot be found directly. However, as the aging cycle data of lithium-ion battery starts when the battery is new, for each experimental battery, the actual capacity calculated from the first cycle experimental data is taken as the initial capacity $Ca{p}_0$ of the battery. After $Ca{p}_k$ and $Ca{p}_0$ are obtained, the SOH value of the full charge data can be calculated through Equation (1).

In dealing with original data, data quality issues cannot be avoided. To ensure accuracy in subsequent modeling, data preprocessing and feature extraction are necessary. Initially, missing values are imputed, and abnormal values are removed. For outliers, this paper first filters out the charging data, whose battery voltage values exceed the battery operating voltage. In addition, some battery data have negative currents, and the charging process should be a process of positive current inflow. The negative current data will affect the calculation of SOH, so the negative current data are filtered out. In addition, the voltage and current value in the actual charging process should be continuously changing, but there are mutation data in the data, which will disrupt the feature extraction process. Therefore, the mutation value is corrected by setting a threshold to detect the mutation, and the original value is replaced by the average value. For missing values, missing data will directly cause the calculation model to fail to run. All the data of voltage, current, and SOC columns are detected separately, and the polynomial interpolation method is used to fill the missing data to fill the missing values. Then, the capacity increase curve (IC) is constructed. The original data comprises voltage, current, state of charge (SOC), and time curves. Therefore, the IC curve is generated based on the original curve, and data dimensionality is added to facilitate feature extraction. Calculation of the IC curve involves differentiating the change in battery power and terminal voltage during charging or discharging. Its calculation method is described as follows:

$$\frac{dQ}{dU}=\frac{\Delta Q}{\Delta U}=\frac{Q_{t_{k+1}}-Q_{t_k}}{U_{t_{k+1}}-U_{t_k}}$$

(3)

where $Q_{t_{k+1}}$ and $Q_{t_k}$ are the battery power at time $k$ and $k+1$, and $U_{t_{k+1} }$ and $U_{t_k}$ are the battery terminal voltages at $k$ and $k+1$. The corresponding curve $dQ/dU-U$ is the IC curve.

After preprocessing the voltage, current, SOC, and IC curves, feature extraction was conducted, and correlation analysis was performed. Five features were selected from each curve to reflect battery degradation.

3. Establishment of SOH Prediction Model

Transfer learning is a well-established research field in the domain of machine learning, which aims to apply previously acquired knowledge from one domain to another unrelated and unknown domain, through leveraging the similarity relationships between them. The central issue in transfer learning is to discover the underlying similarity between the two domains and leverage it to transfer knowledge between them, thereby accomplishing the transfer learning task [25].

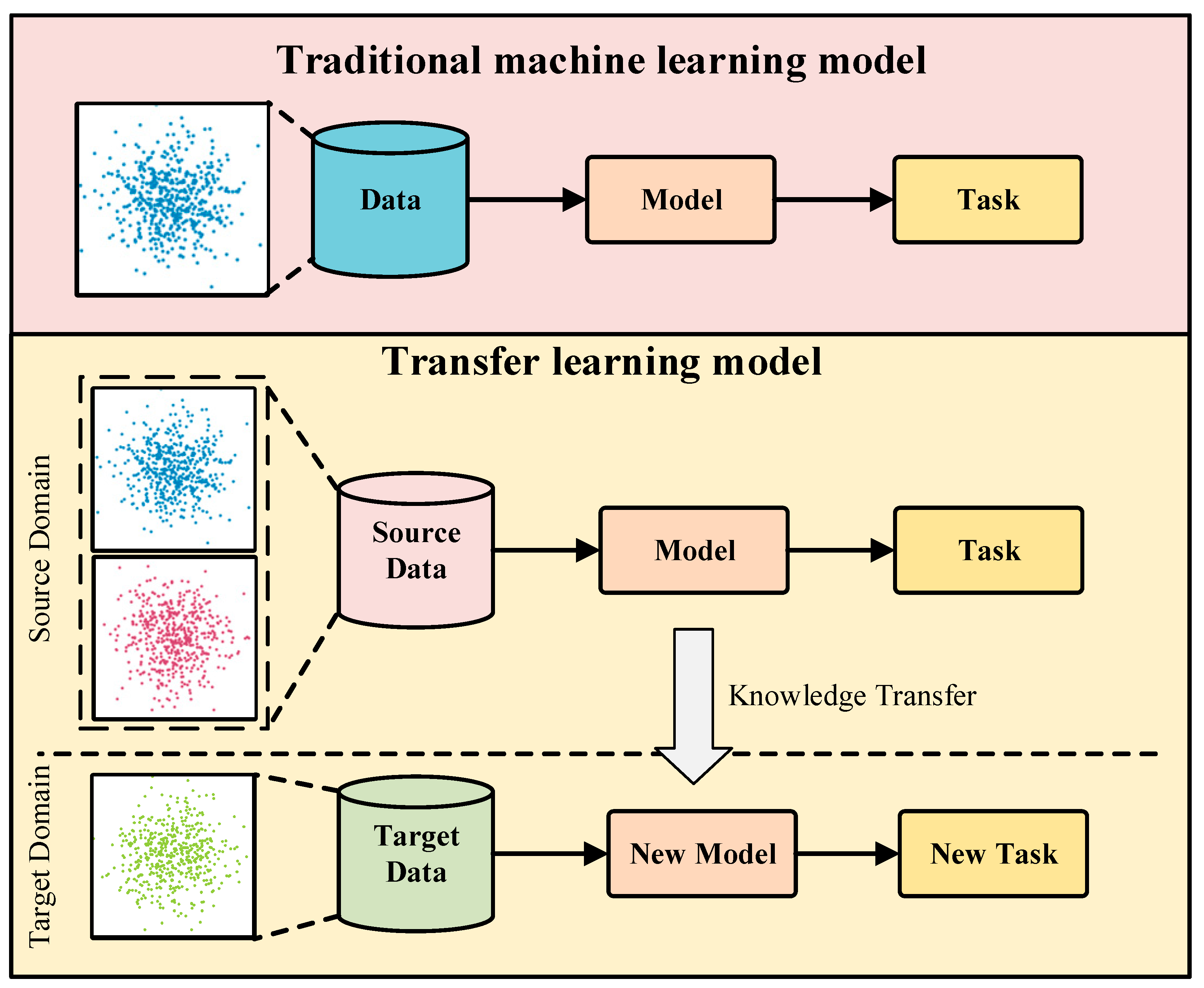
Traditional machine learning methods demand that both the training and test datasets follow the same underlying distribution, with ample labeled data required for model training, as illustrated in Figure 1. However, in practice, acquiring full battery aging data for electric vehicles can be challenging, rendering the operating electric vehicle data insufficient to satisfy these conditions. Transfer learning, on the other hand, presents a promising solution to circumvent these limitations. Through leveraging the similarities between different datasets, transfer learning can compensate for missing battery information in scenarios with limited data samples.

Domain is an important concept in transfer learning. The domain is divided into two parts: the feature space $\chi$ and probability distribution $P(X)$(4), where $X=({\chi }_1,{\chi }_2,{\chi }_3\dots {\chi }_n)\in \chi$ represents n-dimensional data samples in the feature space. Generally speaking, if the two domains are different, they may have different feature spaces or different marginal probability distributions.

$$Domain\to D=(\chi ,P(X))$$

(4)

The domains are divided into source domain and target domain. The source domain is the domain with a lot of labeled data and contains useful information for the target domain, which is the object to be transferred. In this paper, the source domain is the NASA battery aging experimental data; the target domain is the domain that hopes to endow knowledge through transfer. In this paper, the target domain is the lithium-ion battery charging data under vehicle conditions. Lowercase subscripts s and T are usually used to refer to two fields, respectively. $D_s$ represents the source domain, and ${\mathrm{D}}_{\mathrm{t}}$ represents the target domain. The process of transfer learning is to transfer knowledge from the source domain to the target domain, i.e., training a model with a lot of data from the source domain and little data from the target domain, so as to minimize the generalization error in the target domain.

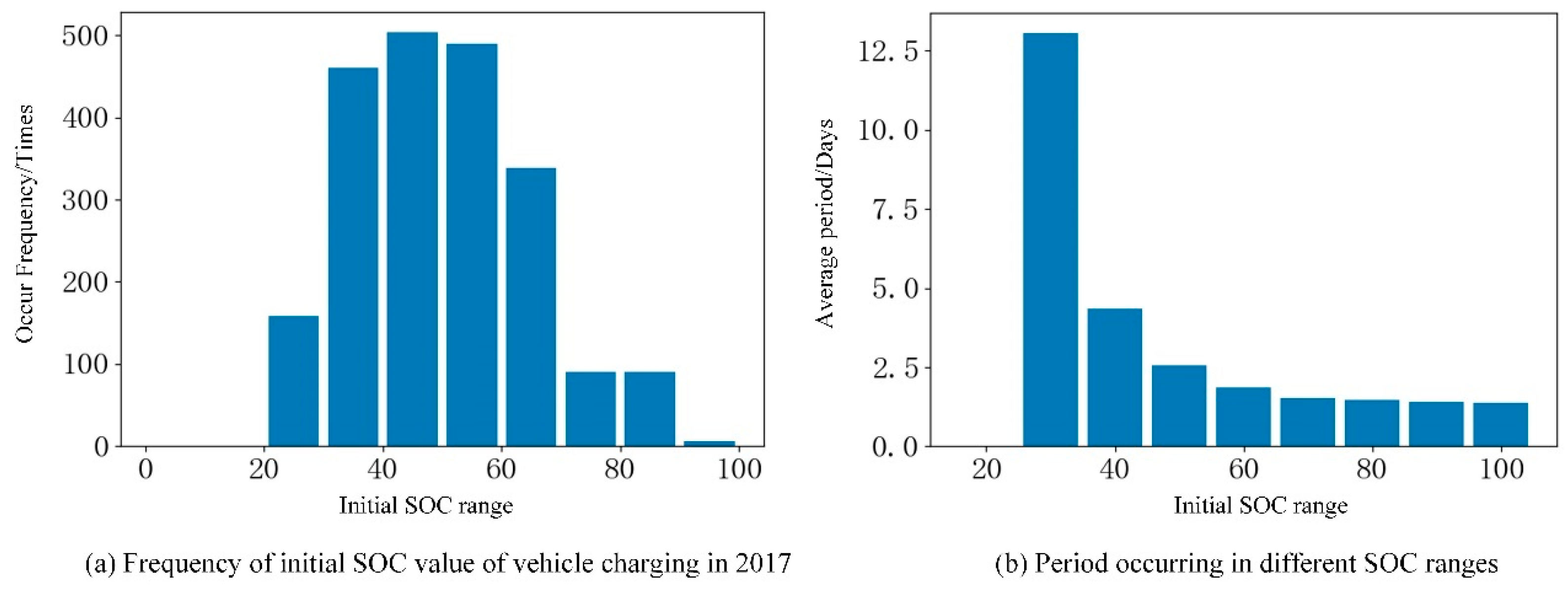
During vehicle operation, car owners often choose to charge their vehicles when the remaining power falls within the range of 30% to 50%, as illustrated in Figure 2. Consequently, the data collected during daily vehicle operation is often fragmented, making it difficult to obtain complete charge and discharge data. Moreover, the number of labeled samples is often limited in such scenarios, making it challenging for traditional machine learning models to achieve the desired level of accuracy. As such, transfer learning has emerged as a promising area of research in small sample learning, leveraging similarity relationships between data and fields to apply previously acquired knowledge to new, unknown fields.

The degradation pattern of batteries under NASA’s experimental conditions and vehicle operating conditions exhibits a comparable overall trend, and the shapes of the constant current charging voltage and current are also similar. This similarity indicates a relatively high correlation between the source domain experimental data and the target domain operational data. As a result, transfer learning can be employed to transfer the shared knowledge of lithium-ion batteries from a vast collection of existing battery aging experimental data to the field of working condition data, leveraging the similarities between the source and target domains.

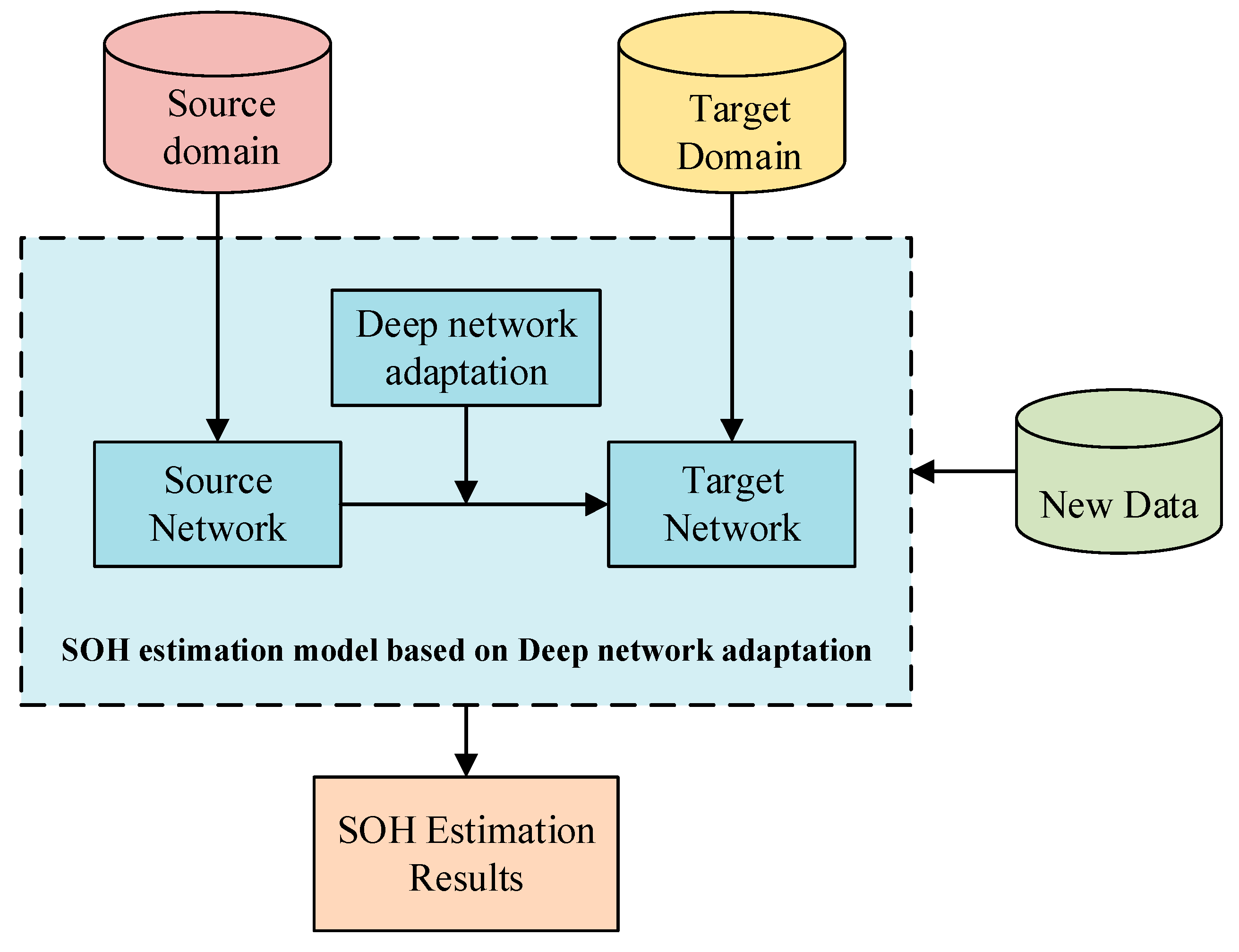
This study proposes a framework for SOH estimation of lithium-ion batteries based on deep network adaptation, as illustrated in Figure 3. Lithium-ion battery data can be categorized into three types based on their origin: (i) new data acquired from sensors during daily electric vehicle charging; (ii) source domain NASA battery experimental data; and (iii) data collected from full charge tests of electric buses in practice. To estimate the SOH of electric vehicles, the proposed method first establishes both the source and target domain networks, followed by the transfer of aging information contained within the source domain data to the target domain network using a depth network adaptive algorithm. When new data are generated through electric vehicle charging, the data are preprocessed, and features are extracted before being input to the trained target domain network, which outputs the SOH value of the current vehicle.

The present study utilizes the depth domain adaptive method to construct an SOH estimation network. In transfer learning, the proximity between two domains is positively correlated with the transfer effectiveness. Domain adaptation, on the other hand, is focused on transfer learning scenarios, in which the tasks in the source and target domains are identical, the feature space is identical, but the feature data distribution varies. The objective of domain adaptation is to facilitate transfer and achieve enhanced transfer learning effects by minimizing the differences in data distribution between the source and target domains.

The formal definition of domain adaptation is given below: given the source domain ${\mathrm{D}}_{\mathrm{s}}$ and target domain ${\mathrm{D}}_{\mathrm{t}}$, where ${\mathrm{D}}_{\mathrm{s}}$ and ${\mathrm{D}}_{\mathrm{t}}$ are consistent with the task and feature space (5), but the feature data distribution is inconsistent (6). The transfer learning problem, in this case, is called domain adaptation [27].

$$\left\{\begin{array}{c}{t}_s=t_T\\ X_s=X_t\end{array}\right.$$

(5)

$$\left\{\begin{array}{c}{Q}_s(y_s|x_s)=Q_t(y_t|x_t)\\ P_s(x_s)\ne P_t(x_t)\end{array}\right.$$

(6)

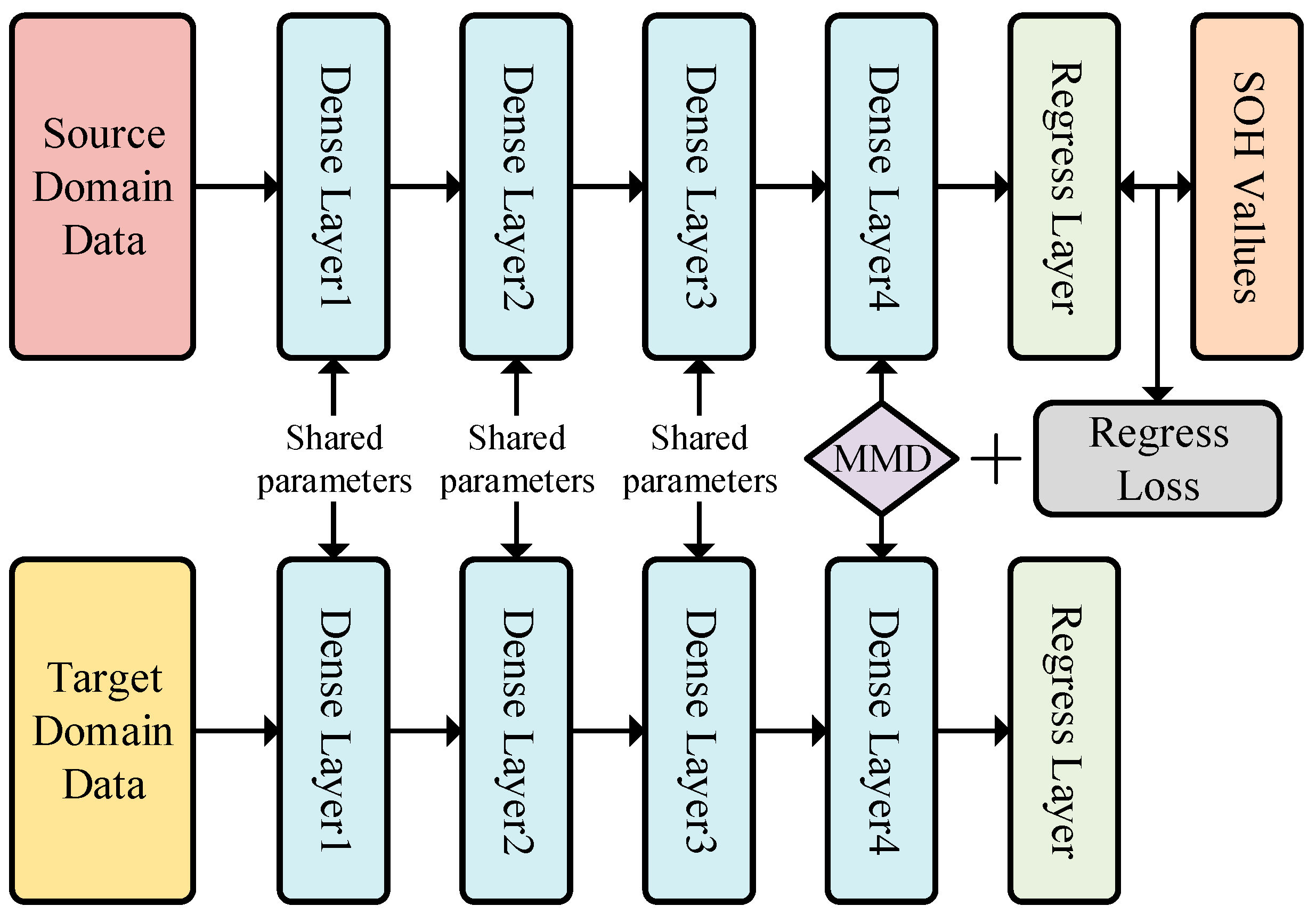
The network architecture developed in this research is illustrated in Figure 4. Two networks, each comprising five fully connected layers, are established in the source and target domains, respectively. An adaptive layer is appended before the regression layer [28]. Deep network adaptation involves the integration of an adaptive layer into the deep learning network. This adaptive layer serves to minimize the data distribution differences between the source and target domains, thereby enabling transfer learning to be accomplished.

In this study, the actual SOH value serves as the label. The specific learning process adopted in this study involves the development of two five-layer perceptron networks. Initially, the parameters of each layer are initialized. Subsequently, in each iteration, the features of both the source and target domains are fed into their respective networks. Once the features pass through the first several layers, the Maximum Mean Difference (MMD) is added to the previous layer of the regression layer, which helps to measure the distance between the two domains. The network parameters of the first three layers are common to both domains and remain the same throughout the training process. The actual SOH value serves as the label. During network training, the conventional loss of the source domain and the distance between the two domains gradually decrease.

The network uses the MAE to measure the loss between the predicted value and the real value of the source domain network (7), where $y_{i(t)}$ represents the real value of the sample $i$, ${\widehat{y}}_{i\left(t\right)}$ represents the predicted value of the sample $i$, $N$ represents the number of samples, and the calculated regression loss is recorded as

$$MSE=\frac{1}{N}{\displaystyle \sum _{i=1}^N{(y_i-{\widehat{y}}_i)}^2}$$

(7)

When calculating the loss $l_R$ between the predicted value and the real value of the source domain network, calculate the distance between the source domain and the target domain at the same time, i.e., calculate the network adaptive loss $l_A$. The loss function of the final model includes both regression loss and adaptive loss, as below (8):

$$loss=l_R+\lambda l_A$$

(8)

$\lambda$ is the parameter in order to measure the weight of regression loss and domain adaptive loss. Through experimental tests, $\lambda$ works best on our data set when it is 0.4.

Once the overall loss function is obtained, it is backpropagated to calculate the error signal of each layer, and the stochastic gradient descent (SGD) algorithm is employed to update the model parameters. The SGD algorithm iterates one sample at a time, which allows for a fast training speed. After updating the parameters, the above iterative steps are repeated until the end of the iteration.

In this model, the maximum mean difference MMD is selected to measure the distance between the two domains, as below (9):

$$\begin{array}{ll}{l}_A& =MM{D}^2\left[F,X_s,X_t\right]\\ & =\left[\frac{1}{m(m-1)}{\displaystyle \sum _{i\ne j}^{m}k}\left(x_{si},x_{sj}\right)+\frac{1}{n(n-1)}{\displaystyle \sum _{i\ne j}^{n}k}\left(x_{ti},x_{tj}\right)+\frac{1}{mn}{\displaystyle \sum _{i,j=1}^{m,n}k}\left(x_{si},x_{tj}\right)\right]\end{array}$$

(9)

where $X_S$ and $X_T$ represent the source domain and target domain, respectively, and $m$ and $n$ represent the numbers of samples in the two domains. In this model, it is the number of nodes in the layer 4, $X_{si}$ represents the output value of the node $i$ of the source domain network layer 4, and $X_{ti}$ represents the output value of the node $i$ of the target domain network full connection layer 4. $k$ represents the kernel function selected by MMD. In MMD measurement, the selection of kernel function plays a very important role. The commonly used kernel functions include Gaussian kernel, polynomial kernel, linear kernel, Laplace kernel, etc. In this model, the linear kernel is used as the kernel function of MMD.

$$k(x,x\prime )=e^{-\frac{{‖x-x\prime ‖}^2}{2{\sigma }^2}}$$

(10)

Therefore, finally, our network adaptive loss $l_A$ can be expressed as follows (11). The number of nodes in the fourth fully connected layer (Figure 4) of the source domain and the target domain is the same, which is uniformly expressed in $\mathrm{n}$.

$$l_A=\left[\frac{1}{n(n-1)}{\displaystyle \sum _{i\ne j}^n\left(e^{-\frac{{‖x_{ti}-x_{tj}‖}^2}{2{\sigma }^2}}+e^{-\frac{{‖x_{si}-x_{sj}‖}^2}{2{\sigma }^2}}\right)}+\frac{1}{mn}{\displaystyle \sum _{i,j=1}^{m,n}{e}^{-\frac{{‖x_{si}-x_{tj}‖}^2}{2{\sigma }^2}}}\right]$$

(11)

The final SOH estimation model is obtained by transferring the target domain network obtained in the previous step to a new five-layer network model with the same structure. The parameters of the transferred network are fine-tuned on the target domain data to obtain the final SOH estimation model. Then, the extracted features of the working condition data are input into the SOH estimation model, and the output is the estimated value of SOH.

4. Experimental Results and Analysis

In this paper, the Pearson Correlation Coefficient (PCC) is used to verify the correlation between the extracted features and SOH values. The features with higher correlation with SOH can better represent attenuation of lithium-ion battery. PCC formula is defined as follows (12). Where ${\sigma }_x$ and ${\sigma }_y$ represent the standard deviation of two variables, and $con\left(X,Y\right)$ represents the covariance of two variables.

$${\rho }_{x,y}=corr(X,Y)=\frac{con(X,Y)}{{\sigma }_x{\sigma }_y}=\frac{E[(X-{\mu }_x)(Y-{\mu }_y)]}{{\sigma }_x{\sigma }_y}$$

(12)

The correlation strength between the extracted features and the SOH is measured using the Pearson correlation coefficient. The results are presented in

Table 1. Correlation degree between the features and SOH values in NASA data condition.

Battery	F1	F2	F3	F4	F5	Correlation
B0005	0.98	0.94	0.97	1.00	0.98	0.97
B0006	0.99	0.96	0.98	1.00	0.99	0.98
B0007	0.98	0.86	0.94	0.99	0.98	0.95
B0018	0.96	0.89	0.93	0.99	0.96	0.95
B0029	0.72	0.80	0.81	0.95	0.72	0.8
B0032	0.84	0.70	0.74	0.95	0.84	0.81
B0033	1.00	0.87	0.87	0.99	1.00	0.94
B0034	0.99	0.86	0.88	0.95	0.99	0.93
B0036	0.83	0.71	0.71	0.91	0.82	0.80
B0030	0.73	0.81	0.80	0.93	0.73	0.80
B0031	0.60	0.73	0.74	0.88	0.61	0.71

and

Table 2. Correlation degree between features and SOH values in EV operating condition.

F1	F2	F3	F4	F5	Correlation
0.89	0.66	0.52	0.86	0.83	0.75

.

It can be seen from the table that the characteristics extracted from each battery in NASA experimental data have high correlation with SOH, most of which have reached more than 0.7, which means they have a high linear correlation with SOH, so they can effectively reflect the aging degree of the battery.

The extracted features from the working condition data are not so highly correlated with the experimental data, but all the correlation degrees are greater than 0.5. Among them, except F3, all the other features are greater than 0.7 or close to 0.7, reaching a high linear correlation with SOH, which can also effectively reflect the aging degree of lithium-ion batteries.

In order to verify whether the transfer learning can transfer the aging information in the source domain to the target domain, the transfer experiment is carried out by using Fine-Tune network transfer algorithm and compared with the direct use of neural network.

In this study, a battery experiment conducted by NASA was used to investigate the effectiveness of transfer learning in predicting battery aging information. Specifically, the experiment utilized two batteries, B0030 and B0031, as target domain data, whereas the remaining batteries were used as source domain data. To evaluate the transfer learning approach, two methods were utilized to divide the training and test data of the target domain: random division and a division that excluded aging information after the state of health (SOH) decreased to 90%. The latter division aimed to assess the ability of transfer learning to effectively transfer missing aging information from the source domain to the target domain, thereby enhancing model prediction accuracy. The results of the experiment are presented in

Table 3. SOH estimation error (MAE) of NASA battery experiment.

	Randomly Divide		Sequence Divide
	Direct	Transfer	Direct	Transfer
Test 1	3.15%	1.83%	5.98%	2.17%
Test 2	4.03%	2.37%	6.72%	2.92%
Test 3	4.57%	2.77%	7.36%	3.36%
Test 4	3.91%	1.89%	7.01%	3.02%
Test 5	4.67%	3.41%	7.09%	3.18%
Average	4.07%	2.46%	6.83%	2.93%

.

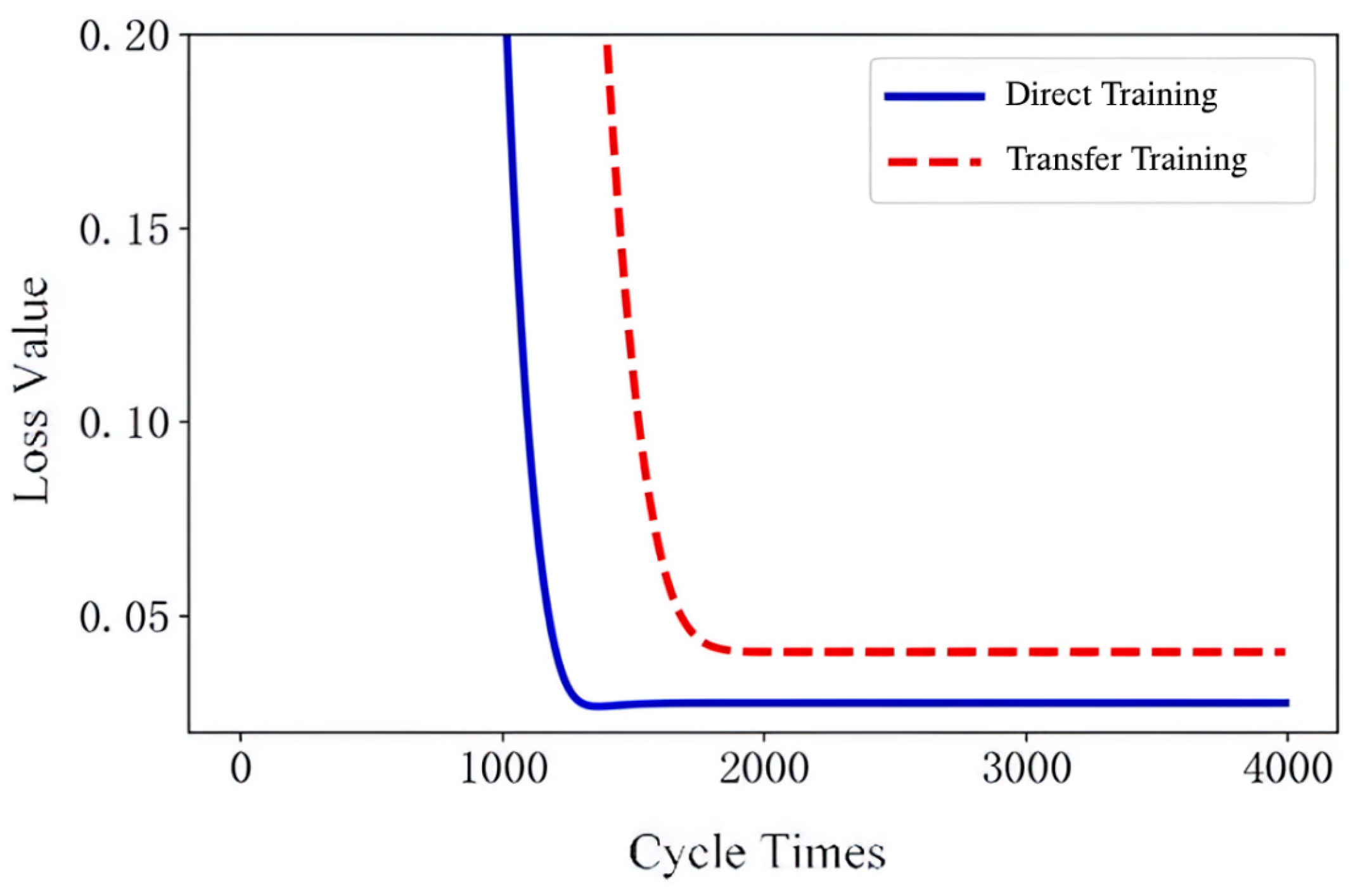
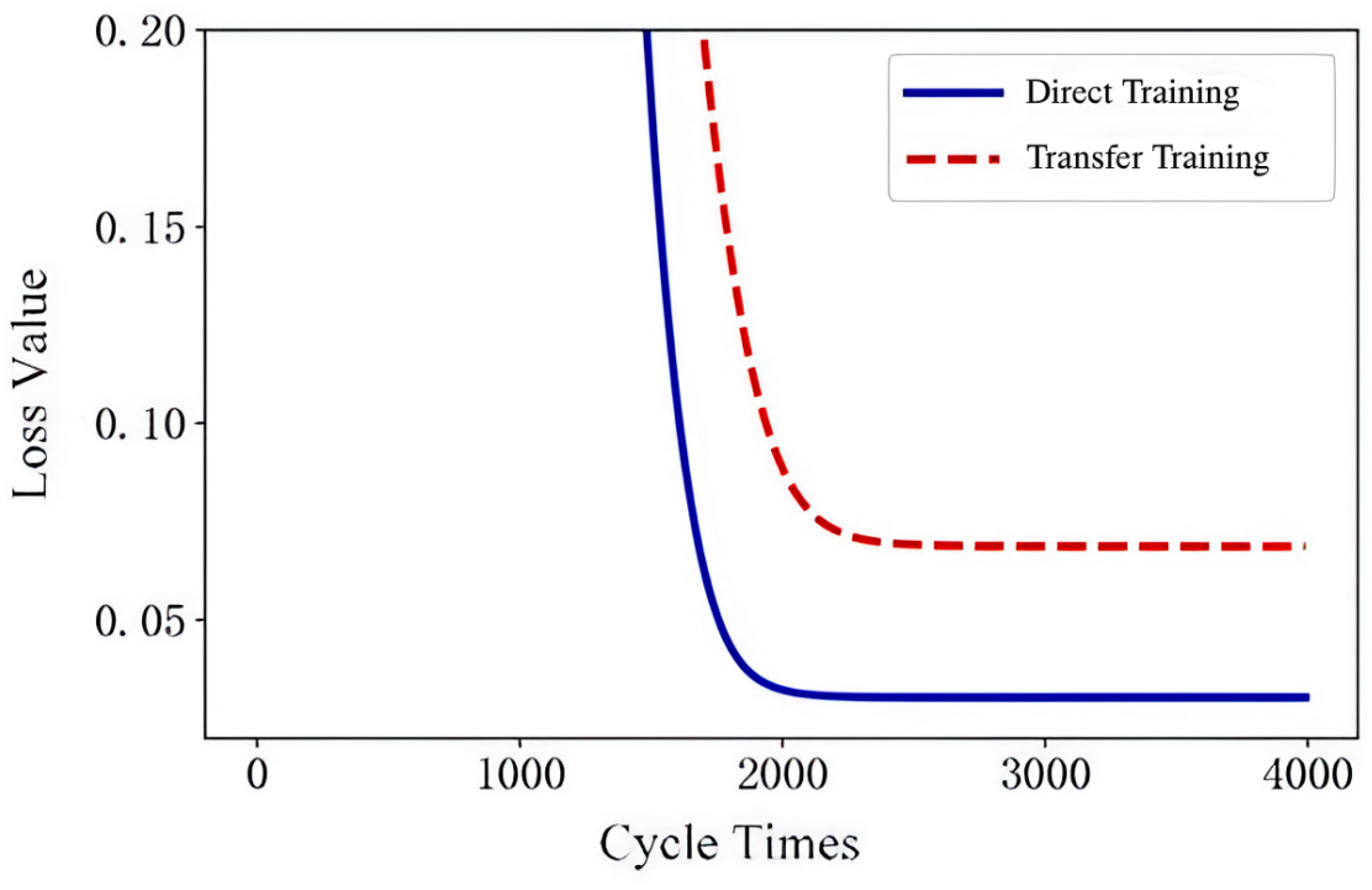
The experimental findings demonstrate that utilization of transfer learning in NASA datasets results in a noteworthy increase in model accuracy, regardless of whether data are divided randomly or sequentially (Figure 5 and Figure 6). Specifically, the error rate associated with sequential division exceeds that of random division, which is consistent with the expectation that the model struggles to estimate SOH (state of health) in the absence of battery aging information. Nevertheless, after transfer learning is applied, the error rate for sequential division decreases from 6.83% to 2.93%, thereby significantly improving the model’s performance. In comparison to sequential partition, the error rate is only marginally higher, by approximately 0.5%, which indicates that transfer learning can compensate for the dearth of battery aging information in the target domain samples.

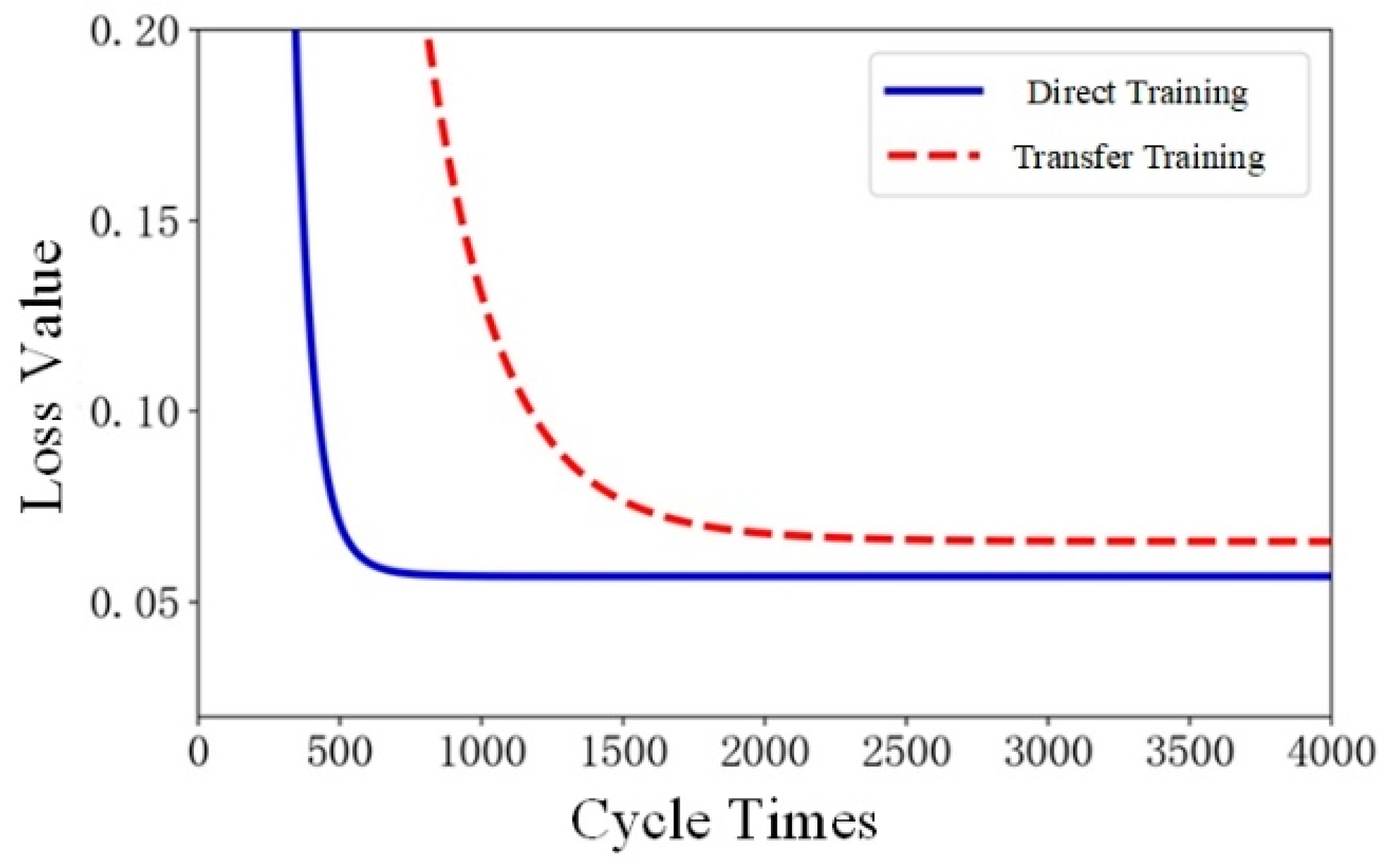
In the study, vehicle operating condition data are utilized as the target domain data, whereas all available NASA battery experimental data serve as the source domain data. Initially, the model is trained on the source domain data to obtain a pre-training model. Subsequently, the parameters of the model are transferred and fine-tuned on the target domain. The average absolute error of the experimental results is presented in

Table 4. SOH estimation error (MAE) of EV operating condition data.

	Direct	Transfer
Test 1	5.83%	4.98%
Test 2	6.88%	5.71%
Test 3	6.84%	5.68%
Average	6.52%	5.46%

and Figure 7.

Based on the experimental results, it is apparent that transfer learning is more effective than direct training in adapting a deep network for estimating the state of health (SOH) between NASA battery experimental data and vehicle operating condition data. The transfer learning approach reduces the error from 6.52% to 5.46% and significantly reduces the time required for model training compared to direct training.

To validate the efficacy of the proposed deep-network-based adaptive SOH estimation method, two commonly used algorithms for SOH estimation, support vector machine regression (SVR) and Gaussian process regression (GPR), were selected as comparison models, along with the Fine-Tune transfer learning algorithm [12,29,30]. SVM and GPR have been extensively used by researchers to predict the SOH value of lithium-ion batteries and have demonstrated good performance in this regard. Therefore, they are suitable as comparison models in this experiment.

For this set of experiments, the deep network adaptation SOH estimation model was trained using all available NASA battery experimental data as source domain data, and the vehicle operating condition data were utilized as the target domain data. The model was trained with the following parameter settings, as detailed in

Table 5. Parameter Settings.

Parameter	Value
Batch size	10
Optimization algorithm	SGD
Learning rate	0.0001
Dropout	0.15
$\lambda$	0.4
MMD Kernel	Linear Kernel

:

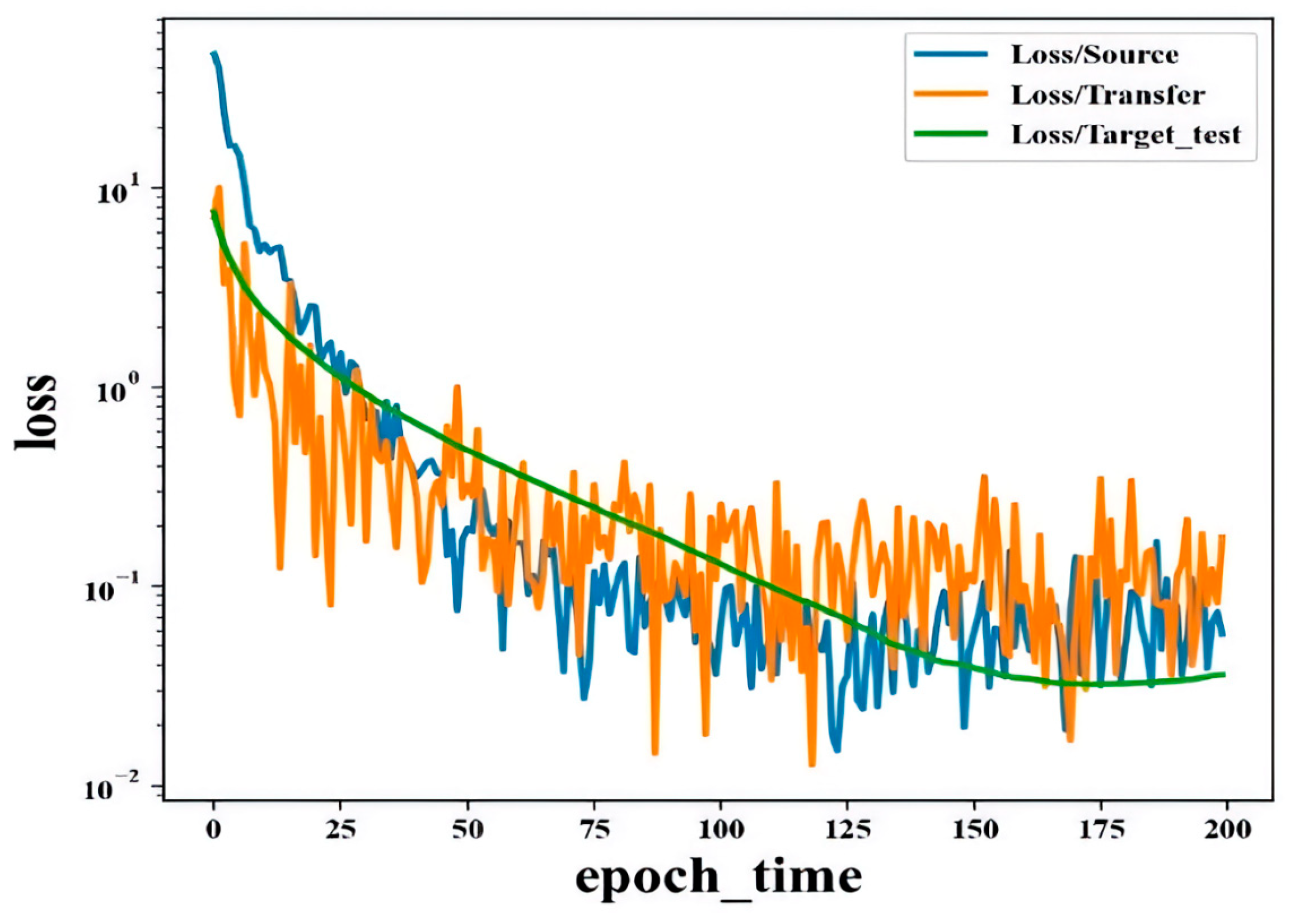
The loss changes in the source domain $l_R$, the changes in two domains network adaptive loss $l_A$, and the loss changes tested on the target domain during the training process are as follows (Figure 8). In order to facilitate observation, the Y axis is set as the logarithmic coordinate axis.

It can be seen from the figure that with the progress of training, the loss of source domain data $l_R$ is decreasing, and the adaptive loss between the two domains $l_A$ is also decreasing, which means that the distance between the two domains is getting closer with the progress of training, and the continuous reduction in target domain loss also confirms the reduction in the distance between the two domains. After the training, the error of the model in the source domain is reduced to 1.9%, and the average error in the target domain is also reduced to 3.0%, which is significantly lower than the model accuracy with the Fine-Tune model.

The present study employs several machine learning techniques, including deep network adaptation, support vector machine, Gaussian process regression, and fine-tuned transfer learning algorithm to predict the SOH values. The performance of these algorithms is compared, and the results are presented in Figure 9. The findings indicate that the deep network adaptation algorithm outperforms other approaches in terms of predicting the SOH value more accurately. Additionally, it demonstrates the potential for better SOH value prediction using vehicle operating condition data.

Table 6. Comparison of estimation results of this study and ADN, SVM, and GPR.

BUS	ADN	SVM	GPR	Fine-Tune
t0457	4.92%	4.99%	6.39%	9.23%
t0747	2.20%	1.78%	2.35%	6.20%
t2475	1.09%	3.17%	2.57%	3.45%
t2741	1.00%	0.25%	2.99%	3.06%
t2747	1.57%	2.77%	1.13%	3.88%
t4643	2.54%	4.97%	2.75%	5.12%
t4707	0.43%	0.67%	1.77%	4.23%
t4712	4.14%	7.21%	6.62%	2.37%
t4740	4.51%	5.59%	6.13%	4.66%
t4742	6.07%	2.19%	2.32%	8.11%
t4942	2.56%	3.54%	10.48%	6.30%
t6743	2.79%	2.22%	5.38%	9.81%
t6941	2.64%	2.90%	6.61%	5.06%
t7451	8.65%	12.89%	12.99%	4.69%
t8747	3.08%	4.61%	6.02%	6.15%
t9408	1.33%	1.83%	3.60%	5.19%
t9430	0.82%	5.03%	3.29%	6.16%
t9451	4.15%	5.94%	4.26%	4.20%
t9470	2.93%	4.64%	4.12%	6.87%
t9471	1.59%	4.47%	4.04%	4.53%
Average	2.95%	4.08%	4.79%	5.46%

presents a comparison of the SOH value estimated by each algorithm with the actual SOH value for each bus. The performance of each method is evaluated and displayed in the table. It is evident from the results that the deep network adaptation algorithm outperforms other approaches in most vehicles, based on the performance metrics assessed.

The overall error rate across all vehicles was observed to decrease to 2.95%, which is deemed satisfactory for daily State of Health (SOH) estimation purposes. Notably, the ADN algorithm exhibited significant advantages over other methods, with error reductions of 27.7%, 38.4%, and 47.5% compared to the SVR, GPR, and Fine-Tune algorithms, respectively. These results demonstrate the successful transfer of battery aging information from the source domain to the target domain via the deep network adaptation approach.

5. Conclusions

In this study, we present a novel approach for estimating the SOH of lithium batteries in EVs through the application of transfer learning techniques using real-world vehicle operation data. Our investigation commences by addressing the inherent challenges associated with EV data collected during actual on-road conditions. Subsequently, we employ data-driven preprocessing and feature extraction methods. We then develop an SOH estimation model based on transfer learning, specifically utilizing deep network adaptation and employing the maximum mean difference as a distance metric between source and target domains.

The results of our proposed model demonstrate a significant enhancement in predictive accuracy when applied to actual vehicle operating condition data, with the average error of the 54 charging data instances from a diverse set of 20 vehicles reduced to a mere 2.95%. Comparative analysis with alternative models, including SVR, GPR, and fine-tuned transfer learning models, reaffirms the superior accuracy and effectiveness of our proposed approach. It is important to note that previous research has been limited in terms of the number of index parameters considered.

As part of our future work, we plan to expand our study by incorporating additional index parameters and exploring more complex transfer learning strategies, aiming to achieve even better performance on more intricate multivariate datasets.