The Assessment of Electric Vehicle Storage Lifetime Using Battery Thermal Management System
Abstract
1. Introduction
- 1. a new BTMS mathematical control model is presented;
- 2. a more accurate heat exchange calculation that fits any liquid-cooled-based system is presented;
- 3. a case study for an off-highway hybrid vehicle based on liquid-cooled BTMS is discussed.
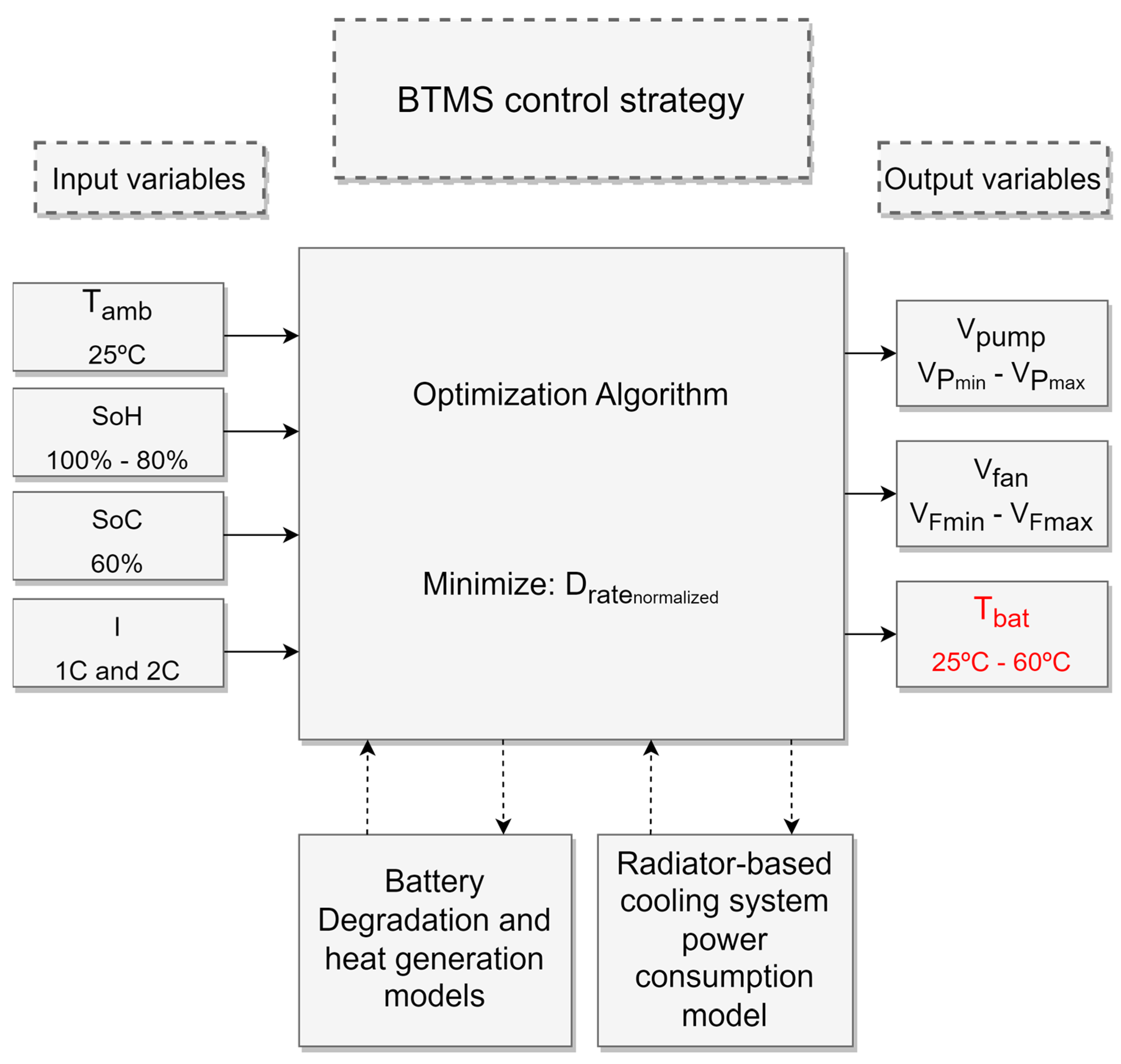
2. BTMS Strategy Methodology
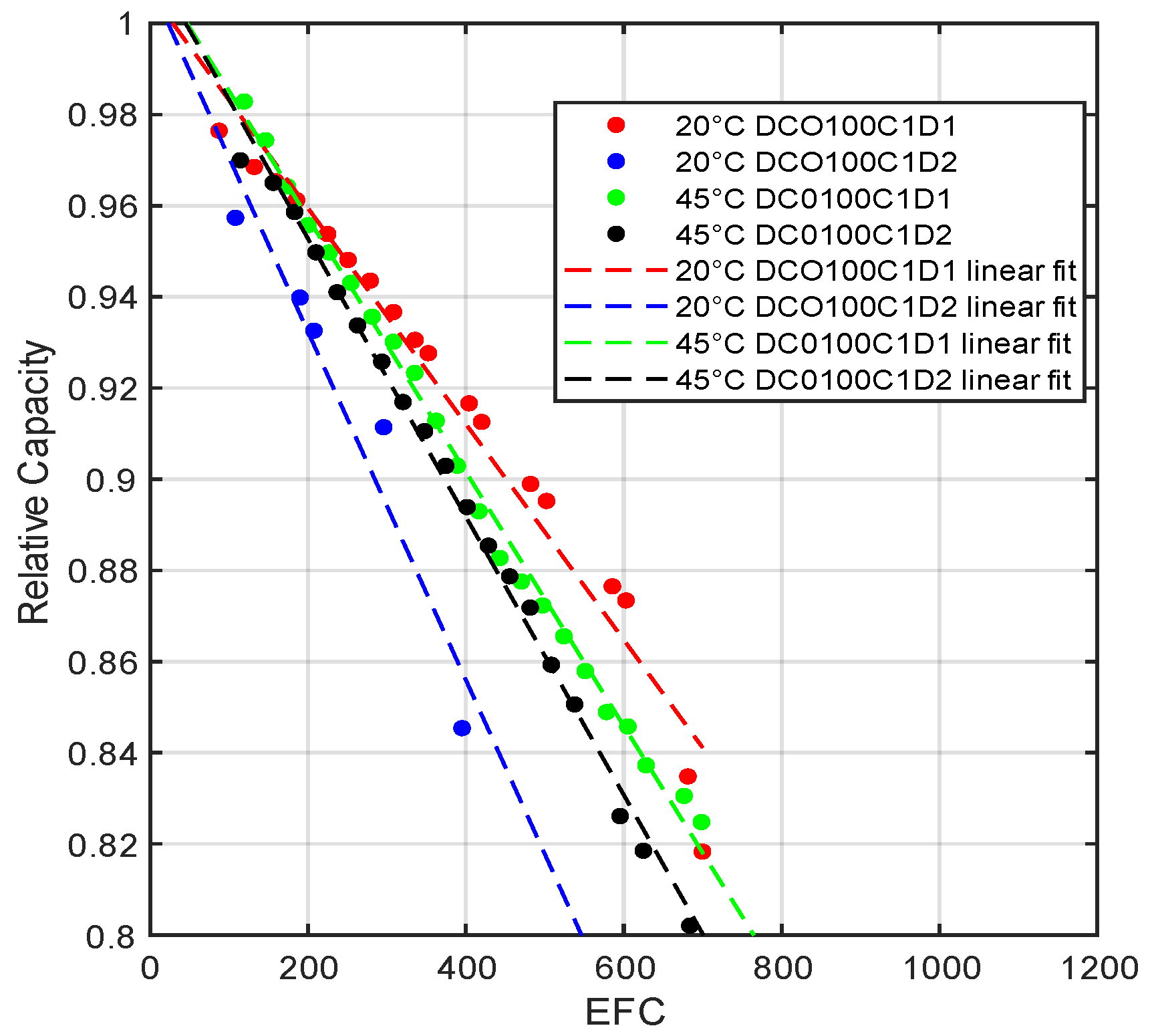
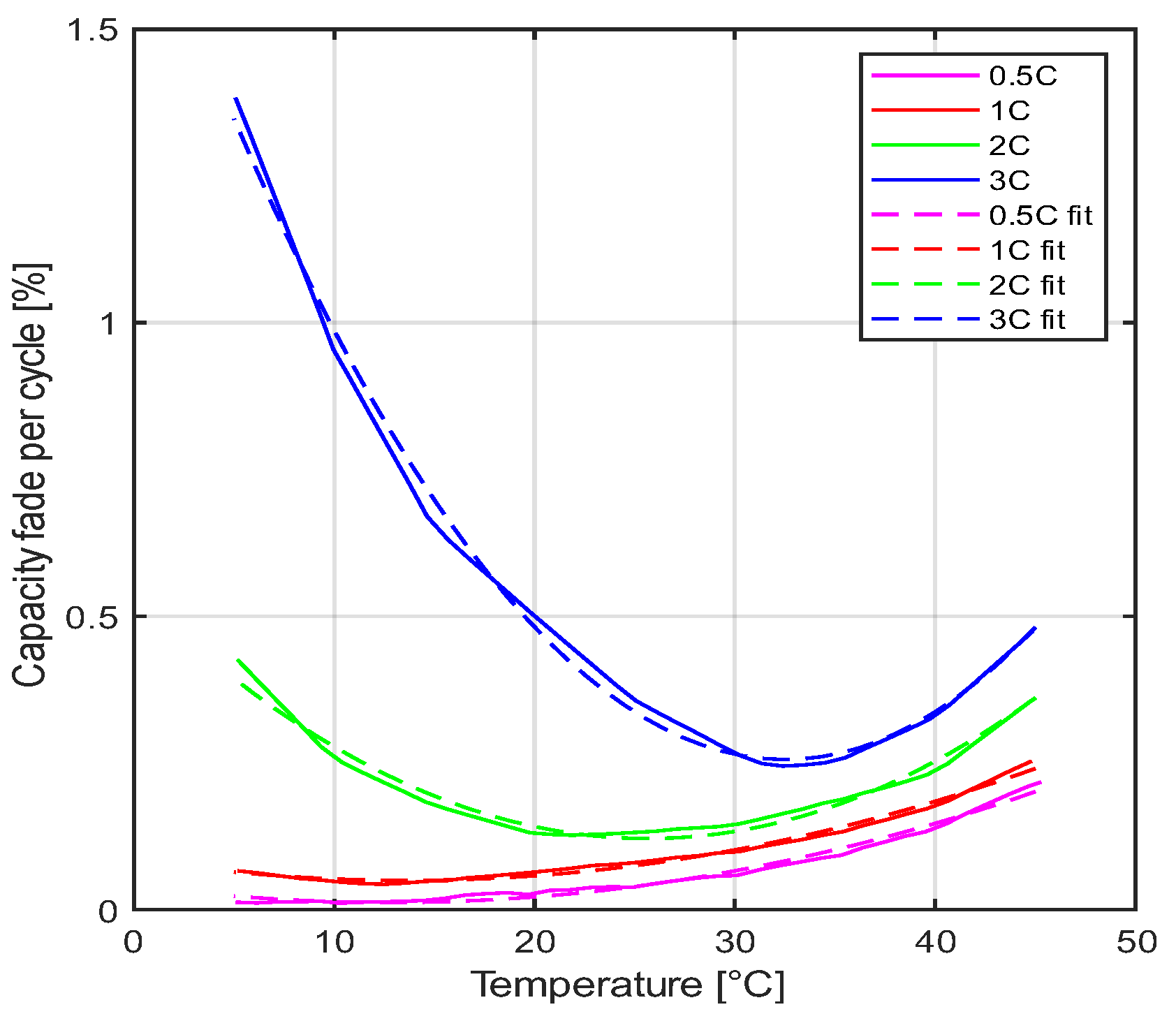
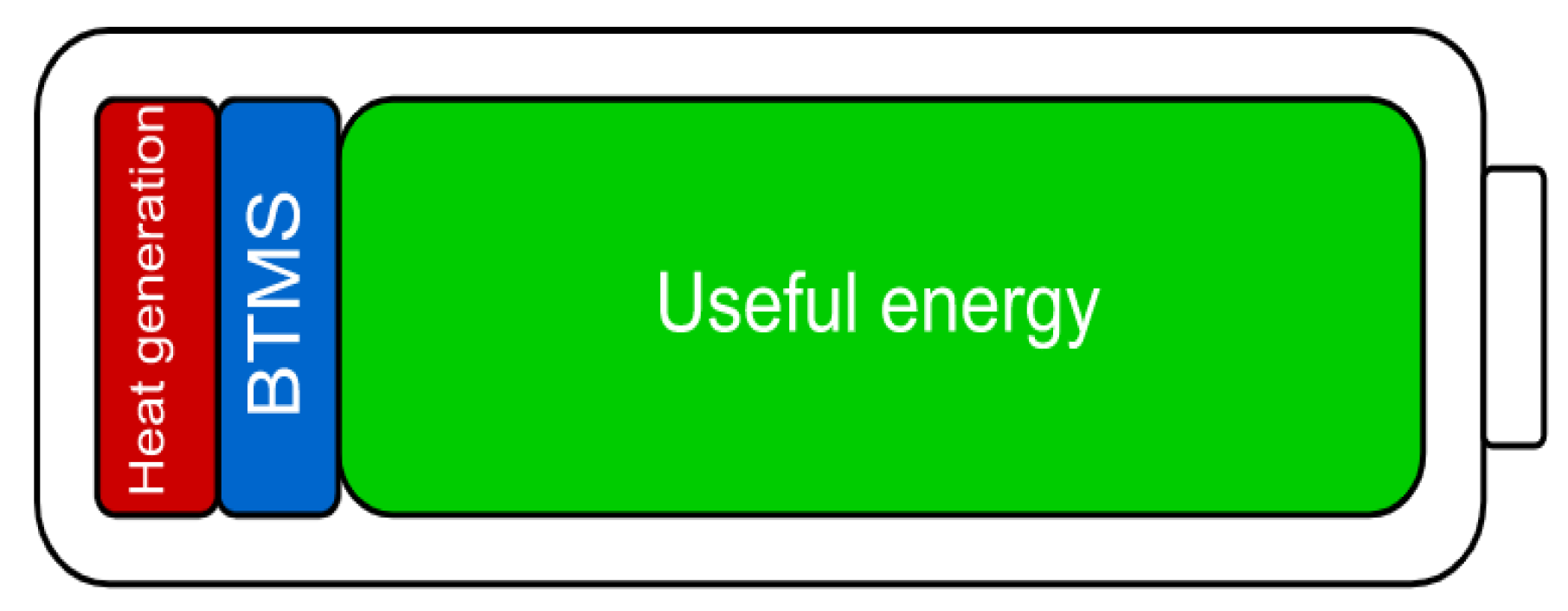
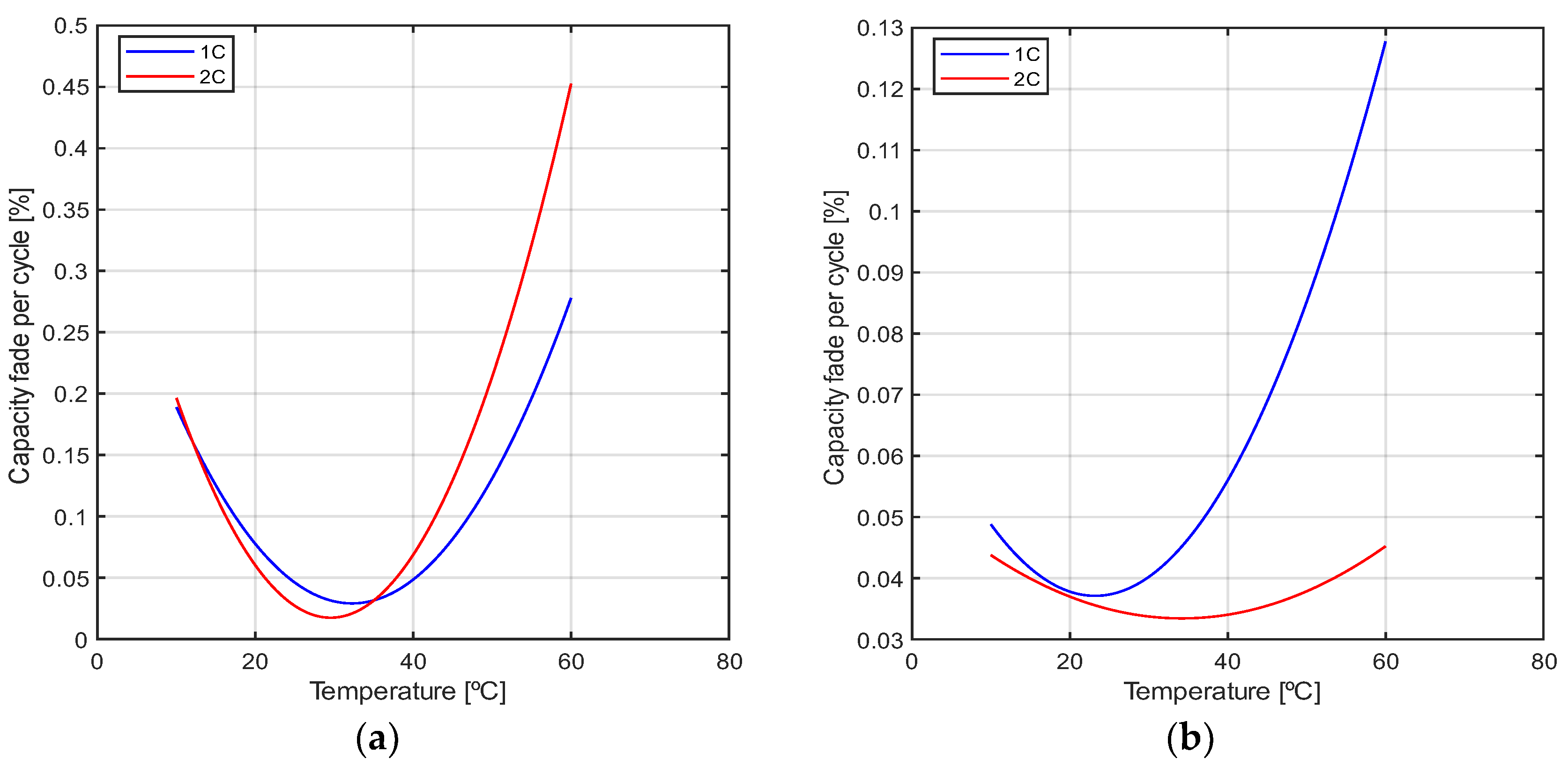
2.1. Degradation Modeling
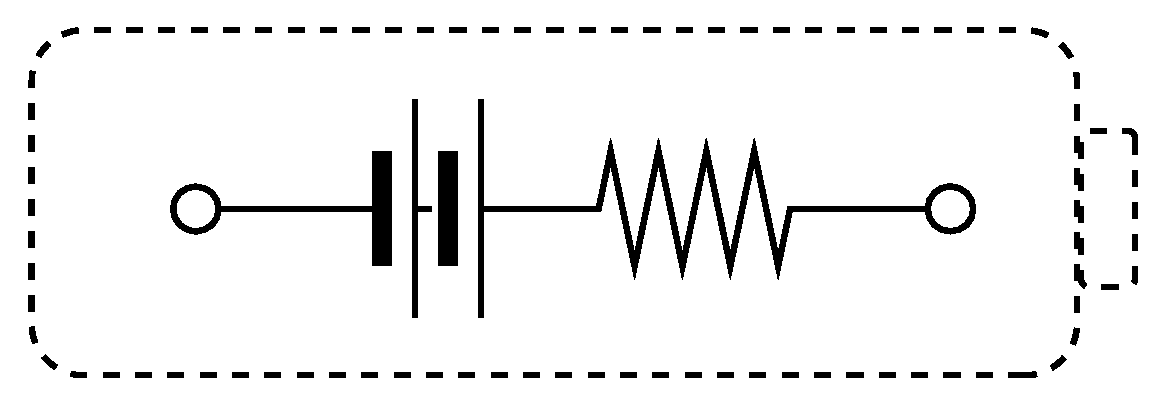
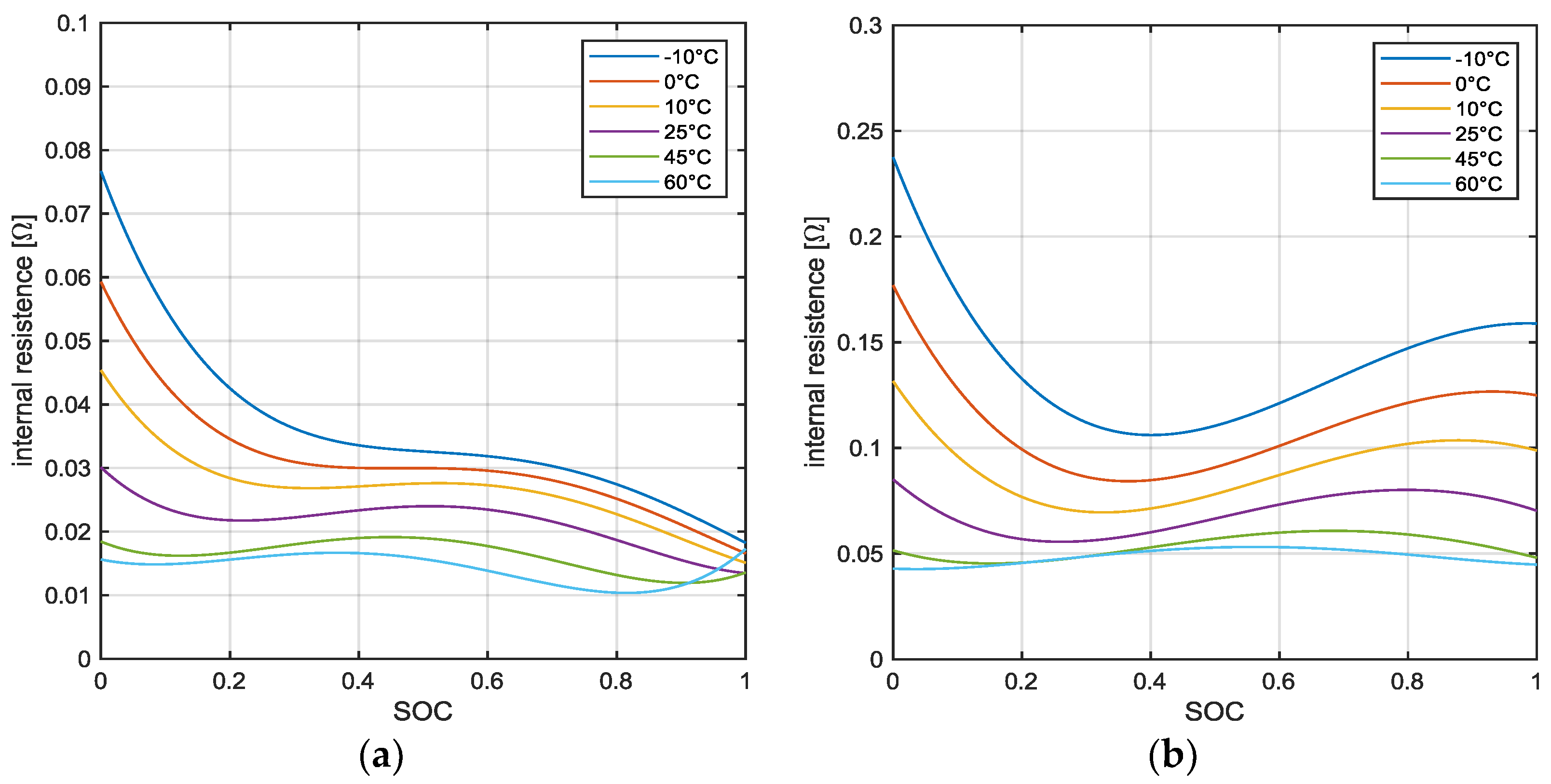
2.2. Cell Heat Generation Modeling
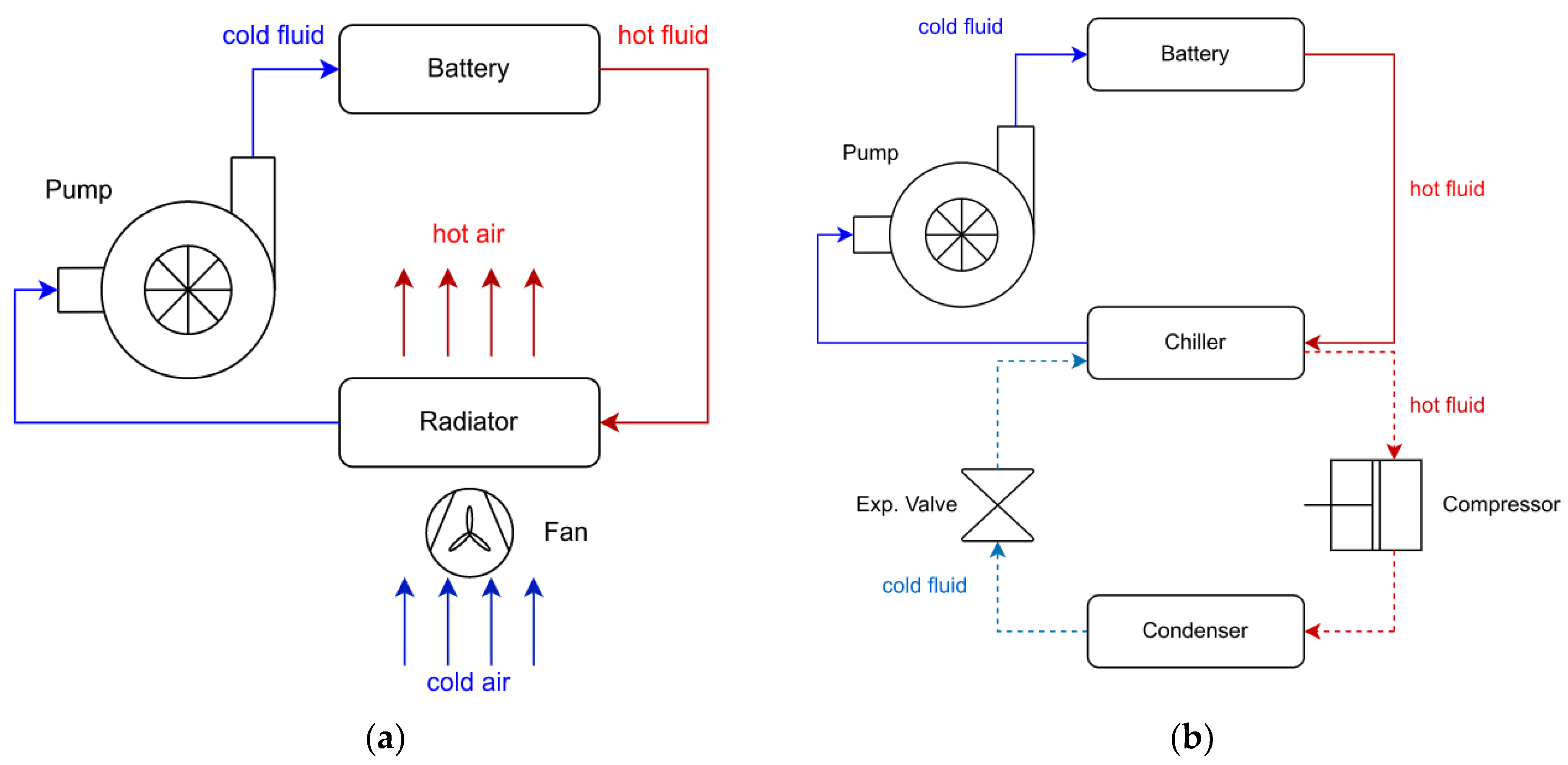
2.3. Cooling System
2.4. Problem Statement
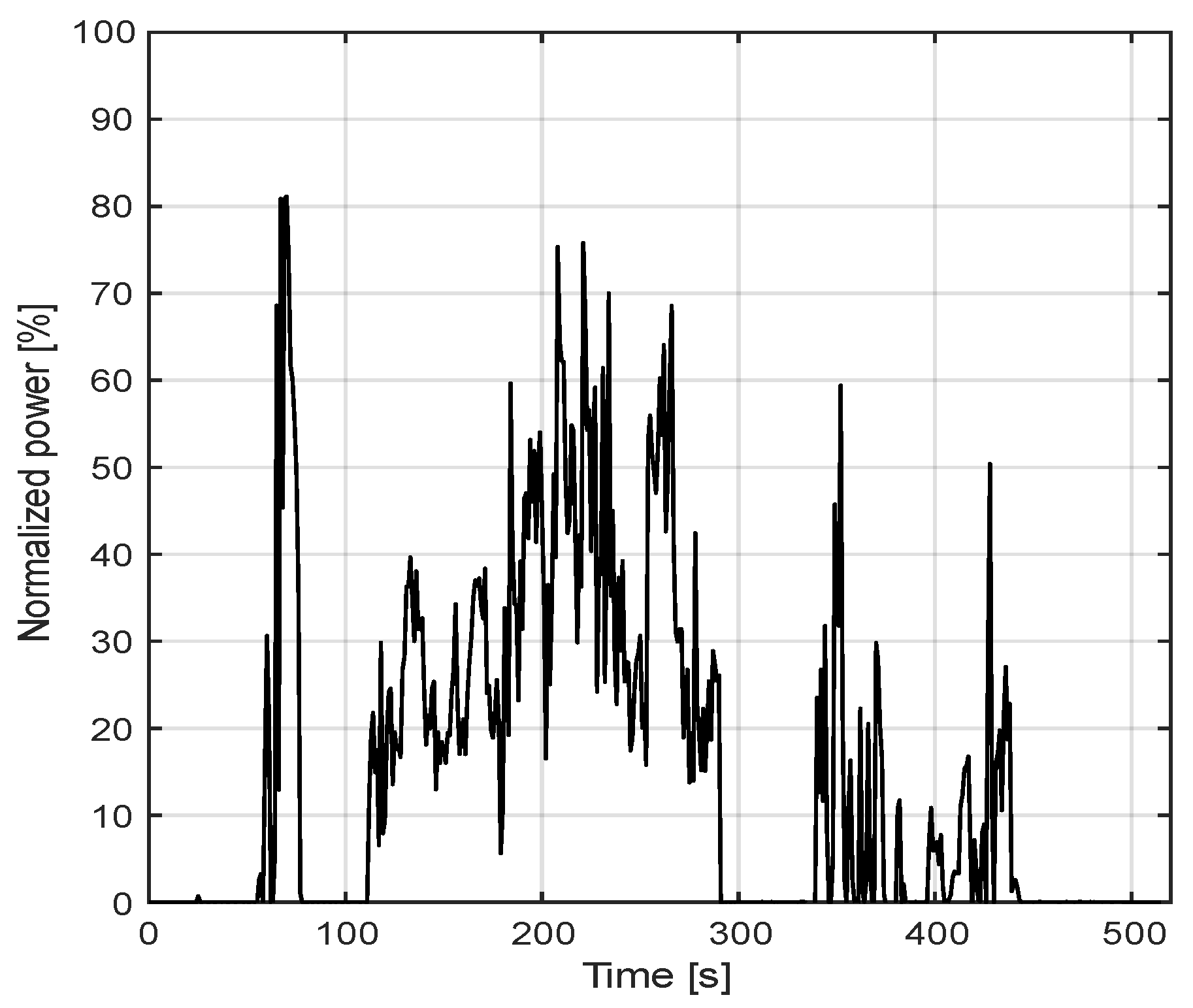
3. Case Study
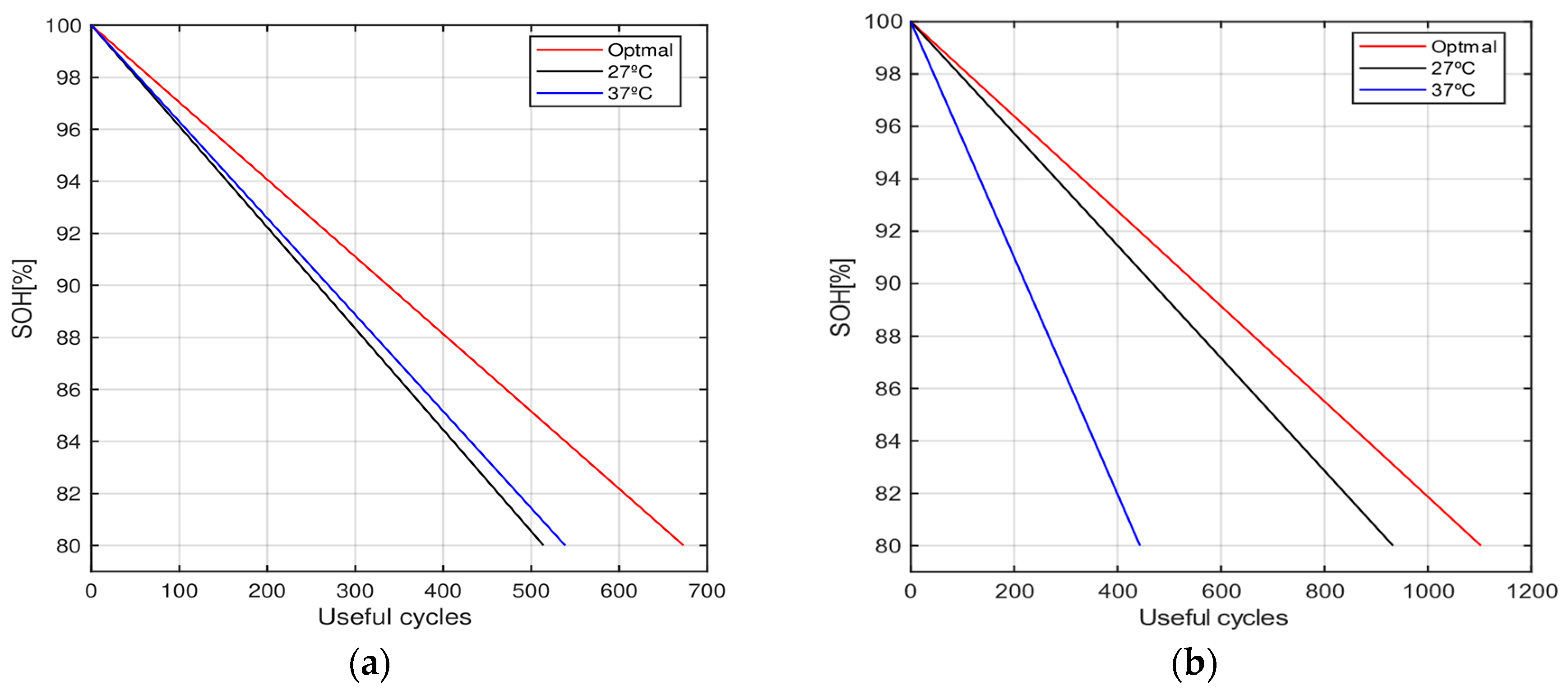
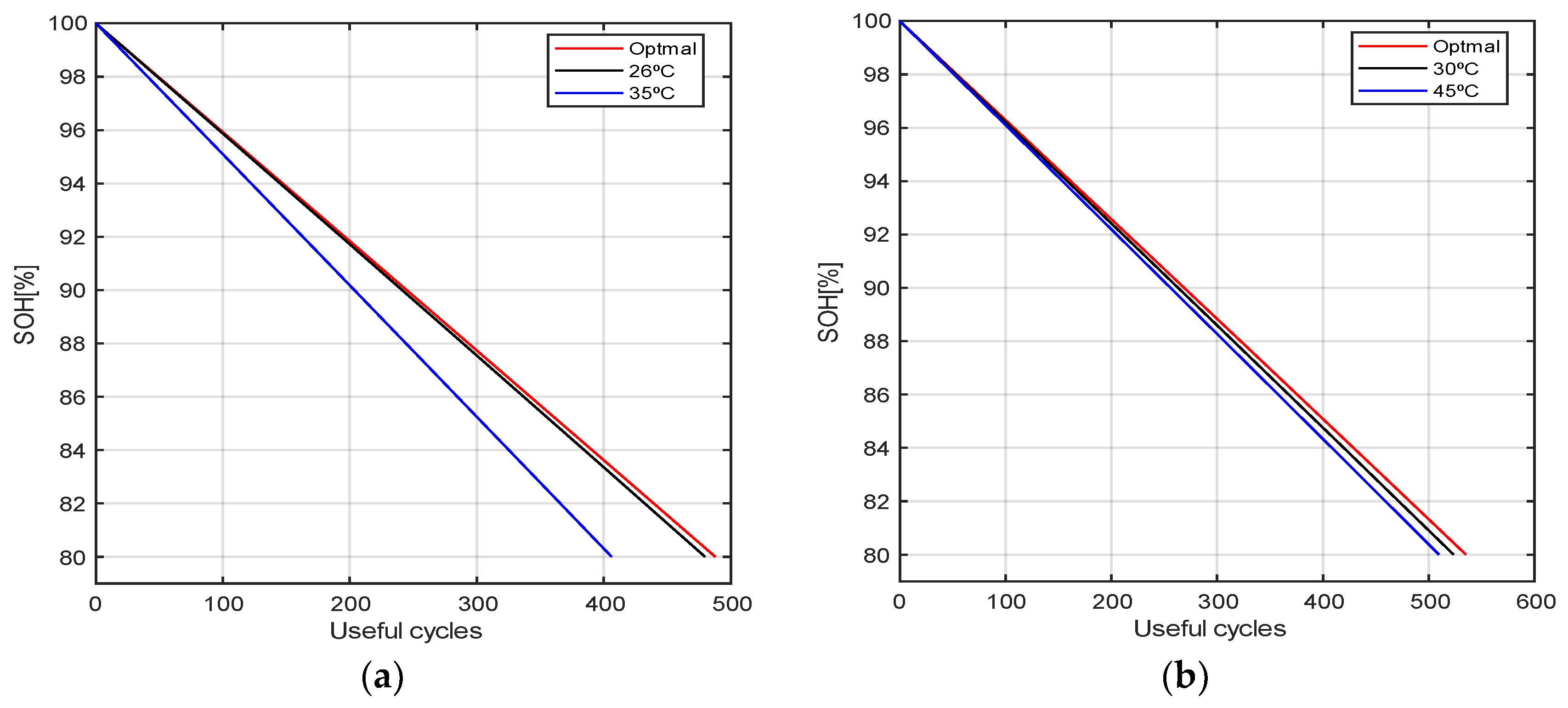
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Masias, A.; Marcicki, J.; Paxton, W.A. Opportunities and challenges of lithium ion batteries in Automotive Applications. ACS Energy Lett. 2021, 6, 621–630. [Google Scholar] [CrossRef]
- Pichler, B. Increasing Electric Vehicle Range with a Recommendation App Providing Context Specific Trip Rankings. Ph.D. Thesis, Universität Linz, Linz, Austria, 2016. [Google Scholar]
- Duan, X.; Jiang, W.; Zou, Y.; Lei, W.; Ma, Z. A coupled electrochemical–thermal–mechanical model for spiral-wound Li-ion batteries. J. Mater. Sci. 2018, 53, 10987–11001. [Google Scholar] [CrossRef]
- Grandjean, T.; Groenewald, J.; McGordon, A.; Widanage, W.; Marco, J. Accelerated internal resistance measurements of lithium-ion cells to support future end-of-life strategies for electric vehicles. Batteries 2018, 4, 49. [Google Scholar] [CrossRef]
- Taffal, M. Electro-Thermal Modeling of Lithium-Ion Battery. Ph.D. Thesis, Politecnico di Torino, Turin, Italy, 2019. [Google Scholar]
- Islam, S.M.; Park, S.-Y.; Balasingam, B. Unification of internal resistance estimation methods for Li-ion batteries using hysteresis-free equivalent circuit models. Batteries 2020, 6, 32. [Google Scholar] [CrossRef]
- Yang, N.; Fu, Y.; Yue, H.; Zheng, J.; Zhang, X.; Yang, C.; Wang, J. An improved semi-empirical model for thermal analysis of lithium-ion batteries. Electrochim. Acta 2019, 311, 8–20. [Google Scholar] [CrossRef]
- Wu, X.; Cui, Z.; Chen, E.; Du, J. Capacity degradation minimization oriented optimization for the pulse preheating of lithium-ion batteries under low temperature. J. Energy Storage 2020, 31, 101746. [Google Scholar] [CrossRef]
- Zhang, L.; Mu, Z.; Gao, X. Coupling analysis and performance study of Commercial 18650 lithium-ion batteries under conditions of temperature and Vibration. Energies 2018, 11, 2856. [Google Scholar] [CrossRef]
- Redondo-Iglesias, E.; Venet, P.; Pelissier, S. Modelling lithium-ion battery ageing in Electric Vehicle Applications—Calendar and cycling ageing combination effects. Batteries 2020, 6, 14. [Google Scholar] [CrossRef]
- Uddin, K.; Perera, S.; Widanage, W.; Somerville, L.; Marco, J. Characterising lithium-ion battery degradation through the identification and tracking of electrochemical battery model parameters. Batteries 2016, 2, 13. [Google Scholar] [CrossRef]
- Yang, X.-G.; Wang, C.-Y. Understanding the trilemma of fast charging, energy density and cycle life of lithium-ion batteries. J. Power Sources 2018, 402, 489–498. [Google Scholar] [CrossRef]
- Zeng, Y.; Chalise, D.; Lubner, S.D.; Kaur, S.; Prasher, R.S. A review of thermal physics and management inside lithium-ion batteries for high energy density and fast charging. Energy Storage Mater. 2021, 41, 264–288. [Google Scholar] [CrossRef]
- Uitz, M.; Sternad, M.; Breuer, S.; Täubert, C.; Traußnig, T.; Hennige, V.; Hanzu, I.; Wilkening, M. Aging of Tesla’s 18650 lithium-ion cells: Correlating solid-electrolyte-interphase evolution with fading in capacity and power. J. Electrochem. Soc. 2017, 164, A3503. [Google Scholar] [CrossRef]
- Wu, Y.; Keil, P.; Schuster, S.F.; Jossen, A. Impact of temperature and discharge rate on the aging of a LiCoO2/LiNi0.8Co0.15Al0.05O2 lithium-ion pouch cell. J. Electrochem. Soc. 2017, 164, A1438. [Google Scholar] [CrossRef]
- Maheshwari, A.; Paterakis, N.G.; Santarelli, M.; Gibescu, M. Optimizing the operation of energy storage using a non-linear lithium-ion battery degradation model. Appl. Energy 2020, 261, 114360. [Google Scholar] [CrossRef]
- Fayaz, H.; Afzal, A.; Samee, A.D.; Soudagar, M.E.; Akram, N.; Mujtaba, M.A.; Jilte, R.D.; Islam, M.T.; Ağbulut, Ü.; Saleel, C.A. Optimization of thermal and structural design in lithium-ion batteries to obtain Energy Efficient Battery Thermal Management System (BTMS): A critical review. Arch. Comput. Methods Eng. 2021, 29, 129–194. [Google Scholar] [CrossRef] [PubMed]
- Hoke, A.; Brissette, A.; Smith, K.; Pratt, A.; Maksimovic, D. Accounting for lithium-ion battery degradation in electric vehicle charging optimization. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 691–700. [Google Scholar] [CrossRef]
- Ma, Y.; Mou, H.; Zhao, H. Cooling optimization strategy for lithium-ion batteries based on triple-step nonlinear method. Energy 2020, 201, 117678. [Google Scholar] [CrossRef]
- Hoke, A.; Brissette, A.; Maksimovic, D.; Kelly, D.; Pratt, A.; Boundy, D. Maximizing lithium ion vehicle battery life through optimized partial charging. In Proceedings of the 2013 IEEE PES Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 4–27 February 2013. [Google Scholar]
- Du, J.; Chen, Z.; Li, F. Multi-objective optimization discharge method for heating lithium-ion battery at low temperatures. IEEE Access 2018, 6, 44036–44049. [Google Scholar] [CrossRef]
- Ruan, H.; Jiang, J.; Sun, B.; Su, X.; He, X.; Zhao, K. An optimal internal-heating strategy for lithium-ion batteries at low temperature considering both heating time and lifetime reduction. Appl. Energy 2019, 256, 113797. [Google Scholar] [CrossRef]
- Casals, L.C.; Rodríguez, M.; Corchero, C.; Carrillo, R.E. Evaluation of the end-of-life of electric vehicle batteries according to the state-of-health. World Electr. Veh. J. 2019, 10, 63. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, C.; Hu, X.; Lin, X.; Zhang, Y.; Li, W. An MPC-based control strategy for electric vehicle battery cooling considering energy saving and battery lifespan. IEEE Trans. Veh. Technol. 2020, 69, 14657–14673. [Google Scholar] [CrossRef]
- Wikner, E.; Thiringer, T. Extending battery lifetime by avoiding high soc. Appl. Sci. 2018, 8, 1825. [Google Scholar] [CrossRef]
- Preger, Y.; Barkholtz, H.M.; Fresquez, A.; Campbell, D.L.; Juba, B.W.; Romàn-Kustas, J.; Ferreira, S.R.; Chalamala, B. Degradation of commercial lithium-ion cells as a function of chemistry and cycling conditions. J. Electrochem. Soc. 2020, 167, 120532. [Google Scholar] [CrossRef]
- Kuntz, P.; Raccurt, O.; Azaïs, P.; Richter, K.; Waldmann, T.; Wohlfahrt-Mehrens, M.; Bardet, M.; Buzlukov, A.; Genies, S. Identification of degradation mechanisms by post-mortem analysis for high power and high energy commercial li-ion cells after electric vehicle aging. Batteries 2021, 7, 48. [Google Scholar] [CrossRef]
- Maheshwari, A.; Heck, M.; Santarelli, M. Cycle aging studies of lithium nickel manganese cobalt oxide-based batteries using electrochemical impedance spectroscopy. Electrochim. Acta 2018, 273, 335–348. [Google Scholar] [CrossRef]
- Golverk, A.A. Mathematical calculation of the performance map of Internal Combustion Engine. SAE Tech. Pap. Ser. 1992. [Google Scholar] [CrossRef]
- Wang, D.; Bao, Y.; Shi, J. Online lithium-ion battery internal resistance measurement application in state-of-charge estimation using the extended Kalman filter. Energies 2017, 10, 1284. [Google Scholar] [CrossRef]
- Jin, X.; Duan, X.; Jiang, W.; Wang, Y.; Zou, Y.; Lei, W.; Sun, L.; Ma, Z. Structural design of a composite board/heat pipe based on the coupled electro-chemical-thermal model in Battery Thermal Management System. Energy 2021, 216, 119234. [Google Scholar] [CrossRef]
- Xie, Y.; Li, W.; Yang, Y.; Feng, F. A novel resistance-based thermal model for lithium-ion batteries. Int. J. Energy Res. 2018, 42, 4481–4498. [Google Scholar] [CrossRef]
- Al-Hallaj, S.; Selman, J.R. Thermal modeling of secondary lithium batteries for electric vehicle/Hybrid Electric Vehicle Applications. J. Power Sources 2002, 110, 341–348. [Google Scholar] [CrossRef]
- Bao, Y.; Dong, W.; Wang, D. Online internal resistance measurement application in lithium ion battery capacity and state of charge estimation. Energies 2018, 11, 1073. [Google Scholar] [CrossRef]
- Wang, Q.; Ping, P.; Zhao, X.; Chu, G.; Sun, J.; Chen, C. Cheminform abstract: Thermal runaway caused fire and explosion of lithium ion battery. ChemInform 2012, 43, 210–224. [Google Scholar] [CrossRef]
- Wark, K. Advanced Thermodynamics for Engineers; McGraw-Hill: New York, NY, USA, 1995. [Google Scholar]
- Bergman, T.L.; Incropera, F.P. Fundamentals of Heat and Mass Transfer 7E: Heat Transfer; Wiley Custom Learning Solutions: Hoboken, NJ, USA, 2011. [Google Scholar]
- Noie, S.H. Investigation of thermal performance of an air-to-air thermosyphon heat exchanger using ε-NTU method. Appl. Therm. Eng. 2006, 26, 559–567. [Google Scholar] [CrossRef]
- Ng, E.Y.; Johnson, P.W.; Watkins, S. An analytical study on heat transfer performance of radiators with non-uniform Airflow Distribution. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2005, 219, 1451–1467. [Google Scholar] [CrossRef]
- Dong, J.; Chen, J.; Chen, Z.; Zhang, W.; Zhou, Y. Heat transfer and pressure drop correlations for the multi-louvered fin compact heat exchangers. Energy Convers. Manag. 2007, 48, 1506–1515. [Google Scholar] [CrossRef]
- Badgujar Pankaj, R.; Rangarajan, S.; Nagaraja, S.R. Analytical performance analysis of cross flow louvered fin automobile radiator. MATEC Web Conf. 2018, 172, 02003. [Google Scholar] [CrossRef]
- Seo, M.; Song, Y.; Kim, J.; Paek, S.W.; Kim, G.-H.; Kim, S.W. Innovative lumped-battery model for state of charge estimation of lithium-ion batteries under various ambient temperatures. Energy 2021, 226, 120301. [Google Scholar] [CrossRef]
- Friesen, A.; Mönnighoff, X.; Börner, M.; Haetge, J.; Schappacher, F.M.; Winter, M. Influence of temperature on the aging behavior of 18650-type lithium ion cells: A comprehensive approach combining electrochemical characterization and post-mortem analysis. J. Power Sources 2017, 342, 88–97. [Google Scholar] [CrossRef]
- Atalay, S.; Sheikh, M.; Mariani, A.; Merla, Y.; Bower, E.; Widanage, W.D. Theory of battery ageing in a lithium-ion battery: Capacity fade, nonlinear ageing and lifetime prediction. J. Power Sources 2020, 478, 229026. [Google Scholar] [CrossRef]
- Liu, C.; Qian, K.; Lei, D.; Li, B.; Kang, F.; He, Y.-B. Deterioration mechanism of LiNi0.8Co0.15Al0.05O2/Graphite–SiOx power batteries under high temperature and discharge cycling conditions. J. Mater. Chem. A 2018, 6, 65–72. [Google Scholar] [CrossRef]
- Zhang, Y.Z.; Xiong, R.; He, H.W.; Qu, X.; Pecht, M. Aging characteristics-based health diagnosis and remaining useful life prognostics for lithium-ion batteries. eTransportation 2019, 1, 100004. [Google Scholar] [CrossRef]
- Waldmann, T.; Wilka, M.; Kasper, M.; Fleischhammer, M.; Wohlfahrt-Mehrens, M. Temperature dependent ageing mechanisms in lithium-ion batteries—A post-mortem study. J. Power Sources 2014, 262, 129–135. [Google Scholar] [CrossRef]
- Engineering ToolBox Ethylene Glycol Heat-Transfer Fluid Properties. Available online: https://www.engineeringtoolbox.com/ethylene-glycol-d_146.html (accessed on 20 October 2021).
| Parameter | Rated Value | Unit |
|---|---|---|
| Torque | 520 | Nm |
| Speed | 3000 | RPM |
| Parameter | Rated Value | Unit |
|---|---|---|
| No of cells | 1776 | - |
| Cell voltage | 4.2 | V |
| Cell capacity | 3 | Ah |
| Pack power capacity | 22 | kWh |
| Parameter | ID | Range | Unit | Type |
|---|---|---|---|---|
| Air flow rate | fmin − fmax | m3/s | Output | |
| Liquid flow rate | pmin − pmax | m3/s | Output | |
| Environmental temperature | Tamb | 25 | °C | Input |
| Discharge rate | I | 3–6 | A | Input |
| State of Health | SoC | 100–80 | % | Input |
| State of Charge | SoH | 60 | % | Input |
| Battery temperature | Tbat | 25–60 | °C | Output |
| State of Charge (%) | ||||||
|---|---|---|---|---|---|---|
| 100 | 96 | 92 | 88 | 84 | 80 | |
| 1C | 26.76 °C | 26.80 °C | 26.83 °C | 26.86 °C | 26.90 °C | 26.93 °C |
| 2C | 35.43 °C | 35.48 °C | 35.53 °C | 35.58 °C | 35.63 °C | 35.68 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pires, R.A., Jr.; Carvalho, S.A.; Cardoso Filho, B.J.; Pires, I.A.; Huebner, R.; Maia, T.A.C. The Assessment of Electric Vehicle Storage Lifetime Using Battery Thermal Management System. Batteries 2023, 9, 10. https://doi.org/10.3390/batteries9010010
Pires RA Jr., Carvalho SA, Cardoso Filho BJ, Pires IA, Huebner R, Maia TAC. The Assessment of Electric Vehicle Storage Lifetime Using Battery Thermal Management System. Batteries. 2023; 9(1):10. https://doi.org/10.3390/batteries9010010
Chicago/Turabian StylePires, Rodrigo A., Jr., Samuel A. Carvalho, Braz J. Cardoso Filho, Igor A. Pires, Rudolf Huebner, and Thales A. C. Maia. 2023. "The Assessment of Electric Vehicle Storage Lifetime Using Battery Thermal Management System" Batteries 9, no. 1: 10. https://doi.org/10.3390/batteries9010010
APA StylePires, R. A., Jr., Carvalho, S. A., Cardoso Filho, B. J., Pires, I. A., Huebner, R., & Maia, T. A. C. (2023). The Assessment of Electric Vehicle Storage Lifetime Using Battery Thermal Management System. Batteries, 9(1), 10. https://doi.org/10.3390/batteries9010010








