Identification of Typical Sub-Health State of Traction Battery Based on a Data-Driven Approach
Abstract
:1. Introduction
2. Voltage Data Analysis
2.1. Data Introduction and Preprocessing
2.2. Types of Sub-Health Status
3. Identification of Sub-Health Status
3.1. Identification Algorithm of Sub-Health State Type
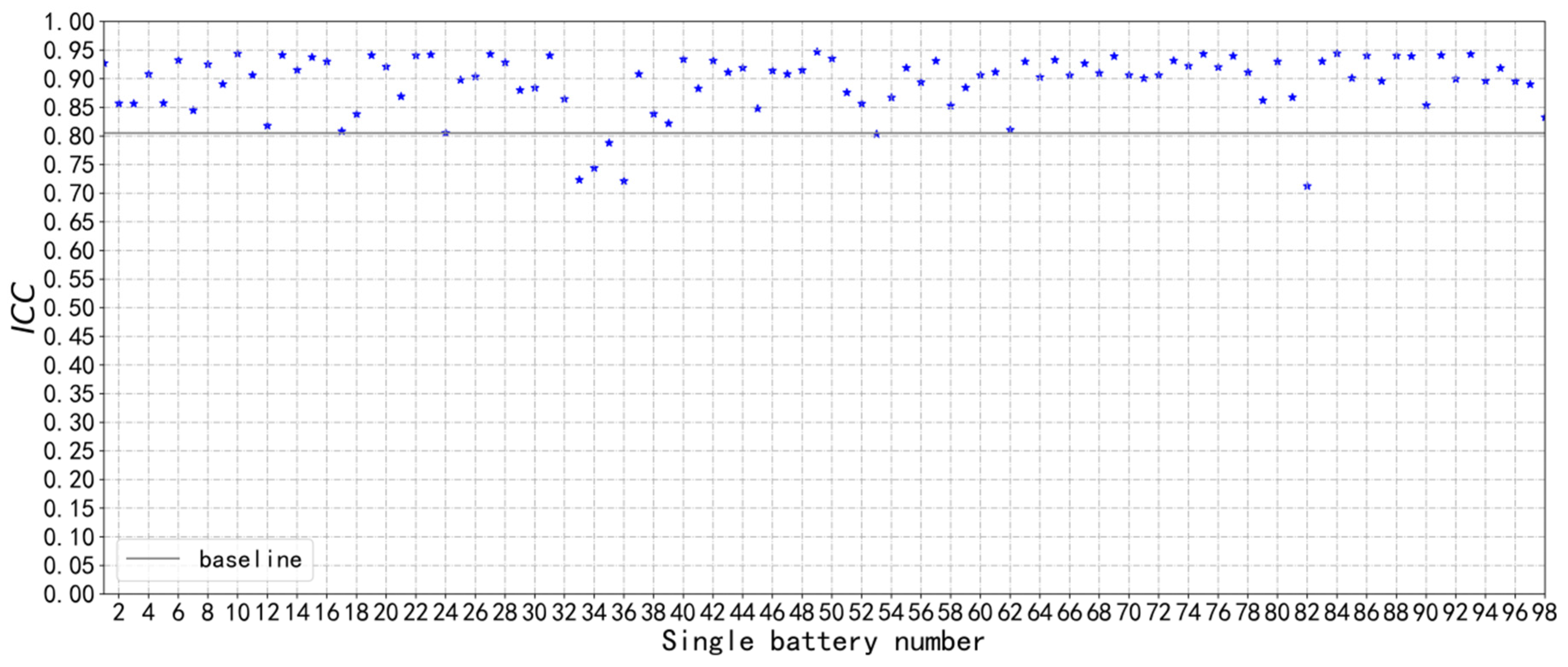
3.1.1. ICC
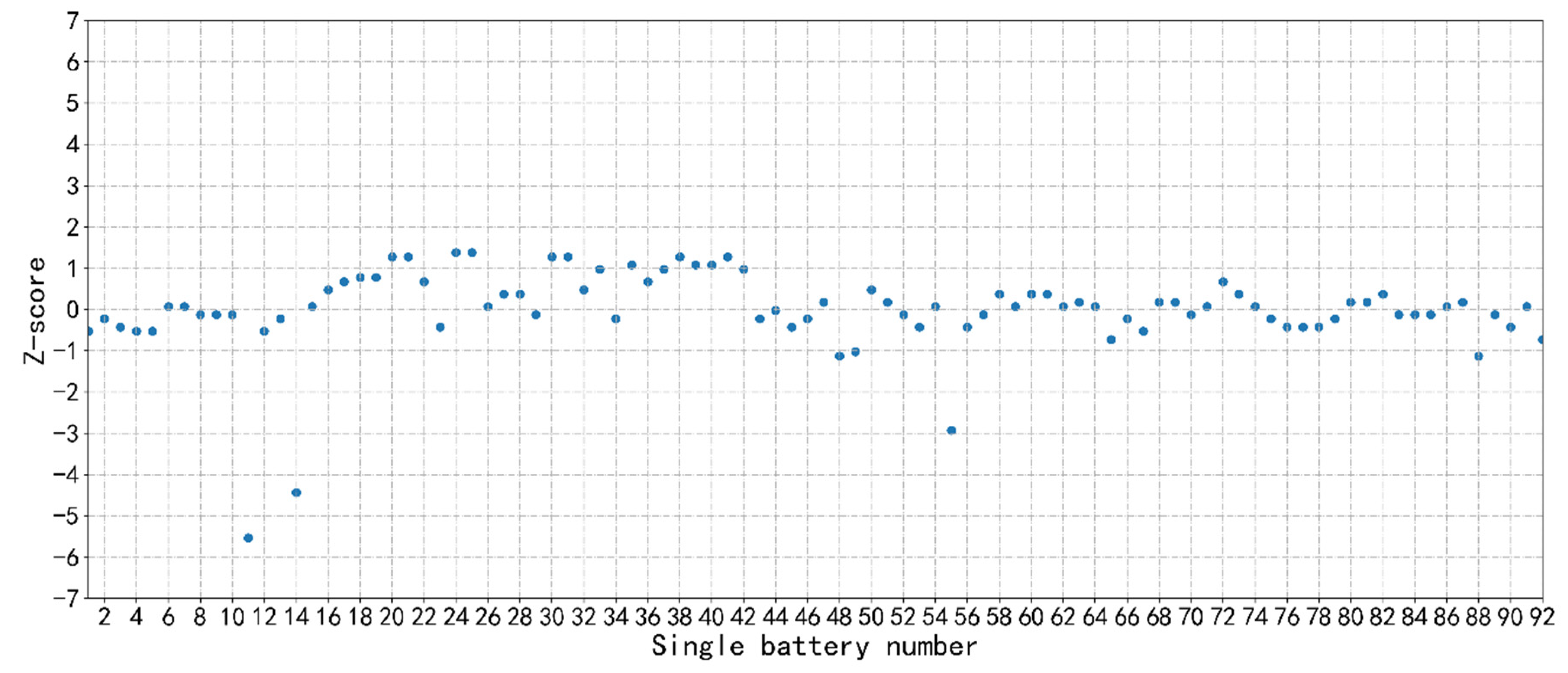
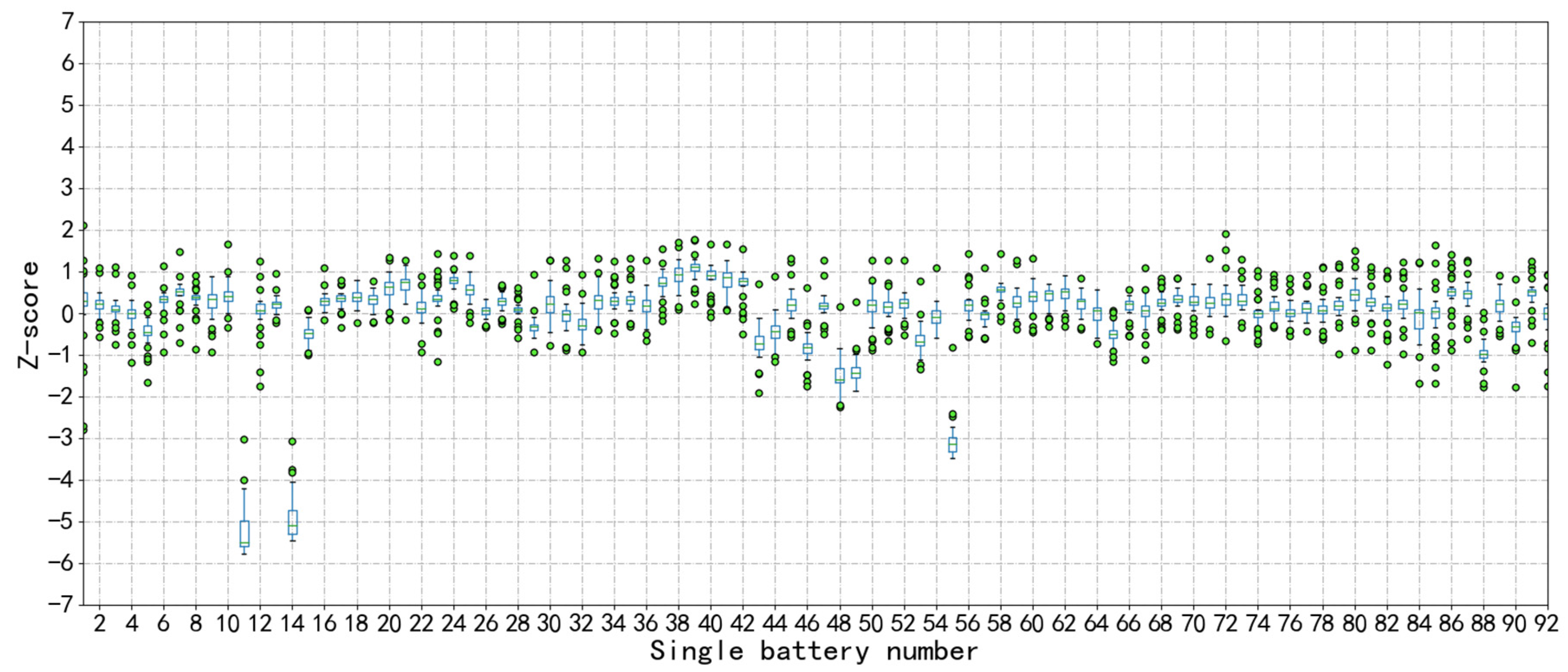
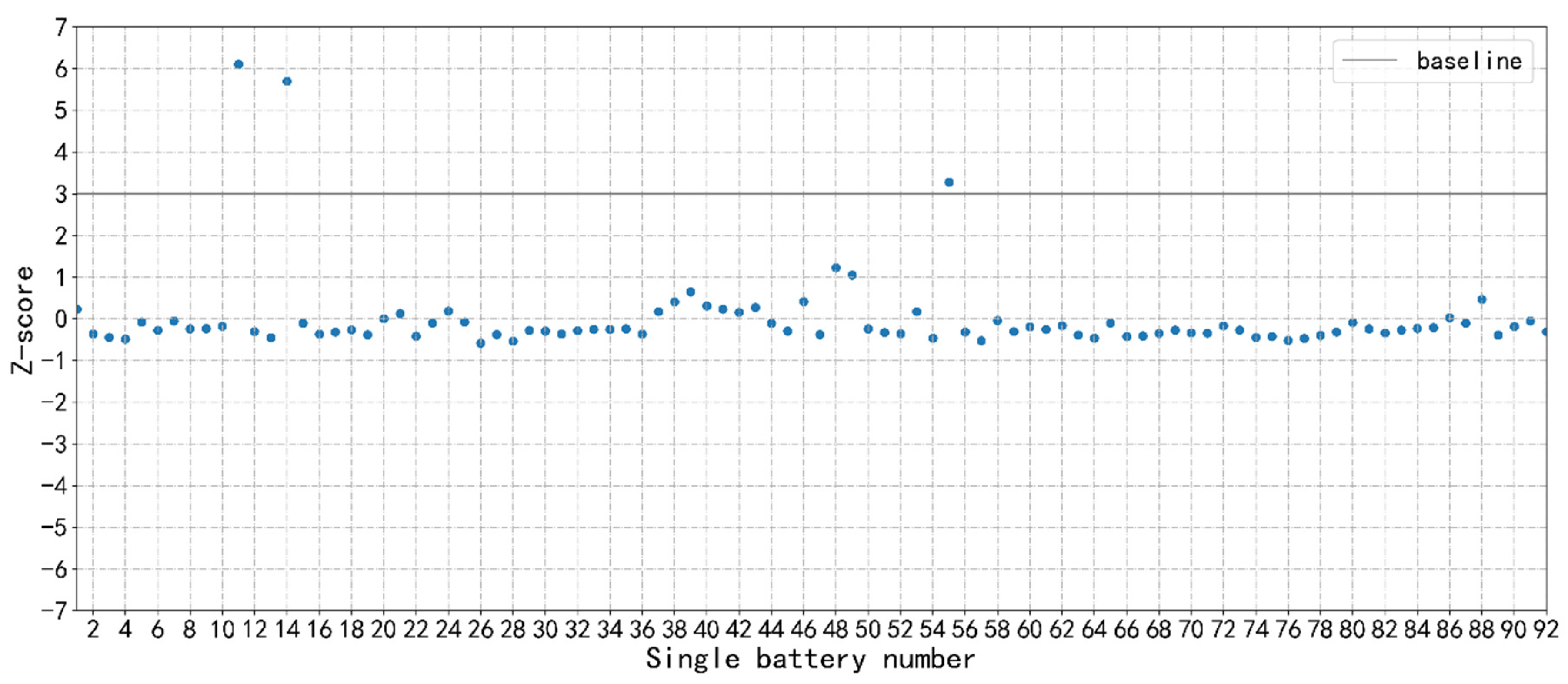
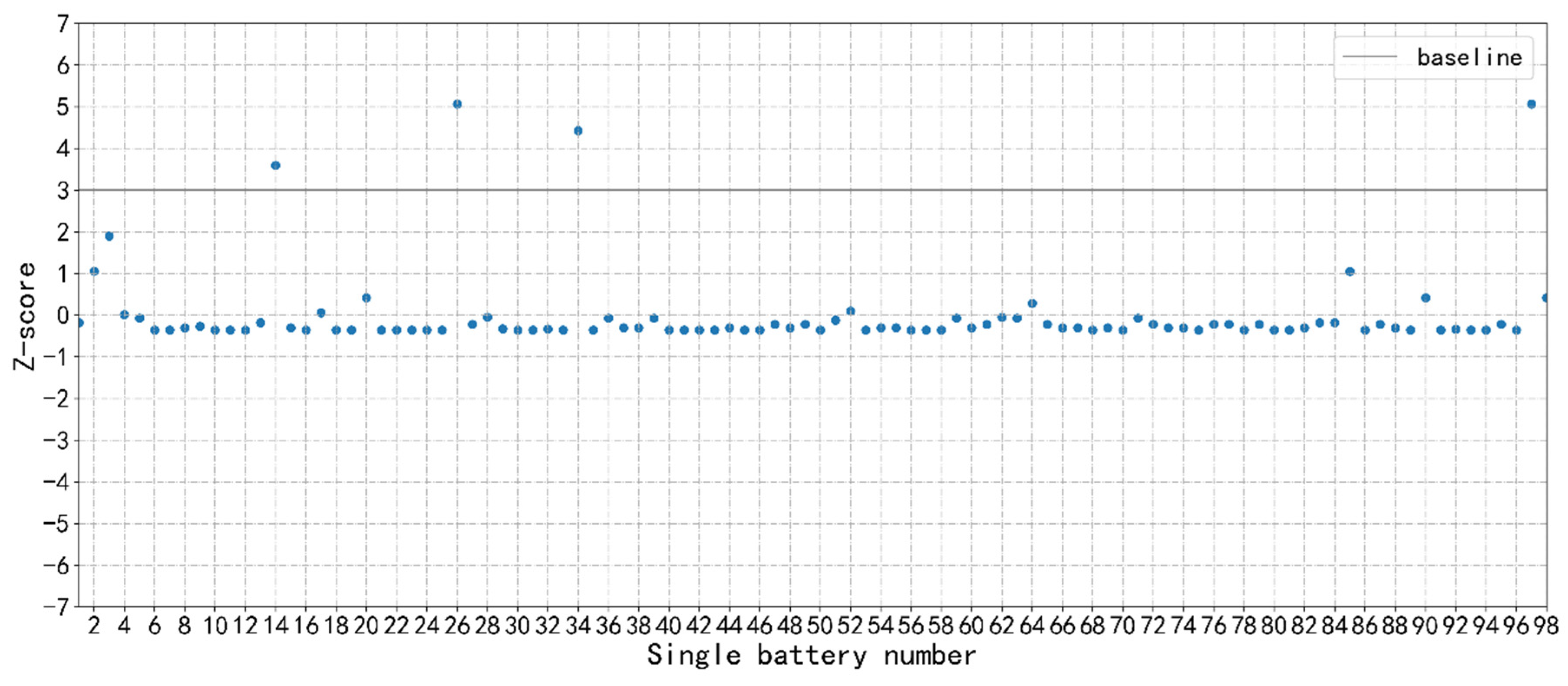
3.1.2. Z-Score
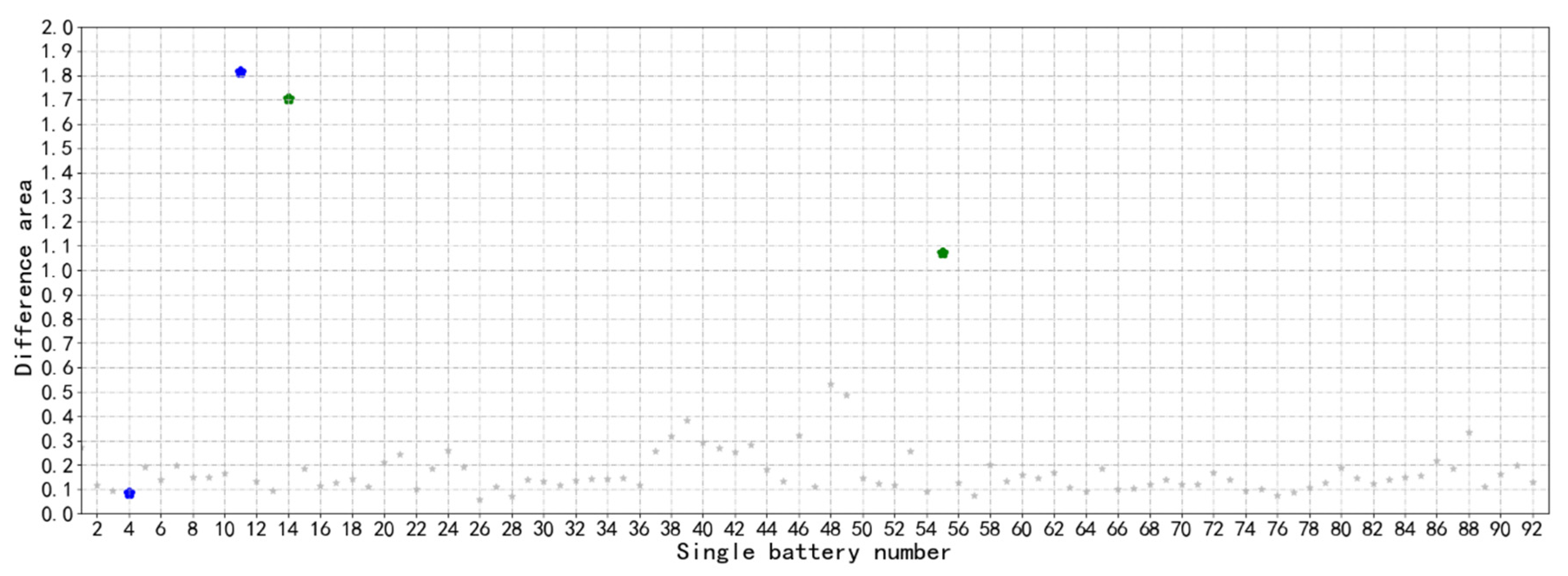
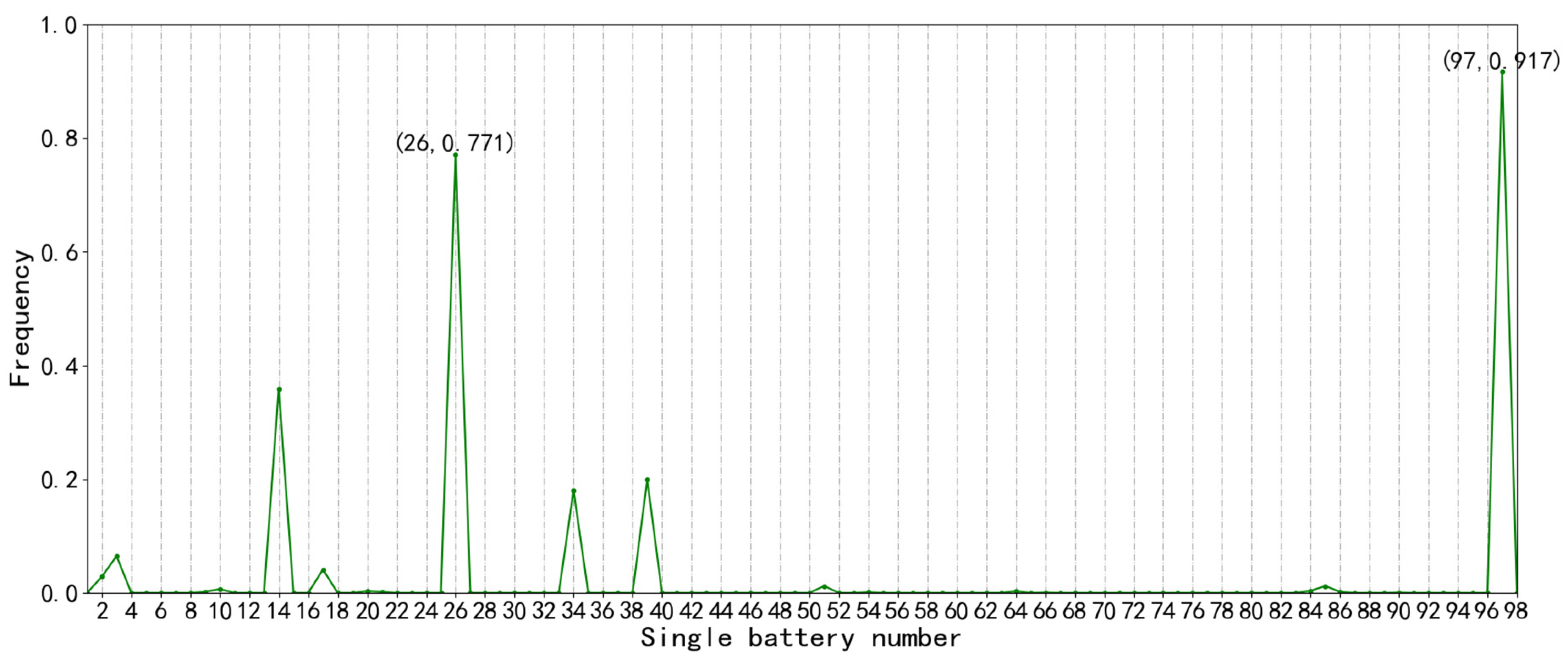
3.1.3. Differential Area Method
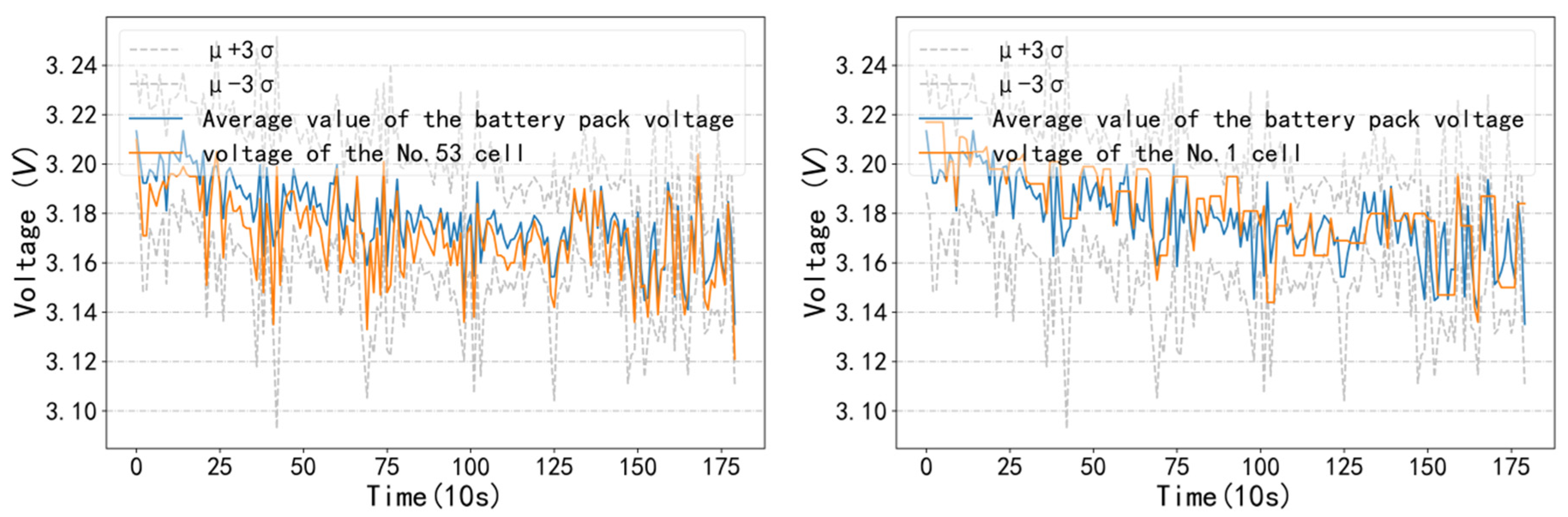
3.2. Identification of Sub-Health Status Type I
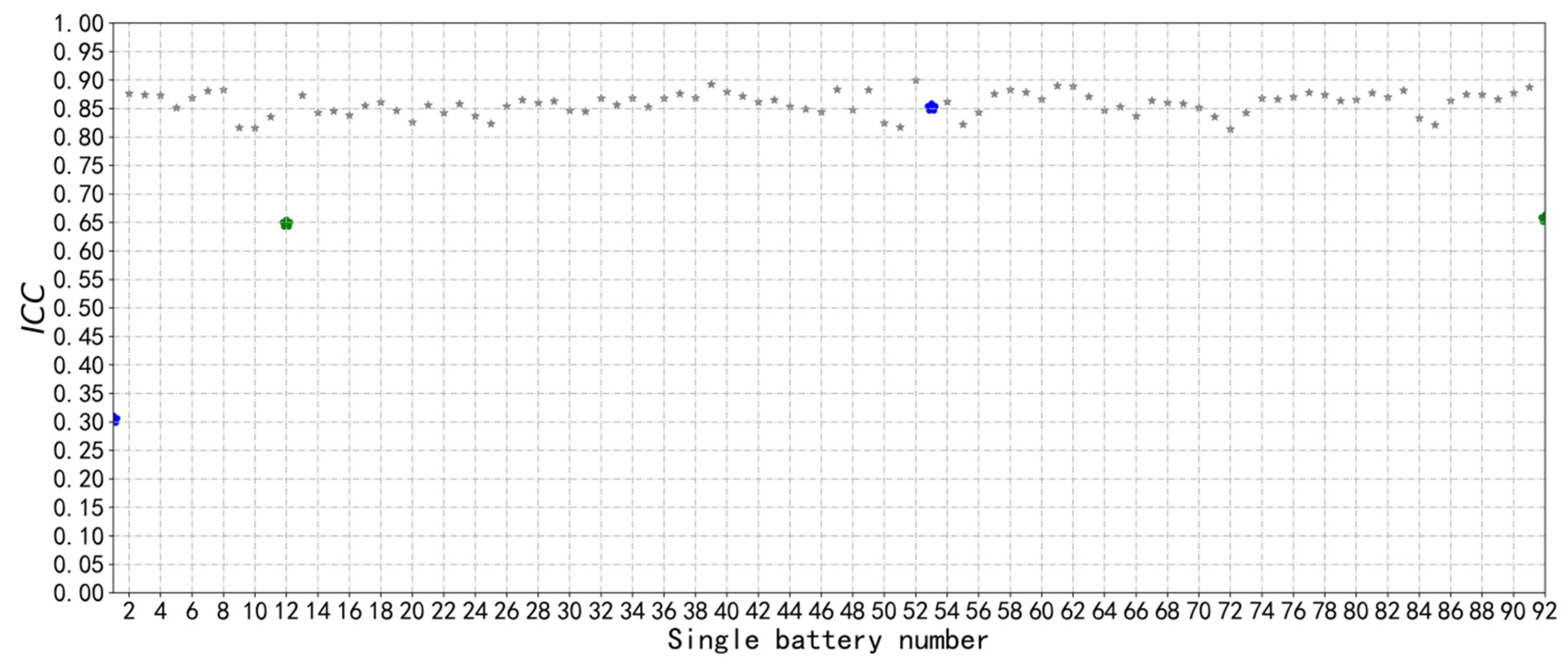
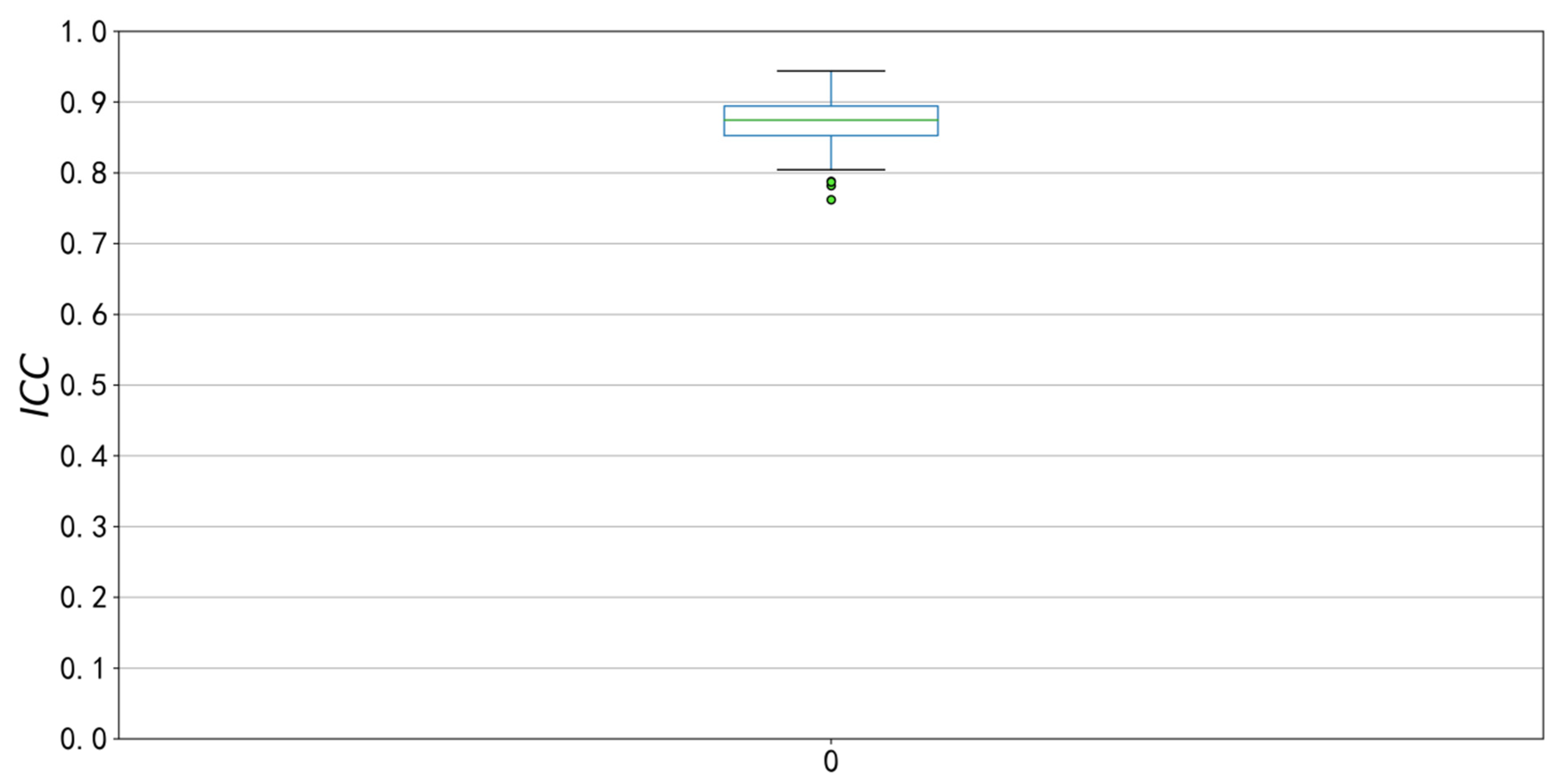
3.2.1. ICC Calculation of Sub-Health State Type
3.2.2. Threshold Calculation of Sub-Health State Type I
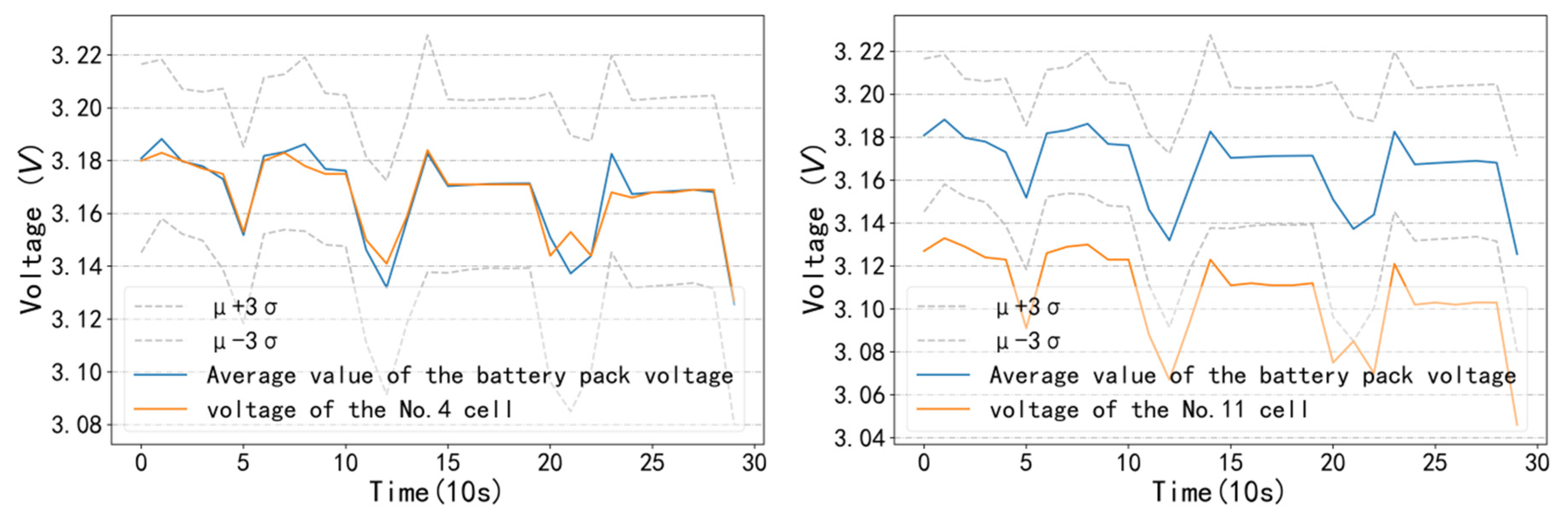
3.3. Identification of Sub-Health State Type II
3.3.1. Z-Score Calculation for Sub-Health Type II
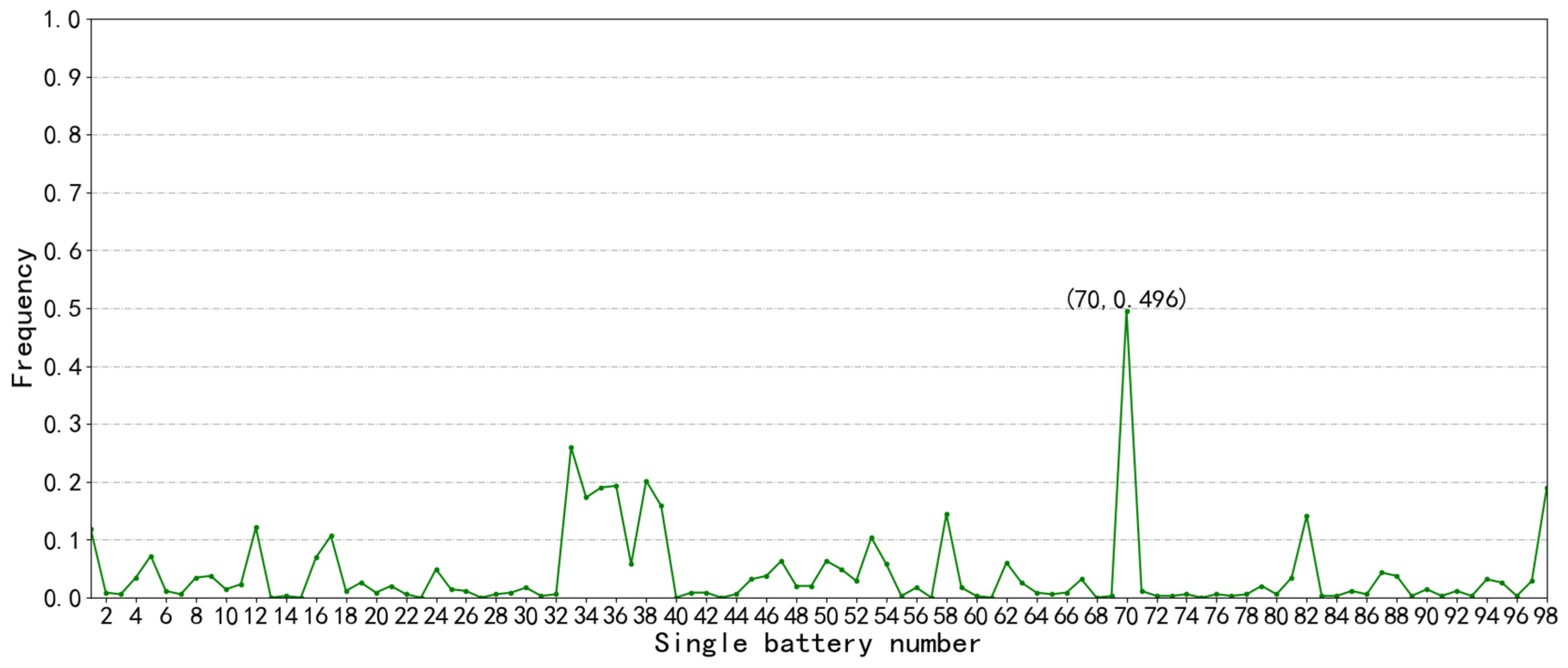
3.3.2. Calculation of Sub-Health Type II by Differential Area Method
3.3.3. Threshold of Sub-Health State Type II Based on the 3δ Rule
4. Method Verification
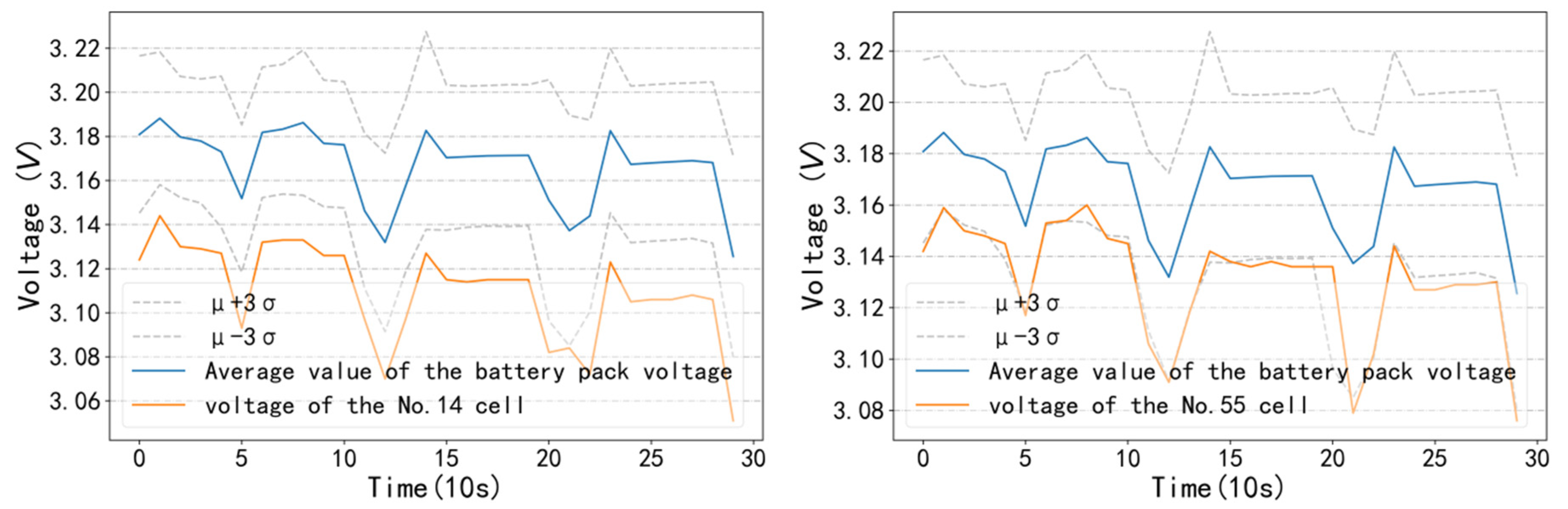
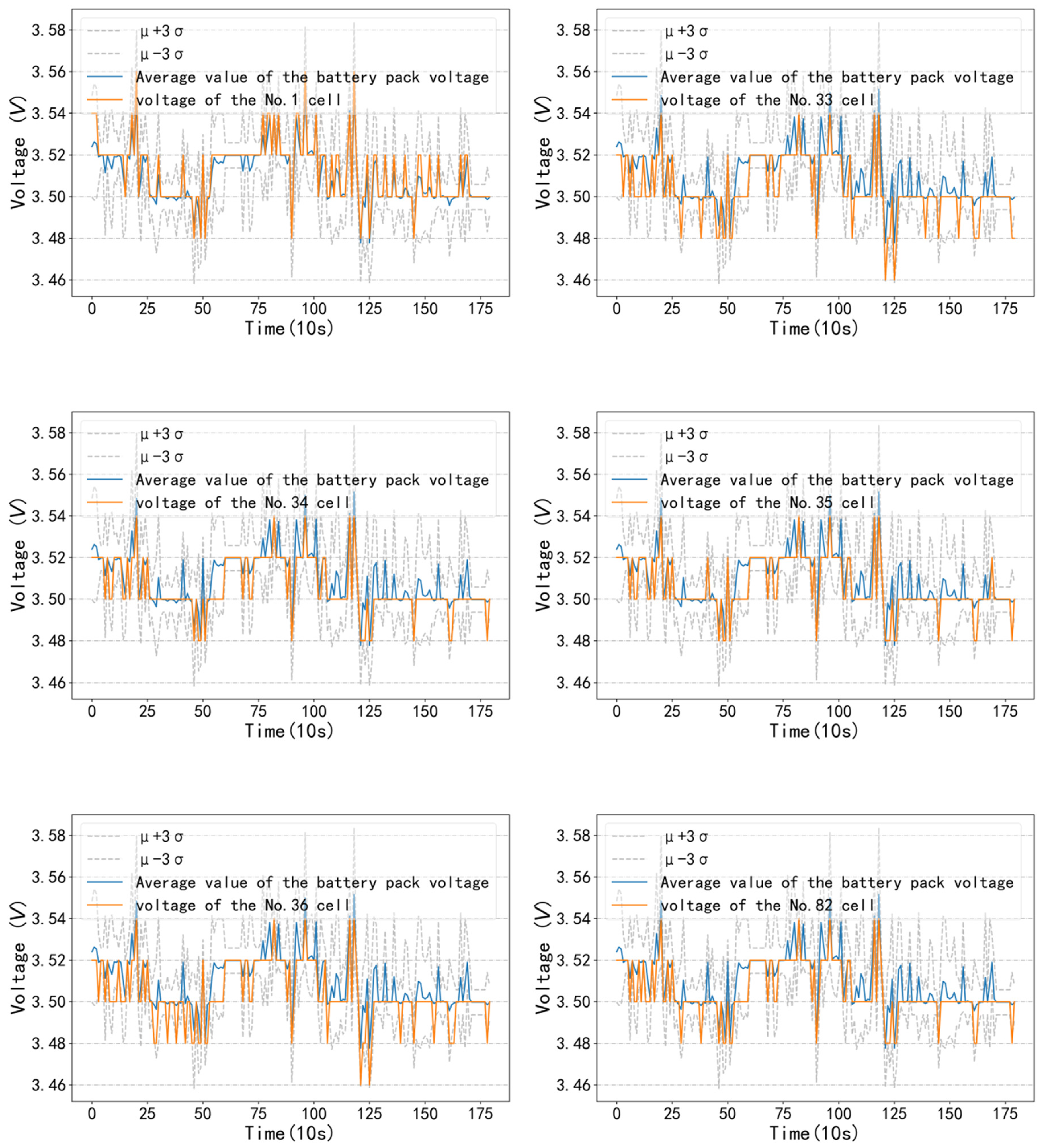
4.1. Verification Methods for Sub-Health State Type I
4.2. Verification Methods for Sub-Health State Type II
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Nomenclature variable | |
| The difference in voltage of a single cell at adjacent time points in the j-th column | |
| Difference between the average values of cell pack voltage at adjacent time points | |
| Mean square error of the error term between and | |
| The mean square error of the block term between and | |
| Sum of squares of deviation from mean of the error term between and | |
| Sum of squares of deviation from mean of the block term between and | |
| Sum of squares of deviation from mean of the treatment term between and | |
| The degree of freedom of the block term between and | |
| The degree of freedom of the error term between and | |
| The number of treatment groups between and | |
| The number of blocks between and | |
| Correction coefficient between and | |
| Total number of data points between and | |
| The i-th time point and the j-th Z-score of single battery voltage | |
| The i-th time point and the j-th single battery voltage | |
| The i-th time point average value of battery pack voltage | |
| The i-th time point standard deviation of battery pack voltage | |
| Subscripts | |
| diff | Difference |
| er | Error |
| bl | Block |
| tr | Treatment |
| Acronyms | |
| ICC | Interclass correlation coefficient |
| EVs | Electric vehicles |
| BMS | Battery management system |
| C | Capacity |
References
- Zhang, S.; Xiong, R.; Gao, J. Battery durability and longevity based power management for plug-in hybrid electric vehicle with hybrid energy storage system. Appl. Energy 2016, 179, 316–328. [Google Scholar] [CrossRef]
- Merkle, L.; Pthig, M.; Schmid, F. Estimate e-Golf Battery State Using Diagnostic Data and a Digital Twin. Batteries 2021, 7, 15. [Google Scholar] [CrossRef]
- Pearre, N.S.; Kempton, W.; Guensler, L.R.; Elango, V.V. Electric vehicles: How much range is required for a day’s driving. Transp. Res. Part C Emerg. Technol. 2011, 19, 1171–1184. [Google Scholar] [CrossRef]
- Li, X.; Zhao, J.; Duan, J.; Panchal, S.; Yuan, J.; Fraser, R.; Fowler, M.; Chen, M. Simulation of cooling plate effect on a battery module with different channel arrangement. J. Energy Storage 2022, 49, 104113. [Google Scholar] [CrossRef]
- Chen, Z.; Li, X.; Shen, J.; Yan, W.; Xiao, R. A Novel State of Charge Estimation Algorithm for Lithium-ion Battery Packs of Electric Vehicles. Energies 2016, 9, 710. [Google Scholar] [CrossRef]
- Dubarry, M.; Vuillaume, N.; Liaw, B.Y. From single cell model to battery pack simulation for Li-ion batteries. J. Power Sources 2009, 18, 500–507. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Zhou, Y. Power battery fault diagnosis system based on fuzzy neural network. Chin. J. Power Sources 2019, 43, 1391–1394. [Google Scholar]
- Baronti, F.; Roncella, R.; Saletti, R. Performance comparison of active balancing techniques for lithium-ion batteries. J. Power Sources 2014, 267, 603–609. [Google Scholar] [CrossRef] [Green Version]
- Rafael, C.; Frederic, H.; Peter, B. Methodology for Determining Time-Dependent Lead Battery Failure Rates from Field Data. Batteries 2021, 7, 39. [Google Scholar] [CrossRef]
- Wu, C.; Zhu, C.; Ge, Y.; Zhao, Y. A review on fault mechanism and diagnosis approach for Li-ion batteries. J. Nanomater. 2015, 2015, 8. [Google Scholar] [CrossRef] [Green Version]
- Tran, M.-K.; Panchal, S.; Khang, T.D.; Panchal, K.; Fraser, R.; Fowler, M. Concept Review of a Cloud-Based Smart Battery Management System for Lithium-Ion Batteries: Feasibility, Logistics, and Functionality. Batteries 2022, 8, 19. [Google Scholar] [CrossRef]
- Zhao, R.; Liu, J.; Gu, J. Simulation and experimental study on lithiumion battery short circuit. Appl. Energy 2016, 173, 29–39. [Google Scholar] [CrossRef]
- Dey, S.; Biron, Z.A.; Tatipamula, S.; Das, N.; Mohon, S.; Ayalew, B.; Pisu, P. On-board Thermal Fault Diagnosis of Lithium-ion Batteries for Hybrid Electric Vehicle Application. IFAC Pap. 2015, 2015, 389–394. [Google Scholar] [CrossRef]
- Yao, L.; Xiao, Y.; Gong, X.; Hou, J.; Chen, X. A novel intelligent method for fault diagnosis of electric vehicle battery system based on wavelet neural network. J. Power Sources 2020, 453, 227870. [Google Scholar] [CrossRef]
- Chen, Z.; Xiong, R.; Tian, J.; Shang, X.; Liu, J. Model-based fault diagnosis approach on external short circuit of lithium-ion battery used in electric vehicles. Appl. Energy 2016, 184, 365–374. [Google Scholar] [CrossRef]
- Dey, S.; Biron, Z.A.; Tatipamula, S.; Das, N.; Mohon, S.; Ayalew, B.; Pisu, P. Model-based real-time thermal fault diagnosis of Lithium-ion batteries. Control. Eng. Pract. 2016, 56, 37–48. [Google Scholar] [CrossRef] [Green Version]
- Han, B.; Wang, D.; Li, S. Research on battery connection reliability based on DC internal resistance. Chin. J. Power Sources 2017, 41, 981–983. [Google Scholar]
- Xia, B.; Chen, Z.; Mi, C.; Robert, B. External short circuit fault diagnosis for lithium-ion batteries. In Proceedings of the Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 15–18 June 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, W.; Chen, W.-T.; Saif, M.; Li, M.-F.; Wu, H. Simultaneous fault isolation and estimation of lithium-ion batteries via synthesized design of luenberger and learning observers. IEEE Trans. Control. Syst. Technol. 2014, 22, 290–298. [Google Scholar] [CrossRef]
- Xu, J.; Liang, D.; Wei, G.; Zhu, C. Series battery pack’s contact resistance fault diagnosis analysis. Trans. China Electrotech. Soc. 2017, 32, 106–112. [Google Scholar] [CrossRef]
- Sidhu, A.; Izadian, A.; Anwar, S. Adaptive Nonlinear Model-Based Fault Diagnosis of Li-ion Batteries. IEEE Trans. Ind. Electron. 2014, 62, 1002–1011. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; He, H. Model-based Sensor Fault Diagnosis of a Lithium-ion Battery in Electric Vehicles. Energies 2015, 6, 6509–6527. [Google Scholar] [CrossRef]
- Dey, S.; Mohon, S.; Pisu, P.; Ayalew, B. Sensor fault detection, isolation, and estimation in lithium-ion batteries. IEEE Trans. Control. Syst. Technol. 2016, 24, 2141–2149. [Google Scholar] [CrossRef]
- Tran, M.-K.; Cunanan, C.; Panchal, S.; Fraser, R.; Fowler, M. Investigation of Individual Cells Replacement Concept in Lithium-Ion Battery Packs with Analysis on Economic Feasibility and Pack Design Requirements. Processes 2021, 9, 2263. [Google Scholar] [CrossRef]
- Chen, Z.; Zheng, C.; Lin, T.; Yang, Q. Multifault Diagnosis of Li-Ion Battery Pack Based on Hybrid System. IEEE Trans. Transp. Electrif. 2022, 8, 1769–1784. [Google Scholar] [CrossRef]
- Hu, J.; He, H.; Wei, Z.; Li, Y. Disturbance-immune and aging-robust internal short circuit diagnostic for lithium-ion battery. IEEE Trans. Ind. Electron. 2021, 69, 1988–1999. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Yao, Y. Fault prognosis of battery system based on accurate voltage abnormity prognosis using long short-term memory neural networks. Appl. Energy 2019, 5, 113381. [Google Scholar] [CrossRef]
- Yang, R.; Xiong, R.; He, H.; Chen, Z. A fractional-order model-based battery external short circuit fault diagnosis approach for all-climate electric vehicles application. J. Clean. Prod. 2018, 187, 950–959. [Google Scholar] [CrossRef]
- Gao, Z.; Cheng, C.S.; Woo, W.L.; Jia, J.; Wei, D.T.W. Genetic algorithm based back-propagation neural network approach for fault diagnosis in lithium-ion battery system. In Proceedings of the 6th International Conference on Power Electronics Systems and Applications, Hong Kong, China, 15–17 December 2015. [Google Scholar] [CrossRef]
- Xia, F.; Ma, X.; Luo, Z.; Zhang, H.; Sun, P. Application of improved D-S evidence theory in fault diagnosis of lithium batteries in electric vehicles. CAAI Trans. Intell. Syst. 2017, 12, 526–537. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z. A novel fault diagnosis method for lithium-Ion battery packs of electric vehicles. Measurement 2018, 10, 402–411. [Google Scholar] [CrossRef]
- Xue, Q.; Li, G.; Zhang, Y.; Shen, S.; Chen, Z.; Liu, Y. Fault diagnosis and abnormality detection of lithium-ion battery packs based on statistical distribution. J. Power Sources 2021, 482, 228964. [Google Scholar] [CrossRef]
- Zou, D.; Chen, H.; Li, X.; Lu, Y.; Huang, P. Consistency evaluation method of lithium battery pack based on cloud charging data. Power Grid Technol. 2022, 2022, 308. [Google Scholar] [CrossRef]
- Dai, H.F.; Wang, N.; Wei, X.Z.; Sun, Z.C.; Wang, J.Y. A review of the research on monomer inconsistency of automotive power lithium-ion batteries. Automot. Eng. 2014, 36, 181–188. [Google Scholar] [CrossRef]
- Kumro, F.G.; Smith, F.M.; Yallop, M.J.; Ciernia, L.A.; Lucy, M.C. Estimates of intra- and interclass correlation coefficients for rump touches and the number of steps during estrus in postpartum cows. J. Dairy Sci 2020, 104, 2318–2333. [Google Scholar] [CrossRef]
- Zidan, M.; Thomas, R.L.; Slovis, T.L. What you need to know aboutstatistics, part II: Reliability of diagnostic and screening tests. Pediatr. Radiol. 2015, 45, 317–328. [Google Scholar] [CrossRef] [PubMed]
- Post, M.W. What to do with “Moderate” reliability and validity coefficients? Arch. Phys. Med. Rehabil. 2016, 97, 1051–1052. [Google Scholar] [CrossRef] [PubMed] [Green Version]



| Vehicle Type | Pure Electric Vehicle |
|---|---|
| Curb weight (kg) | 2420 |
| Energy consumption per hundred kilometers (kwh/100) | 20.5 |
| Maximum speed (km/h) | 155 |
| Rated total energy of battery (kwh) | 82 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Yu, C.; Guo, W.; Wang, Z.; Tan, J. Identification of Typical Sub-Health State of Traction Battery Based on a Data-Driven Approach. Batteries 2022, 8, 65. https://doi.org/10.3390/batteries8070065
Wang C, Yu C, Guo W, Wang Z, Tan J. Identification of Typical Sub-Health State of Traction Battery Based on a Data-Driven Approach. Batteries. 2022; 8(7):65. https://doi.org/10.3390/batteries8070065
Chicago/Turabian StyleWang, Cheng, Chengyang Yu, Weiwei Guo, Zhenpo Wang, and Jiyuan Tan. 2022. "Identification of Typical Sub-Health State of Traction Battery Based on a Data-Driven Approach" Batteries 8, no. 7: 65. https://doi.org/10.3390/batteries8070065
APA StyleWang, C., Yu, C., Guo, W., Wang, Z., & Tan, J. (2022). Identification of Typical Sub-Health State of Traction Battery Based on a Data-Driven Approach. Batteries, 8(7), 65. https://doi.org/10.3390/batteries8070065






