Sensor Fault Detection and Isolation for Degrading Lithium-Ion Batteries in Electric Vehicles Using Parameter Estimation with Recursive Least Squares
Abstract
1. Introduction
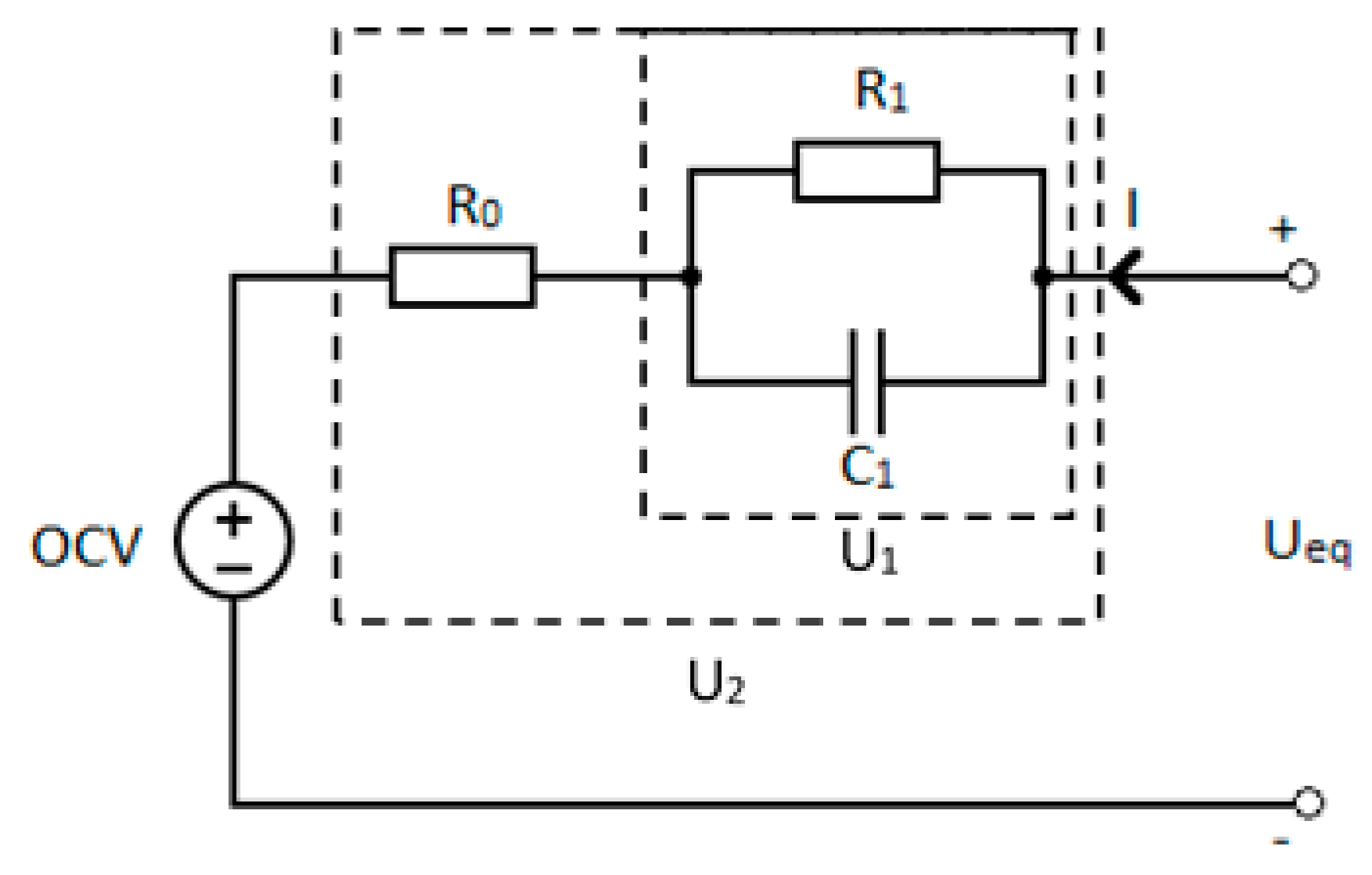
2. Battery Modelling
3. Proposed Fault Diagnosis Scheme
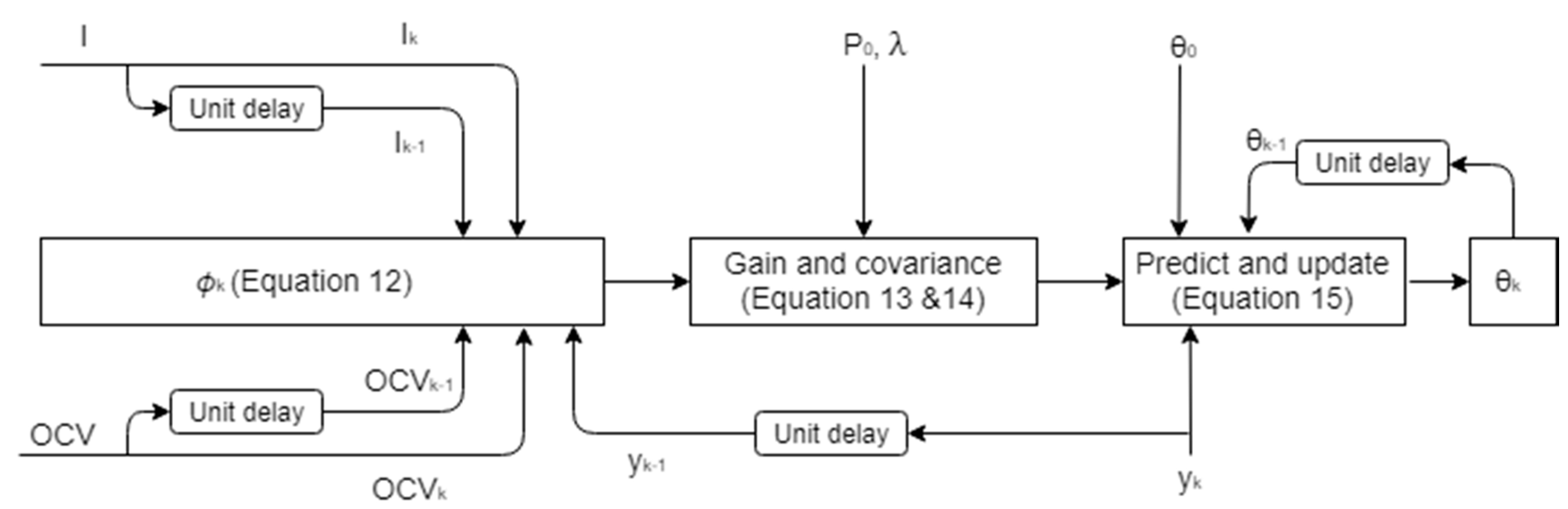
3.1. Recursive Least Squares Estimation
3.2. Sensor Faults
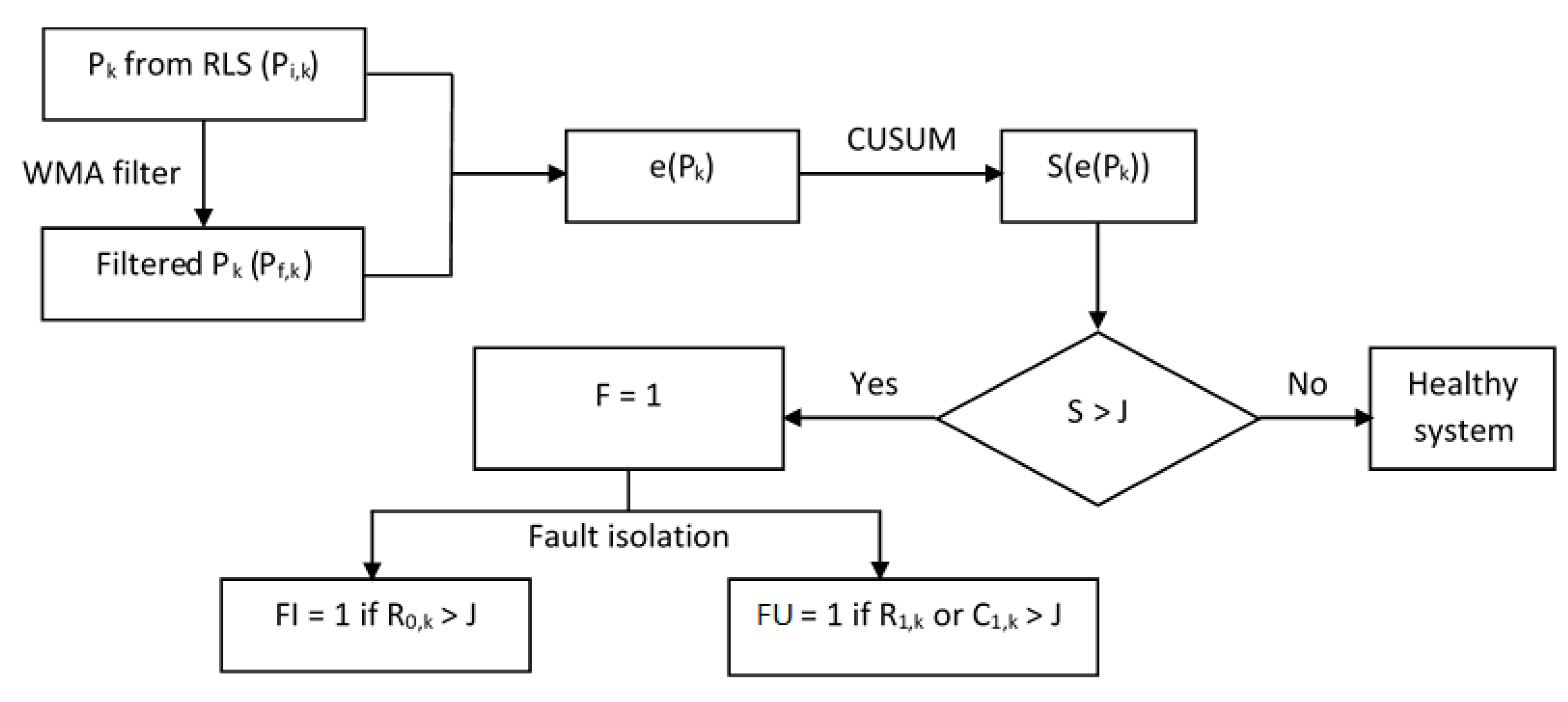
3.3. Online Fault Detection Using Weighted Moving Average Filter and Cumulative Sum Control Chart
4. Effect of Degradation and Faults on ECM Parameters
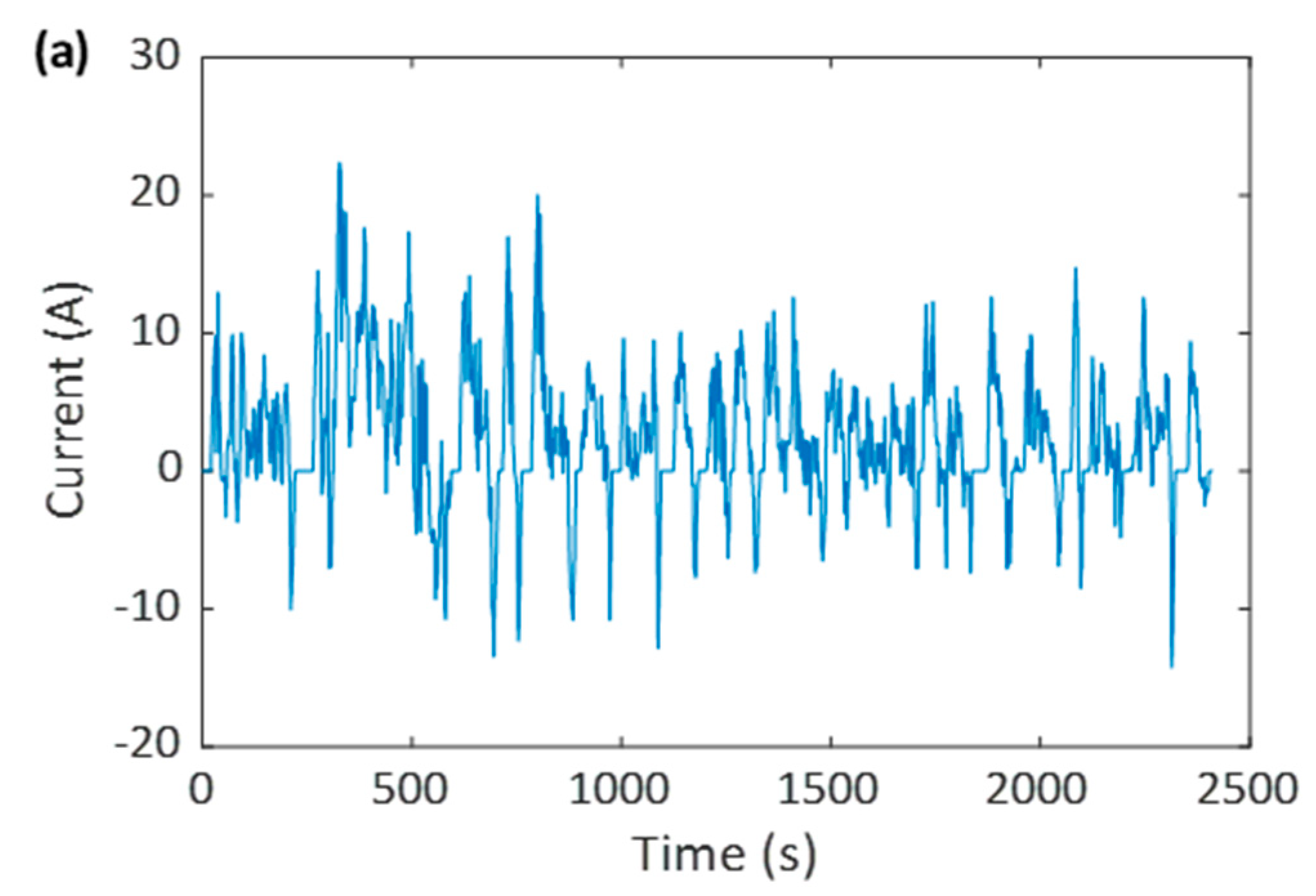
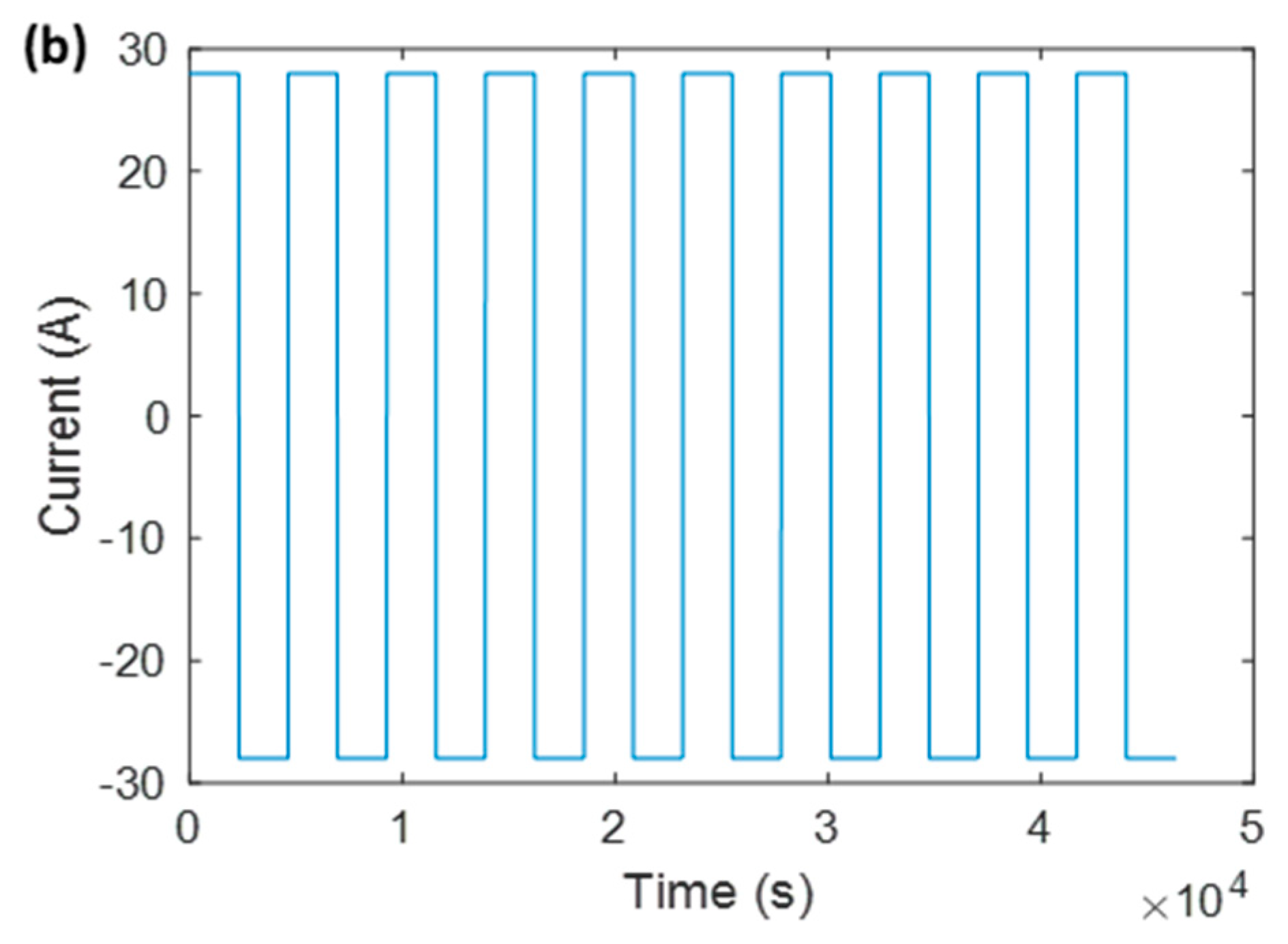
4.1. Experimental Setup
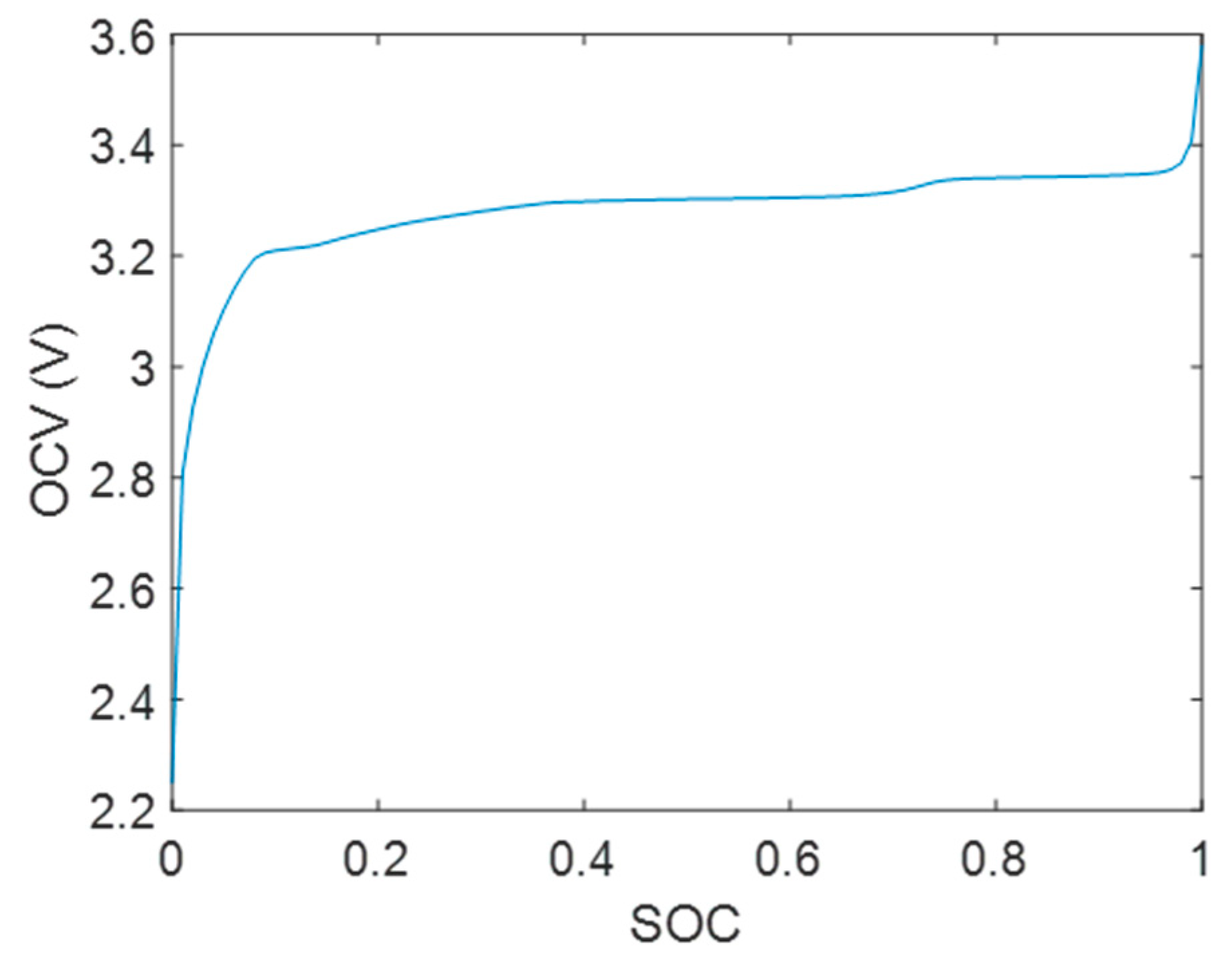
4.2. Cell Characterization Results
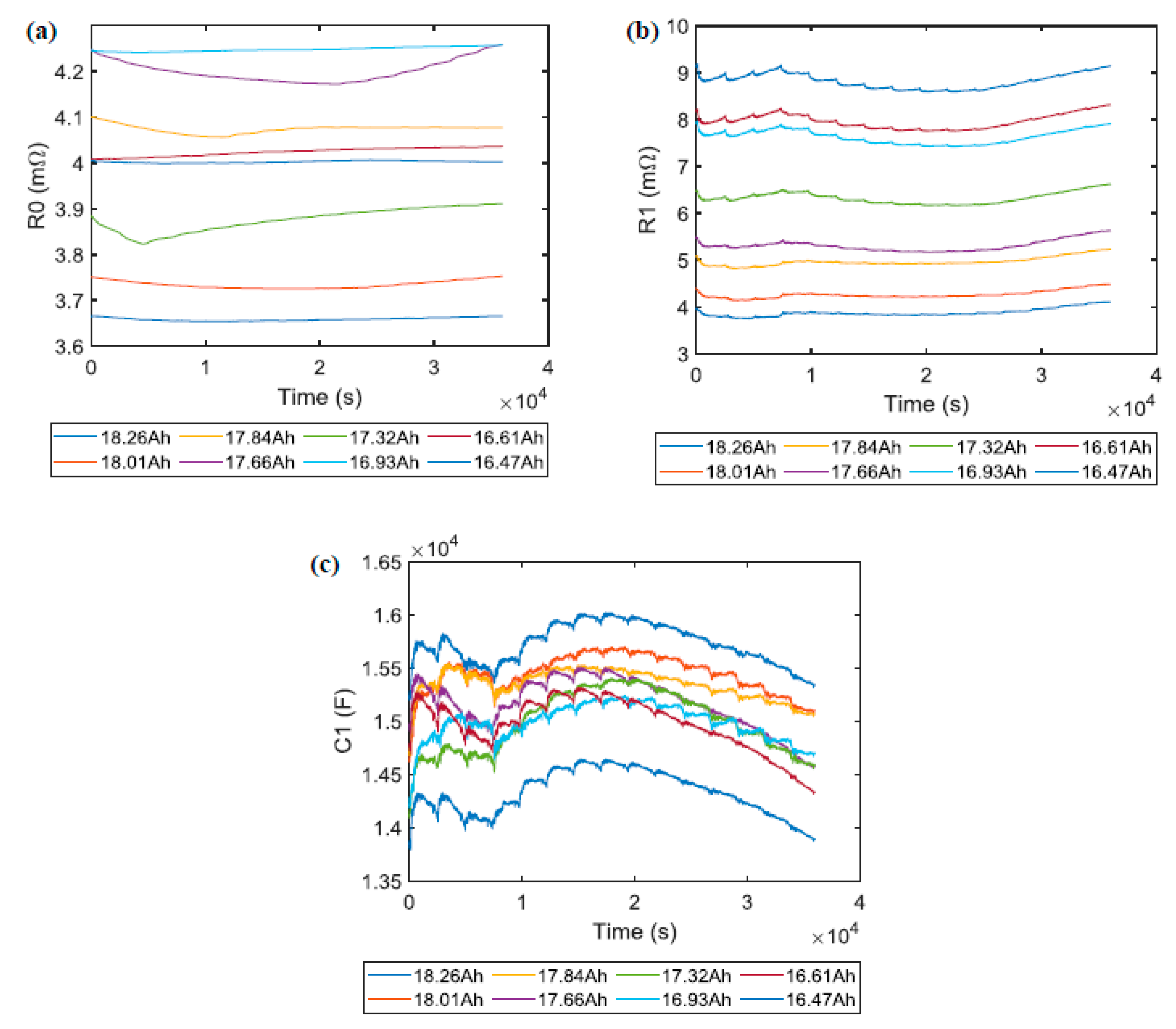
4.3. Effect of Degradation on ECM Parameters
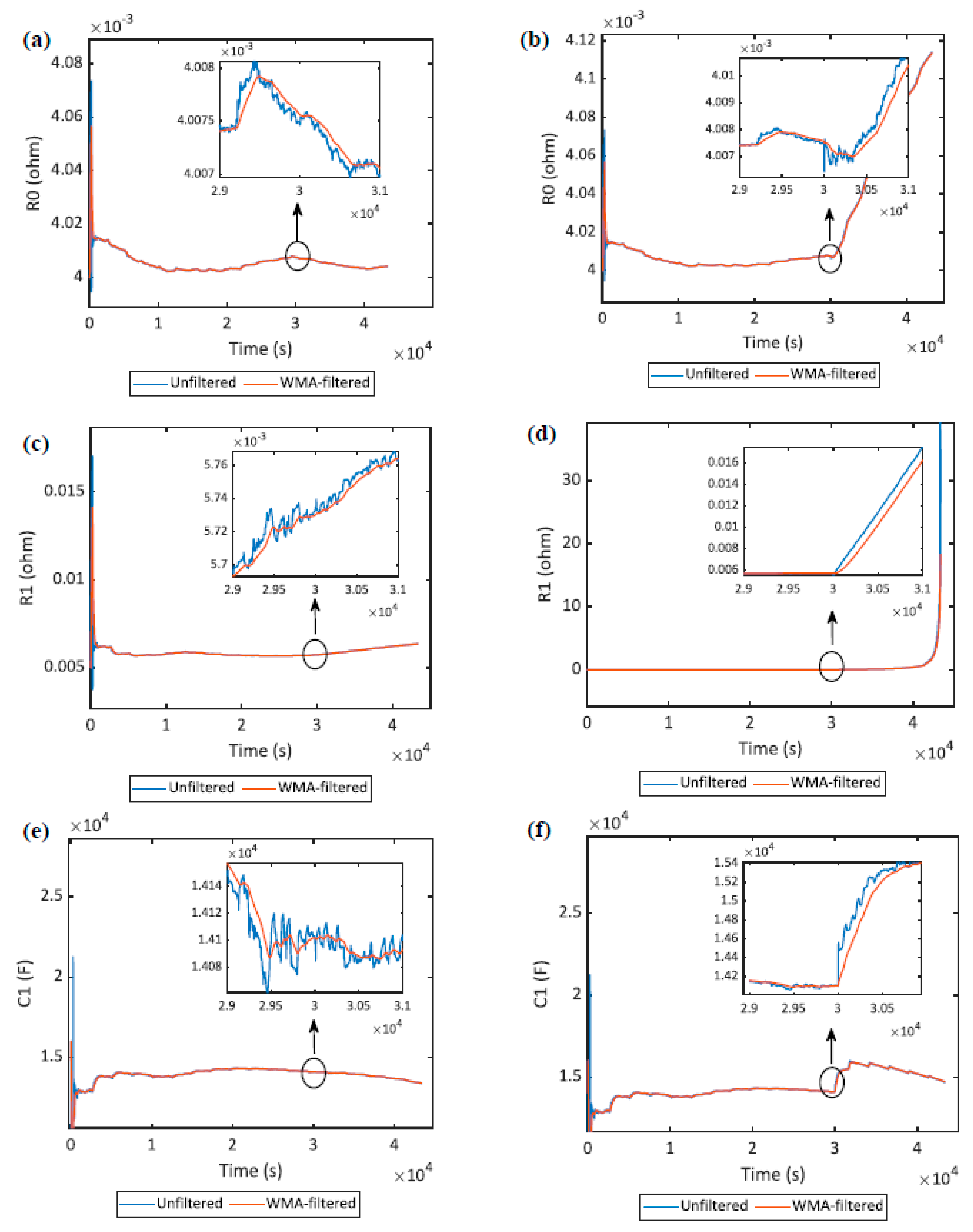
4.4. Effect of Faults on ECM Parameters
4.5. Isolation of Faults
5. Diagnostic Implementation and Evaluation
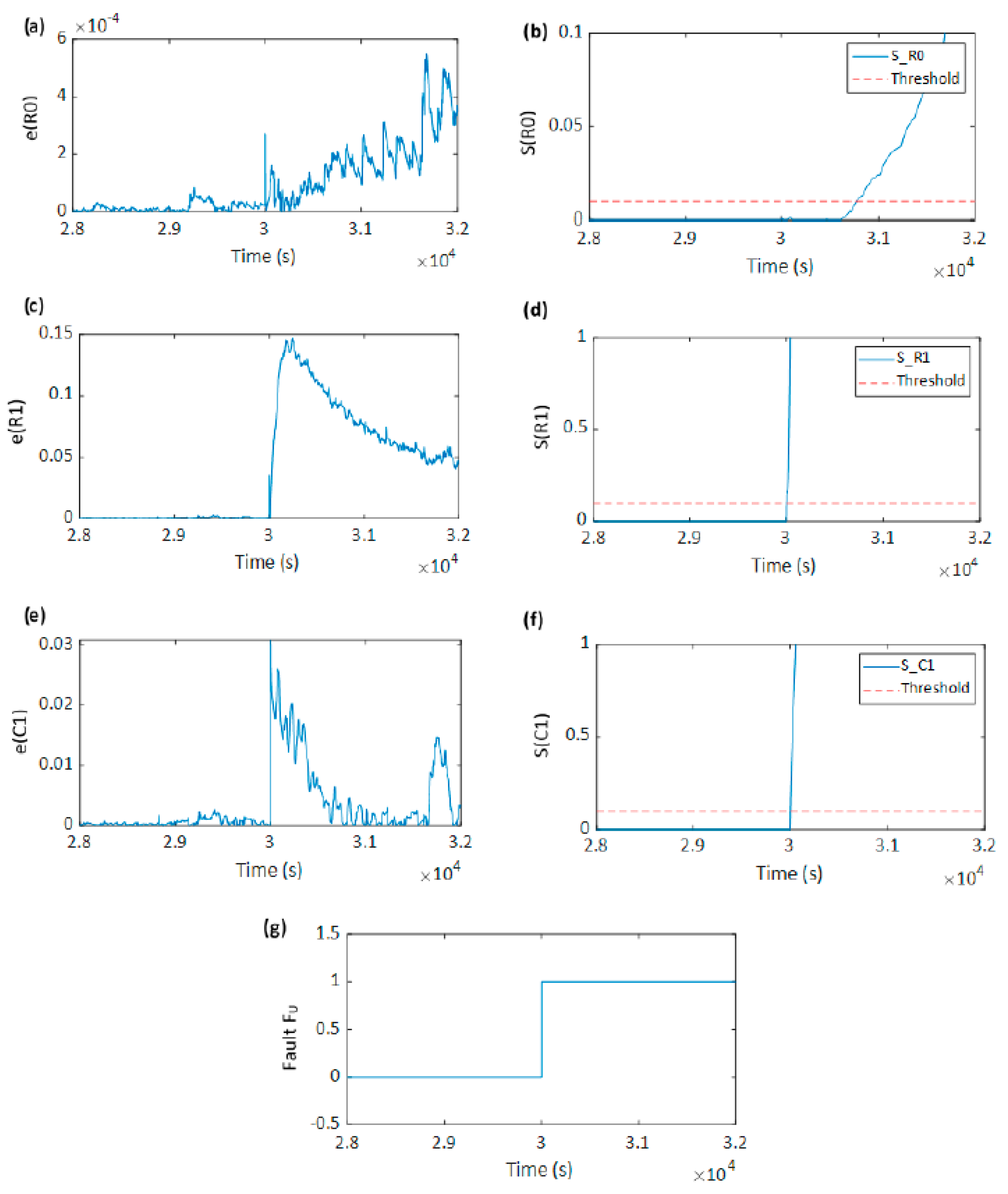
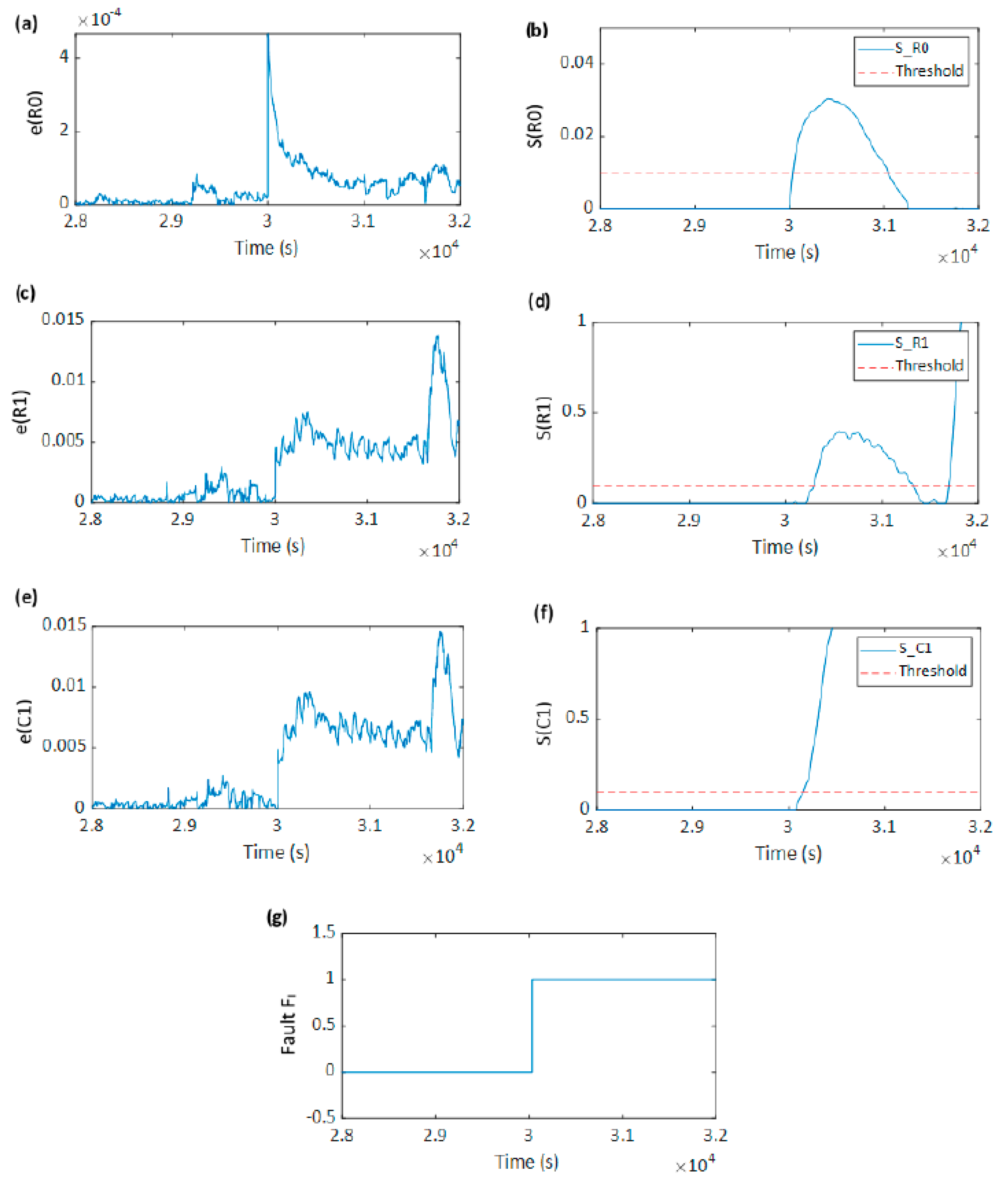
5.1. Voltage Sensor Fault Detection
5.2. Current Sensor Fault Detection
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ould Amrouche, S.; Rekioua, D.; Rekioua, T.; Bacha, S. Overview of energy storage in renewable energy systems. Int. J. Hydrog. Energy 2016, 41, 20914–20927. [Google Scholar] [CrossRef]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Liu, Z.; He, H. Sensor fault detection and isolation for a lithium-ion battery pack in electric vehicles using adaptive extended Kalman filter. Appl. Energy 2017, 185, 2033–2044. [Google Scholar] [CrossRef]
- Liu, Z.; He, H. Model-based Sensor Fault Diagnosis of a Lithium-ion Battery in Electric Vehicles. Energies 2015, 8, 6509–6527. [Google Scholar] [CrossRef]
- Wu, C.; Zhu, C.; Ge, Y.; Zhao, Y. A Review on Fault Mechanism and Diagnosis Approach for Li-Ion Batteries. J. Nanomater. 2015, 2015, 1–9. [Google Scholar] [CrossRef]
- Venkatasubramanian, V.; Rengaswamy, R.; Yin, K.; Ka, S.N. A review of process fault detection and diagnosis Part I: Quantitative model-based methods. Comput. Chem. Eng. 2003, 19, 293–311. [Google Scholar] [CrossRef]
- Marcicki, J.; Onori, S.; Rizzoni, G. Nonlinear Fault Detection and Isolation for a Lithium-Ion Battery Management System. In Proceedings of the ASME 2010 Dynamic Systems and Control Conference, 12–15 September 2010; ASMEDC: Cambridge, MA, USA, 2010; Volume 1, pp. 607–614. [Google Scholar]
- Chen, W.; Chen, W.-T.; Saif, M.; Li, M.-F.; Wu, H. Simultaneous Fault Isolation and Estimation of Lithium-Ion Batteries via Synthesized Design of Luenberger and Learning Observers. IEEE Trans. Control Syst. Technol. 2014, 22, 290–298. [Google Scholar] [CrossRef]
- Liu, Z.; Ahmed, Q.; Zhang, J.; Rizzoni, G.; He, H. Structural analysis based sensors fault detection and isolation of cylindrical lithium-ion batteries in automotive applications. Control Eng. Pract. 2016, 52, 46–58. [Google Scholar] [CrossRef]
- Dey, S.; Mohon, S.; Pisu, P.; Ayalew, B. Sensor Fault Detection, Isolation, and Estimation in Lithium-Ion Batteries. IEEE Trans. Control Syst. Technol. 2016, 24, 2141–2149. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, J.; Yuan, S.; Yang, J.; Zhou, X. A novel method for identification of lithium-ion battery equivalent circuit model parameters considering electrochemical properties. J. Power Sources 2017, 345, 21–29. [Google Scholar] [CrossRef]
- Yang, G.; Li, J.; Fu, Z.; Guo, L. Adaptive state of charge estimation of Lithium-ion battery based on battery capacity degradation model. Energy Procedia 2018, 152, 514–519. [Google Scholar] [CrossRef]
- Dubarry, M.; Berecibar, M.; Devie, A.; Anseán, D.; Omar, N.; Villarreal, I. State of health battery estimator enabling degradation diagnosis: Model and algorithm description. J. Power Sources 2017, 360, 59–69. [Google Scholar] [CrossRef]
- Fleischer, C.; Waag, W.; Heyn, H.-M.; Sauer, D.U. On-Line adaptive battery impedance parameter and state estimation considering physical principles in reduced order equivalent circuit battery models part 2. Parameter and state estimation. J. Power Sources 2014, 262, 457–482. [Google Scholar] [CrossRef]
- Rahimi-Eichi, H.; Ojha, U.; Baronti, F.; Chow, M.-Y. Battery Management System: An Overview of Its Application in the Smart Grid and Electric Vehicles. EEE Ind. Electron. Mag. 2013, 7, 4–16. [Google Scholar] [CrossRef]
- Che Mid, E.; Dua, V. Model-Based Parameter Estimation for Fault Detection Using Multiparametric Programming. Ind. Eng. Chem. Res. 2017, 56, 8000–8015. [Google Scholar] [CrossRef]
- Duong, V.-H.; Bastawrous, H.A.; Lim, K.; See, K.W.; Zhang, P.; Dou, S.X. Online state of charge and model parameters estimation of the LiFePO 4 battery in electric vehicles using multiple adaptive forgetting factors recursive least-squares. J. Power Sources 2015, 296, 215–224. [Google Scholar] [CrossRef]
- Aminikhanghahi, S.; Cook, D.J. A survey of methods for time series change point detection. Knowl. Inf. Syst. 2017, 51, 339–367. [Google Scholar] [CrossRef]
- He, H.; Zhang, X.; Xiong, R.; Xu, Y.; Guo, H. Online model-based estimation of state-of-charge and open-circuit voltage of lithium-ion batteries in electric vehicles. Energy 2012, 39, 310–318. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part I: Fault Diagnosis With Model-Based and Signal-Based Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Lelie, M.; Braun, T.; Knips, M.; Nordmann, H.; Ringbeck, F.; Zappen, H.; Sauer, D. Battery Management System Hardware Concepts: An Overview. Appl. Sci. 2018, 8, 534. [Google Scholar] [CrossRef]
- Perry, M.B. The Weighted Moving Average Technique. In Wiley Encyclopedia of Operations Research and Management Science; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011; p. eorms0964. ISBN 978-0-470-40053-1. [Google Scholar]
- Jeske, D.R.; Montes De Oca, V.; Bischoff, W.; Marvasti, M. Cusum techniques for timeslot sequences with applications to network surveillance. Comput. Stat. Data Anal. 2009, 53, 4332–4344. [Google Scholar] [CrossRef]
- Christopherson, J.P. Battery Test Manual for Electric Vehicles; Idaho National Laboratory: Idaho Falls, ID, USA, 2015.
- Gomez, J.; Nelson, R.; Kalu, E.E.; Weatherspoon, M.H.; Zheng, J.P. Equivalent circuit model parameters of a high-power Li-ion battery: Thermal and state of charge effects. J. Power Sources 2011, 196, 4826–4831. [Google Scholar] [CrossRef]

| Cell Dimension (mm) | 7.25 × 160 × 227 |
| Cell Weight (g) | 496 |
| Nominal Cell Capacity (Ah) | 19 |
| Nominal Cell Voltage (V) | 3.3 |
| Voltage Limit (V) | 2.0 to 3.65 |
| Operating Temperature (°C) | −30 to 55 |
| Cycle | 1 | 2 | 3 | 4 |
| Capacity (Ah) | 18.26 | 18.01 | 17.84 | 17.66 |
| Cycle | 5 | 6 | 7 | 8 |
| Capacity (Ah) | 17.32 | 16.93 | 16.61 | 16.47 |
| Fault Injected | Capacity (Ah) | 18.26 | 17.84 | 16.93 | 16.47 |
| -0.1 V (bias) | Detection Time (s) | 19 | 27 | 14 | 14 |
| +0.5 V (bias) | 3 | 3 | 3 | 3 | |
| +10% (gain) | 4 | 5 | 4 | 4 |
| Fault Injected | Capacity (Ah) | 18.26 | 17.84 | 16.93 | 16.47 |
| −4 A (bias) | Detection Time (s) | 143 | 190 | 560 | 179 |
| +7 A (bias) | 45 | 93 | 38 | 37 | |
| +10% (gain) | 193 | 181 | 180 | 165 |
| DTmax (s) | DTmin (s) | DTmean (s) | FDR (%) | MDR (%) | |
|---|---|---|---|---|---|
| Voltage Sensor Fault | 127 | 2 | 28 | 0 | 0 |
| Current Sensor Fault | 560 | 26 | 172 | 0 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, M.-K.; Fowler, M. Sensor Fault Detection and Isolation for Degrading Lithium-Ion Batteries in Electric Vehicles Using Parameter Estimation with Recursive Least Squares. Batteries 2020, 6, 1. https://doi.org/10.3390/batteries6010001
Tran M-K, Fowler M. Sensor Fault Detection and Isolation for Degrading Lithium-Ion Batteries in Electric Vehicles Using Parameter Estimation with Recursive Least Squares. Batteries. 2020; 6(1):1. https://doi.org/10.3390/batteries6010001
Chicago/Turabian StyleTran, Manh-Kien, and Michael Fowler. 2020. "Sensor Fault Detection and Isolation for Degrading Lithium-Ion Batteries in Electric Vehicles Using Parameter Estimation with Recursive Least Squares" Batteries 6, no. 1: 1. https://doi.org/10.3390/batteries6010001
APA StyleTran, M.-K., & Fowler, M. (2020). Sensor Fault Detection and Isolation for Degrading Lithium-Ion Batteries in Electric Vehicles Using Parameter Estimation with Recursive Least Squares. Batteries, 6(1), 1. https://doi.org/10.3390/batteries6010001






