Classification of the Crystal Structures of Orthosilicate Cathode Materials for Li-Ion Batteries by Artificial Neural Networks
Abstract
1. Introduction
- To analyze the correlation between crystal structures determined by density functional theory (DFT) calculations.
- To utilize an ANN model to predict crystal systems (monoclinic and orthorhombic) of orthosilicate cathodes.
- To evaluate the performance of the ANN models using correlation coefficients.
- To develop user-friendly software for classifying crystal structures.
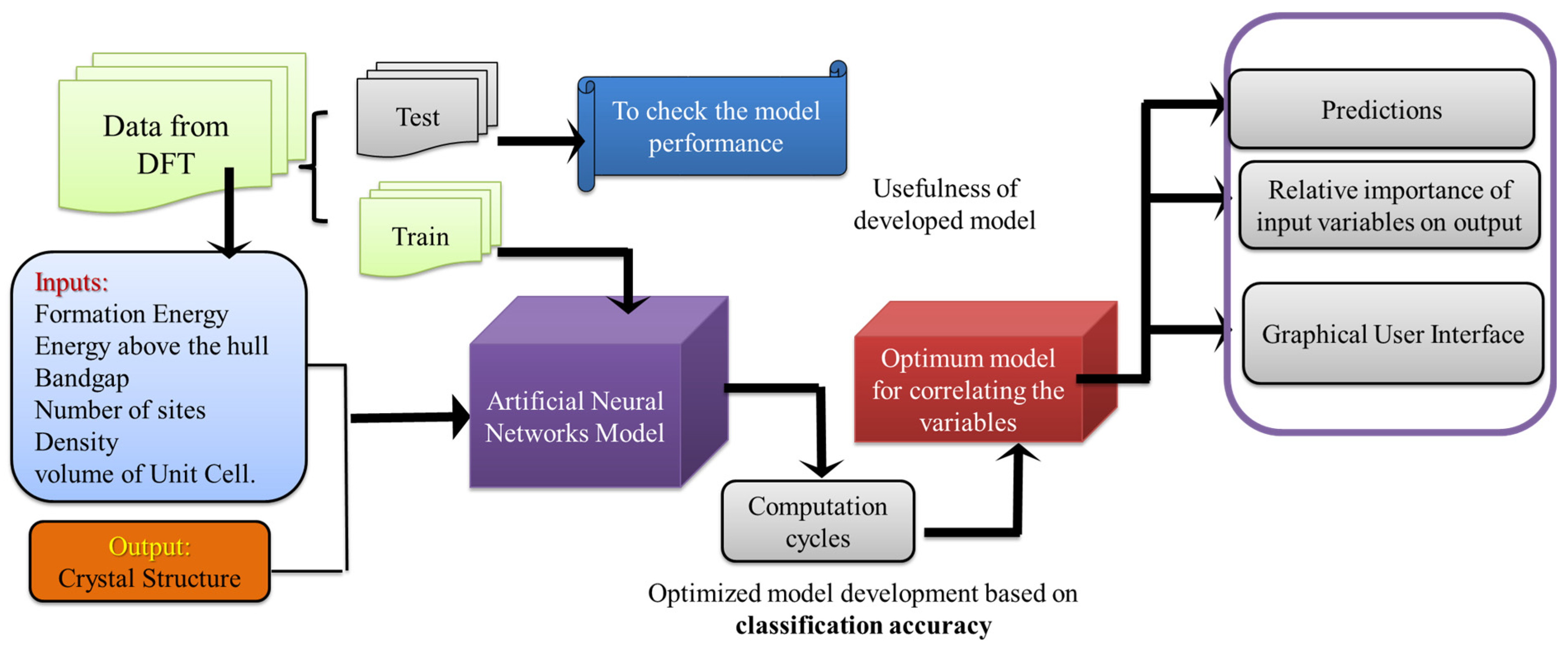
2. Materials and Methods
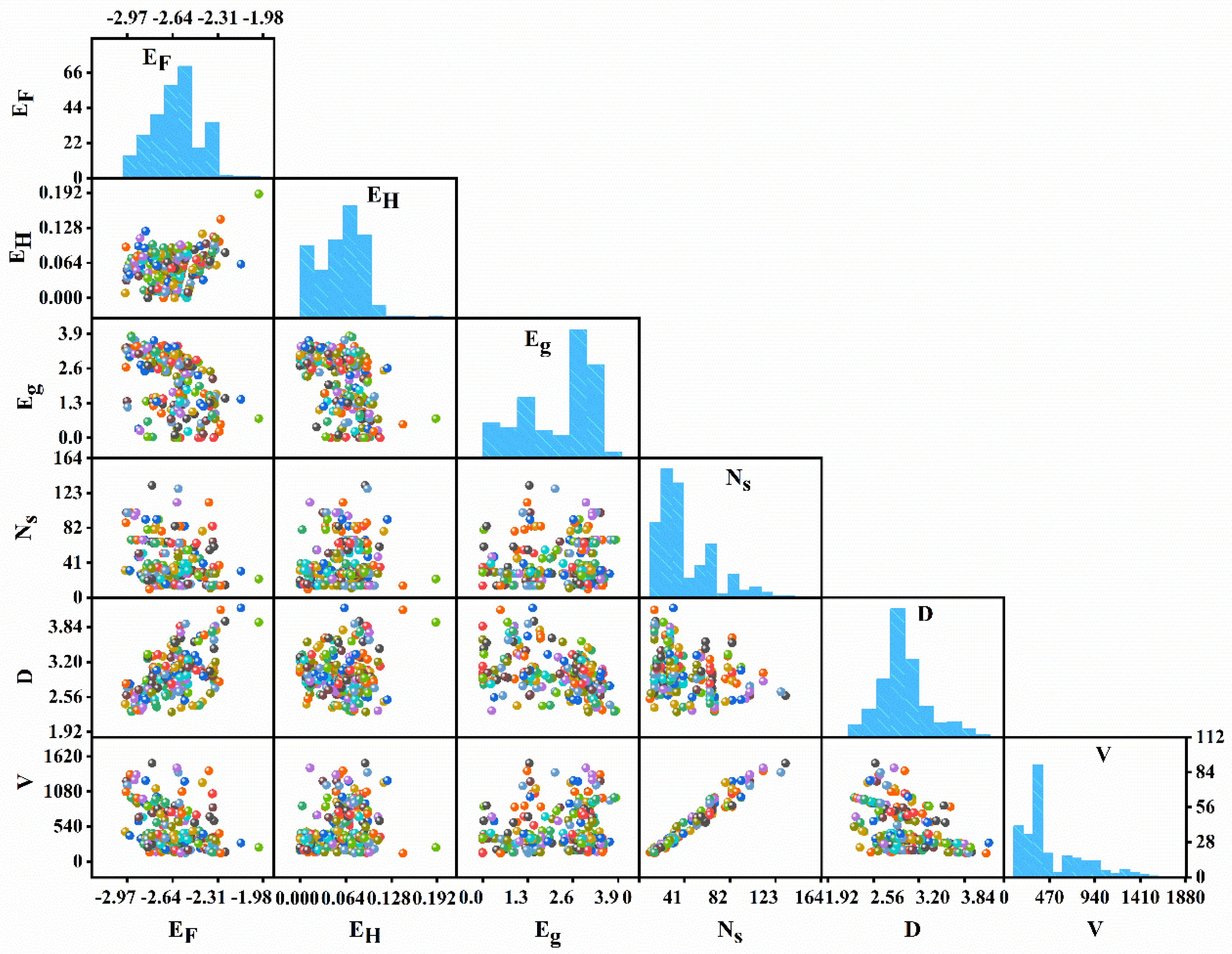
2.1. Experimental Data
2.2. ANN Model Development
3. Results and Discussion
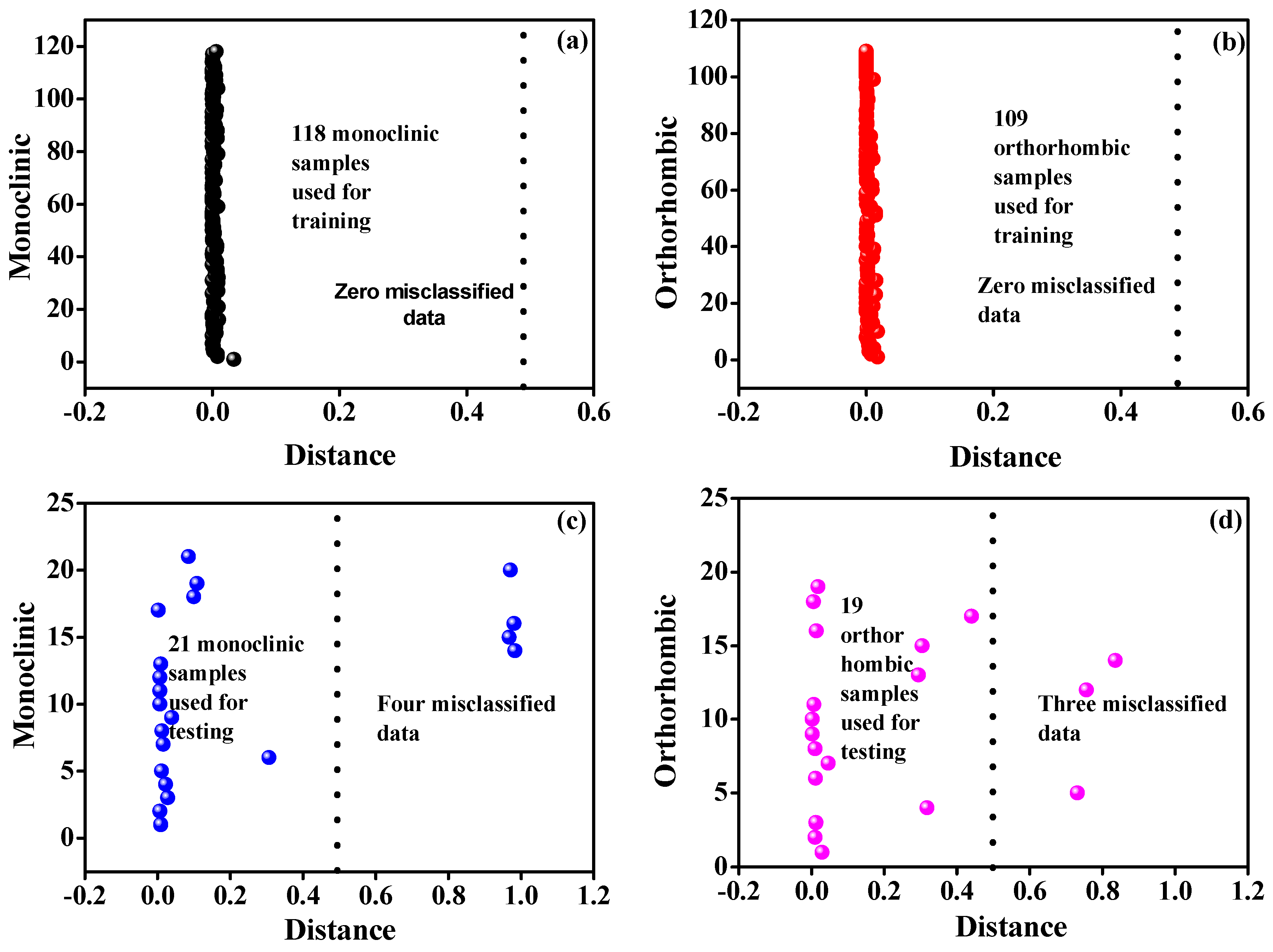
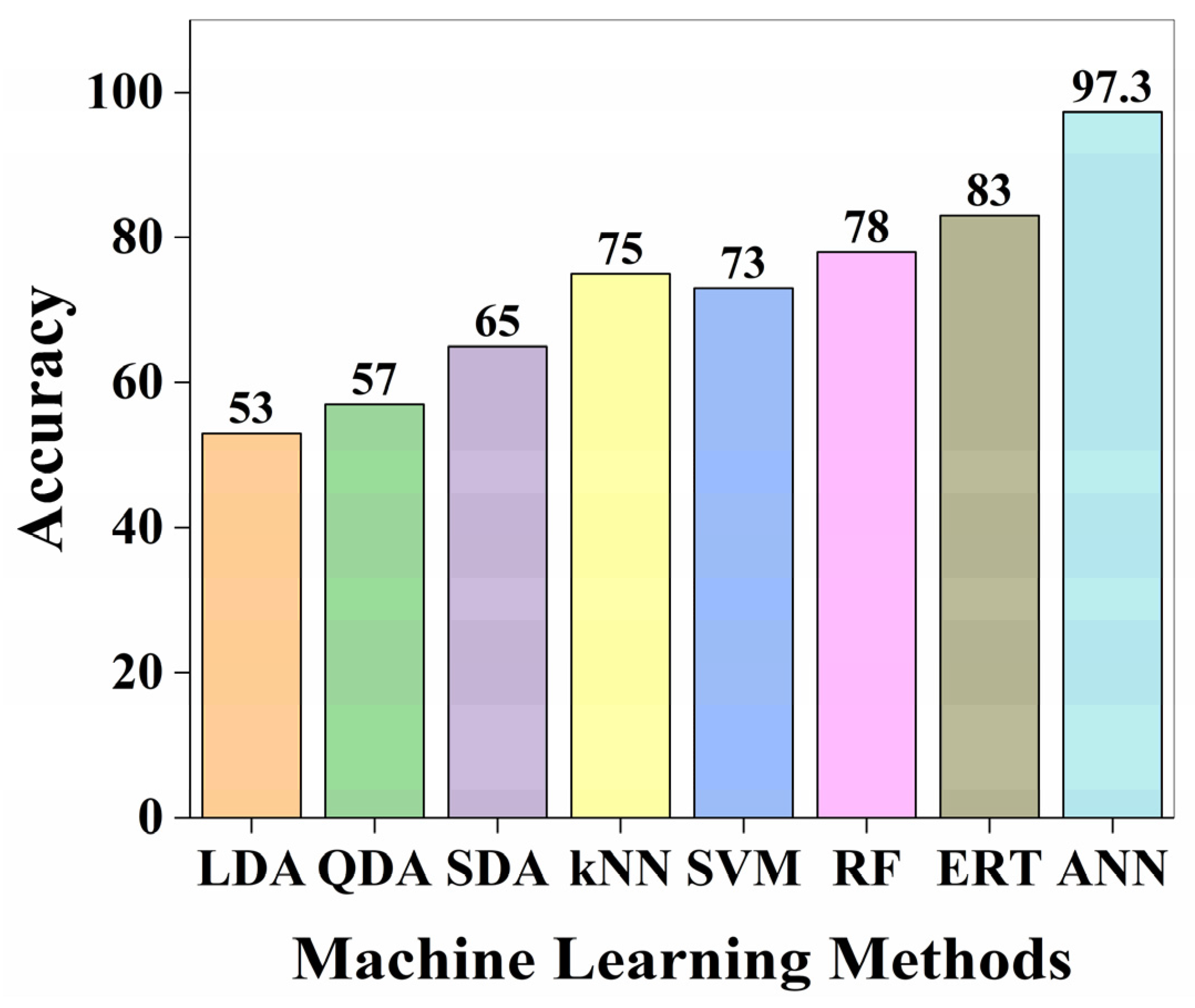
3.1. Model Predictions for Crystal System Classification
3.2. Evaluation of ANN Model Performance Using Confusion Matrix
3.3. Graphical User Interface Design Based on ANN Model Synaptic Weights
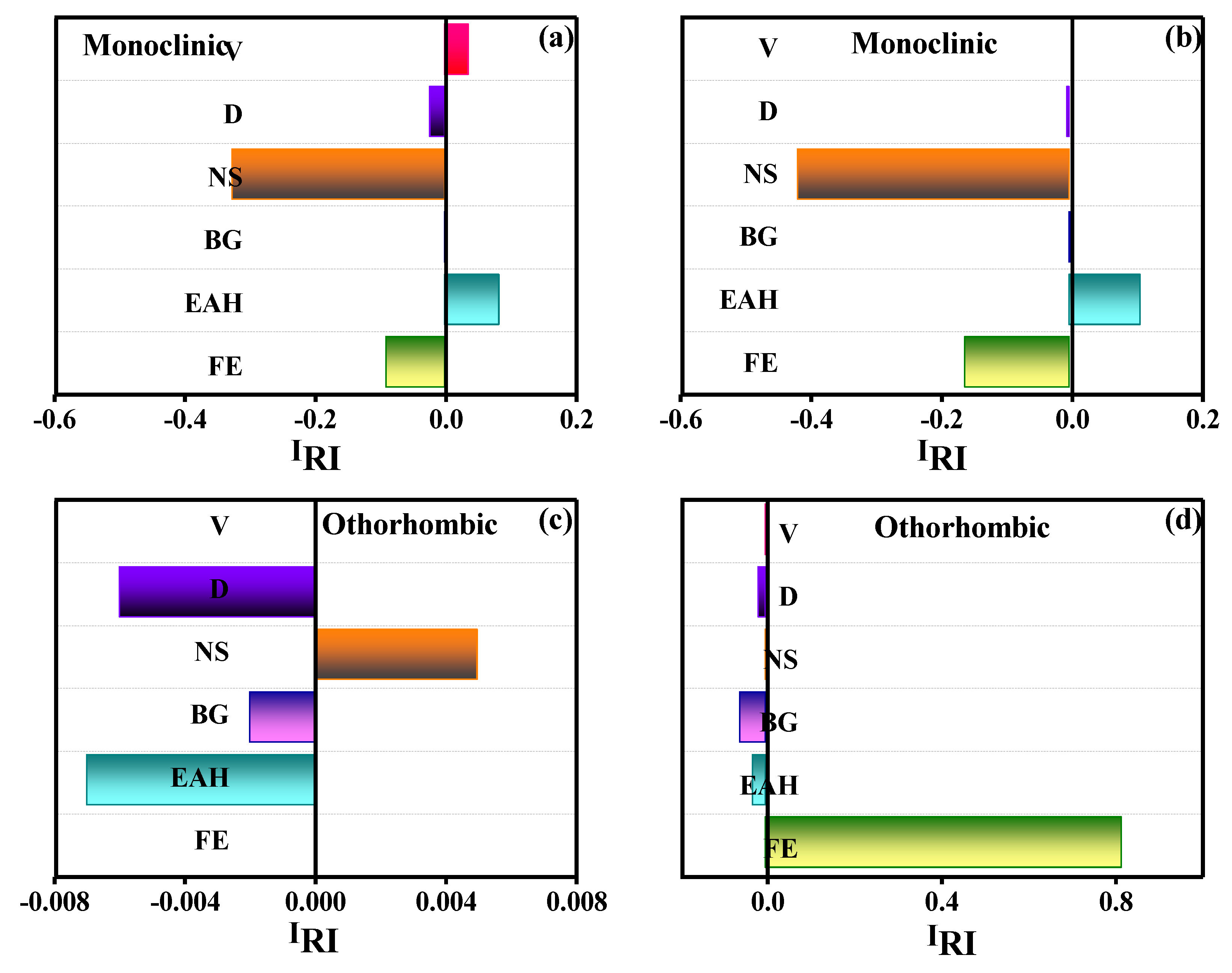
3.4. Identification of Feature Importance
3.5. Study Limitations and Future Directions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Taberna, P.-L.; Mitra, S.; Poizot, P.; Simon, P.; Tarascon, J.-M. High rate capabilities Fe3O4-based Cu nano-architectured electrodes for lithium-ion battery applications. Nat. Mater. 2006, 5, 567. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Hu, Z.; Zhang, K.; Cheng, F.; Chen, J. Intergrown Li2FeSiO4·LiFePo4–C nanocomposites as high-capacity cathode materials for lithium-ion batteries. Chem. Commun. 2013, 49, 3040–3042. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G. Commentary: The materials project: A materials genome approach to accelerating materials innovation. Apl Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
- Dominko, R.; Bele, M.; Gaberšček, M.; Meden, A.; Remškar, M.; Jamnik, J. Structure and electrochemical performance of Li2MnSiO4 and Li2FeSiO4 as potential Li-battery cathode materials. Electrochem. Commun. 2006, 8, 217–222. [Google Scholar] [CrossRef]
- Teixeira, R.S.D.; Calili, R.F.; Almeida, M.F.; Louzada, D.R. Recurrent neural networks for estimating the state of health of lithium-ion batteries. Batteries 2024, 10, 111. [Google Scholar] [CrossRef]
- Sözen, A.; Arcaklioǧlu, E.; Özalp, M. A new approach to thermodynamic analysis of ejector–absorption cycle: Artificial neural networks. Appl. Therm. Eng. 2003, 23, 937–952. [Google Scholar] [CrossRef]
- Wriggers, W.; Milligan, R.A.; McCammon, J.A. Situs: A package for docking crystal structures into low-resolution maps from electron microscopy. J. Struct. Biol. 1999, 125, 185–195. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Jiang, B. Attention mechanism-based neural network for prediction of battery cycle life in the presence of missing data. Batteries 2024, 10, 229. [Google Scholar] [CrossRef]
- Hautier, G.; Fischer, C.; Ehrlacher, V.; Jain, A.; Ceder, G. Data mined ionic substitutions for the discovery of new compounds. Inorg. Chem. 2010, 50, 656–663. [Google Scholar] [CrossRef]
- Zeng, C.; Zheng, R.; Fan, F.; Wang, X.; Tian, G.; Liu, S.; Liu, P.; Wang, C.; Wang, S.; Shu, C. Phase compatible surface engineering to boost the cycling stability of single-crystalline Ni-rich cathode for high energy density lithium-ion batteries. Energy Storage Mater. 2024, 72, 103788. [Google Scholar] [CrossRef]
- Fan, F.; Zheng, R.; Zeng, T.; Xu, H.; Wen, X.; Wang, X.; Tian, G.; Wang, S.; Zeng, C.; Xiang, W.; et al. Cation-ordered Ni-rich positive electrode material with superior chemical and structural stability enabled by atomic substitution for lithium-ion batteries. Chem. Eng. J. 2023, 477, 147181. [Google Scholar] [CrossRef]
- Zeng, C.; Fan, F.; Zheng, R.; Wang, X.; Tian, G.; Liu, S.; Liu, P.; Wang, C.; Wang, S.; Shu, C. Structure and Charge Regulation Strategy Enabling Superior Cycling Stability of Ni-Rich Cathode Materials. ACS Appl. Mater. Interfaces 2024, 16, 11377–11388. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Lippmann, R.P. An introduction to computing with neural nets. IEEE Assp Mag. 1987, 4, 4–22. [Google Scholar] [CrossRef]
- Reddy, N.S.; Panigrahi, B.B.; Ho, C.M.; Kim, J.H.; Lee, C.S. Artificial neural network modeling on the relative importance of alloying elements and heat treatment temperature to the stability of α and β phase in titanium alloys. Comput. Mater. Sci. 2015, 107, 175–183. [Google Scholar] [CrossRef]
- Reddy, N.S.; Krishnaiah, J.; Young, H.B.; Lee, J.S. Design of medium carbon steels by computational intelligence techniques. Comput. Mater. Sci. 2015, 101, 120–126. [Google Scholar] [CrossRef]



| S. No. | Formula | Space Group | Experimental | Ann Predicted |
|---|---|---|---|---|
| 1 | Li2MnSiO4 | Pcmn | Orthorhombic | Orthorhombic |
| 2 | Li2MnSiO4 | Pmnb | Orthorhombic | Orthorhombic |
| 3 | LiMn(SiO3)2 | Pbca | Orthorhombic | Orthorhombic |
| 4 | LiMnSiO4 | Pna21 | Orthorhombic | Orthorhombic |
| 5 | Li2MnSiO4 | Pca21 | Monoclinic | Orthorhombic |
| 6 | Li4Mn2Si4O13 | Pna21 | Orthorhombic | Orthorhombic |
| 7 | Li2Mn2(SiO3)3 | Pnma | Orthorhombic | Orthorhombic |
| 8 | LiMnSiO4 | Imma | Orthorhombic | Orthorhombic |
| 9 | Li2FeSiO4 | Pcmn | Orthorhombic | Orthorhombic |
| 10 | Li2CoSiO4 | Pcmn | Orthorhombic | Orthorhombic |
| 11 | Li2CoSiO4 | C2221 | Orthorhombic | Orthorhombic |
| 12 | LiCoSiO4 | P212121 | Monoclinic | Orthorhombic |
| 13 | LiCoSiO4 | Imcm | Orthorhombic | Orthorhombic |
| 14 | LiMnSiO4 | Pna21 | Monoclinic | Orthorhombic |
| 15 | Li2Co2Si2O7 | C2cm | Orthorhombic | Orthorhombic |
| 16 | LiCoSiO4 | Pb21a | Orthorhombic | Orthorhombic |
| 17 | Li2CoSiO4 | Pca21 | Orthorhombic | Orthorhombic |
| 18 | Li3CoSiO5 | P21nb | Orthorhombic | Orthorhombic |
| 19 | LiCoSiO4 | Cmcm | Orthorhombic | Orthorhombic |
| 20 | Li2MnSiO4 | P21/c | Monoclinic | Monoclinic |
| 21 | Li4MnSi2O7 | Cc | Monoclinic | Monoclinic |
| 22 | Li4Mn2Si3O10 | C2/c | Monoclinic | Monoclinic |
| 23 | Li2Mn3Si3O10 | C2/c | Monoclinic | Monoclinic |
| 24 | Li4MnSi2O7 | C2 | Monoclinic | Monoclinic |
| 25 | LiMnSiO4 | P21 | Monoclinic | Monoclinic |
| 26 | Li2MnSiO4 | P21/c | Monoclinic | Monoclinic |
| 27 | LiMn(SiO3)2 | C2/c | Monoclinic | Monoclinic |
| 28 | Li2Mn(SiO3)2 | Cc | Monoclinic | Monoclinic |
| 29 | Li2MnSiO4 | P21/c | Monoclinic | Monoclinic |
| 30 | Li2Mn(SiO3)2 | C2/c | Monoclinic | Monoclinic |
| 31 | Li2Mn2Si2O7 | P21/c | Monoclinic | Monoclinic |
| 32 | Li10Mn(SiO5)2 | C2/m | Monoclinic | Monoclinic |
| 33 | Li3MnSi2O7 | P21 | Orthorhombic | Monoclinic |
| 34 | Li5Mn(SiO4)2 | C2 | Orthorhombic | Monoclinic |
| 35 | Li2Mn(Si2O5)2 | P21/c | Orthorhombic | Monoclinic |
| 36 | Li2Mn2Si3O10 | Cc | Monoclinic | Monoclinic |
| 37 | Li2Mn2(SiO3)3 | P21/c | Monoclinic | Monoclinic |
| 38 | LiMn(SiO3)2 | C2/c | Monoclinic | Monoclinic |
| 39 | Li2MnSi3O8 | P21 | Orthorhombic | Monoclinic |
| 40 | Li3Mn2(SiO4)2 | P21 | Monoclinic | Monoclinic |
| S. No. | Ef | EH | Eg | Ns | V | D | Exp | ANN |
|---|---|---|---|---|---|---|---|---|
| 241 | −2.62 | 0.005 | 3.027 | 16 | 3.073 | 174.862 | 0 | 1 |
| 242 | −2.619 | 0.007 | 3.407 | 32 | 3.005 | 357.648 | 0 | 1 |
| 243 | −2.61 | 0.012 | 3.026 | 28 | 2.852 | 360.726 | 0 | 1 |
| 247 | −2.887 | 0.04 | 3.144 | 52 | 2.69 | 679.10 | 0 | 1 |
| 253 | −2.65 | 0.054 | 2.582 | 64 | 2.8 | 763.324 | 1 | 0 |
| 261 | −2.291 | 0.144 | 0.511 | 14 | 4.15 | 126.395 | 1 | 0 |
| 263 | −2.453 | 0.072 | 2.84 | 26 | 3.579 | 278.304 | 1 | 0 |
| n = 267 | Actual Value | ||
|---|---|---|---|
| ANN model prediction | 135 TPs | 4 FNs | 139 |
| 3 FPs | 125 TNs | 128 | |
| 138 | 129 | 267 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Premasudha, M.; Srinivasulu Reddy, B.R.; Cho, K.-K.; Hyo-Jun, A.; Sung, J.-K.; Subba Reddy, N.G. Classification of the Crystal Structures of Orthosilicate Cathode Materials for Li-Ion Batteries by Artificial Neural Networks. Batteries 2025, 11, 13. https://doi.org/10.3390/batteries11010013
Premasudha M, Srinivasulu Reddy BR, Cho K-K, Hyo-Jun A, Sung J-K, Subba Reddy NG. Classification of the Crystal Structures of Orthosilicate Cathode Materials for Li-Ion Batteries by Artificial Neural Networks. Batteries. 2025; 11(1):13. https://doi.org/10.3390/batteries11010013
Chicago/Turabian StylePremasudha, Mookala, Bhumi Reddy Srinivasulu Reddy, Kwon-Koo Cho, Ahn Hyo-Jun, Jae-Kyung Sung, and Nagireddy Gari Subba Reddy. 2025. "Classification of the Crystal Structures of Orthosilicate Cathode Materials for Li-Ion Batteries by Artificial Neural Networks" Batteries 11, no. 1: 13. https://doi.org/10.3390/batteries11010013
APA StylePremasudha, M., Srinivasulu Reddy, B. R., Cho, K.-K., Hyo-Jun, A., Sung, J.-K., & Subba Reddy, N. G. (2025). Classification of the Crystal Structures of Orthosilicate Cathode Materials for Li-Ion Batteries by Artificial Neural Networks. Batteries, 11(1), 13. https://doi.org/10.3390/batteries11010013







