Modelling Binder Degradation in the Thermal Treatment of Spent Lithium-Ion Batteries by Coupling Discrete Element Method and Isoconversional Kinetics
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
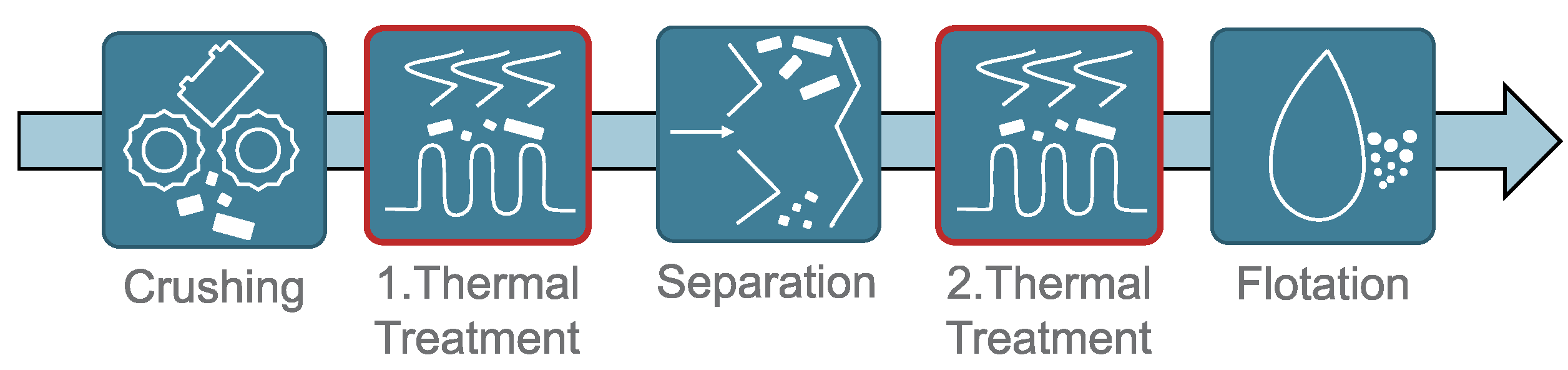
2.2. Experimental Procedure
2.3. Computational Methods
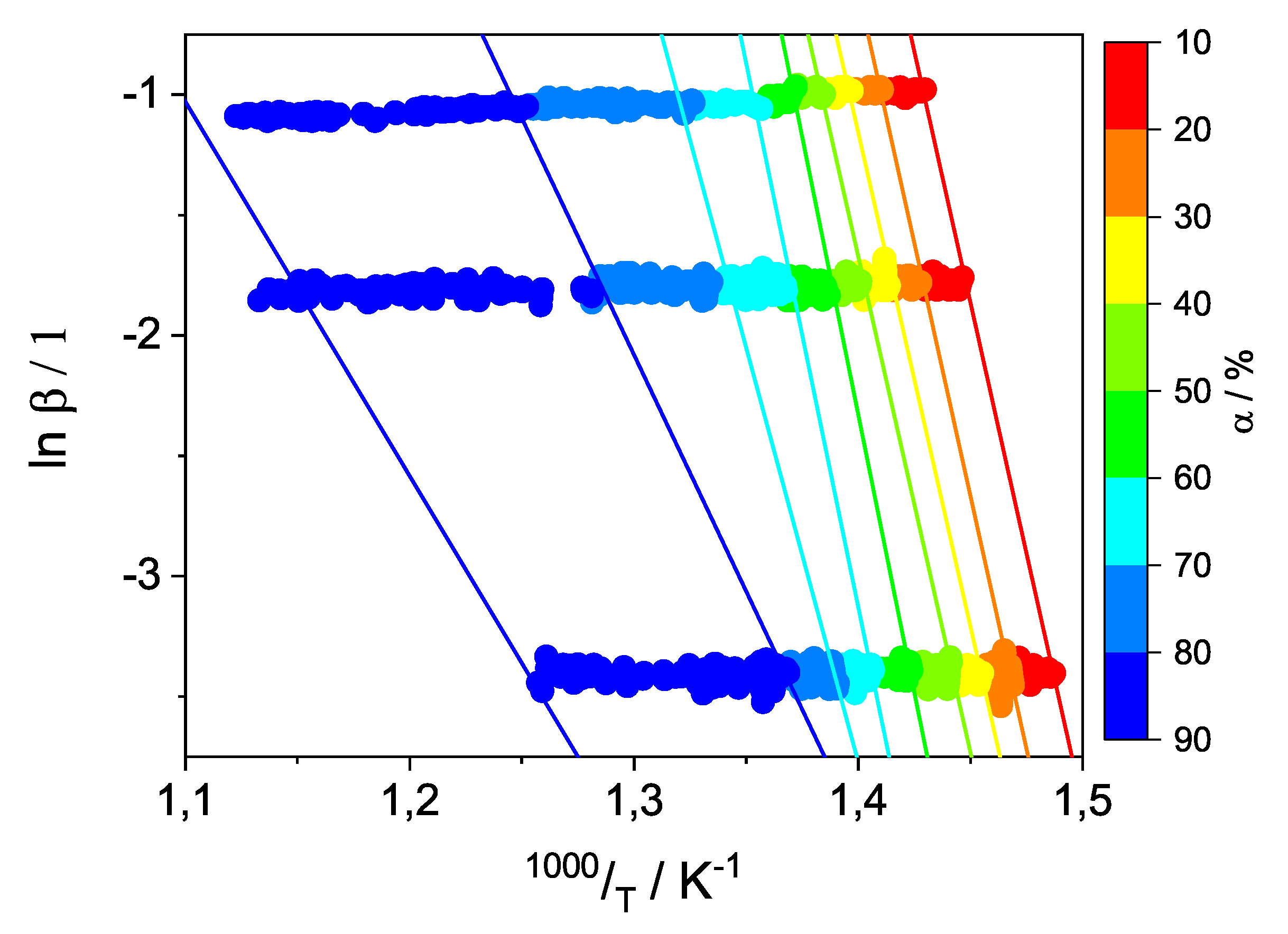
2.3.1. Thermal Degradation Kinetics
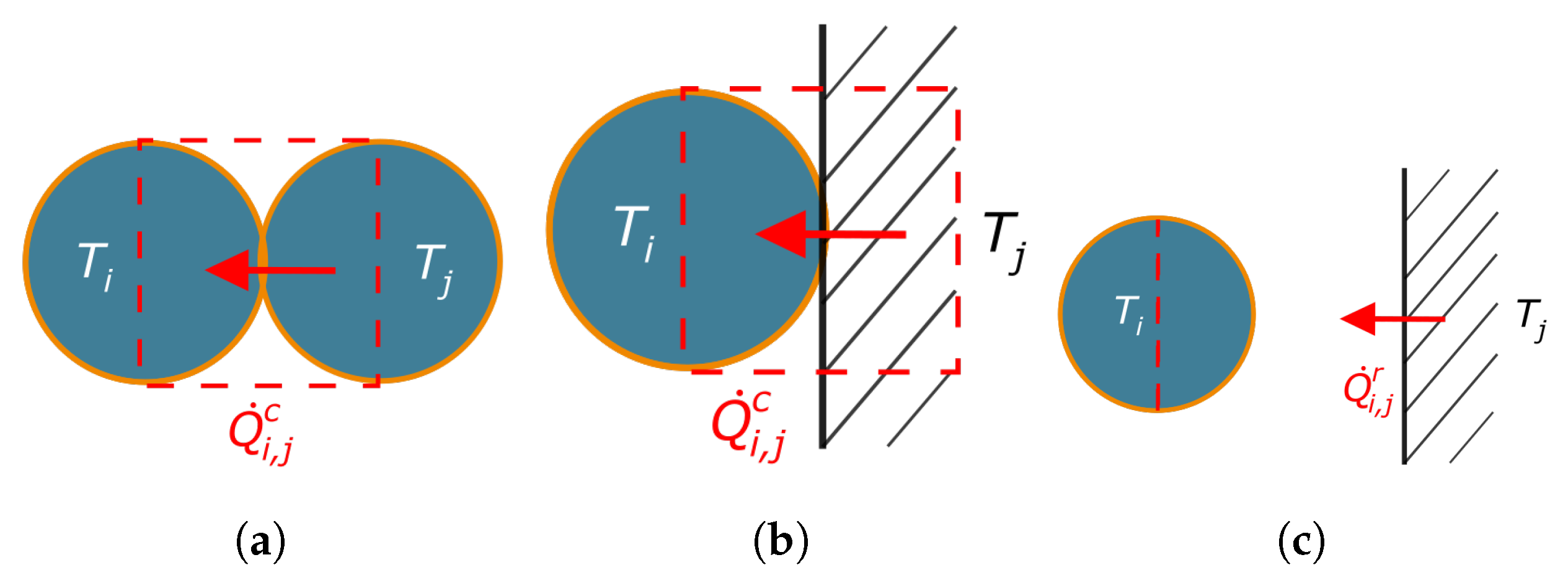
2.3.2. Discrete Element Method (DEM)
Stability of DEM Simulations
Thermophysical Descriptions
- Mode: Calculation according to the overlapping area of objects.
- Mode: Constant by user-defined overlap area.
- Mode: Calculation by projection area , where and is the radius of the smaller object.
Coarse-Graining (CG) Scheme
2.3.3. Representative Black Mass Model (RBMM)
2.3.4. Specific RBMM (sRBMM) for LIBs with a Particular Composition
3. Results and Discussion
3.1. Determining Model Parameters for the sRBMM
3.1.1. Determination and Validation of the Kinetic Model Parameters for PVDF Degradation
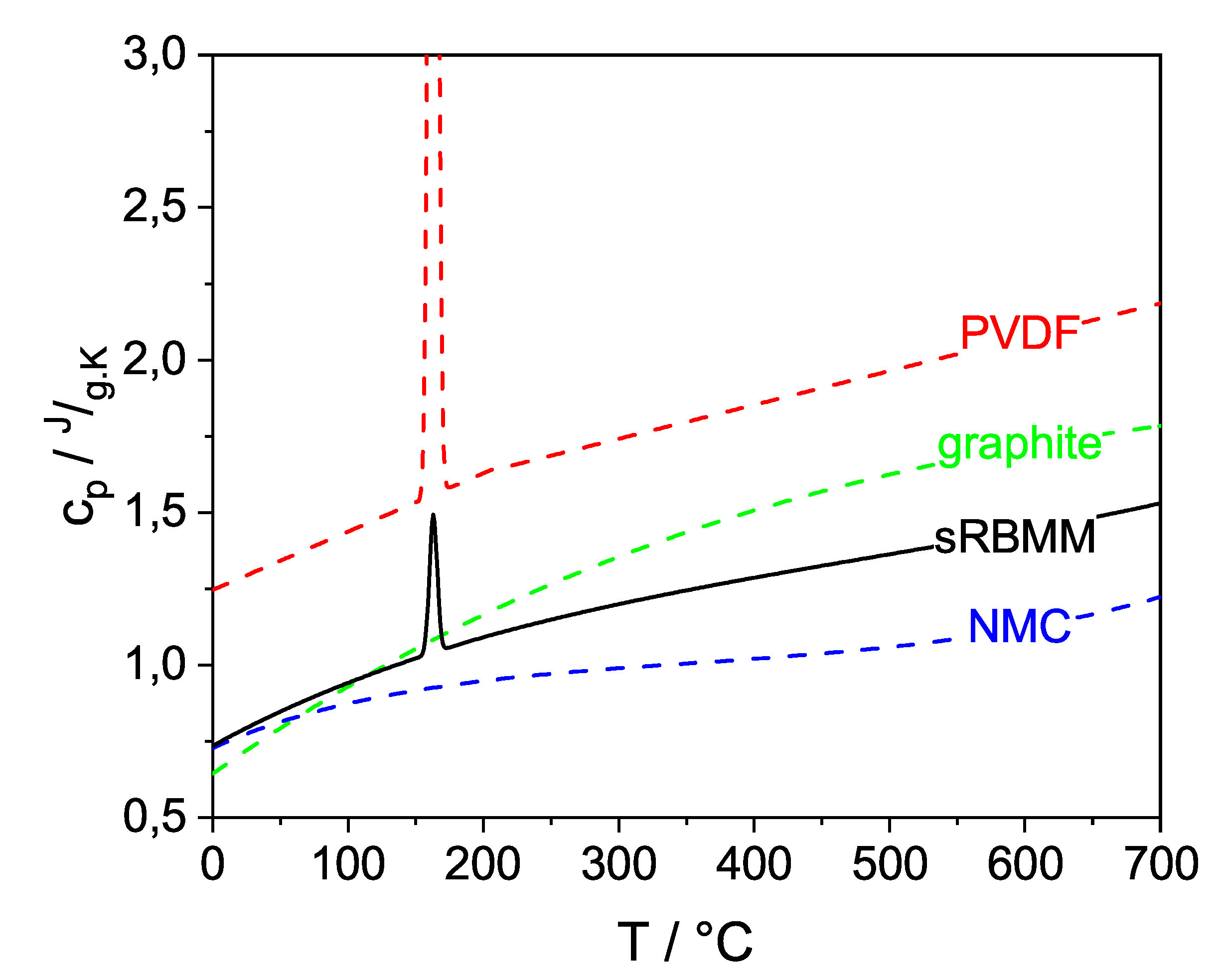
3.1.2. Determining the Parameters for the Mass and the Heat Transfer
3.2. DEM Simulations: Investigation and Validation of the sRBMM
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BM | Black mass |
| BC | Boundary condition |
| CAD | Computer-aided design |
| CMC | Carboxymethyl cellulose |
| DEM | Discrete element method |
| DSC | Difference scanning calorimetry |
| EHT | Effective heat transfer |
| HF | Hydrogen fluoride |
| HR | Heating rate |
| IC | Initial condition |
| LMO | Lithium metal oxide |
| NMC | Nickel manganese cobalt (the metals in the LMO) |
| OFW | Ozawa–Flynn–Wall |
| PVDF | Polyvinylidene fluoride |
| RBMM | Representative Black Mass Model |
| SBR | Styrene butadiene rubber |
| sRBMM | Specific Representative Black Mass Model |
| TGA | Thermogravimetric analysis |
References
- Bürklin, B.; Latz, T.; Schenk, L.; Degen, F.; Diehl, M.; Krätzig, O.; Paulsen, T.; Kampker, A.; Lackner, N.; Neef, C.; et al. Umfeldbericht zum Europäischen Innovationssystem Batterie 2022; Fraunhofer ISI: Karlsruhe, Germany, 2022. [Google Scholar]
- Grohol, M.; Veeh, C. Study on the Critical Raw Materials for the EU 2023: Final Report; Publications Office of the European Union: Luxembourg, 2023. [Google Scholar] [CrossRef]
- Mossali, E.; Picone, N.; Gentilini, L.; Rodrìguez, O.; Pérez, J.M.; Colledani, M. Lithium-ion batteries towards circular economy: A literature review of opportunities and issues of recycling treatments. J. Environ. Manag. 2020, 264, 110500. [Google Scholar] [CrossRef]
- Li, H.; Qiu, H.; Schirmer, T.; Goldmann, D.; Fischlschweiger, M. Tailoring Lithium Aluminate Phases Based on Thermodynamics for an Increased Recycling Efficiency of Li-Ion Batteries. ACS EST Eng. 2022, 2, 1883–1895. [Google Scholar] [CrossRef]
- Li, H.; Ranneberg, M.; Fischlschweiger, M. High-Temperature Phase Behavior of Li2O-MnO with a Focus on the Liquid-to-Solid Transition. JOM 2023, 75, 5796–5807. [Google Scholar] [CrossRef]
- Babanejad, S.; Ahmed, H.; Andersson, C.; Samuelsson, C.; Lennartsson, A.; Hall, B.; Arnerlöf, L. High-Temperature Behavior of Spent Li-Ion Battery Black Mass in Inert Atmosphere. J. Sustain. Metall. 2022, 8, 566–581. [Google Scholar] [CrossRef]
- Vanderbruggen, A.; Hayagan, N.; Bachmann, K.; Ferreira, A.; Werner, D.; Horn, D.; Peuker, U.; Serna-Guerrero, R.; Rudolph, M. Lithium-Ion Battery Recycling- Influence of Recycling Processes on Component Liberation and Flotation Separation Efficiency. ACS EST Eng. 2022, 2, 2130–2141. [Google Scholar] [CrossRef]
- Lombardo, G.; Ebin, B.; Steenari, B.M.; Alemrajabi, M.; Karlsson, I.; Petranikova, M. Comparison of the effects of incineration, vacuum pyrolysis and dynamic pyrolysis on the composition of NMC-lithium battery cathode-material production scraps and separation of the current collector. Resour. Conserv. Recycl. 2021, 164, 105142. [Google Scholar] [CrossRef]
- Nagl, R.; Fan, Z.; Nobis, C.; Kiefer, C.; Fischer, A.; Zhang, T.; Zeiner, T.; Fischlschweiger, M. Study of isobaric vapor–liquid equilibria of diethyl carbonate + ethylene carbonate for lithium-ion battery electrolyte solvent recycling. J. Mol. Liq. 2023, 386, 122449. [Google Scholar] [CrossRef]
- Abdollahifar, M.; Doose, S.; Cavers, H.; Kwade, A. Graphite Recycling from End–of–Life Lithium–Ion Batteries: Processes and Applications. Adv. Mater. Technol. 2023, 8, 2200368. [Google Scholar] [CrossRef]
- Petranikova, M.; Naharro, P.L.; Vieceli, N.; Lombardo, G.; Ebin, B. Recovery of critical metals from EV batteries via thermal treatment and leaching with sulphuric acid at ambient temperature. Waste Manag. 2022, 140, 164–172. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, X.; Zheng, Y.; Wang, Q.; Liu, J.; Xu, S. Boosting efficient and low-energy solid phase regeneration for single crystal LiNi0.6Co0.2Mn0.2O2 via highly selective leaching and its industrial application. Chem. Eng. J. 2023, 451, 139039. [Google Scholar] [CrossRef]
- Liu, X.; Wang, R.; Liu, S.; Pu, J.; Xie, H.; Wu, M.; Liu, D.; Li, Y.; Liu, J. Organic Eutectic Salts–Assisted Direct Lithium Regeneration for Extremely Low State of Health Ni–Rich Cathodes. Adv. Energy Mater. 2023, 13, 2302987. [Google Scholar] [CrossRef]
- Werner, D.; Peuker, U.A.; Mütze, T. Recycling Chain for Spent Lithium-Ion Batteries. Metals 2020, 10, 316. [Google Scholar] [CrossRef]
- Mousa, E.; Hu, X.; Ånnhagen, L.; Ye, G.; Cornelio, A.; Fahimi, A.; Bontempi, E.; Frontera, P.; Badenhorst, C.; Santos, A.C.; et al. Characterization and Thermal Treatment of the Black Mass from Spent Lithium-Ion Batteries. Sustainability 2023, 15, 15. [Google Scholar] [CrossRef]
- Xiao, J.; Li, J.; Xu, Z. Recycling metals from lithium ion battery by mechanical separation and vacuum metallurgy. J. Hazard. Mater. 2017, 338, 124–131. [Google Scholar] [CrossRef] [PubMed]
- Lombardo, G.; Ebin, B.; St. J. Foreman, M.R.; Steenari, B.M.; Petranikova, M. Chemical Transformations in Li-Ion Battery Electrode Materials by Carbothermic Reduction. ACS Sustain. Chem. Eng. 2019, 7, 13668–13679. [Google Scholar] [CrossRef]
- Lombardo, G.; Ebin, B.; St J Foreman, M.R.; Steenari, B.M.; Petranikova, M. Incineration of EV Lithium-ion batteries as a pretreatment for recycling—Determination of the potential formation of hazardous by-products and effects on metal compounds. J. Hazard. Mater. 2020, 393, 122372. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Vanderbruggen, A.; Gugala, E.; Blannin, R.; Bachmann, K.; Serna-Guerrero, R.; Rudolph, M. Automated mineralogy as a novel approach for the compositional and textural characterization of spent lithium-ion batteries. Miner. Eng. 2021, 169, 106924. [Google Scholar] [CrossRef]
- Friedman, H.L. Kinetics of thermal degradation of char–forming plastics from thermogravimetry. Application to a phenolic plastic. J. Polym. Sci. Part C Polym. Symp. 1964, 6, 183–195. [Google Scholar] [CrossRef]
- Ozawa, T. A New Method of Analyzing Thermogravimetric Data. Bull. Chem. Soc. Jpn. 1965, 38, 1881–1886. [Google Scholar] [CrossRef]
- Flynn, J.H.; Wall, L.A. A quick, direct method for the determination of activation energy from thermogravimetric data. J. Polym. Sci. Part B Polym. Lett. 1966, 4, 323–328. [Google Scholar] [CrossRef]
- Akahira, T.; Sunose, T. Method of determining activation deterioration constant of electrical insulating materials. Res. Rep. Chiba Inst. Technol. (Sci. Technol.) 1971, 16, 22–31. [Google Scholar]
- Vyazovkin, S.; Dollimore, D. Linear and Nonlinear Procedures in Isoconversional Computations of the Activation Energy of Nonisothermal Reactions in Solids. J. Chem. Inf. Comput. Sci. 1996, 36, 42–45. [Google Scholar] [CrossRef]
- Vyazovkin, S. Evaluation of activation energy of thermally stimulated solid-state reactions under arbitrary variation of temperature. J. Comput. Chem. 1997, 18, 393–402. [Google Scholar] [CrossRef]
- Vyazovkin, S. Modification of the integral isoconversional method to account for variation in the activation energy. J. Comput. Chem. 2001, 22, 178–183. [Google Scholar] [CrossRef]
- Yeom, S.B.; Ha, E.S.; Kim, M.S.; Jeong, S.H.; Hwang, S.J.; Du Choi, H. Application of the Discrete Element Method for Manufacturing Process Simulation in the Pharmaceutical Industry. Pharmaceutics 2019, 11, 414. [Google Scholar] [CrossRef] [PubMed]
- Bierwisch, C.; Kraft, T.; Riedel, H.; Moseler, M. Three-dimensional discrete element models for the granular statics and dynamics of powders in cavity filling. J. Mech. Phys. Solids 2009, 57, 10–31. [Google Scholar] [CrossRef]
- Poly(Vinylidenfluorid) Average Mw ∼534,000 by GPC, Powder | Sigma-Aldrich. 19 September 2023. Available online: https://export.vwr.com/store/product/25409981/poly-vinylidene-fluoride-m-w-534-000-by-gpc-powder-sigma-aldrich (accessed on 31 December 2023).
- GitHub. ParticulateFlow/LIGGGHTS-PFM: This Is an Academic Adaptation of the LIGGGHTS Software Package, Released by the Department of Particulate Flow Modelling at Johannes Kepler University in Linz, Austria. Available online: http://www.jku.at/pfm (accessed on 20 November 2023).
- Chaudhuri, B.; Muzzio, F.J.; Tomassone, M.S. Modeling of heat transfer in granular flow in rotating vessels. Chem. Eng. Sci. 2006, 61, 6348–6360. [Google Scholar] [CrossRef]
- Department of Particulate Flow Modelling. LIGGGHTS Documentation, Release 21.11. Ph.D. Thesis, Johannes Kepler University Linz, Linz, Austria, 2022. [Google Scholar]
- Bouzennada, T.; Mechighel, F.; Filali, A.; Ghachem, K.; Kolsi, L. Numerical investigation of heat transfer and melting process in a PCM capsule: Effects of inner tube position and Stefan number. Case Stud. Therm. Eng. 2021, 27, 101306. [Google Scholar] [CrossRef]
- Xu, Z.X.; Zhang, C.X.; He, Z.X.; Wang, Q. Pyrolysis Characteristic and kinetics of Polyvinylidene fluoride with and without Pine Sawdust. J. Anal. Appl. Pyrolysis 2017, 123, 402–408. [Google Scholar] [CrossRef]
- Meireles, N. Separation of Anode from Cathode Material from End of Life Li-Ion Batteries (LIBs). Master’s Thesis, Luleå University of Technology, Luleå, Sweden, 2020. [Google Scholar]
- Schreiner, D.; Lindenblatt, J.; Daub, R.; Reinhart, G. Simulation of the Calendering Process of NMC–622 Cathodes for Lithium–Ion Batteries. Energy Technol. 2023, 11, 2200442. [Google Scholar] [CrossRef]
- Richter, F.; Kjelstrup, S.; Vie, P.J.; Burheim, O.S. Thermal conductivity and internal temperature profiles of Li-ion secondary batteries. J. Power Sources 2017, 359, 592–600. [Google Scholar] [CrossRef]
- Mohanty, D.; Hockaday, E.; Li, J.; Hensley, D.K.; Daniel, C.; Wood, D.L. Effect of electrode manufacturing defects on electrochemical performance of lithium-ion batteries: Cognizance of the battery failure sources. J. Power Sources 2016, 312, 70–79. [Google Scholar] [CrossRef]
- Ho, H.; Cheung, W.L.; Gibson, I. Effects of graphite powder on the laser sintering behaviour of polycarbonate. Rapid Prototyp. J. 2002, 8, 233–242. [Google Scholar] [CrossRef]
- Varma-Nair, M.; Wunderlich, B. Heat capacity and other thermodynamic properties of linear macromolecules X. Update of the ATHAS 1980 Data Bank. J. Phys. Chem. Ref. Data 1991, 20, 349–404. [Google Scholar] [CrossRef]
- Masoumi, M. Thermochemical and Electrochemical Investigations of Li(Ni,Mn,Co)O2 (NMC) as Positive Electrode Material for Lithium-Ion Batteries. Ph.D. Dissertation, Karlsruher Instituts für Technologie, Karlsruhe, Germany, 2019. [Google Scholar]
- Spencer, H.M. Empirical Heat Capacity Equations of Gases and Graphite. Ind. Eng. Chem. 1948, 40, 2152–2154. [Google Scholar] [CrossRef]
- Indolia, A.P.; Gaur, M.S. Investigation of structural and thermal characteristics of PVDF/ZnO nanocomposites. J. Therm. Anal. Calorim. 2013, 113, 821–830. [Google Scholar] [CrossRef]
- Sigma-Aldrich. Safety Data Sheet, Produktname: Poly(Vinylidene Fluoride), Produktnummer: 182702, CAS-Nr. 24937-79-9. 2021. Available online: https://www.vanderbilt.edu/vinse/facilities/safety_data_sheets/Poly_vinylidene_fluoride.pdf (accessed on 26 December 2023).
- Gotcu, P.; Pfleging, W.; Smyrek, P.; Seifert, H.J. Thermal behaviour of LixMeO2 (Me = Co or Ni + Mn + Co) cathode materials. Phys. Chem. Chem. Phys. PCCP 2017, 19, 11920–11930. [Google Scholar] [CrossRef] [PubMed]
- Adibekyan, A.; Kononogova, E.; Hameury, J.; Lauenstein, M.; Monte, C.; Hollandt, J. Emissivity measurements on reflective insulation materials. TM Tech. Mess. 2021, 88, 617–625. [Google Scholar] [CrossRef]
- Zimmermann, J.; Mansouri, S.; Nobis, C.; Irmer, M.; Beuermann, S.; Fischlschweiger, M. Influence of Molecular Characteristics and Size Effects in Polystyrene Pyrolysis. Chem. Ing. Tech. 2023, 95, 1339–1343. [Google Scholar] [CrossRef]


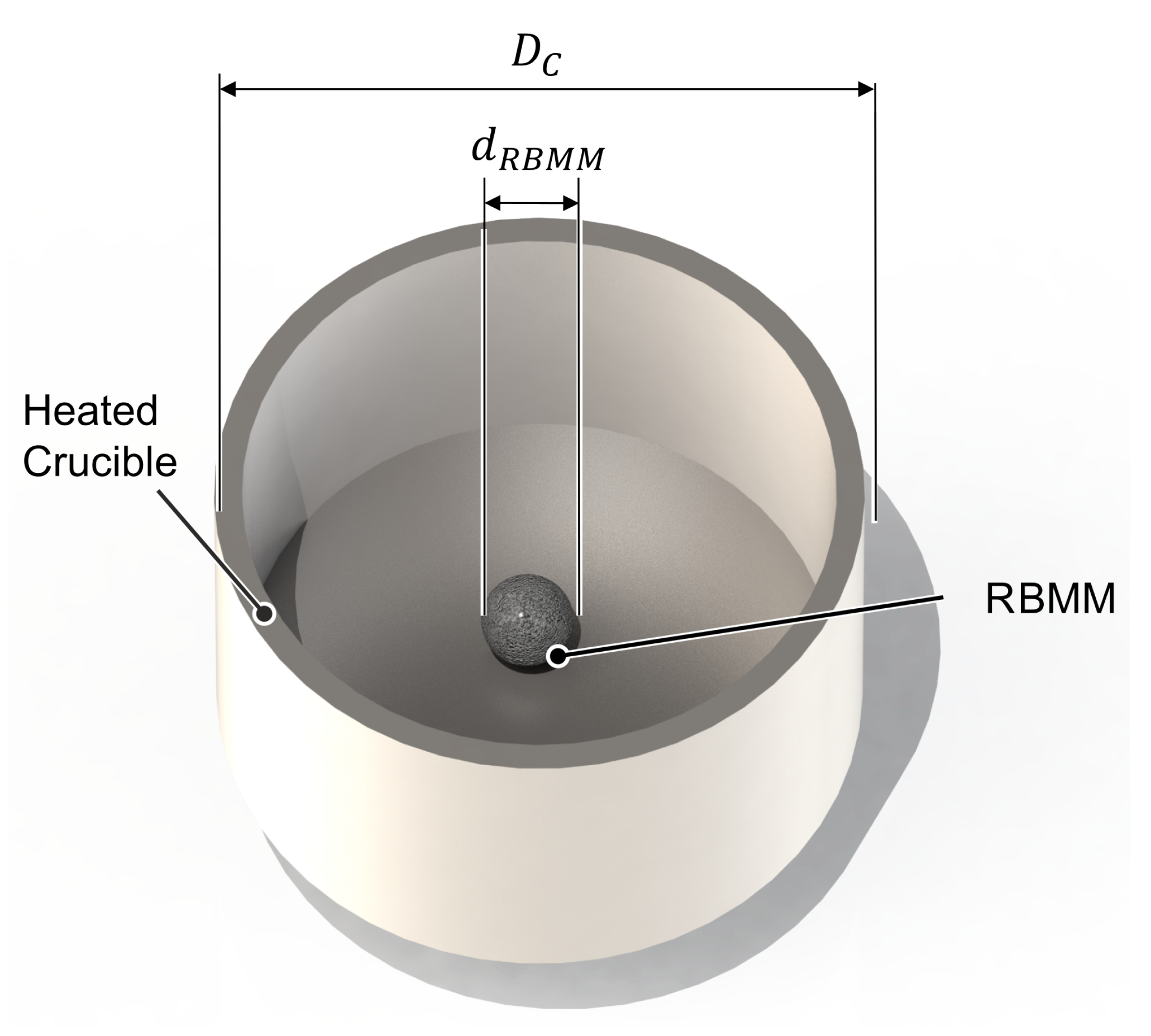
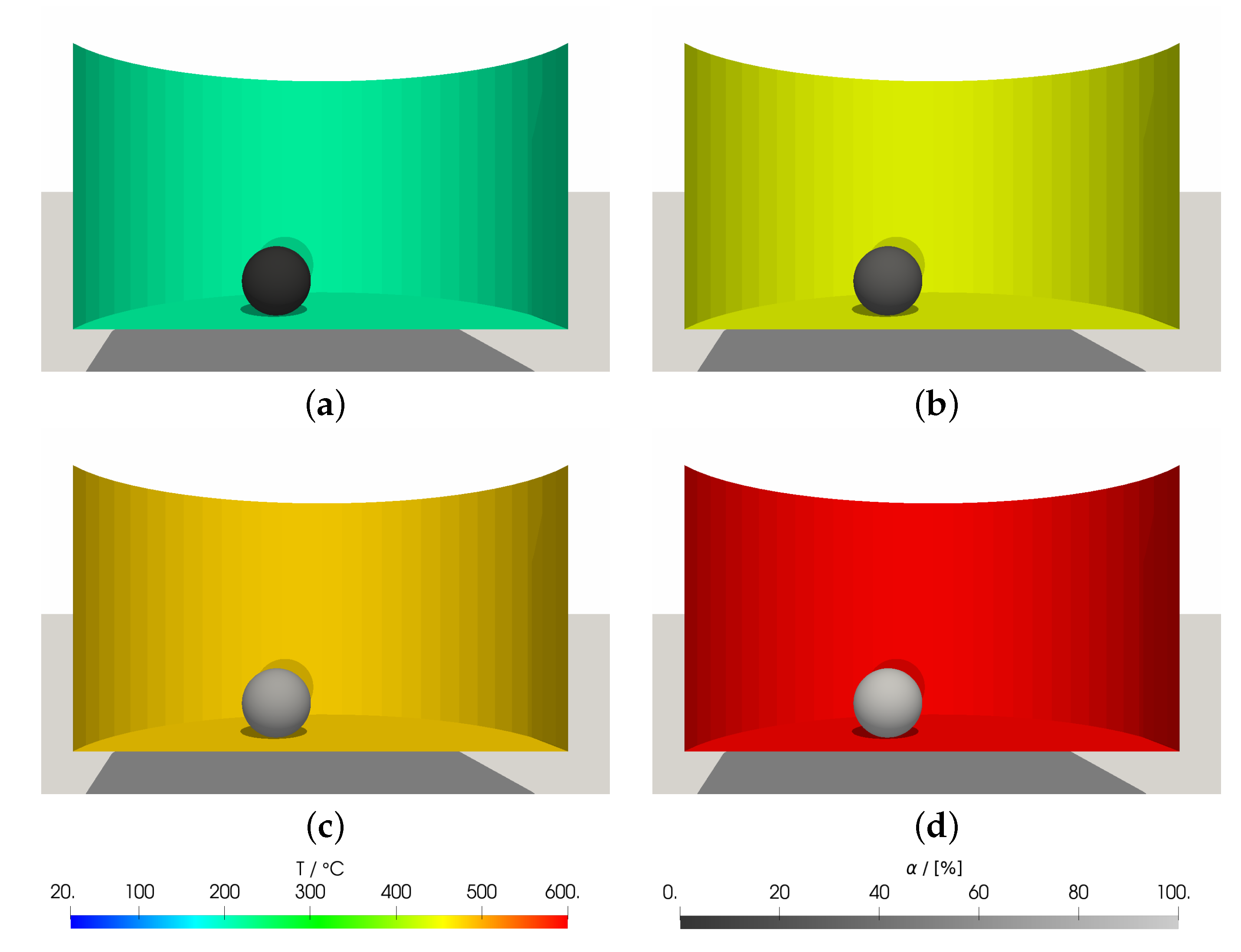
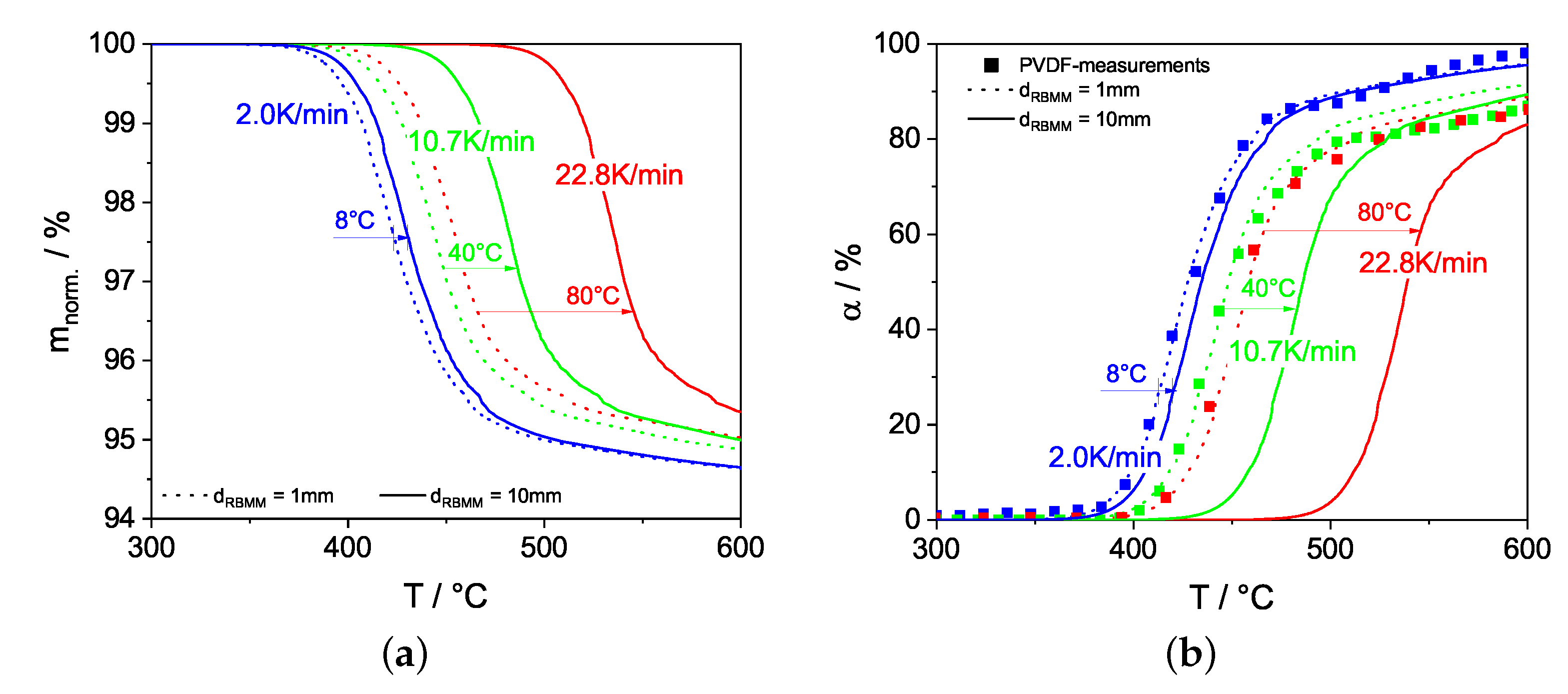
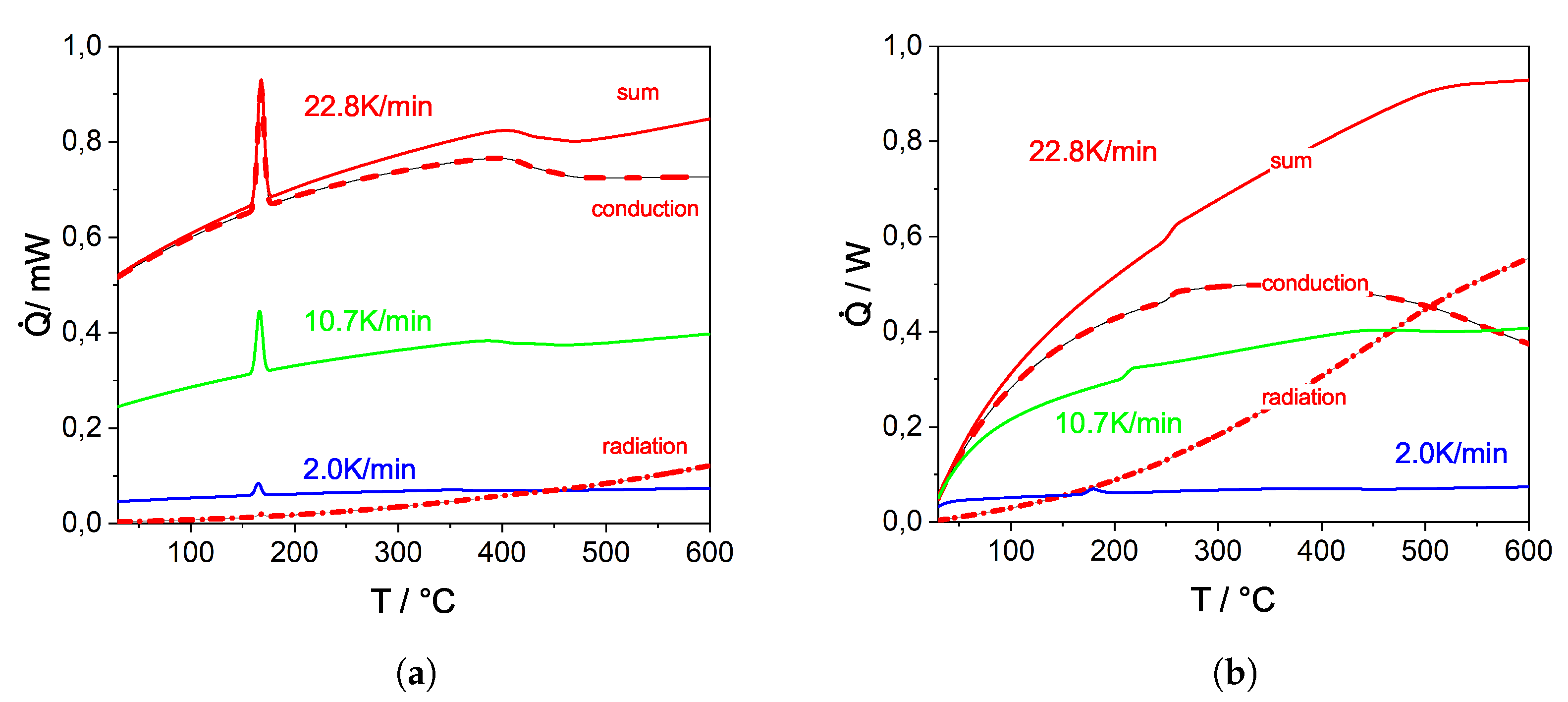
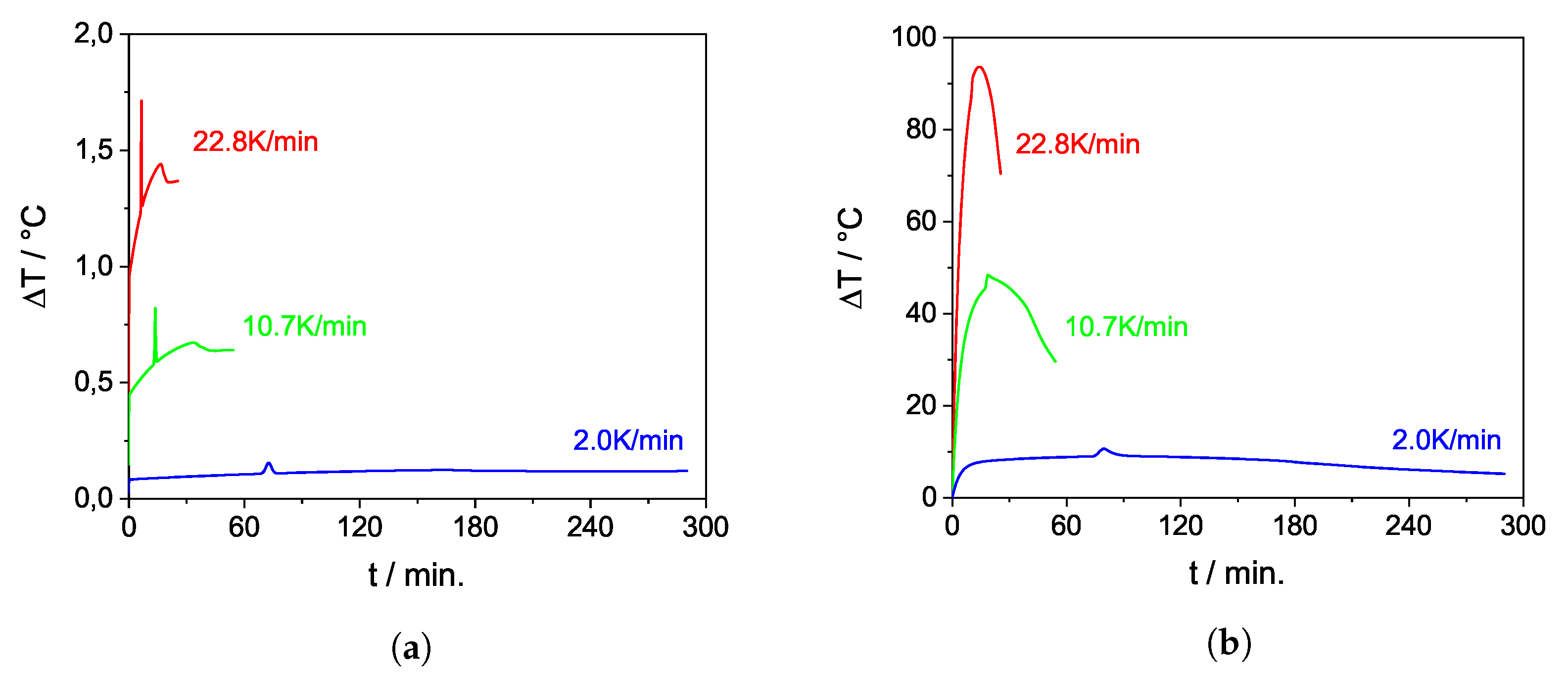
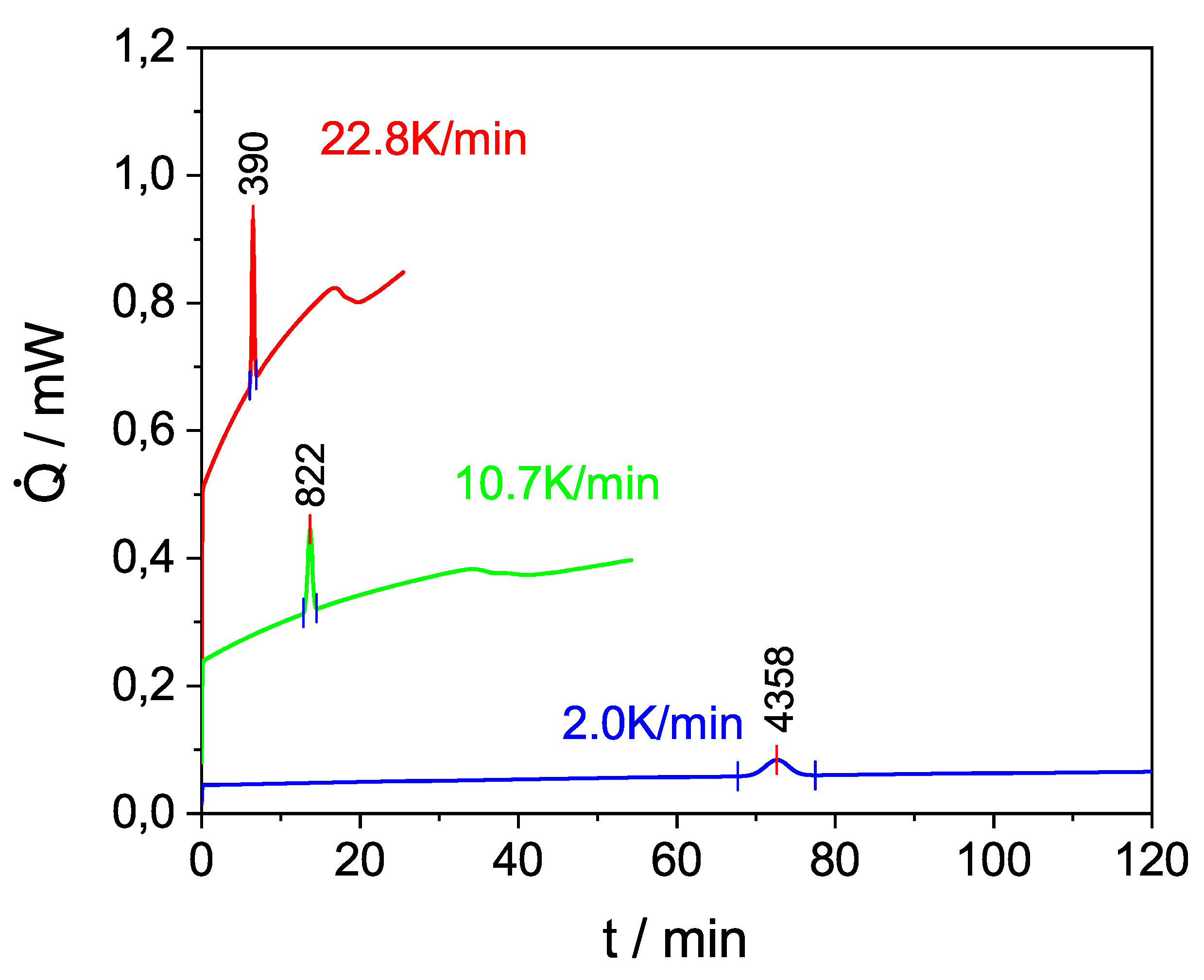

| Property | Value |
|---|---|
| formula | (C2H2F2)x- |
| ∼534,000 by GPC | |
| 1.74 g/mL at 25 °C | |
| 165 °C | |
| −38 °C | |
| >315 °C |
| Uniform RBMM Property | Symbol | |
|---|---|---|
| Variable | Temperature | |
| Extent of conversion | ||
| Parameter | Diameter | |
| Initial density | ||
| Initial mass | ||
| Current density | ||
| Effective heat transfer coefficient | ||
| Emissivity | ||
| Specific heat capacity | ||
| Activation energy | ||
| Pre-exponential factor | ||
| Reaction order | ||
| Final weight fraction |
| Component | Range Min.–Max./wt.% | Chosen Initial Composition for the sRBMM/wt.% |
|---|---|---|
| Binder | 6–10 | 8 (PVDF) |
| LMO | 49–53 | 51 (NMC) |
| Graphite | 41–42 | 41 |
| 30.0 | 3 | 10 | 328.621 | |
| 20 | 328.422 | |||
| 30 | 326.429 | |||
| 40 | 330.896 | |||
| 50 | 367.166 | |||
| 60 | 357.248 | |||
| 70 | 267.864 | |||
| 80 | 149.319 | |||
| 90 | 120.012 |
| Property | Value/Function | References | ||
|---|---|---|---|---|
| Diameter | mm | |||
| Density | 3200 kg/m3 | |||
| Density | 2260 kg/m3 | [36] | ||
| Density | 4740 kg/m3 | [37] | ||
| Porosity | 45% | [37] | ||
| Effective heat transfer | 0.30 W/(m.K) | [38] | ||
| Emissivity | 75% | [39,40] | ||
| Initial composition vector | PVDF: | 8 wt.% | Table 3 | |
| NMC: | 51 wt.% | |||
| Graphite: | 41 wt.% | |||
| Specific heat capacity | PVDF: | [41] | ||
| 5 °C to 330 °C | ||||
| NMC: | [42] | |||
| 40 °C to 750 °C | ||||
| Graphite: | [43] | |||
| 25 °C to 1200 °C | ||||
| Enthalpy of fusion | 40 kJ/kg | [44] | ||
| Melting temperature | 165 °C | [45] | ||
| Dirac Delta | 4 °C | |||
| Condition | Values | |||
|---|---|---|---|---|
| Variation | Diameter of RBMM particle: | mm | ||
| Heating rate | K/min | |||
| IC | Initial temperature | 20 °C | ||
| Initial content of conversion | 0% | |||
| Initial composition vector | Table 5 | |||
| Initial density | Table 5 | |||
| BC | Wall temperature | |||
| Final wall temperature | 600 °C | |||
| Time step | s | |||
| For = 2.0 K/min: | ∼290 min | |||
| Resulting simulation time | For = 10.7 K/min: | ∼55 min | ||
| For = 22.8 K/min: | ∼25 min | |||
| Considered effects | Degradation of binder | Table 4 | ||
| Radiation (wall–particle) | Table 5 | |||
| EHT | Table 5 | |||
Heating Rate/ K/min | Peak Temperature/ | Heat/ | Heat of Fusion/ | |||
|---|---|---|---|---|---|---|
| °C | mJ | kJ/kg | ||||
| 1 mm | 10 mm | 1 mm | 10 mm | 1 mm | 10 mm | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nobis, C.; Mancini, M.; Fischlschweiger, M. Modelling Binder Degradation in the Thermal Treatment of Spent Lithium-Ion Batteries by Coupling Discrete Element Method and Isoconversional Kinetics. Batteries 2024, 10, 63. https://doi.org/10.3390/batteries10020063
Nobis C, Mancini M, Fischlschweiger M. Modelling Binder Degradation in the Thermal Treatment of Spent Lithium-Ion Batteries by Coupling Discrete Element Method and Isoconversional Kinetics. Batteries. 2024; 10(2):63. https://doi.org/10.3390/batteries10020063
Chicago/Turabian StyleNobis, Christian, Marco Mancini, and Michael Fischlschweiger. 2024. "Modelling Binder Degradation in the Thermal Treatment of Spent Lithium-Ion Batteries by Coupling Discrete Element Method and Isoconversional Kinetics" Batteries 10, no. 2: 63. https://doi.org/10.3390/batteries10020063
APA StyleNobis, C., Mancini, M., & Fischlschweiger, M. (2024). Modelling Binder Degradation in the Thermal Treatment of Spent Lithium-Ion Batteries by Coupling Discrete Element Method and Isoconversional Kinetics. Batteries, 10(2), 63. https://doi.org/10.3390/batteries10020063