Abstract
In common irrigation systems, sprinklers are mounted with circular nozzles, but innovative noncircular nozzles can save water and energy by improving fragmentation in a low–intermediate pressure irrigation system. In order to investigate the effects of nozzle orifice shapes (circular, square, and equilateral triangular) on droplet characteristics, experiments using high-speed photography and water droplet spectrum measurement were performed. Using ImageJ to observe with the overlapped droplets and using the self-compiled programs of MATLAB to observe the morphology of droplets, we extracted the outlines of droplets. In addition, several empirical formulas for the prediction of droplets were obtained by way of a regression analysis of the experimental data. In particular, the shape coefficient of the nozzle orifice and the operating pressure of the nozzle were added to these formulas as variable factors to make them applicable to a variety of nozzles and working conditions. The results show that with the increase in shape coefficient, the jet atomization intensifies, and the droplets breaking from the jet will be dense and uniform. The velocity distribution of the droplets conforms to exponential functions (R2 > 0.7). The prediction formulas of diameter and kinetic energy were established with coefficients of determination exceeding 0.95. In low pressure conditions, the specific power multiplies at the end of spraying, and the maximum is proportional to the nozzle orifice coefficient. The impact-driven arm compensates for the disadvantage of the noncircular nozzles with the high irrigation-specific power, by producing a wider diameter gradient of droplets. Therefore, innovative sprinklers based on noncircular nozzles can be applied in a low–intermediate pressure system to increase water use efficiency, reduce energy consumption, and reduce costs.
1. Introduction
The precious resource of water is one of the most basic elements of agriculture. Given the challenges presented by global climate change and energy shortages, it is paramount to develop agricultural technology that will efficiently and effectively utilize irrigation water [1]. Greenhouse horticultural crops are highly efficient at applying irrigation water [2]. The water distribution uniformity significantly affects the growth, productivity, and quality of crops [3,4,5]. Irrigation efficiency is directly impacted by the spraying characteristics of sprinklers, which are an imperative component of the irrigation system. In agriculture irrigation, the spraying performance of a sprinkler is mainly influenced by the structure of the nozzle [6], operating pressure [7], and environmental conditions. The orifice shape of the nozzle has a significant influence on the characteristics of water droplets [8,9]. The noncircular nozzles are designed by changing the orifice shape to improve the spray performance of the nozzle in various applications [10,11]. Li et al. [6] demonstrated the advantages of noncircular nozzles in providing an acceptable water application pattern and fewer large droplets at low operating pressure. Axial switching in noncircular jets improves air entrainment, enhancing dispersion and fragmentation [12]. In other words, noncircular nozzles offer better atomization performance at the slight expense of irrigation range. Therefore, several commercial sprinkler products use noncircular nozzles to ensure acceptable spraying uniformity and reliable irrigation effectiveness in the irrigation of greenhouses, tea plantations, and lawns, which have a low standard for the range of sprinklers, but have high requirements for efficient irrigation uniformity [13], for example, the rotor sprinklers of Rain Bird Co. and the pop-up lawn sprinklers and buried rotary nozzles of Nielsen Irrigation Co., etc.
Spray conditions are essential factors for crop growth and field soil and water conservation; therefore, control of the droplet size and droplet distribution is necessary for the development of agricultural technology [14]. To produce the optimal sprinkler irrigation pattern, the diameter distribution of the droplets should be narrow. This will reduce the size difference between water droplets and make the droplets uniform in size. If the water droplets are too large, damage to the leaves of crops and runoff on the bare soil surface occurs [15]. On the other hand, too small droplets might evaporate and drift before reaching the soil surface because of environmental factors. This could result in the loss of irrigation water or environmental pollution [16].
The formation process of water droplets and distribution characteristics have been investigated intensively [17,18,19,20]. The droplet diameter distribution is mainly researched through experimental measurements. The droplet diameters have previously been measured by using flour pellets, oil immersion, and photographic methods [21]. However, for the measurement of high drop density fields, the overlapping and adhesion of water droplets directly affect the accuracy of measurements [22]. More recently, the rapid development of laser measurement technology has significantly improved measurement accuracy. Laser precipitation monitoring (LPM) and a two-dimensional video disdrometer (2DVD) can accurately measure the multidimensional droplet information, including the droplet diameter, droplet velocity, and landing angle. The jet property is the key factor affecting the prediction of droplet diameters [23]. Several prediction formulations of droplet size distribution have been proposed for different spraying cases, for example, the droplet distribution for impinging jets [24], droplet distribution for the jet form at spill set, and so on [25,26]. Based on these experimental data, droplet size distribution models, such as upper-limit distribution [27], exponential distribution, logarithmic distribution, general gamma distribution [28], and Gaussian distribution were proposed. The droplet size distribution is an important index to quantitatively express the hydraulic performance of the nozzle, which can reflect the water application pattern and even the evaporation drift loss in the spraying process [16]. At the same time, a suitable droplet size distribution formula is also a necessary condition for establishing an accurate spray prediction model. Friso et al. [29] proposed a mathematical model to obtain the droplet size spectrum from the water distribution radial curves. However, these functions or models are mainly aimed at nozzles with a circular orifice and are not applicable to noncircular nozzles. Therefore, it is necessary to investigate the influence of orifice shapes on droplet size distribution in agricultural irrigation sprinklers.
In order to study the influence of nozzle orifice shapes on the water droplet characteristics, three nozzles with different orifice shapes were designed and mounted on the self-designed uniform rotating sprinkler, and two types of experiments were carried out under low–intermediate pressure conditions. We analyzed the droplet diameter distribution characteristics qualitatively and quantitatively, including the distribution of droplet diameter, velocity, kinetic energy, and specific power. Based on the measured droplet spectrum, considering the factors of orifice shape coefficient and operating pressure, corresponding empirical formulas of the droplet distribution characteristics are proposed for noncircular nozzles. These formulas provide initial conditions for establishing a modified spraying model and provide a reference for the application of noncircular sprinklers in an irrigation system.
2. Materials and Methods
2.1. Experimental Setup
In order to investigate the nozzle orifice shape effects on the droplet characteristics, three nozzles with different orifice shapes (e.g., circular, square, and equilateral triangle) were designed according to the equal flow rate method [30]. Figure 1a presents the two-dimensional structure of the nozzle, where the De is the equivalent diameter of the nozzle orifice; the L denotes the length of the nozzle; the A is the orifice area of nozzle, and the X is the perimeter of the orifice. The specific values of the structural parameters are shown in Table 1. In order to research the relationship between orifice shape and spray performance quantitatively, a nozzle shape coefficient Cs was defined as [11]:
where the X is the wetted perimeter of the nozzle orifice, and the A is area of nozzle orifice.

Figure 1.
(a) The two-dimensional structure of the nozzles, (b) the noncircular nozzles, and (c) the self-designed rotating sprinkler device driven by a motor.

Table 1.
Nozzle dimensions and shape parameters of the nozzle orifice.
Figure 1b shows the processed nozzles. These nozzles were fabricated by three-dimensional printing with an accuracy of ±0.1 mm. During the experiments, we mounted these nozzles on a self-designed sprinkler, as shown in Figure 1c. It was refitted based on the PY15 impact sprinkler (Jinlong Spray Irrigation Co., Xinchang, Zhejiang, China). In order to investigate the effect of the orifice shape on spraying performance, we blocked the auxiliary nozzle and reverse fixed the drive arm during the experiment. To ensure the sprinkler rotates at a uniform speed when the driven arm is fixed, we designed a gear transmission device with 6.5 revolutions per minute. The gear was driven by a motor at a given rotation speed, which is controlled by a circuit board.
In this experiment, we installed the sprinkler on a vertical riser with a height of 1.6 m, and the elevation of the sprinkler is 23°. The operating pressure of the irrigation system ranges from 100 to 300 kPa, with 100 kPa intervals, which was monitored by a high-precision pressure gauge (YB-150, accuracy class 0.4, China Red Flag Instrument Co., Ltd., Shanghai, China).
2.2. Experimental Procedure
The experiments were carried out in the sprinkler irrigation laboratory of Jiangsu University, China, which provides an adequate windless test space. Figure 2 is the schematic sketch of the irrigation jet spraying system. After the water jet ejects from the nozzle, there are three states. At first, the jet maintains a stable and complete water column near the orifice. Then, liquid films and ligaments appear on the jet surface due to the shear instability of a Kelvin–Helmholtz and a Rayleigh–Taylor type [31]. Ultimately, the jet is completely broken into water droplets due to instability. In order to investigate the effects of the nozzle orifice shapes on the liquid jet break characteristics during the spraying process, two independent experiments were conducted. The first was a visualized experiment using high-speed photography technology, and the other was a quantitative measurement of water droplet parameters using a two-dimensional video disdrometer (2DVD, Joanneum Research Corp., Graz, Austria).
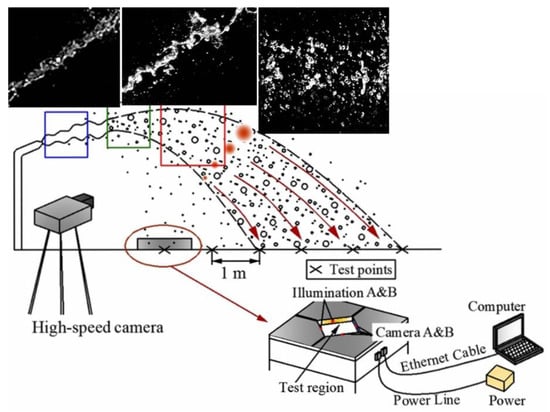
Figure 2.
Schematic diagram of the experiment system.
The visualization system consists of a Phantom Miro M310 camera fitted with a Tuli 100 mm macro lens mounted on a tripod, a 250 Watt custom light source with high brightness, and a black curtain providing a suitable background for shooting. The camera resolution was 1280 × 400 pixels, and the exposure time was 10 µs. The frame acquisition rate was set to 6500 frames per second (fps), and 500 images were obtained per trigger. Images were analyzed in the camera control software (Phantom, Vision Research Inc., Wayne, NJ, USA).
In order to obtain the quantitative parameter information of the sprayed droplets, the two-dimensional video disdrometer was placed along the radial line. The measuring positions were started at 2 m from the sprinkler and set at 1 m intervals along the radial spraying direction. The duration of measurements at each position was at least 3 min to ensure that the number of droplets was more than 500. Two CCD cameras inside the instrument made linear scans of the droplets passing through the test area (100 × 100 mm2) to monitor and record the diameter and velocity information of individual droplets [32]. The test accuracy of the droplet diameter was 0.19 mm, and the velocity accuracy was ±4%.
2.3. Calculation of Droplet Parameters
The water droplet performance parameters that were measured by 2DVD directly were the vertical (Vv, m s−1) and horizontal (Vh, m s−1) velocities and the diameter (d, mm). The relevant parameter calculation equations are as follows [15]:
- (1)
- The resultant velocity (V, m s−1) was calculated as follows:
- (2)
- The specific power Spj, W m−2) was defined as follows:
2.4. Image Processing
We developed an image processing code using commercial software, MATLAB R2020a (MathWorks. Inc., Natick, MA, USA), to obtain the contour lines of the droplet group from raw images of high-speed photography. The water droplets in the images are composed of pixels with different gray scale values, thus the binary image processing algorithm was used to standardize the pixel’s gray level and identify the droplets. Then, the canny edge detector, embedded in MATLAB, was employed to trace the droplet profile in the preprocessed images. The processing steps of high-speed photographic images are shown in Figure 3. In addition, in order to compare and analyze the results more intuitively, we used the Image J software to process the overlapping, adhesive, and irregular droplets in the photos into equivalent droplets with clear boundaries.

Figure 3.
(a) The raw image, (b) binary image, and (c) droplets profile extraction, water droplet identification process using MATLAB.
3. Results and Discussion
3.1. The Morphology of Droplet Break from Different Nozzles
The shape of the nozzle orifice has significant effects on the sprinkler spray characteristics. We took the shooting area of 125 mm × 88 mm in the complete fragmentation zone of 200 kPa as the sample. We used Image J software (1.8.0 National Institutes of Health) to deal with the droplets, segment the overlapped droplets, and recognize and extract the outline of a single droplet with a red curve. The pixel scale of each image is consistent at 4 pixels/mm. Figure 4 shows the morphological characteristics of the droplets in the spray zone. Firstly, the distance of initial complete fragmentation away from the sprinkler is directly proportional to the shape coefficient of the nozzle orifice. The position of complete jet fragmentation for the circular nozzle is 2 m from the nozzle orifice, 1.2 m for the square nozzle, and 1.1 m for the triangular nozzle. Secondly, the number of droplets increases when the orifice shape turns sharper. Counting the number of effective identified droplets from the pictures processed by Image J, the number of equivalent droplets from the triangular nozzle is around 185, and the number is 113 for the square nozzle and 60 for circular nozzle. On the other hand, from the extracted contour of the sprayed droplets, it is also obvious that the number of droplets is directly proportional to the shape coefficient of the nozzle orifice. In Figure 4, after the jet is completely broken, large liquid blocks and strips are the main components in the flow field of the circular jet, accompanied by some droplets separated from these blocks. In the flow field of a square jet, the proportion of large liquid blocks decreases, and the droplet number increases. In the flow field of a triangular jet, the droplets are the protagonist, and there are almost no large liquid blocks. Thirdly, the uniformity of droplet diameter is directly proportional to the shape coefficient of the nozzle orifice. With the increase in the shape coefficient of the nozzle orifice, the number of droplets increases, and the droplet group consists of denser droplets with uniform size. All these results indicated that the triangular nozzle has better atomization, which is manifested by smaller droplets, more droplets, and more uniform particle diameter distribution. According to the research of Hua et al. [12], the fact that noncircular nozzles have better atomization performance is related to the axis-switching phenomenon inside the liquid jet. Axis switching is defined as rotation of the cross-sectional shape of the jet due to its vortex motion [33], and it promotes better mixing and entrainment [34]. These are qualitative analyses on the influence of the shape coefficient of the nozzle orifice on the performance of the droplet. In order to illustrate the specific effects and influence mechanisms of the orifice shape on the sprayed droplets, a quantitative analysis was conducted below.

Figure 4.
The original picture, contour, and outline of droplets sprayed from nozzles with different orifice shapes under 200 kPa. (Circular nozzle, square nozzle, and triangular nozzle, from left to right).
3.2. Characteristics of Droplets Measured by 2DVD
3.2.1. Droplet Diameter
Figure 5 illustrates the distribution of droplet diameters along the spraying direction. For a given nozzle structure, the average diameter of the sprayed droplets increases with the decrease in pressure. For the same pressure condition, the distribution of water droplets by the square nozzle is similar to that of the circular nozzle; however, the size of the water droplets at a given position is much larger than that of the triangular nozzle. Overall, the droplet diameter increases exponentially with the distance from the sprinkler, which conforms to the exponential function. The results show that the basic structure of the functions is as follows:
where d denotes the diameter of a droplet; x presents the distance from the sprinkler, and A and B are fitting coefficients. The coefficients of exponential functions are presented in Table 2.
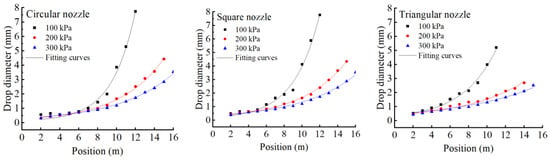
Figure 5.
The exponential relationship between droplet size and orifice shapes.

Table 2.
Exponential relationships between the droplet diameter and distance for different nozzles.
When the shape coefficient of the nozzle orifice Cs is a certain constant, the coefficients A and B increase with the increase in pressure. Positive correlations between pressure and coefficients A and B satisfy the exponential function as well. When the operation pressure of the sprinkler is constant, coefficients A and B increase exponentially with the increase in Cs. Therefore, considering the influence of the shape coefficient of the nozzle orifice and the operating pressure on droplet diameter, an empirical Equation (8) is proposed by fitting multiparameter data using Origin software. Equation (8) is the relationship between droplet diameter and landing position of the noncircular nozzle, and the expression is as follows:
where Cs is the shape coefficient of the nozzle orifice, and P is the operating pressure of the nozzle. R2 is the coefficient of determination, representing a precise fit between the observed data and the estimated values. For noncircular nozzles, this formula provides a prediction model of droplet spectrum information.
In addition to the specific value of the droplet diameter along the spraying direction, the evaluation indicators of droplet diameter distribution also include the distribution dispersion of droplet diameters [35]. According to the experimental data, Figure 6 presents the droplet distribution dispersion characteristics of sprayed droplets, which reveals additional information on the droplet diameter distribution. The volume percentage of the droplet diameter represents the proportion of the number of droplets with a certain diameter to the total number of droplets. The volume percentage curve of the droplet diameter conforms to the Gauss distribution, which is characterized by sharpness and steepness. The majority of the diameters are smaller than 1 mm, and the diameter of the largest number of droplets is 0.4 mm. Moreover, Figure 6 also shows that the cumulative volume distribution is in reasonable agreement with the Rosin–Rammler distribution, which is mathematically expressed as follows [36]:
where denotes the cumulative volume probability function of droplet diameters; denotes the characteristic size of droplets, namely the corresponding diameter when the cumulative percentage is 0.632, and n is a distribution width parameter, which is related to the nozzle type.
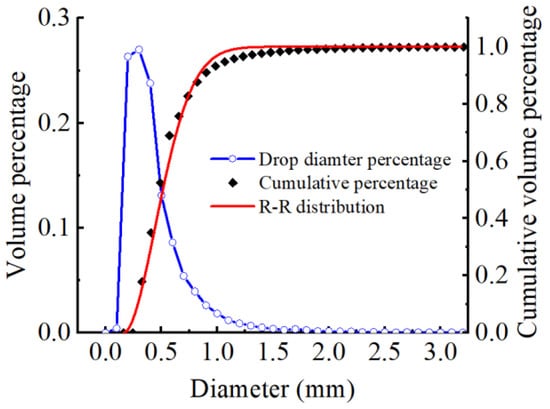
Figure 6.
Distribution characteristics of droplet diameter (Square nozzle with 200 kPa).
In order to obtain the distribution formula of the irrigated droplets, we fitted the droplet diameter in all the experimental conditions by using the Rosin–Rammler function. The specific parameters of n and are presented in Table 3, and all the values are over 0.98.

Table 3.
Rosin–Rammler parameters of the droplet size distribution for different nozzles.
In Table 3, we find that the value of is not only related to the orifice shape coefficient Cs, but also to the operating pressure P. When the shape coefficient is the same,is positively correlated with pressure P. When the pressure is the same,decreases first and then increases with the increases in shape coefficient. The distribution width parameter n represents the width of the droplet distribution. Larger n means a narrower distribution range of the diameters, i.e., a relatively uniform distribution with similar droplet sizes. Conversely, a smaller n indicates a spraying with insufficient fragmentation, where the droplets are of different sizes. The smaller droplets contribute less to the water application distribution. They are prone to evaporation and drift loss due to the influence of environmental winds. Moreover, the larger droplets have a greater impact on the kinetic energy, which has the potential to cause damage to crops and soil. Therefore, the hydraulic spraying performance of a sprinkler can be reflected by the parameter n. The mathematical expression of the parameter n is proportional to the shape coefficient as follows:
3.2.2. Droplet Velocity
The velocity of the sprayed droplets is calculated by Equation (2), and it is a key parameter and basis for calculating the kinetic energy distribution of the irrigation spraying. Figure 7 presents the relationship between the diameter and terminal velocity of droplets sprayed from different nozzle orifices. It can be seen that although the water droplets with the same diameter at different landing positions have different terminal velocities, in general, the droplet diameter is positively correlated with the velocity. In each specific experimental case, the terminal velocity of droplets generally increases with the droplet diameter. When the operating pressure of the nozzle increases, the maximum droplet size and landing velocity increase accordingly, which is reasonable from the perspective of energy conservation. In addition, the dispersion of velocity distribution produced by the circular nozzle is higher. Both the small droplet with high velocity and the large droplet with low velocity were collected in the test, and the relationship between the velocity and diameter of droplets that are produced by the noncircular nozzle is more strictly in line with the positive correlation. The orifice shape has an obvious influence on the velocity of large droplets near the soil surface. The droplets with diameters over 3 mm, which are sprayed from a triangular nozzle, have a much higher velocity than others. A higher velocity represents a higher kinetic energy, which indicates possible damage to crops and soil surface. In addition, the distribution of the droplet velocity for circular nozzles is more dispersed than that of the noncircular nozzles, which shows that the noncircular nozzles have better uniformity on the droplet performance.
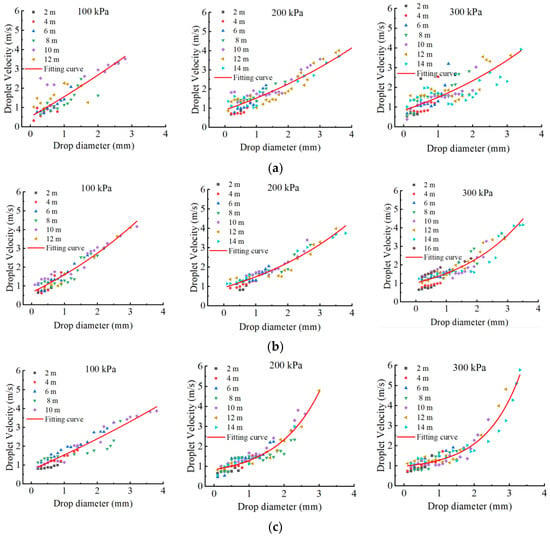
Figure 7.
Relationship between droplet size and velocity for different nozzles. (a) Circular orifice (b) square orifice, and (c) triangular orifice.
In order to obtain a reasonable fitting relationship between the droplet diameter and velocity, we used the exponential function as the fitting function. This allowed us to perform a regression analysis of the data. The fitting functions and corresponding coefficient of determination are shown in Table 4. The relation between the droplet diameter and velocity was previously derived using the logarithmic function [32,37]. Nevertheless, the logarithmic function did not fit very well with the data in our research. The possible reason is that the sprayed droplets in this body of literature are formed by impact structures. A batch of water droplets with small diameters and high velocities are dispersed from the jet by the impact structure. However, the impact-driven arm was removed in our research, and the droplets were broken from free water jet fragmentation. Therefore, the relationship between droplet diameter and velocity is different for the spraying jets based on the sprinkler structure.

Table 4.
Exponential relationships between the droplet diameter and velocity for different nozzles.
3.2.3. Kinetic Energy and Specific Power
The kinetic energy of water droplets reflects the effect of sprinkler irrigation on soil infiltration. Bautista-Capetillo et al. [38] presented an empirical logarithmic equation predicting drop velocity (near the soil surface) from drop diameter based on experiment results. The sprinkler kinetic energy per unit volume is calculated by Equation (4). Figure 8 shows the relationship between the kinetic energy from measured data and distances to the sprinkler. The calculated data were fitted by an exponential function. Similar to the diameter distribution function, the kinetic energy distribution relationship with the distance from the sprinkler is derived from Equation (11).
where is the kinetic energy of the droplets, and the x represents the distance from sprinkler, m. C and D are fitting coefficients. The coefficients and corresponding R2 are shown in Table 5. In order to predict the kinetic energy distribution of droplets sprayed from different nozzles and operating conditions, the shape coefficient of the nozzle orifice and operating pressure are considered in the predicting equation. The proposed equation is Equation (12).
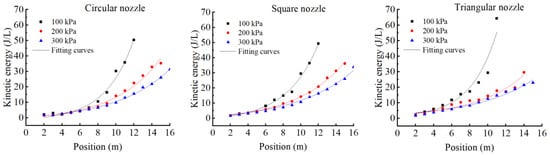
Figure 8.
Kinetic energy distribution and the corresponding fitting curves of three different nozzles.

Table 5.
The exponential relationships between the kinetic energy and distance for different nozzles.
Specific power (SP) is important to assess the effect of sprinkler irrigation on soil and plants. It has been related to the modification of the physical properties of the soil surface (e.g., soil loss due to erosion and reduction in the infiltration rate) [39]. The specific power also reflects the energy distribution of precipitation in a sprinkler irrigation system. The irrigation-specific power is calculated by Equation (3), which connected both with the water application pattern and droplet kinetic energy. Figure 9 illustrates the specific power of the sprinkler with different nozzle orifice shapes. Due to the fact that the sprinkler is rotated without an impact structure, the precipitation is concentrated at the end of the irrigation range. In addition, Figure 8 has already shown that the droplet kinetic energy increases along the spraying direction. Therefore, the distribution of specific power along the spraying direction is nonuniform, and at the end of the spraying range, it has a specific power peak value. When the operating pressure is 300 kPa, the SP distribution of different nozzles is similar. The largest SP is 0.016 W m−2 for the circular nozzle and 0.018 W m−2 for the square triangular nozzles. When the pressure was increased to 200 kPa, the SP maintained the same distribution characteristic. The largest SP is 0.026 W m−2 for the circular nozzle, 0.031 W m−2 for square nozzle, and 0.022 W m−2 for the triangular nozzle. Interestingly, when the operating pressure is down to 100 kPa, the peak of SP multiplies. The peak value of SP is 0.092 W m−2 for the circular nozzle, 0.0965 W m−2 for the square nozzle, and 0.167 W m−2 for triangular nozzle. These values are almost 4.6 to 8.4 times that at 300 kPa. Overall, the peak value of the specific power is both related to the nozzle orifice shape and operating pressure. The peak value increases with the increase in orifice shape coefficient and decreases with the increase in pressure. According to previous research, when the specific power is higher than 0.6 W m−2, the sprinkler irrigation is equivalent to the rainstorm level in natural precipitation, which is easy to induce surface runoff [38]. Since the triangular nozzle has the largest SP and the maximum is far below 0.6 W m−2, the noncircular shape nozzles is applicable for irrigation, even under low irrigation pressure.
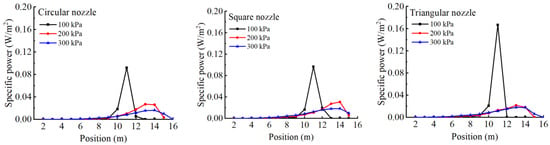
Figure 9.
The specific power distribution along the spraying direction of three nozzle orifice shapes.
3.3. Effects of the Impact Arm on Cumulative Volume Percentage of Droplet Diameters
Impact-driven arms are indispensable devices for mounting noncircular nozzles on real sprinkler products. Therefore, it is necessary to figure out whether the impact-driven arm has positive or negative effects on the sprayed droplet diameters. We tested the diameters of droplets produced by the commercial impact sprinkler (PY15, Jinlong Spray Irrigation Co., Xinchang, Zhejiang, China).
Figure 10 presents the cumulative volume percentage of the sprayed droplets from the sprinklers with and without an impact-driven structure. The results were calculated from the tested data at the given distances of 3, 6, and 9 m away from the sprinkler, with the operating pressure of 200 kPa. The changing trend of cumulative volume distribution curves is similar. In general, within the spraying area near the sprinkler, the droplets sprayed by the sprinkler with impact-driven arms have a bigger diameter. With impact effects of the driven arm, there is a wider range of raindrop spectrum, which means the changing gradient of droplet diameters is greater. It also indicates that the number of tiny droplets (d < 1 mm) decreases with the disperse effect of the impact arm. Moreover, the reduction of the number of tiny droplets is directly proportional to the distance from the sprinkler. The reasonable explain is that in the spraying area near the sprinkler, without impact actions, the spraying water maintains the state of free jet column. The tiny droplets collected in this region are breaks from the surface of the jet because of the shear action between ambient air and the water jet. With the dispersion effect of the impact arm, the water jet breaks into several water blocks; then, these liquid blocks break into droplets with big diameters and land on the spraying region near the sprinkler. Therefore, the droplet diameter measured with the impact structure is bigger than the free water jet.
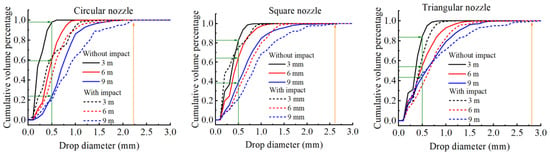
Figure 10.
Comparison between the designed sprinkler and impact-driven sprinkler by the cumulative volume percentage of droplets under 200 kPa.
For the impact-driven sprinkler, the orifice shape of the nozzle also has an influence on droplet diameter distribution. At the same testing location, the slope of the cumulative volume distribution curve decreases with the increase in the orifice shape coefficient. More tiny droplets with diameters smaller than 1 mm are collected in the spraying of circular nozzles than noncircular nozzles. For example, the cumulative volume percentage of droplets with a diameter of 0.5 mm is different under different conditions. In sprinklers without impact-driven structures, at 3 m away from the sprinkler, the proportion of droplets smaller than 0.5 mm sprayed by the noncircular nozzle is ~80%, while the proportion is close to 100% for the circular nozzle. At 9 mm away from the sprinkler, where the precipitation is the highest, the proportion of droplets smaller than 0.5 mm reaches 40% for the noncircular nozzle and only 20% for the circular nozzle. In addition, the shape of the nozzle orifice also affects the maximum droplet diameter. The maximum droplet diameter produced by the circular nozzle is 2.24 mm. The value increases to 2.54 mm for the square nozzle and to 2.76 mm for the triangular nozzle.
4. Conclusions
In this study, the effects the orifice shape has on the sprayed droplet characteristics of the sprinkler, including droplet diameter, velocity, kinetic energy distribution, and specific power distribution, are observed. Due to the noncircular orifice and the absence of an impact-driven arm, the droplet velocity distribution in our research conforms to the exponential function rather than the logarithmic distribution in previous research. The experimental data were used to establish the prediction formulas for droplet diameter and kinetic energy distribution, whose coefficient of determinations are both over 0.95. Particularly, orifice shape coefficient and operating pressure are the parameters in these formulas, so that they can also be applied to noncircular nozzles. At the same time, the effect of water dispersion structure on droplet diameter was also analyzed. The noncircular nozzle is found to have a better dispersion of droplet diameter distribution, allowing for a more optimal water application pattern. In the low–intermediate pressure irrigation system, although the droplets produced by orifices with large shape coefficients have a better diameter distribution, the kinetic energy distribution along the spraying direction is uneven. With lower pressure and a greater shape coefficient, the maximum specific power produced by sprinklers will be larger. The maximum specific power of a sprinkler at low pressure is several times that of medium pressure. This multiple increases with the increase in the shape coefficient of the nozzle orifice. The maximum multiple is 8.4 for the triangular nozzle. An auxiliary dispersion device, such as an impact-driven arm, will transform the sprayed droplet diameter distribution into a wide distribution, effectively compensating for the disadvantage of excessive high specific power at the end of the irrigation range for noncircular nozzles. Therefore, based on the goal of water and energy conservation, we recommend the use of noncircular nozzles in the low–intermediate pressure irrigation system, but an auxiliary water disperse structure is also needed. Additionally, since the water droplet spectrum in our research was obtained in a quiescent atmosphere, the effects of environmental factors on droplet distribution will be studied in the future.
Author Contributions
Formal experiments, L.H. and L.Q.; data analysis, L.H.; writing—original draft preparation, L.H.; writing—review and editing, Y.J. and H.L.; supervision, Y.J.; funding acquisition, H.L., Y.J. and L.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant numbers 51939005, 52009137, and 51809119; the Graduate Research and Innovation Projects of Jiangsu Province, grant number KYCX21_3345; Youth Talent Development Program of Jiangsu University, and the Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD).
Informed Consent Statement
Not applicable.
Acknowledgments
The authors are thankful to the editor and reviewers for their valuable comments in improving the quality of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lyle, W.M.; Bordovsky, J.P. Low Energy Precision Application (LEPA) Irrigation System. Trans. ASAE 1981, 24, 1241–1245. [Google Scholar] [CrossRef]
- Nikolaou, G.; Neocleous, D.; Katsoulas, N.; Kittas, C. Irrigation of greenhouse crops. Horticulturae 2019, 5, 7. [Google Scholar] [CrossRef]
- Contreras, J.I.; Baeza, R.; Alonso, F.; Cánovas, G.; Gavilán, P.; Lozano, D. Effect of distribution uniformity and fertigation volume on the bio-productivity of the greenhouse Zucchini crop. Water 2020, 12, 2183. [Google Scholar] [CrossRef]
- Salokhe, V.M.; Babel, M.S.; Tantau, H.J. Water requirement of drip irrigated tomatoes grown in greenhouse in tropical environment. Agric. Water Manag. 2005, 71, 225–242. [Google Scholar] [CrossRef]
- Guan, H.; Li, J.; Li, Y. Effects of drip system uniformity and irrigation amount on cotton yield and quality under arid conditions. Agric. Water Manag. 2013, 124, 37–51. [Google Scholar] [CrossRef]
- Li, J.; Kawano, H.; Yu, K. Droplet Size Distributions from Different Shaped Sprinkler Nozzles. Trans. ASAE 1994, 37, 1871–1878. [Google Scholar] [CrossRef]
- Cerruto, E.; Manetto, G.; Papa, R.; Longo, D. Modelling spray pressure effects on droplet size distribution from agricultural nozzles. Appl. Sci. 2021, 11, 9283. [Google Scholar] [CrossRef]
- Daskiran, C.; Xue, X.; Cui, F.; Katz, J.; Boufadel, M.C. Impact of a jet orifice on the hydrodynamics and the oil droplet size distribution. Int. J. Multiph. Flow 2022, 147, 103921. [Google Scholar] [CrossRef]
- Nuyttens, D.; Baetens, K.; De Schampheleire, M.; Sonck, B. Effect of nozzle type, size and pressure on spray droplet characteristics. Biosyst. Eng. 2007, 97, 333–345. [Google Scholar] [CrossRef]
- Barik, A.K.; Dash, S.K.; Guha, A. Entrainment of air into an infrared suppression (IRS) device using circular and non-circular multiple nozzles. Comput. Fluids 2015, 114, 26–38. [Google Scholar] [CrossRef]
- Li, J.; Kawano, H. Simulating Water-Drop Movement from Noncircular Sprinkler Nozzles. J. Irrig. Drain. Eng. 1995, 121, 152–158. [Google Scholar] [CrossRef]
- Hua, L.; Li, H.; Jiang, Y. Axis-switching Behavior of Liquid Jets Issued from Non-circular Nozzles under Low-intermediate Pressure. Appl. Eng. Agric. ASABE 2021, 37, 367–378. [Google Scholar] [CrossRef]
- Yan, H.; Hui, X.; Li, M.; Xu, Y. Development in sprinkler irrigation technology in China. Irrig. Drain. 2020, 69, 75–87. [Google Scholar] [CrossRef]
- Sayyadi, H.; Nazemi, A.H.; Sadraddini, A.A.; Delirhasannia, R. Characterising droplets and precipitation profiles of a fixed spray-plate sprinkler. Biosyst. Eng. 2014, 119, 13–24. [Google Scholar] [CrossRef]
- Yan, H.J.; Bai, G.; He, J.Q.; Lin, G. Influence of droplet kinetic energy flux density from fixed spray-plate sprinklers on soil infiltration, runoff and sediment yield. Biosyst. Eng. 2011, 110, 213–221. [Google Scholar] [CrossRef]
- Molle, B.; Tomas, S.; Hendawi, M.; Granier, J. Evaporation and wind drift losses during sprinkler irrigation influenced by droplet size distribution. Irrig. Drain. 2012, 61, 240–250. [Google Scholar] [CrossRef]
- Tuck, C.R.; Butler Ellis, M.C.; Miller, P.C.H. Techniques for measurement of droplet size and velocity distributions in agricultural sprays. Crop Prot. 1997, 16, 619–628. [Google Scholar] [CrossRef]
- Kumar, S.S.; Li, C.; Christen, C.E.; Hogan, C.J.; Fredericks, S.A.; Hong, J. Automated droplet size distribution measurements using digital inline holography. J. Aerosol Sci. 2019, 137, 105442. [Google Scholar] [CrossRef]
- Boddapati, V.; Manish, M.; Sahu, S. A novel approach for conditional measurement of droplet size distribution within droplet clusters in sprays. Exp. Fluids 2020, 61, 42. [Google Scholar] [CrossRef]
- Awan, M.S.; Leigeb, E. Modeling of fog droplet size distributions from infrared light attenuation measurements. Trans. Emerg. Telecommun. Technol. 2014, 25, 294–307. [Google Scholar] [CrossRef]
- De Cock, N.; Massinon, M.; Ouled Taleb Salah, S.; Mercatoris, B.C.N.; Lebeau, F. Droplet Size Distribution Measurements of Iso Nozzles by Shadowgraphy Method. Commun. Agric. Appl. Biol. Sci. 2015, 80, 295–301. [Google Scholar] [PubMed]
- Bocanegra Evans, H.; Dam, N.; Van Der Voort, D.; Bertens, G.; Van De Water, W. Measuring droplet size distributions from overlapping interferometric particle images. Rev. Sci. Instrum. 2015, 86, 023709. [Google Scholar] [CrossRef]
- Perlekar, P.; Biferale, L.; Sbragaglia, M.; Srivastava, S.; Toschi, F. Droplet size distribution in homogeneous isotropic turbulence. Phys. Fluids 2012, 24, 065101. [Google Scholar] [CrossRef]
- Couto, H.S.; Bastos-Netto, D. Modeling droplet size distribution from impinging jets. J. Franklin Inst. 1896, 141, 156. [Google Scholar] [CrossRef]
- Makhnenko, I.; Alonzi, E.R.; Fredericks, S.A.; Colby, C.M.; Dutcher, C.S. A review of liquid sheet breakup: Perspectives from agricultural sprays. J. Aerosol Sci. 2021, 157, 105805. [Google Scholar] [CrossRef]
- Pimentel, R.G.; Dechamplain, A.; Kretschmer, D.; Stowe, R.A.; Harris, P.G. Generalized formulation for droplet size distribution in a spray. In Proceedings of the 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Sacramento, CA, USA, 9–12 July 2006; Volume 7, pp. 5686–5696. [Google Scholar] [CrossRef]
- Roberts, J.H.; Webb, M.J. Measurement of droplet size for wide range particle distributions. AIAA J. 1964, 2, 583–585. [Google Scholar] [CrossRef]
- Emekwuru, N.G. Using the General Gamma Distribution to Represent the Droplet Size Distribution in a Spray Model. In Hydrodynamics-Theory and Model; IntechOpen: London, UK, 2012. [Google Scholar] [CrossRef][Green Version]
- Friso, D.; Bortolini, L. Numerical and volumetric frequency of sprinkler drop-size from water distribution radial curve part I: Mathematical modelling. ARPN J. Eng. Appl. Sci. 2017, 12, 3470–3477. [Google Scholar]
- Jiang, Y.; Li, H.; Hua, L.; Zhang, D.M.; Issaka, Z. Experimental Study on Jet Breakup Morphologies and Jet Characteristic Parameters of Non-circular Nozzles Under Low-intermediate Pressures. Appl. Eng. Agric. ASABE 2019, 35, 617–632. [Google Scholar] [CrossRef]
- Villermaux, E. Fragmentation. Annu. Rev. Fluid Mech. 2007, 39, 419–446. [Google Scholar] [CrossRef]
- Ge, M.; Wu, P.; Zhu, D.; Zhang, L. Analysis of kinetic energy distribution of big gun sprinkler applied to continuous moving hose-drawn traveler. Agric. Water Manag. 2018, 201, 118–132. [Google Scholar] [CrossRef]
- Chen, N.; Yu, H. Mechanism of axis switching in low aspect-ratio rectangular jets. Comput. Math. Appl. 2014, 67, 437–444. [Google Scholar] [CrossRef]
- Meslem, A.; El Hassan, M.; Nastase, I. Analysis of jet entrainment mechanism in the transitional regime by time-resolved PIV. J. Vis. 2011, 14, 41–52. [Google Scholar] [CrossRef]
- Gauno, M.H.; Larsen, C.C.; Vilhelmsen, T.; Moller-Sonnergaard, J.; Wittendorff, J.; Rantanen, J. Evaluation of droplet size distributions using univariate and multivariate approaches. Pharm. Dev. Technol. 2013, 18, 926–934. [Google Scholar] [CrossRef]
- Bailey, A.G.; Balachandran, W.; Williams, T.J. The rosin-rammler size distribution for liquid droplet ensembles. J. Aerosol Sci. 1983, 14, 39–46. [Google Scholar] [CrossRef]
- Chen, R.; Li, H.; Wang, J.; Guo, X. Effects of pressure and nozzle size on the spray characteristics of low-pressure rotating sprinklers. Water 2020, 12, 2904. [Google Scholar] [CrossRef]
- Bautista-Capetillo, C.; Zavala, M.; Playán, E. Kinetic energy in sprinkler irrigation: Different sources of drop diameter and velocity. Irrig. Sci. 2012, 30, 29–41. [Google Scholar] [CrossRef][Green Version]
- Kincaid, D.C. Spraydrop kinetic energy from irrigation sprinklers. Trans. Am. Soc. Agric. Eng. 1996, 39, 847–853. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).