Abstract
A pneumatic oscillating Chinese wolfberry harvester was designed to improve the efficiency of manual harvesting and minimize fruit damage by mechanical harvesting. The shedding model of Chinese wolfberry under pneumatic forces was established based on kinetic analysis, and the flow field characteristics were investigated using computational fluid dynamics (CFD). The position and shape of the fan outlet were determined by comparing the effects of a linear reduction outlet and a Laval reduction outlet on the outlet airflow rate. The size of the oscillating mechanism was optimized with nonlinear constraints to achieve uniform oscillation of the airflow. A three-factor, three-level orthogonal test was conducted on the NingQi 7 wolfberry variety. The flow rate at the outlet, the oscillation frequency, and the outlet distance were the test factors, and the net harvesting rate of ripe fruits, the harvesting rate of green fruits, and the damage rate of ripe fruits were the test indices. The results showed that the net harvesting rate of ripe fruits was 85.21% at an outlet distance of 10 cm, an outlet flow rate of 70 m·s−1, and an oscillation frequency of 2 Hz. This study provides references for the design of pneumatic harvesters for Chinese wolfberry.
1. Introduction
The production of Chinese wolfberry is a labor-intensive industry. Chinese wolfberry fruits are small, and multiple manual harvests are required during the harvesting season, resulting in the high cost of Chinese wolfberry production [1].
Robot picking platform is widely used in the automatic harvesting process of vegetables and fruits. With the help of visual sensors and image recognition technology, the picking robot can obtain various information such as the location and maturity of fruits. With the end-effectors such as air suction, bio-prosthetic hand, and scissors, the picking robot can quickly harvest many kinds of fruits. There is limited research on robot platforms for Lycium barbarum harvesting because of the mature fruit growing along with green fruit and flowers in soft branches at harvesting time. The fruit is also small and numerous. That made it difficult to identify the position of Chinese wolfberry fruit and low efficiency to grab every mature fruit. This makes it difficult for the robotic picking platform to harvest all the ripe fruit during the two to three-day ripening period.
At present, there are two main study directions on mechanical Chinese wolfberry harvesting: vibration harvesting and brush harvesting [2,3,4]. Vibratory harvesting can harvest the fruits of several adjacent branches simultaneously without identifying the location of the fruits, which is more efficient. But because Chinese wolfberry matures in batches, they are harvested every two weeks during the ripening period and more than 10 times throughout the season. Vibratory harvesting is achieved by striking the branches with the vibrating rod of the end effector of the picking machine so that the branches vibrate and the fruits of Chinese wolfberry fall off. In the process of flapping branches, branches are easily broken, and flowers and fruit fall off, which affects the yield of Lycium barbarum in the later period. The brush harvesting method uses friction between the fruit and the opposing rotating rollers, which are made of elastic materials such as silicone and do not damage the ripe fruit, to break off the fruit. The width between the two rollers is slightly smaller than the size of mature wolfberry and larger than the size of green fruit and flowers to avoid damage to green fruit and flowers. The brush picking machine is an auxiliary harvesting device. One hand is needed to hold the picking device while the other hand puts the branches into the rollers’ gap. Only one branch can be harvested at a time, and the picking efficiency is low.
Using positive or negative air pressure to harvest fruit is a low-loss method since the mechanical parts do not contact the branches or fruits. Airflow can act on multiple branches simultaneously to achieve efficient harvesting [5,6,7,8,9]. However, the air blow and air suction method requires large airflow and huge power, and a large amount of energy will be consumed in the process of harvesting. In the traditional Chinese wolfberry planting mode, the working space for picking machines is small, making it difficult for large fans to pass through. At the same time, it was difficult to obtain continuous and stable air pressure due to the pressure loss as the air moved through the pipe. The pneumatic oscillating harvester collected fruit by an inertial force, resulting in low air pressure and flow rate requirements. In the 1960s, pneumatic harvesting of plums, apples, and citrus was investigated. Specifically, most studies focused on citrus harvesting using oscillation and oscillating airflow [10,11,12,13,14,15,16]. Jutras et al. developed a high flow rate and high-velocity pneumatic oscillating citrus harvester. They investigated the effects of the oscillation frequency and air velocity on citrus’s net harvesting rate and leaf damage [11]. Whitney et al. analyzed the generation mechanisms of three oscillation airflow harvesters and found that the polarized disc oscillation increased the harvesting efficiency [12]. Nevertheless, the use of airflow oscillation for harvesting Chinese wolfberry has been rarely investigated.
The research objective of this paper is to explore the relationship between the parameters of the oscillatory flow and the harvest indexes of Lycium barbarum, to determine the effect of the pneumatic oscillating harvesting method in the harvest of Lycium barbarum, and to provide a theoretical basis for the high efficient and low loss harvesting of Lycium barbarum.
2. Structure and Working Principles
2.1. Structure
As shown in Figure 1, the proposed pneumatic oscillating Chinese wolfberry harvester consists of a support, an air source device, and an oscillating device. The support is used to support the oscillating device and the air source device. It can be attached to the ground and moved during harvesting. It is slightly larger than the diameter of the Chinese wolfberry canopy in the length direction so that the air source outlet can be aligned with the branches for harvesting. The air source device consists of an excitation motor, fan blade, fan cover, governor, worm housing, and fan outlet and provides high-velocity airflow. The oscillating device consists of a geared motor and a four-bar mechanism. It drives the air source device to oscillate around the hinge point at a specific frequency to produce oscillating airflow.
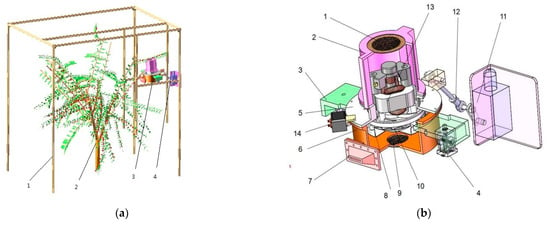
Figure 1.
Structure of the proposed pneumatic oscillating Chinese wolfberry harvester: (a) field view. 1. support 2. plant to be harvested 3. air source device 4. swing device; (b) cutaway view. 1. fan cooling filter 2. upper cover of fan 3. fixed plate of fan 4. hinge 5. lower cover of fan 6. worm shell 7. fan outlet 8. fan cover 9. air inlet filter 10. fan blade 11. gear motor 12. four-rod mechanism 13. excitation motor 14. governor.
2.2. Working Principles
The harvester faces the Chinese wolfberry plant in the row, and the branches to be harvested are placed into the flow field area in front of the outlet. The deceleration motor is initiated, and the crank rotation moves the air source device via the connecting rod. The air source device is hinged to the frame on both sides and can swing relative to the frame. The excitation motor drives the fan attached to the rotor shaft of the motor, causing an airflow. After leaving the edge of the impeller, the air flows out of the fan cover and moves along the inner surface of the worm shell, flowing out of the fan outlet. As the cross-section of the fan outlet decreases and the flow velocity increases, the air flows out of the fan from the outlet and into the external flow field after acceleration. Upon stabilization of the airflow, the velocity of the geared motor is set by the governor, and the air source device is driven by the four-rod mechanism to swing around the hinge point. The airflow moves forward in a wave-like pattern. The wave-like airflow breaks up after contacting the Chinese wolfberry, resulting in a vortex. Under the unsteady flow field, the Chinese wolfberry fruits are subjected to air drag, differential pressure, gravity, and inertia force. Once the external force exceeds the bonding force between the fruits and branches, the fruits are separated from the plant.
2.3. Kinetics of Chinese Wolfberry Fruit Stalk under Oscillating Airflows
Fruit shedding caused by an inertia force can be simplified into three cases. In the first case, the fruit is subjected to an external force along the long axis; the force gradually increases until shedding. The fruit sheds within one oscillation cycle, but a large external force is required. In the second case, the fruit swings several times relative to the branch before reaching the extreme bending stress. In the third case, the fruit undergoes high-frequency, low-amplitude oscillation to reach the fatigue limit, resulting in shedding. Pneumatic harvesting is characterized by a large working space and low energy density. Therefore, in pneumatic oscillating harvesting, the second and third cases are desirable for fruit-stalk separation, and the second case is preferable to maximize harvesting efficiency.
Due to fruit rotation relative to the stalks and the stalks swinging around the branches, the motion is simplified as a vibrating system with two degrees of freedom of rotation. The Chinese wolfberry fruit is subjected to gravity, air drag, and the binding force by the stalk during motion.
2.3.1. Air Drag
The drag generated by the oscillating airflow depends on the time and oscillating position of the fruit. The drag can be calculated by Equation (1):
where ρ is the air density (kg·m−3), v is the relative velocity of the fruit due to airflow (m·s−1), S(θ) is the projected area of the fruit in the direction of the incoming airflow (m), CD is the resistance coefficient, and ω is the angular frequency of the oscillating airflow.
The resistance coefficient is determined by the Reynolds number (Re):
where μ is the dynamic viscosity of the air (Pa-s), and l is the characteristic length (m).
For external flows, vr and l are typically the velocities of the incoming flow from the far front and the object’s length. For internal flows, vr and l are the average flow velocity in the channel and the diameter of the channel. In this study, the external flow was used. Hence, vr was 50 m·s−1, and the length and diameter of typical fruit were used. Thus, it was determined that Re = 3 × 104 (within the range of 700~2 × 105) and CD = 0.44.
Figure 2 shows the projected area of the fruit in the direction of the incoming flow; the Chinese wolfberry fruit is simplified as an ellipsoid, where the X-axis and Y-axis represent the horizontal and vertical directions, respectively. When the angle between the fruit and the vertical direction is θ, the projected area in the incoming flow direction can be calculated by:
where a is the length of the semi-major axis (m), and b is the semi-minor axis length (m).
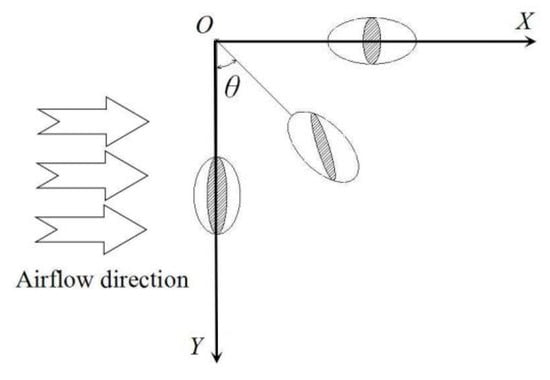
Figure 2.
Schematic of the Chinese wolfberry projection area at different oscillation positions.
The air drag can be calculated by:
2.3.2. Equation of Motion φ
Under oscillating airflow, the fluid force does negative work on the fruit, and its kinetic energy decreases when the oscillation angle exceeds 90°. According to the correlations of tangential acceleration and normal acceleration with the velocity during circular motion, the normal and tangential forces on the fruit during oscillation can be calculated as:
where l0 is the distance from the mass center of the fruit to the stalk-branch contact point (m), and m is the mass of the fruit (kg).
Since the normal and tangential forces on the fruit decrease with decreasing velocity, the fruit will shed as the oscillation angle increases from 0° to 90°. The equations of motion of the fruit under the excitation of the oscillating airflow were established based on aeroelasticity principles. The intrinsic frequency of the Chinese wolfberry fruit vibrating around the branch can be calculated as:
Similar to a natural gust [17], an oscillating airflow can be simplified as a continuous simple harmonic impulse excitation, and its dynamic response function is:
where A2 is the transition from a derivative function of the system to the impulsive excitation.
The analytical solution of the differential equation is the displacement response of the fruit at any moment:
where v is the peak oscillating air velocity, and t is the working period of the oscillating airflow.
The working period of the oscillating air velocity can be determined by:
According to Equation (6), θmax = π/2.
3. CFD Modeling and Flow Field Analysis
According to the above force analysis and model calculation and previous studies of airflow harvesting of citrus and olive, the range of the output air velocity of the fan should be slightly higher than the upper and lower limits of the effective air velocity. In this study, the range was 0–80 m·s−1. A small centrifugal fan (HLX-GS-A3BF501B, main parameters are shown in Table 1) was employed as the airflow source to obtain this air velocity and maintain reasonable mobility of the harvester.

Table 1.
Parameters of the small centrifugal fan.
The location of the fan outlet and the shape of the flow path were modeled in three dimensions and simulated numerically to ensure that the fan reached the required velocity range at the rated velocity and produced uniform velocity in the external flow field.
3.1. Development and Meshing of Flow Paths
A worm casing and an impeller model were created in 3D modeling software, and Boolean operations obtained the fluid solution domain. The outlets in the lower part (see Figure 3a) and on the symmetry plane of the impeller (see Figure 3b) were identified based on the fan’s outline. According to the flow characteristics of one-dimensional airflows, the velocities of compressible and incompressible gases increase as the cross-sectional area of the flow path decreases in the subsonic velocity range. Accordingly, a linear area reduction outlet (see Figure 3a) and a Laval nozzle (shrinkage section) outlet (according to Vitosinski’s formula, see Figure 3b) were designed.
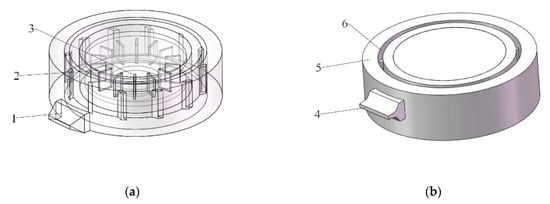
Figure 3.
3D model of the fan runner: (a) linear reduction outlet in the lower part. 1. linear area reduction outlet or Laval nozzle (shrinkage section) outlet in the lower part 2. impeller 3. inlet; (b) Laval outlet on the symmetric plane. 4. linear area reduction outlet or Laval nozzle (shrinkage section) outlet on the symmetric plane 5. passageway 6. worm casing.
An unstructured mesh was developed for the model to accommodate the complex surfaces near the Laval outlet and the blade. At the outlet, interface, and blade surface, the maximum mesh size was 0.002 m, and the growth rate of the mesh was 1.2. At the other locations, the mesh size was smaller than 0.005 m. In the Integrated Computer Engineering and Manufacturing Code for Computational Fluid Dynamics (ICEMCFD), the velocity inlet and pressure outlet were set as the boundary conditions. The intersection plane was set as the interface.
3.2. Model Solving and Flow Field Analysis
Most flows in mechanical and engineering applications of fluids are in a turbulent state. Direct numerical simulations and non-direct methods can calculate turbulence. Direct numerical simulation involves extensive calculations. The Reynolds averaging method (a non-direct method) has been widely applied in the industry because it considers the time-average and pulsation effects [18,19,20,21,22,23]. In this study, the standard k-ε model, which is widely used in engineering, was employed. According to the fan parameters and considering the effect of the load on the fan velocity, the rotation velocity of the blade and the rotating domain was set as 1047 rad·s−1, the inlet flow velocity was set as 20 m·s−1, and the outlet pressure was set as standard atmospheric pressure. The calculation was iterated for 1000 steps. The calculation was terminated when the residuals of the continuity equation, turbulent kinetic energy equation, and momentum conservation equation were below 10−3, and the outlet velocity was stabilized. The velocity distributions at the two outlets without area reduction flow paths are shown in Figure 4a,b, respectively.
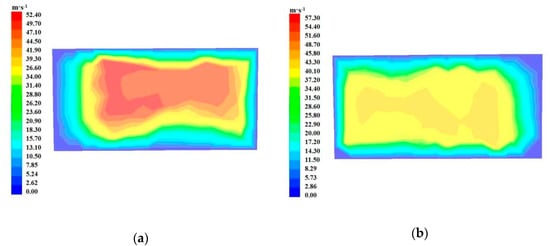
Figure 4.
Velocity cloud without area reduction outlet: (a) outlet in the lower part; (b) outlet on the symmetric plane.
As observed, the velocity distribution at the outlet in the lower part was highly uneven, ranging from 15.7 to 47.1 m·s−1. Sufficient, effective airflow was provided only in a small part near the center. As shown in Figure 4b, the velocity at the outlet on the symmetric plane consisted of three distinct layers: the velocity at the inner layer reached 43 m·s−1, the velocity at the middle layer was 37.2–40.1 m·s−1, and the velocity at the outer layer was 14.3–17.2 m·s−1. A large area had velocity values above 40 m·s−1 at the outlet on the symmetric plane. Considering the velocity decay in the external flow field, neither of the two non-reduction outlets met the flow velocity requirements for airflow oscillation harvesting.
Figure 5 shows the velocity distribution at the two outlets with different reduction flow paths. As observed, both the linear reduction outlet and the Laval outlet exhibited high proportions of high-velocity flows, relieving the attenuation effect of the airflow in the external flow field. A maximum velocity of 94.2 m·s−1 was achieved by the linear reduction outlet in the lower part, whereas the average velocity was less than 72 m·s−1 due to significant fluctuations. A slender high-velocity zone was also observed at the Laval outlet in the lower part, and the velocity decreased to 47.9 m·s−1 as the airflow moved toward the wall. As a result, the effective airflow was unsuitable for the oscillating system consisting of fruits and stalks because the fruits would swing into the low-velocity zone immediately upon contacting the high-velocity airflow. Large areas of high-velocity airflow were observed at both outlets on the symmetric plane, and the linear reduction outlet had a larger average velocity. This result may be attributed to the fact that the outlet length was only 15 mm, and the rapid size contraction in the front section of the Laval outlet led to a significant kinetic energy loss.
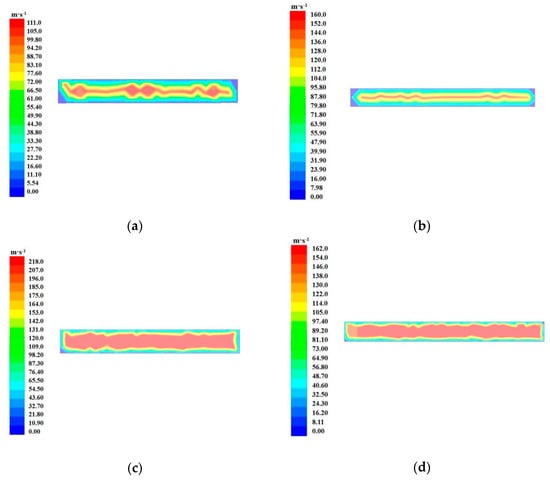
Figure 5.
Velocity clouds of the outlet at different positions: (a) linear reduction outlet in the lower part; (b) Laval outlet in the lower part; (c) linear reduction outlet on the symmetric plane; (d) Laval outlet on the symmetric plane.
In summary, the required range of flow velocities for the test could be achieved using a small centrifugal fan with an outlet on the symmetric plane. A uniform high-velocity flow can be achieved using a linear reduction outlet in cases of short outlet channels.
4. Optimized Design of the Oscillating Mechanism
A four-bar rotating mechanism was used, and the dimensions of each part were optimized separately to achieve periodic oscillation of airflow. During the harvesting of Chinese wolfberry by the proposed pneumatic oscillating harvester, the velocity ratio coefficient should be as close to 1 as possible. The polar angle (β) should be as close to 0° as possible for uniform airflow energy and good stability of the oscillating system. As shown in Figure 6, β and the length of the four poles (l1, l2, l3, l4) satisfy:
where l1 is the crank length (mm), l2 is the length of the connecting rod (mm), l3 is the length of the rocker rod (fan radius, mm), l4 is the length of the connecting frame rod (distance between the fan-frame hinge point and the crank-frame hinge point, mm), φ1 and φ2 are the angles between the crank and the frame (°) when the crank and connecting rod are collinear, and β is the polar angle (°).
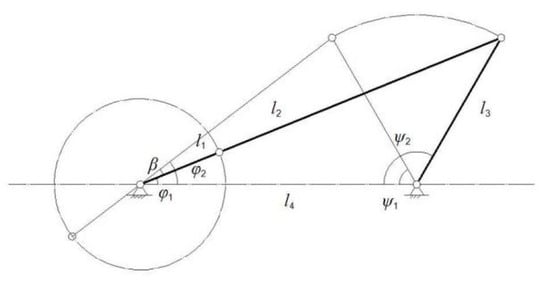
Figure 6.
Position of the maximum swing angle of the rocker.
With the crank as the active part, no dead point was involved. The design of the crank rocker mechanism has to satisfy the edge length condition specified by Grahoff’s theorem:
The rocker of the four-rod mechanism should be rigidly connected to the fan device. The rocker’s output torque should be greater than the load torque generated by the inertial force of the fan device, and the transmission angle (γ) should be no less than 40°. The dimensions of the four-rod mechanism shall satisfy:
Driven by the motor and hinged to the frame, the crank drives the fan via the connecting rod. The fan is hinged to the frame, and l3 should be larger than the fan’s radius (85 mm). l4 equals the distance from the crank-frame hinge point to the fan-frame hinge point. Since the fan has to ensure that the air flows up and down in a swing cycle, the swing angle of the rocker (i.e., fan) was set to 60°. According to the cosine theorem, the dimensions of the four rods shall satisfy:
where ψ1 and ψ2 are the angles (°) between the limit swing position of the rocker and the frame.
The minimum value of β was the objective function, and Equations (10)–(13) were used as the constraints. The optimization equations were established and solved using the nonlinear optimization solver in MATLAB [24,25]. The lengths of the different rods and their corresponding transmission angles were obtained. The velocity ratio coefficients (k) are listed in Table 2.

Table 2.
Optimization results of the four-bar mechanism.
5. Field Tests
5.1. Materials and Method
The experiment was conducted on a Chinese wolfberry farm in Ningxia, China. The wolfberry variety Ningqi 7 was selected for the test, as shown in Figure 7.

Figure 7.
Chinese wolfberry harvesting performance test: 1. Chinese wolfberry harvesting test platform. 2. electronic angle ruler. 3. fruit collection cloth.
We determined the effects of the operation parameters of the harvester on its harvesting efficiency to identify the optimum operating parameters. The oscillation frequency, air velocity, and the distance from the branch to the outlet of the fan (denoted as the outlet distance) were selected as the test factors. The net harvesting rate of ripe fruit (η1%), the damage rate of ripe fruit (η2%), and the harvesting rate of green fruits (η3%) were the test indices, which were calculated using an established method [12]. A three-factor, three-level orthogonal test was conducted using the L27 (313) orthogonal test table to investigate the influence of the factors. The harvesting efficiency and the suitable working range of the proposed harvester were investigated. First, the fan was turned on and adjusted to obtain the desired air velocity. Once the airflow was stabilized, the branches to be harvested were pulled into the flow field area. Each test lasted 20 s, and the average of three replicates was used as the result.
The oscillation frequency, air velocity, and outlet distance are listed in Table 3 [10,11,12,13,14].

Table 3.
Factors and levels of the orthogonal experiment.
5.2. Results and Discussion
Analysis of variance was performed on the test results as shown in Table 4 and Table 5, and the significance levels of the three indicator models were 0.000, 0.008, and 0.001, respectively. The results showed that the oscillation frequency significantly affected the net harvesting rate of ripe fruits but not on the harvesting rate of green fruits or the damage rates of ripe fruits. The air velocity had a significant effect on the net harvesting rate of ripe fruits and the damage rate of ripe fruits, but not on the harvesting rate of green fruits. The outlet distance had a significant effect on the net harvesting rate of ripe fruits but not on the harvesting rate of green fruits and the damage rate of ripe fruits. As observed, all three factors had no significant effects on the harvesting rate of green fruits. This result may be attributed to the strong binding force and the small cross-section of green fruits. Indeed, only a few green fruits fell off, and the total number of green fruits on the branches was low. Hence, the harvesting rate of green fruit varied substantially, and no apparent trend was observed.

Table 4.
Test arrangements and results.

Table 5.
Results of analysis of variance.
5.2.1. Effects of Oscillation Frequency on Different Parameters
As shown in Figure 8, the net harvesting rate of ripe fruits increased and then decreased as the oscillation frequency increased. The net harvesting rate was maximized (88.97%) when the oscillation frequency was 2 Hz. The likely reason is that fruit oscillation was intensified as the oscillation frequency increased. Meanwhile, the period of single airflow action decreased, and the oscillation amplitude of the fruit decreased. At an oscillation frequency of 3 Hz, the oscillation amplitude of some fruits decreased, and they did not reach the critical acceleration. Additionally, the variances of the harvesting rate of green fruits (5–10%) and the damage rate of ripe fruits (10–15%) as a function of the oscillation frequency were insignificant.
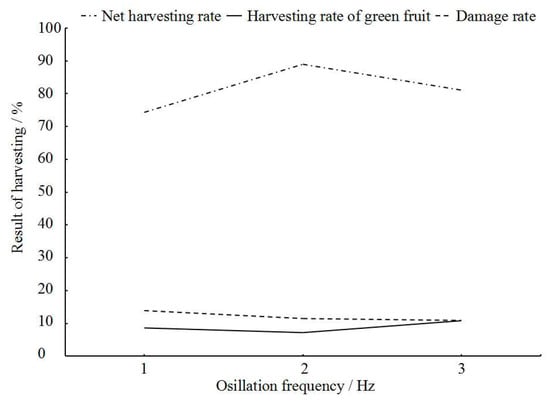
Figure 8.
Effects of oscillation frequency on different parameters.
5.2.2. Effects of Air Velocity on Different Parameters
As shown in Figure 9, as the air velocity increased, the net harvesting rate of ripe fruits increased, and the average net harvesting rate of ripe fruits was maximized (87.03%) when the air velocity reached 70 m·s−1. The average damage rate of ripe fruits decreased with increasing air velocity until it stabilized at 18%. The reason is that the increase in air velocity led to the increased kinetic energy of the fruits per unit time. As a result, more fruits were shed within certain oscillation cycles, and the cycles of oscillating airflow affecting the fruits were reduced. It was observed that fruit shedding could be achieved with fewer oscillation cycles as the airflow increased. This result is consistent with a previous study [13].
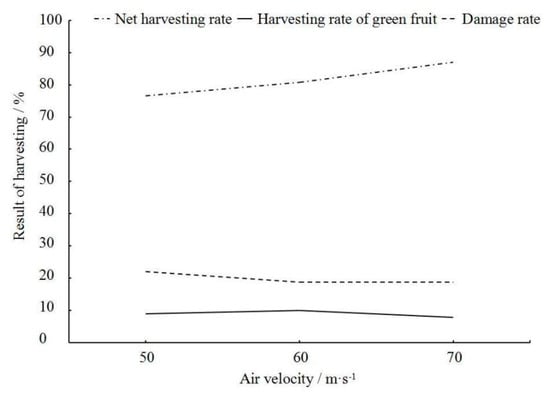
Figure 9.
Effects of air velocity on different parameters.
5.2.3. Effects of the Outlet Distance on Different Parameters
As the outlet distance increased from 5 to 15 cm, the average net harvesting rate of ripe fruits decreased from 87.88% to 85.21% and from 85.21% to 71.29%, as shown in Figure 10. This result may be attributed to the fact that the air velocity and the width of the high-velocity airflow varied slowly within 10 cm from the outlet when the outlet size was constant. When the outlet distance exceeded 10 cm, the air velocity decreased rapidly to the critical level of the effective velocity. Meanwhile, as the width of the high-velocity airflow decreased, the oscillation amplitude did not cover the entire branch. As a result, some fruits were outside the oscillating airflow during the entire process, and the net harvesting rate of ripe fruits decreased rapidly. The harvesting rate of green fruits varied insignificantly (11% to 7.36%). As the outlet distance increased, the damage rate of ripe fruits decreased from 18.58% to 18.47% and then increased rapidly to 22.26. This result may be attributed to the disturbance of the oscillating airflow within 5–10 cm of the outlet. The disturbance caused fruit shedding in relatively few oscillating cycles. Once the outlet distance exceeded 10 cm, the number of oscillating cycles required for fruit shedding increased substantially, and the surface of the ripe fruits was damaged by repeated collision.
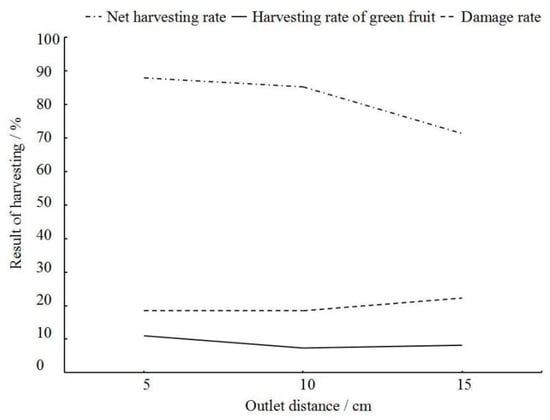
Figure 10.
Effects of outlet distance on different parameters.
In summary, the optimized oscillation frequency, air velocity, and outlet distance for the proposed pneumatic oscillating Chinese wolfberry harvester were 2 Hz, 70 m·s−1, and 10 cm, respectively. In this case, the net harvesting rate of ripe fruits exceeded 85.21%, the harvesting rate of green fruits was 7.76%, and the damage rate of ripe fruits was 18.64%.
6. Conclusions
In this study, Ningqi 7 was taken as the research object. A kinematic model of Chinese wolfberry under an unsteady flow field was established by force analysis and kinematic analysis of the stalk-fruit system. A kind of air oscillating Lycium barbarum picking machine was designed to provide a solution for Lycium barbarum harvesting with low loss.
One of the purposes of this study is to obtain high-speed airflow by using a small fan so that the picking machine can work in the narrow space of the Chinese wolfberry field. The simulation results and field experiments show that the air velocity and action range of the flow from the linear reduction outlet can meet the demand of the Lycium barbarum picking.
How to generate oscillating airflow is one of the difficulties in this study. Jutras et al. adopted a swing guide plate installed at the airflow outlet to adjust the airflow direction. Kokan’s blueberry picker has a rotor at the front of the airflow outlet with a rectangular through-hole that generates a pulse of air as the rotor rotates [26]. Both methods have a phase of blocking the airflow, reducing energy efficiency. Therefore, this study tried a new mode of generating oscillating airflow. The whole fan was installed on the oscillating mechanism to achieve uninterrupted oscillating airflow in the target area. However, this kind of oscillation mechanism has a large mass and large impact force at high frequency, so the test can only be carried out at a low range of frequency(1–3 Hz), which is the range of the first-order natural frequency of Chinese wolfberry plants.
The field harvest experiment showed that it was feasible to harvest Lycium barbarum with pneumatic oscillating, and the airflow speed and frequency had significant effects on Chinese wolfberry harvesting. A higher airflow velocity (70 m·s−1) combined with a suitable oscillation frequency (2 Hz) can achieve the shedding of mature Lycium berry in fewer oscillating cycles, reduce the shedding of green fruits, and avoid the production reduction in the subsequent harvest cycle.
Although the non-contact harvest of Lycium barbarum was realized by the pneumatic oscillating mode under a small power, the net harvesting rate was low, and the damage rate was high. This would not meet the demand of the Lycium barbarum industry for an efficient and low-loss harvest. Next, we will further study the harvesting rules of oscillating air at a higher natural frequency to realize the mechanized harvest of wolfberry and improve the working conditions of farmers.
Author Contributions
Conceptualization, Y.C. and J.C.; methodology, Y.C.; software, Y.C.; validation, Y.C., J.C. and J.Z.; investigation, Y.C., J.C., J.Z. and G.H.; writing—original draft preparation, Y.C.; writing—review and editing, Y.C., J.Z. and G.H.; funding acquisition, J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research and APC were funded by the National Key Research and Development Program of China, grant number 2018YFD0701102.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xu, C.; Liu, S.; Xu, R.; Chen, J.; Qiao, H.; Jin, H.; Lin, C.; Guo, K.; Cheng, H. Investigation of production status in major wolfberry producing areas of China and some suggestions. China J. Chin. Mater. Med. 2014, 39, 1979–1984. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, M.; Zhang, J.; Li, W. Design and experiment of vibrating wolfberry harvester. Trans. CSAM 2018, 49, 97–102. [Google Scholar]
- Chen, J.; Zhao, J.; Chen, Y.; Bu, L.; Hu, G.; Zhang, E. Design and parameters optimization experiment on vibrating and comb brushing harvester for Lycium barbarum. Trans. CSAM 2019, 50, 152–161. [Google Scholar] [CrossRef]
- Xu, L.; Chen, J.; Wu, G.; Yuan, Q.; Ma, S.; Yu, C.; Duan, Z.; Xing, J.; Liu, X. Design and operating parameter optimization of comb brush vibratory harvesting device for Wolfberry. Trans. CSAE 2018, 34, 75–82. [Google Scholar]
- Zhang, W.; Li, Z.; Tan, Y.; Li, W. Optimal design and experiment on variable pacing combing brush picking device for Lycium barbarum. Trans. CSAM 2018, 49, 83–90. [Google Scholar] [CrossRef]
- Lee, S.; Huh, Y.; So, J.; Maeng, S. Vibratory harvesting machine for boxthorn (Lycium Chinese Mill.) berries. Trans. ASABE 2003, 46, 211–221. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiao, H.; Ding, W.; Mei, S. Mechanism simulation analysis and prototype experiment of Lycium barbarum harvest by vibration mode. Trans. CSAE 2015, 31, 20–28. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, Y.; Wang, Y.; Chen, J. Experimental research on parameter optimization of portable vibrating and harvesting device of Chinese Wolfberry. J. Agric. Mech. Res. 2019, 41, 176–182. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Y.; Han, B.; Chen, J. Research on laws of wolfberry dropping based on high-speed camera. J. Agric. Mech. Res. 2018, 11, 166–170. [Google Scholar] [CrossRef]
- Brewer, H.; Fridley, R.; Adrian, P. Field tests show feasibility of blower-shaker for mechanical harvesting of prunes. Calif. Agric. 1961, 15, 5. [Google Scholar]
- Jutras, P.; Coppock, G.; Patterson, J. Harvesting citrus fruit with an oscillating air blast. Trans. ASAE 1963, 6, 192–194. [Google Scholar]
- Whitney, J.; Schultz, D. Analysis of air shaker principles to remove citrus fruit. Trans. ASAE 1975, 18, 1061–1064. [Google Scholar] [CrossRef]
- Berlage, A. Apple harvesting trials with oscillating air jets. Trans. ASAE 1973, 16, 460–461. [Google Scholar] [CrossRef]
- Whitney, J. Design and performance of an air shaker for citrus fruit removal. Trans. ASAE 1972, 10, 52–56. [Google Scholar] [CrossRef]
- Zhang, Z.; Heinemann, P.; Liu, J.; Baugher, T.; Schupp, J. The development of mechanical apple harvesting technology: A review. Trans. ASABE 2016, 59, 1165–1180. [Google Scholar] [CrossRef]
- Sanders, K. Orange harvesting systems review. Biosyst. Eng. 2005, 90, 115–125. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, F.; Wang, Y.; Ma, W. Test for aerodynamic characteristics of a circular cylinder in unsteady wind. J. Vib. Shock 2012, 31, 62–66. [Google Scholar] [CrossRef]
- Zhang, F.; Wei, X.; Chen, K.; Yuan, S.; Wang, Y.; Chen, H. Internal vortex characteristics of side channel pump with convex blade. Trans. CSAM 2020, 51, 115–122. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; Liu, L. Distribution mechanism of airflow in seed tube of different lengths in pneumatic seeder. Trans. CSAM 2020, 51, 55–64. [Google Scholar] [CrossRef]
- Chai, X.; Xu, L.; Sun, Y.; Liang, Z.; Lu, E.; Li, Y. Development of a cleaning fan for a rice combine harvester using computational fluid dynamics and response surface methodology to optimize outlet airflow distribution. Biosyst. Eng. 2020, 232–244. [Google Scholar] [CrossRef]
- Gao, X.; Xu, Y.; He, X.; Zhang, D.; Yang, L.; Cui, T. Design and experiment of diversion turbine of air-assisted high speed maize precision seed metering device. Trans. CSAM 2019, 50, 42–52. [Google Scholar] [CrossRef]
- Jiang, S.; Zhou, J.; Xu, L.; Lin, H.; Zhou, H.; Hou, X. Influence factors of working frequency of pulsed smoke fogger. Trans. CSAM 2019, 50, 85–91. [Google Scholar] [CrossRef]
- Li, H.; Wang, C.; Hu, J.; Yu, H.; Li, Q.; Zhang, X. Simulation and optimum design on airflow distribution chamber of pneumatic forming machine for rice seeding-growing tray. Trans. CSAM 2018, 49, 94–101. [Google Scholar] [CrossRef]
- Wang, M.; Liu, R.; Yang, S. Optimal synthesis of adjustable spherical four-bar mechanisms for function generation. Trans. CSAM 2012, 43, 208–212. [Google Scholar] [CrossRef]
- Liu, G. Optimization design of four bar mechanism based on the improved ant colony algorithm. Trans. CSAM 2006, 37, 149–151. [Google Scholar] [CrossRef]
- BSK. Obrenovac. Available online: www.bsk.rs (accessed on 19 July 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).