Abstract
Crop planning problems have been extensively studied from different perspectives (profit maximization, optimizing available water use, sustainability, etc.). In this paper, a new approach is proposed that considers new forms of customer-producer relationship, involving long-term cooperation agreements where the product volumes are agreed, and the demand is guaranteed in advance. In this context, typical of manufacturing production systems, crop planning must guarantee a given production level on specific dates, thus becoming deterministic in nature. In that context, this paper introduces a lexicographic biobjective optimization approach that, in addition to cost minimization, aims at minimizing the risk of not meeting the agreed demands. The latter is done by maximizing the geographic dispersion of the crops so that weather risk is mitigated. A number of experiments have been carried out to test the proposed approach, showing the high complexity of the solution and opening the door to new solution procedures for a problem that results from interest given to the new type of relationships in the food logistics chain.
1. Introduction
All activities related to agricultural planning are particularly important, given the basic nature of human needs that are fulfilled by their output. A good performance guarantees that all the needed products reach, in an efficient way, the population that requires them. One of the aspects involved, the management of the food supply chain, is especially complex, mainly when talking about perishable products. Thus, the traditional goal of making the products arrive on time to the correct customer must be fulfilled in addition to the specific quality required to avoid health problems, usually with long lead times under considerable uncertainties (volatile markets, weather risks affecting offers, etc.) and all these with small profit margins [1].
According to [2], decisions in agriculture planning cover four main functional areas: production (product selection, volume to be produced, sowing date, resources involved, irrigation, etc.); harvest (dates, tasks scheduling, resources used, etc.); storage (stocks, sales planning, etc.); and distribution (transportation mode, routing, etc.). In this paper, we will deal with the two first areas, in particular with crop planning and the decisions related to harvesting.
Crop planning involves decisions such as product selection and plot size and location, with the goal of maximizing the profits derived from those [3]. However, although easily stated, the problem is complex given the high number of factors that intervene (variety of products to select and their interactions, location alternatives, sociocultural aspects, resources availability, biological aspects of seeds and soil, market requirements…), the prices randomness, and the difficulty to include the crop succession requirements [4], in addition to other uncertainty characteristics of the agriculture business (weather, plagues, fires…). In fact, perishability and uncertainty are two main components in most of the papers dealing with crop planning [5].
Mixed-integer linear programming (MILP) has been the traditional modeling tool to deal with crop planning for many years. Thus, in their review, [1] cite some papers dated 1954. Most of the real problems modeled using Linear Programming (LP) usually consider maximizing profit as their objective function, with available land, workforce, machinery and watering as the production resources considered. However, when considering a more sustainable point of view, the problem becomes multiobjective [6], including additional objectives such as crop rotation, minimizing the use of inputs or working time to improve farmers’ quality of life, or minimizing weather risk.
However, the main difficulties of the problem (uncertainty, linear assumptions, large amount of necessary data) have given rise to a non-successful implementation in many cases [7]. For instance, yield and costs depend not only on some deterministic factors (soil characteristics, watering, seed quality) but also on other aspects related to risk management [8].
When dealing with risk in agriculture management, three main diversification strategies are considered [9]. The first one, product diversification, consists of sowing different products in the land available, reducing in that way the income variance by supplying different markets. This is a simple-to-implement strategy by any farmer just having enough know-how.
The second one (the strategy that we are considering here) is geographic diversification. It consists of planting a product in several, geographically separate plots, avoiding in that way the risks of localized storms or other local problems. Here the goal is to reduce the variance of the harvested crop, which requires the farmer to own several plots in different regions, something which is not always feasible. [10] mentioned that, in addition to this difficulty of land availability, it must be taken into account that production costs increase (transportation, workforce, supervision and, in general, harvest coordination). They conclude that this strategy is more suitable for the bigger farmers who do not need much machinery to be transported.
Finally, cultivar diversification takes into account the time factor, mixing the two previous strategies, thus obtaining both types of advantages. Thus, a product is sown in different regions in such a way that harvesting is done in different seasons, optimizing both the risk of harvest loss and the market price of the products.
While many papers have already considered the fulfilment of a given demand [11,12], in our context, we pursue not only to cover at least the supply orders as other authors did, but avoiding a surplus of production that would need to be discarded given the perishability of these commodities. In addition, to include in the approach the inherent risk of working with agriculture harvesting, we propose for the first time a geographic diversification strategy in the crop planning process, as a means to increase the odds of satisfying the demand.
As previously mentioned, over the years, MILP has proved to be a very flexible tool for modeling all the decision processes in manufacturing, but also in agricultural management. As soon as in 1997, ref. [13] used linear models for crop planning. More recently, many more applications have been published (see, for instance, [14]). Most of the dozens of models developed with that purpose have as their main objective cost minimization [15] taking into consideration factors such as the crop demand, cropping area available, labour costs, fertilizer costs, budget and other resource constraints. In some instances [16], the chemical as well as the physical soil properties are considered (pH, organic matter, permanent wilting point, etc.) in order to identify the best crop selection. In many other cases, water availability and its fair use has been an important issue to be considered as well [17,18]. Produce varieties, planting and harvest periods, and inventory and transportation, are factors to be considered in real planning [19]. Simulation is also used on many occasions to assess or find potentially good alternatives [20,21,22].
One of the characteristics that contributes to the difficulty of planning agricultural activities is the existence of different types of risk (weather, market, environmental, …) affecting the operations. Thus, among the stochastic factors making future crop profits uncertain are temperature or rainfall level, commodity selling price, seed costs, etc., since they affect the crop yield. In this environment with its lack of uncertainty, stochastic programming has been seen as an appropriate tool for many researchers [1]. Alternative scenarios, each with a given probability, can be defined for each potential outcome. In addition, fuzzy modeling has often been used [23,24].
However, as the world population grows and the global food demand increases, the requirements for a more efficient use of the land and farming resources are higher, in order to avoid the pollution and loss of diversity that a wild, intensive agriculture could generate. Sustainable agriculture is understood by [25] as economically viable and environmentally and socially fair. In their case, for instance, instead of cost minimization, a sustainability aspect such as the minimization of the surface area needed to cover crop demands is considered.
Therefore, in this paper, a biobjective optimization model that minimizes cost and maximizes geographic diversity (i.e., minimizes costs and risk of failure to fulfil the demand) is proposed. The main goal of this research is to introduce this new problem, identify its main characteristics, and explore the complexity of the problem in real settlements. Given the size of the problem for real farms, this paper represents a first approach to open the door to more usable solution techniques such as metaheuristics, when dealing with such environments. The structure of the paper is the following; in Section 2, a brief literature review on crop planning modeling is presented, including a section introducing the synchronized demand scenario, typically arising in customer–producer collaborative environments, which has motivated this research. Section 3 formulates the proposed biobjective optimization model, including a first example of how the model introduces a trade-off between cost and risk. Section 4 shows some evidence of the high complexity of the problem in a real setting, and our findings are summarized in Section 5.
2. Crop Planning Problem in Collaborative Environments
The concern about sustainability has made it necessary on many occasions to use multiobjective optimization methods when planning farming operations. Some of the best known methods for multiobjective optimization are ε-constraint (that computes optimal solutions scalarizing all but one objective function in the constraint set, see for example [26]), and goal programming (that defines goals to be fulfilled by the solution, being the objective to satisfy as much as possible those goals, see [27]). Thus, using the latter, ref. [28] defined three goals for the problem of crop planning at a national level: maximization of the return from cultivated land, minimization of the dependency on the import of cereal, and minimization of required investment. Many different combinations of objective functions have been considered but profit maximization and water requirement minimization are those most often considered together [29,30].
Given the high complexity of these optimization problems, it is not unusual that metaheuristics are used to find solutions within a reasonable period of time, mainly when dealing with realistic problems. Ref. [31] present a review of 50 papers, most of them case studies, concluding that the selection of one type of metaheuristic or another is more dependent on the expertise of the research team than on the problem characteristics. Regarding the type of metaheuristics, evolutionary algorithms are the most widely used solution method considered in crop planning [31].
Traditionally, farmers took decisions on their own, trying to guess, based on their experience, how markets would evolve and assessing the resources at their disposal. Once the crop was harvested, they took it to the market and looked for buyers who would pay for it an amount that was dependent on supply and demand.
This view of “two separate worlds” for producers and customers changed a long time ago in some industries (such as retail) because this type of relationship in the end harms both agents: producers risked not finding buyers or not receiving a good price for their crop, while customers risked not obtaining the products in the desired quantities or paying for them at unreasonable prices [32]. That is the reason behind the emergence in the last decades of different developments, such as Collaborative Planning, Forecasting and Replenishment (CPFR), Vendor Managed Inventory (VMI), etc. aimed at establishing and reinforcing a long-term relationship between suppliers and customers, thus enhancing the transparency of the supply chain and increasing the information available for planning and decision-making.
This type of long-term relationship can also be observed in agriculture. Thus, some big retailer chains (a well-known case is the Spanish retailer Mercadona, [33]) have long-term contracts with large farmers and agriculture companies, which, in exchange for guaranteeing an adequate (in terms of quantity, quality and timeliness) supply of products, receive stable and guaranteed demand and revenue levels. Note that the retailers can guarantee the demand level because they have a large amount of data that allow them to forecast the demand with considerable accuracy. Note also that normally the retailer chain demands exclusivity and penalty clauses from the supplier.
In this scenario, which we can call “synchronized demand”, crop planning does not involve selecting the product and the production levels but planning the operations so as to meet the demand of some predefined products, by obtaining, with as much certainty as possible, the given production volume in each period. Thus, decision variables involve when to sow each product, in which plot and when to harvest it. Note that, since the products are generally perishable (lettuce, tomatoes, etc.), sowing more than required is not convenient as the excess production would have to be discarded, which has economic and environmental (in addition to social) costs. Note also that these large agriculture companies have historical data about the yield of the different crops in the different plots under different cultivation practices, thus allowing them to accurately determine when, where, and how much to sow in order to obtain a given crop amount at a given date. This makes this version of crop planning a deterministic decision.
3. Modeling Crop Planning with Synchronized Demand
In this section, we will model the crop planning of a general company managing N farms. As shown in Figure 1, each farm Ff is divided into Kf plots, designated as UPfk. Unlike other authors (e.g., [16]) who consider same-size plots, we assume that the plots may have different sizes, especially those on the border of the farm, which tend to be smaller than the standard size. The distance Dff′ between any two farms is known. This information is necessary to compute transportation costs as well as geographic diversity of the crop plan.
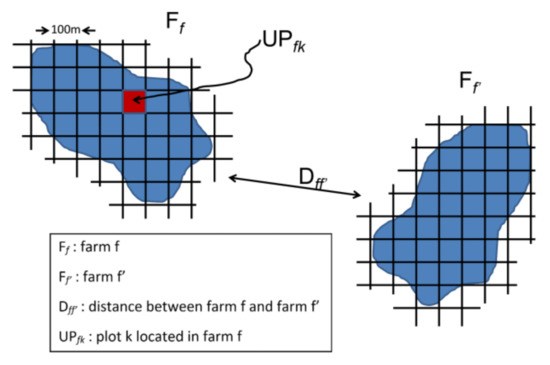
Figure 1.
Geographic distribution of two farms (Ff) and their plots (UPfk), with the notation used in the models.
There is a number P of agricultural products (indexed by index p). The demand for each product for the next T periods (e.g., weeks) is fixed and known. Let dps be the demand of product p in period s. Other data about the different plots (area, irrigation cost, crop growth and yield, etc.) are also available. In particular, as shown in Figure 2, let T(f,p,s,σ) be the yield of product p in farm f as a function of the sowing period s and the number of weeks σ passed after sowing (generally σ ≤ 15 for the types of products considered). These data are key in the decision process, since the growth rate is known for each crop and farm, crop planning becomes deterministic and the production volume obtained for each value of the sowing decision variables can be determined.
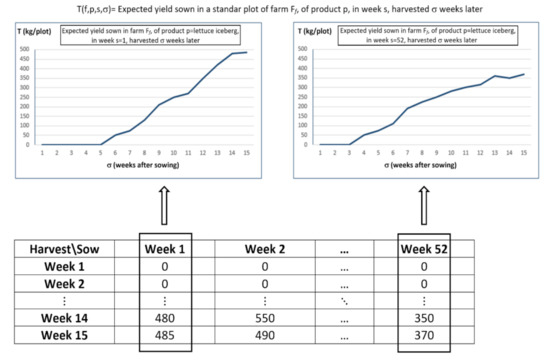
Figure 2.
Expected yield T(f,p,s,σ) in a standard sized plot in farm Ff, for a product p (lettuce Iceberg), sown in week s = 1…52 and harvested σ weeks later. The graph represents data corresponding to weeks 1 and 52.
The problem thus reduces the decision on what crop to sow in each plot in each period s of the planning horizon (the next T weeks) so that the amount harvested in each week is equal to the demand and therefore no waste is generated. This has to be done in a cost-effective way (main costs considered are harvesting and irrigation). In addition, it is desirable that the crops of each product be geographically dispersed so that weather-related problems in one area (storms, floods, hail, tornados, etc.) do not affect all the crop planted, thus reducing the risk of not meeting the amount of produce required in each period. Typical additional constraints for this problem include the infeasibility of planting certain products on certain plots (due to unavailability of irrigation, for example), or that in each period only one crop can be produced in each plot.
In Table 1, we summarize the notation:

Table 1.
Data and decision variables.
Regarding variables xpfksσ, note that σ is bounded in such a way that s + σ ≤ T (nothing can be planned to be harvested beyond the planning horizon), and therefore σ∈ {1, …, min{15,T − s}}.
The proposed optimization model seeks, in the first stage, to minimize operating costs, including the sum of irrigation, harvesting, and machinery costs:
Irrigation costs:
Harvesting costs: The cost of produce picking is proportional to the amount of each product harvested in each farm
Machinery costs:
As mentioned above, the second objective function to be taken into account in a lexicographic way consists of maximizing geographic diversification (with some limitations in the cost increasing). This is done by maximizing, in every period and for every product, the minimum sum Ω of the distances between those farms in which each product is growing in that period (which acts as a proxy of crop dispersion, i.e., risk mitigation).
Note that, by definition, Θpff′s= φpfs⋅φpf′s where φpfs = 1 ⇔ Σkypfks ≥ 1, which is forced by Equations (5)–(7):
Θpff′s ≤ φpfs ∀p,f,f′ ≠ f,s ∈ {0…T − 1}
Θpff′s ≤ φpf′s ∀p,f,f′ ≠ f,s ∈ {0…T − 1}
φpfs ≤ Σkypfks ∀p,f,s ∈ {0…T − 1}
Finally, in the second stage of this lexicographic optimization approach, we have to impose that the values of the cost objective function do not exceed a certain percentage (χ ≥ 1) above the minimal cost TC* obtained in the first stage:
As regards the constraints to be included in both stages:
Satisfying the demand
No more than one crop in any given plot at any period
At any period, the maximum fraction of a given plot that can be planted is unity
Product/plot feasibility
Machine availability (and evaluation of variables zfms for use in the objective function)
Initial conditions: The information on which plots are initially growing in each of the plots (with different harvesting dates) has to be taken into account, among other things to determine the effective demand.
Summing up the number of variables and constraints in the model, we see that, for stage 1, there are PFKT2 continuous variables and FT(PK + M) binary variables, adding further PFT(F + 1) binary variables for stage 2; regarding constraints, the total number is PT + FKT(T2P + P + 2) + MT(F + 1) for stage 1 and another PF(T + 2F) for stage 2. Just to have an idea of the size of the problem, having T = 24 weeks (6 months), P = 10 products, M = 3 machines, F = 5 farms with eight plots per farm, the number of variables in stage 1 is 230,400 continuous and 9960 binary, and a total of 5.5 million constraints.
4. Numerical Experiments and Discussion
4.1. Illustration
In order to illustrate the proposed approach, let us consider a situation involving F = 5 farms, each one divided into eight plots. Data were generated using parameters trying to imitate real environments, with a size able to solve using standard optimizers. The distance between two consecutive farms is 50 km (Dff′ = 50 × (f′ − f), for f′ > f). We have demand for P = 4 products following a uniform distribution during a planning horizon of T = 20 weeks, σ ≤ 15, involving three agricultural machines. Costs were generated using available data from real sources (for instance, irrigation cost CRfk was estimated using government published cost of 800 €/ha/year in the Spanish region of Castille-Leon). Other relevant parameters have been generated following the rational values (for instance, costs CTfp increase from 0.5 €/kg with distance, as well as the movement of machinery, with a minimum cost of movement of 2 €/km; etc.).
For solving the example for the first objective function (cost minimization), we have used both optimization software LINGO© v.17 and CPLEX© 12.8. in a processor Intel Core® i7-6500U, 2.50 GHz, 8 GB RAM. The best solution found has a total cost of 58,935 €. In our case, the most expensive component is the movement of physical resources to the different farms, the second one the irrigation and lastly the harvesting component. We note that, when evaluating for that solution, the value of the corresponding Ω results in a risky plan with Ω = 0 since, for one of the products, all its demand is served from a single farm.
Considering now the second objective (maximization of dispersion Ω for each product as the objective function), the maximum value that we could obtain without taking into consideration that the costs are Ω = 2000. That result is obtained when each product is sown using the most distant farms. Therefore, there is a range of feasible alternatives from the solution with minimum cost (and a high risk Ω = 0) to the solution with Ω = 2000 (and a higher cost). Thus, there should be a trade-off between both objectives: as the dispersion increases (i.e., the risk is smaller), the cost increases.
Figure 3 shows this trade-off as a function of the extra cost we are willing to incur, measured by the parameter χ (χ = 1.0; 1.025; 1.05; …). As can be observed, in this example, individual costs are not monotonic, with small variations as we allow higher total costs (Equation (8)). Finally, the maximum diversification is obtained after paying only an extra cost of 12.5% (total cost 66,273 €).
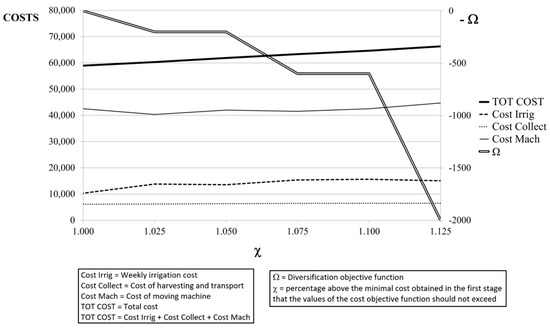
Figure 3.
Evolution of the diversification objective function (Ω), as costs are allowed to increase (controlled by parameter χ) above the minimum value.
4.2. Influence of Parameters in the Problem Complexity
As seen in the previous section, it is possible to trade-off cost increases for geographic diversification improvements (and hence risk reduction). However, the time needed for computation of the optimum solutions for models (1)–(15) becomes extremely large for non-trivial instances, given the number of variables and constraints involved as previously stated. Allegedly, it is not possible to solve optimally for real scenarios, in spite of the increasing importance of the real problem that we are introducing here.
We have performed some experiments to test what parameters have a higher influence in the difficulty of solving this problem. Bounding the computational time to 2 h, even for small instances, the optimization software is able to find only a solution that is in a percentage gap from the unknown optimal solution to the instance (in both cases, using Lingo© as well as CPLEX©). Table 2 shows the results of the gap using Lingo© when the values of some parameters affecting the size of the model double their value, compared with a baseline instance (T = 10, P = 4, F = 5, K = 8, M = 3, σ = 8).

Table 2.
Gap from the optimum solution found after two hours of computation, when the value of some parameters defining the instance doubles.
Results show that the number of products is the factor that makes it more difficult to approach the optimal solution, being the best solution found in the worst case 42% worse than the optimum. Note that the largest number of products planned (8 in our case) is in fact far from the real number of products a regular company could need to plan for (perhaps in the range of 30). On the other hand, the parameter that increases the difficulty of the problem to a lesser degree seems to be the number of periods in the planning horizon (with a gap of 25.61% for T = 20 after two hours of computation).
Figure 4 represents the difficulty of finding optimal solutions, even for instances of this small size, showing how in the previous experiments the gaps evolved with the computation times. In all cases, after 30 min, the search seems to be stagnant, making it clearer how, for a higher number of products, the evolution of the search results is more difficult.
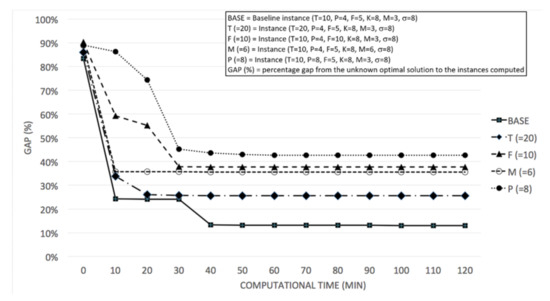
Figure 4.
Evolution of the gap in the two hours computation time for the different instances tested changing the value of one parameter. (Base configuration: T = 10; F = 5; M = 3; P = 4).
5. Conclusions
The relationship among different links in the agri-food supply chain is changing, with long-term agreements that force new planning procedures to fulfil the demand. In this paper, a new crop planning problem under fixed and known demand was defined, and modeled using a biobjective optimization approach that first minimizes cost and then, allowing for some cost increases, maximizes the geographic diversification of the crops to reduce local risks. This is the only way to keep the long-term agreements, since reliability in serving the promised quantities is a hard requirement from the retailers.
To cope with all the characteristics of the problem, the modeling needed was shown to be of a high complexity. In addition, new constraints could be found in real situations depending on the characteristics of the company. For instance, when different types of non-compatible products are sown (i.e., they must be planted apart in different plots), new parameters and constraints must be included in the model to avoid simultaneously the closeness between two of such products in adjacent plots. This implies an even higher complexity and number of variables to be considered in the model.
Therefore, it seems that, for real, very large instances, it is necessary to develop a more efficient metaheuristic solution method, given the inherent impracticalities in trying to solve the optimality of such instances. There is some expertise in the use of metaheuristics in agriculture (see review by [31]). In this case, given the number of variables and constraints involved, it looks as if the only possible methodology to cope with the complexity of the problem is the design of new ad hoc procedures to reach good solutions within a reasonable computation time.
Author Contributions
B.A.-D.: funding acquisition; conceptualization; methodology; writing and editing; G.V.: software; validation; formal analysis. All authors have read and agreed to the published version of the manuscript.
Funding
This research was carried out with the financial support of the Spanish Ministry of Science and the European Regional Development Fund (ERDF), grant DPI2017-85343-P.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Instances and data are available under request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lowe, T.J.; Preckel, P.V. Decision Technologies for Agribusiness Problems: A Brief Review of Selected Literature and a Call for Research. Manuf. Serv. Oper. Manag. 2004, 6, 201–208. [Google Scholar] [CrossRef]
- Ahumada, O.; Villalobos, J.R. Application of planning models in the agri-food supply chain: A review. Eur. J. Oper. Res. 2009, 196, 1–20. [Google Scholar] [CrossRef]
- Prišenk, J.; Vincec, J.; Pavic, L.; Rozman, C.; Turk, J.; Pažek, K. Cropping-Plan Optimization on Agricultural Holdings with a Combination of Linear and Weighted-goal Programming. Appl. Eng. Agric. 2019, 35, 109–116. [Google Scholar] [CrossRef]
- Janová, J. Crop planning optimization model: The validation and verification processes. Cent. Eur. J. Oper. Res. 2011, 20, 451–462. [Google Scholar] [CrossRef]
- Kusumastuti, R.D.; van Donk, D.P.; Teunter, R. Crop-related harvesting and processing planning: A review. Int. J. Prod. Econ. 2016, 174, 76–92. [Google Scholar] [CrossRef]
- Rădulescu, M.; Rădulescu, C.Z.; Zbăganu, G. A portfolio theory approach to crop planning under environmental constraints. Ann. Oper. Res. 2014, 219, 243–264. [Google Scholar] [CrossRef]
- Nevo, A.; Oad, R.; Podmore, T.H. An integrated expert system for optimal crop planning. Agric. Syst. 1994, 45, 73–92. [Google Scholar] [CrossRef]
- Sarker, R.; Talukdar, S.; Haque, A. Determination of optimum crop mix for crop cultivation in Bangladesh. Appl. Math. Model. 1997, 21, 621–632. [Google Scholar] [CrossRef]
- Tadesse, D.; Blank, S.C. Cultivar diversity: A neglected risk management strategy. J. Agric. Resour. Econ. 2003, 28, 217–232. [Google Scholar]
- Nartea, G.V.; Barry, P.J. Risk Efficiency and Cost Effects of Geographic Diversification. Rev. Agric. Econ. 1994, 16, 341–351. [Google Scholar] [CrossRef]
- Alfandari, L.; Lemalade, J.L.; Nagih, A.; Plateau, G. A MIP flow model for crop-rotation planning in a context of forest sustainable development. Ann. Oper. Res. 2011, 190, 149–164. [Google Scholar] [CrossRef]
- Santos, L.M.; Munari, P.; Costa, A.M.; Santos, R.H. A branch-price-and-cut method for the vegetable crop rotation scheduling problem with minimal plot sizes. Eur. J. Oper. Res. 2015, 245, 581–590. [Google Scholar] [CrossRef]
- McCarl, B.A.; Candler, W.V.; Doster, D.H.; Robbins, P.R. Experiences with Farmer Oriented Linear Programming for Crop Planning. Can. J. Agric. Econ. 1977, 25, 17–30. [Google Scholar] [CrossRef]
- Capitanescu, F.; Marvuglia, A.; Navarrete Gutiérrez, T.; Benetto, E. Multi-stage farm management optimization under environmental and crop rotation constraints. J. Clean. Prod. 2017, 147, 197–205. [Google Scholar] [CrossRef]
- Zhang, W.; Wilhelm, W.E. OR/MS decision support models for the specialty crops industry: A literature review. Ann. Oper. Res. 2011, 190, 131–148. [Google Scholar] [CrossRef]
- Cid-Garcia, N.M.; Bravo-Lozano, A.G.; Rios-Solis, Y. A crop planning and real-time irrigation method based on site-specific management zones and linear programming. Comput. Electron. Agric. 2014, 107, 20–28. [Google Scholar] [CrossRef]
- Chetty, S.; Adewumi, A.O. On the performance of new local search heuristics for annual crop planning: Case study of the Vaalharts irrigation scheme. J. Exp. Theor. Artif. Intell. 2014, 27, 159–179. [Google Scholar] [CrossRef]
- Montazar, A. A decision tool for optimal irrigated crop planning and water resources sustainability. J. Glob. Optim. 2011, 55, 641–654. [Google Scholar] [CrossRef]
- Rocco, C.D.; Morabito, R. Production and logistics planning in the tomato processing industry: A conceptual scheme and mathematical model. Comput. Electron. Agric. 2016, 127, 763–774. [Google Scholar] [CrossRef]
- Arunkumar, R.; Jothiprakash, V. Optimal crop plans for a multi-reservoir system having intra-basin water transfer using multi-objective evolutionary algorithms coupled with chaos. Comput. Electron. Agric. 2017, 140, 34–47. [Google Scholar] [CrossRef]
- Fazlali, A.; Shourian, M. A Demand Management Based Crop and Irrigation Planning Using the Simulation-Optimization Approach. Water Resour. Manag. 2017, 32, 67–81. [Google Scholar] [CrossRef]
- Liu, J.; Li, Y.P.; Huang, G.H.; Zhuang, X.W.; Fu, H.Y. Assessment of uncertainty effects on crop planning and irrigation water supply using a Monte Carlo simulation based dual-interval stochastic programming method. J. Clean. Prod. 2017, 149, 945–967. [Google Scholar] [CrossRef]
- Amini, A. Application of Fuzzy Multi-Objective Programming in Optimization of Crop Production Planning. Asian J. Agric. Res. 2015, 9, 208–222. [Google Scholar] [CrossRef][Green Version]
- Itoh, T.; Ishii, H.; Nanseki, T. A model of crop planning under uncertainty in agricultural management. Int. J. Prod. Econ. 2003, 81–82, 555–558. [Google Scholar] [CrossRef]
- Alfandari, L.; Plateau, A.; Schepler, X. A branch-and-price-and-cut approach for sustainable crop rotation planning. Eur. J. Oper. Res. 2015, 241, 872–879. [Google Scholar] [CrossRef]
- Sarker, R.; Ray, T. An improved evolutionary algorithm for solving multi-objective crop planning models. Comput. Electron. Agric. 2009, 68, 191–199. [Google Scholar] [CrossRef]
- Prišenk, J.; Turk, J.; Rozman, Č.; Borec, A.; Zrakić, M.; Pažek, K. Advantages of combining linear programming and weighted goal programming for agriculture application. Oper. Res. 2014, 14, 253–260. [Google Scholar] [CrossRef]
- Sarker, R.; Quaddus, M. Modelling a nationwide crop planning problem using a multiple criteria decision making tool. Comput. Ind. Eng. 2002, 42, 541–553. [Google Scholar] [CrossRef]
- Adeyemo, J.; Otieno, F. Differential evolution algorithm for solving multi-objective crop planning model. Agric. Water Manag. 2010, 97, 848–856. [Google Scholar] [CrossRef]
- Márquez, A.L.; Baños, R.; Gil, C.; Montoya, M.G.; Manzano-Agugliaro, F.; Gil Montoya, F. Multi-objective crop planning using pareto-based evolutionary algorithms. Agric. Econ. 2011, 42, 649–656. [Google Scholar] [CrossRef]
- Memmah, M.-M.; Lescourret, F.; Yao, X.; Lavigne, C. Metaheuristics for agricultural land use optimization. A review. Agron. Sustain. Dev. 2015, 35, 975–998. [Google Scholar] [CrossRef]
- Hammer, M.; Champy, J. Reengineering the Corporation: A Manifesto for Business Revolution; Harper Collins: New York, NY, USA, 1993. [Google Scholar]
- The Economist. 2 June 2011. Available online: http://www.economist.com/node/18775460 (accessed on 3 July 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).