Compositional Nutrient Diagnosis (CND) Applied to Grapevines Grown in Subtropical Climate Region
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Evaluations and Analyses
2.3. Calculations
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- AGRIANUAL. Anuário da Agricultura Brasileira, 23rd ed.; Agribusiness Intelligence: São Paulo, Brazil, 2019. [Google Scholar]
- Piccin, R.; Couto, R.D.R.; Bellinaso, R.J.S.; Gatiboni, L.C.; De Conti, L.; Rodrigues, L.A.T.; Michelon, L.S.; Kulmann, M.S.D.S.; Brunetto, G. Phosphorus forms in leaves and their relationships with must composition and yield in grapevines. Pesquisa Agropecuária Brasileira 2017, 52, 319–327. [Google Scholar] [CrossRef]
- Sparks, D.L.; Page, A.L.; Helmke, P.A.; Loepper, R.H. Methods of Soil Analysis, Part 3: Chemical Methods, 14th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2020; ISBN 0891188258. [Google Scholar]
- Dematte, J.A.; Dotto, A.C.; Bedin, L.G.; Sayão, V.M.; E Souza, A.B. Soil analytical quality control by traditional and spectroscopy techniques: Constructing the future of a hybrid laboratory for low environmental impact. Geoderma 2019, 337, 111–121. [Google Scholar] [CrossRef]
- Carranca, C.; Brunetto, G.; Tagliavini, M. Nitrogen nutrition of fruit trees to reconcile productivity and environmental concerns. Plants 2018, 7, 4. [Google Scholar] [CrossRef] [PubMed]
- Brunetto, G.; Ceretta, C.A.; Melo, G.W.B.; Girotto, E.; Ferreira, P.A.A.; Lourenzi, C.R.; Couto, R.D.R.; Tassinaria, A.; Hammerschmitt, R.K.; Da Silva, L.O.S.; et al. Contribution of nitrogen from urea applied at different rates and times on grapevine nutrition. Sci. Hortic. 2016, 207, 1–6. [Google Scholar] [CrossRef]
- Marschner, P. Marschner’s Mineral Nutrition of Higher Plants, 3rd ed.; Academic Press: London, UK, 2012; ISBN 9780123849052. [Google Scholar]
- Oliveira-Stefanello, L.; Schwalbert, R.; De-Conti, L.; Tassinari, A.; Paula-Garlet, L.; Lourenzi, C.R.; Comin, J.; Loss, A.; Schmitt, D.; Borghezan, M.; et al. Yield and must composition of ’Cabernet Sauvignon’ grapevines subjected to nitrogen application in soil with high organic matter content. Idesia (Arica) 2019, 37, 27–36. [Google Scholar] [CrossRef]
- Parent, L.; Dafir, M. A Theoretical concept of compositional nutrient diagnosis. J. Am. Soc. Hortic. Sci. 1992, 117, 239–242. [Google Scholar] [CrossRef]
- Egozcue, J.J.; Pawlowsky-Glahn, V. Groups of parts and their balances in compositional data analysis. Math. Geol. 2005, 37, 795–828. [Google Scholar] [CrossRef]
- García-Hernández, J.L.; Valdez-Cepeda, R.D.; Murillo-Amador, B.; Morales, F.A.B.; Ruiz-Espinoza, F.H.; Orona-Castillo, I.; Flores-Hernández, A.; Troyo-Diéguez, E. Preliminary compositional nutrient diagnosis norms in Aloe vera L. grown on calcareous soil in an arid environment. Environ. Exp. Bot. 2006, 58, 244–252. [Google Scholar] [CrossRef]
- Wadt, P.G.S.; Anghinoni, I.; Guindani, R.H.P.; De Lima, A.S.T.; Puga, A.P.; Da Silva, G.S.; Prado, R.D.M. Padrões nutricionais para lavouras arrozeiras irrigadas por inundação pelos métodos da CDN chance matemática. Revista Brasileira Ciência Solo 2013, 37, 145–156. [Google Scholar] [CrossRef]
- Urano, E.O.M.; Kurihara, C.H.; Maeda, S.; Vitorino, A.C.T.; Goncalves, M.C.; Marchetti, M.E. Soybean nutritional status evaluation. Pesquisa Agropecuaria Bresileira 2006, 4, 1421–1428. [Google Scholar] [CrossRef]
- Nowaki, R.H.D.; Parent, S.-É.; Filho, A.B.C.; Rozane, D.E.; Meneses, N.B.; Silva, J.A.D.S.D.; Natale, W.; Parent, L.E. Phosphorus over-fertilization and nutrient misbalance of irrigated tomato crops in brazil. Front. Plant Sci. 2017, 8, 825. [Google Scholar] [CrossRef] [PubMed]
- De Souza, H.A.; Vieira, P.F.D.M.J.; Rozane, D.E.; Sagrilo, E.; Leite, L.F.C.; Ferreira, A.C.M. Critical levels and sufficiency ranges for leaf nutrient diagnosis by two methods in soybean grown in the Northeast of Brazil. Revista Brasileira Ciência Solo 2020, 44. [Google Scholar] [CrossRef]
- Da Silva, G.G.C.; Neves, J.C.L.; Alvarez, V.H.; Leite, F.P. Nutritional diagnosis for eucalypt by DRIS, M-DRIS, and CND. Sci. Agricola 2004, 61, 507–515. [Google Scholar] [CrossRef]
- De Paula, B.V.; Arruda, W.S.; Parent, L.E.; De Araujo, E.F.; Brunetto, G. Nutrient diagnosis of Eucalyptus at the factor-specific level using machine learning and compositional methods. Plants 2020, 9, 1049. [Google Scholar] [CrossRef]
- Parent, S.-É.; Parent, L.E.; Rozane, D.E.; Natale, W. Plant ionome diagnosis using sound balances: Case study with mango (Mangifera indica). Front. Plant Sci. 2013, 4, 449. [Google Scholar] [CrossRef]
- Hernandes, A.; Parent, S.-É.; Natale, W.; Parent, L.E. Balancing guava nutrition with liming and fertilization. Rev. Bras. de Frutic. 2012, 34, 1224–1234. [Google Scholar] [CrossRef]
- Rozane, D.E.; Prado, R.D.M.; Natale, W.; Romualdo, L.M.; Franco, C.F. Caracterização biométrica e acúmulo de nutrientes em porta-enxertos de caramboleira cultivada em solução nutritiva. Revista Ciência Agronômica 2013, 44, 426–436. [Google Scholar] [CrossRef]
- De Oliveira, C.T.; Rozane, D.E.; De Amorim, D.A.; De Souza, H.A.; Fernandes, B.S.; Natale, W. Diagnosis of the nutritional status of ‘Paluma’ guava trees using leaf and flower analysis. Rev. Bras. Frutic. 2020, 42, 1–9. [Google Scholar] [CrossRef]
- Melo, G.; Rozane, D.; Brunetto, G. Identification of the critical levels, sufficiency ranges and potential response to nutrient fertilization in vineyards by the DRIS method. Acta Hortic. 2018, 423–430. [Google Scholar] [CrossRef]
- E Parent, L.; Natale, W.; Ziadi, N. Compositional nutrient diagnosis of corn using the Mahalanobis distance as nutrient imbalance index. Can. J. Soil Sci. 2009, 89, 383–390. [Google Scholar] [CrossRef]
- Parent, S.-É.; Parent, L.E.; Egozcue, J.J.; Rozane, D.E.; Hernandes, A.; Lapointe, L.; Gentile, V.H.; Naess, K.; Marchand, S.; Lafond, J.; et al. The plant ionome revisited by the nutrient balance concept. Front. Plant Sci. 2013, 4, 39. [Google Scholar] [CrossRef] [PubMed]
- CQFS-RS/SC. Manual de Calagem e Adubação do RS/SC; Comissão de Quimica e Fertilidade, 11th ed.; Comissão de Quimica e Fertilidade: Porto Alegre, Brazil, 2016. [Google Scholar]
- Tedesco, M.J.; Gianello, C.; Bissani, C.A.; Bohnen, H. Análises de Solo, Plantas e Outros Materiais; UFRGS: Porto Alegre, Brazil, 1995. [Google Scholar]
- Bremner, J.M.; Mulvaney, C.S. Nitrogen total in methods of soil analysis. In Methods of Soil Analysis, Part 2; Page, A.L., Miller, R.H., Keeney, D.R., Eds.; American Society of Agronomy: Madison, WI, USA, 1982; pp. 595–624. [Google Scholar]
- EMBRAPA. Manual de Análises Químicas de Solos, Plantas e Fertilizantes, 2nd ed.; Embrapa Informação Tecnológica: Brasilia, Brasisl, 2009. [Google Scholar]
- Isaac, R.A.; Kerber, J.D.; Walsh, L.M. Atomic Absorption and Flame Photometry: Techniques and Uses in Soil, Plant, and Water Analysis. In Pesticides in Soil and Water; Soil Science Society of America: Madison, WI, USA, 2015; pp. 17–37. [Google Scholar]
- Murphy, J.; Riley, J. A modified single solution method for the determination of phosphate in natural waters. Anal. Chim. Acta 1962, 27, 31–36. [Google Scholar] [CrossRef]
- Krug, F.J.; Mortatti, J.; Pessenda, L.; Zagatto, E.A.G.; Bergamin, H. Flow injection spectrophotometric determination of boron in plant material with azomethine-H. Anal. Chim. Acta 1981, 125, 29–35. [Google Scholar] [CrossRef]
- Gaines, T.P.; Mitchell, G.A. Boron determination in plant tissue by the azomethine H method. Commun. Soil Sci. Plant Anal. 1979, 10, 1099–1108. [Google Scholar] [CrossRef]
- Aitchison, J. The Statistical Analysis of Compositional Data. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 1982, 44, 139–160. [Google Scholar] [CrossRef]
- Aitchison, J. Principles of compositional data analysis. Inst. Math. Stat. Lect. Notes Monogr. Ser. 1994, 73–81. [Google Scholar] [CrossRef]
- Khiari, L.; Parent, L.-É.; Tremblay, N. Selecting the high-yield subpopulation for diagnosing nutrient imbalance in crops. Agron. J. 2001, 93, 802–808. [Google Scholar] [CrossRef]
- Hair, J.J.F.; Black, W.C.; Sant’Anna, A.S. Análise Multivariada De Dados, 6th ed.; Grupo A—Bookman: Porto Alegre, Brazil, 2005; ISBN 9788577805341. [Google Scholar]
- Kurihara, C.H.; Venegas, V.H.A.; Neves, J.C.L.; Novais, R.F.; Staut, L.A. Sufficiency range for nutrient concentration in cotton and soybean leaves, defined through DRIS indexes. Ceres 2013, 60. [Google Scholar] [CrossRef]
- De Souza, H.A.; Rozane, D.E.; Amorim, D.A.; Dias, M.J.T.; Modesto, V.C.; Natale, W. Assessment of nutritional status of guava seedlings using preliminary DRIS norms and sufficiency ranges. J. Plant Nutr. 2015, 38, 1611–1618. [Google Scholar] [CrossRef]
- Van Den Boogaart, K.; Tolosana, R.; Bren, M. “Compositions”: Compositional data analysis in R package. Comput. Geosci. 2013. [Google Scholar] [CrossRef]
- Rozane, D.E.; Mattos, D.; Parent, S.-É.; Natale, W.; Parent, L.É. Meta-analysis in the selection of groups in varieties of citrus. Commun. Soil Sci. Plant Anal. 2015, 46, 1948–1959. [Google Scholar] [CrossRef]
- Brunetto, G.; Ernani, P.; Melo, G.W.B.; Nava, G. Adubação de Videira. In Manual de Calagem e Adubação Para os Estados do Rio Grande do Sul e Santa Catarina; Comissão de Química e Fertilidade do Solo RS/SC; Comissão de Quimica e Fertilidade: Porto Alegre, Brazil, 2016; pp. 189–232. [Google Scholar]
- Khiari, L.; Parent, L.-É.; Tremblay, N. The phosphorus compositional nutrient diagnosis range for potato. Agron. J. 2001, 93, 815–819. [Google Scholar] [CrossRef]
- Dahal, K.; Bhattarai, S.P.; Midmore, D.; Oag, D.R.; Walsh, K. Temporal yield variability in subtropical table grape production. Sci. Hortic. 2019, 246, 951–956. [Google Scholar] [CrossRef]
- Quaggio, J.A.; Raij, B.V. Frutíferas. In Recomendação de Adubação e Calagem Para o Estado São Paulo—Boletim Técnico 100; Raij, B.V., Cantarella, H., Quaggio, J.A., Furlani, A.M.C., Eds.; Instituto Agronômico: Campinas, Brazil, 1997; pp. 121–125. [Google Scholar]
- De Conti, L.; Ceretta, C.A.; Melo, G.W.B.; Tiecher, T.L.; Stefanello, L.; Garlet, L.P.; Mimmo, T.; Cesco, S.; Brunetto, G. Intercropping of young grapevines with native grasses for phytoremediation of Cu-contaminated soils. Chemosphere 2019, 216, 147–156. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.N.; Mobin, M.; Abbas, Z.K.; Alamri, S.A. Fertilizers and Their Contaminants in Soils, Surface and Groundwater. In Encyclopedia of the Anthropocene; Elsevier: Amsterdam, The Netherlands, 2018; Volume 5, pp. 225–240. ISBN 9780128096659. [Google Scholar]
- Latifi, Z.; Jalali, M. Trace element contaminants in mineral fertilizers used in Iran. Environ. Sci. Pollut. Res. 2018, 25, 31917–31928. [Google Scholar] [CrossRef]
- Serra, A.P.; Marchetti, M.E.; Vitorino, A.C.T.; Novelino, J.O.; Camacho, M.A. Desenvolvimento de normas DRIS e CND e avaliação do estado nutricional da cultura do algodoeiro. Revista Brasileira de Ciência do Solo 2010, 34, 97–104. [Google Scholar] [CrossRef]
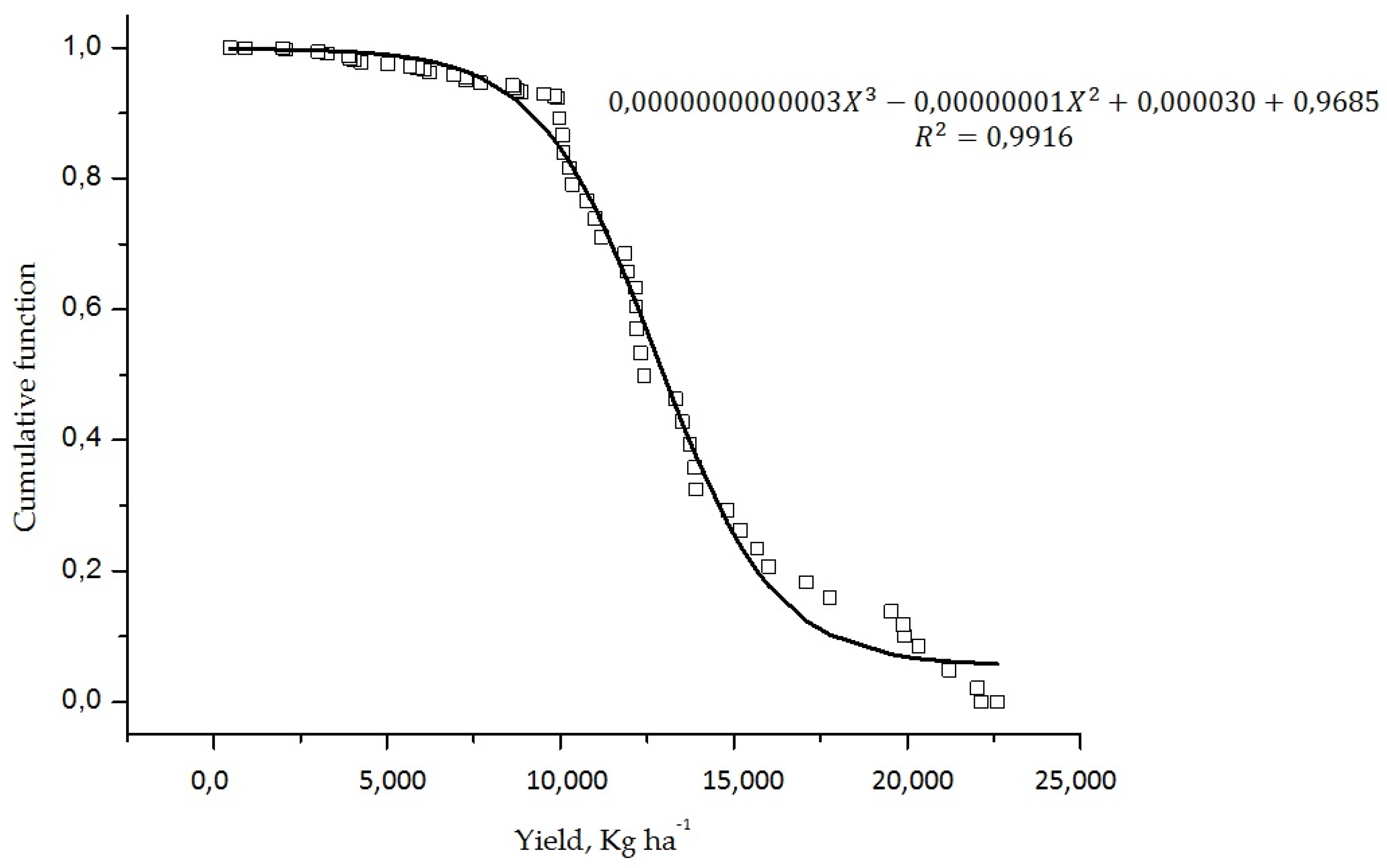
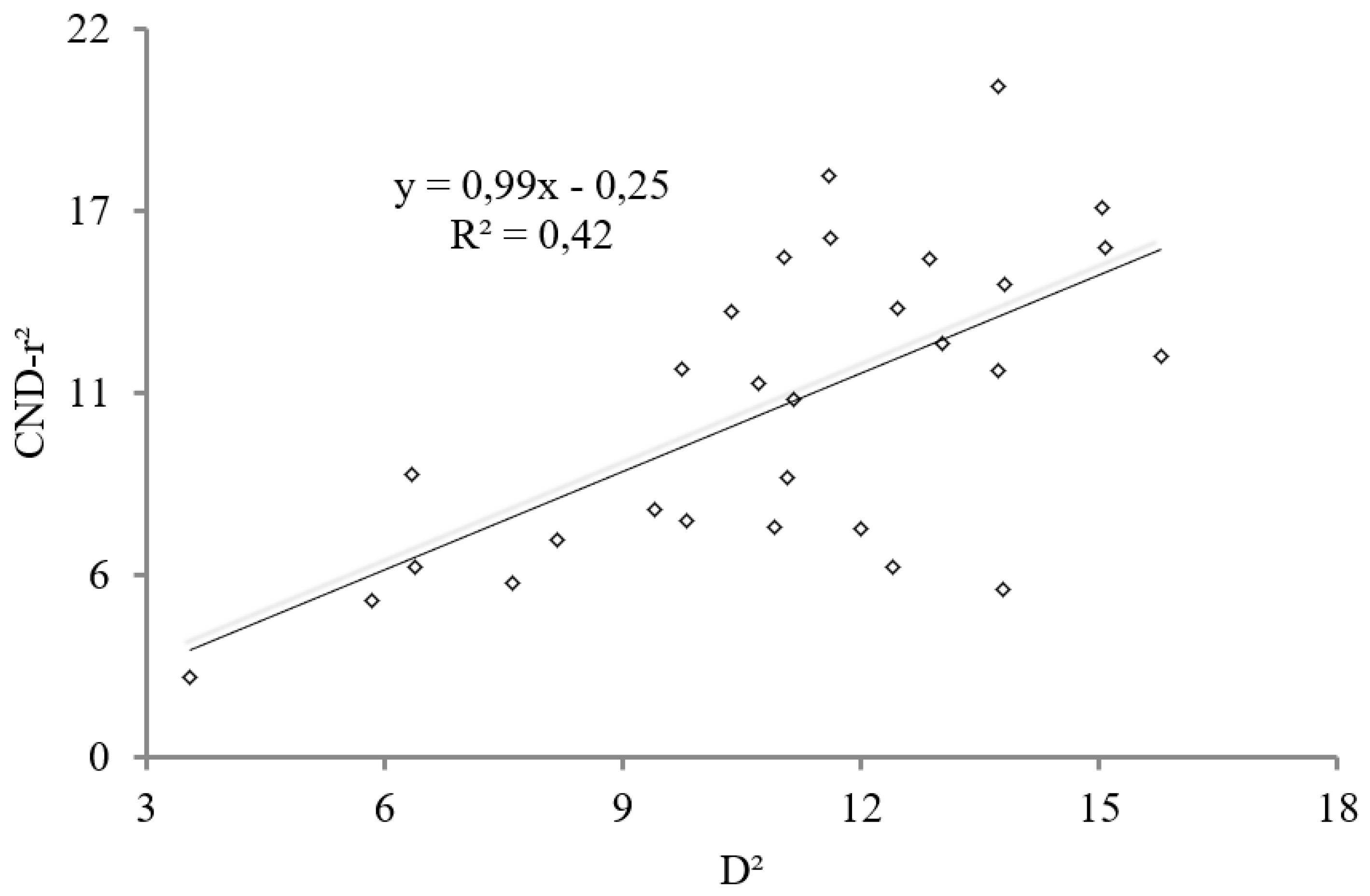
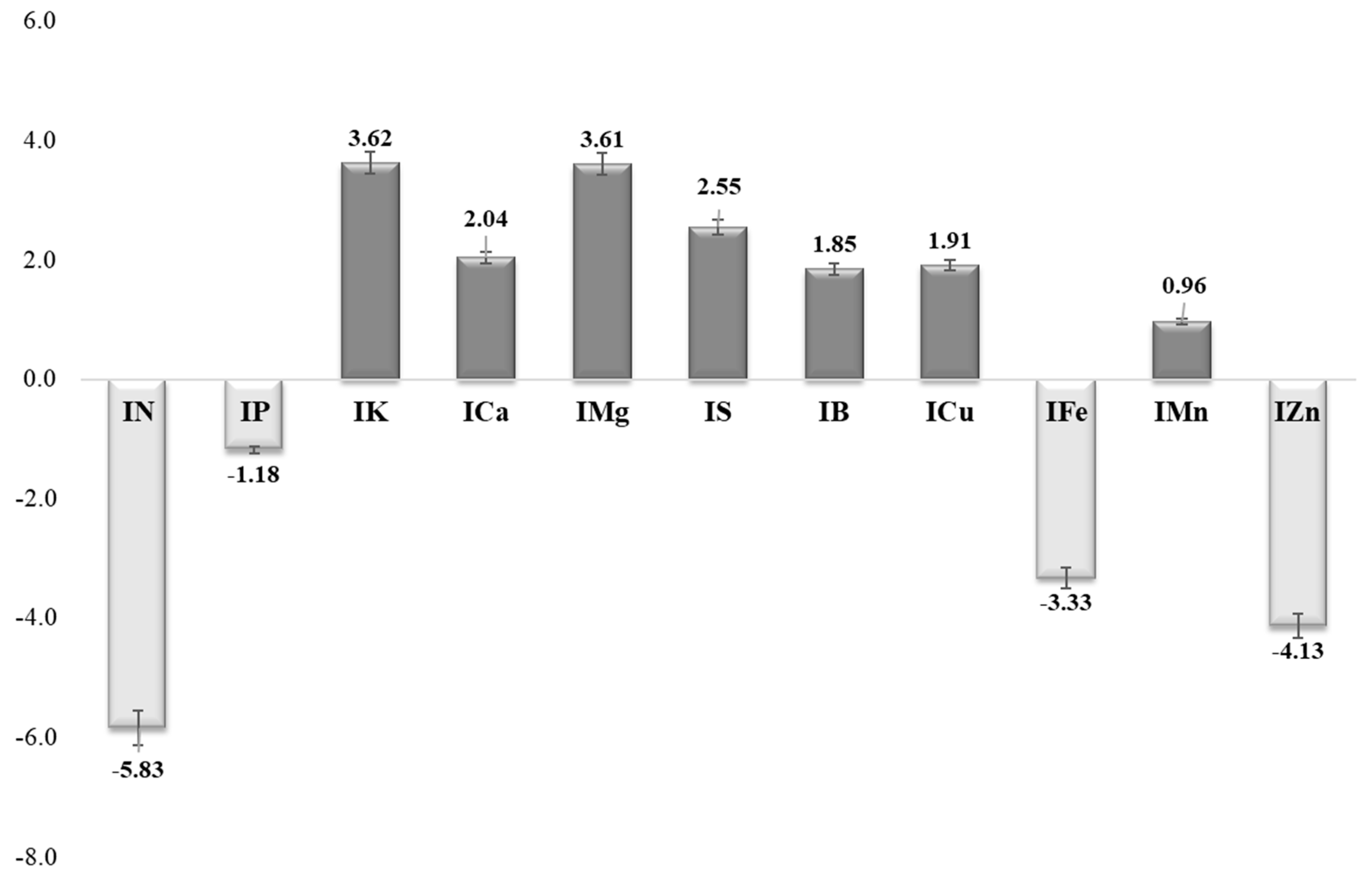
| N | P | K | Ca | Mg | S | B | Cu | Fe | Mn | Zn | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Yield | −01.0 | 0.00 | 0.04 | 0.05 | 0.00 | −0.10 | 0.05 | −0.15 | 0.07 | 0.01 | −0.03 |
| N | 0.52* | −0.17 | 0.08 | 0.13 | 0.56* | 0.05 | 0.25 | 0.07 | 0.04 | 0.23 | |
| P | 0.03 | 0.34 * | 0.53 * | 0.61 * | 0.37 * | 0.40 * | 0.27 * | 0.06 | 0.07 | ||
| K | −0.03 | 0.06 | 0.08 | 0.22 | 0.14 | −0.02 | 0.28 * | 0.02 | |||
| Ca | 0.77 * | 0.44 * | 0.42 * | 0.27 * | 0.01 | 0.10 | 0.05 | ||||
| Mg | 0.45 * | 0.42 * | 0.25 | 0.18 | 0.11 | 0.13 | |||||
| S | 0.40 * | 0.40 * | −0.02 | 0.35 * | 0.35 * | ||||||
| B | 0.33 * | 0.05 | 0.07 | 0.09 | |||||||
| Cu | 0.08 | 0.22 | −0.08 | ||||||||
| Fe | 0.14 | 0.08 | |||||||||
| Mn | 0.04 |
| High Yield Population (n = 29) | |||||||||||
| N | P | K | Ca | Mg | S | B | Cu | Fe | Mn | Zn | |
| Yield | −0.07 | −0.05 | −0.21 | 0.07 | 0.06 | −0.12 | −0.05 | 0.14 | 0.04 | −0.12 | −0.14 |
| N | 0.39 * | −0.11 | 0.02 | −0.03 | 0.64 * | −0.10 | 0.30 | −0.11 | 0.19 | 0.24 | |
| P | 0.07 | 0.29 | 0.51 * | 0.64 * | 0.38 * | 0.71 * | 0.28 | 0.01 | −0.10 | ||
| K | −0.19 | −0.05 | −0.13 | 0.22 | 0.04 | 0.05 | 0.04 | −0.07 | |||
| Ca | 0.78 * | 0.39 * | 0.47 * | 0.27 | −0.15 | 0.09 | 0.10 | ||||
| Mg | 0.34 | 0.43 * | 0.27 | 0.16 | −0.03 | 0.08 | |||||
| S | 0.35 | 0.61 * | −0.06 | 0.43 * | 0.20 | ||||||
| B | 0.48 * | −0.16 | 0.11 | −0.13 | |||||||
| Cu | 0.12 | 0.27 | −0.08 | ||||||||
| Fe | 0.10 | 0.18 | |||||||||
| Mn | 0.05 | ||||||||||
| Low Yield Population (n = 34) | |||||||||||
| N | P | K | Ca | Mg | S | B | Cu | Fe | Mn | Zn | |
| Yield | −0.10 | −0.29 | 0.09 | −0.21 | −0.22 | −0.12 | −0.05 | −0.09 | 0.12 | 0.18 | −0.11 |
| N | 0.66 * | −0.20 | 0.14 | 0.27 | 0.50 * | 0.20 | 0.20 | 0.18 | −0.06 | 0.23 | |
| P | −0.01 | 0.39 * | 0.56 * | 0.60 * | 0.35 * | 0.23 | 0.27 | 0.10 | 0.19 | ||
| K | 0.10 | 0.15 | 0.25 | 0.22 | 0.23 | −0.07 | 0.44 * | 0.07 | |||
| Ca | 0.75 * | 0.51 * | 0.36 * | 0.33 | 0.12 | 0.12 | 0.00 | ||||
| Mg | 0.57 * | 0.40 * | 0.26 | 0.20 | 0.22 | 0.17 | |||||
| S | 0.47 * | 0.26 | 0.00 | 0.29 | 0.46 * | ||||||
| B | 0.26 | 0.19 | 0.05 | 0.25 | |||||||
| Cu | 0.07 | 0.19 | −0.06 | ||||||||
| Fe | 0.16 | 0.03 | |||||||||
| Mn | 0.03 | ||||||||||
| Standards | N | P | K | Ca | Mg | S | B | Cu | Fe | Mn | Zn | |
| Mean | 2.76 | 0.65 | 1.98 | 2.08 | 0.53 | 0.72 | −3.95 | −4.96 | −2.72 | −1.26 | −2.15 | |
| SD | 0.16 | 0.16 | 0.21 | 0.18 | 0.15 | 0.11 | 0.26 | 0.15 | 0.23 | 0.25 | 0.32 | |
| Parameter | IN | IP | IK | ICa | IMg | IS | IB | ICu | IFe | IMn | IZn | CND-r2 |
| LMa | 2.13 | 2.47 | 2.00 | 1.86 | 1.84 | 1.85 | 2.17 | 2.42 | 2.53 | 2.52 | 2.22 | 20.26 |
| LMi | −1.73 | −2.08 | −1.69 | −1.84 | −1.73 | −2.33 | −1.81 | −1.82 | −1.96 | −1.65 | −2.19 | 2.41 |
| SP_m | 0.79 | 0.77 | 0.84 | 0.81 | 0.85 | 0.80 | 0.82 | 0.77 | 0.73 | 0.80 | 0.74 | 3.94 |
| D | 0.36 | 0.30 | 0.25 | 0.04 | −0.01 | −0.11 | −0.01 | 0.40 | 0.41 | 0.32 | −0.25 | 0.16 |
| V | 9.07 | 8.81 | 9.67 | 9.27 | 9.72 | 9.19 | 9.38 | 8.81 | 8.38 | 9.22 | 8.48 | 100.00 |
| Nutrient | Models (1) | R2 | Critical Nutrient (2) |
|---|---|---|---|
| N | IN = 0.1588N—4.2655** | 0.61 | 27 g kg−1 |
| P | IP = 1.2179P—4.0703 ** | 0.74 | 3.3 g kg−1 |
| K | IK = 0.3298K—4.1307 ** | 0.72 | 12 g kg−1 |
| Ca | ICa = 0.2889Ca—4.0095 ** | 0.71 | 14 g kg−1 |
| Mg | IMg = 1.4139Mg—4.1221 ** | 0.62 | 2.9 g kg−1 |
| S | IS = 1.2511S—4.3109 ** | 0.55 | 3.4 g kg−1 |
| B | IB = 0.087B—2.9633 ** | 0.84 | 34 mg kg−1 |
| Cu | ICu = 0.3381Cu—3.9787 ** | 0.71 | 12 mg kg−1 |
| Fe | IFe = 0.0269Fe—3.1331 ** | 0.84 | 116 mg kg−1 |
| Mn | IMn = 0.0063Mn—3.1011 ** | 0.82 | 492 mg kg−1 |
| Zn | IZn = −0.000022Zn2 + 0.023023Zn—3.744291 ** | 0.90 | 201 mg kg−1 |
| Yield | CND-r2= −0.000064 Yield + 12.079888 | 0.006 | - |
| References | N | P | K | Ca | Mg | S |
| g kg−1 | ||||||
| CND—Grapevines (1) | 24–30 | 2.9–3.8 | 11–14 | 12–16 | 2.6–3.3 | 3.1–3.8 |
| Brunetto et al. [41] (2) | 16–24 | 1.2–4.0 | 8–16 | 16–24 | 2.0–6.0 | |
| Quaggio and Raij [44] (3) | 30–35 | 2.4–2.9 | 15–20 | 13–18 | 4.8–5.3 | 3.3–3.8 |
| Mello et al. [22] (4) | 24–30 | 2.9–3.9 | 11–14 | 12–16 | 2.6–3.3 | 3.1–3.8 |
| B | Cu | Fe | Mn | Zn | ||
| mg kg−1 | ||||||
| CND – Grapevines (1) | 27–41 | 10–14 | 91–142 | 398–586 | 148–254 | |
| Brunetto et al. [41] (2) | 30–65 | - | 60–150 | 30–300 | 25–60 | |
| Quaggio and Raij [44] (3) | 45–53 | 18–22 | 97–105 | 67–73 | 30–35 | |
| Mello et al. [22] (4) | 26–39 | 10–14 | 89–140 | 390–578 | 150–256 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rozane, D.E.; Vahl de Paula, B.; Wellington Bastos de Melo, G.; Haitzmann dos Santos, E.M.; Trentin, E.; Marchezan, C.; Stefanello da Silva, L.O.; Tassinari, A.; Dotto, L.; Nunes de Oliveira, F.; et al. Compositional Nutrient Diagnosis (CND) Applied to Grapevines Grown in Subtropical Climate Region. Horticulturae 2020, 6, 56. https://doi.org/10.3390/horticulturae6030056
Rozane DE, Vahl de Paula B, Wellington Bastos de Melo G, Haitzmann dos Santos EM, Trentin E, Marchezan C, Stefanello da Silva LO, Tassinari A, Dotto L, Nunes de Oliveira F, et al. Compositional Nutrient Diagnosis (CND) Applied to Grapevines Grown in Subtropical Climate Region. Horticulturae. 2020; 6(3):56. https://doi.org/10.3390/horticulturae6030056
Chicago/Turabian StyleRozane, Danilo Eduardo, Betania Vahl de Paula, George Wellington Bastos de Melo, Eduardo Maciel Haitzmann dos Santos, Edicarla Trentin, Carina Marchezan, Lincon Oliveira Stefanello da Silva, Adriele Tassinari, Lucas Dotto, Filipe Nunes de Oliveira, and et al. 2020. "Compositional Nutrient Diagnosis (CND) Applied to Grapevines Grown in Subtropical Climate Region" Horticulturae 6, no. 3: 56. https://doi.org/10.3390/horticulturae6030056
APA StyleRozane, D. E., Vahl de Paula, B., Wellington Bastos de Melo, G., Haitzmann dos Santos, E. M., Trentin, E., Marchezan, C., Stefanello da Silva, L. O., Tassinari, A., Dotto, L., Nunes de Oliveira, F., Natale, W., Baldi, E., Toselli, M., & Brunetto, G. (2020). Compositional Nutrient Diagnosis (CND) Applied to Grapevines Grown in Subtropical Climate Region. Horticulturae, 6(3), 56. https://doi.org/10.3390/horticulturae6030056











